Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of solid–liquid phase diagrams of the sulfamethazine–salicylic acid co-crystal†
Dipali
Ahuja
 a,
Michael
Svärd
a,
Michael
Svärd
 *ab and
Åke C.
Rasmuson
*ab
*ab and
Åke C.
Rasmuson
*ab
aSynthesis and Solid State Pharmaceutical Centre, Bernal Institute, Department of Chemical Sciences, University of Limerick, Co. Limerick, Ireland
bDepartment of Chemical Engineering, KTH Royal Institute of Technology, Teknikringen 42, SE-10044 Stockholm, Sweden. E-mail: micsva@kth.se; akera@kth.se
First published on 2nd April 2019
Abstract
The influence of temperature and solvent on the solid–liquid phase diagram of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sulfamethazine–salicylic acid co-crystal has been investigated. Ternary phase diagrams of this co-crystal system have been constructed in three solvents: methanol, acetonitrile and a 7
1 sulfamethazine–salicylic acid co-crystal has been investigated. Ternary phase diagrams of this co-crystal system have been constructed in three solvents: methanol, acetonitrile and a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) dimethylsulfoxide–methanol mixture, at three temperatures. The system exhibits congruent dissolution in acetonitrile and the co-crystal solubility has been determined by a gravimetric technique. The Gibbs energy of co-crystal formation from the respective solid components has been estimated from solubility data, together with the corresponding enthalpic and entropic component terms. The Gibbs energy of formation ranges from −5.7 to −7.7 kJ mol−1, with the stability increasing with temperature. In methanol and the DMSO–methanol mixture, the co-crystal dissolves incongruently. It is shown that the solubility ratio of the pure components cannot be used to predict with confidence whether the co-crystal will dissolve congruently or incongruently. The size of the region where the co-crystal is the only stable solid phase is inversely related to the pure component solubility ratio of salicylic acid and sulfamethazine.
3 (v/v) dimethylsulfoxide–methanol mixture, at three temperatures. The system exhibits congruent dissolution in acetonitrile and the co-crystal solubility has been determined by a gravimetric technique. The Gibbs energy of co-crystal formation from the respective solid components has been estimated from solubility data, together with the corresponding enthalpic and entropic component terms. The Gibbs energy of formation ranges from −5.7 to −7.7 kJ mol−1, with the stability increasing with temperature. In methanol and the DMSO–methanol mixture, the co-crystal dissolves incongruently. It is shown that the solubility ratio of the pure components cannot be used to predict with confidence whether the co-crystal will dissolve congruently or incongruently. The size of the region where the co-crystal is the only stable solid phase is inversely related to the pure component solubility ratio of salicylic acid and sulfamethazine.
Introduction
Co-crystals are crystalline molecular complexes comprising two or more neutral components that in pure form are solid at room temperature. The components appear in the co-crystal in a specific stoichiometry, bonded by non-covalent interactions, especially hydrogen bonding. Co-crystals are of considerable interest to the pharmaceutical industry because of their ability to modify the physical properties of the active pharmaceutical ingredient (API), without affecting the molecular structure.1–3 Co-crystal formation has indeed proved to be a useful tool to alter a wide range of properties including melting point, hygroscopicity, dissolution rate, thermal stability, solubility and hence bioavailability.4–10 Different methods can be used to synthesize co-crystals, such as dry and wet grinding,11–17 evaporation crystallization,18–21 spray drying,22–24 and sonication,25–27 but solution and cooling crystallization remain the most popular for scale up.16,28–31 A few other methods for co-crystal synthesis including hot melt extrusion,32 supercritical fluid technology33,34 and laser irradiation,35 have been reported in literature. Most research on co-crystals so far has focused on finding new co-crystals and rationalising whether co-crystals will be formed or not. Much less work has focused on their physical properties and how these depend on the coformer.36–38 There is also a limited amount of work performed so far on various aspects of their manufacturing.39–41For design and operation of a crystallization process for the manufacture of co-crystals, a complete and detailed phase diagram is crucial as it reveals the stability regions for the different crystalline phases. Based on a proper phase diagram identifying the region where the co-crystal is the stable solid phase, the conditions for manufacturing can be determined. Parameters like solvent and temperature can significantly affect the solubility of the co-crystal and alter the shape of the phase diagram.28,42 It has been suggested that a large solubility difference between the two components most likely leads to an incongruent system.42 Of general importance is whether the co-crystal dissolves congruently or not, the width of the region where the co-crystal is stable, and the co-crystal solubility. The wider the co-crystal region, the more robust the process of manufacturing becomes. If the co-crystal dissolves congruently a simple cooling crystallization can be performed, and the design of the process is even more facilitated. However, if the starting solution composition is adjusted appropriately,19,20 a non-congruent system is no major obstacle as long as the co-crystal region is not too narrow.
It is important to understand the co-crystal stability and formation in terms of key thermodynamic parameters like Gibbs energy. In the literature, only a few studies specifically treat thermodynamics of co-crystals. Nehm et al. defined the solubility product of a co-crystal as the product of the component concentrations and demonstrated it for the carbamazepine–nicotinamide co-crystal system.43 In 2007, Chiarella et al. showed that crystallization from a solution containing stoichiometric amounts of pure components might or might not form pure co-crystal based on solvent choice, and explained this on the basis of phase diagrams for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 trans-cinnamic acid–nicotinamide co-crystal.28 The factors responsible for the formation and stability of co-crystals with different stoichiometry using carbamazepine–4-aminobenzoic acid as a model system have been identified by Rodríguez-Hornedo et al.44 ter Horst et al. utilized thermodynamic principles to develop a method for co-crystal screening.45 In 2012, Leyssens et al. showed the importance of the solvent for synthesis and stability of diverse stoichiometric caffeine–maleic acid co-crystals.46 In acetone where the relative solubility between the pure components is high, the 2
1 trans-cinnamic acid–nicotinamide co-crystal.28 The factors responsible for the formation and stability of co-crystals with different stoichiometry using carbamazepine–4-aminobenzoic acid as a model system have been identified by Rodríguez-Hornedo et al.44 ter Horst et al. utilized thermodynamic principles to develop a method for co-crystal screening.45 In 2012, Leyssens et al. showed the importance of the solvent for synthesis and stability of diverse stoichiometric caffeine–maleic acid co-crystals.46 In acetone where the relative solubility between the pure components is high, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal is inaccessible, whereas in ethyl acetate with a reduced relative solubility, this zone becomes accessible. Croker et al. reported the formation of a new co-crystal with p-toluenesulfonamide and triphenylphosphine and studied the effect of the solvent by constructing phase diagrams in two solvents: acetonitrile and dichloromethane.19 Zhang and Rasmuson studied the thermodynamics and crystallization of theophylline–oxalic acid and theophylline–glutaric acid 1
1 co-crystal is inaccessible, whereas in ethyl acetate with a reduced relative solubility, this zone becomes accessible. Croker et al. reported the formation of a new co-crystal with p-toluenesulfonamide and triphenylphosphine and studied the effect of the solvent by constructing phase diagrams in two solvents: acetonitrile and dichloromethane.19 Zhang and Rasmuson studied the thermodynamics and crystallization of theophylline–oxalic acid and theophylline–glutaric acid 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystals.47,48 They estimated Gibbs energies of co-crystal formation from solubility data and investigated the effect of polymorphism on the phase diagrams. In 2017, Bacchi et al. constructed ternary phase diagrams for a liquid API, propofol, with solid coformers: bipyridine and phenazine.49 They employed co-crystallization to stabilize the liquid drug in a crystalline form.
1 co-crystals.47,48 They estimated Gibbs energies of co-crystal formation from solubility data and investigated the effect of polymorphism on the phase diagrams. In 2017, Bacchi et al. constructed ternary phase diagrams for a liquid API, propofol, with solid coformers: bipyridine and phenazine.49 They employed co-crystallization to stabilize the liquid drug in a crystalline form.
Sulfonamides are considered able to form co-crystals, as they possess both hydrogen bond donor and acceptor groups. Sulfamethazine (SMT), a sulfonamide drug, is an antimicrobial and an anti-infective agent. It is used as a veterinary medicine to treat a variety of infections. In humans, it is used for the treatment of urinary tract infection, chlamydia, malaria, rheumatoid fever and toxoplasmosis.50 It belongs to the BCS class II, i.e. it is known to have a high permeability but a low solubility, and consequently a low bioavailability. For pure solid SMT, only one pure component crystal structure has been reported, belonging to the monoclinic crystal system.51,52 SMT can form co-crystals with several carboxylic acids. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal between SMT and salicylic acid (SA) has been reported.53 The chemical structures of SMT and SA are depicted in Fig. 1.
1 co-crystal between SMT and salicylic acid (SA) has been reported.53 The chemical structures of SMT and SA are depicted in Fig. 1.
In this work, the SMT–SA co-crystal system is used as a model for construction and analysis of phase diagrams. We have investigated the thermodynamics of the SMT–SA co-crystal in three different solvent systems. Ternary phase diagrams have been constructed in methanol and acetonitrile at 10, 20, 30 °C and in a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) dimethyl sulfoxide–methanol mixture at 20, 30 and 40 °C. The objectives of this work include identifying the stability regions of the co-crystal in the three solvent systems, and studying the effect of coformer solubility and temperature on the appearance, shape, and symmetry of the phase diagrams. We have also estimated the Gibbs energy of co-crystal formation from the solubility data. The volumetric productivity and co-crystal yields in the three systems are discussed.
3 (v/v) dimethyl sulfoxide–methanol mixture at 20, 30 and 40 °C. The objectives of this work include identifying the stability regions of the co-crystal in the three solvent systems, and studying the effect of coformer solubility and temperature on the appearance, shape, and symmetry of the phase diagrams. We have also estimated the Gibbs energy of co-crystal formation from the solubility data. The volumetric productivity and co-crystal yields in the three systems are discussed.
Experimental work
Materials
Sulfamethazine (CAS Registry Number 57-68-1), purity >99%, salicylic acid (CAS Registry Number 69-72-7), purity >99% and methanol (CAS Registry Number 67-56-1, HPLC grade, purity >99.9%) were purchased from Sigma-Aldrich. Acetonitrile (CAS Registry Number 75-05-8, HPLC grade, purity >99.9%) was purchased from Fisher Chemicals and dimethyl sulfoxide (CAS Registry Number 67-68-5, purity >99.8%) was purchased from Acros Organics. All the chemicals were used as received. Necessary precautions were taken to minimize exposure of solvents to the moisture in ambient air – in particular for DMSO due to its hygroscopic nature.Solvents were selected with the ambition to cover congruent as well as incongruent conditions, with the starting point in the expectation that a symmetric and congruent system would be obtained when the pure components had similar solubility, and asymmetric and incongruent systems obtained for larger solubility differences. Preliminary solubility experiments were carried out, based on which the three solvent systems were selected. The solvents evaluated were methanol, acetonitrile, water, chloroform, acetone, ethyl acetate, dimethyl sulfoxide, N,N-dimethyl acetamide, N,N-dimethyl formamide, and dimethyl sulfoxide–methanol mixtures of different ratios. The preliminary solubility experiments revealed a high SA to SMT solubility ratio in ethyl acetate and in methanol. Methanol was chosen as an example of a likely incongruent dissolution over ethyl acetate on the basis of a higher SMT solubility. In acetonitrile the solubility ratio was lower than in acetone, and was selected as a likely congruent dissolution system. In chloroform, the settling velocity of solid was low because of similar densities of SMT, SA and chloroform, and in water the problem was the same. Hence, for practical reasons, water and chloroform were not selected. SMT exhibits about the same low solubility in all solvents tested except for DMSO, DMA and DMF. However, SMT forms solvates in pure DMSO, DMF and DMA.54 A few DMSO–methanol mixtures were evaluated with the intent to keep the DMSO content high. A 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol mixture, prepared by mixing 7 volume parts of DMSO and 3 volume parts of methanol, was chosen as it fulfils the three targets, i.e. high SMT solubility, no solvate formation and a low solubility ratio.
3 (v/v) DMSO–methanol mixture, prepared by mixing 7 volume parts of DMSO and 3 volume parts of methanol, was chosen as it fulfils the three targets, i.e. high SMT solubility, no solvate formation and a low solubility ratio.
Equipment
PXRD data was collected in reflectance mode using an Empyrean diffractometer (PANalytical, Phillips) equipped with Cu Kα1,2 radiation (γ = 1.5406 Å) operating at 40 kV and 40 mA at room temperature. Samples were scanned between 2θ values of 5 and 40° at a step size of 0.01313° 2θ with step time 73 s per step on a spinning silicon holder. HPLC analysis was performed on an “Agilent Technologies 1260 Infinity Series” comprising of a solvent 1260 Quat delivery pump, auto-injector, absorbance UV spectrophotometric detector (275 nm) and Agilent Chem Station software. A Macharey-Nagel EC 100/4.6 Nucleodur C18 column was used with methanol/2% acetic acid (88/12, v/v) as the mobile phase. An OHAUS Explorer analytical balance with a resolution of 10−4 g was used for weighing of chemicals. The solubility experiments were carried out in 30 mL glass vials with magnetic stirrer bars, using a Grant ST26 stainless steel thermostatic water bath; 26 L, 505 × 300 × 200 mm; equipped with a Grant C2G cooling unit and a Grant GR150 control unit; stability ±0.01 °C and uniformity ±0.05 °C, with a serial submersible 60 points magnetic stirrer plate (2Mag) placed on the base and a submersible water pump (1400 L h−1) to enhance circulation in the bath.Co-crystal preparation
The co-crystal was synthesized using the solvent drop grinding method. Equimolar amounts of sulfamethazine (SMT) and salicylic acid (SA) were finely ground for about 15–20 minutes by hand. A few drops of acetonitrile were added followed by further grinding for 10–15 minutes to form a white dry powder. The powder was characterized by PXRD and DSC.Determination of solubility
Solubility of the pure compounds (SMT and SA) was determined gravimetrically in methanol and acetonitrile at 10, 20 and 30 °C. HPLC was employed to determine the solubility in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) dimethyl sulfoxide–methanol mixture at 20, 30 and 40 °C. The first step to both the techniques involved preparing saturated solutions, for each of which an amount of solid solute in excess of the solubility was added to ∼5 mL of the solvent at the desired temperature. The solutions were equilibrated for a period of 24 hours under continuous agitation. The agitation was then stopped, and the solids allowed to settle for a period of 10 minutes (methanol, acetonitrile), or 60 minutes (DMSO–methanol) due to slow settling. Samples of the saturated supernatant clear liquid was pipetted out using a syringe. For gravimetric determination, approx. 1 mL of the solution was filtered into a pre-weighed glass vial (m1) using a 0.2 μm PTFE syringe filter. The vial was weighed immediately and the mass recorded as m2. The solvent was then allowed to evaporate by placing the vial for a sufficient time (usually overnight) in a fume hood until dry and the mass recorded. The dried vial was then moved to a vacuum oven at 50 °C for 1 hour, after which no further decrease in weight could be recorded. The mass of the vial containing dry solids (m3) was recorded. The syringes, vials and the filters were pre-heated before sampling solutions at high temperatures. The solubility was calculated as (m3 − m1)/(m2 − m3). Each reported concentration value is an average of four completely separate experiments.
3 (v/v) dimethyl sulfoxide–methanol mixture at 20, 30 and 40 °C. The first step to both the techniques involved preparing saturated solutions, for each of which an amount of solid solute in excess of the solubility was added to ∼5 mL of the solvent at the desired temperature. The solutions were equilibrated for a period of 24 hours under continuous agitation. The agitation was then stopped, and the solids allowed to settle for a period of 10 minutes (methanol, acetonitrile), or 60 minutes (DMSO–methanol) due to slow settling. Samples of the saturated supernatant clear liquid was pipetted out using a syringe. For gravimetric determination, approx. 1 mL of the solution was filtered into a pre-weighed glass vial (m1) using a 0.2 μm PTFE syringe filter. The vial was weighed immediately and the mass recorded as m2. The solvent was then allowed to evaporate by placing the vial for a sufficient time (usually overnight) in a fume hood until dry and the mass recorded. The dried vial was then moved to a vacuum oven at 50 °C for 1 hour, after which no further decrease in weight could be recorded. The mass of the vial containing dry solids (m3) was recorded. The syringes, vials and the filters were pre-heated before sampling solutions at high temperatures. The solubility was calculated as (m3 − m1)/(m2 − m3). Each reported concentration value is an average of four completely separate experiments.
Because of the high boiling point (189 °C) and accordingly low volatility of DMSO, the gravimetric method was not feasible for DMSO–methanol solutions. Solution concentrations were determined by HPLC for the determination of the solubility of SMT and SA in this solvent system. This entailed the construction of calibration curves i.e. peak area vs. concentration using stock solutions of known concentrations of SMT and SA in DMSO–methanol. The calibration lines showed good linearity (R2 = 0.99). The saturated solution samples were filtered into clean glass vials. Peak areas for the saturated solutions of SMT and SA at different temperatures were obtained and the corresponding concentrations in turn obtained using the calibration curves.
Determination of the ternary phase diagram
Invariant points represent solution concentrations at which two solid phases (SMT + co-crystal or SA + co-crystal) are at equilibrium with the same solution. These points were determined by equilibrating different mixtures of the two solid co-crystal components with the solvent and then analyzing both the solid and the solution phase. At constant temperature, SMT and SA were mixed with the solvent and magnetically stirred for 24 hours to reach equilibrium. Following this, the solid material and the saturated solution were separated by filtration. An aliquot of the saturated solution was diluted with pure solvent and analysed by HPLC. The concentration of SMT and SA, respectively, was determined from the calibration curves in the pure solvent. Using another aliquot of the saturated solution, gravimetry was employed to determine the solute and solvent content in the liquid phase. The solid material was analyzed by PXRD and DSC. The solubility of the pure components and the concentrations corresponding to the invariant points were plotted in a ternary diagram using the Prosim Ternary Diagram software.55Process experiments
Isothermal slurry conversion experiments19,20,56 were carried out for investigation of the manufacturing of the co-crystal. Guided by the determined ternary phase diagram in each solvent at 30 °C, two points were selected inside the region where the co-crystal only is thermodynamically stable. The two points were selected to compare a high and a low solid loading (refer to Table 3 for mass fractions). Pure solid components and the solvent were mixed in proportions corresponding to each point, and the mixture was stirred for 24 hours. The solids were then separated from the solution by filtration and allowed to dry. The mass of the dry solids was recorded (product mass) and was confirmed by PXRD to be co-pure crystals. The co-crystal yield was calculated as the mass of obtained co-crystals divided by the total mass of API and coformer used, and the volumetric productivity was calculated as the mass of obtained co-crystals divided by the total slurry volume (API, coformer and solvent).Results and discussion
Solid phase characterization
Pure SMT and SA, as well as the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal, each have only one reported crystalline form. In the present work, the structures with the CSD refcodes SLFNMD10, SALIAC19 and GEYSAE have been used. The PXRD pattern obtained for the 1
1 co-crystal, each have only one reported crystalline form. In the present work, the structures with the CSD refcodes SLFNMD10, SALIAC19 and GEYSAE have been used. The PXRD pattern obtained for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal matches with the simulated pattern obtained from the structure GEYSAE (Fig. 2a) confirming the purity of the co-crystal. The co-crystal features strong hydrogen bonding interactions between the hydroxyl and carbonyl functionalities of SA with the pyrimidine ring nitrogen and the sulfonamide N–H group of the SMT, respectively forming a R22(8) type synthon (Fig. 2b).
1 co-crystal matches with the simulated pattern obtained from the structure GEYSAE (Fig. 2a) confirming the purity of the co-crystal. The co-crystal features strong hydrogen bonding interactions between the hydroxyl and carbonyl functionalities of SA with the pyrimidine ring nitrogen and the sulfonamide N–H group of the SMT, respectively forming a R22(8) type synthon (Fig. 2b).
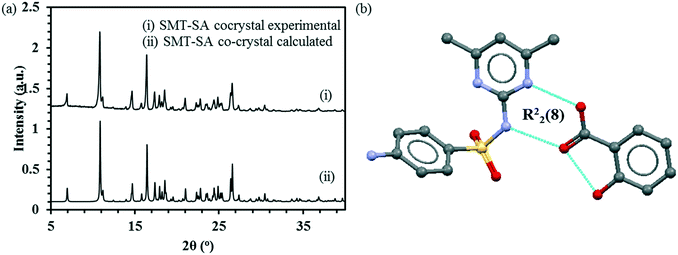 | ||
Fig. 2 Experimental and calculated PXRD patterns for SMT–SA co-crystal (a), main hydrogen-bond motif in the crystal structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–SA co-crystal (b).51 1 SMT–SA co-crystal (b).51 | ||
Solubility, ternary phase diagram, effect of solvent and temperature
The solubility of SMT and SA in the three solvents at three temperatures are given in Table 1, as averages of n = 4 experiments, together with standard deviations. The solubility values of both coformers in methanol and acetonitrile agree well with those reported in the literature.57,58 The temperature dependence of the solubility of pure SMT and SA in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol mixture is shown in Fig. 3 as van't Hoff plots. In all solvents, the solubility of SA is higher than that of SMT, by approx. a factor 60 in methanol, 12 in acetonitrile and 3 in the DMSO–methanol mixture, at 30 °C.
3 (v/v) DMSO–methanol mixture is shown in Fig. 3 as van't Hoff plots. In all solvents, the solubility of SA is higher than that of SMT, by approx. a factor 60 in methanol, 12 in acetonitrile and 3 in the DMSO–methanol mixture, at 30 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol at three temperatures
3 (v/v) DMSO–methanol at three temperatures
| Solvent | T (°C) | Solubility (g solute/g solvent) | Solubility (mol L−1) | Standard deviation (mol L−1, n = 4) | Solubility ratio (SA/SMT) (M/M) | |||
|---|---|---|---|---|---|---|---|---|
| SMT | SA | SMT | SA | SMT | SA | |||
| Methanol | 10 | 0.0092 | 0.4788 | 0.0262 | 2.7456 | 0.0010 | 0.0014 | 104.7 |
| 20 | 0.0140 | 0.5688 | 0.0399 | 3.2615 | 0.0011 | 0.0015 | 81.7 | |
| 30 | 0.0228 | 0.7007 | 0.0650 | 4.0178 | 0.0013 | 0.0018 | 61.8 | |
| Acetonitrile | 10 | 0.0102 | 0.0634 | 0.0291 | 0.3742 | 0.0014 | 0.0019 | 12.8 |
| 20 | 0.0151 | 0.0881 | 0.0431 | 0.5051 | 0.0018 | 0.0016 | 11.7 | |
| 30 | 0.0209 | 0.1265 | 0.0592 | 0.6827 | 0.0015 | 0.0017 | 11.5 | |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol 3 (v/v) DMSO–methanol |
20 | 0.4762 | 0.7011 | 1.7237 | 5.1152 | 0.0084 | 0.0079 | 2.96 |
| 30 | 0.5029 | 0.7345 | 1.8202 | 5.3727 | 0.0074 | 0.0081 | 2.95 | |
| 40 | 0.5232 | 0.7620 | 1.8940 | 5.5602 | 0.0078 | 0.0071 | 2.93 | |
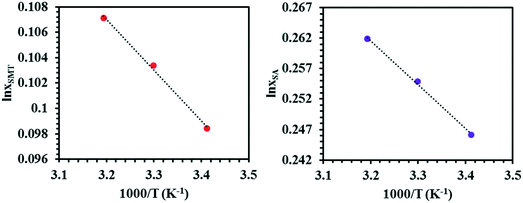 | ||
Fig. 3 Van't Hoff plots for SMT and SA in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol mixture, where xSMT and xSA correspond to mole fraction solubility of SMT and SA, respectively. 3 (v/v) DMSO–methanol mixture, where xSMT and xSA correspond to mole fraction solubility of SMT and SA, respectively. | ||
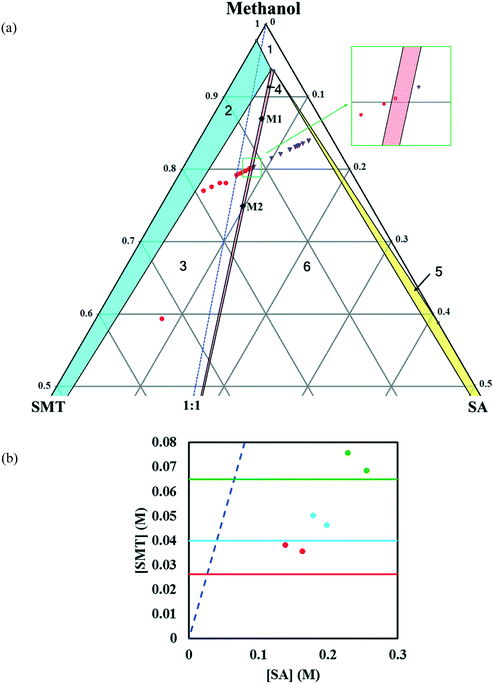
In methanol, the phase diagram (Fig. 4a) is rather asymmetric as would be expected given the high solubility ratio of SA to SMT (Table 1), and the co-crystal region is significantly skewed towards the more soluble component, SA. In addition, the region where the co-crystal is the stable solid phase is very narrow. A very narrow co-crystal region makes the manufacturing process more difficult to design and operate. The dissolution of the co-crystal is incongruent, i.e. it is not possible to establish a solid–liquid equilibrium between the co-crystal solid phase and a stoichiometric solution. For this reason, the solubility of the co-crystal cannot be determined by traditional methods. Continued dissolution of this co-crystal would tend to move the solution composition to the point where the stable solid phase is a mixture of SMT and co-crystal, i.e. the invariant point. The phase diagram at three temperatures as a function of SMT and SA concentrations has been depicted in Fig. 4b.
In acetonitrile, the solubility of SMT is slightly higher while that of SA is lower, leading to a reduced solubility ratio between the two components (Table 1). The phase diagram is quite symmetric and the co-crystal dissolves congruently. Since the solubility of SA is still approximately 12 times higher than that of SMT, the co-crystal region is slightly skewed towards the SA side of the diagram, i.e. towards the more soluble component (Fig. 5a). The co-crystal region is clearly broader than in methanol. Since the co-crystal dissolves congruently the solubility of the co-crystal can be gravimetrically determined (Table 2). The SMT concentration at equilibrium with the co-crystal is slightly higher than the SMT concentration at equilibrium with pure SMT (Fig. 6a), whereas the SA concentration at equilibrium with the co-crystal is lower than the SA concentration at equilibrium with pure SA. The van't Hoff plot of the solubility data for the co-crystal is shown in Fig. 6b, from the slope (−ΔH/R) of which the van't Hoff enthalpy of solution is determined to be +22.2 kJ mol−1 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex). The corresponding values for the pure components SMT and SA in acetonitrile are +25.4 and +20.8 kJ mol−1, respectively. The co-crystal value is not too far from the average of the values of the pure components.
1 complex). The corresponding values for the pure components SMT and SA in acetonitrile are +25.4 and +20.8 kJ mol−1, respectively. The co-crystal value is not too far from the average of the values of the pure components.
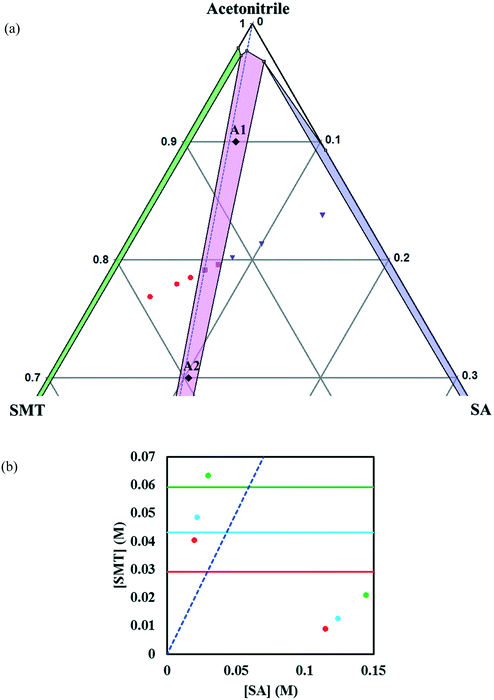 | ||
Fig. 5 Zoom-in view of the ternary phase diagram of SMT–SA co-crystal system in acetonitrile at 30 °C. Values are in mass fractions. The blue dotted line is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric line. Regions and various points in the diagram are as same as marked in Fig. 4. The points A1 and A2 (black filled diamonds) represent starting compositions for co-crystal yield and volumetric productivity determination (a), phase diagrams at 10 (red), 20 (light blue) and 30 °C (green) in acetonitrile. The horizontal lines are the solubilities of SMT at 10, 20, 30 °C in acetonitrile. The points (filled circles) depict the invariant points at the three temperatures (b). 1 stoichiometric line. Regions and various points in the diagram are as same as marked in Fig. 4. The points A1 and A2 (black filled diamonds) represent starting compositions for co-crystal yield and volumetric productivity determination (a), phase diagrams at 10 (red), 20 (light blue) and 30 °C (green) in acetonitrile. The horizontal lines are the solubilities of SMT at 10, 20, 30 °C in acetonitrile. The points (filled circles) depict the invariant points at the three temperatures (b). | ||
| Solvent | T (°C) | Solid phases at equilibrium | Invariant point (mole fraction) | K sp (M2) | S AB (M) | ΔGa (kJ mol−1) | |||
|---|---|---|---|---|---|---|---|---|---|
| x SMT | x SA | x solvent | HPLC | Gravimetry | |||||
| a Gibbs energy of co-crystal formation. | |||||||||
| Methanol | 10 | SMT + co-crystal | 0.0015 | 0.0056 | 0.9929 | 5.8 × 10−3 | −6.0 | ||
| SA + co-crystal | 0.0014 | 0.0066 | 0.9920 | 5.4 × 10−3 | |||||
| 20 | SMT + co-crystal | 0.0020 | 0.0072 | 0.9908 | 8.9 × 10−3 | −6.5 | |||
| SA + co-crystal | 0.0018 | 0.0080 | 0.9902 | 8.2 × 10−3 | |||||
| 30 | SMT + co-crystal | 0.0030 | 0.0092 | 0.9878 | 1.7 × 10−2 | −6.8 | |||
| SA + co-crystal | 0.0027 | 0.0103 | 0.9870 | 1.6 × 10−2 | |||||
| Acetonitrile | 10 | SMT + co-crystal | 0.0022 | 0.0010 | 0.9968 | 7.9 × 10−4 | −5.9 | ||
| SA + co-crystal | 0.0004 | 0.0059 | 0.9936 | 1.0 × 10−3 | |||||
| Co-crystal | 0.0015 | 0.0015 | 0.9969 | 8.6 × 10−4 | 0.0293 | 0.0304 | |||
| 20 | SMT + co-crystal | 0.0025 | 0.0012 | 0.9963 | 1.1 × 10−3 | −6.9 | |||
| SA + co-crystal | 0.0006 | 0.0064 | 0.9929 | 1.7 × 10−3 | |||||
| Co-crystal | 0.0017 | 0.0017 | 0.9966 | 1.5 × 10−3 | 0.0388 | 0.0404 | |||
| 30 | SMT + co-crystal | 0.0033 | 0.0015 | 0.9952 | 1.8 × 10−3 | −7.2 | |||
| SA + co-crystal | 0.0010 | 0.0075 | 0.9914 | 3.0 × 10−3 | |||||
| Co-crystal | 0.0026 | 0.0026 | 0.9948 | 2.7 × 10−3 | 0.0524 | 0.0534 | |||
DMSO–methanol (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, v/v) 3, v/v) |
20 | SMT + co-crystal | 0.0678 | 0.0708 | 0.8613 | 1.59 | −6.8 | ||
| SA + co-crystal | 0.0031 | 0.1949 | 0.8019 | 0.23 | |||||
| 30 | SMT + co-crystal | 0.0696 | 0.0738 | 0.8566 | 1.71 | −6.3 | |||
| SA + co-crystal | 0.0042 | 0.2035 | 0.7923 | 0.33 | |||||
| 40 | SMT + co-crystal | 0.0721 | 0.0758 | 0.8521 | 1.84 | −6.2 | |||
| SA + co-crystal | 0.0051 | 0.2143 | 0.7806 | 0.44 | |||||
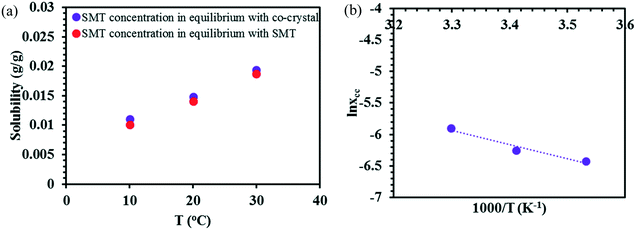 | ||
| Fig. 6 The experimental solubility of pure SMT and the co-crystal in acetonitrile (a), van't Hoff plot of the co-crystal in acetonitrile (b). | ||
A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal ‘AB’ equilibrates with the API ‘A’ and the coformer ‘B’ in the saturated solution as per eqn (1). The corresponding equilibrium constant can be expressed in terms of thermodynamic activities. In eqn (2), Ksp refers to the solubility product of the co-crystal, when the activity of the solid co-crystal is taken as unity. Assuming that the contributions from activity coefficients (γ) can be neglected, Ksp can be approximated by the product of concentrations of its co-crystal components, with concentrations in mol L−1. This assumption is valid for ideal solutions, and approximately so for dilute solutions where γA and γB are independent of concentration. The constant Ksp reflects the strength of interactions between the API and coformer in the co-crystal relative to interactions with the solvent in solution.43 The co-crystal intrinsic solubility (SAB) can be estimated from eqn (3) at 10, 20 and 30 °C in acetonitrile (congruent case) using concentrations obtained from HPLC well matching those determined by the gravimetric method (Table 2).
1 co-crystal ‘AB’ equilibrates with the API ‘A’ and the coformer ‘B’ in the saturated solution as per eqn (1). The corresponding equilibrium constant can be expressed in terms of thermodynamic activities. In eqn (2), Ksp refers to the solubility product of the co-crystal, when the activity of the solid co-crystal is taken as unity. Assuming that the contributions from activity coefficients (γ) can be neglected, Ksp can be approximated by the product of concentrations of its co-crystal components, with concentrations in mol L−1. This assumption is valid for ideal solutions, and approximately so for dilute solutions where γA and γB are independent of concentration. The constant Ksp reflects the strength of interactions between the API and coformer in the co-crystal relative to interactions with the solvent in solution.43 The co-crystal intrinsic solubility (SAB) can be estimated from eqn (3) at 10, 20 and 30 °C in acetonitrile (congruent case) using concentrations obtained from HPLC well matching those determined by the gravimetric method (Table 2).
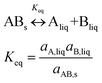 | (1) |
| Ksp = aA,liqaB,liq = γA[A]γB[B] ≈ [A][B] | (2) |
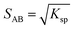 | (3) |
| A(s) + B(s) → AB(s) | (4) |
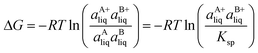 | (5) |
Based on the solubility data, the Gibbs energy of formation of the co-crystal from its pure solid components (eqn (4)) can be determined by eqn (5), where 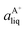 and
and 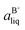 denote the activities of the solute in a solution in equilibrium with the pure co-crystal components respectively. aAliq and aBliq are the activities of the co-crystal components in a solution in equilibrium with pure co-crystal.56 By approximating the activities with the concentrations in mol L−1, the free energy change can be estimated. Using the co-crystal solubility data in acetonitrile (a congruent system), the Gibbs energy of co-crystal formation at 10, 20 and 30 °C is estimated to be −5.7, −7.1 and −7.7 kJ mol−1, respectively. The Gibbs energy of formation has also been estimated using the average Ksp in the three solvent systems; the data is reported in Table 2. The values are all quite close to the values obtained from the co-crystal solubility data. Altogether, the negative value of the Gibbs energy change reveals that the formation of the 1
denote the activities of the solute in a solution in equilibrium with the pure co-crystal components respectively. aAliq and aBliq are the activities of the co-crystal components in a solution in equilibrium with pure co-crystal.56 By approximating the activities with the concentrations in mol L−1, the free energy change can be estimated. Using the co-crystal solubility data in acetonitrile (a congruent system), the Gibbs energy of co-crystal formation at 10, 20 and 30 °C is estimated to be −5.7, −7.1 and −7.7 kJ mol−1, respectively. The Gibbs energy of formation has also been estimated using the average Ksp in the three solvent systems; the data is reported in Table 2. The values are all quite close to the values obtained from the co-crystal solubility data. Altogether, the negative value of the Gibbs energy change reveals that the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal from pure solid SMT and SA is a spontaneous process, and that the co-crystal is thermodynamically stable compared to a physical mixture of pure SMT and SA solid phases. With increasing temperature, the free energy change becomes more negative, signifying an increased stability of the co-crystal.
1 co-crystal from pure solid SMT and SA is a spontaneous process, and that the co-crystal is thermodynamically stable compared to a physical mixture of pure SMT and SA solid phases. With increasing temperature, the free energy change becomes more negative, signifying an increased stability of the co-crystal.
The entropic (eqn (7)) and enthalpic (eqn (8)) components of the Gibbs energy of formation can be determined:
| ΔG = ΔH − TΔS | (6) |
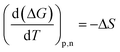 | (7) |
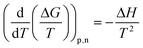 | (8) |
The calculated Gibbs energies are plotted in the appropriate coordinates in Fig. 7, from which estimates of the entropy and the enthalpy of formation are determined from the slopes. The entropy of co-crystal formation is found to be 0.1015 kJ K−1 mol−1, i.e. the co-crystal formation is associated with a positive entropy change. The estimated co-crystal enthalpy of formation is +23.1 kJ mol−1, which agrees closely with the average value of +22.8 kJ mol−1 obtained using eqn (6). Hence, the SMT–SA co-crystal formation from its solid components is shown to be an endothermic processes, i.e. energy needs to be provided to synthesize the co-crystal. Obviously, the conclusion is that the formation of the co-crystal is entirely driven by a favorable entropy increase.
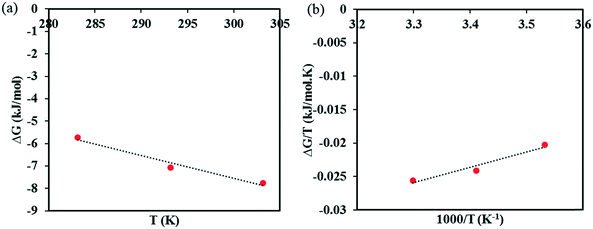 | ||
| Fig. 7 A plot of ΔG vs. T to find the entropy of SMT–SA co-crystal formation (a), Gibbs–Helmholtz plot to determine the enthalpy of SMT–SA co-crystal formation (b). | ||
The 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) mixture of DMSO and methanol was chosen to reach a higher solubility of SMT. The solubility ratio between the two co-crystal components in this solvent is very low (∼2.9), and hence this system is expected to be congruent. However, as shown in Fig. 8a, the system is in fact shown to be incongruent, even though the co-crystal region is very broad and only slightly skewed away from the 1
3 (v/v) mixture of DMSO and methanol was chosen to reach a higher solubility of SMT. The solubility ratio between the two co-crystal components in this solvent is very low (∼2.9), and hence this system is expected to be congruent. However, as shown in Fig. 8a, the system is in fact shown to be incongruent, even though the co-crystal region is very broad and only slightly skewed away from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric line (Fig. 8a). The effect of temperature on the phase diagram is shown in Fig. 8b.
1 stoichiometric line (Fig. 8a). The effect of temperature on the phase diagram is shown in Fig. 8b.
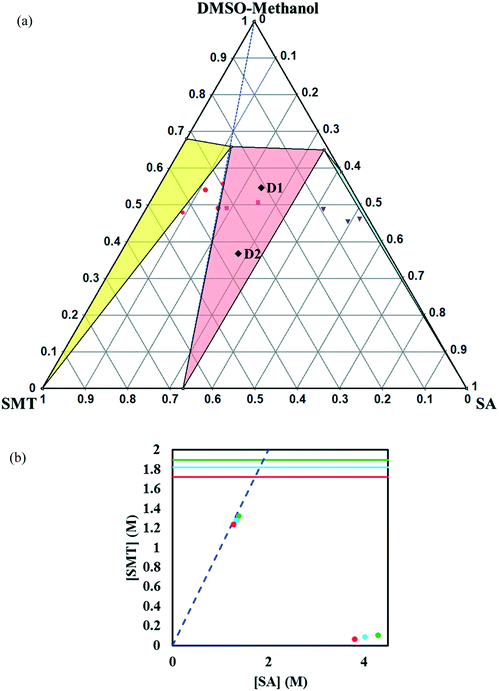 | ||
Fig. 8 Full-scale ternary phase diagram of the SMT–SA co-crystal system in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol mixture at 30 °C. Values are in mass fractions. The blue dotted line is the 1 3 (v/v) DMSO–methanol mixture at 30 °C. Values are in mass fractions. The blue dotted line is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric line. Regions and various points in the diagram areas are same as marked in Fig. 4. The points D1 and D2 (black filled diamonds) represent starting compositions for co-crystal yield and volumetric productivity determination (a), phase diagrams at 20 (red), 30 (light blue) and 40 °C (green) in 7 1 stoichiometric line. Regions and various points in the diagram areas are same as marked in Fig. 4. The points D1 and D2 (black filled diamonds) represent starting compositions for co-crystal yield and volumetric productivity determination (a), phase diagrams at 20 (red), 30 (light blue) and 40 °C (green) in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol. The horizontal lines are the solubilities of SMT at 20, 30, 40 °C in 7 3 (v/v) DMSO–methanol. The horizontal lines are the solubilities of SMT at 20, 30, 40 °C in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 DMSO–methanol. The points (filled circles) depict the invariant points at the three temperatures (b). 3 DMSO–methanol. The points (filled circles) depict the invariant points at the three temperatures (b). | ||
In accordance with the SA to SMT solubility ratio, the co-crystal shows incongruent dissolution in methanol where the ratio is high and congruent dissolution in acetonitrile where the ratio is low. However, for an even lower solubility ratio in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol the co-crystal unexpectedly shows incongruent behaviour. The nature of co-crystal dissolution was confirmed by separate co-crystal dissolution experiments. In methanol and DMSO–methanol, the originally pure cocrystal solid phase transformed into a mixture of solid SMT and co-crystal, whereas in acetonitrile, a pure co-crystal solid was maintained. So even if the co-crystal dissolves nearly congruent in 7
3 (v/v) DMSO–methanol the co-crystal unexpectedly shows incongruent behaviour. The nature of co-crystal dissolution was confirmed by separate co-crystal dissolution experiments. In methanol and DMSO–methanol, the originally pure cocrystal solid phase transformed into a mixture of solid SMT and co-crystal, whereas in acetonitrile, a pure co-crystal solid was maintained. So even if the co-crystal dissolves nearly congruent in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol it is perfectly clear that the system is incongruent. In addition, the co-crystal region for this system does not change systematically towards the SMT axis compared to the acetonitrile system as would have been expected from the difference in the solubility ratio. Accordingly, it can be concluded that the coformer to API solubility ratio for the SA–SMT system cannot be safely used as a guide to the nature of the co-crystal dissolution behaviour. However, quite clearly the solvent has a major influence on the nature of co-crystal dissolution and the overall appearance of the phase diagram.
3 (v/v) DMSO–methanol it is perfectly clear that the system is incongruent. In addition, the co-crystal region for this system does not change systematically towards the SMT axis compared to the acetonitrile system as would have been expected from the difference in the solubility ratio. Accordingly, it can be concluded that the coformer to API solubility ratio for the SA–SMT system cannot be safely used as a guide to the nature of the co-crystal dissolution behaviour. However, quite clearly the solvent has a major influence on the nature of co-crystal dissolution and the overall appearance of the phase diagram.
With increasing temperature the solubility of all the solid phases increase, which leads to a shift of the various solid state regions down towards the solid SMT–SA axis in the ternary phase diagram. This leads to a larger region for the solution phase region (see Fig. S9–S11 in the ESI†). Temperature changes did not bring about any remarkable changes on the overall appearance of the phase diagram.
The experimentally determined invariant points for the three solvents in terms of mole fractions are given in Table 2, together with the corresponding Ksp values obtained from eqn (3). Obviously, the value depends on the solvent. The order in which Ksp varies is DMSO–methanol > methanol > acetonitrile. In each solvent, the Ksp value and the corresponding co-crystal solubility increase with temperature. In methanol and acetonitrile, there is just a small difference in the Ksp values obtained from the two invariant points. However, in the DMSO–methanol mixture, the Ksp difference is much higher, most likely because at higher concentrations the error associated with neglecting the activity coefficients becomes larger. For the congruent acetonitrile case, the Ksp for the co-crystal is between the Ksp values obtained from the two invariant points.
The width of the region where the co-crystal is the most stable phase can be measured as the linear distance between the two invariant points as per eqn (9).
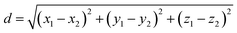 | (9) |
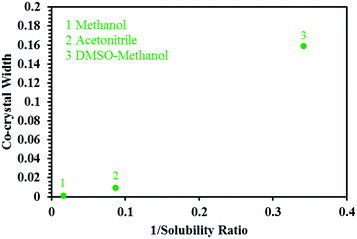
Based on this, the width of the co-crystal region decreases in the order DMSO–methanol > acetonitrile > methanol, and is inversely proportional to the solubility ratio between the two co-crystal components (SA/SMT, Table 1) i.e. the smaller the solubility ratio, the wider the co-crystal region (Fig. 9).
The co-crystal yield and productivity results are given in Table 3. The starting overall compositions of pure solid SMT, SA and solvent in the experiments are marked in Fig. 4, 5 and 8 by (M1, M2), (A1, A2) and (D1, D2), respectively. The farther away from the solid–liquid equilibrium line this initial overall composition point is placed, the greater is the surplus of material that can transform into solid co-crystal, and hence the higher the potential co-crystal yield and productivity. The difference in yield for the different solvents primarily depends on the co-crystal solubility. A high solubility leaves a greater amount dissolved in the solution at the end of the process. The yield can be improved by adding more pure solid components at a stoichiometric ratio. The very narrow co-crystal region in methanol requires a high precision in dosing the components. In spite of a large co-crystal region in DMSO–methanol, a limiting factor for DMSO–methanol is the high boiling point, which makes it difficult to completely remove the toxic solvent. Irrespective of the system being congruent or incongruent, the pure co-crystal can be synthesized by slurry co-crystallization as long as the liquid composition starting point is along the curve where the co-crystal is in equilibrium with the solution. It may be noted that it is favourable from a yield point of view if the phase diagram is skewed towards the coformer axis, since this corresponds to a lower concentration of SMT in the solution.
| Pointa | Input reagents (mass fraction) | Co-crystal mass (g) | Co-crystal yield (g g−1) | Volumetric productivity (g mL−1) | ||
|---|---|---|---|---|---|---|
| SMT | SA | Solvent | ||||
| a M (methanol), A (acetonitrile), D (DMSO–methanol). | ||||||
| M1 | 0.0700 | 0.0600 | 0.8700 | 0.1423 | 0.55 | 0.06 |
| M2 | 0.1530 | 0.0980 | 0.7490 | 0.4574 | 0.91 | 0.21 |
| A1 | 0.0620 | 0.0380 | 0.9000 | 0.1460 | 0.73 | 0.06 |
| A2 | 0.1968 | 0.1032 | 0.7000 | 0.5819 | 0.96 | 0.26 |
| D1 | 0.2100 | 0.2430 | 0.5470 | 0.0910 | 0.10 | 0.05 |
| D2 | 0.3540 | 0.2780 | 0.3680 | 0.4857 | 0.38 | 0.29 |
Conclusions
Ternary phase diagrams have been constructed for sulfamethazine and salicylic acid in three solvents: methanol, acetonitrile and a dimethyl sulfoxide–methanol 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture, at three temperatures. The shape of the phase diagram depends strongly on the solvent. The choice of solvent can make the co-crystal system congruent or incongruent, and can significantly affect the width of the co-crystal region. The co-crystal dissolves incongruently in methanol and 7
3 mixture, at three temperatures. The shape of the phase diagram depends strongly on the solvent. The choice of solvent can make the co-crystal system congruent or incongruent, and can significantly affect the width of the co-crystal region. The co-crystal dissolves incongruently in methanol and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) DMSO–methanol mixture, whereas it shows congruent dissolution in acetonitrile. The impact of temperature on the phase diagram is weak over the 20 °C range investigated. The solubility ratio of the two co-crystal components does not afford a simple reliable method to predict whether the co-crystal system becomes congruent or incongruent. The Gibbs energy of the SMT–SA co-crystal formation from its solid pure components is estimated to be −5.7, −7.1, and −7.7 kJ mol−1 at 10, 20 and 30 °C, revealing that the co-crystal is thermodynamically stable in relation to the pure components. In all three solvents, a slurry conversion process can provide a high yield and a high volumetric productivity.
3 (v/v) DMSO–methanol mixture, whereas it shows congruent dissolution in acetonitrile. The impact of temperature on the phase diagram is weak over the 20 °C range investigated. The solubility ratio of the two co-crystal components does not afford a simple reliable method to predict whether the co-crystal system becomes congruent or incongruent. The Gibbs energy of the SMT–SA co-crystal formation from its solid pure components is estimated to be −5.7, −7.1, and −7.7 kJ mol−1 at 10, 20 and 30 °C, revealing that the co-crystal is thermodynamically stable in relation to the pure components. In all three solvents, a slurry conversion process can provide a high yield and a high volumetric productivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research conducted with the financial support of the Synthesis and Solid State Pharmaceutical Centre (SSPC), funded by Science Foundation Ireland (SFI), co-funded under the European Regional Development Fund under Grant Number 12/RC/2275, as well as support from the Bernal Institute and the Department of Chemical Sciences, both at the University of Limerick.References
- N. Schultheiss and A. Newman, Cryst. Growth Des., 2009, 9, 2950–2967 CrossRef CAS PubMed.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- G. Bolla and A. Nangia, Chem. Commun., 2016, 52, 8342–8360 RSC.
- R. D. B. Walsh, M. W. Bradner, S. Fleischman, L. A. Morales, B. Moulton, N. Rodriguez-Hornedo and M. J. Zaworotko, Chem. Commun., 2003, 186–187, 10.1039/B208574G.
- S. G. Fleischman, S. S. Kuduva, J. A. McMahon, B. Moulton, R. D. Bailey Walsh, N. Rodríguez-Hornedo and M. J. Zaworotko, Cryst. Growth Des., 2003, 3, 909–919 CrossRef CAS.
- J. F. Remenar, S. L. Morissette, M. L. Peterson, B. Moulton, J. M. MacPhee, H. R. Guzmán and Ö. Almarsson, J. Am. Chem. Soc., 2003, 125, 8456–8457 CrossRef CAS PubMed.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1013–1021 CrossRef CAS.
- S. Karki, T. Friščić, L. Fábián, P. R. Laity, G. M. Day and W. Jones, Adv. Mater., 2009, 21, 3905–3909 CrossRef CAS.
- S. F. Chow, M. Chen, L. Shi, A. H. L. Chow and C. C. Sun, Pharm. Res., 2012, 29, 1854–1865 CrossRef CAS PubMed.
- M. Samipillai and S. Rohani, J. Cryst. Growth, 2019, 507, 270–282 CrossRef CAS.
- M. C. Etter and G. M. Frankenbach, Chem. Mater., 1989, 1, 10–12 CrossRef CAS.
- N. Shan, F. Toda and W. Jones, Chem. Commun., 2002, 2372–2373 RSC.
- T. Friscic, L. Fabian, J. C. Burley, W. Jones and W. D. S. Motherwell, Chem. Commun., 2006, 5009–5011 RSC.
- S. S. A. Abidi, Y. Azim, S. N. Khan and A. U. Khan, J. Pharm. Biomed. Anal., 2018, 149, 351–357 CrossRef CAS PubMed.
- A. Mukherjee, R. D. Rogers and A. Myerson, CrystEngComm, 2018, 20, 3817–3821 RSC.
- B. Yadav, S. Balasubramanian, R. B. Chavan, R. Thipparaboina, V. Naidu and N. R. Shastri, Cryst. Growth Des., 2018, 18, 1047–1061 CrossRef CAS.
- A. V. Trask and W. Jones, in Organic Solid State Reactions, ed. F. Toda, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 41–70 Search PubMed.
- M. R. Caira, Mol. Pharmaceutics, 2007, 4, 310–316 CrossRef CAS PubMed.
- D. M. Croker, M. E. Foreman, B. N. Hogan, N. M. Maguire, C. J. Elcoate, B. K. Hodnett, A. R. Maguire, Å. C. Rasmuson and S. E. Lawrence, Cryst. Growth Des., 2012, 12, 869–875 CrossRef CAS.
- S. Zhang, H. Chen and A. C. Rasmuson, CrystEngComm, 2015, 17, 4125–4135 RSC.
- P. Vishweshwar, J. A. McMahon, M. L. Peterson, M. B. Hickey, T. R. Shattock and M. J. Zaworotko, Chem. Commun., 2005, 4601–4603 RSC.
- A. Alhalaweh and S. P. Velaga, Cryst. Growth Des., 2010, 10, 3302–3305 CrossRef CAS.
- S. P. Patil, S. R. Modi and A. K. Bansal, Eur. J. Pharm. Sci., 2014, 62, 251–257 CrossRef CAS PubMed.
- A. Alhalaweh, W. Kaialy, G. Buckton, H. Gill, A. Nokhodchi and S. P. Velaga, AAPS PharmSciTech, 2013, 14, 265–276 CrossRef CAS PubMed.
- T. Friščić, S. L. Childs, S. A. Rizvi and W. Jones, CrystEngComm, 2009, 11, 418–426 RSC.
- D. H. Leung, S. Lohani, R. G. Ball, N. Canfield, Y. Wang, T. Rhodes and A. Bak, Cryst. Growth Des., 2012, 12, 1254–1262 CrossRef CAS.
- S. Aher, R. Dhumal, K. Mahadik, A. Paradkar and P. York, Eur. J. Pharm. Sci., 2010, 41, 597–602 CrossRef CAS PubMed.
- R. A. Chiarella, R. J. Davey and M. L. Peterson, Cryst. Growth Des., 2007, 7, 1223–1226 CrossRef CAS.
- M. Eraković, V. Nemec, T. Lež, I. Porupski, V. Stilinović and D. Cinčić, Cryst. Growth Des., 2018, 18, 1182–1190 CrossRef.
- K. V. Drozd, A. N. Manin, A. V. Churakov and G. L. Perlovich, CrystEngComm, 2017, 19, 4273–4286 RSC.
- M. Malamatari, S. A. Ross, D. Douroumis and S. P. Velaga, Adv. Drug Delivery Rev., 2017, 117, 162–177 CrossRef CAS PubMed.
- K. Boksa, A. Otte and R. Pinal, J. Pharm. Sci., 2014, 103, 2904–2910 CrossRef CAS PubMed.
- C. Pando, A. Cabanas and I. A. Cuadra, RSC Adv., 2016, 6, 71134–71150 RSC.
- L. Padrela, M. A. Rodrigues, S. P. Velaga, H. A. Matos and E. G. de Azevedo, Eur. J. Pharm. Sci., 2009, 38, 9–17 CrossRef CAS PubMed.
- V. Titapiwatanakun, A. W. Basit and S. Gaisford, Cryst. Growth Des., 2016, 16, 3307–3312 CrossRef CAS.
- S.-W. Zhang, A. P. Brunskill, E. Schwartz and S. Sun, Cryst. Growth Des., 2017, 17, 2836–2843 CrossRef CAS.
- G. L. Perlovich, CrystEngComm, 2018, 20, 3634–3637 RSC.
- C. Loschen and A. Klamt, Cryst. Growth Des., 2018, 18, 5600–5608 CrossRef CAS.
- V. Todaro, Z. A. Worku, L. M. Cabral and A. M. Healy, AAPS PharmSciTech, 2019, 20, 28 CrossRef PubMed.
- A. S. Pessoa, G. P. S. Aguiar, J. V. Oliveira, A. J. Bortoluzzi, A. Paulino and M. Lanza, J. Supercrit. Fluids, 2019, 145, 93–102 CrossRef CAS.
- L. H. do Amaral, F. A. do Carmo, M. I. Amaro, V. P. de Sousa, L. C. R. P. da Silva, G. S. de Almeida, C. R. Rodrigues, A. M. Healy and L. M. Cabral, AAPS PharmSciTech, 2018, 19, 2687–2699 CrossRef CAS PubMed.
- A. Ainouz, J.-R. Authelin, P. Billot and H. Lieberman, Int. J. Pharm., 2009, 374, 82–89 CrossRef CAS PubMed.
- S. J. Nehm, B. Rodríguez-Spong and N. Rodríguez-Hornedo, Cryst. Growth Des., 2006, 6, 592–600 CrossRef CAS.
- A. Jayasankar, L. S. Reddy, S. J. Bethune and N. Rodríguez-Hornedo, Cryst. Growth Des., 2009, 9, 889–897 CrossRef CAS.
- J. H. ter Horst, M. A. Deij and P. W. Cains, Cryst. Growth Des., 2009, 9, 1531–1537 CrossRef CAS.
- T. Leyssens, G. Springuel, R. Montis, N. Candoni and S. Veesler, Cryst. Growth Des., 2012, 12, 1520–1530 CrossRef CAS.
- S. Zhang and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 1153–1161 CrossRef CAS.
- S. Zhang and Å. C. Rasmuson, CrystEngComm, 2012, 14, 4644–4655 RSC.
- A. Bacchi, D. Capucci, M. Giannetto, M. Mattarozzi, P. Pelagatti, N. Rodriguez-Hornedo, K. Rubini and A. Sala, Cryst. Growth Des., 2016, 16, 6547–6555 CrossRef CAS.
- S. Ghosh, P. P. Bag and C. M. Reddy, Cryst. Growth Des., 2011, 11, 3489–3503 CrossRef CAS.
- A. K. Basak, S. K. Mazumdar and S. Chaudhuri, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 492–494 CrossRef.
- R. K. Tiwari, M. Haridas and T. P. Singh, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 655–657 CrossRef.
- U. Patel, M. Haridas and T. P. Singh, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 1264–1267 CrossRef.
- D. Ahuja, P. Bannigan and A. C. Rasmuson, CrystEngComm, 2017, 19, 6481–6488 RSC.
- www.prosim.net.
- S. Zhang and A. C. Rasmuson, CrystEngComm, 2012, 14, 4644–4655 RSC.
- F. L. Nordström and Å. C. Rasmuson, J. Chem. Eng. Data, 2006, 51, 1668–1671 CrossRef.
- D. R. Delgado, O. A. Almanza, F. Martínez, M. A. Peña, A. Jouyban and W. E. Acree, J. Chem. Thermodyn., 2016, 97, 264–276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ce00124g |
| This journal is © The Royal Society of Chemistry 2019 |