 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Meta-biomaterials
Amir A.
Zadpoor

Additive Manufacturing Laboratory, Department of Biomechanical Engineering, Delft University of Technology (TU Delft), Mekelweg 2, Delft 2628 CD, The Netherlands. E-mail: a.a.zadpoor@tudelft.nl; Fax: +31-15-2784717; Tel: +31-15-2781021
First published on 14th October 2019
Abstract
Meta-biomaterials are designer biomaterials with unusual and even unprecedented properties that primarily originate from their geometrical designs at different (usually smaller) length scales. This concept has been primarily used in the context of orthopedic biomaterials with the ultimate aim of improving the bone tissue regeneration performance of implants and decreasing the risk of implant-associated infections. In this paper, we review the ways though which geometrical design at the macro-, micro-, and nanoscales combined with advanced additive manufacturing techniques (3D printing) could be used to create the unusual properties of meta-biomaterials. Due to their intended applications in orthopedics, metallic and hard polymeric biomaterials have received the most attention in the literature. However, the reviewed concepts are, at least in principle, applicable to a wide range of biomaterials including ceramics and soft polymers. At the macroscale, we discuss the concepts of patient-specific implants, deployable meta-implants, and shape-morphing implants. At the microscale, we introduce the concept of multi-physics meta-biomaterials while also covering the applications of auxetic meta-biomaterials for improving the longevity of orthopedic implants. At the nanoscale, the different aspects of the geometrical design of surface nanopatterns that simultaneously stimulate the osteogenic differentiation of stem cells and kill bacteria are presented. The concept of origami-based meta-biomaterials and the applications of self-folding mechanisms in the fabrication of meta-biomaterials are addressed next. We conclude with a discussion on the available evidence regarding the superior performance of meta-biomaterials and suggest some possible avenues for future research.
1. Introduction
For decades, developing biomaterials that address clinical challenges has chiefly meant the synthesis of a new material such as a new biopolymer or a new metallic alloy. Recently, however, an alternative paradigm has been emerging motivated by the recent discoveries of how the desired mechanical, physical, and biological properties as well as advanced (bio-)functionalities could be achieved through geometrical designs at the macro-, micro-, and nanoscales. This marks the birth of the so-called “designer biomaterials” where smart application of physical and biological principles combined with computational models guide us in designing geometries that give rise to the desired properties and functionalities. This approach of using physical principles and computational models to design materials with novel properties and advanced functionalities is sometimes called “rational design”1 and has recently generated tremendous enthusiasm and interest worldwide. The first applications of the rational design process for the development of advanced functional materials have been in technological areas other than biomedicine. The resulting materials are often called “metamaterials”.Metamaterials are often defined as architected materials that, owing to their rationally designed small-scale architecture, exhibit extraordinary properties not usually seen in natural materials. This is a generally valid attempt at a definition for technological metamaterials where the aim of the rational design process is to achieve exotic mechanical,2–8 acoustic,9–12 or electromagnetic13–16 properties. This definition, however, does not capture the entire picture when it comes to ‘meta-biomaterials’ whose aim is to replace biological tissues either temporarily (to facilitate their regeneration) or permanently (as implantable medical devices). In fact, biological tissues are the nature's magnum opus and, as such, possess a host of extraordinary properties that man-made meta-biomaterials can only hope to imitate. The list of unusual properties exhibited by biological tissues is long and includes negative Poisson's ratios,17 a combination of ultrahigh stiffness with ultrahigh toughness (i.e., contradictory designs requirements for engineering materials),18–20 and interfacing extremely soft materials with extremely hard materials (e.g., in bone-tendon or bone-cartilage connections).21,22
Indeed, in the case of meta-biomaterials, we are searching for designs that enable us to achieve properties that are readily available in nature particularly in the living matter. In particular, millions of years of evolution has equipped organisms with ingenious ways to meet multiple, often contradictory, design criteria. Living tissues, therefore, present favorable combinations of mechanical, mass transport, and biological properties including combinations that are ordinarily considered mutually exclusive. Given that the temporary or permanent replacements of biological tissues should mimic their properties, meta-biomaterials can be defined as ‘architected materials that mimic the unusual combinations of properties exhibited by living tissues’. This, of course, does not preclude designing meta-biomaterials whose properties are purposefully or due to (fabrication) limitations different from those of the tissues they replace, as the native properties of tissues under homeostatic conditions are not necessarily the best ones for transient states such as those of a regenerating tissue.
In addition to the differences highlighted above, meta-biomaterials are different from the vast majority of other metamaterials studied to date in that they target multiple types of (physical) properties. In that sense, meta-biomaterials can be considered ‘multi-physics metamaterials’ as opposed to single-physics metamaterials such as mechanical, acoustic, or optical metamaterials. The rational design of meta-biomaterials, therefore, requires the application of multi-physics computational approaches at multiple length and time scales to devise micro-architectures that gives rise to the desired multi-physics properties.
Furthermore, the rational design of meta-biomaterials requires a multi-scale approach, because mimicking the functionalities of biological tissues is otherwise impossible. As previously mentioned, the hierarchical design23,24 is partially responsible for the extraordinary properties of biological tissues particularly because, together with functional gradients, it allows for meeting contradictory design requirements. This is contrast with the vast majority of technological metamaterials demonstrated to date where only two distinct scales, namely the micro- and macro-scales, are recognizable. Indeed, the limitations of the two length scales approach have been also recognized by other metamaterials communities. For example, a number of hierarchical mechanical metamaterials25,26 with extraordinary and otherwise impossible combination of properties, such as high stiffness and auxetic behavior27 have recently appeared in the literature.
Given the importance of the different length scales in the design of meta-biomaterials, this review has been organized according to the length-scale at which the unusual properties and functionalities of meta-biomaterials are created and observed including the macro-, micro-, and nanoscales. In practice, realizing meta-biomaterials with precisely controlled geometrical designs requires the application of advanced additive manufacturing (AM = 3D printing) techniques. We will, therefore, pay also some attention to AM techniques and their application for fabrication of meta-biomaterials. After discussing each length scale separately, we will turn our focus to the unique technical challenges that are associated with combining geometrical designs at different scales and the solutions proposed for overcoming those challenges including those based on (self-folding) origami. In terms of the application area, the main focus of this article will be meta-biomaterials that aim to enhance the bone tissue regeneration performance and, thus, the longevity of orthopaedic implants while minimizing the risk of implant-associated infections.
2. Macroscale design
One of the first applications of the form-freedom offered by AM techniques for improving the longevity of orthopaedic implants has been through patient-specific designs that ensure the implant can exactly match the patients’ anatomy. Due to this anatomical matching, patient-specific implants are expected to result in improved primary stability, thereby increasing the lifetime of implants in orthopaedic, trauma, and maxillofacial surgeries. An exact matching of the complex anatomical shapes exhibited by various bones28,29 often requires the use of complex geometrical designs (Fig. 1a). Such a design route constitutes the simplest way through which complex geometrical designs at the macroscale could be used for improving the performance of implants and has been explored by a large number of researchers.30 The design and fabrication of patient-specific implants is, however, not the only way to benefit from the advantages of complex designs at the macroscale. Two new categories of the so-called ‘meta-implants’ have been recently introduced that take full advantage of complex designs at the macroscale to equip orthopaedic implants with unprecedented functionalities such as deployability and shape-morphing behaviors.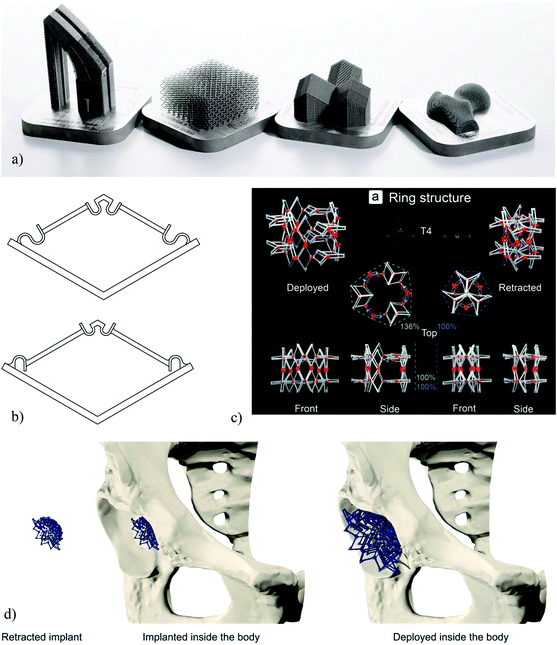 | ||
| Fig. 1 (a) A number of AM orthopaedic implants (reprinted from ref. 46 with permission from Elsevier, Copyright 2018). (b) The basic bi-stable elements used for the design of multi-stable deployable implants.38 (c) A deployable implant made through an arrangement of bi-stable implants.38 (d) A schematic demonstration of the concept of deployable implants.38 | ||
2.1. Deployable meta-implants
The form-freedom offered by AM techniques could be used to create deployable implants where the implant is compact in its retracted state and could, therefore, be brought to the surgical site with minimum invasiveness. Once the implant is in its intended implantation site, a deployment mechanism is activated to change the state of the implant to its fully deployed state where it takes its full size and is fully load-bearing. The shape and mechanical properties of the implant, therefore, change through the deployment mechanism.Similar ideas have been used in cardiovascular stents where the stent is brought to its implantation site in a compressed state and is released from its compressed state to recover its shape elastically. The stent will, then, open the blood vessel up at the point of its application. The superelastic features offered by shape memory alloys such as NiTi31,32 could be used to facilitate such deployment mechanisms by ensuring the full recovery of the stent from its highly compressed state. This simple deployment mechanism is practical in the case of cardiovascular stents, because the forces required to keep our very flexible blood vessels open are very small as compared to musculoskeletal forces and that there are tensile forces imposed by the blood flow (i.e., blood pressure) that assist in keeping the stent open. Similar design principle cannot be used in orthopedic implants, because they need to withstand very large forces that amount to several times the body weight and are primarily compressive. That is why the design and fabrication of deployable orthopedic implants is much more complex than the design of deployable stents, and requires alternative design and AM paradigms.
The main design paradigm proposed in the design of deployable implants is the concept of multi-stability in physics and mechanics33–37 where the mechanisms are designed to have two (i.e., bi-stable) or more (i.e., multi-stable) stable configurations. Each of those stable states are associated with a specific shape and set of mechanical properties. To change the equilibrium state of the implant, an energy barrier should be overcome in a specific direction. The direction of the required deployment forces is particularly important in this regard, because they should be in the opposite direction as the main loading direction of the implant to make sure the deployed implant cannot go back to its undeployed state once it has been implanted.
In the first design of deployable meta-implants, the concept of bi-stability (Fig. 1b) was used to design deployable implants.38 Such bi-stable elements work on the basis of a snap-through behavior that associates the different equilibrium states of the element with different sizes and mechanical properties. The basic snap-through elements were then arranged in a variety of ways to create different types of deployable implants that could be deployed either in the radial or axial directions (e.g., see Fig. 1c and d). The deployment force can be applied using an inflating balloon that exerts a tensile force to push the implants from their retracted state to their fully deployed state where the implant is subjected to primarily compressive forces. The insertion of an inflating balloon is a non-invasive procedure that is already used in some conventional surgical procedures such as kyphoplasty,39 which is a vertebral augmentation technique for the treatment of the compression fractures of vertebrae. The fact that similar processes are already in widespread clinical use, should facilitate the adoption of the concept. A measurement of the deployment forces and mechanical properties associated with the different designs of the deployable implants (i.e., different arrangements of the bi-stable elements) has shown that they are highly dependent on the exact arrangements of the basic elements.38 This provides a design paradigm within which a large number of design variations befitting different applications could be achieved from a single design of bi-stable element. Given the fact that AM of multi-stable elements is challenging, the availability of such a general design paradigm could deliver multiple advantages in terms of the manufacturability of deployable implants.
2.2. Shape-morphing meta-implants
As previously mentioned, patient-specific implants whose shapes exactly matches the patients’ anatomy offer many clinical advantages including improved primary and possibly also secondary fixation. However, they are often much more expensive, laborious, and time consuming to design and manufacture. The design and manufacturing of one such implant could take up to a few months depending on the complexity of the case and the number of iterations required between the designers and the responsible surgeon. These iterations and extended lead times could also increase the cost of the implant to many times that of off-the-shelf implants while making patient-specific implants not an option when the surgery needs to be performed within a short time span (e.g., in the case of trauma patients). It is important to note that most of the costs of patient-specific implants are associated with the design process where expert designers need to use clinical images and expensive medical image processing software to design the exact shape of the implant and iterate their designs with the responsible surgeon.An alternative approach based on the so-called “metallic clay”40 concept has been recently proposed where the implant is not designed to match the anatomy of a specific patient but rather to exhibit shape-morphing and shape-locking behaviors (Fig. 2a). This concept is in many ways similar to the way clay is used: initially, the implant can be basically formed into any shape using the relevant tools and/or by expert hands. Once the desired shape has been achieved, the clay is fired (i.e., baked) to freeze it in the intended shape. A similar concept could be used for the design of shape-morphing implants that will, in principle, be generic and, thus, available off-the-shelf. The shape of the implants can be morphed into the desired shape during the surgery. Subsequently, a locking mechanism is activated to freeze the shape of the implant.
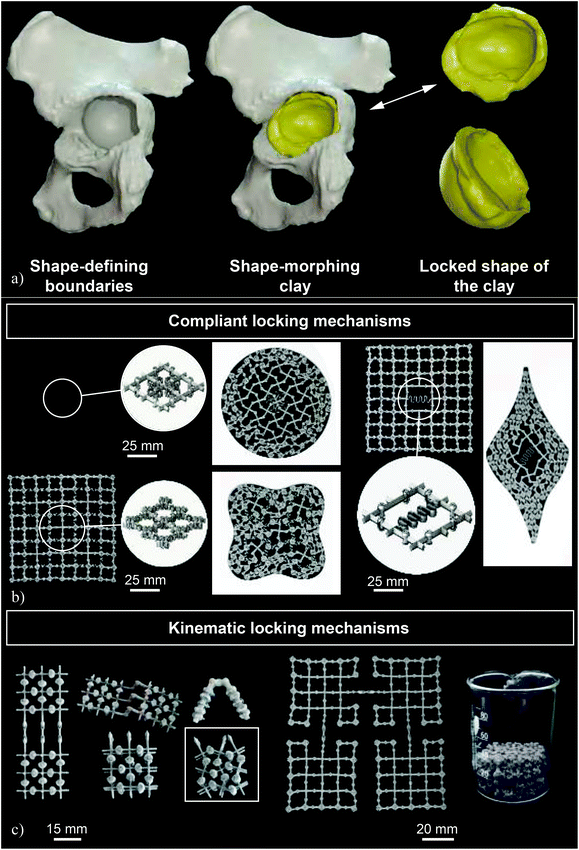 | ||
| Fig. 2 (a) A schematic drawing illustrating the concept of metallic clay as applied for the treatment of acetabular defects (reprinted from ref. 40 with permission from Elsevier, Copyright 2019). (b) Some examples of the prototypes made to demonstrate the concept of joints as well as the concept of complaint locking mechanisms (reprinted from ref. 40 with permission from Elsevier, Copyright 2019). (c) A number of prototypes made to demonstrate the concept of kinematic locking mechanisms (reprinted from ref. 40 with permission from Elsevier, Copyright 2019). | ||
The concept of metallic clay requires two major mechanisms, namely shape-morphing and shape-locking mechanisms. The shape-morphing capability is afforded to the implant through incorporation of many joints (Fig. 2b and c). The joints may be complaint or kinematic (or a combination of both) depending on the specific requirements of the implant. In kinematic joints, the shape-morphing behavior is created through the relative (rigid body) movements of the different parts of the joints with respect to each other, while the elements of complaint joints40 need to undergo material deformation. Similarly, the locking mechanisms could be either complaint (Fig. 2b) or kinematic (Fig. 2c). In the case of kinematic locking mechanisms, a moving barrier blocks the degrees-of-freedom of the joints, thereby locking the implant in its current shape. Complaint locking mechanisms, however, use elastic forces to lock the implant in its current shape. Given the complex geometries involved, the non-assembly fabrication of a large number of (kinematic) joints, such as those used in shape-morphing metallic implants is only possible through an efficient use of AM and a re-design of traditional joints to make it possible to fabricate them without any need for support structures.40 If successful, the metallic-clay concept could change the design paradigm particularly for such surgeries as the treatment of acetabular defects where well-defined bony contours exist that relatively effortlessly define the desired shape of the implant. Given the minimum amount of material that is used in the design of deployable and shape-morphing implants, simultaneously satisfying the requirements regarding the mechanical performance and shape-morphing capabilities poses a major challenge that needs to be overcome through the smart application of optimal design approaches such as topology optimization.
3. Microscale design
The next scale of geometrical design concerns the design of the micro-architecture of meta-biomaterials. This is the scale whose rational design is the closest to the traditional definition of the term metamaterials within the contexts of mechanical and acoustic metamaterials. The aim of microscale scale design is to rationally design the geometry of the constituting unit cells of a porous structure in such a way that its effective properties at the macroscale meet certain design objectives. In most cases, the objective is to achieve (a combination of) material properties that are unique and not attainable in traditional ways.In addition to adjusting the material properties, microscale geometrical design could be used to facilitate the other ways through which the performance of meta-biomaterials could be improved. Two of these mechanisms are particularly noteworthy. First, AM porous structures possess up to several orders of magnitude larger (internal) surface areas as compared to their solid counterparts. This could, in turn, result in an amplified effect of surface bio-functionalization approaches (e.g., see ref. 41–45) such as those applied for preventing implant-associated infections and improving the osteogenic response of biomaterials. Second, the internal pore space of meta-biomaterials could be used to accommodate drug delivery vehicles and to adjust their release profiles.
In the following sub-sections, we review some examples of the unusual properties that could result from the rational geometrical design of meta-biomaterials and describe how they could contribute towards an improved performance of orthopedic implants.
3.1. Meta-biomaterials as multi-physics metamaterials
As opposed to most other metamaterials where the targeted properties are usually of one type, meta-biomaterials need to simultaneously satisfy multiple design criteria regarding properties of different physical natures, essentially requiring a multi-physics design approach. The different types of properties include mechanical properties (i.e., quasi-static mechanical properties and fatigue behavior), mass transport properties (i.e., permeability and diffusivity), and morphology-dependent biological properties (e.g., curvature, pore size). While the native bone tissue possesses all those properties, replicating the same in synthetic biomaterials is often very challenging, if not impossible.The microscale design of meta-biomaterials is usually performed either using beam-based or sheet-based geometries.46,47 In the case of beam-based geometries, the basic unit cells making up the micro-architecture of the meta-biomaterials are designed using structural elements with large length to diameter ratios (i.e., beams or struts). Some examples of such unit cells are space-filling polyhedra and modifications thereof. The unit cells of sheet-based geometries, on the other hand, are made from sheets whose thickness is much smaller than their other dimensions (Fig. 3a). While the relationship between the geometrical design and the resulting properties including quasi-static mechanical properties,48–52 fatigue lives,53–60 and permeability61,62 have been extensively studied for strut-based geometries, relatively limited information is available regarding sheet-based geometries. A recent study,63 however, has shown that a specific class of sheet-based geometries, namely triply periodic minimal surfaces, are extremely successful in satisfying the multi-physics design requirements laid out for meta-biomaterials and could offer a combination of bone-mimicking elastic modulus, a very high yield strength, extremely long fatigue lives, and bone-mimicking transport properties, as well as a bone-mimicking mean surface curvature of zero.64 This unique and ideal combination of material properties and this extremely high level of multi-physic bone mimicry is a good example of how a proper selection of the geometrical design at the microscale could lead to favorable properties at the higher length scales. Of course, it is important to realize that replicating the properties of the native bony tissue, which is in an equilibrium, homeostatic state, may not be the best way to stimulate bone tissue regeneration. However, the advantages of microscale geometrical design within the context of meta-biomaterials remain relevant regardless of the chosen design objective, because microscale geometrical design could be also applied to satisfy any alternative design objectives.
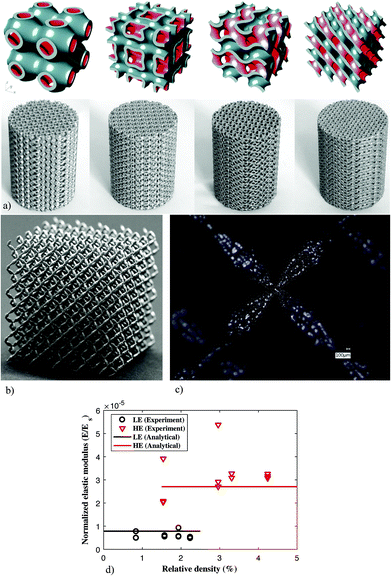 | ||
| Fig. 3 (a) Some examples of the meta-biomaterials designed using different types of triply periodic minimal surfaces and fabricated using selective laser melting.63,115 (b) Pentamode metamaterials made from Ti-6Al-4V65 and (c) the double-cone shape of their struts.65 (d) The Ashby's law between relating relative density to the mechanical properties of cellular structures breaks down in the case of pentamode metamaterials.65 | ||
Another example of the use of microscale geometrical design for creating unprecedented properties is reported in a study on pentamode metamaterials.65 A specific design of pentamode metamaterials was proposed in 1995![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 but was never realized in practice until 2012 where a first realization using a low-stiffness polymeric material was reported.67 However, the low mechanical properties of the materials from which those specimens were made, meant that they were of limited use for practical applications. In 2017, pentamode metamaterials were realized for the first time from a medical-grade titanium alloy with extremely high mechanical properties (i.e., Ti-6Al-4V, elastic modulus = 110 GPa).65 The specific shape of the beam-like elements making up the diamond-type unit cell of these structures, namely the double-cones that are attached to each other at their base (Fig. 3b and c), makes AM of this type of metamaterials very challenging particularly from metals.
66 but was never realized in practice until 2012 where a first realization using a low-stiffness polymeric material was reported.67 However, the low mechanical properties of the materials from which those specimens were made, meant that they were of limited use for practical applications. In 2017, pentamode metamaterials were realized for the first time from a medical-grade titanium alloy with extremely high mechanical properties (i.e., Ti-6Al-4V, elastic modulus = 110 GPa).65 The specific shape of the beam-like elements making up the diamond-type unit cell of these structures, namely the double-cones that are attached to each other at their base (Fig. 3b and c), makes AM of this type of metamaterials very challenging particularly from metals.
There are two specific reasons why the properties offered by pentamode metamaterials are interesting within the context of meta-biomaterials. First, it has been shown that pentamode metamaterials could be designed to exhibit mechanical properties described by any elasticity tensor that is thermodynamically admissible.66 Pentamode metamaterials, therefore, offer a general design platform that could be used to create any set of mechanical properties that may be suitable for bone tissue regeneration regardless of what the final design criteria turn out to be. Second, it has been shown that, for this particular class of materials, the universally valid Ashby's law, which postulates a power law type relationship between the relative density and mechanical properties of cellular materials, breaks down (Fig. 3d).65,68 The breakdown of this law has to do with the fact that almost all of the stress is transferred through the apex of the double-cones, meaning that the dimensions of the base of the cones could be changed at will, without affecting the effective mechanical properties of the metamaterial. As a result, it is possible to decouple the mechanical properties of the lattice structure from its relative density. Given the fact that the mass transport properties of porous structures are highly dependent on their relative density (or porosity),69,70 pentamode mechanical metamaterials offer a route to the decoupling of the mechanical and mass transport properties of meta-biomaterials. A decoupled design of mechanical and mass transport properties is particularly interesting given the fact that they often require conflicting choices in terms of the geometrical design.
Proper design of the geometry at the microscale requires knowledge regarding the boundaries of possible properties. Since many mechanical and physical properties that were previously thought to be impossible can now be achieved, a natural question to ask is, ‘are there any well-defined boundaries for the multi-physics boundaries of meta-biomaterials?’ If yes, what are those boundaries? In the case of some of the mechanical properties (e.g., elastic modulus), some of those boundaries have been established before (e.g., Hashin–Shtrikman bounds71). The property bounds are, however, less clear in the case of some other types of multi-physics properties and need to be further researched in the future.
3.2. Auxetic meta-biomaterials
Auxetic metamaterials72–74 are a special case of mechanical metamaterials with negative values of the Poisson's ratio. A negative value of the Poisson's ratio means that, contrary to the vast majority of natural material, auxetic metamaterials expand upon stretching and shrink upon compression. This unusual behavior has many applications in other engineering areas including a high energy absorption capacity75 that may be also relevant for the design of orthopedic implants. The main application of auxetic meta-biomaterials, however, does not have much to do with their conventional applications and boils down to the rational design of the geometry and mechanical properties of implants in such a way that they could optimize the bone-implant contact.In the specific case of hip stems, a rational distribution of the mechanical properties of auxetic and non-auxetic meta-biomaterials (Fig. 4a and b) enables an unprecedented and unique feature that cannot be obtained in any other way. Hip stems are loaded under bending, meaning that one side of the implant (i.e., the lateral side) is under tension while the other side (i.e., the medial side) is under compression. If the implant is made from a conventional material with a positive Poisson's ratio, the side that is under compression will expand laterally, meaning that it presses against the surrounding bony tissue. Compression against the surrounding bones is favorable, as it minimizes the risk of interface failure while stimulating bone tissue regeneration at the interface and preventing the wear particles from entering the potential sites of interface failure between the implant and the surrounding bone. The side of the implant that is under tension, however, shrinks laterally, meaning that it tends to go away from the surrounding bony structures. This could result in tensile interface stresses and, thus, interface failure. Moreover, wear particles could more easily enter the bone-implant interface and cause an inflammatory response that eventually leads to wear particle-related osteolysis.76 The only way to prevents one of the sides of the implant from laterally shrinking is to design the implant in such a way that it is partially made from an auxetic material and partially from a conventional material (Fig. 4c). AM auxetic meta-biomaterials allow for such a construction to be realized. Indeed, full-field strain measurements performed on simulated implantations using digital image correlation (i.e., a full-field strain measurement technique77,78) have confirmed the presence of compressive stresses on both sides of orthopedic meta-implants designed and printed using such a design approach.79 Further steps need to be taken to validate these observations in ex vivo and in vivo settings.
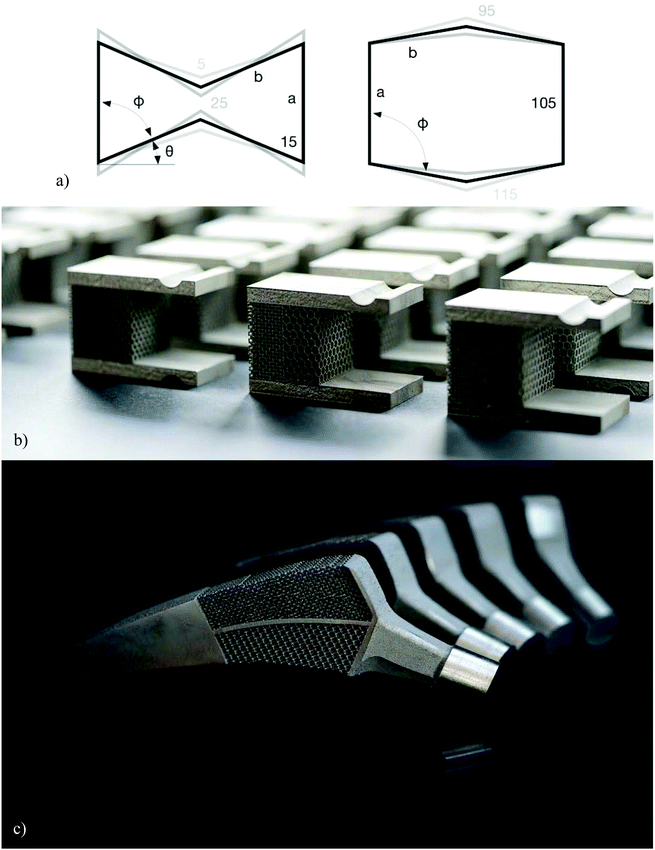 | ||
| Fig. 4 (a) From left to right, the shapes of the unit cell used for creating auxetic and conventional metamaterials.79 (b) A combination of the positive and negative values of the Poisson's ratio could be used to create compression around the periphery of hip stems (c).79 | ||
3.3. Biodegradable porous biomaterials
AM of porous biodegradable metals such as magnesium alloys,80 pure iron,81 and zinc82 has recently become possible. It is, therefore, now possible to fabricate meta-biomaterials made from biodegradable metals. This could take the bone-substituting properties of AM metallic meta-biomaterials to the next level, as it would be possible to synthesize bone-substituting meta-biomaterials that are fully biodegradable and could, thus, result in full bone regeneration in segmental critical size bony defects. The microscale geometrical design of the porous structures has a role to play within this context. Given the fact that the biodegradation rate of metals and alloys almost always deviates from the desired rate of biodegradation, a mechanism through which the rate of biodegradation could be adjusted is highly desirable. A few recent studies have shown that it is, indeed, possible to fine-tune the biodegradation rate of such biomaterials using specific types of geometrical design, such as functionally graded geometries.83 In most cases, what could be done through geometrical design is locally increasing the surface area and, thus, the rate of biodegradation. It is, therefore, beneficial to start from materials such as iron or zinc whose rate of biodegradation is relatively low. The increase of the surface area could then be used to adjust the rate of biodegradation to a desired value, which is higher than the innate rate of biodegradation of the specific material at hand. Similar to the other types of biodegradable metals, the effects of biodegradation process and biodegradation products on the performance of host cells and the foreign body response should be carefully studied before any clinical applications can be realized.Finally, it is important to realize that it is possible to combine the benefits of the macroscale geometrical design with those of the microscale geometrical design, as advanced AM techniques allow for the fabrication of geometries that both at the macro- and microscales conform to specific designs.
4. Nanoscale design
On our journey towards smaller length scales, nanoscale is the next scale. At this length scale, we are primarily concerned with surface nanopatterns where specific nanofeatures (Fig. 5a) with controlled shapes and dimensions are used to induce certain bio-functionalities. The primarily functionalities of interest for the kind of meta-biomaterials we are dealing with are osteogenic and bactericidal properties. | ||
| Fig. 5 (a) Some examples of the nanofeatures created on the surface of origami-based meta-biomaterials using EBID.104 (b) The response of pre-osteoblast to nanopatterned surfaces. (c) Staphylococcus aureus can be killed by nanopatterns.95 | ||
4.1. Osteogenic nanopatterns
Determining stem cell fate is one of the most important approaches to improving the bone tissue regeneration performance of biomaterials. Up until recently, this was primarily pursued through the application of biochemical factors (e.g., growth factors) that stimulate the osteogenic differentiation of stem cells. In the recent years, however, there has been accumulation of evidence indicating that physical cues, such as the substrate stiffness and the geometrical design of nanopatterns play important roles in determining cell behavior.84–88 The pathways through which nanopatterns affect stem cell fate are generally mechanobiological in nature. The geometrical design of nanopatterns affects the integrin pathways and focal adhesions, leads to cytoskeletal re-organization, changes cellular morphology (Fig. 5b), and modulates gene expressions through direct mechanical forces applied to the nucleus or as an indirect consequence of the forces sensed by the other parts of the cell.89–94 A systematic review of osteogenic surface nanopatterns91 has found multiple studies in which nanofeatures with dimensions that are (at least partially) below 100 nm induce the osteogenic differentiation of mesenchymal stem cells in absence of osteogenic supplements. The nanopatterns that cover the surfaces of meta-biomaterials should, therefore, be designed such that they replicate the osteogenic behavior observed in such studies. This allows for drug-free induction of the osteogenic behavior. Replacing pharmaceutics by surface nanopatterns has the added advantages that the certification process of the resulting medical device is more streamlined than implants that incorporate pharmaceutical agents and/or stem cells. However, the small size of the individual nanopillars means that high-end nanofabrication techniques (see section 4.3) need to be used for surface patterning. Moreover, large-scale nanopatterning of biomaterials surfaces may be a time-consuming process depending on the type of the applied nanofabrication technique.4.2. Bactericidal nanopatterns
Surface nanopatterns could be also used to kill both Gram-positive and Gram-negative bacteria,95 thereby preventing implant-associated infections. The action mechanism of bactericidal nanopatterns is mechanical in nature: high aspect ratio nanofeatures strain the bacterial cell wall to the point of rupture (Fig. 5c). Bactericidal nanopatterns are present in nature as well, for example, on the wings of a number of insects such as dragonflies and cicadae.96 A systematic review of the nanopatterns that exhibit bactericidal behavior has shown that nanopillar arrays with the following dimensions induce bactericidal behavior: “heights of 100–1000 nm, diameters of 10–300 nm, and interspacings of <500 nm”.97There is an overlap between the range of nanopillar dimensions that lead to an osteogenic behavior and those resulting in a bactericidal one. It is, therefore, possible to create multi-functional surface nanopatterns that simultaneously stimulate stem cell differentiation towards an osteogenic lineage and kill bacteria.98 Finding the dimensions for which the different beneficial effects of surface nanopatterns overlap, while the adverse effects such as cytotoxicity are absent, is a major challenge partially due to the fact that systematic experiments on nanopatterned surface with different dimensions is technically challenging. Computational models (e.g., see ref. 99) could be useful in this regard, as they allow for considering the effects of surface nanopatterns on both mammalian and bacteria cells and identifying a limited range of parameters that could be later used in experimental analyses.
4.3. Nanofabrication techniques
Given the fact that the desired nanofeatures should be precisely controlled and are often geometrically complex, high-end nanofabrication techniques need to applied for such nanopatterning purposes. Among AM techniques, two specific techniques, namely two-photon polymerization (2PP)100 and electron beam induced deposition (EBID),101 are particularly suited for this purpose. In terms of the length scales they could achieve, 2PP can easily achieve features sizes in the range of a few hundred nanometers while EBID could go down in terms of feature sizes to a few nanometers. In addition to AM approaches, lithography-based approaches such as electron beam-based nanolithography supplemented with inductively coupled plasma etching could be used for fabricating nanofeatures in the range of a few hundred nanometers.102 Between themselves, these techniques could create almost any desired geometrical design with a high level of precision and repeatability. There is, however, a major caveat in all these approaches: most advanced nanopatterning techniques are only applicable to flat surfaces. Given the fact that the vast majority of our meta-biomaterial designs are three-dimensional in nature, it is not possible to apply surface nanopatterns to lattice structures. Moreover, the internal surface areas of meta-biomaterials, which are by far the largest part of the surface area of lattice structures, is not accessible once the AM process has been finished. This technological limitation makes it impossible to combine the beneficial effects of macroscale and microscale geometrical designs with those of surface nanopatterns. Alternative approaches are, therefore, required.5. Origami-inspired meta-biomaterials
The ancient Japanese art of paper folding (origami) could be used to combine the advantages of macroscale and microscale geometrical designs with those of surface nanopatterns. Given the fact that surface nanopatterning techniques work only on flat surfaces and that access to the entire surface area is required, it is imperative that the fabrication of meta-biomaterials should start from a flat state. Once the surface nanopatterns are applied, a self-folding mechanism should be triggered to achieve the shape-shifting required for transforming the geometry of meta-biomaterials to the desired three-dimensional lattice. In order for this approach to work, we need to overcome two major challenges. First, we need to develop a folding strategy including the crease patterns and a folding sequence to enable going from a flat state to a complex three-dimensional lattice shape. Second, there is a need for a self-folding mechanism to make this shape-shifting possible in practice. We will discuss both of those aspects in the following sub-sections of this section.5.1. Folding strategies and foldability
One of the most fundamental questions regarding the origami-based approach is whether it is possible to fold the three-dimensional lattice structures required for the geometrical design of meta-biomaterials from a flat state.103 This fundamental question needs to be answered separately for beam-based and sheet-based lattice structures, as these two types of geometries could be fundamentally different.It is important to realize that the development of folding strategies is much more complex for the practical applications of origami as compared to traditional origami. That is because, in the practical applications of origami, the panels that need to be folded have a finite thickness as compared to the negligible thickness of paper in traditional origami. That finite thickness needs to be accommodated during the folding process. Moreover, locking mechanisms need to be designed within the folding panels such that the folded panels lock into each other, thereby affording increased mechanical properties to the folded structures. These challenges should not only be considered for the design of the crease patterns and folding sequences, but have also consequences for the self-folding mechanisms that will be discussed later in section 5.2.
As far as beam-based lattice structures are concerned, a recent study has shown that it is possible to fold a wide range of lattice structures from a flat state using three distinct folding strategies (e.g., see Fig. 6a).104 Depending on the type of the unit cell based on which the lattice structure is made, one of those three types of folding strategies needs to be used. Using the proposed strategies, it is possible to fold a variety of meta-biomaterials with different types of materials properties including auxetic meta-biomaterials that are based on re-entrant unit cells.
 | ||
| Fig. 6 (a) The folding of a cellular structure from a flat state. Three different folding strategies are proposed for the different types of unit cells.104 (b) The lattice structures based on triply periodic minimal surfaces have a mean surface curvature of zero and belong to the realm of hyperbolic geometry.116 (c) The folding of lattice structures based on triply periodic minimal surfaces from a flat state.116 (d) Frames incorporating joints combined with a pre-stretched sheet are used to fold the patches making up the minimal surfaces from a flat state. Micro-computed tomography measurements of the surface curvature confirm the near-zero mean curvatures achieved using this approach.116 (e) Joining patches together to create a larger frame allows for the folding of unit cells and lattice structures from a flat state.116 | ||
In the case of sheet-based unit cells that are based on triply periodic minimal surfaces, the problem is more complex. While flat sheets belong to the realm of Euclidean geometry, minimal surface are hyperbolic in nature. There is, therefore, an additional geometrical barrier that needs to be overcome when trying to fold minimal surfaces from a flat state. Given the important feature of triply periodic minimal surfaces (i.e., a mean surface curvature of zero), it is important to be able to fold minimal surfaces from a flat state. Indeed, the fact that surface curvature highly influences tissue regeneration is a relatively recent discovery, which has been gaining more traction within the last few years.105–113 Since the mean surface curvature of trabecular bone is close to zero,64,114 it is often assumed63,115–117 that origami-based meta-biomaterials need to be able to achieve such a surface curvature in order to maximize their potential for enhancing the tissue regeneration performance of orthopedic implants.
A recently proposed folding strategy enables the folding of minimal surfaces from a flat state by incorporating rationally designed joints within a rigid frame, which is covered by a pre-stretched sheet. The pre-stretched sheet drives the frame towards the state of minimum energy, which corresponds to mean surface curvature of (almost) zero. This folding strategy has been applied to a variety of minimal surfaces (Fig. 6b and c) and has been demonstrated to generate actual minimal surface whose mean surface curvature is very close to zero (Fig. 6d and e).116 Using a pre-stretched sheet and the concept of kinematic joints, this approach, enables transforming the shape of the meta-biomaterials from a flat Euclidian state to a complex three-dimensional shape that belongs to the realm of hyperbolic geometry and is suitable for imparting the unusual properties expected from meta-biomaterials.
5.2. Self-folding
The self-folding of lattice structures, which are suitable for the fabrication of meta-biomaterials, from a flat state is a challenging process given several challenges that exist in this regard. First, the self-folding process should be capable of programming (multiple) time delays in the folding sequences so as to realize the complex folding strategies that are required for the folding of multi-storey structures. Second, the applied self-folding mechanisms should be scalable in order to enable the folding of microscale structures. Finally, the self-folding mechanisms should successfully activate the locking mechanisms that are designed for enhancing the mechanical properties of the folded lattices. Multiple approaches have been proposed in the literature to address some or all of the abovementioned challenges.The first proposed approach works on the basis of stored elastic energy, which is released and drives the self-folding of the material from its flat state. This technique has been applied for the self-folding of both beam-based and sheet-based lattices (Fig. 7a and 6d, e).104 The advantage of this approach is that it is relatively easy to implement and does not require specific materials. Moreover, the current implementations of this techniques have been successful in activating the locking mechanisms that are incorporated into the design of lattice structures.104 However, it is very difficult to program sequential shape shifting using this approach. In addition, downscaling this approach to the microscale would be very challenging.
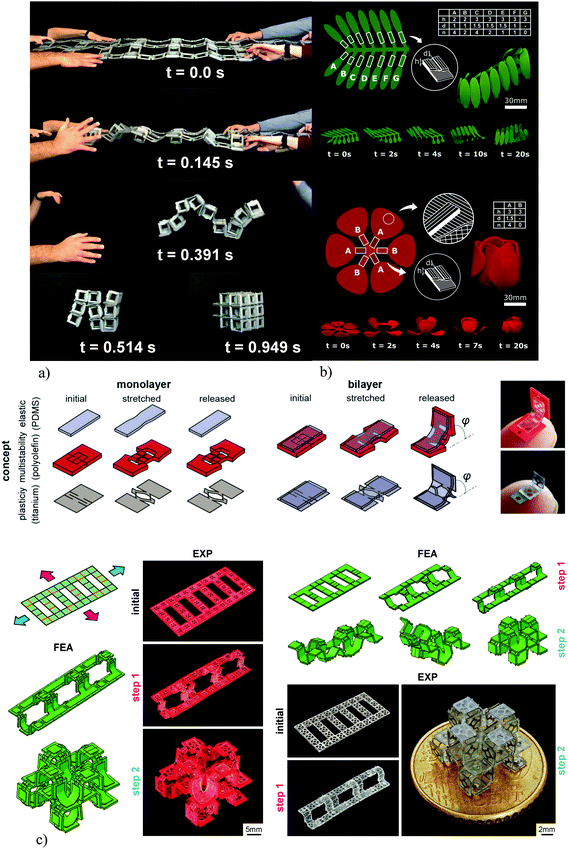 | ||
| Fig. 7 (a) The self-folding behavior of macroscale lattice structures working on the basis of pre-stretched elements.104 (b) The sequential self-folding of initially flat constructs was programmed into the material using FDM 3D printers.118 (c) The mechanical self-folding of origami-based lattice structures. Kirigami can be used to induce instability in flat sheets. When combined with both plastically deforming or elastic materials, these bi-layer constructs exhibit the desired shape-shifting behavior.120 | ||
An alternative approach in which inexpensive 3D printers working on the basis of fused deposition modeling (FDM) and widely available off-the-shelf shape memory polymers (i.e., polylactic acid filaments) were used for the programming of shape shifting in initially flat materials addresses some of the above-mentioned limitations (Fig. 7b).118,119 The shape shifting behavior could be programmed into the fabric of the printed material based on the direction of the printed filaments.118,119 Moreover, such an approach would allow for the programing of complex shape shifting sequences using the concept of material porosity, where porosity adjusts the speed of heat transfer through the printed panels, thereby programming time delays into the shape shifting sequences. Finally, as compared to using elastic energy, it is possible to scale the size of the specimens further down. However, this approach is highly dependent on the type of the material used (i.e., shape memory polymers) and cannot be applied to any material of choice. Moreover, approaching very small dimensions is still challenging, given the limitations of the FDM 3D printing process in terms of the nozzle size.
Mechanical shape shifting could address the limitations of the self-folding approaches that work on the basis of shape memory materials. In this case, the shape shifting behavior is a result of the mechanical instabilities that are developed in the material as a consequence of applying external forces (i.e., compressive or tensile forces). The advantage of mechanical shape shifting is that it is applicable to a wide range of materials. Moreover, the mechanical principles used in this approach are highly scalable, meaning that it is relatively easy to create lattice structures with microscale feature sizes. Programing sequential shape shifting is also possible, as forces can be applied in different directions and with time delays to program the complex shape shifting sequences that are required for the fabrication of multi-storey lattice structures. A recent study120 has combined the concept of kirigami with that origami to create self-folding multi-storey lattice structures at the microscale. The role of kirigami cut patterns is to create local instability when subjected to globally applied tensile forces (Fig. 7c).120 The flat sheets are designed in a multi-layer fashion to give rise to the required out-of-plane deformations (Fig. 7c). To demonstrate its versatility, this approach has been applied to both metallic and polymeric materials without any requirements regarding their chemical compositions and shape memory behavior (Fig. 7d).120
Together, the abovementioned approaches to self-folding origami solve most of the challenges faced when trying to self-fold meta-biomaterials from a flat state. It is, however, important to realize that most of the self-folding techniques proposed to date are only demonstrated to work for a limited number of unit cells. Upscaling those approaches such that any number of unit cells could be manufactured at a reasonable cost and within a manageable time remains a major challenge.
6. Discussion
We reviewed the recently introduced concept of meta-biomaterials that, as opposed to traditional biomaterials, is highly dependent on multiple ideas borrowed from physics, mechanics, and mathematics. Ultimately, however, it is important to assess how meta-biomaterials perform in comparison with the other types of biomaterials.6.1. Evidence of superior performance
Similar to all other emerging concepts, an important question regarding the concept of meta-biomaterials is, ‘why do we think meta-biomaterials hold great promise as future biomaterials?’ The answer to this question is surprisingly simple in the case of meta-biomaterials. Meta-biomaterials and the concept of multi-scale geometrical design enable us to realize biomaterials that exploit already existing action mechanisms. For example, the primary literature from biology, biophysics, biomechanics, and biomaterials communities has already shown that bone-mimicking mechanical and mass transport properties as well as certain types of surface curvature and nanotopography improve tissue regeneration performance of biomaterials and minimize the risk of biomaterial-associated infections. The promise of the meta-biomaterials concept is to use geometrical design and AM to ‘realize’ those properties and design features and to pack them into one single piece of biomaterial. The possibility to incorporate multiple beneficial properties and design features is expected to allow such biomaterials to simultaneously benefit from multiple action mechanisms and any synergistic effects thereof.More concretely, there are different levels of pre-clinical and clinical evidence available to support the superior performance achieved through the geometrical design of meta-biomaterials. In general, the level of evidence is higher for the larger length scales as compared to the smaller ones, partially due to the fact that the research into the geometrical design at the smaller scales has recently started and partially due to the various challenges that are associated with the design and fabrication of meta-biomaterials at the smaller scales and have prevented researchers from stepping towards clinical assessments.
At the macroscale, several clinical studies have already demonstrated the advantages of patient-specific implants.30 The available evidence supporting the superior performance of meta-biomaterials designed at the microscale is quite abundant particularly using in vitro cell culture studies and animal experiments, which both have been widely used for the assessment of the different hypotheses mentioned in section 3.1 regarding the beneficial effects of micro-architectural design in improving the tissue regeneration performance of meta-biomaterials and preventing the risk of implant-associated infections. For example, an animal experiment has shown decreasing the elastic modulus of AM porous metallic biomaterials could lead to enhanced bone tissue regeneration in vivo.121 Moreover, multiple in vitro, ex vivo, and in vivo studies have shown the advantages of the increased surface area and the ample pore space of such biomaterials for the application of surface bio-functionalization techniques and accommodating drug delivery vehicles.41,122–127 Among those studies, some used the surface treatments and drug delivery vehicles for improving the bone tissue regeneration performance of meta-biomaterials,124–126 while others aimed to decrease the risk of implant-associated infections.41,122,123,127
At the nanoscale, there are only a few in vivo studies44 available that clearly show the advantages of surface nanopatterns for improving the bone tissue regeneration performance of meta-biomaterials. As for the bactericidal effects, there are several in vitro studies that have demonstrated the bactericidal effects of surface nanopatterns.41,95,98,123,127–129 However, not much is known regarding the in vivo performance of meta-biomaterials with nanopatterned surfaces in terms of preventing the risk of implant-associated infections.
6.2. Future directions and challenges
Even though there is some evidence supporting the importance of geometrical design at different individual scales, the collective effects of multiple types of geometrical designs at different length scales have not been studied before. It is, therefore, suggested that future studies should study the isolated and modulated effects of geometrical designs at multiple length scales including any potential synergistic behaviors on the bone tissue regeneration performance and the risk of implant-associated infections in orthopedic implants.In addition to the assessment of the biological performance of meta-biomaterials, there are many other aspects regarding their geometrical design and fabrication that require further research as well. In fact, the research into novel geometrical designs of meta-biomaterials has just started. Given that the properties achieved through geometrical design are often unusual and even unprecedented, the space of possible applications for such properties is largely unexplored. For example, auxetic meta-biomaterials could be used to create stress distributions in the bone-implant complex that are otherwise impossible to achieve. This possibility has, thus far, not been extensively explored. It is expected that many other applications in the design of orthopedic implants can be found for auxetic meta-biomaterials. The application of advanced computational models could be particularly useful in this regard.
Previous studies have used computational solid and fluid mechanisms models to predict the mechanical properties and mass transport properties corresponding to various geometrical designs.61,130–135 However, a host of other types of computational models could be also used to inform the geometrical design of meta-biomaterials at different scales. In particular, the theoretical models of bone tissue growth and adaptation136–138 could be used to predict the effects of geometrical design on adjusting the bone tissue regeneration performance of meta-biomaterials. Moreover, more realistic mechanical loading conditions could be obtained using large-scale musculoskeletal models139–143 or at least simpler mass-spring-damper models144–147 that describe the dynamics of the human body movement. More realistic loading conditions can further improve the predictive capability of computational models. Moreover, some refined versions of topology optimization techniques148–154 could be used to more formally define the problem of geometrically designing the meta-biomaterials so as to achieve a specific set of material parameters.
The application of multiple materials in the design of meta-biomaterials has not been explored as well. The availability of multiple materials that could be spatially distributed could lead to new frontiers in terms of achieving unprecedented properties.155–157
In order to expand the scope of research into meta-biomaterials and to address the abovementioned research questions, there are multiple challenges that need to be overcome. Most of those challenges can be categorized as being either manufacturing-related or design-related. In terms of manufacturing, bridging the various length scales that are relevant for the fabrication of meta-biomaterials remains challenging. Moreover, a lot of progress needs to be made regarding the nanoscale fabrication of nanopatterned surfaces. The currently available techniques such as 2PP and EBID are relatively slow, which is why it is important to combine them with such techniques as step and repeat nanoimprinting to enlarge the surface areas that could be covered with the nanopatterns. As for the self-folding behavior, while the currently available techniques meet the basic requirements for the fabrication of meta-biomaterials, there is still a need for achieving smaller dimensions, improved controllability, and enhanced mechanical properties to streamline the preclinical and clinical evaluations of meta-biomaterials. The design-related challenges are also numerous. In particular, it is often not clear what exact geometries would give rise to an arbitrary set of desired properties. Given the fact that the targeted properties are multi-physics in nature, multi-physics computational models are needed to establish the relationship between geometrical designs and the resulting properties of meta-biomaterials. In addition to multiple types of physics (e.g., mechanical and mass transport models), theoretical models of cellular behavior, the dynamics of tissue adaptation, and the collective behavior of cells and bacteria are required to better predict the effects of various geometrical designs on the transient processes of bone tissue regeneration and biofilm formation. These types of multi-physics, multi-domain models are, however, rare and often need to be developed from ground up and corroborated against available experimental data. Addressing these important challenges are expected to define the research into meta-biomaterials for years to come.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research has received funding from the European Research Council under the ERC grant agreement no. [677575].References
- J. T. Overvelde, J. C. Weaver, C. Hoberman and K. Bertoldi, Rational design of reconfigurable prismatic architected materials, Nature, 2017, 541(7637), 347 CrossRef CAS.
- S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, 3D soft metamaterials with negative Poisson's ratio, Adv. Mater., 2013, 25(36), 5044–5049 CrossRef CAS.
- J. Berger, H. Wadley and R. McMeeking, Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness, Nature, 2017, 543(7646), 533 CrossRef CAS.
- K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke, Flexible mechanical metamaterials, Nat. Rev. Mater., 2017, 2(11), 17066 CrossRef CAS.
- Y. Chen, T. Li, F. Scarpa and L. Wang, Lattice metamaterials with mechanically tunable Poisson's ratio for vibration control, Phys. Rev. Appl., 2017, 7(2), 024012 CrossRef.
- J. Christensen, M. Kadic, O. Kraft and M. Wegener, Vibrant times for mechanical metamaterials, MRS Commun., 2015, 5(3), 453–462 CrossRef CAS.
- B. Florijn, C. Coulais and M. van Hecke, Programmable mechanical metamaterials, Phys. Rev. Lett., 2014, 113(17), 175503 CrossRef.
- T. A. Hewage, K. L. Alderson, A. Alderson and F. Scarpa, Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative poisson's ratio properties, Adv. Mater., 2016, 28(46), 10323–10332 CrossRef CAS.
- H. Chen and C. Chan, Acoustic cloaking in three dimensions using acoustic metamaterials, Appl. Phys. Lett., 2007, 91(18), 183518 CrossRef.
- S. A. Cummer, J. Christensen and A. Alù, Controlling sound with acoustic metamaterials, Nat. Rev. Mater., 2016, 1(3), 16001 CrossRef.
- J. Mei, G. Ma, M. Yang, Z. Yang, W. Wen and P. Sheng, Dark acoustic metamaterials as super absorbers for low-frequency sound, Nat. Commun., 2012, 3, 756 CrossRef.
- L. Zigoneanu, B.-I. Popa and S. A. Cummer, Three-dimensional broadband omnidirectional acoustic ground cloak, Nat. Mater., 2014, 13(4), 352 CrossRef CAS.
- K. Fan and W. J. Padilla, Dynamic electromagnetic metamaterials, Mater. Today, 2015, 18(1), 39–50 CrossRef CAS.
- A. J. Hoffman, L. Alekseyev, S. S. Howard, K. J. Franz, D. Wasserman, V. A. Podolskiy, E. E. Narimanov, D. L. Sivco and C. Gmachl, Negative refraction in semiconductor metamaterials, Nat. Mater., 2007, 6(12), 946 CrossRef CAS PubMed.
- D. Schurig, J. Mock, B. Justice, S. A. Cummer, J. B. Pendry, A. Starr and D. R. Smith, Metamaterial electromagnetic cloak at microwave frequencies, Science, 2006, 314(5801), 977–980 CrossRef CAS.
- C. M. Watts, X. Liu and W. J. Padilla, Metamaterial electromagnetic wave absorbers, Adv. Mater., 2012, 24(23), OP98–OP120 CAS.
- R. Gatt, M. V. Wood, A. Gatt, F. Zarb, C. Formosa, K. M. Azzopardi, A. Casha, T. P. Agius, P. Schembri-Wismayer and L. Attard, Negative Poisson's ratios in tendons: an unexpected mechanical response, Acta Biomater., 2015, 24, 201–208 CrossRef.
- F. Barthelat, H. Tang, P. Zavattieri, C.-M. Li and H. D. Espinosa, On the mechanics of mother-of-pearl: a key feature in the material hierarchical structure, J. Mech. Phys. Solids, 2007, 55(2), 306–337 CrossRef CAS.
- Y. Shao, H.-P. Zhao, X.-Q. Feng and H. Gao, Discontinuous crack-bridging model for fracture toughness analysis of nacre, J. Mech. Phys. Solids, 2012, 60(8), 1400–1419 CrossRef.
- H. Tang, F. Barthelat and H. D. Espinosa, An elasto-viscoplastic interface model for investigating the constitutive behavior of nacre, J. Mech. Phys. Solids, 2007, 55(7), 1410–1438 CrossRef CAS.
- G. M. Genin and S. Thomopoulos, The tendon-to-bone attachment: Unification through disarray, Nat. Mater., 2017, 16(6), 607 CrossRef CAS.
- L. Rossetti, L. Kuntz, E. Kunold, J. Schock, K. Müller, H. Grabmayr, J. Stolberg-Stolberg, F. Pfeiffer, S. Sieber and R. Burgkart, The microstructure and micromechanics of the tendon–bone insertion, Nat. Mater., 2017, 16(6), 664 CrossRef CAS.
- P. Fratzl and R. Weinkamer, Nature's hierarchical materials, Prog. Mater. Sci., 2007, 52(8), 1263–1334 CrossRef CAS.
- Z. Liu, M. A. Meyers, Z. Zhang and R. O. Ritchie, Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications, Prog. Mater. Sci., 2017, 88, 467–498 CrossRef CAS.
- Y. Tang, G. Lin, L. Han, S. Qiu, S. Yang and J. Yin, Design of hierarchically cut hinges for highly stretchable and reconfigurable metamaterials with enhanced strength, Adv. Mater., 2015, 27(44), 7181–7190 CrossRef CAS.
- X. Zheng, W. Smith, J. Jackson, B. Moran, H. Cui, D. Chen, J. Ye, N. Fang, N. Rodriguez and T. Weisgraber, Multiscale metallic metamaterials, Nat. Mater., 2016, 15(10), 1100 CrossRef CAS.
- D. Rayneau-Kirkhope, Stiff auxetics: Hierarchy as a route to stiff, strong lattice based auxetic meta-materials, Sci. Rep., 2018, 8(1), 12437 CrossRef CAS.
- N. Sarkalkan, H. Weinans and A. A. Zadpoor, Statistical shape and appearance models of bones, Bone, 2014, 60, 129–140 CrossRef.
- D. Wagner, L. Kamer, P. M. Rommens, T. Sawaguchi, R. G. Richards and H. Noser, 3D statistical modeling techniques to investigate the anatomy of the sacrum, its bone mass distribution, and the trans-sacral corridors, J. Orthop. Res., 2014, 32(11), 1543–1548 CrossRef.
- P. Tack, J. Victor, P. Gemmel and L. Annemans, 3D-printing techniques in a medical setting: a systematic literature review, Biomed. Eng. Online, 2016, 15(1), 115 CrossRef PubMed.
- M. Azaouzi, A. Makradi and S. Belouettar, Deployment of a self-expanding stent inside an artery: a finite element analysis, Mater. Des., 2012, 41, 410–420 CrossRef CAS.
- D. Stoeckel, A. Pelton and T. Duerig, Self-expanding nitinol stents: material and design considerations, Eur. Radiol., 2004, 14(2), 292–301 CrossRef.
- H. Fu, K. Nan, W. Bai, W. Huang, K. Bai, L. Lu, C. Zhou, Y. Liu, F. Liu and J. Wang, Morphable 3D mesostructures and microelectronic devices by multistable buckling mechanics, Nat. Mater., 2018, 17(3), 268 CrossRef CAS.
- B. Haghpanah, L. Salari-Sharif, P. Pourrajab, J. Hopkins and L. Valdevit, Multistable shape-reconfigurable architected materials, Adv. Mater., 2016, 28(36), 7915–7920 CrossRef CAS.
- S. Shan, S. H. Kang, J. R. Raney, P. Wang, L. Fang, F. Candido, J. A. Lewis and K. Bertoldi, Multistable architected materials for trapping elastic strain energy, Adv. Mater., 2015, 27(29), 4296–4301 CrossRef CAS.
- S. Waitukaitis, R. Menaut, B. G.-g. Chen and M. van Hecke, Origami multistability: From single vertices to metasheets, Phys. Rev. Lett., 2015, 114(5), 055503 CrossRef.
- Y. Yang, M. A. Dias and D. P. Holmes, Multistable kirigami for tunable architected materials, Phys. Rev. Mater., 2018, 2(11), 110601 CrossRef CAS.
- F. S. L. Bobbert, S. Janbaz and A. A. Zadpoor, Towards deployable meta-implants, J. Mater. Chem. B, 2018, 6(21), 3449–3455 RSC.
- S. Garfin and C. Bono, Kyphoplasty and Vertebroplasty for the Treatment of Painful Osteoporotic Vertebral Compression Fractures, Advances in Spinal Fusion, CRC Press, 2003, pp. 43–60 Search PubMed.
- S. Leeflang, S. Janbaz and A. A. Zadpoor, Metallic clay, Addit. Manuf., 2019, 28, 528–534 CrossRef CAS.
- S. Amin Yavari, L. Loozen, F. L. Paganelli, S. Bakhshandeh, K. Lietaert, J. A. Groot, A. C. Fluit, C. Boel, J. Alblas and H. C. Vogely, Antibacterial behavior of additively manufactured porous titanium with nanotubular surfaces releasing silver ions, ACS Appl. Mater. Interfaces, 2016, 8(27), 17080–17089 CrossRef CAS.
- S. A. Yavari, S. Ahmadi, J. van der Stok, R. Wauthlé, A. Riemslag, M. Janssen, J. Schrooten, H. Weinans and A. A. Zadpoor, Effects of bio-functionalizing surface treatments on the mechanical behavior of open porous titanium biomaterials, J. Mech. Behav. Biomed. Mater., 2014, 36, 109–119 CrossRef.
- S. A. Yavari, Y. C. Chai, A. J. Böttger, R. Wauthle, J. Schrooten, H. Weinans and A. A. Zadpoor, Effects of anodizing parameters and heat treatment on nanotopographical features, bioactivity, and cell culture response of additively manufactured porous titanium, Mater. Sci. Eng., C, 2015, 51, 132–138 CrossRef PubMed.
- S. A. Yavari, J. van der Stok, Y. C. Chai, R. Wauthle, Z. T. Birgani, P. Habibovic, M. Mulier, J. Schrooten, H. Weinans and A. A. Zadpoor, Bone regeneration performance of surface-treated porous titanium, Biomaterials, 2014, 35(24), 6172–6181 CrossRef.
- S. A. Yavari, R. Wauthlé, A. J. Böttger, J. Schrooten, H. Weinans and A. A. Zadpoor, Crystal structure and nanotopographical features on the surface of heat-treated and anodized porous titanium biomaterials produced using selective laser melting, Appl. Surf. Sci., 2014, 290, 287–294 CrossRef.
- A. A. Zadpoor, Mechanical performance of additively manufactured meta-biomaterials, Acta Biomater., 2019, 85, 41–59 CrossRef CAS.
- A. A. Zadpoor, Additively manufactured porous metallic biomaterials, J. Mater. Chem. B, 2019, 7, 4088–4117 RSC.
- R. Hedayati, S. Ahmadi, K. Lietaert, B. Pouran, Y. Li, H. Weinans, C. Rans and A. Zadpoor, Isolated and modulated effects of topology and material type on the mechanical properties of additively manufactured porous biomaterials, J. Mech. Behav. Biomed. Mater., 2018, 79, 254–263 CrossRef CAS.
- R. Hedayati, S. Janbaz, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, How does tissue regeneration influence the mechanical behavior of additively manufactured porous biomaterials?, J. Mech. Behav. Biomed. Mater., 2017, 65, 831–841 CrossRef CAS.
- R. Hedayati, M. Sadighi, M. Mohammadi Aghdam and A. A. Zadpoor, Mechanical properties of additively manufactured thick honeycombs, Materials, 2016, 9(8), 613 CrossRef.
- A. A. Zadpoor, Mechanics of additively manufactured biomaterials, J. Mech. Behav. Biomed. Mater., 2017, 70, 1–6 CrossRef CAS.
- A. A. Zadpoor and R. Hedayati, Analytical relationships for prediction of the mechanical properties of additively manufactured porous biomaterials, J. Biomed. Mater. Res., Part A, 2016, 104(12), 3164–3174 CrossRef CAS.
- S. Ahmadi, R. Hedayati, Y. Li, K. Lietaert, N. Tümer, A. Fatemi, C. Rans, B. Pouran, H. Weinans and A. Zadpoor, Fatigue performance of additively manufactured meta-biomaterials: The effects of topology and material type, Acta Biomater., 2018, 65, 292–304 CrossRef CAS.
- S. Ahmadi, R. Kumar, E. Borisov, R. Petrov, S. Leeflang, Y. Li, N. Tümer, R. Huizenga, C. Ayas and A. Zadpoor, From microstructural design to surface engineering: A tailored approach for improving fatigue life of additively manufactured meta-biomaterials, Acta Biomater., 2019, 83, 153–166 CrossRef CAS.
- M. Dallago, V. Fontanari, E. Torresani, M. Leoni, C. Pederzolli, C. Potrich and M. Benedetti, Fatigue and biological properties of Ti-6Al-4V ELI cellular structures with variously arranged cubic cells made by selective laser melting, J. Mech. Behav. Biomed. Mater., 2018, 78, 381–394 CrossRef CAS.
- R. Hedayati, H. Hosseini-Toudeshky, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Computational prediction of the fatigue behavior of additively manufactured porous metallic biomaterials, Int. J. Fatigue, 2016, 84, 67–79 CrossRef CAS.
- F. Li, J. Li, H. Kou and L. Zhou, Porous Ti6Al4V alloys with enhanced normalized fatigue strength for biomedical applications, Mater. Sci. Eng., C, 2016, 60, 485–488 CrossRef CAS PubMed.
- K. Lietaert, A. Cutolo, D. Boey and B. Van Hooreweder, Fatigue life of additively manufactured Ti6Al4V scaffolds under tension-tension, tension-compression and compression-compression fatigue load, Sci. Rep., 2018, 8(1), 4957 CrossRef.
- B. Van Hooreweder, Y. Apers, K. Lietaert and J.-P. Kruth, Improving the fatigue performance of porous metallic biomaterials produced by Selective Laser Melting, Acta Biomater., 2017, 47, 193–202 CrossRef CAS.
- S. A. Yavari, S. Ahmadi, R. Wauthle, B. Pouran, J. Schrooten, H. Weinans and A. Zadpoor, Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials, J. Mech. Behav. Biomed. Mater., 2015, 43, 91–100 CrossRef PubMed.
- S. Truscello, G. Kerckhofs, S. Van Bael, G. Pyka, J. Schrooten and H. Van Oosterwyck, Prediction of permeability of regular scaffolds for skeletal tissue engineering: a combined computational and experimental study, Acta Biomater., 2012, 8(4), 1648–1658 CrossRef CAS.
- X.-Y. Zhang, G. Fang, S. Leeflang, A. A. Zadpoor and J. Zhou, Topological design, permeability and mechanical behavior of additively manufactured functionally graded porous metallic biomaterials, Acta Biomater., 2019, 84, 437–452 CrossRef CAS.
- F. Bobbert, K. Lietaert, A. A. Eftekhari, B. Pouran, S. Ahmadi, H. Weinans and A. Zadpoor, Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties, Acta Biomater., 2017, 53, 572–584 CrossRef CAS.
- H. Jinnai, Y. Nishikawa, M. Ito, S. D. Smith, D. A. Agard and R. J. Spontak, Topological similarity of sponge-like bicontinuous morphologies differing in length scale, Adv. Mater., 2002, 14(22), 1615–1618 CrossRef CAS.
- R. Hedayati, A. Leeflang and A. Zadpoor, Additively manufactured metallic pentamode meta-materials, Appl. Phys. Lett., 2017, 110(9), 091905 CrossRef.
- G. W. Milton and A. V. Cherkaev, Which elasticity tensors are realizable?, J. Eng. Mater. Technol., 1995, 117(4), 483–493 CrossRef.
- M. Kadic, T. Bückmann, N. Stenger, M. Thiel and M. Wegener, On the practicability of pentamode mechanical metamaterials, Appl. Phys. Lett., 2012, 100(19), 191901 CrossRef.
- M. Kadic, T. Bückmann, R. Schittny, P. Gumbsch and M. Wegener, Pentamode metamaterials with independently tailored bulk modulus and mass density, Phys. Rev. Appl., 2014, 2(5), 054007 CrossRef.
- S. J. Hollister, Porous scaffold design for tissue engineering, Nat. Mater., 2005, 4(7), 518 CrossRef CAS.
- D. A. Shimko, V. F. Shimko, E. A. Sander, K. F. Dickson and E. A. Nauman, Effect of porosity on the fluid flow characteristics and mechanical properties of tantalum scaffolds, J. Biomed. Mater. Res., Part B, 2005, 73(2), 315–324 CrossRef.
- Z. Hashin and S. Shtrikman, A variational approach to the theory of the elastic behaviour of multiphase materials, J. Mech. Phys. Solids, 1963, 11(2), 127–140 CrossRef.
- K. E. Evans and A. Alderson, Auxetic materials: functional materials and structures from lateral thinking!, Adv. Mater., 2000, 12(9), 617–628 CrossRef CAS.
- H. M. Kolken and A. Zadpoor, Auxetic mechanical metamaterials, RSC Adv., 2017, 7(9), 5111–5129 RSC.
- K. Wang, Y.-H. Chang, Y. Chen, C. Zhang and B. Wang, Designable dual-material auxetic metamaterials using three-dimensional printing, Mater. Des., 2015, 67, 159–164 CrossRef.
- S. Mohsenizadeh, R. Alipour, M. S. Rad, A. F. Nejad and Z. Ahmad, Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading, Mater. Des., 2015, 88, 258–268 CrossRef.
- J. Gallo, M. Slouf and S. B. Goodman, The relationship of polyethylene wear to particle size, distribution, and number: A possible factor explaining the risk of osteolysis after hip arthroplasty, J. Biomed. Mater. Res., Part B, 2010, 94(1), 171–177 Search PubMed.
- K. Genovese, S. Leeflang and A. A. Zadpoor, Microscopic full-field three-dimensional strain measurement during the mechanical testing of additively manufactured porous biomaterials, J. Mech. Behav. Biomed. Mater., 2017, 69, 327–341 CrossRef CAS.
- L. Grassi, S. P. Väänänen, S. A. Yavari, H. Weinans, J. S. Jurvelin, A. A. Zadpoor and H. Isaksson, Experimental validation of finite element model for proximal composite femur using optical measurements, J. Mech. Behav. Biomed. Mater., 2013, 21, 86–94 CrossRef.
- H. M. Kolken, S. Janbaz, S. M. Leeflang, K. Lietaert, H. H. Weinans and A. A. Zadpoor, Rationally designed meta-implants: a combination of auxetic and conventional meta-biomaterials, Mater. Horiz., 2018, 5(1), 28–35 RSC.
- Y. Li, J. Zhou, P. Pavanram, M. Leeflang, L. Fockaert, B. Pouran, N. Tümer, K.-U. Schröder, J. Mol, H. Weinans, H. Jahr and A. A. Zadpoor, Additively manufactured biodegradable porous magnesium, Acta Biomater., 2018, 67, 378–392 CrossRef CAS PubMed.
- Y. Li, H. Jahr, K. Lietaert, P. Pavanram, A. Yilmaz, L. Fockaert, M. Leeflang, B. Pouran, Y. Gonzalez-Garcia, H. Weinans, J. Mol, J. Zhou and A. A. Zadpoor, Additively manufactured biodegradable porous iron, Acta Biomater., 2018, 77, 380–393 CrossRef CAS.
- P. Wen, Y. Qin, Y. Chen, M. Voshage, L. Jauer, R. Poprawe and J. H. Schleifenbaum, Laser additive manufacturing of Zn porous scaffolds: Shielding gas flow, surface quality and densification, J. Mater. Sci. Technol., 2019, 35(2), 368–376 CrossRef.
- Y. Li, H. Jahr, P. Pavanram, F. Bobbert, U. Puggi, X. Zhang, M. Leeflang, H. Weinans and J. ZhouZadpoor, Additively manufactured functionally graded biodegradable porous iron, Acta Biomater., 2019, 96, 646–661 CrossRef CAS.
- D. E. Discher, P. Janmey and Y.-l. Wang, Tissue cells feel and respond to the stiffness of their substrate, Science, 2005, 310(5751), 1139–1143 CrossRef CAS.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Matrix elasticity directs stem cell lineage specification, Cell, 2006, 126(4), 677–689 CrossRef CAS.
- B. Geiger, J. P. Spatz and A. D. Bershadsky, Environmental sensing through focal adhesions, Nat. Rev. Mol. Cell Biol., 2009, 10(1), 21 CrossRef CAS.
- F. Guilak, D. M. Cohen, B. T. Estes, J. M. Gimble, W. Liedtke and C. S. Chen, Control of stem cell fate by physical interactions with the extracellular matrix, Cell Stem Cell, 2009, 5(1), 17–26 CrossRef CAS.
- A. Higuchi, Q.-D. Ling, Y. Chang, S.-T. Hsu and A. Umezawa, Physical cues of biomaterials guide stem cell differentiation fate, Chem. Rev., 2013, 113(5), 3297–3328 CrossRef CAS.
- Z. Chen, A. Bachhuka, F. Wei, X. Wang, G. Liu, K. Vasilev and Y. Xiao, Nanotopography-based strategy for the precise manipulation of osteoimmunomodulation in bone regeneration, Nanoscale, 2017, 9(46), 18129–18152 RSC.
- M. J. Dalby, N. Gadegaard and R. O. Oreffo, Harnessing nanotopography and integrin–matrix interactions to influence stem cell fate, Nat. Mater., 2014, 13(6), 558 CrossRef CAS.
- S. Dobbenga, L. E. Fratila-Apachitei and A. A. Zadpoor, Nanopattern-induced osteogenic differentiation of stem cells–A systematic review, Acta Biomater., 2016, 46, 3–14 CrossRef CAS.
- K. Nune, R. Misra, X. Gai, S. Li and Y. Hao, Surface nanotopography-induced favorable modulation of bioactivity and osteoconductive potential of anodized 3D printed Ti-6Al-4V alloy mesh structure, J. Biomater. Appl., 2018, 32(8), 1032–1048 CrossRef CAS PubMed.
- B. K. K. Teo, S. T. Wong, C. K. Lim, T. Y. Kung, C. H. Yap, Y. Ramagopal, L. H. Romer and E. K. Yim, Nanotopography modulates mechanotransduction of stem cells and induces differentiation through focal adhesion kinase, ACS Nano, 2013, 7(6), 4785–4798 CrossRef CAS.
- E. K. Yim, E. M. Darling, K. Kulangara, F. Guilak and K. W. Leong, Nanotopography-induced changes in focal adhesions, cytoskeletal organization, and mechanical properties of human mesenchymal stem cells, Biomaterials, 2010, 31(6), 1299–1306 CrossRef CAS.
- M. Ganjian, K. Modaresifar, M. R. Ligeon, L. B. Kunkels, N. Tümer, L. Angeloni, C. W. Hagen, L. G. Otten, P. L. Hagedoorn and I. Apachitei, Nature Helps: Toward Bioinspired Bactericidal Nanopatterns, Adv. Mater. Interfaces, 2019, 6, 1900640 CrossRef.
- A. Elbourne, R. J. Crawford and E. P. Ivanova, Nano-structured antimicrobial surfaces: From nature to synthetic analogues, J. Colloid Interface Sci., 2017, 508, 603–616 CrossRef CAS PubMed.
- K. Modaresifar, S. Azizian, M. Ganjian, L. E. Fratila-Apachitei and A. A. Zadpoor, Bactericidal effects of nanopatterns: A systematic review, Acta Biomater., 2018, 83, 29–36 CrossRef.
- D. S. Widyaratih, P.-L. Hagedoorn, L. G. Otten, M. Ganjian, N. Tümer, I. Apachitei, C. W. Hagen, L. E. Fratila-Apachitei and A. A. Zadpoor, Towards osteogenic and bactericidal nanopatterns?, Nanotechnology, 2019, 30(20), 20LT01 CrossRef CAS.
- M. Mirzaali, I. Van Dongen, N. Tümer, H. Weinans, S. A. Yavari and A. Zadpoor, In-silico quest for bactericidal but non-cytotoxic nanopatterns, Nanotechnology, 2018, 29(43), 43LT02 CrossRef CAS.
- K. S. Lee, D. Y. Yang, S. H. Park and R. H. Kim, Recent developments in the use of two-photon polymerization in precise 2D and 3D microfabrications, Polym. Adv. Technol., 2006, 17(2), 72–82 CrossRef CAS.
- W. Van Dorp and C. W. Hagen, A critical literature review of focused electron beam induced deposition, J. Appl. Phys., 2008, 104(8), 10 CrossRef.
- C. Hammann, C. T. H. Heerkens, C. Hagen, A. Zadpoor and L. Fratila-Apachitei, Direct submicron patterning of titanium for bone implants, Microelectron. Eng., 2018, 195, 13–20 CrossRef CAS.
- S. J. Callens and A. A. Zadpoor, From flat sheets to curved geometries: Origami and kirigami approaches, Mater. Today, 2018, 21(3), 241–264 CrossRef.
- S. Janbaz, N. Noordzij, D. S. Widyaratih, C. W. Hagen, L. E. Fratila-Apachitei and A. A. Zadpoor, Origami lattices with free-form surface ornaments, Sci. Adv., 2017, 3(11), eaao1595 CrossRef.
- N. D. Bade, R. D. Kamien, R. K. Assoian and K. J. Stebe, Curvature and Rho activation differentially control the alignment of cells and stress fibers, Sci. Adv., 2017, 3(9), e1700150 CrossRef.
- N. D. Bade, T. Xu, R. D. Kamien, R. K. Assoian and K. J. Stebe, Gaussian Curvature Directs Stress Fiber Orientation and Cell Migration, Biophys. J., 2018, 114(6), 1467–1476 CrossRef CAS.
- C. M. Bidan, K. P. Kommareddy, M. Rumpler, P. Kollmannsberger, Y. J. Bréchet, P. Fratzl and J. W. Dunlop, How linear tension converts to curvature: geometric control of bone tissue growth, PLoS One, 2012, 7(5), e36336 CrossRef CAS.
- R. M. Gouveia, E. Koudouna, J. Jester, F. Figueiredo and C. J. Connon, Template curvature influences cell alignment to create improved human corneal tissue equivalents, Adv. Biosyst., 2017, 1(12), 1700135 CrossRef.
- L. Pieuchot, J. Marteau, A. Guignandon, T. Dos Santos, I. Brigaud, P.-F. Chauvy, T. Cloatre, A. Ponche, T. Petithory and P. Rougerie, Curvotaxis directs cell migration through cell-scale curvature landscapes, Nat. Commun., 2018, 9(1), 3995 CrossRef.
- M. Rumpler, A. Woesz, J. W. Dunlop, J. T. van Dongen and P. Fratzl, The effect of geometry on three-dimensional tissue growth, J. R. Soc., Interface, 2008, 5(27), 1173–1180 CrossRef.
- J. R. Vetsch, R. Müller and S. Hofmann, The influence of curvature on three-dimensional mineralized matrix formation under static and perfused conditions: an in vitro bioreactor model, J. R. Soc., Interface, 2016, 13(123), 20160425 CrossRef.
- M. Werner, S. B. Blanquer, S. P. Haimi, G. Korus, J. W. Dunlop, G. N. Duda, D. W. Grijpma and A. Petersen, Surface curvature differentially regulates stem cell migration and differentiation via altered attachment morphology and nuclear deformation, Adv. Sci., 2017, 4(2), 1600347 CrossRef.
- M. Werner, N. A. Kurniawan, G. Korus, C. V. Bouten and A. Petersen, Mesoscale substrate curvature overrules nanoscale contact guidance to direct bone marrow stromal cell migration, J. R. Soc., Interface, 2018, 15(145), 20180162 CrossRef.
- H. Jinnai, H. Watashiba, T. Kajihara, Y. Nishikawa, M. Takahashi and M. Ito, Surface curvatures of trabecular bone microarchitecture, Bone, 2002, 30(1), 191–194 CrossRef CAS.
- F. Bobbert and A. Zadpoor, Effects of bone substitute architecture and surface properties on cell response, angiogenesis, and structure of new bone, J. Mater. Chem. B, 2017, 5(31), 6175–6192 RSC.
- S. J. Callens, N. Tümer and A. A. Zadpoor, Hyperbolic origami-inspired folding of triply periodic minimal surface structures, Appl. Mater. Today, 2019, 15, 453–461 CrossRef.
- A. A. Zadpoor, Bone tissue regeneration: the role of scaffold geometry, Biomater. Sci., 2015, 3(2), 231–245 RSC.
- T. Van Manen, S. Janbaz and A. A. Zadpoor, Programming 2D/3D shape-shifting with hobbyist 3D printers, Mater. Horiz., 2017, 4(6), 1064–1069 RSC.
- T. Van Manen, S. Janbaz and A. A. Zadpoor, Programming the shape-shifting of flat soft matter, Mater. Today, 2018, 21, 144–163 CrossRef CAS.
- T. Van Manen, S. Janbaz, M. Ganjian and A. A. Zadpoor, Kirigami-enabled self-folding origami, Mater. Today, 2019 DOI:10.1016/j.mattod.2019.08.001.
- N. Reznikov, O. R. Boughton, S. Ghouse, A. E. Weston, L. Collinson, G. W. Blunn, J. R. Jeffers, J. P. Cobb and M. M. Stevens, Individual response variations in scaffold-guided bone regeneration are determined by independent strain-and injury-induced mechanisms, Biomaterials, 2019, 194, 183–194 CrossRef CAS PubMed.
- S. Bakhshandeh, Z. Gorgin Karaji, K. Lietaert, A. C. Fluit, C. E. Boel, H. C. Vogely, T. Vermonden, W. E. Hennink, H. Weinans and A. A. Zadpoor, Simultaneous Delivery of Multiple Antibacterial Agents from Additively Manufactured Porous Biomaterials to Fully Eradicate Planktonic and Adherent Staphylococcus aureus, ACS Appl. Mater. Interfaces, 2017, 9(31), 25691–25699 CrossRef CAS PubMed.
- M. Croes, S. Bakhshandeh, I. van Hengel, K. Lietaert, K. van Kessel, B. Pouran, B. van der Wal, H. Vogely, W. Van Hecke, A. Fluit, C. E. Boel, J. Albas, A. A. Zadpoor, H. Weinans and S. Amin Yavari, Antibacterial and immunogenic behavior of silver coatings on additively manufactured porous titanium, Acta Biomater., 2018, 81, 315–327 CrossRef CAS.
- Z. Gorgin Karaji, M. Speirs, S. Dadbakhsh, J.-P. Kruth, H. Weinans, A. Zadpoor and S. Amin Yavari, Additively manufactured and surface biofunctionalized porous nitinol, ACS Appl. Mater. Interfaces, 2017, 9(2), 1293–1304 CrossRef CAS.
- J. Van der Stok, M. Koolen, M. De Maat, S. A. Yavari, J. Alblas, P. Patka, J. Verhaar, E. Van Lieshout, A. A. Zadpoor and H. Weinans, Full regeneration of segmental bone defects using porous titanium implants loaded with BMP-2 containing fibrin gels, Eur. Cells Mater., 2015, 2015(29), 141–154 CrossRef.
- J. Van der Stok, H. Wang, S. Amin Yavari, M. Siebelt, M. Sandker, J. H. Waarsing, J. A. Verhaar, H. Jahr, A. A. Zadpoor, S. C. Leeuwenburgh and H. Weinans, Enhanced bone regeneration of cortical segmental bone defects using porous titanium scaffolds incorporated with colloidal gelatin gels for time-and dose-controlled delivery of dual growth factors, Tissue Eng., Part A, 2013, 19(23–24), 2605–2614 CrossRef CAS.
- I. A. Van Hengel, M. Riool, L. E. Fratila-Apachitei, J. Witte-Bouma, E. Farrell, A. A. Zadpoor, S. A. Zaat and I. Apachitei, Selective laser melting porous metallic implants with immobilized silver nanoparticles kill and prevent biofilm formation by methicillin-resistant Staphylococcus aureus, Biomaterials, 2017, 140, 1–15 CrossRef CAS.
- C. D. Bandara, S. Singh, I. O. Afara, A. Wolff, T. Tesfamichael, K. Ostrikov and A. Oloyede, Bactericidal effects of natural nanotopography of dragonfly wing on Escherichia coli, ACS Appl. Mater. Interfaces, 2017, 9(8), 6746–6760 CrossRef CAS.
- D. P. Linklater, S. Juodkazis and E. P. Ivanova, Nanofabrication of mechano-bactericidal surfaces, Nanoscale, 2017, 9(43), 16564–16585 RSC.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanical properties of regular porous biomaterials made from truncated cube repeating unit cells: Analytical solutions and computational models, Mater. Sci. Eng., C, 2016, 60, 163–183 CrossRef CAS PubMed.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanics of additively manufactured porous biomaterials based on the rhombicuboctahedron unit cell, J. Mech. Behav. Biomed. Mater., 2016, 53, 272–294 CrossRef CAS.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanical behavior of additively manufactured porous biomaterials made from truncated cuboctahedron unit cells, Int. J. Mech. Sci., 2016, 106, 19–38 CrossRef.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Analytical relationships for the mechanical properties of additively manufactured porous biomaterials based on octahedral unit cells, Appl. Math. Model., 2017, 46, 408–422 CrossRef.
- S. C. Kapfer, S. T. Hyde, K. Mecke, C. H. Arns and G. E. Schröder-Turk, Minimal surface scaffold designs for tissue engineering, Biomaterials, 2011, 32(29), 6875–6882 CrossRef CAS PubMed.
- H. Montazerian, E. Davoodi, M. Asadi-Eydivand, J. Kadkhodapour and M. Solati-Hashjin, Porous scaffold internal architecture design based on minimal surfaces: A compromise between permeability and elastic properties, Mater. Des., 2017, 126, 98–114 CrossRef CAS.
- G. Campoli, H. Weinans and A. A. Zadpoor, Computational load estimation of the femur, J. Mech. Behav. Biomed. Mater., 2012, 10, 108–119 CrossRef.
- P. F. Egan, K. A. Shea and S. J. Ferguson, Simulated tissue growth for 3D printed scaffolds, Biomech. Model. Mechanobiol., 2018, 1–15 Search PubMed.
- A. A. Zadpoor, G. Campoli and H. Weinans, Neural network prediction of load from the morphology of trabecular bone, Appl. Math. Model., 2013, 37(7), 5260–5276 CrossRef.
- E. Montefiori, B. Kalkman, A. Clarke, M. Paggiosi, E. McCloskey and C. Mazzà, A subject-specific musculoskeletal model to estimate joint loading at different walking speeds, Gait Posture, 2018, 66(Suppl. 1), S28 CrossRef.
- F. Azari, N. Arjmand, A. Shirazi-Adl and T. Rahimi-Moghaddam, A combined passive and active musculoskeletal model study to estimate L4-L5 load sharing, J. Biomech., 2018, 70, 157–165 CrossRef CAS.
- D. Cazzola, T. P. Holsgrove, E. Preatoni, H. S. Gill and G. Trewartha, Cervical spine injuries: A whole-body musculoskeletal model for the analysis of spinal loading, PLoS One, 2017, 12(1), e0169329 CrossRef.
- D. L. Crouch, L. Pan, W. Filer, J. W. Stallings and H. Huang, Comparing Surface and Intramuscular Electromyography for Simultaneous and Proportional Control Based on a Musculoskeletal Model: A Pilot Study, IEEE Trans. Neural Syst. Rehabil. Eng., 2018, 26(9), 1735–1744 Search PubMed.
- D. G. Lloyd and T. F. Besier, An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo, J. Biomech., 2003, 36(6), 765–776 CrossRef PubMed.
- A. A. Nikooyan and A. A. Zadpoor, An improved cost function for modeling of muscle activity during running, J. Biomech., 2011, 44(5), 984–987 CrossRef.
- A. A. Nikooyan and A. A. Zadpoor, Effects of muscle fatigue on the ground reaction force and soft-tissue vibrations during running: a model study, IEEE Trans. Biomed. Eng., 2012, 59(3), 797–804 Search PubMed.
- A. A. Zadpoor and A. A. Nikooyan, Modeling muscle activity to study the effects of footwear on the impact forces and vibrations of the human body during running, J. Biomech., 2010, 43(2), 186–193 CrossRef.
- A. A. Zadpoor, A. A. Nikooyan and A. R. Arshi, A model-based parametric study of impact force during running, J. Biomech., 2007, 40(9), 2012–2021 CrossRef PubMed.
- A. Asadpoure and L. Valdevit, Topology optimization of lightweight periodic lattices under simultaneous compressive and shear stiffness constraints, Int. J. Solids Struct., 2015, 60, 1–16 CrossRef.
- L. Cheng, J. Liu, X. Liang and A. C. To, Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design, Comput. Methods Appl. Mech. Eng., 2018, 332, 408–439 CrossRef.
- Y.-H. Kuo, C.-C. Cheng, Y.-S. Lin and C.-H. San, Support structure design in additive manufacturing based on topology optimization, Struct. Multidiscipl. Optim., 2018, 57(1), 183–195 CrossRef.
- H. Li, Z. Luo, L. Gao and P. Walker, Topology optimization for functionally graded cellular composites with metamaterials by level sets, Comput. Methods Appl. Mech. Eng., 2018, 328, 340–364 CrossRef.
- P. Vogiatzis, M. Ma, S. Chen and X. D. Gu, Computational design and additive manufacturing of periodic conformal metasurfaces by synthesizing topology optimization with conformal mapping, Comput. Methods Appl. Mech. Eng., 2018, 328, 477–497 CrossRef.
- Y. Wang, H. Xu and D. Pasini, Multiscale isogeometric topology optimization for lattice materials, Comput. Methods Appl. Mech. Eng., 2017, 316, 568–585 CrossRef.
- W. Zhang, J. Song, J. Zhou, Z. Du, Y. Zhu, Z. Sun and X. Guo, Topology optimization with multiple materials via moving morphable component (MMC) method, Int. J. Numer. Methods Eng., 2018, 113(11), 1653–1675 CrossRef.
- S. Janbaz, F. Bobbert, M. Mirzaali and A. Zadpoor, Ultra-programmable buckling-driven soft cellular mechanisms, Mater. Horiz., 2019, 6, 1138–1147 RSC.
- S. Janbaz, M. McGuinness and A. A. Zadpoor, Multimaterial control of instability in soft mechanical metamaterials, Phys. Rev. Appl., 2018, 9(6), 064013 CrossRef.
- M. Mirzaali, A. Caracciolo, H. Pahlavani, S. Janbaz, L. Vergani and A. Zadpoor, Multi-material 3D printed mechanical metamaterials: Rational design of elastic properties through spatial distribution of hard and soft phases, Appl. Phys. Lett., 2018, 113(24), 241903 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |

