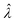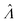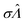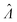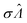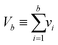Open Access Article
Open Access ArticleGeneral methods for quantitative interpretation of results of digital variable-volume assays†
Toan
Huynh
 ,
Samantha A.
Byrnes
,
Samantha A.
Byrnes
 ,
Tim C.
Chang
,
Bernhard H.
Weigl
,
Tim C.
Chang
,
Bernhard H.
Weigl
 and
Kevin P.
Nichols
and
Kevin P.
Nichols
 *
*
Intellectual Ventures Laboratory, 14360 SE Eastgate Way, Bellevue, WA 98007, USA. E-mail: knichols@intven.com
First published on 24th October 2019
Abstract
In digital assays, devices are typically considered to require precisely controlled volumes since variation in compartment volumes causes biases in concentration estimates. To enable more possibilities in device design, we derived two methods to accurately calculate target concentrations from raw results when the compartment volume may vary and may not follow known parametrically described distributions. The Digital Variable Volume (dvv) method uses volumes of ON compartments (those with positive signals) and the total sample volume, while the Digital Variable Volume Approximation (dvva) method uses the number of ON compartments, the total number of compartments, and a set of separately measured volumes. We verified the trueness of the dvv and dvva methods using simulated assays where volumes followed an empirical distribution (based on measured droplet volumes) and well known distributions with a wide range of standard deviations. We applied both methods to digital PCR experiments with polydisperse volumes, and also derived equations to estimate standard errors and limits of detection. The dvv method allows the compartment volume to follow any distribution in each assay run, the dvva method allows for quantification without in-assay volume measurements, and both methods potentially enable new designs of digital assays.
1. Introduction
In digital assays, targets are partitioned into separate compartments, which are processed to give ON/OFF (positive/negative) signals (usually with amplification) depending on whether the compartments have any or no target entities. Digital assays have been developed to detect various target types (nucleic acids,1–3 proteins,4,5 and cells5,6), and implemented in commercial systems.7,8 These systems require the compartments to have uniform volumes,9 posing a challenge in precise microfabrication and limiting total addressable sample volumes due to the volume limitations of most microfluidic systems. Simple, non-microfluidic, methods to make compartments typically result in widely distributed compartment volumes,10–14 making quantification inaccurate using traditional statistics.15 Herein, we report general statistical methods to quantify results of digital assays with any volume distributions, termed Digital Variable Volume (dvv), and Digital Variable Volume Approximation (dvva).Previously developed methods to infer results of digital assays with polydisperse volumes assume that the compartment volumes follow truncated normal (Gaussian) distributions16 or gamma distributions.17 These methods provide accurate results when the volumes follow the specified distributions, or when the standard deviations are small. However, in systems where compartments are made by a simple method, such as vortexing,13,14 the volume distribution does not have a known analytical form and spans orders of magnitude. A method to account for general volume variation was previously published18 but has not been shown to work with very wide volume distributions (e.g. those of manually made droplets13,14 with standard deviations exceeding a few times the mean). Another method was built upon results for multivolume digital PCR (MVdPCR)19 but with the assumption that the compartment volumes are non-identical, and without the confidence intervals of the estimated concentrations.
We aimed to derive the dvv and dvva methods so that they are compatible with any volume distribution, no matter how wide it is or if it follows any known function. These methods differ in the type of information available due to different experimental setups. The dvv method is applicable when the volumes of ON compartments are measured in each assay run and the total sample volume is known. The dvva method is useful when one knows the number of ON compartments, the total number of compartments, and a set of pre-measured compartment volumes as an estimate of the volume distribution.
In this paper, we describe the derivation of the dvv and dvva methods. We then compare the truness of the dvv and dvva methods to that of some previously published methods,16–18 using both assay results simulated with different volume distributions and experimental results. We also provide trueness maps of those methods and simple approximation methods. We then characterize the precision of dvv and dvva, and provide a simple approximation of the limit of detection.
2. Materials and methods
Mathematical symbols that are generally used throughout the whole paper are defined in Table 1. Some other symbols used only locally are defined where they first appear.2.1. Computation
Calculations and simulations were done using Python (3.6.4) with scipy (1.0.0) and numpy (1.14.1) on a laptop computer.Volumes following the gamma distributions were simulated using the method numpy.random.gamma. The shape was μV2/σV2, and the scale was μV2/σV (σV is volume standard deviation).
Volumes following the lognormal distributions were simulated using the method numpy.random.lognormal. The mean of the underlying normal distribution was 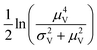 , and the standard deviation of the underlying normal distribution was
, and the standard deviation of the underlying normal distribution was 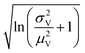 .
.
The simulation of volumes following the truncated normal distributions was limited to those with smaller standard deviations, due to a theoretical upper limit on the coefficient of variation (σV/μV), which we now prove. We can calculate the actual mean (μV) and standard deviation (σV) of a truncated normal distribution defined on (0, ∞) using the underlying mean (μ0) and standard deviation (σ0).20
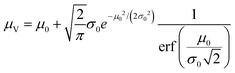 | (1) |
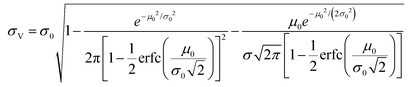 | (2) |
The larger σ0, the larger the coefficient of variation, σV/μV. With erf (0) = 0 and erfc (0) = 1, as σ0 approaches infinity, σV/μV approaches a constant.
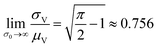 | (3) |
Therefore, random volumes following truncated normal distribution were simulated with a limited range of standard deviations (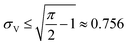 with μV = 1). Volumes following the truncated normal distributions were simulated using the method scipy.stats.truncnorm.rvs. To achieve the desired μV and σV, the mean (μ0) and standard deviation (σV) of the underlying normal distribution were calculated by numerically solving the system of eqn (1) and (2). The parameters for the scipy.stats.truncnorm.rvs method include the lower bound of (0 − μ0)/σ0, upper bound of effectively infinity (numpy.finfo(numpy.float64).max), location of μ0, and scale of σ0.
with μV = 1). Volumes following the truncated normal distributions were simulated using the method scipy.stats.truncnorm.rvs. To achieve the desired μV and σV, the mean (μ0) and standard deviation (σV) of the underlying normal distribution were calculated by numerically solving the system of eqn (1) and (2). The parameters for the scipy.stats.truncnorm.rvs method include the lower bound of (0 − μ0)/σ0, upper bound of effectively infinity (numpy.finfo(numpy.float64).max), location of μ0, and scale of σ0.
Volume simulation was verified by comparing histograms of simulated volumes with the theoretical probability distribution functions (Fig. S1†).
For a compartment with volume vi, at bulk concentration λ, the assay result was simulated via a Poisson random number (with mean of viλ), using the method numpy.random.poisson.
2.2. Generation and characterization of droplets that describe the empirical distribution
The volume values were obtained in the same procedure previously described.13 Droplets were generated by vortexing the aqueous phase and non-aqueous phase together in a 1.5 mL microcentrifuge tube. Samples were thermocycled then transferred to an imaging chamber and characterized using a microscope (20× objective on a Nikon Eclipse Ti2 inverted microscope with epifluorescence illumination and a 14-bit Nikon DS-Qi2 CMOS camera (Nikon Instruments, Melville, NY, USA)). The stability of polydisperse droplets prepared using this same technique was previous demonstrated13 and the stability of the reagents used in this work has been previously noted.21,222.3. Digital PCR experiments
Digital PCR experiments were performed as previously described.14 In each digital PCR experiment, polydisperse droplets were prepared using 100 μL of the PCR reagents (see details below) and 200 μL of BioRad oil/surfactant mixture (BioRad, Hercules, CA, USA). These fluids were vortexed at maximum speed for 30 seconds to create a population of polydisperse droplets with diameters in the range of 1.5 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm. The median diameter was 56 μm and corresponds to 90 pL.
000 μm. The median diameter was 56 μm and corresponds to 90 pL.
DNA targets were amplified using the BioRad Supermix for ddPCR (BioRad, Hercules, CA, USA). Input DNA concentrations were varied from 0.8 to 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 copies per μL. Final primer and probe concentrations were 500 nM and 250 nM, respectively. The assay utilized the targeted the E. coli rodA gene (forward primer [GCAAACCACCTTTGGTCG], reverse primer [CTGTGGGTGTGGATTGACAT], and probe [TexasRed-AACCCCTACAACCGGCAGAATACC-BHQ2]).23 The droplet-based reactions were run in either a C100 or C1000 thermocycler (BioRad, Hercules, CA, USA) using the following protocol: 95 °C for 10 minutes, 40 cycles of 95 °C for 30 seconds and 60 °C for 1 minute.
000 copies per μL. Final primer and probe concentrations were 500 nM and 250 nM, respectively. The assay utilized the targeted the E. coli rodA gene (forward primer [GCAAACCACCTTTGGTCG], reverse primer [CTGTGGGTGTGGATTGACAT], and probe [TexasRed-AACCCCTACAACCGGCAGAATACC-BHQ2]).23 The droplet-based reactions were run in either a C100 or C1000 thermocycler (BioRad, Hercules, CA, USA) using the following protocol: 95 °C for 10 minutes, 40 cycles of 95 °C for 30 seconds and 60 °C for 1 minute.
In each experiment, droplets were imaged in a 100 μm-deep cell counting chamber slide (Countess slide, ThermoFisher C10228) using a Nikon Eclipse Ti2 inverted microscope with epifluorescence illumination and a 14-bit Nikon DS-Qi2 CMOS camera (Nikon Instruments, Melville, NY, USA). Large stitched images were acquired using 26 × 13 individual fluorescence images with a 20× objective, an automated x–y stage, and a 15% overlap. Droplets in the countess slides were focused manually prior to imaging. The Nikon NIS-Elements AR software was used to control the image acquisition.
The MATLAB (Mathworks, Natick, MA, USA) image analysis software was used to automate the quantification of ON droplets in each image. Briefly, images were cropped to remove edges with uneven illumination, converted to a black and white format, and thresholded before ON droplets were identified. The MATLAB Image Processing Toolbox (Mathworks, Natick, MA, USA) was used for droplet size identification and counting of ON droplets. In particular, images were analyzed using the imfindcircles function in the MATLAB Image Processing Toolbox. The size range was set to 2–50, with ObjectPolarity set to bright, Sensitivity set to 0.90–0.95, and EdgeThreshold set to 0.10–0.15. The resulting radii were converted to droplet volumes in pL.
3. Results
3.1. Derivation
For each assay, the bulk concentration needs to be calculated using a certain inference method. The dvv and dvva methods are based on maximum likelihood estimation; the concentration estimate is the one that maximizes the likelihood of observing a certain experimental result. The choice of maximum likelihood estimation was inspired by its use in MVdPCR19 (where each assay utilizes a handful of predetermined, precisely controlled volumes), which has been inspired by limiting dilution assays for microorganism counting.24,25 In particular, an important feature is that results from different volumes are readily combined by way of multiplying the likelihoods. Below, we derive the expressions used to calculate the concentration estimates and the standard errors using the maximum likelihood framework.
The main goal is to calculate the bulk concentration (λ) or its logarithm (Λ). The calculated values (estimators) are denoted as 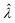 and
and 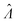 , respectively. All symbols are defined in Table 1.
, respectively. All symbols are defined in Table 1.
We begin by calculating the probability that a particular compartment with turns ON given the volume (v) and bulk concentration (λ) (eqn (4)). It is the same as the probability of having more than one target in the compartment, based on the Poisson distribution with the mean of vλ. This probability is useful in subsequent derivation steps.
 | (4) |
Herein, we operate under the assumption that eqn (4) is correct. Mathematically, the assay in each compartment follows Poisson statistics. In practice, this condition requires the following. First, the target particles are much smaller than the smallest compartment size, so that it is possible for each compartment to have from 0 to a very large number of target particles. Second, the assay in each compartment happens without interference from any other compartment (i.e. no cross-talks, blocking, etc.). Third, the subject (e.g. a pond) has to contain a much larger number of target particles (e.g. bacteria) in comparison to the expected number of targets in a sample (e.g. 1 mL of pond water) (even if the concentration is low), and the distribution of the particles is spatially homogeneous. Fourth, target particles are separate and independent from each other, i.e. the co-occupation of any two particles in the same compartment is due to independent events.
The likelihood l(λ) of observing a certain assay result, i.e. particular numbers of ON and OFF compartments (a and b, respectively) with the associated volumes is the product of individual likelihoods calculated using eqn (4).
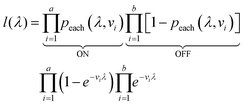 | (5) |
We need to find the λ value that maximizes l(λ). We use the natural logarithm of the concentration (Λ ≡ ln(λ)) and the loglikelihood function (L(Λ) ≡ ln(l(λ))) to conveniently calculate the standard errors and enforce the requirement for positive concentrations. The calculation of the standard error is also more appropriate for Λ than for λ because the distribution of Λ is less skewed.24,25 Therefore, the goal is now finding the Λ value that maximizes L(Λ). The expression for L(Λ) and the first and second derivatives are shown below.
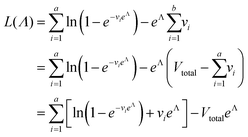 | (6) |
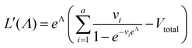 | (7) |
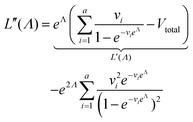 | (8) |
To calculate 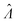 , we can numerically find the root of the first derivative (eqn (7)), i.e. solve the equation below.
, we can numerically find the root of the first derivative (eqn (7)), i.e. solve the equation below.
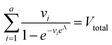 | (9) |
Eqn (9) agrees with the result obtained by using an equation for MVdPCR (eqn (10) in Kreutz et al.19), treating individual compartments as pre-determined compartments in MVdPCR. Although this approach was taken previously with the assumption that none of the volumes are identical,26 the derivation of eqn (9) herein shows that this assumption is mathematically unnecessary.
Plugging L′(Λ) = 0 into eqn (8), we have L′′(Λ) < 0. So the 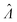 value found using eqn (9) indeed maximizes L(Λ). Also, using the derivatives at
value found using eqn (9) indeed maximizes L(Λ). Also, using the derivatives at 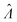 , the standard error of Λ can also be calculated using the observed Fisher information,
, the standard error of Λ can also be calculated using the observed Fisher information, 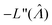 .27
.27
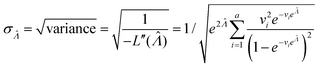 | (10) |
This 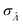 can be used to calculate the confidence interval. Calculating
can be used to calculate the confidence interval. Calculating 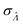 using the expected Fisher information is not feasible because the volume distribution is unknown. In fact, to use the dvv method, the volume distribution is not required and need not be the same from one experiment to another.
using the expected Fisher information is not feasible because the volume distribution is unknown. In fact, to use the dvv method, the volume distribution is not required and need not be the same from one experiment to another.
In general, we can calculate the probability a compartment turns ON using the volume distribution (specified by the probability density function f(v)).
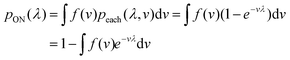 | (11) |
Previously, f(v) has been chosen to follow the gamma distribution17 or truncated normal distribution.16 However, in practice, f(v) may not be described by a simple function. and even when it is, a set of pre-measured volumes still needs to be experimentally obtained to characterize f(v). Therefore, for the dvv a method, a set of separately measured volumes, M ≡ v1, v2, …, vm, is used instead of f(v).
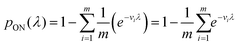 | (12) |
The likelihood function can then be obtained using the binomial distribution (for the case of a ON compartments out of n compartments with the probability of pON(λ)).
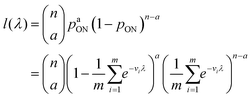 | (13) |
As motivated above, we can calculate the loglikelihood function with the change of variable Λ ≡ ln(λ), and subsequently, its first and second derivatives.
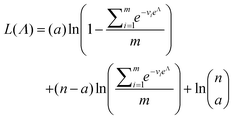 | (14) |
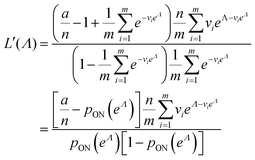 | (15) |
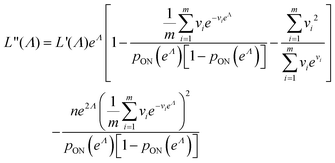 | (16) |
To maximize L(Λ), we can find the root of L′(Λ) (eqn (17)), and verify that it corresponds to a maximum by checking the sign of the second derivative (eqn (18)). An interesting observation is that eqn (17) can also be obtained by using a/n to estimate pON(λ).
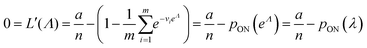 | (17) |
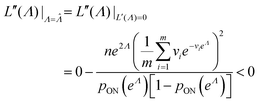 | (18) |
We can then calculate 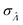 using the expected Fisher information, −〈L′′(Λ)〉.27 The second derivative, L′′(Λ), is a linear function of
using the expected Fisher information, −〈L′′(Λ)〉.27 The second derivative, L′′(Λ), is a linear function of 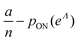 (eqn (16)). We can plug
(eqn (16)). We can plug 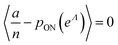 in eqn (15) and plug the subsequent result in eqn (16) to obtain the following expression for
in eqn (15) and plug the subsequent result in eqn (16) to obtain the following expression for 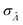 .
.
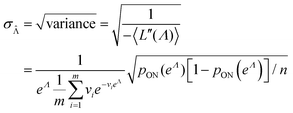 | (19) |
In this particular case, the standard error calculated using the observed Fisher information, 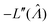 ,27 is also the same as eqn (19) evaluated at
,27 is also the same as eqn (19) evaluated at 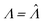 . This can be verified by plugging
. This can be verified by plugging 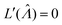 into
into 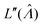 (eqn (16)).
(eqn (16)).
 , we consider the scenario when every compartment has the volume of v. Plugging m = 1 and vi = v in eqn (19) we have
, we consider the scenario when every compartment has the volume of v. Plugging m = 1 and vi = v in eqn (19) we have | (20) |
Using the first and second partial derivatives with respects to Λ, we can calculate the optimal Λ (denoted Λ0) and the minimum  .
.
 | (21) |
 | (22) |
 (or
(or  ). Previously published methods are Nonparametric Volume Modeling18 (volmod), Poisson Plus16 (pp), Poisson Plus Approximation16 (ppa), and Huggett–Cowen–Foy17 (hcf). Quick approximation methods are those using the count (number of ON compartments) (cnt), the arithmetic mean volume (amv), or the geometric mean volumes (gmv). The list of the methods (including dvv and dvva) and the corresponding equations is provided in Table 2.
). Previously published methods are Nonparametric Volume Modeling18 (volmod), Poisson Plus16 (pp), Poisson Plus Approximation16 (ppa), and Huggett–Cowen–Foy17 (hcf). Quick approximation methods are those using the count (number of ON compartments) (cnt), the arithmetic mean volume (amv), or the geometric mean volumes (gmv). The list of the methods (including dvv and dvva) and the corresponding equations is provided in Table 2.
| Method | Input | Equation |
|---|---|---|
| Digital variable volume (dvv) | A, Vtotal |
|
| Digital variable volume | ||
| Approximation (dvva) | a, n, M |
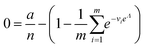
|
| Nonparametric volume | ||
| Modeling18 (volmod) | a, n, M | An iterative process |
| Poisson Plus16 (pp) | a, n, μV, σV |
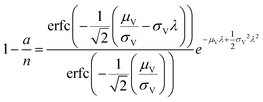
|
| Poisson Plus approximation16 (ppa) | a, n, μV, σV |
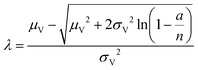
|
| Huggett–Cowen–Foy17 (hcf) | a, n, μV, σV |
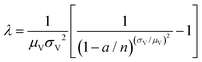
|
| Count (cnt) | a, n |
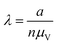
|
| Arithmetic mean volume (amv) | a, n, μV |
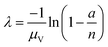
|
| Geometric mean volume (gmv) |
μ
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V V
|
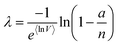
|
3.2. Trueness
We characterized the truness of the methods by applying them to simulated assay results and experimental digital PCR results.14 In particular, the metric is the bias in the natural logarithm of the concentration, which is the difference between the estimators (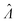 ) obtained by the specified methods and the corresponding known quantities (Λ) set in the simulation or measured by a reference method (in the cases of experimental results).
) obtained by the specified methods and the corresponding known quantities (Λ) set in the simulation or measured by a reference method (in the cases of experimental results).
The standard deviation of the empirical distribution is 1.96. Random volumes following this distribution were simulated using inverse transform sampling.28 The standard deviations of the gamma and lognormal distributions were chosen from 0.01 to 5.01 and included the standard deviation of the empirical distribution (1.96). The gamma, lognormal, and truncated normal (truncated at 0 to ensure volumes are positive) distributions with different standard deviations (in the range of 0.01–5.01) were also used. Eqn (3) also implies that the pp method16 is not compatible with distributions with coefficients of variation larger than such limit.
We compared the trueness of the dvv, dvva, volmod, pp, and hcf methods with volume distributions that have the same standard deviation as that of the empirical distribution of 1.96 (Fig. 1). The truncated normal distributions were not considered due to the limit discussed above (eqn (3)), so only the empirical, gamma, and lognormal distributions were used. The dvv and dvva methods were accurate in the whole range of true Λ and in all distributions. The volmod method underestimated in cases of gamma distributions with larger standard deviations, but were accurate in all other cases (including the empirical and lognormal distributions with large standard deviations). The hcf method was accurate with the gamma distribution as expected (it is based on the gamma distribution). With the lognormal distribution, the hcf method was accurate at lower Λ values only and over-estimated at higher ones. The pp method under-estimated at all concentrations with all distributions. This result is expected because the truncated normal distribution behind the pp method cannot have a standard deviation of 1.96 while the mean is 1 (eqn (3)). Note that the confidence intervals for the hcf method were abnormally wide with the empirical and lognormal distributions, and were narrow with the gamma distribution. This observation further emphasizes the need for the appropriate volume distribution in the model, or the use of methods such as dvv or dvva to bypass that need.
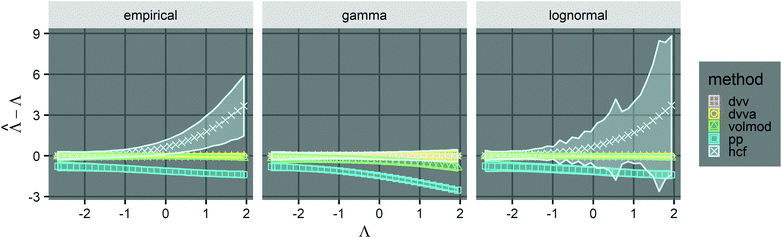 | ||
Fig. 1 Trueness of the dvv, dvva, volmod, hcf, and pp methods in analyzing simulated assay results. The plots show the bias (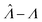 ) calculated from simulated assay results versus input Λ. The shaded areas indicate the 95% confidence intervals calculated from the standard deviations. Compartment volumes were simulated following the empirical, gamma, and lognormal distributions, with parameters matching that of the empirical distributions (μV = 1 and σV = 1.96). The bulk concentration was varied over 2 orders of magnitude (λ ∈ [0.069, 6.93] ⇔ Λ ∈ [−2.67, 1.94]). The number of pre-measured volumes, m, was 2000, and the number of compartments, n, in each assay was 1000. Each point shows the average of results from 1500 assays. Such number of assays was chosen to ensure the sample size is large enough, and the simulated results (e.g. ) calculated from simulated assay results versus input Λ. The shaded areas indicate the 95% confidence intervals calculated from the standard deviations. Compartment volumes were simulated following the empirical, gamma, and lognormal distributions, with parameters matching that of the empirical distributions (μV = 1 and σV = 1.96). The bulk concentration was varied over 2 orders of magnitude (λ ∈ [0.069, 6.93] ⇔ Λ ∈ [−2.67, 1.94]). The number of pre-measured volumes, m, was 2000, and the number of compartments, n, in each assay was 1000. Each point shows the average of results from 1500 assays. Such number of assays was chosen to ensure the sample size is large enough, and the simulated results (e.g. ) converge (Fig. S2†). ) converge (Fig. S2†). | ||
To provide an overview of the trueness of different methods in a wide range of distributions, we also calculated error maps of the inference methods (Table 2) over wide ranges of Λ and σV (Fig. 2), with different distribution types (gamma, lognormal, and truncated normal). After averaging over many simulation runs, the bias (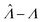 ) was 0 throughout for both the dvv dvva methods. The volmod method was correct in most conditions, except those with very large volume standard deviations. As expected, the hcf method had no errors with the gamma distribution, but led to errors with the other distribution types. Similarly, the pp method gave correct results for truncated normal distributions, but not others. In general, methods other than dvv and dvva were accurate at lower bulk concentrations and volume standard deviations, while the dvv and dvva methods were accurate in all cases considered.
) was 0 throughout for both the dvv dvva methods. The volmod method was correct in most conditions, except those with very large volume standard deviations. As expected, the hcf method had no errors with the gamma distribution, but led to errors with the other distribution types. Similarly, the pp method gave correct results for truncated normal distributions, but not others. In general, methods other than dvv and dvva were accurate at lower bulk concentrations and volume standard deviations, while the dvv and dvva methods were accurate in all cases considered.
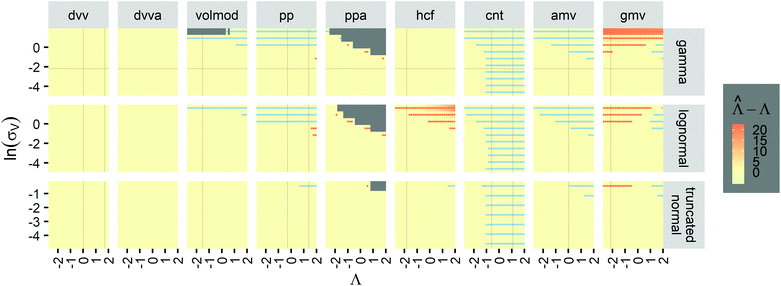 | ||
Fig. 2 Trueness maps of inference methods (Table 2) with different volume distributions (gamma, lognormal, and truncated normal), standard deviations (σV ∈ [0.01, 5.01] ⇔ ln(σV) ∈ [−4.61, 1.61]), and bulk concentrations (Λ ∈ [−2.67, 1.94]), with μV = 1. The color maps show the difference between 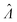 (calculated from simulated assay results) and input Λ. The orange and blue dots indicate locations of 20% overestimation of λ ( (calculated from simulated assay results) and input Λ. The orange and blue dots indicate locations of 20% overestimation of λ (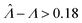 ) and 17% underestimation of λ ( ) and 17% underestimation of λ (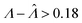 ), respectively. The number of pre-measured volumes, m, was 2000, and the number of compartments, n, in each assay was 1000. Each point shows the average of results from 1500 assays. Dark gray areas indicate where the calculation is invalid. For the truncated normal distribution, ln(σV) ≤ −0.461, because σV ≤ 0.756 when μV = 1 according to eqn (3). ), respectively. The number of pre-measured volumes, m, was 2000, and the number of compartments, n, in each assay was 1000. Each point shows the average of results from 1500 assays. Dark gray areas indicate where the calculation is invalid. For the truncated normal distribution, ln(σV) ≤ −0.461, because σV ≤ 0.756 when μV = 1 according to eqn (3). | ||
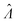 values with different methods using experimental results of digital PCR assays in vortexed droplets14 (Fig. 3). The dvv, dvva, volmod methods gave
values with different methods using experimental results of digital PCR assays in vortexed droplets14 (Fig. 3). The dvv, dvva, volmod methods gave 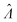 values similar to the expected ones (as confirmed by a commercial digital PCR assay). As expected from the simulation (Fig. 2 and 3), the hcf method overestimated at higher concentrations, and the pp method slightly underestimated in some occasions.
values similar to the expected ones (as confirmed by a commercial digital PCR assay). As expected from the simulation (Fig. 2 and 3), the hcf method overestimated at higher concentrations, and the pp method slightly underestimated in some occasions.
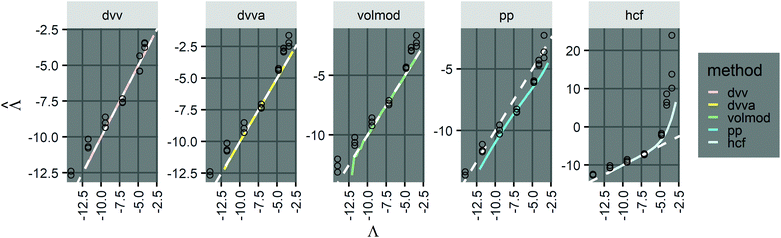 | ||
Fig. 3 Application to experimental data (droplet digital PCR14). Plots show the relationship between 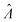 values calculated using the dvv, dvva, hcf, and pp methods versus the expected Λ = ln (λ) values. The solid lines indicate the corresponding simulation results (averaged over 1500 simulation runs). The white dashed lines indicate where values calculated using the dvv, dvva, hcf, and pp methods versus the expected Λ = ln (λ) values. The solid lines indicate the corresponding simulation results (averaged over 1500 simulation runs). The white dashed lines indicate where 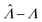 . The known input concentrations (λ) were 8.0 × 10−7, 8.0 × 10−6, 8.0 × 10−5, 8.0 × 10−4, 8.0 × 10−3, 1.6 × 10−2, and 3.2 × 10−2 copies per pL, and the corresponding Λ values were −14.04, −11.74, −9.43, −7.13, −4.83, −4.14, and −3.44. Note that the y-axis scale in each panel was chosen to present the data fully and clearly, and may be different from those of other panels. . The known input concentrations (λ) were 8.0 × 10−7, 8.0 × 10−6, 8.0 × 10−5, 8.0 × 10−4, 8.0 × 10−3, 1.6 × 10−2, and 3.2 × 10−2 copies per pL, and the corresponding Λ values were −14.04, −11.74, −9.43, −7.13, −4.83, −4.14, and −3.44. Note that the y-axis scale in each panel was chosen to present the data fully and clearly, and may be different from those of other panels. | ||
However, results using all methods were noisy and were obtained with only 3 technical replicates. As previously pointed out,14 there remains challenges in imaging and measuring droplets with sizes spanning a wide range. Future experiments with more replicates and better droplet counting methods (e.g. using a confocal microscope or a flow-through reader) will allow for a more expansive validation process.
3.3. Precision
Having established that the dvv and dvva methods have good trueness (Fig. 2), we investigate the precision, using the standard error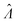 .
.
It is useful to characterize when the calculation is more or less precise, i.e. the standard errors are smaller or larger, respectively. Using 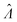 obtained with the dvv method for simulated assay results,
obtained with the dvv method for simulated assay results, 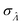 was calculated over wide ranges of Λ and σV (Fig. 4). The quantity
was calculated over wide ranges of Λ and σV (Fig. 4). The quantity 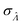 did not markedly increase until σV ≈ 0.5. Similarly, the most-precise Λ is near the best-case estimate of ≈0.466 (eqn (21)). Note that at smaller σV, the landscapes are similar across different distribution types, and at larger σV, the most-precise Λ also increases.
did not markedly increase until σV ≈ 0.5. Similarly, the most-precise Λ is near the best-case estimate of ≈0.466 (eqn (21)). Note that at smaller σV, the landscapes are similar across different distribution types, and at larger σV, the most-precise Λ also increases.
 | ||
Fig. 4 Maps of the standard error (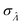 ) at different volume standard deviations (σV) and log bulk concentrations (Λ), with different types of volume distributions (gamma, lognormal, and truncated normal), using the dvv method. Each panel corresponds to a volume distribution type, and provides the landscape of the standard error as a function of Λ and σV. The white dashed line denotes the optimal Λ (eqn (21)). The magenta lines denote the contours (interval = 0.002). Each standard error (each point on the maps) was calculated from 1500 ) at different volume standard deviations (σV) and log bulk concentrations (Λ), with different types of volume distributions (gamma, lognormal, and truncated normal), using the dvv method. Each panel corresponds to a volume distribution type, and provides the landscape of the standard error as a function of Λ and σV. The white dashed line denotes the optimal Λ (eqn (21)). The magenta lines denote the contours (interval = 0.002). Each standard error (each point on the maps) was calculated from 1500 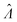 values, each of which was calculated using the dvv method from raw results of an simulated assay. In each assay, the number of compartments was n = 1000. The dark gray area corresponds to where the truncated normal distribution is not defined (σV ≤ 0.756 according to eqn (3)). The mean volume, μV, was 1. values, each of which was calculated using the dvv method from raw results of an simulated assay. In each assay, the number of compartments was n = 1000. The dark gray area corresponds to where the truncated normal distribution is not defined (σV ≤ 0.756 according to eqn (3)). The mean volume, μV, was 1. | ||
The dvva method is called “approximation” because the pre-measured volumes are used to approximate the true volume distribution. The more pre-measured volumes (larger m), the better this approximation. Indeed, as m becomes larger, the dvva 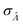 becomes smaller and approaches the dvv
becomes smaller and approaches the dvv 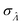 (Fig. 5).
(Fig. 5).
The standard errors of 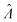 can be obtained using eqn (10) for the dvv method, and eqn (19) for the dvva method. The use of standard errors of
can be obtained using eqn (10) for the dvv method, and eqn (19) for the dvva method. The use of standard errors of 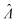 is appropriate (especially when confidence intervals of assay results are desired) because
is appropriate (especially when confidence intervals of assay results are desired) because 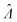 values follow normal distributions (Fig. S3†). However, these expressions are expected to provide approximations only. If the dvv method is used, the standard error provided by eqn (10) is conditional upon the set of individual compartment volumes, each of which is a random variable based on the true volume distribution. The use of eqn (19) for dvva is more forgiving, because, even though the set of pre-measured volumes is also a random variable based on the true volume distribution, it only needs to be representative enough. Indeed, the error plots (Fig. 6, S3†) indicates that eqn (10) (for dvv) underestimated at lower concentrations and overestimated at higher concentrations, while eqn (19) (for dvva) gave results similar to the simulated values, with a little underestimation at higher concentrations.
values follow normal distributions (Fig. S3†). However, these expressions are expected to provide approximations only. If the dvv method is used, the standard error provided by eqn (10) is conditional upon the set of individual compartment volumes, each of which is a random variable based on the true volume distribution. The use of eqn (19) for dvva is more forgiving, because, even though the set of pre-measured volumes is also a random variable based on the true volume distribution, it only needs to be representative enough. Indeed, the error plots (Fig. 6, S3†) indicates that eqn (10) (for dvv) underestimated at lower concentrations and overestimated at higher concentrations, while eqn (19) (for dvva) gave results similar to the simulated values, with a little underestimation at higher concentrations.
 | ||
Fig. 6 Maps of errors in using derived expressions to calculate standard errors of  . The error is defined as . The error is defined as 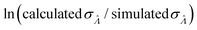 . The calculated . The calculated 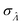 is the standard errors calculated using eqn (10) for the dvv method, and eqn (19) for the dvva method, averaged over different simulated assays of the same conditions, as specified by the volume distribution type, volume standard deviation, and input concentrations. The emprirical is the standard errors calculated using eqn (10) for the dvv method, and eqn (19) for the dvva method, averaged over different simulated assays of the same conditions, as specified by the volume distribution type, volume standard deviation, and input concentrations. The emprirical 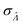 for each assay condition is the sample standard deviation of for each assay condition is the sample standard deviation of 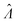 obtained by simulated assays. The simulation parameters are the same as those used to obtain Fig. 2. obtained by simulated assays. The simulation parameters are the same as those used to obtain Fig. 2. | ||
3.4. Limit of detection
We then investigated how volume variation affects the assays’ sensitivity, using the limit of detection (LOD). Herein, the LOD is defined as the concentration at which at least 1 ON compartment is observed in q fraction of experiments. In particular, we choose q = 95%. The LOD can be approximated by considering the probability of sampling at least 1 target entity in each whole assay (with the total volume of Vtotal = nμV). Plugging this volume and q in eqn (4) we have the following.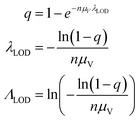 | (23) |
Note that λLOD scales with 1/n and does not depend on the volume distribution. To verify this observation, we simulated limits of detection over different volume distribution types and standard deviations (details in the ESI†). Indeed, eqn (23) agrees well with results simulated over different n, σV values (0.01–5.01), and distribution types (empirical, gamma, lognormal, and truncated normal) (Fig. 7).
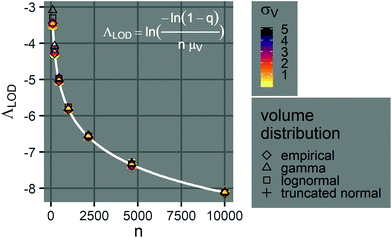 | ||
Fig. 7 Limits of detection of Λ. The plot shows the relationship between the limit of detection, ΛLOD, and the number of compartments per assay, n (100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), when the mean volume is a constant (μV = 1). The points indicate simulated ΛLOD at different σV values (0.01–5.01), with different volume distributions (empirical, gamma, lognormal, and truncated normal). The white curve represents the analytical expression (eqn (23)). Note that at each n value, many points representing different volume distributions cluster at the white curve. 000), when the mean volume is a constant (μV = 1). The points indicate simulated ΛLOD at different σV values (0.01–5.01), with different volume distributions (empirical, gamma, lognormal, and truncated normal). The white curve represents the analytical expression (eqn (23)). Note that at each n value, many points representing different volume distributions cluster at the white curve. | ||
4. Discussion
4.1. Choice of method
The dvv and dvva methods can both be used to accurately calculate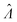 (Fig. 1 and 2) with computational simplicity by numerically solving eqn (9) and (17), respectively. However, they require different inputs, and therefore, are suitable for different scenarios. The dvv method is more precise (Fig. 5), and does not rely on any assumptions about the volume distribution. However, the volume of each ON compartment needs to be measured, adding a requirement on the experimental setup. This requirement is already satisfied in some systems, such as imaging based ones with the hardware capability, and the software to convert images into volumes can be developed in a straightforward fashion.4,13,14,19 On the other hand, the dvva method only requires the ability to detect and count ON compartments. A low-resolution/low-magnification imaging system or a flow-through system may already have this capability. However, the experimental setup has to be consistent enough so that the volume distribution is similar over different realizations of the assay (e.g. like a setup previously described13,14). Ideally, many pre-measured volumes should be obtained to accurately reflect the true volume distribution and to improve the precision (Fig. 5). Therefore, with respect to instrumentation, the choice between the dvv and dvva methods is based on the compromise between the simplicity of compartmentalization and detection.
(Fig. 1 and 2) with computational simplicity by numerically solving eqn (9) and (17), respectively. However, they require different inputs, and therefore, are suitable for different scenarios. The dvv method is more precise (Fig. 5), and does not rely on any assumptions about the volume distribution. However, the volume of each ON compartment needs to be measured, adding a requirement on the experimental setup. This requirement is already satisfied in some systems, such as imaging based ones with the hardware capability, and the software to convert images into volumes can be developed in a straightforward fashion.4,13,14,19 On the other hand, the dvva method only requires the ability to detect and count ON compartments. A low-resolution/low-magnification imaging system or a flow-through system may already have this capability. However, the experimental setup has to be consistent enough so that the volume distribution is similar over different realizations of the assay (e.g. like a setup previously described13,14). Ideally, many pre-measured volumes should be obtained to accurately reflect the true volume distribution and to improve the precision (Fig. 5). Therefore, with respect to instrumentation, the choice between the dvv and dvva methods is based on the compromise between the simplicity of compartmentalization and detection.
According to previously published results, the volmod method was expected to be compatible with any volume distribution.18 Surprisingly, it was found to be inaccurate at larger volume standard deviations (Fig. 2). A possible reason for this discrepancy was how the method is implemented. The published implementation includes user-determined parameters such as the number of volumes to be simulated, and the number of iterations. Default values were used in this paper. Future investigation in how volmod is implemented would be useful. An additional motivation for such investigation is that the volmod implementation in R is about 3 orders of magnitude slower than the dvva implementation in Python described herein (Fig. S5†).
Even though other methods (Table 2) may not be as accurate as the dvv and dvva methods in some cases (Fig. 1 and 2), calibration can be performed when using them, as previously suggested.15 For example, curves of 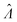 versus Λ with biases are monotonically increasing, implying the possibility of calibration (Fig. 1). If the volume distribution is well approximated by functions specified by a few parameters (such as a gamma function), the calibration can be simpler than generally recognized.15 If the volume distribution cannot be simply described by a few parameters, many experiments have to be performed. In such case, depending on the specific scenarios, one needs to choose between having larger numbers of experiments (for calibration) and adding the capability of volume measurements.
versus Λ with biases are monotonically increasing, implying the possibility of calibration (Fig. 1). If the volume distribution is well approximated by functions specified by a few parameters (such as a gamma function), the calibration can be simpler than generally recognized.15 If the volume distribution cannot be simply described by a few parameters, many experiments have to be performed. In such case, depending on the specific scenarios, one needs to choose between having larger numbers of experiments (for calibration) and adding the capability of volume measurements.
4.2. Volume polydispersity
There are important points to consider about digital assays with polydisperse volumes in general, regardless of the inference method. First, a crucial assumption is that any compartment with one or more targets turns ON. This assumption may not always hold. For example, when the volume distribution is very wide, some compartments with very large volumes have very low concentrations of targets. If the signal is generated in a linear fashion, such as enzymatic amplification,4 the bulk concentration is underestimated. Fortunately, this issue is mitigated if the signal is generated with super-linear amplification, such as in the case of nucleic acid amplification.14 On the other hand, if a compartment is extremely small, the generated signal may not be easily detected. Therefore, one must pay extra attention to the processes of signal conversion and detection with a larger volume variation.Second, the analysis of the LOD revealed an important insight about assay systems with variable volumes. The finding that the LOD does not depend on the volume distribution, and only scales with 1/Vtotal (or 1/n when μV is a constant) (eqn (23)) indicates that the assay sensitivity is not affected by volume variation. This implies that for detection purposes, any method of compartmentalization can be employed without concerns about volume precision or trueness, even when compartments are droplets with really wide volume distributions.13,14
Third, whether the main goal is sensitive detection, quantification, or both, digital assays can now be performed without complex and expensive microfluidic devices. This development enables the design of digital assays geared toward resource-limited settings. The total addressable volume can consequentially be increased to achieve better sensitivity (eqn (23)) and mitigate the noise due to volume variation.
4.3. Possible generalization to deal with other stochastic factors
Volume variation is an important concern when developing and using digital assays. However, there are many other processes that can stochastically affect assay outcomes. For example, bacteria may have some noise in processing signal, or DNA molecules may randomly be lost to surfaces before amplification. Both the dvv and dvva methods can be generalized to work with stochasticity in other parts of the setup. In particular, peach (eqn (4)) can be a function of other variables, and can be plugged into eqn (5) to perform dvv, or eqn (11) to perform dvva (with separately measured values of the other random variables). If peach can be rearranged into eqn (4) with veffective instead of v, then all derived equations are readily applicable.4.4. Experimental considerations when implementing dvv and dvva
The main advantage of the dvv and dvva is the independence from assumptions about the distributions of the compartment volumes. However, they both rely on volumetric measurements, which may have errors. When dvv is used, in each assay run, errors in volumes of ON compartments and total sample volume manifest directly into the equation to solve for bulk concentration (eqn (9)). When dvva is used, errors in individual pre-measured volumes (vi), if not systematic, may still lead to a set of pre-measured volumes (M ≡ {v1, v2, …, vm}) that is still representative of the true volume distribution, and still lead to correct calculations of the bulk concentrations (eqn (17)). In addition, the pre-measured volumes (M ≡ {v1, v2, …, vm}) can be obtained separately from the assays, using accurate and precise instruments (e.g. confocal microscopes26 and channel-based microfluidic devices29). Therefore, while dvv may be more precise (Fig. 5), dvva may be more robust.Another possible experimental error is the variation in the signal intensity, which has been observed in many digital PCR experiments.30–34 Such error would change the number of terms in the left hand side of eqn (9) (for dvv) and the a/n ratio in eqn (9) (for dvva). In both cases, if the errors are not systematic, their effects on different compartments may partially cancel each other out. However, it would still be better to apply clustering techniques to better distinguish ON and OFF compartments as previously suggested.30–34 Furthermore, an alternative is to use the likelihood of observing a certain signal intensity (instead of an ON/OFF response like in eqn (4)) as a function of the compartment volume and the bulk concentration, and apply a similar maximum likelihood estimation framework as described herein. In such case, however, the assay requires the instrument to measure intermediate signal intensities and is no longer digital.
5. Conclusions
We described the dvv and dvva methods with equations to calculate the estimators of the natural logarithm of the concentration and standard errors. Both methods provided accurate estimators from simulated and experimental assays, even when the volume standard deviations were a few times larger then the means. The dvv method requires the measurements of ON compartments in each assay, but does not require the volume distribution to be same in different assays. The dvva method requires a set of separately measured volumes representative of the distributions in all assay runs, but does not require volume measurements for each independent assay run. With the simplicity in computation of these methods, they can be readily integrated with pre-built systems, or used separately to analyze raw results on typical computers. In the future, they can be extended to consider other stochastic processes in digital assays. In general, these methods enable the quantification in a class of digital assays where compartmentalization can be done using simple methods, allowing for simpler designs and higher volume capacities.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding was provided by Intellectual Ventures’ Global Good Fund. We gratefully acknowledge Bill Gates and Nathan Myhrvold for their support and supervision. We also thank our colleague David Gasperino for helpful discussion, and Elizabeth Phillips for help in background information gathering.References
- P. J. Sykes, S. H. Neoh, M. J. Brisco, E. Hughes, J. Condon and A. A. Morley, BioTechniques, 1992, 13, 444–449 CAS.
- A. A. Morley, Biomol. Detect. Quantif., 2014, 1, 1–2 CrossRef PubMed.
- A. S. Basu, SLAS Technol., 2017, 22, 369–386 Search PubMed.
- D. M. Rissin, C. W. Kan, T. G. Campbell, S. C. Howes, D. R. Fournier, L. Song, T. Piech, P. P. Patel, L. Chang, A. J. Rivnak, E. P. Ferrell, J. D. Randall, G. K. Provuncher, D. R. Walt and D. C. Duffy, Nat. Biotechnol., 2010, 28, 595–599 CrossRef CAS PubMed.
- A. S. Basu, SLAS Technol., 2017, 22, 387–405 Search PubMed.
- J. Q. Boedicker, L. Li, T. R. Kline and R. F. Ismagilov, Lab Chip, 2008, 8, 1265–1272 RSC.
- A. G. Chunyk, A. Joyce, S. K. Fischer, M. Dysinger, A. Mikulskis, A. Jeromin, R. Lawrence-Henderson, D. Baker and D. Yeung, AAPS J., 2018, 20, 10 CrossRef PubMed.
- L. Dong, Y. Meng, Z. Sui, J. Wang, L. Wu and B. Fu, Sci. Rep., 2015, 5, 13174 CrossRef CAS PubMed.
- A. B. Košir, C. Divieto, J. Pavšič, S. Pavarelli, D. Dobnik, T. Dreo, R. Bellotti, M. P. Sassi and J. Žel, Anal. Bioanal. Chem., 2017, 409, 6689–6697 CrossRef PubMed.
- A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841 RSC.
- J. A. Boxall, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Ind. Eng. Chem. Res., 2010, 49, 1412–1418 CrossRef CAS.
- F. Y. Ushikubo and R. L. Cunha, Food Hydrocolloids, 2014, 34, 145–153 CrossRef CAS.
- S. A. Byrnes, E. A. Phillips, T. Huynh, B. H. Weigl and K. P. Nichols, Analyst, 2018, 143, 2828–2836 RSC.
- S. A. Byrnes, T. C. Chang, T. Huynh, A. Astashkina, B. H. Weigl and K. P. Nichols, Anal. Chem., 2018, 90, 9374–9380 CrossRef CAS PubMed.
- J. Tellinghuisen, Anal. Chem., 2016, 88, 12183–12187 CrossRef CAS PubMed.
- N. Majumdar, S. Banerjee, M. Pallas, T. Wessel and P. Hegerich, Sci. Rep., 2017, 7, 9617 CrossRef PubMed.
- J. F. Huggett, S. Cowen and C. A. Foy, Clin. Chem., 2015, 61, 79–88 CrossRef CAS PubMed.
- M. Vynck and O. Thas, Anal. Chem., 2018, 90, 6540–6547 CrossRef CAS PubMed.
- J. E. Kreutz, T. Munson, T. Huynh, F. Shen, W. Du and R. F. Ismagilov, Anal. Chem., 2011, 83, 8158–8168 CrossRef CAS PubMed.
- W. H. Greene, Econometric analysis, Prentice Hall, 7th edn, 2012, p. 1188 Search PubMed.
- L. B. Pinheiro, V. A. Coleman, C. M. Hindson, J. Herrmann, B. J. Hindson, S. Bhat and K. R. Emslie, Anal. Chem., 2012, 84, 1003–1011 CrossRef CAS PubMed.
- T. Demeke and D. Dobnik, Anal. Bioanal. Chem., 2018, 410, 4039–4050 CrossRef CAS PubMed.
- E. Chern, S. Siefring, J. Paar, M. Doolittle and R. Haugland, Lett. Appl. Microbiol., 2011, 52, 298–306 CrossRef CAS PubMed.
- W. G. Cochran, Biometrics, 1950, 6, 105 CrossRef CAS PubMed.
- S. N. E. E. Fazekas de St Groth, J. Immunol. Methods, 1982, 49, R11–R23 CrossRef PubMed.
- G. S. Yen, B. S. Fujimoto, T. Schneider, J. E. Kreutz and D. T. Chiu, J. Am. Chem. Soc., 2019, 141, 1515–1525 CrossRef CAS PubMed.
- B. Efron and D. V. Hinkley, Biometrika, 1978, 65, 457–483 CrossRef.
- L. Devroye, Proceedings of COMPSTAT 2010 - 19th International Conference on Computational Statistics, Keynote, Invited and Contributed Papers, 2010, pp. 3–18.
- J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127–9133 CrossRef CAS.
- M. Jones, J. Williams, K. Gärtner, R. Phillips, J. Hurst, J. Frater, K. Gartner, K. Gärtner, R. Phillips, J. Hurst and J. Frater, J. Virol. Methods, 2014, 202, 1–8 CrossRef PubMed.
- W. Trypsteen, M. Vynck, J. de Neve, P. Bonczkowski, M. Kiselinova, E. Malatinkova, K. Vervisch, O. Thas, L. Vandekerckhove and W. de Spiegelaere, Anal. Bioanal. Chem., 2015, 407, 5827–5834 CrossRef CAS.
- D. Attali, R. Bidshahri, C. Haynes and J. Bryan, F1000Research, 2016, 5, 1411 Search PubMed.
- A. Chiu, M. Ayub, C. Dive, G. Brady and C. J. Miller, Bioinformatics, 2017, 33, 2743–2745 CrossRef CAS PubMed.
- B. K. Jacobs, E. Goetghebeur, J. Vandesompele, A. De Ganck, N. Nijs, A. Beckers, N. Papazova, N. H. Roosens and L. Clement, Anal. Chem., 2017, 89, 4461–4467 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Extra figures referred to in the main text. A zip file containing code and raw data. See DOI: 10.1039/C9AN01479A |
| This journal is © The Royal Society of Chemistry 2019 |

![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)