Considerations for uranium isotope ratio analysis by atmospheric pressure ionization mass spectrometry

Abstract

The accurate measurement of uranium isotope ratios from trace samples lies at the foundation of achieving nuclear nonproliferation. These challenging measurements necessitate both the continued characterization and evaluation of evolving mass spectrometric technologies as well as the propagation of sound measurement approaches. For the first time in this work, we present the analysis of uranium isotope ratio measurements from discrete liquid injections with an ultra-high-resolution hybrid quadrupole time-of-flight mass spectrometer. Also presented are important measurement considerations for evaluating the performance of this type and other atmospheric pressure and ambient ionization mass spectrometers for uranium isotope analysis. Specifically, as the goal of achieving isotope ratios from as little as a single picogram of solid material is approached, factors such as mass spectral sampling rate, collision induced dissociation (CID) potentials, and mass resolution can dramatically alter the measured isotope ratio as a function of mass loading. We present the ability to accurately measure ²³⁵UO₂⁺/²³⁸UO₂⁺ down to 10s of picograms of solubilized uranium oxide through a proper consideration of mass spectral parameters while identifying limitations and opportunities for pushing this limit further.

---

Introduction

The need for sensitive and accurate uranium isotopic measurements remains imperative to nuclear safeguards of interest to the International Atomic Energy Agency (IAEA). Specifically, direct determination of uranium isotopic ratios enables the desired monitoring of nuclear enrichment compliance and capabilities.^1,2 As technologies improve, it is important to evaluate state-of-the-art mass spectrometry (MS) approaches for these aims. As such, the analytical performance of a wide range of isotope ratio (IR)MS-based instrumentation and techniques have been investigated, including secondary ion mass spectrometry (SIMS),^3–10 thermal ionization (TI) MS,^11,12 inductively coupled plasma (ICP)-MS,^13,14 isotope dilution (ID) MS,¹⁵ extractive electrospray ionization (EESI)-MS,^16,17 and atmospheric plasma-based sources such as microwave plasma torch (MPT)-MS,¹⁸ solution-cathode glow discharge (SCGD),¹⁹ and liquid sampling-atmospheric pressure glow discharge (LS-APGD) ionization coupled with Orbitrap MS.^20–23

The IAEA and related agencies maintain interest in uranium isotopic measurements across two critical regimes, specifically, bulk sample analysis and particle analysis. The bulk sample analysis of uranium isotopes often focuses on uranium hexafluoride (UF₆), although uranium oxides and uranyl nitrate are also measured. These analyses are not limited by sample size and isotope abundance measurement uncertainties are guided by the IAEA's International Target Values (ITVs) for Measurement Uncertainties in Safeguarding Nuclear Materials.²⁴ The ITV performance metrics for bulk analysis are specified for minimum sizes often in the range of grams or milliliters of materials. Gas source (GS) MS, multi-collector (MC)ICP-MS, and more recently, LS-APGD-MS have been employed for the mass spectrometric analysis of bulk samples targeting ITV metrics.^22–25 Alternatively, the sample-limited particle analysis regime focuses on trace levels of materials. These analyses are typically conducted in combination with a particle isolation stage and include techniques such as SIMS,^3,4,26,27 TIMS,^28,29 and laser ablation (LA) ICP-MS.^30,31 The analysis of particles yields distributions of individual isotope ratio measurements that may statistically vary based on the amount of material present (particle size) and instrument sensitivity.

Outside of the traditional MS techniques and instrumentation used for uranium isotopic measurements, ‘newer’ technologies with advanced mass analyzers such as ion traps and time-of-flight have the potential to impact these analyses. Studies evaluating new MS technologies for this purpose often report concentration-based limits of detection (LODs) of individual uranium isotopes in as much as 100s of nanograms of dissolved uranium.^17–19 While the mere detection of uranium is important, the questions pertinent to the IAEA for both bulk and particle analyses typically require at least simultaneous detection of ²³⁵U to give a measure of whether undeclared uranium enrichment has occurred. In addition, as the evaluation of evolving MS technologies advances from bulk analysis to sample-limited analysis, isotopic ratio measurements must be conducted on as little as picograms of material in a discrete manner. In these samples, much more leeway is given in measurement result metrics/uncertainties since there are often orders of magnitude lower amounts of uranium atoms relative to the sample results governed by the aforementioned analytical ITVs.

In this article, we present new approaches that expand the information set for MS evaluation of uranium isotopes with respect to mass-based LODs, emphasizing the quest toward the single picogram LOD for the ²³⁵U/²³⁸U isotopic ratio in an analytically challenging depleted uranium material (where ²³⁸U is 237× higher in abundance than ²³⁵U). We describe how this isotopic ratio was impacted by MS system parameters while for the first time reporting on the use of an ultra-high-resolution hybrid quadrupole time-of-flight mass spectrometer for uranium detection. The result is a metrological rubric for future MS technology evaluation studies of uranium materials, particularly for the application of smaller amounts of uranium material in a trace, non-bulk analysis.

Experimental methods

Isotope ratio determination for uranium was conducted on an ultra-high-resolution (UHR) hybrid quadrupole time-of-flight (QTOF) mass spectrometer (maXis II, Bruker Daltonic GmbH, Bremen, Germany). A single-element uranium ICP-MS standard, derived from uranyl nitrate (UO₂(NO₃)₂), was purchased from Inorganic Ventures (Christiansburg, Virginia, USA) and volumetrically diluted in 95/5 (volume/volume) TraceSELECT grade methanol/water (details in the ESI‡). Certified abundances of the standard were ²³⁸U: (99.6 ± 0.1)% and ²³⁵U: (0.42 ± 0.05)%, both reported with expanded uncertainties (coverage factor, k = 2). Discrete sample introductions and subsequent ionization were achieved by a 6-port divert valve with a 5 μL sample loop and a traditional pneumatically-assisted electrospray ionization (ESI) source. TraceSELECT grade solutions specify a maximum of 0.5 ppb uranium (≈2.8 pg UO₂) background contaminant level for the 5 μL injections used here (it is recognized that as LODs approach 1 pg, better than 0.5 ppb U background will be required). A spray solution of 95/5 (volume fraction) methanol/water was delivered using a syringe pump (Legato 100, KD Scientific, Holliston, MA, USA). Certain commercial products are identified in order to adequately specify the procedure; this does not imply endorsement or recommendation by NIST, nor does it imply that such products are necessarily the best available for the purpose.

A cursory optimization of the ESI and other system parameters was conducted resulting in the values found in Table 1. The quadrupole and collision cell parameters were optimized for the transmission of ions in the general region from m/z 200 to m/z 300, covering the major uranium-based cations. No targeted fragmentation of ions was completed here, as care was taken throughout system optimization to minimize ion transmission losses that would negate the ultimate goal of providing isotopic ratios at the lowest possible mass loadings. The incorporated 45 μs transfer time and 15 μs pre-pulse storage time were also set to define the ion accumulation prior to each TOF-pulse, effectively limiting the mass range.

Table 1 Parameters employed for UHR-MS

Endplate potential	500 V	Dry gas flow	7.5 L min^−1
Capillary potential	4250 V	Dry gas temp.	250 °C
Nebulizing gas (N2)	100 kPa	Flow rate	100 μL min^−1
Funnel 1 RF	200 Vpp	Multipole RF	200 Vpp
In-source CID	125 eV
Ion energy	2 eV	Low mass	100 m/z
Collision energy	5 eV	Collision RF	200 Vpp
Transfer time	45 μs	Pre pulse storage	15 μs
Cycle time	62 μs	Pulse width	5 μs
Repetition rate	16.129 kHz
Detector potential	2245 V	Spectra range	m/z 200–300
Noise	11 LSB

---

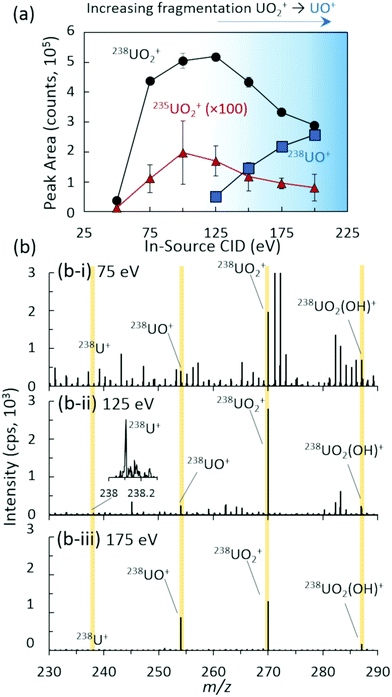
The nature of the uranium standard and system conditions yielded an ion distribution in positive mode dominated by the UO₂⁺ cation, with observed cations for U⁺, UO⁺, UO₂(OH)⁺, and UO₂(H₂O)⁺ as demonstrated in Fig. 1. Alternative ionization methods such as EESI, MPT, or SCGD, and different mass spectrometer parameters may yield different ion species distributions.^16–19 Previous investigations using a range of ambient and atmospheric pressure liquid-,^32–36 laser-,³⁷ and plasma-based^20,38,39 ionization schemes have employed in-source collision induced dissociation (CID) for the direct manipulation of large ion distributions common to inorganic species. Unlike MS/MS CID within the collision cell, which targets a specific m/z parent ion, in-source CID imparts the fragmentation or declustering energy to all incoming ions. Given the wide ion distribution observed here, in-source CID was implemented instead of a more targeted MS/MS fragmentation of a single cation from that distribution. In-source CID was controlled by varying the energy imparted between the two ion funnels within the differentially pumped stages between the inlet and triple quadrupole regions (Fig. S1‡). The DC potential applied to ion funnel 1 was increased, accelerating all incoming ions into ion funnel 2 and increasing the frequency and energy of collisions with the remaining gas molecules.

Fig. 1 (a) Integrated peak areas of ²³⁸UO₂⁺, ²³⁸UO⁺, and ²³⁵UO₂⁺ as a function of in-source collision induced dissociation (CID) energy for 567 pg UO₂ injections. Data points and uncertainties represent average peak areas and expanded standard deviations (k = 2) of seven replicate injections from each extracted ion chronogram. (b) Representative mass spectra and ion distributions at (i) 75 eV, (ii) 125 eV, and (iii) 175 eV in-source CID energies.

The ion distribution as a function of in-source CID was analytically characterized for overall abundance (Fig. 1) and isotope ratio, ²³⁵UO₂/²³⁸UO₂ (Fig. S2‡), yielding an optimal value of approximately 125 eV for the maximum UO₂⁺ cation signal. All peak areas in Fig. 1 and throughout the study were baseline subtracted (see the ESI‡ for details). Lower values of in-source CID allowed excessive clusters and adducts to remain intact, minimizing the overall uranium signal in the m/z range investigated. This also yielded a higher abundance of chemical noise from organic species (Fig. 1(b-i)). In contrast, higher values of in-source CID yielded increasing fragmentation of UO₂⁺ to UO⁺ (Fig. 1(b-iii)). Of note is that the instrument's limited range of in-source CID energies were insufficient to fully fragment the complete ion distribution (UO⁺, UO₂⁺, UO₂(OH)⁺, and UO₂(H₂O)⁺) to U⁺, which prevented a single ion distribution.

Results and discussion

We evaluated the performance and isotope ratio measurement capabilities of the hybrid QTOF for diminishing discrete uranium injections. The injection of discrete liquid packets enabled the measurement of isotope ratios for a known quantity (mass) of sample and was critical to determining the prospects and limitations of ultimately achieving useful isotope ratios with this form of instrumentation. Extracted ion chronograms (XICs) for all relevant ions were tracked and used to derive peak areas. Preliminary optimization of general system parameters was conducted, yielding the values identified above and in Table 1. The mass spectral acquisition parameters, specifically the spectra rate and rolling averaging functions, revealed important effects on the isotopic ratio accuracy and precision for diminishing mass loadings. Proper consideration and understanding of the role that these parameters played was imperative for identifying and avoiding potentially misleading isotope ratio data. With the quadrupoles employed as ion guides between the dual ion funnel region and the orthogonal TOF mass analyzer, factors such as ion capacity and field defects, typical of ion trap mass analyzers, did not play a significant role in the isotope ratio measurements in this study.

Rolling averaging

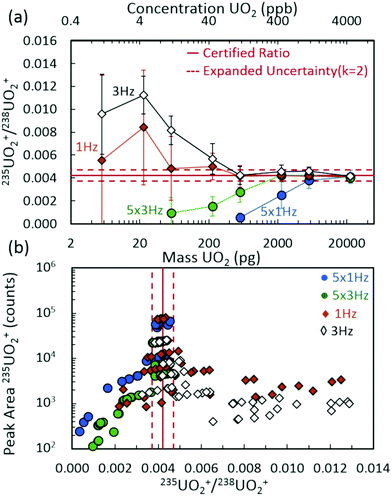
Fig. 2(a) demonstrates the ²³⁵UO₂⁺/²³⁸UO₂⁺ isotope ratio as a function of injected UO₂ mass (and equivalent UO₂ concentrations) for spectra rates of 1 Hz and 3 Hz, both without rolling averaging and with averaging of five spectra. All acquisition conditions exhibited accurate isotope ratio measurements for the highest mass loadings considered (approximately 5 ng to 20 ng) with single digit relative standard deviations (RSDs) across multiple discrete injections (Fig. 3). However, as the injected mass of UO₂ decreased, the isotope ratio for averaging conditions (5 × 1 Hz and 5 × 3 Hz) diverged low from the certified value. For a given spectra rate, a further increase in the rolling average setting directly led to undercounting of the minor isotope for relatively constant major isotope peak areas, driving the isotope ratio low (Fig. S3 and S4‡). This was also observed in the scatter plot of the minor isotope peak area (²³⁵UO₂⁺) as a function of the measured isotope ratio (left-hand side of Fig. 2(b)). Undercounting of the minor isotope when employing spectra averaging was further exacerbated by reduction in the spectra rate from 3 Hz to 1 Hz (Fig. 2(a) and S5‡). This phenomenon also increased the RSD of the isotope ratio measurements (Fig. 3), while spectra averaging led to a high RSD for a given spectra rate as the mass loading decreased.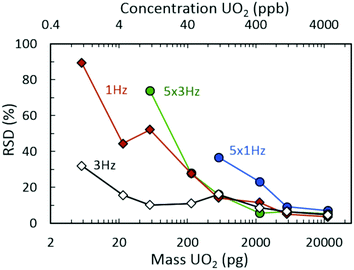

Fig. 2 (a) Isotope ratio (²³⁵UO₂⁺/²³⁸UO₂⁺) measurements as a function of UO₂ injection mass for multiple spectra rates and rolling averages. Data points and uncertainties expressed as the average peak area ratios and expanded standard deviations (k = 2) of seven replicate injections. (b) Scatter plot representing the peak area of ²³⁵UO₂⁺ as a function of measured isotope ratio for investigated spectra rates and rolling averages.

Fig. 3 Relative standard deviation (RSD) measurements for isotope ratio (²³⁵UO₂⁺/²³⁸UO₂⁺) determination as a function of UO₂ injection mass from seven replicate injections.

The discrete nature of sample injections led to temporally vanishing signal profiles for the minor ²³⁵U isotope as mass loadings decreased (Fig. S5‡). Importantly, the interplay of time scales associated with mass spectra acquisition must be understood to make accurate isotope ratio measurements from discrete samples as the goal of isotope ratios down to single picograms of material is approached. As demonstrated in Fig. 4, the temporal extent (i.e., peak width) of the minor isotope peak (t_peak) exhibited in the extracted ion chronogram monotonically decreased with decreasing injection mass (Fig. S5 and S6‡). Under ideal conditions, the peak timescale (width) would be 3 seconds for a 5 μL injection at 100 μL min⁻¹. However, diffusion, dispersion, and instrument settings led to varying levels of ion packet broadening. For the rolling average cases (5 × 1 Hz and 5 × 3 Hz), as the peak time scale (t_peak) approached the averaging time scale (t_ave) (dashed horizontal lines in Fig. 4), the isotope ratio began to deviate from the certified value (Fig. 2(a)). As the mass per injection decreased, this deviation was first observed for the 5 × 1 Hz conditions, given the long averaging time scale (t_ave≈ 5 s). A further decrease in injection mass led to the divergence of the 5 × 3 Hz (t_ave ≈ 1.67 s) isotope ratios from the certified value. The interaction between similar averaging and peak time scales led to a mismatch between the individual step size (in time) of each spectrum and the function (extracted ion chronogram peak) being integrated (peak area measurement). This mismatch effectively led to averaging in zero values for the minor isotope intensity, which largely contributed to the observed undercounting (Fig. S5‡). This phenomenon was observed for a wide range of rolling average values and spectra rates (Fig. S7–S9‡).

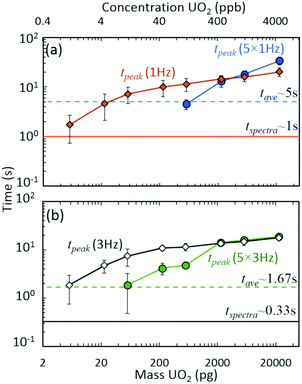Fig. 4 Interacting time scales for discrete injection isotope ratio determination: averaging (t_ave), spectra rate (t_spectra), and peak duration (t_peak) time scales. Approximate peak time scales as a function of UO₂ injection mass for (a) 1 Hz and (b) 3 Hz spectra rates. Data derived from Fig. 2 results. Data points and uncertainties represent the averages and expanded standard deviations (k = 2) of seven replicate injections.

No spectral averaging

When rolling averaging was not incorporated, the effective step size for peak area determination was defined by the spectra time scale (solid horizontal lines in Fig. 3). The right-hand side of Fig. 2(b) includes data without spectra averaging where isotope ratios were systematically high compared to the certified value, due mostly to the ²³⁵UO₂⁺ signal being dominated by spectral noise (and hence, not reflecting actual counts of the uranium species). Compared to averaging, the 1 Hz and 3 Hz acquisition cases maintained accurate isotope ratio measurements at lower UO₂ mass injections. The isotope ratios began to deviate away from the certified value for mass injections at or below 200 pg, but were still close to the expanded uncertainty range down to approximately 50 pg. To frame these levels in the context of nuclear safeguards, 50 pg of either pure UO₂ or pure U₃O₈ equates to a particle size of just over 2 μm in diameter.

Below 50 pg, the isotope ratios increased above the certified value due to a perceived overcounting of the minor isotope, but more likely due to interfering random chemical noise. As the injected mass decreased, the fraction of the minor isotope signal attributed to chemical noise increased, further increasing the uncertainty in the isotope ratio measurement while decreasing the isotope ratio accuracy (Fig. S6‡). These observations appeared to be a result of a competitive ionization environment, a common phenomenon in ESI-based MS (Fig. S10‡).^40–43 In the region around the minor isotope, m/z 267, the chemical noise in blank injections remained approximately a few hundred counts per second (cps) across the experiment duration. However, the analysis of UO₂ injections exhibited decreasing low level chemical noise as the injection mass increased (Fig. 5(insets) and S10(b)‡). The aspects of droplet desolvation and ionization of species in ESI led to certain species preferentially ionizing to the detriment of other species. The limited available charge was preferentially maintained by the higher concentrations of uranium nitrate relative to chemical noise species as droplets desolvated (Fig. S10‡). As the uranium nitrate concentration decreased, more of the chemical noise species maintained charge. For example, the XICs of such a species at m/z 267.12 (near the ²³⁵UO₂⁺ cation at m/z 267.03) exhibited the maximum injection peak intensity for the lowest UO₂ injection masses (Fig. S11‡). The overall intensity of the noise XIC peak decreased with increasing UO₂ injection masses to the point of complete suppression during the injection, followed by an increase back to baseline levels (Fig. S11‡).

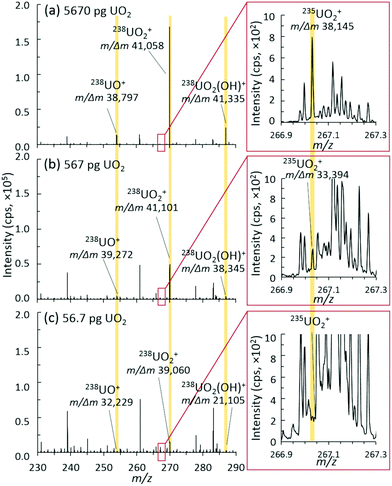Fig. 5 Representative mass spectra, ion distributions, and mass resolution for (a) 5670 pg, (b) 567 pg, and (c) 56.7 pg discrete UO₂ injection mass loadings.

In addition to the effects of chemical noise and competitive ionization as the spectra rate increased, the magnitude of the divergence away from the certified ratio increased. This was determined to be a direct result of decreasing signal intensity for both uranium isotopes as a function of increasing spectra rate (Fig. S12‡). As the spectra rate increased, the corresponding increase in quenching events (proportional to spectra rate, i.e., 1 Hz = 1 quench, 3 Hz = 3 quenches) in the collision cell, subsequent filling of narrow pseudo potential wells,⁴⁴ and the dead time for communication between the instrument detector and processing software/computer for each spectrum (1 Hz = 1 communication delay, 3 Hz = 3 communication delays) led to a significant decrease in detected uranium signal. The combination of limited signal intensity, increased chemical noise, and matrix effects (competitive ionization) also led to increases in the measurement uncertainty for decreasing mass injections (Fig. 3).

This discussion on spectral rates illustrates a cautionary tale: how measurements are made is critical to achieving accurate and precise isotope ratio data. It is easy to be misled into thinking that sound measurement approaches for large amounts of sample material will directly translate to sound measurements for the interrogation of trace levels of material. As such it is imperative that instrument performance be evaluated, and unique measurement approaches be developed, at low level mass loadings to identify and avoid misinterpretation of results stemming from procedural implementations for high level loading.

Accordingly, as new MS instrumentation options are evaluated for uranium isotopic analysis of small sample sizes, the ability to separate out interference and/or spectral noise is critical, especially for the minor isotopes. Fig. 5 shows the mass spectra of the uranium species region and the insets of the minor isotope ²³⁵UO₂⁺ region for three different mass loadings. The mass resolution for all U-based species (UO⁺, UO₂⁺, and UO₂(OH)⁺) was consistently measured at about 40 000 m/Δm. As mass loadings decreased into the 10s of picogram range, this mass resolution was maintained for the detected ²³⁸U species. For the ²³⁵U species, this mass resolution was maintained through 100s of picograms, but suffered from a lower signal-to-noise (S/N) ratio at 10s of picograms. With enough material present, a mass resolution near 40 000 m/Δm is sufficient to separate the challenging ²³⁵UH⁺ from ²³⁶U⁺, which many nuclear forensics MS instruments cannot directly achieve.⁴ However, despite the inherent capabilities of the hybrid QTOF presented herein, a better understanding and control of spectral noise will need to be achieved to realize the full benefits of such a high mass resolution.

Conclusions

The continued progression of mass spectrometric technologies requires the development of rigorous metrology to evaluate unique measurement paradigms. One such measurement, the accurate determination of uranium isotope ratios from discrete picogram level samples, plays a central role for the nuclear forensics and nonproliferation communities. Here, we provided an evaluation of a hybrid QTOF mass spectrometer for the measurement of discrete liquid uranium samples. Most notably, mass spectral acquisition parameters played a significant role in the accuracy and precision of isotope ratio measurements for decreasing mass loadings. For mass loadings approaching picogram levels, the temporal response of discrete samples approaches, and even becomes shorter than, the time scales for spectra acquisition, which directly led to inaccurate measurement of the minor isotope and erroneous isotope ratios. An understanding of these competing time scales is imperative to measurement confidence.

Many of the recent developments in mass spectrometry have targeted various -omics, pharmaceutical, and biopharmaceutical fields. Traditionally these applications are not material limited; therefore, instrumentation, signal processing, and data presentation have been developed to meet these needs. For applications concerned with vanishing temporal signals and sample abundances, a full understanding of the ion transmission efficiency, as well as signal acquisition and processing becomes critical to recognizing the role that ion loss, noise, and dead time play in the measurement of minor isotopes.

In addition to understanding the measurement science for low-level discrete injections, the results demonstrated here incorporated electrospray flow rates and associated source parameters that best resulted in a steady spray and tight discrete peaks within the extracted ion chronograms. However, this relatively high flow rate also led to inefficient ionization and gas phase introduction of ionic species, as well as matrix effects and competitive ionization, in turn limiting the levels of UO₂ for which accurate isotope ratios were measured. Altering this injection paradigm from ESI, beyond nanoESI, to vanishingly small discrete injections of highly charged species may drastically enhance the ion transport and fate^45,46 and reduce matrix effects, improving sensitivities and isotope ratio determination. Similarly, altering the ionization method may improve sensitivity through enhanced ionization efficiency or reduced matrix effects for these analyses.^16–18 Employing tandem mass spectrometry may also eliminate some of the chemical noise artifacts encountered, however the appreciable signal loss typical of MS/MS would certainly hinder sensitivity for low mass loadings.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. D. L. Donohue, Anal. Chem., 2002, 74, 28 A–35 A.
2. E. Kuhn, D. Fischer and M. Ryjinski, IAEA Report, 2001, No. IAEA-SM-367.
3. N. Sharp, J. D. Fassett and D. S. Simons, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2016, 34, 03H115.
4. D. S. Simons and J. D. Fassett, J. Anal. At. Spectrom., 2017, 32, 393–401.
5. M. Betti, G. Tamborini and L. Koch, Anal. Chem., 1999, 71, 2616–2622.
6. F. Esaka, K. T. Esaka, C. G. Lee, M. Magara, S. Sakurai, S. Usuda and K. Watanabe, Talanta, 2007, 71, 1011–1015.
7. G. Tamborini, M. Betti, V. Forcina, T. Hiernaut, B. Giovannone and L. Koch, Spectrochim. Acta, Part B, 1998, 53, 1289–1302.
8. P. M. L. Hedberg, P. Peres, J. B. Cliff, F. Rabemananjara, S. Littmann, H. Thiele, C. Vincent and N. Albert, J. Anal. At. Spectrom., 2011, 26, 406–413.
9. P. M. L. Hedberg, P. Peres, F. Fernandes, N. Albert and C. Vincent, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2018, 36, 03F108.
10. P. M. L. Hedberg, P. Peres, F. Fernandes and L. Renaud, J. Anal. At. Spectrom., 2015, 30, 2516–2524.
11. S. Richter and S. A. Goldberg, Int. J. Mass Spectrom., 2003, 229, 181–197.
12. S. Richter, H. Kuhn, Y. Aregbe, M. Hedberg, J. Horta-Domenech, K. Mayer, E. Zuleger, S. Burger, S. Boulyga, A. Kopf, J. Poths and K. Mathew, J. Anal. At. Spectrom., 2011, 26, 550–564.
13. C.-C. Shen, R. Lawrence Edwards, H. Cheng, J. A. Dorale, R. B. Thomas, S. Bradley Moran, S. E. Weinstein and H. N. Edmonds, Chem. Geol., 2002, 185, 165–178.
14. H. Cheng, R. Lawrence Edwards, C.-C. Shen, V. J. Polyak, Y. Asmerom, J. Woodhead, J. Hellstrom, Y. Wang, X. Kong, C. Spötl, X. Wang and E. Calvin Alexander, Earth Planet. Sci. Lett., 2013, 371–372, 82–91.
15. A. Hasozbek, K. J. Mathew, G. Orlowicz, N. Hui, B. Srinivasan, M. Soriano and U. Narayanan, J. Radioanal. Nucl. Chem., 2013, 296, 447–451.
16. C. Liu, B. Hu, J. Shi, J. Li, X. Zhang and H. Chen, J. Anal. At. Spectrom., 2011, 26, 2045–2051.
17. M. Luo, B. Hu, X. Zhang, D. Peng, H. Chen, L. Zhang and Y. Huan, Anal. Chem., 2010, 82, 282–289.
18. Y. Li, M. Yang, R. Sun, T. Zhong and H. Chen, J. Mass Spectrom., 2016, 51, 159–164.
19. A. J. Schwartz, K. L. Williams, G. M. Hieftje and J. T. Shelley, Anal. Chim. Acta, 2017, 950, 119–128.
20. E. D. Hoegg, C. J. Barinaga, G. J. Hager, G. L. Hart, D. W. Koppenaal and R. K. Marcus, J. Am. Soc. Mass Spectrom., 2016, 27, 1393–1403.
21. E. D. Hoegg, C. J. Barinaga, G. J. Hager, G. L. Hart, D. W. Koppenaal and R. K. Marcus, J. Anal. At. Spectrom., 2016, 31, 2355–2362.
22. E. D. Hoegg, R. K. Marcus, G. J. Hager, G. L. Hart and D. W. Koppenaal, J. Anal. At. Spectrom., 2018, 33, 251–259.
23. E. D. Hoegg, R. K. Marcus, D. W. Koppenaal, J. Irvahn, G. J. Hager and G. L. Hart, Rapid Commun. Mass Spectrom., 2017, 31, 1534–1540.
24. M. Zhao, M. Penkin, C. Norman and S. Balsley, ESARDA Bull., 2012, 48, 3–24.
25. S. Richter, A. Alonso-Munoz, R. Eykens, U. Jacobsson, H. Kuehn, A. Verbruggen, Y. Aregbe, R. Wellum and E. Keegan, Int. J. Mass Spectrom., 2008, 269, 145–148.
26. F. Esaka, C.-G. Lee, M. Magara and T. Kimura, Anal. Chim. Acta, 2012, 721, 122–128.
27. F. Esaka and M. Magara, Talanta, 2014, 120, 349–354.
28. M. Kraiem, S. Richter, H. Kühn and Y. Aregbe, Anal. Chim. Acta, 2011, 688, 1–7.
29. C. G. Lee, K. Iguchi, J. Inagawa, D. Suzuki, F. Esaka, M. Magara, S. Sakurai, K. Watanabe and S. Usuda, J. Radioanal. Nucl. Chem., 2007, 272, 299–302.
30. N. Dzigal, E. Chinea-Cano, S. Walsh and A. Limbeck, Talanta, 2017, 167, 583–592.
31. N. S. Lloyd, R. R. Parrish, M. S. A. Horstwood and S. R. N. Chenery, J. Anal. At. Spectrom., 2009, 24, 752–758.
32. K. M. Evans-Nguyen, A. Quinto, T. Hargraves, H. Brown, J. Speer and D. Glatter, Anal. Chem., 2013, 85, 11826–11834.
33. T. P. Forbes and E. Sisco, Anal. Chem., 2014, 86, 7788–7797.
34. A. T. Blades, P. Jayaweera, M. G. Ikonomou and P. Kebarle, J. Chem. Phys., 1990, 92, 5900–5906.
35. P. Jayaweera, A. T. Blades, M. G. Ikonomou and P. Kebarle, J. Am. Chem. Soc., 1990, 112, 2452–2454.
36. J. T. Watson and O. D. Sparkman, Introduction to Mass Spectrometry, John Wiley & Sons, Ltd., West Sussex, 2007.
37. T. P. Forbes and E. Sisco, Anal. Chim. Acta, 2015, 892, 1–9.
38. K. M. Evans-Nguyen, J. Gerling, H. Brown, M. Miranda, A. Windom and J. Speer, Analyst, 2016, 141, 3811–3820.
39. T. P. Forbes, E. Sisco, M. Staymates and G. Gillen, Anal. Methods, 2017, 9, 4988–4996.
40. D. L. Buhrman, P. I. Price and P. J. Rudewiczcor, J. Am. Soc. Mass Spectrom., 1996, 7, 1099–1105.
41. L. L. Jessome and D. A. Volmer, LC GC N. Am., 2006, 24, 498.
42. R. King, R. Bonfiglio, C. Fernandez-Metzler, C. Miller-Stein and T. Olah, J. Am. Soc. Mass Spectrom., 2000, 11, 942–950.
43. P. J. Taylor, Clin. Biochem., 2005, 38, 328–334.
44. S. Beck, A. Michalski, O. Raether, M. Lubeck, S. Kaspar, N. Goedecke, C. Baessmann, D. Hornburg, F. Meier, I. Paron, N. A. Kulak, J. Cox and M. Mann, Mol. Cell. Proteomics, 2015, 14, 2014–2029.
45. A. Li, Y. Zi, H. Guo, Z. L. Wang and F. M. Fernández, Nat. Nanotechnol., 2017, 12, 481.
46. A. Li, A. Hollerbach, Q. Luo and R. G. Cooks, Angew. Chem., Int. Ed., 2015, 54, 6893–6895.

---

Footnotes

† Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States.

‡ Electronic supplementary information (ESI) available: Additional experimental details, figures, and data as noted in the text. See DOI: 10.1039/c8an01716f

---