Lithium ion dynamics in LiZr₂(PO₄)₃ and Li_1.4Ca_0.2Zr_1.8(PO₄)₃

Abstract

High ionic conductivity, electrochemical stability and small interfacial resistances against Li metal anodes are the main requirements to be fulfilled in powerful, next-generation all-solid-state batteries. Understanding ion transport in materials with sufficiently high chemical and electrochemical stability, such as rhombohedral LiZr₂(PO₄)₃, is important to further improve their properties with respect to translational Li ion dynamics. Here, we used broadband impedance spectroscopy to analyze the electrical responses of LiZr₂(PO₄)₃ and Ca-stabilized Li_1.4Ca_0.2Zr_1.8(PO₄)₃ that were prepared following a solid-state synthesis route. We investigated the influence of the starting materials, either ZrO₂ and Zr(CH₃COO)₄, on the final properties of the products and studied Li ion dynamics in the crystalline grains and across grain boundary (g.b.) regions. The Ca²⁺ content has only little effect on bulk properties (4.2 × 10⁻⁵ S cm⁻¹ at 298 K, 0.41 eV), but, fortunately, the g.b. resistance decreased by 2 orders of magnitude. Whereas, ⁷Li spin-alignment echo nuclear magnetic resonance (NMR) confirmed long-range ion transport as seen by conductivity spectroscopy, ⁷Li NMR spin–lattice relaxation revealed much smaller activation energies (0.18 eV) and points to rapid localized Li jump processes. The diffusion-induced rate peak, appearing at T = 282 K, shows Li⁺ exchange processes with rates of ca. 10⁹ s⁻¹ corresponding, formally, to ionic conductivities in the order of 10⁻³ S cm⁻¹ to 10⁻² S cm⁻¹.

---

1. Introduction

In the years to come, all-solid-state Li or Na batteries¹ are expected to replace conventional systems² that still rely on flammable aprotic electrolytes. Ceramic cells may take advantage of highly flexible design possibilities if batteries with dimensions in the mm range are considered.^3,4 Moreover, ceramic batteries are going to withstand higher temperatures than their analogous cells with liquid components.⁵

For their realization, ceramic electrolytes with sufficiently high ionic conductivities are, however, needed.^5–9 The overall performance of NaSICON-type (Na SuperIonic CONductor) conductors^10,11 has attracted renewed interest to study the influence of synthesis conditions and dopants on morphology and ion dynamics. Earlier reports have shown that LiM₂(PO₄)₃ (M: Ge, Ti, Sn, Hf, Zr) exhibits good chemical stabilities under ambient conditions. This property comes along with a wide electrochemical stability window.^12,13 LiTi₂(PO₄)₃ is known as a very good Li-ion conductor but it suffers from the fact that Ti(IV) can easily be reduced to Ti(III) when in contact with metallic Li.¹⁴

In contrast to LiTi₂(PO₄)₃-based ceramics, including those in which Ti⁴⁺ is partly replaced by Al³⁺, LiZr₂(PO₄)₃ (LZP) shows a much better stability against Li anodes. If in contact with a Li metallic anode LZP forms stable decomposing products, such as Li₃P and layer-structured Li₈ZrO₆, that are able to conduct Li ions when present as thin layers. Importantly, this interphase also reveals sufficiently good wetting properties with respect to both Li metal and the electrolyte.¹⁵ LZP crystallizes with different structures, ionic conductivities sensitively depend on both the overall morphology and the defect chemistry involved. The ionic conductivity can be improved by incorporating different metals such as Y³⁺, Sc³⁺, Al³⁺, La³⁺ or Ca²⁺; this strategy is usually accompanied by a stabilization of the rhombohedral structure.^13,16–22 LZP is typically prepared at calcination temperatures of ca. 1173 K, the phase appearing under these conditions is denoted as the α-phase of LZP, which is subdivided in a orthorhombic form (α) and a monoclinic one (α′). At higher sintering temperatures, that is, approximately at 1423 K, the highly conductive rhombohedral structure α-LiZr₂(PO₄)₃ crystallizing with R3̄c symmetry is formed. α′-LiZr₂(PO₄)₃, obtained at lower temperatures, is usually a mixture of monoclinic LZP and triclinic LZP; its ionic conductivity is reported to be in the order of 10⁻⁸ S cm⁻¹ whereas α-LiZr₂(PO₄)₃ shows values around 10⁻⁵ S cm⁻¹.^15,22–25

In this work, the structure variation of different educts on the product formed is discussed. We analysed Li ion dynamics in LiZr₂(PO₄)₃ and Li_1+2xCa_xZr_2−x(PO₄)₃ (LCZP) by both broadband impedance spectroscopy^26,27 and ⁷Li nuclear magnetic resonance (NMR) spectroscopy, i.e., by recording diffusion-induced spin–lattice relaxation rates.^28–30 The latter are sensitive to both short-range and long-range ion transport through the crystal lattice of LZP. As we deal with powder samples with crystallite diameters in the μm range, NMR rates measured in the laboratory frame of reference are solely sensitive to bulk ion dynamics.

2. Experimental

2.1. Sample preparation

LiZr₂(PO₄)₃ (LZP) was prepared via a classic solid-state reaction by mixing stoichiometric amounts of Li₂CO₃ (Sigma Aldrich ≥99%), (NH₄)₂HPO₄ (Sigma Aldrich ≥99.9%) with either ZrO₂ (Sigma Aldrich ≥99%) or Zr(CH₃COO)₄ (= Zr(ac)₄). The starting compounds were mechanically milled for 2 hours by using a high-energy planetary ball mill (Fritsch Pulverisette 7 Premium line) at a rotation speed of 400 rpm. We used ZrO₂ beakers (45 mL), which were filled with 180 balls made of ZrO₂ (5 mm in diameter). The subsequent calcination process was carried out in Al₂O₃ crucibles at 900 °C (heating rate 10 °C min⁻¹) for 10 hours, where the decomposition of the hydrogen phosphate starts and initiates the reaction with Li₂CO₃. The resulting white powder was milled again for 2 hours at 400 rpm to guarantee a good contact between the particles. Finally, the mixture was pressed with 0.4 tons into pellets with a diameter of 5 mm. The pellets were filled into Al₂O₃ crucibles and sintered at 1150 °C (heating rate 10 °C min⁻¹) for 20 hours. To incorporate Ca²⁺ into LZP we used CaCO₃ (Alfa Aesar, >99%). An excess of 10 wt% Li₂CO₃ should compensate the loss of lithium during the high temperature heating process leading to Li_1.4Ca_0.2Zr_1.8(PO₄)₃ (LCZP). For the synthesis of LZP (and LCZP) using Zr(CH₃COO)₄ we needed to prepare the acetate as follows.³¹ 20 mmol Zirconium oxochloride (Sigma-Aldrich 99.99%) was dissolved under reflux in 100 mL of a mixture of MeCOOH (Sigma-Aldrich ≥99.5%) and Me(COO)₂O (Sigma Aldrich ≥99%) (1 : 9). After the mixture was allowed to cool to room temperature, a white crystalline deposit appeared. Finally, it was filtered and dried at 60 °C under vacuum.

2.2. X-ray powder diffraction

The sample obtained after the calcination process and the finally sintered product were characterized by X-ray powder diffraction (XRPD). We used a Bruker D8 Advance diffractometer operating with Bragg Brentano geometry and Cu K_α radiation. Diffractograms were recorded in air atmosphere and at room temperature covering a 2θ range from 20° to 100° with a step size of 0.02° (2 s per step). Rietveld analysis (X-PertHighScorePlus (PANanalytical)) was used to refine the diffraction data.

2.3. Impedance spectroscopy

For the impedance measurements the sintered samples were equipped with gold electrodes by a sputtering process. Gold electrodes with a layer thickness of 100 nm were applied on both sides with a sputter coater (LEICA EM SCD 050) to ensure a good electrical contact. To avoid any influence of moisture, the samples were dried at 60 °C under vacuum prior to the impedance measurements.

Impedance spectra were recorded with a Novocontrol Concept 80 broadband dielectric spectrometer equipped with a BDS 1200 cell combined with an active ZGS cell (Novocontrol). We measured complex impedances over a frequency range of ten decades (10 mHz to 10 MHz). The temperature in the sample holder was varied from 173 K to 473 K in steps of 20 K; the temperature program was automatically controlled by a QUATRO cryosystem (Novocontrol). During the measurements a dry nitrogen atmosphere was build up around the sample in the cryostat to avoid any contamination with water and/or oxygen.

2.4. Nuclear magnetic resonance measurements

For the time-domain NMR measurements, the powder samples LiZr₂(PO₄)₃ and Li_1.4Ca_0.2Zr_1.8(PO₄)₃ were sealed in Duran glass tubes (ca. 4 cm in length and 3 mm in diameter). During the sealing procedure they were kept under dynamic vacuum to safely protect them from any contact with humid air. We used ⁷Li NMR line shape measurements, spin lattice relaxation (SLR) experiments as well as ⁷Li spin alignment echo (SAE) NMR to collect information about Li activation energies and jump rates. Longitudinal NMR SLR rates (1/T₁) as well as spin-lock rates (1/T_1ρ) were measured with a Bruker Avance III spectrometer that is connected to a shimmed cryomagnet with a nominal magnetic field of 7 Tesla. This field corresponds to a ⁷Li Larmor frequency of ω₀/2π = 116 MHz. For the measurements at temperatures ranging from 173 K to 583 K a ceramic temperature probe (Bruker Biospin) was used. Depending on temperature and at a power level of 180 W the π/2 pulse length ranged from 2.2 μs to 2.4 μs.

⁷Li NMR SLR rates (1/T₁ = R₁) in the laboratory frame were acquired with the well-known saturation recovery pulse sequence. This sequence uses a comb of closely spaced π/2 pulses to destroy any longitudinal magnetization M_z. The subsequent recovery of M_z was detected as a function of waiting time t_d with a π/2 reading pulse: 10 × π/2 − t_d − π/2 – acquisition.^32,33 To construct the magnetization transients M_z(t_d), we plotted the area under the free induction decays vs. t_d. The transients M_z(t_d) were parameterized with stretched exponentials, M_z(t_d) ∝ 1 − exp(−(t/T₁)^γ), to extract the rates R₁. Additionally, rotating frame ⁷Li NMR SLRρ rates 1/T_1ρ (= R_1ρ) were measured by means of the spin lock technique: π/2-p_lock – acquisition.³² Here, we used a locking frequency ω₁/2π of 20 kHz. The duration of the spin-lock pulse t_lock was varied from 10 μs to 460 ms. To ensure full longitudinal relaxation between each scan the recycle delay was set to 5 × T₁. The R_1ρ rates were obtained by analyzing the resulting transients M_ρ(t_lock) with stretched exponentials with the form M_ρ(t_lock) ∝ exp(−(t_lock/T_1ρ)^κ). The stretching exponent γ varied from 1 to 0.8, the exponent κ ranges from 1 to 0.6.

Finally, mixing time (t_m) dependent ⁷Li SAE NMR decay curves were recorded with the help of the Jeener–Broekaert^34,35 three-pulse sequence: (90°)X-t_p–(45°)Y-t_m–45°-acq. We used a constant preparation time t_p of 25 μs to acquire two-time sinus–sinus single-spin correlation functions. The mixing time was varied from 30 μs up to several seconds. A suitable phase cycle^34,36 was employed to suppress unwanted coherences and to eliminate, as best as possible, dipolar contributions affecting the echo that appears after the reading pulse.³⁶ Fourier transformation of the spin alignment echoes, starting from the top of the signal, yields ⁷Li SAE NMR spectra useful to highlight quadrupole intensities due to the interaction of the quadrupole moment of the ⁷Li spin (spin-quantum number I = 3/2) and a non-vanishing electric field gradient.

3. Results and characterization

3.1. Characterization via X-ray powder diffraction

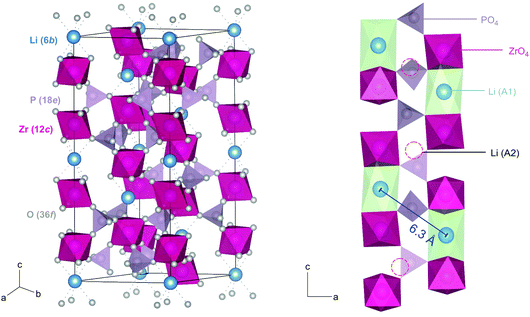
The purity of the crystalline samples synthesized was examined by XRPD. As mentioned above, diffraction patterns were collected at room temperature and under air atmosphere. The first XRPD pattern was recorded directly after the calcination process, i.e., after removal of CO₂, NH₃ and H₂O at 900 °C, the pattern is depicted in Fig. S1.† After this calcination step (10 hours), we see that LiZr₂(PO₄)₃ crystallizes with monoclinic structure (space group P12₁/c1, see Fig. S1 (ESI)†). Sintering the samples yields a crystalline material that is in agreement with the rhombohedral NaSICON structure³⁷ (space group R3̄c, Fig. 1);¹⁹ the corresponding XRPD pattern is shown in Fig. 2. This phase is isostructural with the sibling compound LiTi₂(PO₄)₃.³⁸ The increase in conductivity before and after sintering, i.e., the difference in ionic transport properties of monoclinic and rhombohedral LZP is illustrated in Fig. S1b.†

Fig. 1 Left: Rhombohedral crystal structure of LiZr₂(PO₄)₃. The tetrahedra in purple represent PO₄-units, octahedra in pink show ZrO₆, while the blue spheres denote the Li⁺ ions. Li⁺ is octahedrally coordinated by oxygen anions of the ZrO₆ octahedra. Right: Section of the rhombohedral crystal structure to show interstitial sites A2; the Li ions may use to jump between the regularly occupied sites A1. The A1–A1 distance is 6.3 Å, which is, presumably, much too large for a direct jump process.

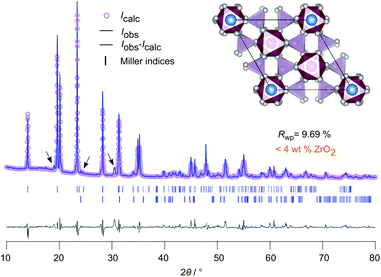Fig. 2 Rietveld refinement of LZP using ZrO₂ as educt. The sample was sintered at 1150 °C for 20 hours in a closed Al₂O₃-crucible. LZP crystallizes with space group R3̄cH, see Table S1† for further information. Selected reflections have been indexed with vertical bars. A very small amount (<4 wt%) of ZrO₂ was detected. The inset shows the ab-plane of the rhombohedral NaSICON structure with the viewing direction along the c-axis.

The Zr₂(PO₄)₃ framework of rhombohedral NaSICON-type LZP consists of two ZrO₆ octahedra and three PO₄ tetrahedra sharing O atoms. The octahedral and tetrahedral units are alternating with the cations to form infinite chains parallel to the ternary axis of the structure. Each PO₄ unit shares its oxygen with four ZrO₆ octahedra of three Zr₂(PO₄)₃ units to form the NaSICON framework. A 3D network of conduction pathways is formed that is used by the ions to diffuse through the crystal. In this case the Li ions (6b) are octahedrally coordinated by oxygen ions (36f) at the intersection of three conduction channels (A1). The A1 sites are located between pairs of ZrO₆ octahedra along the c-axis, while the (vacant) interstitial sites (□) A2 can be found between O₃ZrO₃A1O₃Zr-□-O₃ZrO₃A1. Since the A1–A1 distance in LZP is rather larger, we assume that interstitial sites, such as A2, are involved in Li⁺ diffusion. Because of the large spatial separation of Li ions in LZP, we expect rather low homonuclear dipole–dipole interactions resulting in narrow ⁷Li NMR lines even in the rigid lattice regime, see below.

In Fig. 2 the result of our Rietveld analysis of the diffraction pattern of LiZr₂(PO₄)₃ synthesized by using ZrO₂ as educt is shown. Our structure solution indeed points to rhombohedral symmetry characterized by the space group R3̄cH (ICSD, no. 201935), as already found by the study of Petit et al.¹⁹Via high-temperature neutron diffraction (T ≥ 423 K), Catti et al. reported on two Li⁺ positions displaced from the A1 and A2 sites (see Fig. S2†).²⁴ Here, in addition to the main rhombohedral phase, a minor impurity of ZrO₂ (<4 wt%) is seen (see black bars). Rietveld analysis yields the following lattice properties a (= b) = 8.824 Å and c = 22.456 Å; V = 1514.24 ų. By doping this sample with 5 wt% and 10 wt% Ca²⁺ the cell volume decreases (1512.64 ų (5 wt% Ca), 1506.22 ų (10 wt% Ca)) as expected; for further information we refer to Table S1 in the ESI.†

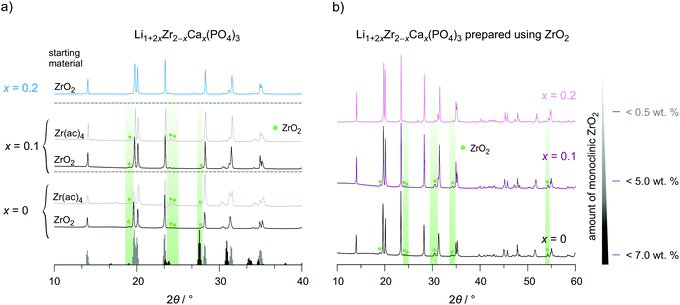
The preparation route with Zr(CH₃COO)₄ as starting material yields almost the same lattice parameters but the amount of non-reacted material is much higher and reaches values as high as 25 wt%. The incorporation of aliovalent Ca²⁺ ions, on the other hand, helps obtaining phase pure LZP with rhombohedral structure, as is illustrated in Fig. 3. The amount of unreacted ZrO₂ continuously decreases with increasing Ca-content. This behavior is also found for LCZP prepared with the help of Zr(ac)₄. Nonetheless, the amount of ZrO₂ remains much higher (>15 wt%) than that in samples prepared from ZrO₂ directly. Dots in Fig. 3 denote reflections belonging to ZrO₂. Worth noting, here we do not find any additional Bragg reflections that belong to triclinic LZP in all diffractograms. These have been seen in earlier reports.^22,39–41 We recognize that small variations in synthesis conditions, including heat treatment and cooling rates, might sensitively affect the phase purity of the final compounds.

Fig. 3 (a) X-ray powder diffraction pattern of the crystalline LiZr₂(PO₄)₃ and Li_1+2xZr_2−xCa_x(PO₄)₃ (x = 0.1 and 0.2). All samples were prepared by a classical solid-state route with either ZrO₂ as starting material (black) or Zr(CH₃COO)₄ (light grey). The vertical lines (in grey) at the bottom denote the reflections of rhombohedral LZP, those of monoclinic ZrO₂ are indicated by green dots. (b) XRPD pattern of Li_1+2xZr_2−xCa_x(PO₄)₃ prepared with the help of ZrO₂. The diffraction pattern reveal that the amount of the impurity phase ZrO₂ decreases with increasing Ca²⁺-content.

According to XRPD we decided to study, in detail, ion dynamics of the following samples: LiZr₂(PO₄)₃ prepared from ZrO₂ and Zr(ac)₄ as well as Li_1+2xZr_2−xCa_x(PO₄)₃ (x = 0.1 and 0.2) prepared with the help of ZrO₂. Similar to LiTi₂(PO₄)₃ and other NaSICON-type materials α-LiZr₂(PO₄)₃ shows low relative densities, here ranging from 78% to 84%.

3.2. Impedance spectroscopy

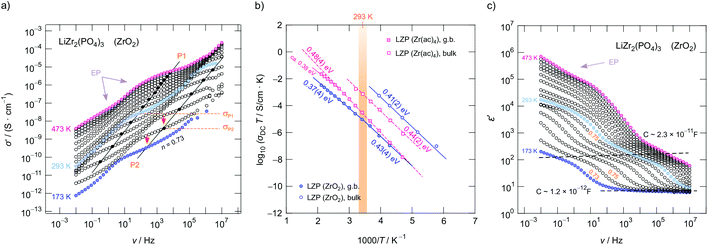
To study how Li⁺ ion transport is affected by x as well as to investigate whether the starting materials influence the dynamic parameters, we measured complex impedances over a large temperature and frequency range.^26,42 Exemplarily, in Fig. 4a conductivity isotherms of rhombohedral LiZr₂(PO₄)₃ are shown. Isotherms are obtained by plotting the real part, σ′, of the complex conductivity σ of LiZr₂(PO₄)₃ as a function of frequency ν. They are composed of four regimes. (i) At low frequencies (and sufficiently high temperatures and, thus, high ionic mobility) electrode polarization (EP) appears owing to the piling-up of ions near the surface of the blocking Au electrodes applied. In many cases a stepwise decay of σ′ is seen (cf. the two arrows in Fig. 4a). (ii) The polarization regime passes into so-called conductivity plateaus (P1) governing the isotherms at intermediate temperatures and low frequencies. If this plateau is identified with a bulk response, it reflects long-range ion transport and is given by the dc-conductivity σ_dc. By moving to higher frequency a shallow dispersive regime with a weak frequency dependence shows up. It directly merges into another plateau (iii, P2), which finally passes over in the high-frequency dispersive regime (iv) which can roughly be approximated with Jonscher's power law.

Fig. 4 (a) Conductivity isotherms of Ca-free LZP (synthesized from ZrO₂) recorded at temperatures ranging from 173 K to 473 K; isotherms have been recorded in steps of 20 K. We observed two plateaus P1 and P2 that correspond to the grain boundary (g.b., P1) and bulk response (P2). (b) Arrhenius plot of the DC conductivities associated with P1 and P2. The solid and dashed line show line fits with an Arrhenius law yielding activation energies ranging from 0.39 eV to 0.52 eV. Circles represent LZP synthesized from ZrO₂ and rectangles show results of LZP that was synthesized from Zr(ac)₄. LZP prepared from ZrO₂ shows the highest bulk ion conductivity that is characterized by 0.41 eV. (c) Real part of the complex permittivity as a function of frequency. P1 and P2 seen in (a) produce a two-step increase of ε′ characterized by permittivities and capacities being typical for a bulk electrical response and a response including ion-blocking grain boundaries. The same characteristics are seen for LZP prepared from Zr(ac)₄. Both processes can be approximated with a power law of the form ε′(ν) = ε(∞) + A_sν^−p with p ≠ f(T) ≈ 0.75, wherein ε(∞) represents the permittivity at very high frequencies.

In Fig. 4a the inflexion points of the plateaus P1 and P2 are highlighted by filled circles; straight lines connect these circles. The dispersive region belonging to plateau P2 is best seen at 173 K, it can be approximated with Jonscher's power law:⁴³σ′ = σ_dc + A₀νⁿ. Here A₀ is the so-called dispersion parameter and n represents the power law exponent, which takes a value of 0.73 at 173 K. To analyse our data in terms of dimensionality effects, we also studied the frequency dependence of the real part of the complex permittivity; the corresponding isotherms (ε′ vs. ν) are plotted in Fig. 4c; the plateaus P1 and P2 produce a two-step increase of ε′ when coming from high frequencies. As for σ′, also ε′(ν) can be approximated with exponents around 0.75 for P2, see Fig. 4c. Such Jonscher exponents are expected for 3D ionic conduction.⁴⁴

To determine which capacitances C govern the responses P1 and P2, we used the equation for a parallel-plate capacitor for an estimation C = ε₀ε_rA/d. Here ε₀ represents the electric field constant (8.854 × 10⁻¹² F m⁻¹), A the area and d the thickness of the sample. While the DC plateau (P2) at high frequencies is characterized by C = 1.2(1) × 10⁻¹² F, for the plateau at lower ν we found C = 2.3(2) × 10⁻¹¹ F. Therefore, the plateau associated with C in the pF range represents the bulk response, whereas P1 seen at lower frequencies is additionally governed by grain boundary contributions (g.b.) for which capacitances in the order of 10⁻¹¹ F are typically expected.⁴⁵

In the Arrhenius plot of Fig. 4b, σ_DCT of the two plateaus P1 and P2 is plotted vs. the inverse temperature T. σ_DCT does not change when several heating and cooling runs were performed. The lines in Fig. 4b refer to fits according to σ_DCT(P1, P2) ∝ exp(−E_a/(k_BT)); k_B denotes the Boltzmann's constant and E_a the corresponding activation energy. For LiZr₂(PO₄)₃ prepared from ZrO₂ we obtain E_a(P2) of 0.41(1) eV (in agreement with ref. 15 (0.40 eV) and ref. 25 (0.39 eV)), whereas for LiZr₂(PO₄)₃, when using Zr(ac)₄ as starting material, E_a increases to 0.44(1) eV (see Fig. 4b). At room temperature, the ionic conductivities of P2 are 3.6(2) × 10⁻⁵ S cm⁻¹ and 3.4(2) × 10⁻⁶ S cm⁻¹, respectively. For the sake of clarity, in Table 1 all activation energies E_a are listed, the table also includes values referring to Li_1+2xCa_xZr_2−x(PO₄)₃ (x = 0.1, x = 0.2) that has been prepared from ZrO₂.

Table 1 Comparison of activation energies E_a and prefactors σ₀ of the Arrhenius lines shown in Fig. 4b. The values refer to Ca-free and Ca-containing LiZr₂(PO₄)₃. Values in the brackets represent data determined by blocking grain boundaries (P2). Results for Ca-bearing LZP are also included

composition	E a/eV	log10(σ0/S cm^−1 K)	Starting material
a At lower temperatures the activation energy increases to 0.43(4) eV.
LiZr2(PO4)3	0.44(2) (0.48(4))	4.97(1) (3.86(2))	Zr(ac)4
LiZr2(PO4)3	0.41(2) (0.37(4)^a)	4.91(2) (1.49(7))	ZrO2
Li1.2Ca0.1Zr1.9(PO4)3	0.43(1) (0.52(9))	5.44(4) (4.14(7))	ZrO2
Li1.4Ca0.2Zr1.8(PO4)3	0.41(2) (0.38(4))	5.08(2) (3.49(1))	ZrO2

---

Unfortunately, by using Nyquist diagrams (see Fig. S3†), which show complex plane plots of the imaginary part Z′′ of the complex impedance, Z, vs. its real part Z′, the faster relaxation process, corresponding to P2, cannot be resolved properly. Instead, we used the complex modulus M′′(ν) representation⁴⁶ to visualize the two processes, see Fig. 5a and 6 (Fig. 6b includes data for Li_1+2xCa_xZr_2−x(PO₄)₃ prepared from ZrO₂).

Fig. 5 (a) Frequency dependence of the imaginary part of the electric modulus M′′, of LiZr₂(PO₄)₃ prepared from Zr(ac)₄. Spectra were recorded at the temperatures indicated. The lines are to guide the eye. As suggested by σ′(ν), two distinct peaks are visible denoted as M1 and M2. The temperature dependence of the corresponding relaxation rate τ_M⁻¹ is shown in (b). For comparison, the results of LiZr₂(PO₄)₃ (prepared from ZrO₂) and Li_1.4Zr_1.8Ca_0.2(PO₄)₃ (also prepared from ZrO₂) are included as well. Error margins are at least ± 0.1 eV.

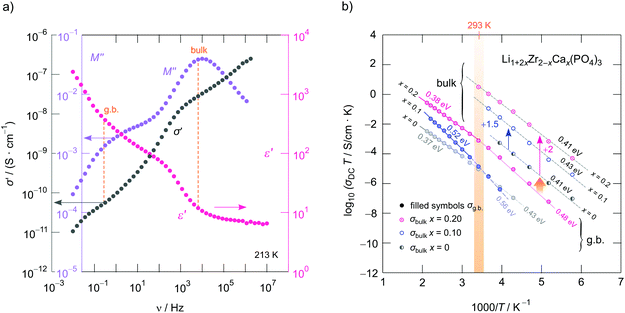Fig. 6 (a) Frequency dependence of the imaginary part M′′ of the complex modulus, the real part, ε′, of the permittivity as well as the real part, σ′, of the complex conductivity of LiZr₂(PO₄)₃ (prepared from ZrO₂). The isotherm was recorded at 213 K. The maxima in M′′ clearly refer to the plateaus P1 and P2 seen in σ′(ν). For comparison, the change of ε′(ν) is shown, too. (b) Arrhenius plot of the ionic conductivities referring to the plateaus P1 and P2 (σ_DCT vs. 1000/T) of cation-mixed crystalline Li_1+2xZr_2−xCa_x(PO₄)₃. Solid lines and dashed lines represent fits according to an Arrhenius law yielding the activation energies E_a as indicated. While solid lines refer to conductivities influenced by the grain boundary contributions, the dashed lines represent bulk ion dynamics in Li_1+2xZr_2−xCa_x(PO₄)₃. For the sake of clarity, the bulk ion conductivities for the samples with x = 0.20 and x = 0.10 have been plotted using an offset of +2 and +1.5 on the logarithmic scale. These conductivities coincide with those of the Ca-free sample. Activation energies with error margins are listed in Table 1.

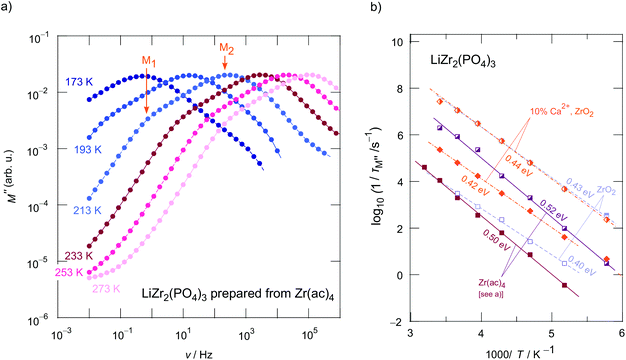
At sufficiently low temperatures two relaxation peaks M1 and M2 appear (see the orange arrows in Fig. 5a). These peaks are separated by two orders of magnitude on the frequency scale. This distance on the frequency scale is comparable with the ratio of σ_DC,P2 : σ_DC,P1; thus, they refer, as is seen in Fig. 6 to the plateaus P1 and P2 governing σ′(ν). As expected the two electrical relaxation frequencies mirror the ratio in conductivities. The peak with the larger amplitude (M2) corresponds to P2 in σ′(ν), the one with the smaller amplitude (M1) represents a relaxation process with a longer relaxation time (cf. P1), see also Fig. 6. As an estimation, M′′ is proportional to the inverse capacitance, M′′ ∝ 1/C.^45,47 Thus, we expect peak M2 to be characterized by a larger amplitude (3.4 pF) than M1 (30.1 pF). C₁/C₂ ≈ 10 is in good agreement with the amplitude ratio seen in Fig. 5a and 6a.

In order to compare activation energies extracted from σ_DC(P1, P2) we determined characteristic electrical relaxation frequencies 1/τ_M using the modulus peaks of Fig. 5a. 1/τ_M refers to frequencies at which the peaks appear. A comparison of activation energies for selected compounds is shown in Fig. 5b; errors are, at least, in the order of ±0.01 eV.

As mentioned in the beginning, Ca²⁺ incorporation increases the ionic conductivity of LZP. Fig. 6b shows the change in σ_DCT(P1, P2) of Li_1+2xCa_xZr_2−x(PO₄)₃ prepared from ZrO₂ for x = 0, x = 0.1 and x = 0.2. Most importantly, while σ_DCT(P2), which refers to bulk ion dynamics, is only slightly affected by x (E_a ranges from 0.41 eV to 0.43 eV, see Fig. 6b and Table 1 that also includes the prefactors), Ca²⁺ incorporation mainly reduces the g.b. resistance. We clearly see that σ_DCT(P1) is by two orders of magnitude larger than that of the sample with x = 0, see Fig. 6b. Most likely, the sintering process benefits from a Ca-rich composition, which helps reducing the blocking nature of surface regions of the Li_1+2xCa_xZr_2−x(PO₄)₃ crystallites. For x = 0.2 we obtain σ_DC(P2) = 4.2 × 10⁻⁵ S cm⁻¹ at 293 K. This value is only slightly lower than that of Li et al.¹⁵ (3.8 × 10⁻⁵ S cm⁻¹) when samples are compared that have been prepared by conventional sintering. If pellets were fired by spark plasma sintering, bulk values of 1.8 × 10⁻⁴ S cm⁻¹ were reported.¹⁵ It would be interesting to see, in coming studies, whether Ca²⁺, here acting as a sintering aid, segregates in the g.b. regions; such segregation would explain the finding that ion transport in the bulk regions is only little affected by Ca²⁺ incorporation.

Careful inspection of σ_DCT(P1) reveals that, if the samples with x = 0.2 is considered as an example (Fig. 6b), a slight kink is seen for temperatures well above room temperature; the activation energy changes from 0.48 eV to 0.38 eV at higher T. Presumably, Ca²⁺ in the grain boundaries influences the Li⁺ arrangements in these regions. Li⁺ order/disorder phenomena might lead to such changes.

3.3. Ion dynamics as seen by NMR measurements

Fig. 7a gives an overview of the ⁷Li NMR SLR rate measurements performed using an Arrhenius representation plotting the R_1(ρ) rates as a function of the inverse temperature. To identify the thermally activated regions, we measured R_1(ρ) of Li_1.4Ca_0.2Zr_1.8(PO₄)₃ over a wide temperature range to detect the maxima of diffusion-induced rate peaks.⁴⁸ Here we focused on the sample with the composition Li_1.4Ca_0.2Zr_1.8(PO₄)₃ as it shows the lowest bulk activation energy and the lowest amount of residual ZrO₂.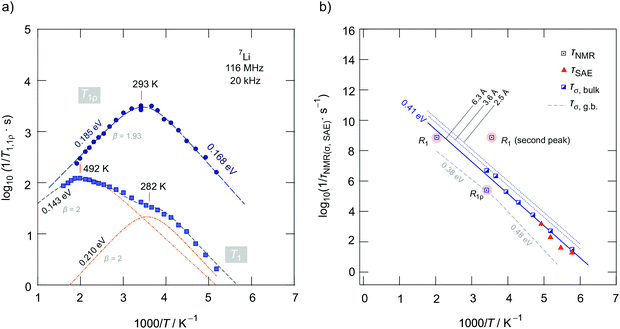

Fig. 7 (a) Arrhenius plot of the ⁷Li NMR relaxation rates R₁ and R_1ρ of Li_1.4Ca_0.2Zr_1.8(PO₄)₃ (prepared via the route using ZrO₂) measured in the laboratory frame of reference (116 MHz) and in the rotating frame of reference (20 kHz, nominal locking frequency). Dashed lines represent BPP-type fits to determine activation energies, prefactors and asymmetry parameters β. Temperatures indicate T_max of the rate peaks. The superposition of the R₁ rate peaks can be approximated with two symmetric peaks (β = 2). (b) Li⁺ jump rates as deduced from the diffusion-induced rate peaks R₁ and R_1ρ. For comparison, we also included jump rates that we estimated from frequency-dependent conductivity measurements and ⁷Li SAE NMR. See text for further explanations and Table 2 for error margins of the activation energies shown.

Below 183 K the rates R₁ reveal a non-diffusive background regime. In this temperature range longitudinal relaxation is induced by lattice vibrations or coupling of the Li spins with paramagnetic impurities.^48–50 At higher temperatures we expect the SLR rate to be increasingly induced by Li⁺ hopping processes. Such processes lead to magnetic and electric field fluctuations that cause longitudinal relaxation.⁴⁸ Indeed, the rates increase with temperature and, in both cases R₁ and R_1ρ, characteristic diffusion-induced rate peaks appear. Importantly, we recognize that R₁ passes through two maxima located at T_max = 282 K and 492 K, respectively. In general, at T_max the motional correlation rate 1/τ_c is related to ω₀via the relation τ_cω₀ ≈ 1. The so-called motional correlation rate 1/τ_c is identical, within a factor of two, with the Li⁺ jump rate 1/τ.^48,50 For R_1ρ, this maximum condition changes to τ_cω₁ ≈ 0.5.⁵¹ As ω₀ and ω₁ differ by more than three orders of magnitude, we are able to characterize Li⁺ motional correlation rates in LCZP with values in both the kHz and MHz range.⁵²

Here, we approximated the superposition of the two R₁ rate peaks by a sum of two Lorentzian-shaped spectral density functions J(ω₀, T) ∝ τ_c/(1 + (ω₀τ_c)^β) according to the concept introduced by Bloembergen, Purcell and Pound (BPP) for 3D isotropic diffusion,^53,54 see dashed line in Fig. 7a that follows the R₁ rates. For each peak we used a single term to deconvolute the temperature dependence of the overall R₁ rates measured, cf. the dashed-dotted lines in Fig. 7a, which will be discussed below. The rate 1/τ_c usually obeys the Arrhenius relation 1/τ_c = 1/τ_c,0 exp(−E_a/(k_BT)); 1/τ_c,0 represents the pre-exponential factor that is typically identified as the “attempt frequency” of the jump process.⁵⁵

In general, J(ω₀, T) is the Fourier transform of the underlying motional correlation function G(t′).⁴⁸ If G(t′) is or can be well approximated with a single exponential, β equals 2. Values smaller than 2 are expected for correlated motion, which is, e.g., seen for cations exposed to an irregularly shaped potential landscape. In such a landscape short-ranged Li⁺ diffusion will be different to long-range ion transport. In particular, forth-and-back jumps or, more generally speaking, localized motions will govern the rate R₁ in the low-temperature regime, which is characterized by τ_cω₀ ≫ 1. In this regime we have J(ω₀) ∝ τ_c⁻¹ω₀^−β with (1 < β ≤ 2). β < 2 produces asymmetric rate peaks which are often found for structurally complex ion conductors with a non-uniformly shaped energy landscape. Ion dynamics in this regime are anticipated to be affected by correlation effects because of both structural disorder and strong Coulomb interactions of the moving ions.⁵⁶ As the peak is asymmetric, the activation energy on this side of the peak, E_{a, low}, is lower than that of the high-temperature flank, E_{a, high}; the two values are linked to each other via E_{a, low} = (β_(ρ) − 1)E_{a, high}. In the regime τ_cω₀ ≪ 1, that is, on the high-temperature side of the peak, many jump events are sensed during one Larmor precession and the probability is high that also these jumps contribute to longitudinal relaxation which are characterized by higher activation energies. Usually, on this side of the rate peak R₁(1/T) long-range Li ion dynamics is sensed; in this limit we obtain J(ω₀) ∝ τ_c.²⁹

In the present case, approximating the rate peaks with a sum of two BPP-type spectral densities yields activation energies of E_a,1 = 0.210(5) eV and E_a,2 = 0.143(5) eV. As both rate peaks join up, information on β are difficult to obtain. Here, the fitting routine yields β = 2 for the two peaks resulting in symmetric peaks with E_{a, low} = E_{a, high} = E_a,i (i = 1, 2). Note that the peak at higher T (i = 2) is only partly visible which influences the precise determination of E_{a, high}. We clearly recognize that E_a,i as determined from R₁ SLR NMR turned out to be significantly lower than E_a obtained from σ_DC measurements describing bulk ion dynamics. The fact that E_a,i < E_{a, DC} shows that the number of jump events seen by NMR does not include all types of jumps needed for long-range diffusion. Obviously, the spin-fluctuations sensed by NMR are already sufficient to generate a full R₁ peak. Thus, we conclude that the Li⁺ ions in LCZP are highly mobile on a short-range length scale while long-range ion transport is, however, characterized by much larger activation energies than 0.2 eV. This situation resembles that of Li⁺ ion dynamics in argyrodite-type Li₆PS₅I, which has been studied recently by our group.⁴² Here, we assume that rapid forward–backward exchange processes between the sites A1 and A2 might be responsible for the peaks seen in NMR spin–lattice relaxometry. A2 sites might be occupied in samples with x > 0. Here, especially the peak appearing at T_max = 282 K for Li_1.4Ca_0.2Zr_1.8(PO₄)₃ points to rapid (localized) exchange processes with residence times in the order of several ns. According to ω₀τ_c ≈ 1 we estimate that at T_max the jump rate should be in the order of 1/τ = 7.3 × 10⁸ s⁻¹ ≈ 10⁹ s⁻¹. A very similar behavior has recently been seen also for NaSICON-type Na_3.4Sc_0.4Zr_1.6(SiO₄)₂PO₄.

To complement our R₁ measurements, we carried out spin-lock NMR SLR measurements at a locking frequency of 20 kHz. As expected we detected a prominent spin-lock NMR peak R_1ρ(1/T) at much lower temperature than 492 K. A single peak appears at T_max = 293 K. It turned out to be slightly asymmetric with an activation energy of E_{a, high} = 0.185(5) eV and E_{a, low} = 0.168(5) eV. At first glance we would say that the R_1ρ peak might correspond to the R₁ peak seen at T_max = 492 K. Keeping, however, both the locking frequency of only 20 kHz and the rather low activation energy of 0.185 eV in mind, the R_1ρ peak belonging to R₁(1/T) with T_max = 492 K would be expected to appear at much lower temperatures than ambient. Even if we replace ω₁ by an effective frequency ω_{1, eff} (>ω₁), which takes local magnetic fields into account that increase ω₁, no satisfactory joint fit results that is characterized by the same E_a and the same τ_c,0 for the two peaks. Here, only unreliably high ω_{1, eff} values reaching the MHz range would result in a joint fit connecting the two peaks. Table 2 shows an overview of the results obtained from analyzing the three peaks individually by BPP-type spectral density functions. It also includes the amplitudes C_NMR in R_1(ρ) = C_NMRJ(ω₀, T). We see that the amplitudes of the two R₁ rate peaks differ by approximately one order of magnitude. Most likely, stronger quadrupolar relaxation governs the peak appearing at higher T. The corresponding prefactor 1/τ₀ is relatively low, while that of the peak showing up at 282 K (1/τ₀ = 5.9 × 10¹² s⁻¹) is consistent with frequencies typically expected for phonons.

Table 2 Results of analyzing the ⁷Li NMR rate peaks R₁ and R_1ρ of Li_1.4Ca_0.2Zr_1.8(PO₄)₃. The coupling constant C_NMR, which is the amplitude of the rate peak, J(ω₀) = C_NMRτ_c/(1 + (ω₀τ_c)^β, turned out to be in the range of 1010 and 10¹¹ s⁻². Values in the order of 10⁻¹³ s for τ₀ correspond to (inverse) phonon frequencies

	E a (= Ea, high)	C NMR	β (ρ)	τ 0
a The value in brackets refers to Ea, low of the R1ρ peak seen at 293 K.
R 1 (Tmax = 492 K)	0.143(5) eV	1.8(1) × 10^11 s^−2	2	4.1(2) × 10^−11 s
R 1 (Tmax = 282 K)	0.210(5) eV	2.5(1) × 10^10 s^−2	1.93	1.7(2) × 10^−13 s
R 1,ρ (Tmax = 293 K)	0.185(5) eV	1.5(1) × 10^9 s^−2	2	2.8(1) × 10^−9 s
	(0.168(5) eV)^a

---

The above-mentioned jump rate derived from SLR NMR at T_max (1/τ = 7.3 × 10⁸ s⁻¹) can be converted into diffusion coefficients with the help of the Einstein–Smoluchowski equation according to D_NMR = a²/(6τ), which is valid for 3D diffusion.²⁹ As an estimation, by inserting a = 6.3 Å, which is simply the shortest Li–Li distance, we obtain D_NMR = a²/(6τ) = 4.8 × 10⁻¹¹ m² s⁻¹. Assuming the interstitial sites A2 participating in exchange processes D_NMR reduces to 1.8 × 10⁻¹¹ m² s⁻¹. A distance of a = 6.3 Å is, of course, by far too long for a single hopping process. In the structural model of Catti et al. the distance reduced to 4.2 Å at 423 K.²⁴

In the Arrhenius plot of Fig. 7b we compare the rates 1/τ from NMR (1/τ_NMR) with those obtained after converting σ_DC into jump rates by using the Nernst Einstein equation. As we do not know the exact jump distance, we calculated 1/τ_σ for three different values of a. 1/τ_σ represents an average value mainly influenced by Li⁺ jumps necessary for long-range ion transport. Most likely, the R₁ peak appearing at 492 K is more related to jump processes enabling the ions to move over longer distances. The large discrepancy between 1/τ_NMR(282 K) and 1/τ_σ once again visualizes that the R₁(1/T) peak at low T reflects localized jump processes. We do not find evidences that this peak originates from any phase transitions, as the phase-pure Ca-bearing samples show rhombohedral structure. For comparison, in Fig. 7b we also included 1/τ_σ rates estimated from conductivity values that characterize the influence of grain boundaries. Interestingly, 1/τ_NMR(293 K, R_1ρ) = 2.5 × 10⁵ s⁻¹, which we estimated via the relation ω₁τ_c ≈ 0.5, see above, agrees with 1/τ_{σ, g.b}. In contrast to R₁, which as far as μm-sized crystallites are considered, is mainly affected by bulk processes, the corresponding spin-lock NMR rates R_1ρ seems to be (also partly) sensitive to ion dynamics also influenced by interfacial processes. This behaviour is consistent with the following comparison. At frequencies in the kHz range (ω₁/2π = 20 kHz) and at T = 282 K the isotherms σ′(ν) are mainly influenced by the g.b. response rather than bulk ion dynamics.

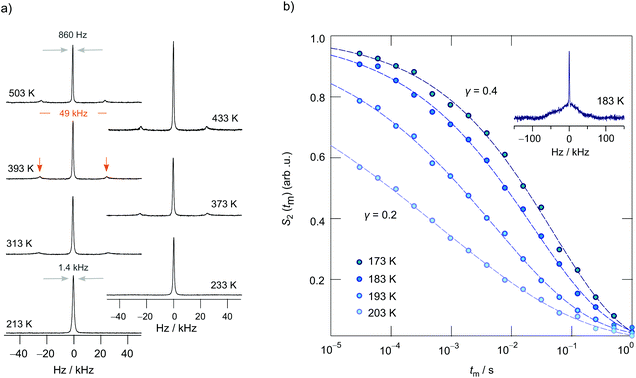
To shed more light on long-range ion dynamics, we used ⁷Li NMR line shape measurements and ⁷Li SAE NMR experiments^46,57–60 to further characterize ionic transport in LCZP. Via SAE NMR we should be able to get access to diffusion parameters that characterize ion transport over longer distances as the method is sensitive to exchange processes on the time scale that is comparable to that of DC conductivity measurements.⁴⁸ In Fig. 8a variable-temperature ⁷Li NMR spectra of Li_1.4Ca_0.2Zr_1.8(PO₄)₃ are shown. Remarkably, at temperatures as low as 213 K a relatively narrow NMR line is detected whose width is only 1.4 kHz. Usually, we would expect a width in the order of several kHz due to ⁷Li–⁷Li dipolar interactions. Here, the large Li–Li distance of 6.3 Å between the A1 sites, and between A1 sites and Li ions occupying interstitial sites in samples with x > 0, leads to relatively weak dipole–dipole interactions producing a narrow line already in the rigid-lattice regime. With increasing temperature, the line undergoes a slight narrowing process because of Li diffusion that averages dipolar couplings. Finally, at even higher temperatures, i.e., in the extreme narrowing regime, its width is only governed by the inhomogeneity of the external magnetic field.

Fig. 8 (a) ⁷Li NMR spectra of Li_1.4Ca_0.2Zr_1.8(PO₄)₃ recorded at the temperatures indicated. The NMR line transforms from a Gaussian shape at low temperatures to a Lorentzian one at elevated T. Clearly visible and well-defined quadrupole powder patterns emerge at temperatures higher than 313 K. (b) ⁷Li SAE NMR decay curves of LCZP whose spectra are shown in (a). Decay curves follow stretched exponentials (0.2 < γ < 0.4) which are shown as solid lines. Data have been recorded at a Larmor frequency of 116 MHz. See text for further details. Inset: Fourier transform of a spin-alignment echo, starting from the top of the echo, which was recorded at a fixed t_p of 20 μs and a short mixing time of t_m = 100 μs. In addition to a “central line” a rather broad quadrupole foot is visible illustrating the distribution of EFGs seen by the Li ions in the dynamic regime of the rigid lattice.

Interestingly, at 313 K two satellite lines emerge that belong to a first-order quadrupole powder pattern arising from the interaction of the quadrupole moment of the ⁷Li nucleus (I = 3/2) with a non-vanishing electric field gradient (EFG) at the nuclear site. The EFG is produced by the electric charge distribution in the direct neighborhood of the ⁷Li nucleus. This additional interaction alters the Zeeman levels and, thus, also the associated (angular) Zeeman frequency ω₀ towards ω₀ ± ω_Q.^32,54 The singularities seen in Fig. 8a correspond to the 90° satellite transitions of a powder pattern, which typically show up at sufficiently high T; this feature belongs to the universal characteristics of crystalline materials studied by NMR.^32,50,61 Their distance on the frequency scale, if we simply assume an EFG with axial symmetry, corresponds to δ/2. δ is the quadrupole coupling constant. A distance of 49 kHz leads to δ = 98 kHz,⁵⁸ which is in fair agreement with the value reported by Petit et al.²⁰ Here, this value should, however, be interpreted as an average value, as we cannot exclude a small distribution of EFGs the ions are exposed to at very low temperatures. At very low T, the intensity of the singularities is too low to be detectable by single pulse experiments. Instead, echo experiments should be used that are able to avoid receiver dead time effects. In Fig. 8b (see inset) a spectrum is shown that is the Fourier transform of a stimulated echo. Indeed, a sharp central line is located on top of a broad quadrupole foot. Hence, we conclude that the Li ions are exposed to a distribution of EFGs.

Fluctuations in ω_Q seen by the ions when jumping between electrically inequivalent sites can be used to record sinus–sinus two-time correlation functions. In Fig. 8a the change of the ⁷Li SAE amplitude S₂ is shown vs. the logarithmic mixing time t_m. S₂ depends on both the preparation time t_p and t_m. Here, we measured the decay curve at fixed t_p (= 20 μs) but variable mixing time. Stretched exponentials of the form S₂ ∝ exp(−(t_m/τ_SAE)^λ), with a stretching factor λ ranging from 0.21 to 0.37, are best suited to describe the dependence of S₂(t_p = const., t_m) in this temperature regime. In general, stretching factors deviating from λ = 1 indicate non-Debye-like motional process. For example, such deviations can arise from motions in disordered matrices or in confined dimensions^59,62 leading to motional correlation functions whose decay slows down with increasing observation time. With increasing T the inflexion point of the echo decay curves shifts towards shorter t_m. At the same time, the shape of S₂ steadily becomes more stretched until a value of λ = 0.21 is reached at T = 203 K. At sufficiently long mixing times the curves S₂(t_p = const., t_m) always reach S_2,∞ = 0, which either indicates a rather large number of quadrupole frequencies involved or which points to the influence of dipolarly coupled spins, as is well-described in literature.³⁶ The rates 1/τ_SAE governing the stretched decay functions are included in Fig. 7b. We recognize that they are in fair agreement with those rates, 1/τ_{σ, bulk}, which were estimated from bulk ionic conductivities of Li_1.4Ca_0.2Zr_1.8(PO₄)₃.

4. Conclusion

We used a conventional solid-state reaction procedure to synthesize NaSICON-type LiZr₂(PO₄)₃ and investigated both its ionic conductivity and Li⁺ diffusivity by broadband conductivity measurements and NMR spectroscopy. Ca²⁺ incorporation helps prepare Li_1+2xZr_2−xCa_x(PO₄)₃ crystallizing with rhombohedral symmetry. While bulk ion dynamics is not influenced by the Ca²⁺ content, the grain boundaries in LZCP turn out to be less blocking for Li⁺ ions as compared to the sample with x = 0. We observed an increase in the low-frequency ionic conductivity by two orders of magnitude when increasing x from x = 0 to x = 0.2. For Li_1.4Ca_0.2Zr_1.8(PO₄)₃⁷Li NMR relaxometry revealed rapid localized Li⁺ jump processes with activation energies of 0.21 eV and 0.14 eV. The diffusion-induced rate peak seen at 282 K points to a very high jump rate in the order of 10⁹ s⁻¹ at this temperature. On the other hand, ⁷Li spin-alignment echo spectroscopy confirmed that long-range ion transport in the bulk regions of Li_1.4Zr_1.8Ca_0.2(PO₄)₃ needs to be characterized by an activation energy of 0.41 eV as determined by variable-frequency conductivity measurements.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 769929. We thank the Deutsche Forschungsgemeinschaft for further support (FOR1277, WI3600(2-1;4-2). Further support by the K-project ‘safe battery’ (FFG) is highly appreciated.

References

1. J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141.
2. D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29.
3. J. I. Hur, L. C. Smith and B. Dunn, Joule, 2018, 2, 1187–1201.
4. E. Quartarone and P. Mustarelli, Chem. Soc. Rev., 2011, 40, 2525–2540.
5. J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
6. Z. Z. Zhang, Y. J. Shao, B. Lotsch, Y. S. Hu, H. Li, J. Janek, L. F. Nazar, C. W. Nan, J. Maier, M. Armand and L. Q. Chen, Energy Environ. Sci., 2018, 11, 1945–1976.
7. Y. Inaguma, K. Funayama, A. Aimi, D. Mori, Y. Hamasaki, K. Ueda, M. Ikeda, T. Ohno and K. Mitsuishi, Solid State Ionics, 2018, 321, 29–33.
8. A. Sakuda, A. Hayashi and M. Tatsumisago, Sci. Rep., 2013, 3, 2261.
9. A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856.
10. M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064.
11. M. Guin, F. Tietz and O. Guillon, Solid State Ionics, 2016, 293, 18–26.
12. H. Xie, J. B. Goodenough and Y. Li, J. Power Sources, 2011, 196, 7760–7762.
13. V. Ramar, S. Kumar, S. R. Sivakkumar and P. Balaya, Electrochim. Acta, 2018, 271, 120–126.
14. S. Hasegawa, N. Imanishi, T. Zhang, J. Xie, A. Hirano, Y. Takeda and O. Yamamoto, J. Power Sources, 2009, 189, 371–377.
15. Y. T. Li, W. D. Zhou, X. Chen, X. J. Lu, Z. M. Cui, S. Xin, L. G. Xue, Q. X. Jia and J. B. Goodenough, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13313–13317.
16. H. Xie, Y. Li and J. B. Goodenough, RSC Adv., 2011, 1, 1728–1731.
17. C. R. Mariappan, P. Kumar, A. Kumar, S. Indris, H. Ehrenberg, G. Vijaya Prakash and R. Jose, Ceram. Int., 2018, 44, 15509–15516.
18. L. Xiaojuan, F. Xue, L. Wenwei, L. Haitao and Z. Yunjie, Adv. Engin. Res., International Conference on Advances in Energy, Environment and Chemical Engineering, 2015, pp. 227–230, DOI:  DOI:10.2991/aeece-15.2015.45.
19. D. Petit, P. Colomban, G. Collin and J. P. Boilot, Mater. Res. Bull., 1986, 21, 365–371.
20. D. Petit and B. Sapoval, Solid State Ionics, 1986, 21, 293–304.
21. M. Casciola, U. Costantino, L. Merlini, I. G. K. Andersen and E. K. Andersen, Solid State Ionics, 1988, 26, 229–235.
22. M. Catti and S. Stramare, Solid State Ionics, 2000, 136–137, 489–494.
23. M. Catti, S. Stramare and R. Ibberson, Solid State Ionics, 1999, 123, 173–180.
24. M. Catti, A. Comotti and S. Di Blas, Chem. Mater., 2003, 15, 1628–1632.
25. H. El-Shinawi, C. Greaves and J. Janek, RSC Adv., 2015, 5, 17054–17059.
26. F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590.
27. S. Lunghammer, Q. Ma, D. Rettenwander, I. Hanzu, F. Tietz and H. M. R. Wilkening, Chem. Phys. Lett., 2018, 701, 147–150.
28. B. Stanje, D. Rettenwander, S. Breuer, M. Uitz, S. Berendts, M. Lerch, R. Uecker, G. Redhammer, I. Hanzu and M. Wilkening, Ann. Phys., 2017, 529, 1700140.
29. M. Uitz, V. Epp, P. Bottke and M. Wilkening, J. Electroceram., 2017, 38, 142–156.
30. V. Epp, Q. L. Ma, E. M. Hammer, F. Tietz and M. Wilkening, Phys. Chem. Chem. Phys., 2015, 17, 32115–32121.
31. N. P. Kuz'mina, A. E. Altsybeev, I. P. Malkerova, A. S. Alikhanyan and I. E. Korsakov, Russ. J. Inorg. Chem., 2006, 51, 1750–1754.
32. V. Epp, Ö. Gün, H. J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123.
33. E. Fukushima and S. B. W. Roeder, Experimental Pulse NMR. A Nuts and Bolts Approach, Addison-Wesley Publ. Comp., Reading, 1981.
34. R. Böhmer, J. Magn. Reson., 2000, 147, 78–88.
35. J. Jeener and P. Broekaert, Phys. Rev., 1967, 157, 232–240.
36. F. Qi, G. Diezemann, H. Böhm, J. Lambert and R. Böhmer, J. Magn. Reson., 2004, 169, 225–239.
37. C. Masquelier, C. Wurm, J. Rodríguez-Carvajal, J. Gaubicher and L. Nazar, Chem. Mater., 2000, 12, 525–532.
38. A. Aatiq, M. Ménétrier, L. Croguennec, E. Suard and C. Delmas, J. Mater. Chem., 2002, 12, 2971–2978.
39. K. Arbi, M. Ayadi-Trabelsi and J. Sanz, J. Mater. Chem., 2002, 12, 2985–2990.
40. I. A. Stenina, Y. A. Velikodnyi, V. A. Ketsko and A. B. Yaroslavtsev, Inorg. Mater., 2004, 40, 967–970.
41. J. Sanz, J. M. Rojo, R. Jiménez, J. E. Iglesias and J. Alamo, Solid State Ionics, 1993, 62, 287–292.
42. I. Hanghofer, M. Brinek, S. L. Eisbacher, B. Bitschnau, M. Volck, V. Hennige, I. Hanzu, D. Rettenwander and H. M. R. Wilkening, Phys. Chem. Chem. Phys., 2019, 21, 8489–8507.
43. A. K. Jonscher, Nature, 1977, 267, 673–679.
44. D. L. Sidebottom, Phys. Rev. Lett., 1999, 83, 983–986.
45. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138.
46. B. Ruprecht, H. Billetter, U. Ruschewitz and M. Wilkening, J. Phys.: Condens. Matter, 2010, 22, 245901.
47. S. Breuer, D. Prutsch, Q. L. Ma, V. Epp, F. Preishuber-Pflügl, F. Tietz and M. Wilkening, J. Mater. Chem. A, 2015, 3, 21343–21350.
48. M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53–65.
49. M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291–9300.
50. A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302.
51. A. Kuhn, M. Kunze, P. Sreeraj, H. D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2–8.
52. M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291–9300.
53. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712.
54. A. Abragam, The Principles of Nuclear Magnetism, Claredon Press, Oxford, 1961.
55. P. M. Richards, in Topics in Current Physics, ed. M. B. Salamon, Springer, Berlin, 1979, vol. 15.
56. A. Bunde, P. Maass and M. Meyer, Phys. A, 1992, 191, 433–437.
57. P. Bottke, D. Rettenwander, W. Schmidt, G. Amthauer and M. Wilkening, Chem. Mater., 2015, 27, 6571–6582.
58. M. Wilkening and P. Heitjans, J. Phys.: Condens. Matter, 2006, 18, 9849–9862.
59. M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024311.
60. M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B, 2008, 78, 054303.
61. R. Bertermann, W. Müller-Warmuth, C. Jansen, F. Hiltmann and B. Krebs, Solid State Ionics, 1999, 117, 245–255.
62. P. Bottke, Y. Ren, I. Hanzu, P. G. Bruce and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 1894–1901.

---

Footnote

† Electronic supplementary information (ESI) available: Further X-ray powder patterns, results from structure solution and Nyquist plots. See DOI: 10.1039/c9dt01786k

---