 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: Generalized Langevin dynamics: construction and numerical integration of non-Markovian particle-based models
Gerhard
Jung
*ab,
Martin
Hanke
c and
Friederike
Schmid
a
aInstitut für Physik, Johannes Gutenberg-Universität Mainz, Staudingerweg 9, 55128 Mainz, Germany. E-mail: jungge@uni-mainz.de; friederike.schmid@uni-mainz.de
bGraduate School of Excellence Materials Science in Mainz, Staudingerweg 9, 55128 Mainz, Germany
cInstitut für Mathematik, Johannes Gutenberg-Universität Mainz, Staudingerweg 9, 55128 Mainz, Germany. E-mail: hanke@mathematik.uni-mainz.de
First published on 30th November 2018
Abstract
Correction for ‘Generalized Langevin dynamics: construction and numerical integration of non-Markovian particle-based models’ by Gerhard Jung et al., Soft Matter, 2018, DOI: 10.1039/c8sm01817k.
Algorithm 1 presented in the manuscript on page 4 contains a significant typographical error which was introduced in the typesetting process. Line 13 of Algorithm 1 in the published manuscript is:
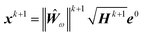 and has been corrected to
and has been corrected to 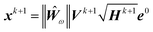 . The full and correct algorithm is repeated below.
. The full and correct algorithm is repeated below.
The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
| This journal is © The Royal Society of Chemistry 2018 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)

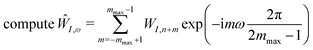
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif)

![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif)
