Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ice-templated poly(vinylidene fluoride) ferroelectrets
Yan
Zhang
 *a,
Chris R.
Bowen
*a,
Chris R.
Bowen
 a and
Sylvain
Deville
a and
Sylvain
Deville
 b
b
aDepartment of Mechanical Engineering, University of Bath, Bath, UK. E-mail: yanzhangmaterial@hotmail.com
bLaboratoire de Synthèse et Fonctionnalisation des Céramiques, UMR 3080 CNRS/Saint-Gobain, Saint-Gobain Research Provence, Cavaillon, France
First published on 7th December 2018
Abstract
Ferroelectrets are piezoelectrically-active polymer foams that can convert externally applied loads into electric charge for sensor or energy harvesting applications. Existing processing routes used to create pores of the desired geometry and degree of alignment appropriate for ferroelectrets are based on complex mechanical stretching and chemical dissolution steps. In this work, we present the first demonstration of the use of freeze casting as a cost effective and environmentally friendly approach to produce polymeric ferroelectrets. The pore morphology, phase analysis, relative permittivity and direct piezoelectric charge coefficient (d33) of porous poly(vinylidene fluoride) (PVDF) based ferroelectrets with porosity volume fractions ranging from 24% to 78% were analysed. The long-range alignment of pore channels produced during directional freezing is shown to be beneficial in forming a highly polarised structure and high d33 ∼ 264 pC N−1 after breakdown of air within the pore channels during corona poling. This new approach opens a way to create tailored pore structures and voids in ferroelectret materials for transducer applications related to sensors and vibration energy harvesting.
Introduction
Piezoelectric materials manifest themselves by the generation of a charge when subjected to mechanical loads. The direct piezoelectric effect can be used to sense dynamic pressure, acceleration, or change in force and there is also potential for scavenging energy from motion in the surrounding environment.1 Ferroelectric materials are a sub-class of piezoelectric materials and exhibit piezoelectric properties as a result of a remnant polarisation due to the presence of aligned domains, which have been of interest in sensor and energy harvesting applications.2 In order to evaluate the performance of such materials, relevant figures of merit have been widely used, such as dij2/εσ33 for piezoelectric energy harvesting applications, and dij/εσ33 for sensor applications, where dij is the piezoelectric charge coefficient, and εσ33 is the permittivity of the material at constant stress. These figures of merit indicate that a low permittivity, and high piezoelectric activity are beneficial for both sensor and energy harvesting applications. Ferroelectric ceramics often exhibit high figures of merit for high sensor sensitivity or high energy capability, but they are relatively high density and exhibit poor mechanical flexibility. Ferroelectric polymers exhibit a relatively low piezoelectric activity, but they have a low permittivity, are lightweight and exhibit flexibility which is important for flexible electronics, wearables and stretchable electronics.3As an alternative to ferroelectric materials, ferroelectrets are a class of piezoelectrically-active foam manufactured from a non-polar porous polymer whereby gas, such as air, within the pore space can be subjected to electrical breakdown when subjected to a high electric field during a poling process. This process results in opposing electric charges being deposited on the upper and lower surfaces of the pores.4 As a result of a poling process, a dipole-like structure is formed where the dipole moment is changed by the application of a mechanical stress, thereby leading to a piezoelectric response. The piezoelectric d33 charge coefficient, a measure of the charge generated per unit force, can be an order of magnitude greater than those found in conventional ferroelectric polymers, such as polyvinylidene fluoride (PVDF) and can be comparable or even greater than ferroelectric ceramics5–7 while maintaining a high compliance due to their polymeric nature. For example, for sensor applications a ferroelectret polymer exhibited a sensing figure of merit of d33/εσ33 that was 10–150 times higher than a ferroelectric PVDF polymer and over a thousand times higher than a lead zirconate titanate ceramic (PZT), due to its high d33 values and low permittivity; for example d33 ∼ 25–700 pC N−1 and εσ33 ∼ 1.12–1.23 for a porous polypropylene based ferroelectret polymer.8,9 Ferroelectret polymers with an average pore diameter of 0.9 μm or a pore height of 4.5 μm and pore width of 1.55 μm were also demonstrated to produce 44.9 nW10 and 4.35 mW11 for energy harvesting applications. Therefore, ferroelectrets have gained much interest in low-level mechanical energy harvesting12 and sensing4 based on their combination of relatively high piezoelectric coefficient and low permittivity.
To create ferroelectret materials with a high electro-mechanical response, it is desirable to have a pore structure that exhibits a cellular geometry or is ‘lens-shaped’ so that pores are elongated in the lateral extension; this can be typically >10 μm long and only a few μm in height.13,14 Such a morphology is beneficial due to the relatively low elastic stiffness of such an anisotropic pore structure in the polarisation direction.15,16 Micron-size pores are desirable to achieve micro-discharges within pores, which are interpreted in terms of in terms of Townsend breakdown17 which follows Paschen's law18 and large electric fields are required in very small pores. As a result, the majority of existing processing routes have focused on creating cellular, elongated or lens-shaped microstructures for ferroelectrets. Current processing routes include biaxial stretching of polymers with embedded foreign particles followed by chemically dissolution of the embedded foreign particles,10,11 or the injection of the polymer by high-pressure gas to further modify the pore size and shape.19,20
Freeze casting, also termed the ice-templating method,21 is an effective and facile technique to prepare materials with tailored pore morphology and anisotropic porosity. This approach involves freezing a colloidal suspension under a unidirectional gradient temperature, followed by sublimation of the solvent. The aligned pore channels formed parallel to the freezing direction are a direct replica of the solvent after solidification. Freeze casting has potential to be a cost effective and environmentally friendly approach, and it is feasible to tailor pore characteristics and form aligned pores in almost all types of materials: ceramics, polymers, metals and their composites.21 To date, more than 30 different types of polymers with straight, aligned and elongated pore channels have been formed by freeze casting for catalysis, separation, biomedical and thermal insulation applications.21 However, there has been no report to date on the freeze casting of polymers to create polymeric ferroelectrets.
In this work we have used freeze casting of PVDF to produce a porous ferroelectret material. PVDF is a classical ferroelectric polymer which is partially crystalline and has the dipole moment perpendicular to the polymer chain, especially when the polar all-trans β-phase is dominant.22 Copolymers of the materials have been employed to achieve a higher crystallinity for improved ferroelectric properties; these include poly(vinylidene fluoride-trifluoroethylene) (PVDF-TrFE) and poly(vinylidene fluoride-hexafluoropropylene) (PVDF-HFP).23,24 PVDF has been selected since freeze casting has been previously employed to form a PVDF microporous membrane with pore sizes <10 μm whose Young's modulus and water flux ability were explored,25 but no piezoelectric properties were reported. In this paper we have examined the fabrication of the optimised pore structure in PVDF formed by freeze casting, with proof of its ferroelectret nature and corresponding piezoelectric response. A range of polymer solutions at different polymer loading levels were assessed for freeze casting and the microstructure, phase identity, direct d33 piezoelectric charge coefficients and permittivity of the polymers were examined in detail.
Experimental
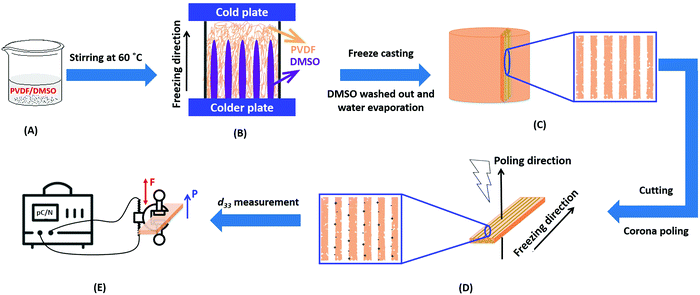
Poly(vinylidene fluoride) (PVDF, 6010) powders were used from Solef® (Belgium) and used in the as-received condition. A schematic of the freeze casting process applied to PVDF is shown in Fig. 1. PVDF powders with different weight fractions of 0.2, 0.4, 0.6, 0.8, 1 and 1.2 g were dissolved in 10 g solvent of dimethyl sulfoxide (DMSO, anhydrous ≥99.9%, freezing point of 19 °C, Sigma-Aldrich) and stirred at 60 °C for overnight to achieve homogenous solutions; see Fig. 1(A). Other widely used polar solvents (e.g. N-methyl-2-pyrrolidone/NMP, dimethylformamide/DMF, dimethylacetamide/DMAc) with lower melting points of −20 to −61 °C were not suitable for the demoulding step at room temperature. The prepared PVDF/DMSO solutions were then poured into polydimethylsiloxane (PDMS) mould with a diameter of 20 mm and height of 10 mm. The bottom face of the mould was held on the surface of liquid N2 and the top face of the mould held at an ambient temperature of ∼20 °C to unidirectionally freeze the solution. In a conventional freeze casting process,26 freeze drying is undertaken at low temperature and pressure in order to sublimate the solvent from a solid to a gas. In this work, freeze drying of the frozen PVDF/DMSO was not chosen since DMSO has the potential to contaminate not only the vacuum pump,27 but has an unpleasant sulfur smell28 with potential health risks during sublimation of the solvent,29 especially when the concentration >1% v/v.30 After freezing, the samples were therefore demoulded and immediately immersed into water to dissolve and remove the solidified DMSO, which was repeated 7–8 times to complete removal of the DMSO. The samples were then dried in an oven at 40 °C for 24 h to eliminate the remaining water, see Fig. 1B. The dried samples were then frozen in liquid N2, followed by cutting to a thickness of ∼1.5 mm parallel to the freeze-cast direction using a sharp blade (Fig. 1C). Materials were cut parallel to the freezing direction to pole the pores that were aligned and elongated in the direction normal to the polarisation direction. Corona poling was conducted by applying a DC voltage of 26.8 kV with the needle height of 14 mm for 30 min at ambient temperature to break down the air whose breakdown strength of ∼30 kV cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 (Fig. 1D). All samples were silver electroded (RS Components, Product No. 186-3600, UK) on both sides normal to the freeze-cast direction for piezoelectric and dielectric characterisation.
31 (Fig. 1D). All samples were silver electroded (RS Components, Product No. 186-3600, UK) on both sides normal to the freeze-cast direction for piezoelectric and dielectric characterisation.
The microstructure of the samples was examined by scanning electron microscopy (SEM, JSM6480LV, Tokyo, Japan) and the bulk density of the specimens was measured using Archimedes’ principle. The piezoelectric strain coefficient (d33) was measured using a Berlincourt Piezometer (PM25, Take Control, UK) for a period of 0.5–6 days after corona poling to examine aging of the piezoelectric response. To confirm that the measured d33 values originate from the piezoelectric effect, the sample orientation was reversed to ensure the piezoelectric coefficient changes from a positive to negative polarity. The relative permittivity (ε) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) were measured in the frequency range of 1 to 106 Hz with an oscillating voltage of 1 Vrms using an Agilent Technology 4192A impedance analyzer. Fourier transform infrared spectra (FT-IR) of the materials were recorded using a Perkin Elmer Spectrum 100 with a diamond universal ATR attachment. The phase structure of the ceramics was examined by X-ray diffraction (BRUKER D8-Advance, USA) with Cu radiation with 2θ ranging from 10° to 60°.
δ) were measured in the frequency range of 1 to 106 Hz with an oscillating voltage of 1 Vrms using an Agilent Technology 4192A impedance analyzer. Fourier transform infrared spectra (FT-IR) of the materials were recorded using a Perkin Elmer Spectrum 100 with a diamond universal ATR attachment. The phase structure of the ceramics was examined by X-ray diffraction (BRUKER D8-Advance, USA) with Cu radiation with 2θ ranging from 10° to 60°.
Results
Microstructural observations of the freeze cast porous PVDF materials, phase analysis, dielectric spectroscopy and piezoelectric properties of the poled freeze-cast materials are now described.Microstructure
Fig. 2A–F show the porous structure of PVDF prepared from the solutions with weight ratios of PVDF/DMSO from 0.2/10 to 1.2/10. At a ratio of 0.2/10 with the minimum PVDF content, adjacent pore channels with a pore size less than 5 μm were formed that were overlapped, see Fig. 2A. A further increase in the weight ratios from 0.4/10 (Fig. 2B) to 0.8/10 (Fig. 2D) led to the formation of more aligned pore channels along the freeze-cast direction, and the pore size normal to the freeze-cast direction decreased from 25 ± 3 μm in the 0.4/10 sample to 20 ± 2 μm in the 0.8/10 sample (Fig. 2D). At low magnification aligned pores can be observed on the upper sample surface, where in Fig. 3A mm-scale length pores can be seen in the freeze-cast PVDF with a PVDF/DMSO ratio of 0.4/10. A similar low magnification side view, see inset of Fig. 3B, reveals the elongated pore morphology. Compared to commercially available ferroelectrets,19 the freeze-cast polymers had a larger pore length with similar pore shape and pore size which might facilitate the generation and deposition of plasma charges on the inner pore surface under the action of a high electric field during the poling process. A further increase in the amount of PVDF to a ratio of 1.0/10 (Fig. 2E) and 1.2/10 (Fig. 2F) resulted in an overlapped pore morphology (Fig. 2E) with the formation of more rounded pores, as in Fig. 2F, rather than an aligned structure; this is similar to the structure of ice-templated ceramics when the solid loading is too high.32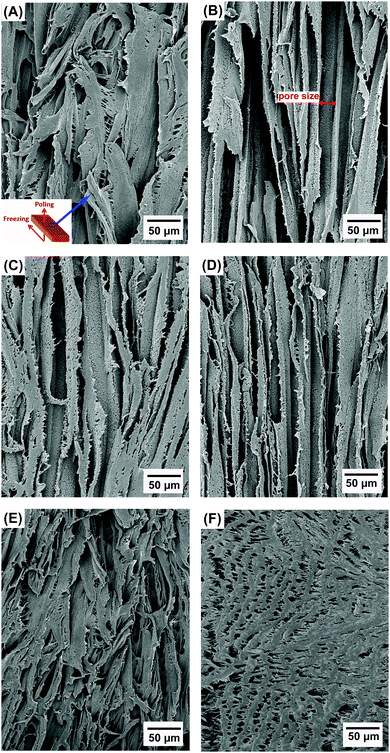 | ||
| Fig. 2 Scanning electron micrographs of porous freeze cast PVDF with increasing weight ratios of PVDF/DMSO. (A) 0.2/10, (B) 0.4/10, (C) 0.6/10, (D) 0.8/10, (E) 1.0/10, (F) 1.2/10. | ||
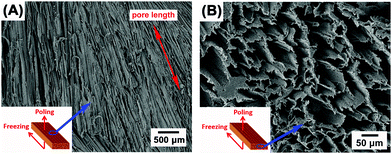 | ||
| Fig. 3 Scanning electron micrographs of (A) the mm-scale pore length and (B) the prism/elongated pore morphology of the freeze-cast PVDF with the weight ratio of 0.4/10. | ||
In general, larger pores are formed from the PVDF/DMSO solution at low PVDF concentrations during directional freezing, since the porous structure is a replica of DMSO crystals. However, for a low PVDF content of 0.2/10, the capillary force33 formed by water during evaporation during drying leads to shrinkage of the pore channels, thereby making the adjacent pore channels overlap, as shown in Fig. 2A. With an increase of PVDF concentration, there is a reduced effect of the capillary force on pore deformation (Fig. 2B–D) for the 0.4/10 to 0.8/10 samples, due to the lower amount of water left in the samples. However, if the PVDF concentration is too high there is a loss of directionality and smaller equi-axed pores were formed; this is possibly due to the high viscosity of the solution during freeze casting,34 (Fig. 2E and F).
Phase analysis
Fig. 4 shows the FT-IR and XRD spectra of the freeze cast porous PVDF with different weight ratios of PVDF/DMSO. The FT-IR transmittance spectra are shown in the 550–1500 cm−1 (Fig. 4A), and 800–900 cm−1 (Fig. 3B) ranges. No characteristic peak for either the α- or β-phase was found in all freeze cast samples. Some peaks could be attributed to both β- and γ-phases, namely 1176 cm−1 (Fig. 4A) and 840 cm−1 (Fig. 4B).35,36 However, the representative peak at 1234 cm−1 can be exclusively used to identify the γ-phase characteristic band,37,38 which is uniquely assigned to the γ-crystalline form.39,40 A small peak at 811 cm−1 was also observed, and is also a peak exclusively attributed to the γ-phase.35Fig. 4C and D show the X-ray diffraction of the polymers with different weight ratios of PVDF/DMSO. A typical semi-crystalline peak appeared in the XRD curves indicating the semi-crystalline nature of the materials for all weight ratios of PVDF/DMSO. All PVDF samples exhibited peaks centred at a diffraction angle of 20.04° (110)37 which further confirmed the γ-phase crystal polymorph was dominant in the final materials. Therefore both infrared spectroscopy and XRD spectra in Fig. 4 indicate that the γ-phase was the predominant crystalline presence in the porous PVDF for all PVDF/DMSO weight ratios, which was in agreement with previous conclusions that γ-phase usually was normally obtained from the DMSO solvent,41,42 regardless of the preparation temperature.43,44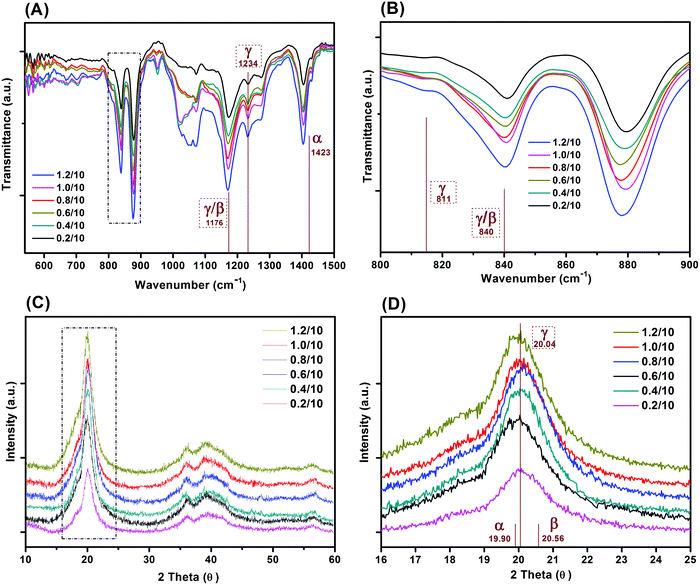 | ||
| Fig. 4 (A) FTIR and (B) XRD spectra of porous PVDF with different weight ratios of PVDF/DMSO, (C and D) are FTIR and XRD spectra in the range of 800–900 cm−1 and 16–25°, respectively. | ||
Piezoelectric and frequency dependent dielectric properties
Fig. 5A–D shows the porosity variation and piezoelectric performance of the poled porous PVDF with weight ratios of PVDF/DMSO ranging from 0.2/10 to 1.2/10. The apparent porosity increased from 35 vol% for 0.2/10 sample to reach the maximum value of 78 vol% for 0.4/10, followed by a decrease to 24 vol% for 1.2/10 (Fig. 5A). The higher porosity level of the aligned porous structure may provide more space to retain the plasma charges for piezoelectric activity. As the PVDF/DMSO weight ratio increased from 0.2/10 to 0.8/10, the d33 values increased from 41 ± 1 pC N−1 for 0.2/10 to 264 ± 2 pC N−1 for 0.4/10; this was followed by a decrease in d33 for ratios higher than 0.6/10; see Fig. 5B. The d33 values obtained for these materials were comparable with ferroelectrets prepared from stretching and gas injection methods,7,45,46 and a commercial ferroelectret with a reported values of 25 pC N−1 to 200 pC N−1.47 In addition, Fig. 5B and Table 1 clearly shows the almost equal in magnitude and opposite charge accumulations at the two-opposing poled-sides in terms of negatively-poled and positively-poled in all the porous PVDF samples, indicating the piezoelectric origin of measured electrical charge from the applied force.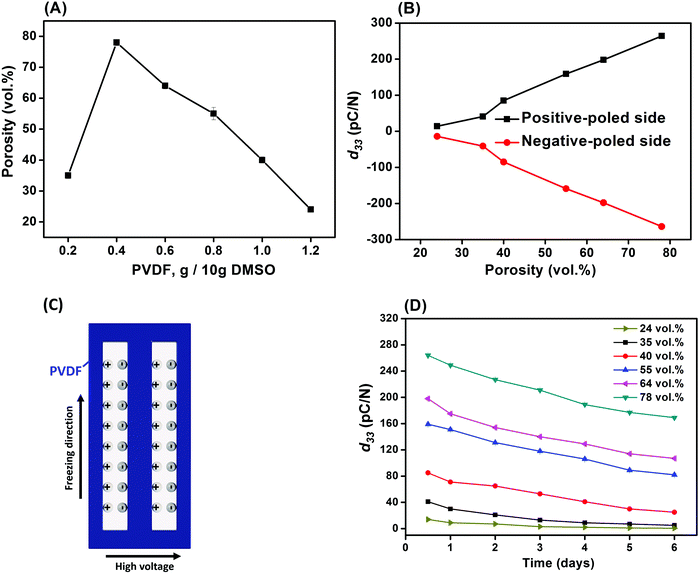 | ||
| Fig. 5 (A) Porosity, (B) piezoelectric coefficient (d33), (C) schematic of the plasma discharges on the surface and (D) aging performance of the porous PVDF. | ||
| d 33 (pC N−1) | PVDF/DMSO | |||||
|---|---|---|---|---|---|---|
| 0.2/10 | 0.4/10 | 0.6/10 | 0.8/10 | 1.0/10 | 1.2/10 | |
| Positive side | 41 ± 1 | 264 ± 2 | 198 ± 3 | 159 ± 3 | 85 ± 2 | 14 ± 1 |
| Negative side | −39 ± 2 | −260 ± 3 | −198 ± 2 | −157 ± 2 | −83 ± 2 | −13 ± 1 |
It is known that among the five crystalline polymorphs in PVDF, namely α, β, γ, δ and ε, the α and ε phases are non-polar with no electroactive response,48 while the ferroelectric properties are related to the polar phases of β, γ, and δ. β-PVDF is the most desired phase for ferroelectric applications since it exhibits the highest piezoelectric properties of the available PVDF polymorphs, with β-rich PVDF exhibiting a d33 ∼−30 pC N−1,49 compared to a lower d33 ∼−7 pC N−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 in γ-rich PVDF due to the smaller dipole moment. Therefore, the ferroelectric γ-phase in the freeze cast materials in this work (Fig. 4), is unlikely to be the main contributor to the high piezoelectric response of the freeze cast porous PVDF since the d33 values are typically well in excess of 7 pC N−1. This indicates that the porous semi-crystallized PVDF fabricated by ice-templating were piezoelectric, due to the formation of the dipole-like structure via applying a high electric field normal to the freezing direction and pore direction. This is in contrast to electret materials where charge flow is produced by either the change in a dielectric gap or the variation of the overlapping area.51 Therefore, it can be concluded that the freeze-cast PVDF for all the weight ratios were ferroelectret in nature and, as shown in Fig. 5C. After applying a high poling electric field normal to the freezing direction, the air inside the aligned pore channel were subject to electrical breakdown, thereby depositing the opposite charges on the surface of the pore channel to form the dipole-like structure. Due to the high compliance of the porous polymer material, the polarisation and dipole moment is changed on application of a mechanical stress, thereby leading to an electro-mechanical response. While the polar nature of the polymer in not vital to achieve a ferroelectret response, the use of a polar and high permittivity polymer, such as PVDF, acts to increase the permittivity contrast between the polymer and pore space and concentrates the electric field in the low permittivity pore space as a consequence of Gauss's law (Ef = q/A·ε, where q is charge, A is area, ε is permittivity of the polymer, and Ef is electric field). This field concentration in the pore space facilitates Townsend breakdown to create the ferroelectret.
50 in γ-rich PVDF due to the smaller dipole moment. Therefore, the ferroelectric γ-phase in the freeze cast materials in this work (Fig. 4), is unlikely to be the main contributor to the high piezoelectric response of the freeze cast porous PVDF since the d33 values are typically well in excess of 7 pC N−1. This indicates that the porous semi-crystallized PVDF fabricated by ice-templating were piezoelectric, due to the formation of the dipole-like structure via applying a high electric field normal to the freezing direction and pore direction. This is in contrast to electret materials where charge flow is produced by either the change in a dielectric gap or the variation of the overlapping area.51 Therefore, it can be concluded that the freeze-cast PVDF for all the weight ratios were ferroelectret in nature and, as shown in Fig. 5C. After applying a high poling electric field normal to the freezing direction, the air inside the aligned pore channel were subject to electrical breakdown, thereby depositing the opposite charges on the surface of the pore channel to form the dipole-like structure. Due to the high compliance of the porous polymer material, the polarisation and dipole moment is changed on application of a mechanical stress, thereby leading to an electro-mechanical response. While the polar nature of the polymer in not vital to achieve a ferroelectret response, the use of a polar and high permittivity polymer, such as PVDF, acts to increase the permittivity contrast between the polymer and pore space and concentrates the electric field in the low permittivity pore space as a consequence of Gauss's law (Ef = q/A·ε, where q is charge, A is area, ε is permittivity of the polymer, and Ef is electric field). This field concentration in the pore space facilitates Townsend breakdown to create the ferroelectret.
Since the piezoelectric properties of the ferroelectret originate from charged pores, it is of interest to evaluate their surface potential decay with time. The piezoelectric coefficient (d33) of all samples decreased rapidly from 0.5 to 6 days followed by a slow reduction in d33 values from 5 to 6 days measured after corona poling, as shown in Fig. 5D. A logarithmic function was used to define the aging rate based on 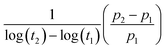 ,52 where t1 and t2 are the time periods after the pores were charged by corona poling, and p1 and p2 are the corresponding piezoelectric coefficients of the ferroelectret based PVDF. This approach has been previously used to examine aging in polarised ferroelectrics. The absolute value of the aging rate of the ferroelectret based PVDF in this work was ∼7–19%, which was larger than ferroelectric ceramic PMN-PT with the aging rate of ∼4–10%.53 Normally the surface potential, or d33 values, fall rapidly in the first week for ferroelectrets based on polydimethylsiloxane (PDMS),54 PDMS/polyvinyl alcohol (PVA),55 ethylene vinyl acetate copolymer (EVA)/biaxially oriented polypropylene (BOPP),14 and fluorinated ethylene propylene (FEP)/polytetrafluoroethylene (PTFE),56 then reach a more stable value, which can last for at least six weeks using porous polyethylene terephthalate (PET)/ethylene vinyl acetate copolymer (EVA).57 The high charge capturing ability and low elastic modulus of the porous polymer have been considered as the main reasons for the stabilisation of the piezoelectric response in the ambient atmosphere with time.57 In addition to the electrical properties of the polymer, such as dielectric loss and conductivity, the ratio between the width and length of the elongated pore channel, the thickness of the sample, and surface modification are likely to play a key roles in sustaining the charges at the pores, leading to reduced aging of the ferroelectrets.
,52 where t1 and t2 are the time periods after the pores were charged by corona poling, and p1 and p2 are the corresponding piezoelectric coefficients of the ferroelectret based PVDF. This approach has been previously used to examine aging in polarised ferroelectrics. The absolute value of the aging rate of the ferroelectret based PVDF in this work was ∼7–19%, which was larger than ferroelectric ceramic PMN-PT with the aging rate of ∼4–10%.53 Normally the surface potential, or d33 values, fall rapidly in the first week for ferroelectrets based on polydimethylsiloxane (PDMS),54 PDMS/polyvinyl alcohol (PVA),55 ethylene vinyl acetate copolymer (EVA)/biaxially oriented polypropylene (BOPP),14 and fluorinated ethylene propylene (FEP)/polytetrafluoroethylene (PTFE),56 then reach a more stable value, which can last for at least six weeks using porous polyethylene terephthalate (PET)/ethylene vinyl acetate copolymer (EVA).57 The high charge capturing ability and low elastic modulus of the porous polymer have been considered as the main reasons for the stabilisation of the piezoelectric response in the ambient atmosphere with time.57 In addition to the electrical properties of the polymer, such as dielectric loss and conductivity, the ratio between the width and length of the elongated pore channel, the thickness of the sample, and surface modification are likely to play a key roles in sustaining the charges at the pores, leading to reduced aging of the ferroelectrets.
Fig. 6 shows the dielectric properties of the porous PVDF measured from 1 Hz to 1 MHz with different weight ratios ranging from 0.2/10 to 1.2/10, respectively. The relative permittivity of all the porous PVDF samples exhibited a frequency dependence at low frequency (∼30 Hz) and a more frequency independent behaviour at higher frequencies (>1 kHz, Fig. 6A), which is a common behaviour for disordered materials and obeys the universal law of dielectric response.58 The low frequency dispersion in permittivity is likely to be due to a small amount of conductivity in the sample59 and this observation agrees with the higher dielectric loss (loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) in the materials at low frequency, see Fig. 6B.
δ) in the materials at low frequency, see Fig. 6B.
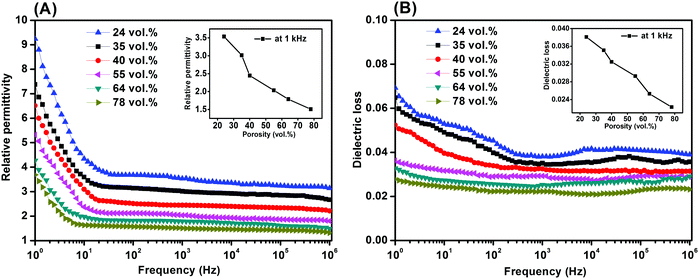 | ||
| Fig. 6 (A) Relative permittivity and (B) dielectric loss of the porous PVDF with different porosities and PVDF/DMSO ratios. | ||
If the permittivity at a frequency of 1 kHz is examined for all the samples (inset of Fig. 6A), the relative permittivity (εr) initially decreased from εr ∼ 3.0 at 0.2/10 to a minimum of εr ∼ 1.5 at a weight ratio of 0.4/10, it then increased to a maximum value of εr ∼ 3.5 as the ratio increased to 1.2/10. Based on the microstructural observations of porosity, Fig. 2, the increase in the level of porosity of PVDF as the PVDF/DMSO weight ratios increased from 0.2/10 (35% porosity) to 0.4/10 (78% porosity) led to a reduction in permittivity of the porous PVDF since the relative permittivity of PVDF9 is εr ∼ 10, compared to air with εr ∼ 1. The increase in relative permittivity as the PVDF/DMSO weight ratios increased from 0.6/10 to 1.2/10 (Fig. 6A, inset) was a result of the decrease in porosity from 64% to 24%. Fig. 6B also revealed that the change in dielectric loss varied in accordance with the change of the relative permittivity and porosity; see inset of Fig. 6A at 1 kHz, which indicated that the overall loss of the material originated from the PVDF material.
The combination of low permittivity and high piezoelectric activity can lead to high sensor sensitivity due to high g33 (= d33/εσ33) coefficients which is a measure of the electric field per unit stress in the polarisation direction, e.g. g33 = 19.9 V m N−1 for the 0.4/10 porous PVDF at 1 kHz compared with g33 = 0.067 V m N−1 for a ferroelectric porous lead zirconate titanate (PZT) ceramic.60 In addition, the figures-of-merit, d332/εσ33, for evaluating the performance as an energy harvester were 50 to 4 × 104 (pC N−1)2, compared with ∼53 (pC N−1)2 for ferroelectric PVDF5 and ∼99 (pC N−1)2 in ferroelectric PZT,9 leading to interest in ferroelectrets for piezoelectric energy harvesting applications.1,12,19,20,33,45,51,55 Future avenues can include further optimisation of pore geometry or exploitation of the technique on low dielectric loss porous polymer systems with high permittivity, longer charge and thermal stability, along with energy generation and sensor performance for practical flexible transducer applications.
Conclusions
In contrast to conventional processing methods to prepare ferroelectret materials with a cellular pore morphology, we have developed a new strategy to fabricate PVDF ferroelectret materials using an ice-templating method. Ferroelectret polymers are foams with charged pores and have the potential to be used in flexible wearable electronics, sensors and energy harvesters. The generated internal quasi-permanent macro-dipoles in the pore void can be induced by Townsend breakdown by application of a high electric field, which leads to a piezoelectric response. The ice-templated porous PVDF polymers formed by this new processing route exhibited elongated pore channels which were beneficial to achieve a high ferroelectret response. A maximum piezoelectric d33 coefficient of ∼264 pC N−1 was obtained for a porous ferroelectret PVDF with a pore size of 25 μm, which is significantly higher than a d33 of 30 pC N−1 for dense β-phase ferroelectric PVDF films. Future work could seek to examine water soluble and low dielectric loss polymers as ferroelectret candidates and employ a freeze drying process to realize solvent sublimation. In conclusion, this is the first demonstration of freeze casting in terms of its reliability and stability in the formation of ferroelectret polymers with highly aligned pore structures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Y. Zhang acknowledges support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant, Agreement No. 703950 (H2020-MSCA-IF-2015-EF-703950-HEAPPs). Prof. C. R. Bowen, would like to acknowledge the funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 320963 on Novel Energy Materials, Engineering Science and Integrated Systems (NEMESIS). The authors are thankful for the helpful advice and inspiring discussions with Mr Sujoy Kumar Ghosh from Jadavpur University, India.References
- C. R. Bowen, H. A. Kim, P. M. Weaver and S. Dunn, Energy Environ. Sci., 2014, 7, 25–44 RSC.
- Y. Zhang, M. Xie, V. Adamaki, H. Khanbareh and C. R. Bowen, Chem. Soc. Rev., 2017, 46, 7757–7786 RSC.
- E. Kim, H. Tu, C. Lv, H. Jiang, H. Yu and Y. Xu, Appl. Phys. Lett., 2013, 102, 033506 CrossRef.
- S. Bauer, R. Gerhard-Multhaupt and G. M. Sessler, Phys. Today, 2004, 57, 37–43 CrossRef CAS.
- A. De Neef, C. Samuel, G. Stoclet, M. Rguiti, C. Courtois, P. Dubois, J. Soulestin and J.-M. Raquez, Soft Matter, 2018, 14, 4591–4602 RSC.
- P. Hemalatha, D. Ponnamma and M. Al-Maadeed, Soft Matter, 2018, 14, 8803–8813 RSC.
- S. K. Ghosh, A. Biswas, S. Sen, C. Das, K. Henkel, D. Schmeisser and D. Mandal, Nano Energy, 2016, 30, 621–629 CrossRef CAS.
- V. Bovtun, J. Döring, J. Bartusch, U. Beck, A. Erhard and Y. Yakymenko, Appl. Phys. A: Mater. Sci. Process., 2007, 88, 737–743 CrossRef CAS.
- K. L. Walter Heywang and W. Wersing, Piezoelectricity, Springer-Verlag Berlin Heidelberg, 2008 Search PubMed.
- S. K. Ghosh, T. K. Sinha, B. Mahanty and D. Mandal, Energy Technol., 2015, 3, 1190–1197 CrossRef.
- B. Mahanty, S. K. Ghosh, S. Garain and D. Mandal, Mater. Chem. Phys., 2017, 186, 327–332 CrossRef CAS.
- J. Hillenbrand, P. Pondrom and G. M. Sessler, Appl. Phys. Lett., 2015, 106, 183902 CrossRef.
- A. Kachroudi, S. Basrour, L. Rufer and F. Jomni, J. Phys.: Conf. Ser., 2016, 773, 012072 CrossRef.
- J. Zhong, Q. Zhong, G. Chen, B. Hu, S. Zhao, X. Li, N. Wu, W. Li, H. Yu and J. Zhou, Energy Environ. Sci., 2016, 9, 3085–3091 RSC.
- M. Wegener, W. Wirges and R. Gerhard-Multhaupt, Adv. Eng. Mater., 2005, 7, 1128–1131 CrossRef CAS.
- A. Mellinger, M. Wegener, W. Wirges, R. R. Mallepally and R. Gerhard-Multhaupt, Ferroelectrics, 2006, 331, 189–199 CrossRef CAS.
- R. W. Crowe, J. K. Bragg and V. G. Thomas, Phys. Rev., 1954, 96, 10–14 CrossRef.
- X. Qiu, A. Mellinger and R. Gerhard, Appl. Phys. Lett., 2008, 92, 052901 CrossRef.
- S. Anton, K. Farinholt and A. Erturk, J. Intell. Mater. Syst. Struct., 2014, 25, 1681–1692 CrossRef.
- N. Wu, X. Cheng, Q. Zhong, J. Zhong, W. Li, B. Wang, B. Hu and J. Zhou, Adv. Funct. Mater., 2015, 25, 4788–4794 CrossRef CAS.
- S. Deville, Freezing Colloids: Observations, Principles, Control, and Use, Springer International Publishing, 2017 Search PubMed.
- R. Hasegawa, Y. Takahashi, Y. Chatani and H. Tadokoro, Polym. J., 1972, 3, 600 CrossRef CAS.
- J. Nunes-Pereira, S. Ribeiro, C. Ribeiro, C. J. Gombek, F. M. Gama, A. C. Gomes, D. A. Patterson and S. Lanceros-Méndez, Polym. Test., 2015, 44, 234–241 CrossRef CAS.
- N. Moussaif and R. Jérôme, Polymer, 1999, 40, 6831–6839 CrossRef CAS.
- C. Mu, Y. Su, M. Sun, W. Chen and Z. Jiang, J. Membr. Sci., 2010, 361, 15–21 CrossRef CAS.
- S. Deville, E. Saiz, R. K. Nalla and A. P. Tomsia, Science, 2006, 311, 515–518 CrossRef CAS PubMed.
- http://www.labconco.com/articles/how-to-freeze-dry-the-6-most-challenging-samples .
- L. I. Boral, Lab. Med., 1983, 14, 246–251 CrossRef.
- J. Hebling, L. Bianchi, F. G. Basso, D. L. Scheffel, D. G. Soares, M. R. O. Carrilho, D. H. Pashley, L. Tjäderhane and C. A. de Souza Costa, Dent. Mater., 2015, 31, 399–405 CrossRef CAS PubMed.
- J. Galvao, B. Davis, M. Tilley, E. Normando, M. R. Duchen and M. F. Cordeiro, FASEB J., 2014, 28, 1317–1330 CrossRef CAS PubMed.
- P. A. Tipler, College Physics, Worth Publishers Inc.,U.S., 1987 Search PubMed.
- S. Deville, E. Saiz and A. P. Tomsia, Acta Mater., 2007, 55, 1965–1974 CrossRef CAS.
- Z. Zhang, C. Yao, Y. Yu, Z. Hong, M. Zhi and X. Wang, Adv. Funct. Mater., 2016, 26, 6760–6765 CrossRef CAS PubMed.
- Y. Zhang, K. Zhou, Y. Bao and D. Zhang, Mater. Sci. Eng., C, 2013, 33, 340–346 CrossRef CAS PubMed.
- X. Cai, T. Lei, D. Sun and L. Lin, RSC Adv., 2017, 7, 15382–15389 RSC.
- L. He, B. Cui, N. Jia, J. Sun, G. Xia, H. Zhang and R. Song, J. Macromol. Sci., Part B: Phys., 2016, 55, 503–517 CrossRef CAS.
- P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706 CrossRef CAS.
- N. Jia, Q. Xing, X. Liu, J. Sun, G. Xia, W. Huang and R. Song, J. Colloid Interface Sci., 2015, 453, 169–176 CrossRef CAS PubMed.
- S. Ramasundaram, S. Yoon, K. J. Kim and C. Park, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 2173–2187 CrossRef CAS.
- M. M. Abolhasani, F. Zarejousheghani, Z. Cheng and M. Naebe, RSC Adv., 2015, 5, 22471–22479 RSC.
- M. Benz, W. B. Euler and O. J. Gregory, Macromolecules, 2002, 35, 2682–2688 CrossRef CAS.
- J. Martin, D. Zhao, T. Lenz, I. Katsouras, D. M. de Leeuw and N. Stingelin, Mater. Horiz., 2017, 4, 408–414 RSC.
- Y. J. Park, Y. S. Kang and C. Park, Eur. Polym. J., 2005, 41, 1002–1012 CrossRef CAS.
- S. Satapathy, S. Pawar, P. K. Gupta and K. B. R. Varma, Bull. Mater. Sci., 2011, 34, 727 CrossRef CAS.
- Z. Luo, D. Zhu, J. Shi, S. Beeby, C. Zhang, P. Proynov and B. Stark, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 1360–1368 CAS.
- L. Zhenhua, Z. Dibin and B. Steve, Smart Mater. Struct., 2016, 25, 045010 CrossRef.
- https://www.emfit.com/copy-of-s-series-sensor .
- L. Ruan, X. Yao, Y. Chang, L. Zhou, G. Qin and X. Zhang, Polymers, 2018, 10, 228 CrossRef.
- S. R. Khaled, D. Sameoto and S. Evoy, Smart Mater. Struct., 2014, 23, 033001 CrossRef.
- A. C. Lopes, C. M. Costa, C. J. Tavares, I. C. Neves and S. Lanceros-Mendez, J. Phys. Chem. C, 2011, 115, 18076–18082 CrossRef CAS.
- T. Kai, L. Shuwei, L. Sun Woh, M. Jianmin and H. Xiao, J. Micromech. Microeng., 2014, 24, 065022 CrossRef.
- A. Barzegar, R. Bagheri and A. K. Taheri, J. Appl. Phys., 2001, 89, 2322–2326 CrossRef CAS.
- J. H. Park, F. Xu and S. Trolier-McKinstry, J. Appl. Phys., 2001, 89, 568–574 CrossRef CAS.
- K. Achraf, B. Skandar, R. Libor, S. Alain and J. Fathi, Smart Mater. Struct., 2016, 25, 105027 CrossRef.
- J. Shi, Z. Luo, D. Zhu and S. P. Beeby, J. Phys.: Conf. Ser., 2016, 773, 012051 CrossRef.
- B. Wang, J. Zhong, Q. Zhong, N. Wu, X. Cheng, W. Li, K. Liu, L. Huang, B. Hu and J. Zhou, Adv. Electron. Mater., 2016, 2, 1500408 CrossRef.
- J. Zhong, Q. Zhong, X. Zang, N. Wu, W. Li, Y. Chu and L. Lin, Nano Energy, 2017, 37, 268–274 CrossRef CAS.
- A. K. Jonscher, Nature, 1977, 267, 673 CrossRef CAS.
- D. P. Almond and C. R. Bowen, Phys. Rev. Lett., 2004, 92, 157601 CrossRef CAS PubMed.
- P. Guillaussier, C. Audoly and D. Boucher, Ferroelectrics, 1996, 187, 121–128 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |