DOI:
10.1039/C8SM01765D
(Paper)
Soft Matter, 2018,
14, 9436-9444
Electrostatic interaction of particles trapped at fluid interfaces: effects of geometry and wetting properties
Received
28th August 2018
, Accepted 6th November 2018
First published on 8th November 2018
Abstract
The electrostatic interaction between pairs of spherical or macroscopically long, parallel cylindrical colloids trapped at fluid interfaces is studied theoretically for the case of small inter-particle separations. Starting from the effective interaction between two planar walls and by using the Derjaguin approximation, we address the issue of how the electrostatic interaction between such particles is influenced by their curvatures and by the wetting contact angle at their surfaces. Regarding the influence of curvature, our findings suggest that the discrepancies between linear and nonlinear Poisson–Boltzmann theory, which have been noticed before for planar walls, also occur for spheres and macroscopically long, parallel cylinders, though their magnitude depends on the wetting contact angle. Concerning the influence of the wetting contact angle θ simple relations are obtained for equally sized particles which indicate that the inter-particle force varies significantly with θ only within an interval around 90°. This interval depends on the Debye length of the fluids and on the size of the particles but not on their shape. For unequally sized particles, a more complicated relation is obtained for the variation of the inter-particle force with the wetting contact angle.
I. Introduction
Colloidal particles trapped at a fluid interface usually adopt configurations which are energetically more favorable compared to those occurring in the adjacent bulk phase(s).1,2 This can be exploited for a wide spectrum of systems ranging from micrometer down to nanometer in size and from biological to industrial processes, including the stabilization of Pickering emulsions,3 the transport of drugs and nutrients in biological systems,4 the formation of artificial cells,5 oil recovery, water purification, mineral processing, maintaining proper foaminess of cosmetic and food products,2 and the fabrication of various nanostructured devices.6,7 The trapping phenomenon depends on the wetting properties, the size, and the shape of the colloidal particles, because it hinges on the particle-mediated reduction of the fluid–fluid interfacial area, and consequently on the net reduction of the free energy of the system.2
On a mesoscopic level, the wetting properties of a colloidal particle are described best by the contact angle θ of the fluid–fluid interface with respect to the particle surface (see Fig. 1). Following the standard convention, we measure θ inside the more polar phase. For oil–water systems this implies that a particle is hydrophilic if θ < 90°, hydrophobic if θ > 90°, and neutrally wetted for θ = 90°. Within the continuum model, the equilibrium contact angle θ of a particle is determined solely by energies associated with the three interfaces (two particle–liquid and one liquid–liquid) according to the well-known Young equation.8,9 In general, particles, which are partially wetted by both fluid phases, attach most stably to an interface because the corresponding trapping energy often exceeds several orders of kBT.2,10
 |
| | Fig. 1 Cross-sectional view in the y = 0 plane of a system with two spherical or parallel cylindrical colloids (yellow discs) floating at a fluid interface indicated by the horizontal line. The projection of the center of the left particle onto the interface is chosen as the center (0, 0, 0) of the Cartesian coordinate system used to describe the system. The fluid medium below the interface is called medium “1” and the one above the interface medium “2”. The particles are chemically identical, such that the contact surfaces with one of the media carry the same charge densities and the same wetting contact angles θ. The particles may differ in size with radius R1 on the left and R2 on the right particle. The horizontal distance of the particles is characterized by the width L of the gap between both particles as depicted by the vertical dashed lines. The equilibrium heights of the centers of the left and right particles from the interface are given by |D1| and |D2|, respectively, with θ ∈ [0, π] determining the sign of D1 and D2 according to the relations D1 = −R1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and D2 = −R2 θ and D2 = −R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ. | |
Wetting properties are crucial not only for the adsorption of a single particle at an interface, but also for the interaction between several of them. For example, whereas very hydrophobic silica particles (θ ≥ 129°) form well-ordered monolayer structures (with inter-particle separations of several particle diameter) at octane–water interfaces, less hydrophobic (θ ≤ 115°) particles fail to do so.11,12 This can be attributed to different strengths of the repulsive electrostatic force, which acts mainly through the oil-phase because the electrostatic field is well screened inside the aqueous phase at the high salt concentrations used. Moreover, the capillary interaction due to the overlap of the interface deformation field around each particle also depends on the contact angle θ. However, here we disregard deformations of the interface, which can be significant if the particle surfaces are rough13 or the particles are large (radius ≳ 10 μm),14–19 and we focus only on the electrostatic interaction between the colloids.
Whereas the electrostatic interaction between particles trapped at a fluid interface has been studied extensively since the pioneering studies by Pieranski20 and Hurd,21 most of the investigations deal with the case of particles situated far away from each other. At long distances the electrostatic pair-interaction takes the particularly simple form of an interaction between two electric dipoles, which are generated by the asymmetric counterion distribution at the particle surfaces in contact with the two fluid phases. It has been shown that in this case the linearization of the Poisson–Boltzmann (PB) theory is applicable.21 Recent studies, directed towards the opposite limit of small inter-particle separations, have been performed within the linearized PB theory22–24 or by considering a flat plate geometry22,24,25 in order to simplify the problem. Whereas the former approximation is often violated at short separations, the latter represents the ideal situation of a contact angle of exactly 90° and the absence of particle curvature. However, in reality, the contact angle θ can vary significantly to either side of 90°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,10,19,26 and whether the particle curvature plays any important role at short inter-particle separations still remains to be addressed within the nonlinear PB theory.
2,10,19,26 and whether the particle curvature plays any important role at short inter-particle separations still remains to be addressed within the nonlinear PB theory.
Accordingly, in this contribution, we investigate the electrostatic interaction between spherical and parallel cylindrical colloids with an arbitrary contact angle appearing at a fluid interface. As long as the size of the particles is sufficiently larger than both the length scale of the interaction and the inter-particle separation, which is usually the case for short inter-particle separations we are interested in, one can apply the Derjaguin approximation (DA) using results of the corresponding case of planar walls.27 Having recently solved this two-plate problem exactly (i.e., without using the superposition approximation) within the nonlinear PB theory,25 we proceed one step further and compute the force between a pair of spheres or parallel cylinders. A similar approach has already been employed and proved to be valid in this context.28,29 However, the present study differs from those treatments in several aspects. Whereas ref. 28 deals with macroscopically long cylinders trapped at an oil–water interface and having a constant surface potential, which is most suitable for metallic particles, we consider dielectric particles described by constant charge densities at their surfaces. Moreover, to keep our analysis general and to be consistent with experimental observations,30–34 we consider the particle surfaces to be charged in both fluid phases, which is not the case in ref. 28. On the other hand, ref. 29 describes the interaction between spherical particles by using the superposition approximation, which has been shown to be qualitatively wrong for small inter-particle separations,22 and it discards any interaction between the particle–water surface of one particle and the particle–oil surface of the other particle. As explained in the next section, this latter contribution to the interaction energy is included in our calculation via the line contribution.
II. Model and formalism
As depicted in Fig. 1, we consider two particles with radii R1 and R2 placed at a fluid–fluid interface described by a three-dimensional Cartesian coordinate system. The projection of the center of the left particle onto the interface is chosen as the origin (0, 0, 0) of the coordinate system. The particles are either two spheres or two macroscopically long, parallel cylinders with axes in y-direction; their cross-sections in the plane y = 0 are shown in Fig. 1. The fluid–fluid interface is indicated by the horizontal line at x = 0. Although the particles can differ in size, they are taken to be chemically identical such that the surfaces of both particles in contact with the same fluid phase carry the same surface charge density, and that the contact angle θ is the same for both particles. This is a simplifying assumption because chemically identical particles in general need not to be equally charged.35 In equilibrium the centers of the left and the right particle are located at x = D1 and x = D2, respectively. Depending upon the contact angle θ ∈ [0, π], both D1 = −R1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and D2 = −R2
θ and D2 = −R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ can be negative (for
θ can be negative (for  ; the case considered in Fig. 1) as well as positive (for
; the case considered in Fig. 1) as well as positive (for  ). In between the particles a gap of width L occurs (see the vertical dashed lines in Fig. 1) so that the horizontal center-to-center distance is L + R1 + R2. The fluid phase below (above) the interface occupying the half-space x < 0 (x > 0) is denoted by medium “1” (“2”). Both fluids are modeled as structureless, continuous media with dielectric constant εi = εr,iε0, i ∈ {1, 2}, where εr,i is the relative permittivity of medium i and ε0 is the vacuum permittivity. The ionic strength of added salt in medium i ∈ {1, 2} is denoted by Ii. The corresponding Debye screening length in each medium is given by
). In between the particles a gap of width L occurs (see the vertical dashed lines in Fig. 1) so that the horizontal center-to-center distance is L + R1 + R2. The fluid phase below (above) the interface occupying the half-space x < 0 (x > 0) is denoted by medium “1” (“2”). Both fluids are modeled as structureless, continuous media with dielectric constant εi = εr,iε0, i ∈ {1, 2}, where εr,i is the relative permittivity of medium i and ε0 is the vacuum permittivity. The ionic strength of added salt in medium i ∈ {1, 2} is denoted by Ii. The corresponding Debye screening length in each medium is given by  where
where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B = e2/(4πε0kBT) is the vacuum Bjerrum length with e > 0, kB, and T being the elementary charge, the Boltzmann constant, and the absolute temperature, respectively. Within our description at the mean-field level, the length scale of interest is the Debye length as both the local charge density and the electrostatic interaction vary on this scale. Phenomena which occur on smaller length scales, e.g., the structuring of liquids on the molecular length scale, are not considered. Here we consider medium “2” to be the less polar phase in the sense that κ2−1 > κ1−1. With this the criteria for the applicability of the DA are that both radii R1 and R2 have to be much larger than κ2−1 and L.
B = e2/(4πε0kBT) is the vacuum Bjerrum length with e > 0, kB, and T being the elementary charge, the Boltzmann constant, and the absolute temperature, respectively. Within our description at the mean-field level, the length scale of interest is the Debye length as both the local charge density and the electrostatic interaction vary on this scale. Phenomena which occur on smaller length scales, e.g., the structuring of liquids on the molecular length scale, are not considered. Here we consider medium “2” to be the less polar phase in the sense that κ2−1 > κ1−1. With this the criteria for the applicability of the DA are that both radii R1 and R2 have to be much larger than κ2−1 and L.
Within the DA, one basically decomposes the two interacting particles into infinitesimal surface elements. Assuming that the elementary surface pieces, which face each other, interact like flat parallel surfaces, the total interaction between the two curved objects is obtained via integration over the whole surface. Here, however, the particle surfaces are homogeneously charged only separately inside each medium, the properties of which in general differ. As a result, a three-phase contact line is formed where a particle surface intersects the fluid interface; two such contact lines on opposing particles interact as well. But this does not introduce any additional constraint for applying the DA. In the spirit of the DA, each of these two contact lines can be divided in infinitesimal pieces and the total contribution due to the line interaction can be obtained as long as the interaction between two parallel lines is known. Therefore, in order to apply the DA, one needs to know the interaction of parallel flat surfaces dipped into medium “1” or medium “2” and the interaction between two parallel three-phase contact lines. These are exactly the quantities we calculated in ref. 25 numerically by solving the nonlinear PB equation. To be more precise, the relevant quantities, as defined in ref. 25, are ωγ,i(r), which is the interaction energy per total surface area between two parallel, planar surfaces dipped at a distance r into medium i ∈ {1, 2}, and ωτ(r), which is the interaction energy per total line length between two parallel three-phase contact lines at a distance r. Please note that the interaction of the surface of one particle in contact with medium “1” and that of the other particle in contact with medium “2” is included in the line contribution ωτ(r). In order to tackle the problem efficiently, we first fit simple functions to the numerical data for ωγ,1(r), ωγ,2(r), and ωτ(r) obtained by full minimization of the nonlinear PB grand potential. It turns out that a reasonably good fitting can be obtained by superposing exponential contributions as follows:
| | 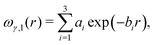 | (1) |
| |  | (2) |
and
| |  | (3) |
For two flat plates, all interactions decay exponentially in the limit of large separations:
ωγ,i(
r → ∞) ∼ exp(−
κir) and
ωτ(
r → ∞) ∼ exp(−
κ2r) (note the convention
κ2−1 >
κ1−1). As a result, when fitting the data over a sufficiently large interval of
r (
i.e., a few Debye lengths), the slowest of the decay rates
bi in
eqn (1) equals
κ1 and the slowest of the decay rates
di in
eqn (2) as well as the slowest of the decay rates
hi in
eqn (3) equal
κ2. All three interactions,
i.e.,
ωγ,1,
ωγ,2, and
ωτ result in forces onto the particles, which can be obtained by taking the negative derivative with respect to the appropriate distance between the facing surface or line elements, followed by integrating over the particles. Due to the geometry of the problem, the electrostatic force between the particles acts only in the horizontal
z-direction. Please note that the movement of the particles in the vertical
x-direction is suppressed by the steep and strong trapping potential.
2 In the following, we denote the
z-component of the electrostatic force, which the left particle in
Fig. 1 exerts on the right one, by
F(
L), and we decompose it, according to
F(
L) =
F1(
L) +
F2(
L) +
F3(
L), into the surface contribution
F1(
L) due to the surface interaction
ωγ,1 in medium “1”, the surface contribution
F2(
L) due to the surface interaction
ωγ,2 in medium “2”, and the line contribution
F3(
L) due to the line interaction
ωτ.
III. Results and discussion
In this section we discuss the variation of the force F(L) between the particles as function of the particle sizes (radii R1 and R2), the particle separation L, and the contact angle θ. For our discussion we consider two typical experimental setups and in each case the results for a pair of spheres as well as a pair of parallel cylinders are presented. Between the two systems considered below, the data for flat wall interactions for water–lutidine interfaces are taken from ref. 25 and those for water–octanol interfaces are newly generated here. We mention that all numerical examples presented here have been chosen such that the conditions for applying the DA are satisfied. Consequently, systems featuring oil with very low dielectric constants, such as decane or octane, have been excluded because the corresponding Debye length κ2−1 is too large for them to satisfy the condition R1, R2 ≫ κ2−1, even for micron size colloids.
A. Water–lutidine interface
First, we consider a system consisting of polystyrene particles placed at a water–lutidine (2,6-dimethylpyridine) interface at temperature T = 313 K. The added salt is NaI with bulk ionic strengths I1 = 1 mM and I2 = 0.85 mM. The relative permittivities are εr,1 = 72 for the water-rich phase (medium “1”) and εr,2 = 62 for the lutidine-rich phase (medium “2”). The chemically identical particles are assumed to be similarly charged; the magnitude of the surface charge density in contact with the aqueous phase is σ1 = 0.1e nm−2 and that in contact with the oil-phase is σ2 = 0.01e nm−2. Differences in the solubilities of the ions in the two fluids result in a potential difference between the bulk of the two media, which is called the Donnan potential or Galvani potential difference,36 and which, for our system, is assumed to be 1kBT/e. These numbers correspond to a standard set of parameters as used in ref. 25. They are either taken or estimated from various experimental studies.31,37–42
1. Spheres.
In the case of two interacting spheres at a fluid interface, after performing the surface and line integrations, for the three distinct, lateral force contributions the following expressions are obtained:| |  | (4) |
| | 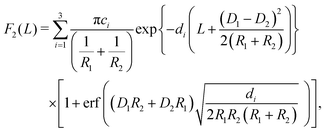 | (5) |
where erf(x) denotes the error function,46 and| | 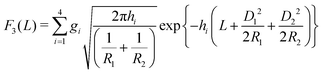 | (6) |
with D1 = −R1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and D2 = −R2
θ and D2 = −R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Variations of the total force F(L) = F1(L) + F2(L) + F3(L) in the units of 103κ1/β with the scaled separation κ1L for different system parameters are shown in Fig. 2. Here β = 1/(kBT) is the inverse thermal energy. As one can infer from Fig. 2(a), for equally-sized spheres (R1 = R2 = R) with a contact angle of θ = 90°, the effective force scales linearly with the size of the particles and decays exponentially with increasing separation between the particles. Both the linear scaling with R and the exponential decay with L can be directly inferred from the inset of Fig. 2(a) where the ratio of the dimensionless force βF/κ1 to the scaled radius κ1R is plotted as a function of the scaled separation κ1L using a semi-logarithmic scale, revealing data collapse. The exponential decay is expected to occur in the sense that all effective interactions decay exponentially for a pair of interacting flat plates, which remains unaffected while using the DA, and the linear scaling with R is a direct consequence of the DA. Fig. 2(b and c) display the variation of the scaled force with contact angle θ for equally-sized particles. As one can see, for κ1R ≈ 100 (b), the force increases with decreasing contact angle but de facto it varies only within the interval 80° < θ < 100°. A similar phenomenon is observed for κ1R ≈ 30 (c) albeit with variation in a slightly broader interval 75° < θ < 105°. Fig. 2(d and e) show the variation of the force with contact angle θ as function of separation distance κ1L for unequally-sized spheres. For the relatively small size-asymmetry in Fig. 2(d), the force between the particles can increase in a certain range of separation between the particles as the contact angle θ is decreased slightly from 90° downwards. Otherwise the force is weaker than the one obtained for a neutral wetting situation θ = 90°. For the larger size-asymmetry in Fig. 2(e), the force becomes weaker as soon as the contact angle θ differs from 90°. However, in both cases, as considered in Fig. 2(d and e), the force between the particles decreases upon increasing θ in the interval θ > 90°. Finally, in Fig. 2(f), we compare the force obtained within the linearized and the nonlinear PB theory for equally sized spheres. As one can see from the plot, the forces differ by almost an order of magnitude even at large separations such as κ1L ≈ 6 for θ = 90°. It turns out that with increasing contact angle θ this difference diminishes; see the inset of Fig. 2(f), where both curves are of almost the same magnitude. This is expected since the portion of the particles immersed in the more polar phase, for which the electrostatic interaction is stronger because κ1 ≈ κ2 [κ1 ≈ 0.1059 nm−1, κ2 ≈ 0.1053 nm−1] and σ1 ≫ σ2, decreases with increasing contact angle. Note that this situation differs from the one in ref. 11 and 12 in which κ1 ≫ κ2. A similar discrepancy appeared while comparing the interactions within the linear and nonlinear theory for parallel flat surfaces.25 Thus taking into account particle curvature does not significantly change this result.
θ. Variations of the total force F(L) = F1(L) + F2(L) + F3(L) in the units of 103κ1/β with the scaled separation κ1L for different system parameters are shown in Fig. 2. Here β = 1/(kBT) is the inverse thermal energy. As one can infer from Fig. 2(a), for equally-sized spheres (R1 = R2 = R) with a contact angle of θ = 90°, the effective force scales linearly with the size of the particles and decays exponentially with increasing separation between the particles. Both the linear scaling with R and the exponential decay with L can be directly inferred from the inset of Fig. 2(a) where the ratio of the dimensionless force βF/κ1 to the scaled radius κ1R is plotted as a function of the scaled separation κ1L using a semi-logarithmic scale, revealing data collapse. The exponential decay is expected to occur in the sense that all effective interactions decay exponentially for a pair of interacting flat plates, which remains unaffected while using the DA, and the linear scaling with R is a direct consequence of the DA. Fig. 2(b and c) display the variation of the scaled force with contact angle θ for equally-sized particles. As one can see, for κ1R ≈ 100 (b), the force increases with decreasing contact angle but de facto it varies only within the interval 80° < θ < 100°. A similar phenomenon is observed for κ1R ≈ 30 (c) albeit with variation in a slightly broader interval 75° < θ < 105°. Fig. 2(d and e) show the variation of the force with contact angle θ as function of separation distance κ1L for unequally-sized spheres. For the relatively small size-asymmetry in Fig. 2(d), the force between the particles can increase in a certain range of separation between the particles as the contact angle θ is decreased slightly from 90° downwards. Otherwise the force is weaker than the one obtained for a neutral wetting situation θ = 90°. For the larger size-asymmetry in Fig. 2(e), the force becomes weaker as soon as the contact angle θ differs from 90°. However, in both cases, as considered in Fig. 2(d and e), the force between the particles decreases upon increasing θ in the interval θ > 90°. Finally, in Fig. 2(f), we compare the force obtained within the linearized and the nonlinear PB theory for equally sized spheres. As one can see from the plot, the forces differ by almost an order of magnitude even at large separations such as κ1L ≈ 6 for θ = 90°. It turns out that with increasing contact angle θ this difference diminishes; see the inset of Fig. 2(f), where both curves are of almost the same magnitude. This is expected since the portion of the particles immersed in the more polar phase, for which the electrostatic interaction is stronger because κ1 ≈ κ2 [κ1 ≈ 0.1059 nm−1, κ2 ≈ 0.1053 nm−1] and σ1 ≫ σ2, decreases with increasing contact angle. Note that this situation differs from the one in ref. 11 and 12 in which κ1 ≫ κ2. A similar discrepancy appeared while comparing the interactions within the linear and nonlinear theory for parallel flat surfaces.25 Thus taking into account particle curvature does not significantly change this result.
 |
| | Fig. 2 Variation of the lateral component of the force F(L) due to the electrostatic interaction between a pair of spherical colloidal particles, expressed in units of 103κ1/β, as function of their scaled separation κ1L for (a) equally sized (R1 = R2 = R) spheres of varying radius with contact angle θ = 90°, (b) equally sized (κ1R ≈ 100) particles with varying θ, (c) equally sized (κ1R ≈ 30) particles with varying θ, (d) unequally sized (2κ1R1 = κ1R2 ≈ 100) particles with varying θ, (e) unequally sized (10κ1R1 = κ1R2 ≈ 300) particles with varying θ, and (f) equally sized (κ1R ≈ 100) particles with θ = 90° within linear and nonlinear PB theory. As shown by panel (a) and its inset, the force increases linearly with increasing R and decays exponentially with increasing separation κ1L. Panels (b) and (c) suggest that, for equally sized spheres, the force increases significantly with decreasing contact angle θ only within an interval around 90°. Outside this interval the force remains de facto constant and the interval of θ, across which the force actually varies, widens upon decreasing κ1R. For unequally sized spheres, if the size asymmetry is moderate, the force may increase as well as decrease if the contact angle deviates from 90° (panel (d)). However, if the size contrast is high, the force becomes weaker once θ is slightly shifted away from 90° in either direction (panel (e)). From panel (f) and the inset therein one can infer that the discrepancy between the linear and the nonlinear results diminishes with increasing θ. | |
All these observations are in accordance with the force expressions given in eqn (4)–(6). For micron-sized particles considered here, in most of the cases the line contribution to the total interaction is negligible. Therefore, the total force F(L) is dominated by the surface contributions F1(L) (eqn (4)) and F2(L) (eqn (5)). For θ = 90°, which is the case considered in Fig. 2(a), one has D1 = D2 = 0. Moreover, with R1 = R2 = R, eqn (4) and (5) reduce to 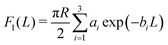 and
and  , respectively, which transparently explain the linear variation of the force with the particle size R (the coefficients ai and ci do not depend on R) and its exponential decay as function of the separation L. The decay rate in the limit of large distances is determined by the smaller of the two Debye lengths κ1−1 and κ2−1 (please note that for our system κ1−1 ≈ κ2−1). For R1 = R2 = R with an arbitrary contact angle θ, one has D1 − D2 = 0 so that the dependence on θ appears in eqn (4) and (5) only through the terms involving the error functions, which reduce to
, respectively, which transparently explain the linear variation of the force with the particle size R (the coefficients ai and ci do not depend on R) and its exponential decay as function of the separation L. The decay rate in the limit of large distances is determined by the smaller of the two Debye lengths κ1−1 and κ2−1 (please note that for our system κ1−1 ≈ κ2−1). For R1 = R2 = R with an arbitrary contact angle θ, one has D1 − D2 = 0 so that the dependence on θ appears in eqn (4) and (5) only through the terms involving the error functions, which reduce to  and
and 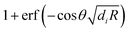 , respectively. Since the error function levels off to |erf(x)| ≈ 1 for |x| ≳ 2, the variation of the force with respect to θ in eqn (4) saturates once the slowest decay rate bi, which in the present case is κ1, satisfies the inequality
, respectively. Since the error function levels off to |erf(x)| ≈ 1 for |x| ≳ 2, the variation of the force with respect to θ in eqn (4) saturates once the slowest decay rate bi, which in the present case is κ1, satisfies the inequality
| |  | (7) |
Similarly, in
eqn (5) the saturation is obtained once the slowest decay rate
di,
i.e.,
κ2 satisfies the inequality
| |  | (8) |
Note that once the slowest decay rates
bi and
di satisfy these conditions, all the other decay rates will do so, too. For
κ1R ≈ 100 (and therefore,
κ2R ≈ 100 as
κ1 ≈
κ2), both
eqn (7) and (8) predict that the force varies appreciably only within the interval 78° ≤
θ ≤ 102°, which one precisely observes in
Fig. 2(b). Decreasing the contact angle
θ from

implies that the particles become more hydrophilic. Consequently, the contribution
F1(
L) to the total force increases while
F2(
L) decreases upon decreasing
θ. Finally, at
θ ≈ 78° the former attains a non-zero finite value and the latter vanishes (please note the different signs in front of the error functions in
eqn (4) and (5)). On the other hand, increasing the contact angle
θ from

implies that the particles become more hydrophobic. As a result, the contribution
F2(
L) increases and
F1(
L) decreases with the former attaining a non-zero finite value while the latter is vanishing at
θ ≈ 102°. Upon decreasing
κ1R, the interval of
θ over which the force varies broadens as can be inferred from
Fig. 2(c). For unequal particles sizes,
i.e., for
R1 ≠
R2, the dependence on
θ in
eqn (4) and (5) originate from both the exponential and the error function. For moderate size-asymmetry, like the one considered in
Fig. 2(d), a competition between these two functions determines the variation of the force with
θ. However, for the extremely asymmetric case considered in
Fig. 2(e), the difference
D1 −
D2 is large and the exponential terms dominate as soon as
θ differs slightly from 90°.
2. Cylinders.
For macroscopically long, parallel cylinders, the expressions for the lateral force contributions, expressed per length Ly in the y-direction, are given by:| |  | (9) |
| | 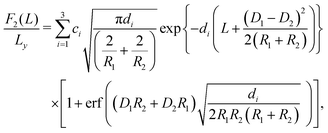 | (10) |
and| |  | (11) |
We note that for geometrical reasons these expressions are slightly different from those obtained for spheres in eqn (4)–(6). In particular, the contact lines for cylinders are just straight lines and in order to obtain F3(L) there is no need to use the DA. Fig. 3 shows the variation of the z-component of the total force F(L) = F1(L) + F2(L) + F3(L), per length Ly in the y-direction and in units of 102κ12/β, which the left cylinder exerts on the right one as function of the scaled separation κ1L for the sizes R1 and R2 and for the contact angle θ. Except for a few features, the findings are qualitatively the same as those obtained for spheres in Fig. 2. For example, for R1 = R2 = R and θ = 90°, the force between two cylinders also decays exponentially with varying separation L between them and increases with increasing size R, but for the cylinders the increase is proportional to 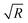 ; see Fig. 3(a) and the inset therein. This is evident from the prefactors of the exponential functions in eqn (9) and (10). The variation of the force with respect to θ as well as eqn (7) and (8) remain the same as for the spheres, because the θ-dependent terms in eqn (9) and (10) have exactly the same form as in eqn (4) and (5). This behavior is confirmed by Fig. 3(b–e). Finally, the comparison of the effective force for θ = 90° within linearized and nonlinear PB theory reveals a significant discrepancy between the predictions of the two approaches, which becomes smaller for larger contact angles θ, i.e., as the portion of the particles, dipped into the more polar phase, decreases (see Fig. 3(f)).
; see Fig. 3(a) and the inset therein. This is evident from the prefactors of the exponential functions in eqn (9) and (10). The variation of the force with respect to θ as well as eqn (7) and (8) remain the same as for the spheres, because the θ-dependent terms in eqn (9) and (10) have exactly the same form as in eqn (4) and (5). This behavior is confirmed by Fig. 3(b–e). Finally, the comparison of the effective force for θ = 90° within linearized and nonlinear PB theory reveals a significant discrepancy between the predictions of the two approaches, which becomes smaller for larger contact angles θ, i.e., as the portion of the particles, dipped into the more polar phase, decreases (see Fig. 3(f)).
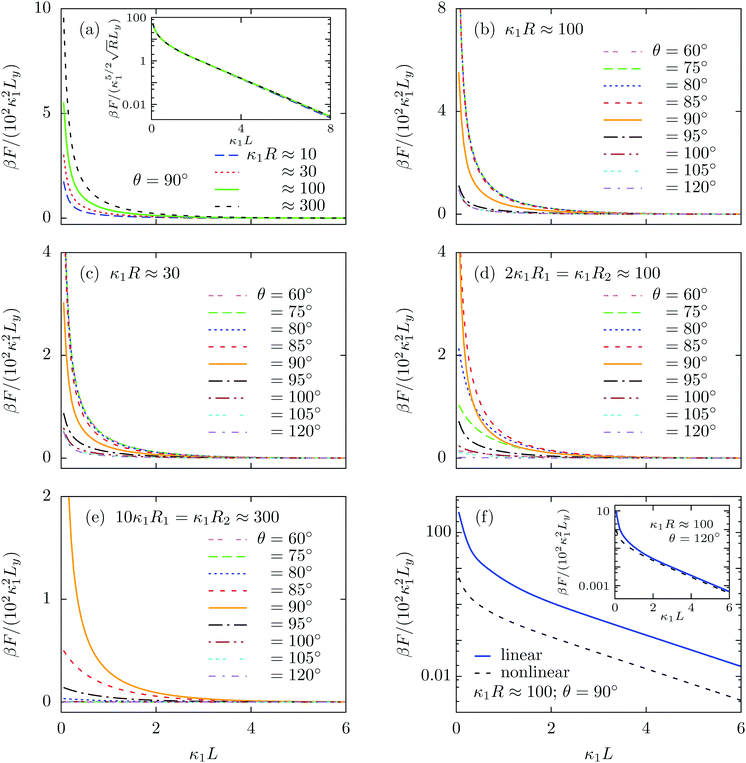 |
| | Fig. 3 Variation of the z-component (see Fig. 1) of the force F(L), per length Ly in the y-direction, due to the electrostatic interaction between a pair of parallel cylindrical colloids, expressed in units of 102κ12/β, as function of their scaled separation κ1L for (a) equally sized (R1 = R2 = R) cylinders of varying radius with contact angle θ = 90°, (b) equally sized (κ1R ≈ 100) particles with varying θ, (c) equally sized (κ1R ≈ 30) particles with varying θ, (d) unequally sized (2κ1R1 = κ1R2 ≈ 100) particles with varying θ, (e) unequally sized (10κ1R1 = κ1R2 ≈ 300) particles with varying θ, and (f) equally sized (κ1R ≈ 100) particles with θ = 90° within linear and nonlinear PB theory. As shown by panel (a) and its inset, the force increases  with increasing R and decays exponentially with increasing separation κ1L. Panels (b) and (c) suggest that, for equally sized cylinders, the force increases significantly with decreasing contact angle θ only within an interval around 90°. Outside this interval the force remains de facto constant and the interval of θ, across which the force actually varies, widens upon decreasing κ1R. For unequally sized cylinders, if the size asymmetry is moderate, the force may increase as well as decrease if the contact angle deviates from 90° (panel (d)). However, if the size contrast is high, the force becomes weaker once θ is slightly shifted away from 90° in either direction (panel (e)). From panel (f) and the inset therein one can infer that the discrepancy between the linear and the nonlinear results diminishes with increasing θ. with increasing R and decays exponentially with increasing separation κ1L. Panels (b) and (c) suggest that, for equally sized cylinders, the force increases significantly with decreasing contact angle θ only within an interval around 90°. Outside this interval the force remains de facto constant and the interval of θ, across which the force actually varies, widens upon decreasing κ1R. For unequally sized cylinders, if the size asymmetry is moderate, the force may increase as well as decrease if the contact angle deviates from 90° (panel (d)). However, if the size contrast is high, the force becomes weaker once θ is slightly shifted away from 90° in either direction (panel (e)). From panel (f) and the inset therein one can infer that the discrepancy between the linear and the nonlinear results diminishes with increasing θ. | |
B. Water–octanol interface
Water and lutidine, which are immiscible for sufficiently high temperatures, form a special system in that the bulk properties, i.e., the relative permittivities and the bulk ionic strengths, and consequently the Debye screening lengths, are not very different for the two fluid phases. In contrast to that, in the present subsection we consider another system with silica particles trapped at a water–octanol interface. At room temperature T = 300 K these two fluids differ starkly with respect to their bulk properties with εr,1 = 80 for water and εr,2 = 10.3 for octanol. The partitioning of ions at such an interface leads to highly contrasting bulk ionic strengths: for I1 = 10 mM one has I2 = 2.9 × 10−3 mM; the corresponding resulting Donnan potential equals 3.8kBT/e.43,44 Under these conditions, the inverse Debye length in the water phase is κ1 ≈ 0.324 nm−1 and the one in the oil phase (octanol) is κ2 ≈ 0.015 nm−1. The magnitude of the surface charge densities in contact with the two fluid phases also differ significantly; we consider σ1 = 0.01e nm−2 and σ2 = 0.0005e nm−2.11,12,45
The resulting interactions between the particles are shown in Fig. 4 for a pair of spheres (panels (a) and (c)) as well as for a pair of cylinders (panels (b) and (d)). From Fig. 4(a and b) one can infer that the total force F(L) between equally sized particles increases with increasing radii (R1 = R2 = R), both for spheres and cylinders. Whereas for spheres this increase is linear in the particle size (see the inset in Fig. 4(a)), in the case of cylinders it scales  (see the inset in Fig. 4(b)), which is evident from the data collapse in the insets. Although the line interaction becomes relatively more important in the case of the water–octanol system – due to a greater mismatch of the system parameters (ionic strengths, permittivities, and charge densities) compared to those of the water–lutidine system – these findings suggest that for micron-sized particles the interaction is still dominated by the surface parts. Fig. 4(c and d) show the variation of the inter-particle forces F(L) as function of the wetting contact angle θ for spheres and cylinders, respectively. At very short separations, the force varies only within a narrow interval 85° ≲ θ ≲ 95°. However, at relatively large separations it varies within a wider interval 75° ≲ θ ≲ 105° of the contact angle. These findings are also in accordance with eqn (7) and (8). For the system considered here, eqn (7) predicts that F1(L) varies appreciably within the interval 86° ≲ θ ≲ 94° whereas, according to eqn (8), F2(L) varies within the interval 71° ≲ θ ≲ 109°. At very short separations, the total force is dominated by the surface contribution in medium “1” (aqueous phase) due to higher surface charge densities at the particle surfaces. Therefore, if θ is decreased from 90°, i.e., when the particles become increasingly hydrophilic, the force increases, followed by saturation at around θ = 85°, as predicted by eqn (7). On the other hand, if θ is increased beyond 90° the particles become more hydrophobic. Up to θ ≈ 95°, for which F1 vanishes, the total force decreases as F1 decreases. Beyond that, a slight increase of the total force is observed due to F2 which, as predicted by eqn (8), increases up to θ ≈ 109°. As the separation between the particles is increased, in medium “1” the interaction decays very fast due to a strong screening by the higher amount of salt present. Consequently, at relatively large separations the total force is dominated by the surface contribution in medium “2” (oil phase) and, within the interval 75° ≲ θ ≲ 105°, it increases monotonically with increasing contact angle. It is important to note that eqn (7) and (8) are derived by using the fact that the error function erf(x) saturates for |x| ≳ 2, with the most significant variation occurring only for |x| ≲ 1.5. Therefore, the variation of F2(L) within the intervals 71° ≲ θ ≲ 75° and 105° ≲ θ ≲ 109° are very slow and hardly visible. Since here the silica particles are considered to be weakly charged, the discrepancy between the linear and the nonlinear PB theories become less significant. Still, the forces within the two approaches differ by a factor of 2 even at separations κ1L ≈ 10 for θ = 90°.
(see the inset in Fig. 4(b)), which is evident from the data collapse in the insets. Although the line interaction becomes relatively more important in the case of the water–octanol system – due to a greater mismatch of the system parameters (ionic strengths, permittivities, and charge densities) compared to those of the water–lutidine system – these findings suggest that for micron-sized particles the interaction is still dominated by the surface parts. Fig. 4(c and d) show the variation of the inter-particle forces F(L) as function of the wetting contact angle θ for spheres and cylinders, respectively. At very short separations, the force varies only within a narrow interval 85° ≲ θ ≲ 95°. However, at relatively large separations it varies within a wider interval 75° ≲ θ ≲ 105° of the contact angle. These findings are also in accordance with eqn (7) and (8). For the system considered here, eqn (7) predicts that F1(L) varies appreciably within the interval 86° ≲ θ ≲ 94° whereas, according to eqn (8), F2(L) varies within the interval 71° ≲ θ ≲ 109°. At very short separations, the total force is dominated by the surface contribution in medium “1” (aqueous phase) due to higher surface charge densities at the particle surfaces. Therefore, if θ is decreased from 90°, i.e., when the particles become increasingly hydrophilic, the force increases, followed by saturation at around θ = 85°, as predicted by eqn (7). On the other hand, if θ is increased beyond 90° the particles become more hydrophobic. Up to θ ≈ 95°, for which F1 vanishes, the total force decreases as F1 decreases. Beyond that, a slight increase of the total force is observed due to F2 which, as predicted by eqn (8), increases up to θ ≈ 109°. As the separation between the particles is increased, in medium “1” the interaction decays very fast due to a strong screening by the higher amount of salt present. Consequently, at relatively large separations the total force is dominated by the surface contribution in medium “2” (oil phase) and, within the interval 75° ≲ θ ≲ 105°, it increases monotonically with increasing contact angle. It is important to note that eqn (7) and (8) are derived by using the fact that the error function erf(x) saturates for |x| ≳ 2, with the most significant variation occurring only for |x| ≲ 1.5. Therefore, the variation of F2(L) within the intervals 71° ≲ θ ≲ 75° and 105° ≲ θ ≲ 109° are very slow and hardly visible. Since here the silica particles are considered to be weakly charged, the discrepancy between the linear and the nonlinear PB theories become less significant. Still, the forces within the two approaches differ by a factor of 2 even at separations κ1L ≈ 10 for θ = 90°.
 |
| | Fig. 4 Panel (a): Variation of the lateral component of the force F(L), expressed in units of 103κ1/β, due to electrostatic interaction between a pair of equally sized (R1 = R2 = R) spheres of varying radius with contact angle 90° as function of their scaled separation κ1L. The force increases linearly with increasing size of the particles which is evident from the data collapse in the inset. Panel (b): Variation of the z-component (see Fig. 1) of the force F(L), per length Ly in the y-direction, expressed in units of κ12/β, due to electrostatic interaction between a pair of equally sized cylinders of varying radius with contact angle 90°, as function of their scaled separation κ1L. Contrary to what one observes for spheres, the force between cylinders is proportional to 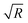 . Panel (c): Variation of the lateral component of the force F(L), expressed in units of 103κ1/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) spheres with various contact angles θ, as function of their scaled separation κ1L. Panel (d): Variation of the z-component of the force F(L), per length Ly in the y-direction, expressed in units of κ12/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) cylinders for various contact angles θ, as function of their scaled separation κ1L. Both for spheres and cylinders the force varies within a narrow interval of the contact angle at very short separations. The force increases if the particles are more hydrophilic within this interval of θ. At relatively large separations, however, this interval slightly broadens but the force increases if the particles become more hydrophobic. . Panel (c): Variation of the lateral component of the force F(L), expressed in units of 103κ1/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) spheres with various contact angles θ, as function of their scaled separation κ1L. Panel (d): Variation of the z-component of the force F(L), per length Ly in the y-direction, expressed in units of κ12/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) cylinders for various contact angles θ, as function of their scaled separation κ1L. Both for spheres and cylinders the force varies within a narrow interval of the contact angle at very short separations. The force increases if the particles are more hydrophilic within this interval of θ. At relatively large separations, however, this interval slightly broadens but the force increases if the particles become more hydrophobic. | |
IV. Conclusions
To conclude, by using the Derjaguin approximation and a fitting procedure for numerical results for the effective interaction between parallel, planar surfaces in contact with two demixed fluids in between, we have calculated the force due to the electrostatic interaction between pairs of spheres or cylinders at close distance from each other at a fluid–fluid interface. The comparison between the results obtained within linear and nonlinear PB theory shows that the former overestimates the force both for spheres and for cylinders, even at distances of several Debye lengths. Concerning the results within the nonlinear theory, we have investigated the effects of varying the sizes and the contact angle of the particles. Our general study is applicable also to pairs of particles which differ in size. For equally-sized spheres and cylinders the force always decays exponentially with increasing separation, and it scales ∝R for spheres and  for cylinders, where R is the common radius of the particles. Importantly, for equally-sized particles (both spherical and cylindrical) we have found an interval around the contact angle of 90°, beyond which the force de facto does not vary. We have also obtained simple relations (eqn (7) and (8)) involving the Debye lengths of the two media and the radii of the particles for calculating the width of this interval. These robust results can be expected to be useful for describing more general or complex particle interactions at fluid interfaces, which is important for various application perspectives of such systems.
for cylinders, where R is the common radius of the particles. Importantly, for equally-sized particles (both spherical and cylindrical) we have found an interval around the contact angle of 90°, beyond which the force de facto does not vary. We have also obtained simple relations (eqn (7) and (8)) involving the Debye lengths of the two media and the radii of the particles for calculating the width of this interval. These robust results can be expected to be useful for describing more general or complex particle interactions at fluid interfaces, which is important for various application perspectives of such systems.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Open Access funding provided by the Max Planck Society.
References
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156 CrossRef CAS.
-
B. P. Binks and T. S. Horozov, Colloidal Particles at Liquid Interfaces, Cambridge University Press, Cambridge, 2006 Search PubMed.
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001 RSC.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Márquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006 CrossRef CAS PubMed.
- M. Li, R. L. Harbron, J. V. M. Weaver, B. P. Binks and S. Mann, Nat. Chem., 2013, 5, 529 CrossRef CAS PubMed.
- A. Böker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231 RSC.
- B. M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Nano Lett., 2016, 16, 157 CrossRef CAS PubMed.
- T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65 CrossRef.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100, 503 CrossRef.
- T. S. Horozov, R. Aveyard, J. H. Clint and B. P. Binks, Langmuir, 2003, 19, 2822 CrossRef CAS.
- T. S. Horozov, R. Aveyard, B. P. Binks and J. H. Clint, Langmuir, 2005, 21, 7405 CrossRef CAS PubMed.
- D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E, 2000, 62, 5263 CrossRef CAS.
- P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145 CrossRef CAS PubMed.
- M. Oettel, A. Domínguez and S. Dietrich, Phys. Rev. E, 2005, 71, 051401 CrossRef CAS PubMed.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- M. Oettel and S. Dietrich, Langmuir, 2008, 24, 1425 CrossRef CAS PubMed.
- L. Parolini, A. D. Law, A. Maestro, D. M. A. Buzza and P. Cicuta, J. Phys.: Condens. Matter, 2015, 27, 194119 CrossRef PubMed.
- S. E. Anachkov, I. Lesov, M. Zanini, P. A. Kralchevsky, N. A. Denkov and L. Isa, Soft Matter, 2016, 12, 7632 RSC.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569 CrossRef CAS.
- A. J. Hurd, J. Phys. A: Math. Gen., 1985, 18, L1055 CrossRef CAS.
- A. Majee, M. Bier and S. Dietrich, J. Chem. Phys., 2014, 140, 164906 CrossRef PubMed.
- Z. Lian, J. Chem. Phys., 2016, 145, 014901 CrossRef PubMed.
- A. Majee, T. Schmetzer and M. Bier, Phys. Rev. E, 2018, 97, 042611 CrossRef PubMed.
- A. Majee, M. Bier and S. Dietrich, J. Chem. Phys., 2016, 145, 064707 CrossRef.
- S. G. Booth and R. A. W. Dryfe, J. Phys. Chem. C, 2015, 119, 23295 CrossRef CAS.
-
W. B. Russell, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, Cambridge, 1989 Search PubMed.
- M. P. Lyne, B. D. Bowen and S. Levine, J. Colloid Interface Sci., 1992, 150, 374 CrossRef CAS.
- F. Martínez-López, M. A. Cabrerizo-Vílchez and R. Hidalgo-Álvarez, J. Colloid Interface Sci., 2000, 232, 303 CrossRef PubMed.
- R. Aveyard, J. H. Clint, D. Nees and V. N. Paunov, Langmuir, 2000, 16, 1969 CrossRef CAS.
- R. Aveyard, B. P. Binks, J. H. Clint, P. D. I. Fletcher, T. S. Horozov, B. Neumann, V. N. Paunov, J. Annesley, S. W. Botchway, D. Nees, A. W. Parker, A. D. Ward and A. N. Burgess, Phys. Rev. Lett., 2002, 88, 246102 CrossRef CAS PubMed.
- B. J. Park, J. P. Pantina, E. M. Furst, M. Oettel, S. Reynaert and J. Vermant, Langmuir, 2008, 24, 1686 CrossRef CAS PubMed.
- P. Gao, X. C. Xing, Y. Li, T. Ngai and F. Jin, Sci. Rep., 2014, 4, 4778 CrossRef CAS PubMed.
- C. P. Kelleher, A. Wang, G. I. Guerrero-García, A. D. Hollingsworth, R. E. Guerra, B. J. Krishnatreya, D. G. Grier, V. N. Manoharan and P. M. Chaikin, Phys. Rev. E, 2015, 92, 062306 CrossRef PubMed.
- A. Majee, M. Bier and R. Podgornik, Soft Matter, 2018, 14, 985 RSC.
-
V. S. Bagotsky, Fundamentals of Electrochemistry, Wiley, Hoboken, NJ, 2006 Search PubMed.
- R. W. Rampolla and C. P. Smyth, J. Am. Chem. Soc., 1958, 80, 1057 CrossRef CAS.
- P. D. Gallagher, M. L. Kurnaz and J. V. Maher, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 7750 CrossRef.
- C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516 CrossRef CAS.
- H. D. Inerowicz, W. Li and I. Persson, J. Chem. Soc., Faraday Trans., 1994, 90, 2223 RSC.
-
D. R. Lide, Handbook of Chemistry and Physics, CRC, Boca Raton, 82nd edn, 2001–2002 Search PubMed.
- M. Bier, A. Gambassi and S. Dietrich, J. Chem. Phys., 2012, 137, 034504 CrossRef PubMed.
- R. Gulaboski, V. Mirčeski and F. Scholz, Electrochem. Commun., 2002, 4, 277 CrossRef CAS.
- F. Quentel, V. Mirčeski and M. L'Her, J. Solid State Electrochem., 2008, 12, 31 CrossRef CAS.
- K. D. Danov, P. A. Kralchevsky and M. P. Boneva, Langmuir, 2004, 20, 6139 CrossRef CAS PubMed.
-
Handbook of Mathematical Functions, ed. M. Abramowitz and I. A. Stegun, Dover, New York, 1964 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Markus
Bier
*ab,
Markus
Bier
 *abc and
S.
Dietrich
ab
*abc and
S.
Dietrich
ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,10,19,26 and whether the particle curvature plays any important role at short inter-particle separations still remains to be addressed within the nonlinear PB theory.
2,10,19,26 and whether the particle curvature plays any important role at short inter-particle separations still remains to be addressed within the nonlinear PB theory.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and D2 = −R2
θ and D2 = −R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ can be negative (for
θ can be negative (for  ; the case considered in Fig. 1) as well as positive (for
; the case considered in Fig. 1) as well as positive (for  ). In between the particles a gap of width L occurs (see the vertical dashed lines in Fig. 1) so that the horizontal center-to-center distance is L + R1 + R2. The fluid phase below (above) the interface occupying the half-space x < 0 (x > 0) is denoted by medium “1” (“2”). Both fluids are modeled as structureless, continuous media with dielectric constant εi = εr,iε0, i ∈ {1, 2}, where εr,i is the relative permittivity of medium i and ε0 is the vacuum permittivity. The ionic strength of added salt in medium i ∈ {1, 2} is denoted by Ii. The corresponding Debye screening length in each medium is given by
). In between the particles a gap of width L occurs (see the vertical dashed lines in Fig. 1) so that the horizontal center-to-center distance is L + R1 + R2. The fluid phase below (above) the interface occupying the half-space x < 0 (x > 0) is denoted by medium “1” (“2”). Both fluids are modeled as structureless, continuous media with dielectric constant εi = εr,iε0, i ∈ {1, 2}, where εr,i is the relative permittivity of medium i and ε0 is the vacuum permittivity. The ionic strength of added salt in medium i ∈ {1, 2} is denoted by Ii. The corresponding Debye screening length in each medium is given by  where
where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B = e2/(4πε0kBT) is the vacuum Bjerrum length with e > 0, kB, and T being the elementary charge, the Boltzmann constant, and the absolute temperature, respectively. Within our description at the mean-field level, the length scale of interest is the Debye length as both the local charge density and the electrostatic interaction vary on this scale. Phenomena which occur on smaller length scales, e.g., the structuring of liquids on the molecular length scale, are not considered. Here we consider medium “2” to be the less polar phase in the sense that κ2−1 > κ1−1. With this the criteria for the applicability of the DA are that both radii R1 and R2 have to be much larger than κ2−1 and L.
B = e2/(4πε0kBT) is the vacuum Bjerrum length with e > 0, kB, and T being the elementary charge, the Boltzmann constant, and the absolute temperature, respectively. Within our description at the mean-field level, the length scale of interest is the Debye length as both the local charge density and the electrostatic interaction vary on this scale. Phenomena which occur on smaller length scales, e.g., the structuring of liquids on the molecular length scale, are not considered. Here we consider medium “2” to be the less polar phase in the sense that κ2−1 > κ1−1. With this the criteria for the applicability of the DA are that both radii R1 and R2 have to be much larger than κ2−1 and L.
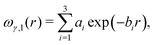



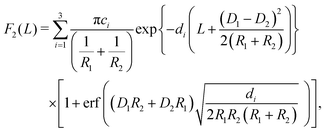
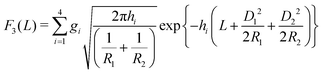
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and D2 = −R2
θ and D2 = −R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Variations of the total force F(L) = F1(L) + F2(L) + F3(L) in the units of 103κ1/β with the scaled separation κ1L for different system parameters are shown in Fig. 2. Here β = 1/(kBT) is the inverse thermal energy. As one can infer from Fig. 2(a), for equally-sized spheres (R1 = R2 = R) with a contact angle of θ = 90°, the effective force scales linearly with the size of the particles and decays exponentially with increasing separation between the particles. Both the linear scaling with R and the exponential decay with L can be directly inferred from the inset of Fig. 2(a) where the ratio of the dimensionless force βF/κ1 to the scaled radius κ1R is plotted as a function of the scaled separation κ1L using a semi-logarithmic scale, revealing data collapse. The exponential decay is expected to occur in the sense that all effective interactions decay exponentially for a pair of interacting flat plates, which remains unaffected while using the DA, and the linear scaling with R is a direct consequence of the DA. Fig. 2(b and c) display the variation of the scaled force with contact angle θ for equally-sized particles. As one can see, for κ1R ≈ 100 (b), the force increases with decreasing contact angle but de facto it varies only within the interval 80° < θ < 100°. A similar phenomenon is observed for κ1R ≈ 30 (c) albeit with variation in a slightly broader interval 75° < θ < 105°. Fig. 2(d and e) show the variation of the force with contact angle θ as function of separation distance κ1L for unequally-sized spheres. For the relatively small size-asymmetry in Fig. 2(d), the force between the particles can increase in a certain range of separation between the particles as the contact angle θ is decreased slightly from 90° downwards. Otherwise the force is weaker than the one obtained for a neutral wetting situation θ = 90°. For the larger size-asymmetry in Fig. 2(e), the force becomes weaker as soon as the contact angle θ differs from 90°. However, in both cases, as considered in Fig. 2(d and e), the force between the particles decreases upon increasing θ in the interval θ > 90°. Finally, in Fig. 2(f), we compare the force obtained within the linearized and the nonlinear PB theory for equally sized spheres. As one can see from the plot, the forces differ by almost an order of magnitude even at large separations such as κ1L ≈ 6 for θ = 90°. It turns out that with increasing contact angle θ this difference diminishes; see the inset of Fig. 2(f), where both curves are of almost the same magnitude. This is expected since the portion of the particles immersed in the more polar phase, for which the electrostatic interaction is stronger because κ1 ≈ κ2 [κ1 ≈ 0.1059 nm−1, κ2 ≈ 0.1053 nm−1] and σ1 ≫ σ2, decreases with increasing contact angle. Note that this situation differs from the one in ref. 11 and 12 in which κ1 ≫ κ2. A similar discrepancy appeared while comparing the interactions within the linear and nonlinear theory for parallel flat surfaces.25 Thus taking into account particle curvature does not significantly change this result.
θ. Variations of the total force F(L) = F1(L) + F2(L) + F3(L) in the units of 103κ1/β with the scaled separation κ1L for different system parameters are shown in Fig. 2. Here β = 1/(kBT) is the inverse thermal energy. As one can infer from Fig. 2(a), for equally-sized spheres (R1 = R2 = R) with a contact angle of θ = 90°, the effective force scales linearly with the size of the particles and decays exponentially with increasing separation between the particles. Both the linear scaling with R and the exponential decay with L can be directly inferred from the inset of Fig. 2(a) where the ratio of the dimensionless force βF/κ1 to the scaled radius κ1R is plotted as a function of the scaled separation κ1L using a semi-logarithmic scale, revealing data collapse. The exponential decay is expected to occur in the sense that all effective interactions decay exponentially for a pair of interacting flat plates, which remains unaffected while using the DA, and the linear scaling with R is a direct consequence of the DA. Fig. 2(b and c) display the variation of the scaled force with contact angle θ for equally-sized particles. As one can see, for κ1R ≈ 100 (b), the force increases with decreasing contact angle but de facto it varies only within the interval 80° < θ < 100°. A similar phenomenon is observed for κ1R ≈ 30 (c) albeit with variation in a slightly broader interval 75° < θ < 105°. Fig. 2(d and e) show the variation of the force with contact angle θ as function of separation distance κ1L for unequally-sized spheres. For the relatively small size-asymmetry in Fig. 2(d), the force between the particles can increase in a certain range of separation between the particles as the contact angle θ is decreased slightly from 90° downwards. Otherwise the force is weaker than the one obtained for a neutral wetting situation θ = 90°. For the larger size-asymmetry in Fig. 2(e), the force becomes weaker as soon as the contact angle θ differs from 90°. However, in both cases, as considered in Fig. 2(d and e), the force between the particles decreases upon increasing θ in the interval θ > 90°. Finally, in Fig. 2(f), we compare the force obtained within the linearized and the nonlinear PB theory for equally sized spheres. As one can see from the plot, the forces differ by almost an order of magnitude even at large separations such as κ1L ≈ 6 for θ = 90°. It turns out that with increasing contact angle θ this difference diminishes; see the inset of Fig. 2(f), where both curves are of almost the same magnitude. This is expected since the portion of the particles immersed in the more polar phase, for which the electrostatic interaction is stronger because κ1 ≈ κ2 [κ1 ≈ 0.1059 nm−1, κ2 ≈ 0.1053 nm−1] and σ1 ≫ σ2, decreases with increasing contact angle. Note that this situation differs from the one in ref. 11 and 12 in which κ1 ≫ κ2. A similar discrepancy appeared while comparing the interactions within the linear and nonlinear theory for parallel flat surfaces.25 Thus taking into account particle curvature does not significantly change this result.
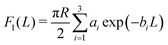 and
and  , respectively, which transparently explain the linear variation of the force with the particle size R (the coefficients ai and ci do not depend on R) and its exponential decay as function of the separation L. The decay rate in the limit of large distances is determined by the smaller of the two Debye lengths κ1−1 and κ2−1 (please note that for our system κ1−1 ≈ κ2−1). For R1 = R2 = R with an arbitrary contact angle θ, one has D1 − D2 = 0 so that the dependence on θ appears in eqn (4) and (5) only through the terms involving the error functions, which reduce to
, respectively, which transparently explain the linear variation of the force with the particle size R (the coefficients ai and ci do not depend on R) and its exponential decay as function of the separation L. The decay rate in the limit of large distances is determined by the smaller of the two Debye lengths κ1−1 and κ2−1 (please note that for our system κ1−1 ≈ κ2−1). For R1 = R2 = R with an arbitrary contact angle θ, one has D1 − D2 = 0 so that the dependence on θ appears in eqn (4) and (5) only through the terms involving the error functions, which reduce to  and
and 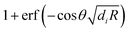 , respectively. Since the error function levels off to |erf(x)| ≈ 1 for |x| ≳ 2, the variation of the force with respect to θ in eqn (4) saturates once the slowest decay rate bi, which in the present case is κ1, satisfies the inequality
, respectively. Since the error function levels off to |erf(x)| ≈ 1 for |x| ≳ 2, the variation of the force with respect to θ in eqn (4) saturates once the slowest decay rate bi, which in the present case is κ1, satisfies the inequality

 implies that the particles become more hydrophilic. Consequently, the contribution F1(L) to the total force increases while F2(L) decreases upon decreasing θ. Finally, at θ ≈ 78° the former attains a non-zero finite value and the latter vanishes (please note the different signs in front of the error functions in eqn (4) and (5)). On the other hand, increasing the contact angle θ from
implies that the particles become more hydrophilic. Consequently, the contribution F1(L) to the total force increases while F2(L) decreases upon decreasing θ. Finally, at θ ≈ 78° the former attains a non-zero finite value and the latter vanishes (please note the different signs in front of the error functions in eqn (4) and (5)). On the other hand, increasing the contact angle θ from  implies that the particles become more hydrophobic. As a result, the contribution F2(L) increases and F1(L) decreases with the former attaining a non-zero finite value while the latter is vanishing at θ ≈ 102°. Upon decreasing κ1R, the interval of θ over which the force varies broadens as can be inferred from Fig. 2(c). For unequal particles sizes, i.e., for R1 ≠ R2, the dependence on θ in eqn (4) and (5) originate from both the exponential and the error function. For moderate size-asymmetry, like the one considered in Fig. 2(d), a competition between these two functions determines the variation of the force with θ. However, for the extremely asymmetric case considered in Fig. 2(e), the difference D1 − D2 is large and the exponential terms dominate as soon as θ differs slightly from 90°.
implies that the particles become more hydrophobic. As a result, the contribution F2(L) increases and F1(L) decreases with the former attaining a non-zero finite value while the latter is vanishing at θ ≈ 102°. Upon decreasing κ1R, the interval of θ over which the force varies broadens as can be inferred from Fig. 2(c). For unequal particles sizes, i.e., for R1 ≠ R2, the dependence on θ in eqn (4) and (5) originate from both the exponential and the error function. For moderate size-asymmetry, like the one considered in Fig. 2(d), a competition between these two functions determines the variation of the force with θ. However, for the extremely asymmetric case considered in Fig. 2(e), the difference D1 − D2 is large and the exponential terms dominate as soon as θ differs slightly from 90°.

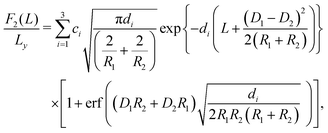

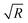 ; see Fig. 3(a) and the inset therein. This is evident from the prefactors of the exponential functions in eqn (9) and (10). The variation of the force with respect to θ as well as eqn (7) and (8) remain the same as for the spheres, because the θ-dependent terms in eqn (9) and (10) have exactly the same form as in eqn (4) and (5). This behavior is confirmed by Fig. 3(b–e). Finally, the comparison of the effective force for θ = 90° within linearized and nonlinear PB theory reveals a significant discrepancy between the predictions of the two approaches, which becomes smaller for larger contact angles θ, i.e., as the portion of the particles, dipped into the more polar phase, decreases (see Fig. 3(f)).
; see Fig. 3(a) and the inset therein. This is evident from the prefactors of the exponential functions in eqn (9) and (10). The variation of the force with respect to θ as well as eqn (7) and (8) remain the same as for the spheres, because the θ-dependent terms in eqn (9) and (10) have exactly the same form as in eqn (4) and (5). This behavior is confirmed by Fig. 3(b–e). Finally, the comparison of the effective force for θ = 90° within linearized and nonlinear PB theory reveals a significant discrepancy between the predictions of the two approaches, which becomes smaller for larger contact angles θ, i.e., as the portion of the particles, dipped into the more polar phase, decreases (see Fig. 3(f)).
 with increasing R and decays exponentially with increasing separation κ1L. Panels (b) and (c) suggest that, for equally sized cylinders, the force increases significantly with decreasing contact angle θ only within an interval around 90°. Outside this interval the force remains de facto constant and the interval of θ, across which the force actually varies, widens upon decreasing κ1R. For unequally sized cylinders, if the size asymmetry is moderate, the force may increase as well as decrease if the contact angle deviates from 90° (panel (d)). However, if the size contrast is high, the force becomes weaker once θ is slightly shifted away from 90° in either direction (panel (e)). From panel (f) and the inset therein one can infer that the discrepancy between the linear and the nonlinear results diminishes with increasing θ.
with increasing R and decays exponentially with increasing separation κ1L. Panels (b) and (c) suggest that, for equally sized cylinders, the force increases significantly with decreasing contact angle θ only within an interval around 90°. Outside this interval the force remains de facto constant and the interval of θ, across which the force actually varies, widens upon decreasing κ1R. For unequally sized cylinders, if the size asymmetry is moderate, the force may increase as well as decrease if the contact angle deviates from 90° (panel (d)). However, if the size contrast is high, the force becomes weaker once θ is slightly shifted away from 90° in either direction (panel (e)). From panel (f) and the inset therein one can infer that the discrepancy between the linear and the nonlinear results diminishes with increasing θ. (see the inset in Fig. 4(b)), which is evident from the data collapse in the insets. Although the line interaction becomes relatively more important in the case of the water–octanol system – due to a greater mismatch of the system parameters (ionic strengths, permittivities, and charge densities) compared to those of the water–lutidine system – these findings suggest that for micron-sized particles the interaction is still dominated by the surface parts. Fig. 4(c and d) show the variation of the inter-particle forces F(L) as function of the wetting contact angle θ for spheres and cylinders, respectively. At very short separations, the force varies only within a narrow interval 85° ≲ θ ≲ 95°. However, at relatively large separations it varies within a wider interval 75° ≲ θ ≲ 105° of the contact angle. These findings are also in accordance with eqn (7) and (8). For the system considered here, eqn (7) predicts that F1(L) varies appreciably within the interval 86° ≲ θ ≲ 94° whereas, according to eqn (8), F2(L) varies within the interval 71° ≲ θ ≲ 109°. At very short separations, the total force is dominated by the surface contribution in medium “1” (aqueous phase) due to higher surface charge densities at the particle surfaces. Therefore, if θ is decreased from 90°, i.e., when the particles become increasingly hydrophilic, the force increases, followed by saturation at around θ = 85°, as predicted by eqn (7). On the other hand, if θ is increased beyond 90° the particles become more hydrophobic. Up to θ ≈ 95°, for which F1 vanishes, the total force decreases as F1 decreases. Beyond that, a slight increase of the total force is observed due to F2 which, as predicted by eqn (8), increases up to θ ≈ 109°. As the separation between the particles is increased, in medium “1” the interaction decays very fast due to a strong screening by the higher amount of salt present. Consequently, at relatively large separations the total force is dominated by the surface contribution in medium “2” (oil phase) and, within the interval 75° ≲ θ ≲ 105°, it increases monotonically with increasing contact angle. It is important to note that eqn (7) and (8) are derived by using the fact that the error function erf(x) saturates for |x| ≳ 2, with the most significant variation occurring only for |x| ≲ 1.5. Therefore, the variation of F2(L) within the intervals 71° ≲ θ ≲ 75° and 105° ≲ θ ≲ 109° are very slow and hardly visible. Since here the silica particles are considered to be weakly charged, the discrepancy between the linear and the nonlinear PB theories become less significant. Still, the forces within the two approaches differ by a factor of 2 even at separations κ1L ≈ 10 for θ = 90°.
(see the inset in Fig. 4(b)), which is evident from the data collapse in the insets. Although the line interaction becomes relatively more important in the case of the water–octanol system – due to a greater mismatch of the system parameters (ionic strengths, permittivities, and charge densities) compared to those of the water–lutidine system – these findings suggest that for micron-sized particles the interaction is still dominated by the surface parts. Fig. 4(c and d) show the variation of the inter-particle forces F(L) as function of the wetting contact angle θ for spheres and cylinders, respectively. At very short separations, the force varies only within a narrow interval 85° ≲ θ ≲ 95°. However, at relatively large separations it varies within a wider interval 75° ≲ θ ≲ 105° of the contact angle. These findings are also in accordance with eqn (7) and (8). For the system considered here, eqn (7) predicts that F1(L) varies appreciably within the interval 86° ≲ θ ≲ 94° whereas, according to eqn (8), F2(L) varies within the interval 71° ≲ θ ≲ 109°. At very short separations, the total force is dominated by the surface contribution in medium “1” (aqueous phase) due to higher surface charge densities at the particle surfaces. Therefore, if θ is decreased from 90°, i.e., when the particles become increasingly hydrophilic, the force increases, followed by saturation at around θ = 85°, as predicted by eqn (7). On the other hand, if θ is increased beyond 90° the particles become more hydrophobic. Up to θ ≈ 95°, for which F1 vanishes, the total force decreases as F1 decreases. Beyond that, a slight increase of the total force is observed due to F2 which, as predicted by eqn (8), increases up to θ ≈ 109°. As the separation between the particles is increased, in medium “1” the interaction decays very fast due to a strong screening by the higher amount of salt present. Consequently, at relatively large separations the total force is dominated by the surface contribution in medium “2” (oil phase) and, within the interval 75° ≲ θ ≲ 105°, it increases monotonically with increasing contact angle. It is important to note that eqn (7) and (8) are derived by using the fact that the error function erf(x) saturates for |x| ≳ 2, with the most significant variation occurring only for |x| ≲ 1.5. Therefore, the variation of F2(L) within the intervals 71° ≲ θ ≲ 75° and 105° ≲ θ ≲ 109° are very slow and hardly visible. Since here the silica particles are considered to be weakly charged, the discrepancy between the linear and the nonlinear PB theories become less significant. Still, the forces within the two approaches differ by a factor of 2 even at separations κ1L ≈ 10 for θ = 90°.
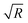 . Panel (c): Variation of the lateral component of the force F(L), expressed in units of 103κ1/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) spheres with various contact angles θ, as function of their scaled separation κ1L. Panel (d): Variation of the z-component of the force F(L), per length Ly in the y-direction, expressed in units of κ12/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) cylinders for various contact angles θ, as function of their scaled separation κ1L. Both for spheres and cylinders the force varies within a narrow interval of the contact angle at very short separations. The force increases if the particles are more hydrophilic within this interval of θ. At relatively large separations, however, this interval slightly broadens but the force increases if the particles become more hydrophobic.
. Panel (c): Variation of the lateral component of the force F(L), expressed in units of 103κ1/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) spheres with various contact angles θ, as function of their scaled separation κ1L. Panel (d): Variation of the z-component of the force F(L), per length Ly in the y-direction, expressed in units of κ12/β, due to electrostatic interaction between a pair of equally sized (κ1R ≈ 800) cylinders for various contact angles θ, as function of their scaled separation κ1L. Both for spheres and cylinders the force varies within a narrow interval of the contact angle at very short separations. The force increases if the particles are more hydrophilic within this interval of θ. At relatively large separations, however, this interval slightly broadens but the force increases if the particles become more hydrophobic. for cylinders, where R is the common radius of the particles. Importantly, for equally-sized particles (both spherical and cylindrical) we have found an interval around the contact angle of 90°, beyond which the force de facto does not vary. We have also obtained simple relations (eqn (7) and (8)) involving the Debye lengths of the two media and the radii of the particles for calculating the width of this interval. These robust results can be expected to be useful for describing more general or complex particle interactions at fluid interfaces, which is important for various application perspectives of such systems.
for cylinders, where R is the common radius of the particles. Importantly, for equally-sized particles (both spherical and cylindrical) we have found an interval around the contact angle of 90°, beyond which the force de facto does not vary. We have also obtained simple relations (eqn (7) and (8)) involving the Debye lengths of the two media and the radii of the particles for calculating the width of this interval. These robust results can be expected to be useful for describing more general or complex particle interactions at fluid interfaces, which is important for various application perspectives of such systems.


