Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the collapse transition of weakly charged polymers by ion-specific screening and adsorption†
Richard
Chudoba
 abc,
Jan
Heyda
abc,
Jan
Heyda
 *d and
Joachim
Dzubiella
*d and
Joachim
Dzubiella
 *bc
*bc
aInstitut für Physik, Humboldt-Universität zu Berlin, Newtonstraße 15, D-12489 Berlin, Germany. E-mail: richard.chudoba@helmholtz-berlin.de
bPhysikalisches Institut, Albert-Ludwigs Universität Freiburg, Hermann-Herder-Straße 3, D-79104 Freiburg im Breisgau, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
cResearch Group Simulations of Energy Materials, Helmholtz-Zentrum Berlin, Hahn-Meitner-Platz 1, D-14109 Berlin, Germany
dDepartment of Physical Chemistry, University of Chemistry and Technology, Prague, Technická 5, CZ-16628 Praha 6, Czech Republic. E-mail: jan.heyda@vscht.cz
First published on 8th November 2018
Abstract
The experimentally observed swelling and collapse response of weakly charged polymers to the addition of specific salts displays quite convoluted behavior that is not easy to categorize. Here we use a minimalistic implicit-solvent/explicit-salt simulation model with a focus on ion-specific interactions between ions and a single weakly charged polyelectrolyte to qualitatively explain the observed effects. In particular, we demonstrate ion-specific screening and bridging effects cause collapse at low salt concentrations whereas the same strong ion-specific direct interactions drive re-entrant swelling at high concentrations. Consistently with experiments, a distinct salt concentration at which the salting-out power of anions inverts from the reverse to direct Hofmeister series is observed. At this so called isospheric point, the ion-specific effects vanish. Furthermore, with additional simplifying assumptions, an ion-specific mean-field model is developed for the collapse transition which quantitatively agrees with the simulations. Our work demonstrates the sensitivity of the structural behavior of charged polymers to the addition of specific salt beyond simple screening and shall be useful for further guidance of experiments.
1 Introduction
Biopolymers as well as functional synthetic polymers in solution are subject to a complex set of interactions that are decisive for their molecular structure and function, e.g., as for folded versus unfolded states for proteins, or, more general, collapsed versus swollen states of a polymer.1 Typically those solvated polymers are weakly charged and constitute relatively heterogeneous, partially polar, partially hydrophobic, macromolecules. Hence their polymeric structure is greatly affected by the solvation environment. Apart from the solvent type (e.g., water), the polymer conformation can be conveniently controlled by the concentration and type of added cosolutes. In particular, ion-specific, also called Hofmeister, effects2,3 of salts on biopolymeric structure and phase behavior have been studied and highlighted in recent years in an overwhelming amount of literature.4–8The Hofmeister effects on the polymeric structure and the phase behavior are very complex and polymer specific. In order to increase the accessibility to the problem, often model systems are employed. For instance, ureido copolymers are only partially miscible in water below their upper critical solution temperature (UCST), which can be modulated by addition of salts.9 Another example is the poly-N-isopropylacrylamide (PNIPAM) homopolymer or elastin-like polypeptides (ELPs), which both exhibit hydrophobic collapse transitions at their respective lower critical solution temperatures (LCST).10–12 These collapse transitions are analogous to cold-denaturation of proteins, in which ion-specific interactions (Hofmeister effects) play a prominent role.
Poly(allylamine)-co-poly(allylurea) (PAU) copolymers undergo a UCST transition at physiological conditions. The formation of hydrogen bonds among ureido groups is proposed as the underlying mechanism. The UCST is influenced by the copolymer composition and rises as the ureido content increases. Amine groups in the copolymer are protonated at pH ∼ 7.5 making the polymer weakly positively charged.9
PNIPAM is a neutral polymer with a LCST at 32 °C. Charge groups can be introduced into the polymer structure by copolymerization, typically with weak or strong acids or bases.15–17 The electrostatic repulsion between charged monomers then leads to an increase of the LCST in pure water and a strong response to added salt at millimolar salt concentration when charge screening sets in.
ELPs constitute a particularly nice model system as they can be expressed by bacteria in a strictly monodisperse fashion with different repeating sequences.13,18–20 It is possible, for instance, to synthesize pentapeptide sequences of the generic form (VPGXG)n, where X stands for any amino acid except proline.21,22 One can thus easily modulate the hydrophilic, hydrophobic, and charged character of the ELPs22 together with their LCST.20,23 Salt-specific effects were studied not only for a few neutral ELPs (e.g., V-120),13,24,25 but also for the weakly positively charged KV6-120,8,14 and the weakly negatively charged DV2F-64.10
For completely neutral polymers, e.g., pure PNIPAM or neutral ELPs, only two regimes of salt action were reported in the literature,13,26 see Fig. 1(a). (I) A linear and rather steep decrease of the cloud point temperature (an approximate but direct experimental measure of the LCST) with salt concentration was observed for most strongly hydrated salts, such as sulfates, acetates, fluorides, and chlorides. (II) An initial weak increase of the cloud point temperature at low salt concentrations, typically below 1 M, with a subsequent decrease at higher concentrations. Only recently a third regime, which was predicted by computer simulations27 and is characterized by a strongly attractive bridging interaction, was found. Guanidinium thiocyanate, one of the most potent protein denaturants, steeply decreases the cloud point temperature below 1.5 M, and the temperature grows even more rapidly above 1.5 M salt.25 The relation of this to the phenomenon of cononsolvency in solvent mixtures is under discussion.28 Charged ELPs possess a more complex behavior due to the ion-specific screening at low salt concentrations,8,10,14cf.Fig. 1(b), similar to the stability behavior of charged proteins.4
 | ||
| Fig. 1 Experimental data of cloud point measurements plotted versus the concentration of various sodium salts (with anions as given in the legend on the right side) added to the polymer solution. (a) The change of the LCST of the uncharged ELP V5A2G3-120.13,14 (b) The change of the LCST of the weakly positively charged ELP KV6-112.14 (c) The cloud point of the weakly positively charged PAU exhibiting an UCST.9 | ||
It is now of fundamental importance to characterize the regimes in which salt-specific effects operate. This would allow one to build a predictive model, which may be applied for determination of protein stability, but also for designing biomaterials of desired properties in their native environments. Computer simulations have already provided insight in the action of various solvents and cosolutes in coarse-grained simulations27,29–35 or all-atom simulations.23,36–38 Typically the results are interpreted by theories for chain structure and swelling,39e.g., due to counterion condensation at highly charged polymers40–44 or specific steric interactions.45–50 Yet, a quantitative description of ion-specific counterion condensation relies on all-atom simulations.51,52 Driven by increasing interest in cononsolvency and the action of mixed solutes on the polymer structure, a whole body of mean-field theories has been developed especially for the description of the coil-to-globule transition in mixed solvents.27,28,53–58
Recently, we have developed a thermodynamic approach for neutral polymers (such as PNIPAM, or neutral ELPs) within the framework of preferential binding,8,59 which helps to interpret the salt-specific thermodynamic fingerprints of cosolute–polymer interactions.60 A similar model was used and extended to include non-specific screening effects for weakly charged polymers.61 In this work we aim to fully understand the complex data for charged elastin8,10,14 (selected data shown in Fig. 1(b)). For this purpose we devise a generic simulation model of a charged polymer with different charge fractions in uni-univalent salt solutions. The ion-specificity of salts enters by systematically varying the polymer–ion interactions, i.e., from more repulsive, mimicking rather strongly hydrated ions (traditionally called ‘kosmotropes’), to very attractive, mimicking rather weakly hydrated ions (originally named as ‘chaotropes’).3 Our previous simulations of neutral polymers exhibiting simple UCST have already demonstrated a non-trivial response of the polymer, where collapse by depletion, swelling through weak attraction, and re-entrant collapse by strong attractions have been observed.27 As indicated by experiments, the situation becomes more complex in charged systems, where screening and synergistic cation and anion interactions with the polymer are expected. In this work, we therefore complement the simulations with a new theory that extends our Flory-type mean-field model for neutral polymers with approaches for ion-specific screening.61,62
2 Model and methods
In our model, a single polymer chain containing Nmer = 200 coarse-grained monomer units is used. Monomers bearing a charge +e or −e are evenly (equidistantly) distributed along the chain to obtain the desired charge fractions ξ of 0, 5 and 10%, for cationic or anionic chains, respectively. Furthermore, coarse-grained ions (counter-ions of the polyelectrolyte and uni-univalent electrolyte) are explicitly resolved in the implicit solvent environment. All beads, i.e., monomers and ions, interact via effective pair potentials in the form of the Lennard-Jones (LJ) potential, that is | (1) |
The charged particles furthermore interact through the standard Coulomb potential. The relative permittivity of the background corresponds to water at room temperature with a dielectric constant εr = 78. This results in the Bjerrum length lB = e2/4πε0εrkBT = 0.7 nm at T = 298 K, where e is the elementary charge, ε0 the vacuum permittivity, and kB is the Boltzmann constant.
The bonds between adjacent monomers in the polymer chain are modeled with a harmonic potential with a spring constant k = 100kBT nm−2 and a bond length b = 0.38 nm.27 Neither angular nor torsional potential is applied. Non-bonded interactions between adjacent monomers are excluded.
The non-interacting polymer chain having Nmer = 200 segments each b = 0.38 nm long is considered as an ideal reference of our simulation setup. The ideal radius of gyration equals  .
.
The solvation characteristics of ions cannot be captured directly in the implicit solvent model. Instead the value of the second virial coefficient B2 for the monomer–ion interaction (without electrostatics) can be used as a global measure of the hydrated character and ion-specific affinity to the polymer. Repulsive ions prefer to stay in the bulk solution because of a net repulsion between them and the uncharged polymer. That corresponds to a positive B2 value of the monomer–ion interaction. On the other hand, attractive ions tend to preferentially adsorb to the polymer surface, which gives a net negative B2 value of the monomer–ion interaction. The value of B2 can be computed from the pairwise potential (eqn (5)). The effective nonbonded potential in the LJ form conveniently allows a gradual change of ion characteristics from repulsive to attractive, i.e. ε ≲ 0.3kBT gives a positive B2 value (a net repulsion), while ε ≳ 0.3kBT yields a negative B2 value (a net attraction).
The implicit-solvent simulations are symmetric regarding the positive and negative charge. However, as known from experiments, anions exhibit a greater variety of interactions with ELPs than common cations.8 To investigate a broader range of interaction types and yet to stay consistent with the experiments, we varied the anion–polymer interaction strength while keeping the strength of the cation–polymer interaction unchanged. The affinity of the ions to the polymer is controlled by εcation and εanion in the LJ potential acting between a monomer (regardless of its charge) and a cation, or an anion, respectively. The value of εcation = 0.1kBT is kept constant, corresponding to strongly repulsive cations. The value of εanion varies between 0.1kBT and 0.9kBT, altering the value of the second virial coefficient of the interaction between anions and the polymer. The actual B2 values of the interactions employed in the simulations are summarized in Table S1 (ESI†).
The non-electrostatic interaction between two ions (either anions, cations or cation–anion pairs) is determined by εij = 0.3kBT in all simulations, corresponding to the zero value of the second virial coefficient B2 for a purely non-electrostatic interaction.
The non-bonded pair interaction between monomers reflects the quality of the implicit solvent towards the polymer, i.e., varying solvent and polymer temperature. Our simple polymer model without solvent and explicit T-dependent interactions exhibits a UCST, while all qualitative trends including LCST are reflected, however, in an inverse manner. LJ potentials with εmer between 0.1kBT and 0.9kBT are used when scanning for the near-critical (collapse transition) solvent condition.
The value of σ = 0.3385 nm in the LJ potential is kept constant for all interactions,27 except for the interaction between cation and monomer, where σ = 0.4787 nm corresponds to even stronger repulsion of common cations, e.g. Na+, from rather apolar monomers.24,36
Langevin dynamics (LD) simulations in Gromacs 5.163 in the NVT ensemble are performed. The friction constant γ is set to 1.0 ps−1. The stochastic processes correspond to the temperature T = 298 K. The time step of the velocity Verlet integrator is set to 7.5 fs. Together with the reduced molar mass 8.635 g mol−1 of all coarse-grained particles, the polymer conformations are sampled efficiently. The electrostatic potential is computed using the particle mesh Ewald method.64 To efficiently employ this method in a system with a low particle density, the value of the cut-off distance in real space and the number of grid points in Fourier reciprocal space are optimized, as described in Table S2 (ESI†).
A single coarse-grained polymer chain and salt ions are placed into a cubic simulation box to prepare 0.0 M (counterions only), 0.1 M, 0.4 M, 1.0 M, and 2.0 M salt solutions (Fig. 2). Periodic boundary conditions are applied. The default volume of the simulation box 8304 nm3 is reduced to one fourth when the polymer holds a compact globular conformation and the salt concentration is ≥1 M. The compositions of the systems are described in detail in Table S2 (ESI†). A trajectory of 525 ns is obtained in every simulation run. The initial 25 ns is considered as an equilibration phase and thus excluded from the analysis. Standard Gromacs tools, namely gmx polystat and gmx rdf, are used for the data analysis. Further statistical evaluations are performed in R.65 The uncertainties of the quantities are determined as a standard error obtained from ten independent parts of the simulation trajectory.
3 Mean-field theory
In this section, we present a mean-field theory to describe the change of critical conditions of the polymer in the presence of cosolute, e.g., salt. The theory ansatz closely corresponds to the simulation setup as introduced in the previous section. Thus a generic weakly charged polymer in an implicit solvent with an explicit salt is considered.All interactions within the theory are described by a virial expansion, i.e., the nonbonded interactions presented in the simulations in the LJ-form are integrated into the virial expansion coefficients. Moreover, the electroneutrality condition is postulated to deal with electrostatic interactions stemming from the polymer's own charge.
We choose an NpT ensemble for the polymer which is in contact with a reservoir of cosolutes at a constant chemical potential. Cosolute molecules are allowed to exchange between the ensemble and the reservoir. At equilibrium the Gibbs free energy is minimized in such a system. The polymer is simply modeled as an elastic, penetrable sphere that can change its radius upon the sorption of cosolutes. (Polymer conformational degrees of freedom are thus averaged out into an effective blob, like in the classical Flory approaches where only the polymer size is a variable.) Hence, the total Gibbs free energy of the polymer phase which is in contact with a salt reservoir containing i cosolute constituents, i.e., anions and cations in our system, can be defined as
 | (2) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i is the electrochemical potential of the respective constituent in the reservoir, p is the osmotic pressure, and Fpol is the total Helmholtz free energy of the polymer including the absorbed cosolute.
i is the electrochemical potential of the respective constituent in the reservoir, p is the osmotic pressure, and Fpol is the total Helmholtz free energy of the polymer including the absorbed cosolute.
The electrochemical potential ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i can be expressed with the explicit electrostatic term as
i can be expressed with the explicit electrostatic term as
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i = μi + zieϕ, i = μi + zieϕ, | (3) |
 | (4) |
The interactions between particles are described by a virial expansion up to the fourth order in our model. Note, the expansion at least up to the third order is required to guarantee a physically relevant solution for the negative second virial coefficient. The second viral coefficient Bij2 between the particles i and j can be easily evaluated from the Lennard-Jones pair potential UijLJ,27,66
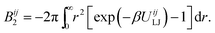 | (5) |
We approximate all three body interactions using the third virial coefficient Bijk3 = 2.00σ6, consistently with our previous work.27 The four body interactions are modeled analogously with the fourth virial coefficient of hard spheres with a diameter σ, Bijkl4 = 2.64σ9. The values approximately correspond to the virial expansion coefficients of homogeneous LJ fluids within the considered range of ε.67,68
The polymer chain itself is modeled as an elastic (entropic) spring54,58,69
 | (6) |
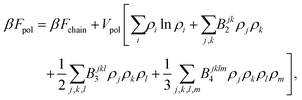 | (7) |
The reservoir is modeled as a real gas which follows the fourth order virial expansion
 | (8) |
 | (9) |
 | (10) |
In order to find the equilibrium we numerically minimize the Gibbs free energy of the polymer Gpol (eqn (2)) with respect to its effective volume Vpol and the number of cosolute particles Ni. Note that the theory can model both UCST and LCST polymers, depending on the input, in particular, the T-dependence of the viral coefficients.
Knowing the equilibrium concentration of the ions inside the polymer phase, the Donnan potential can be evaluated using eqn (3) directly, for either cations, or anions. The chemical part μi of the electrochemical potential ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i of the respective cosolute i inside the polymer phase can be expressed from eqn (7), computing the derivative
i of the respective cosolute i inside the polymer phase can be expressed from eqn (7), computing the derivative
 | (11) |
Detailed evaluation of the Donnan potential is provided in the ESI.†
The mean effective volume of the polymer can be obtained as a Boltzmann weighted average. The fluctuations in the radius of the polymer (〈R4pol〉/〈R2pol〉2 − 1) are computed as a function of the solvent quality (εmer). At the critical solution temperature (CST) the fluctuations maximize.70 The n-th moment of Rpol was computed using the Boltzmann distribution
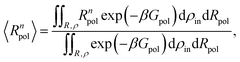 | (12) |
Note that our mean-field theory can be considered valid only close to the coil-to-globule equilibrium when the polymer chain forms a rather compact conformation. The further assumptions are that the fraction of charged monomers has to be low and the salt concentration relatively high, i.e., the neutral reference state is only slightly perturbed.
A similar thermodynamic description has been recently developed for microgels, albeit a different procedure to find the thermodynamic equilibrium was employed.62 Salt-specific effects on weakly charged copolymers can be captured qualitatively by a simplified theory which treats the ion-specific and non-specific electrostatic contributions on a simple additive level, as demonstrated on PNIPAM copolymers.61 In contrast, the theory developed in this work includes the ion-specific and non-specific interactions in a self-consistent way.
The equations are solved using numeric solvers of the Wolfram Mathematica 11.2 software package.71
4 Results and discussion
4.1 Solvent quality near critical conditions
In order to find conditions close to the swollen-to-collapse transition, a solvent quality parameter, i.e., an effective interaction between monomers εmer, is varied from 0.1kBT to 0.9kBT. The polymer chain conformation changes from an extended coil to a collapsed globule in this solvent quality range, as shown in Fig. 3.The radius of gyration of an uncharged polymer chain (ξ = 0.00) at εmer ≃ 0.4kBT almost exactly corresponds to the radius of gyration of the ideal, non-interacting polymer chain Ridg. The radius of gyration increases with the charge fraction of the polymer and the transition is shifted to higher εmer values. However, a small concentration of salt (0.1 M) already suppresses this trend due to the charge screening, as shown in Fig. 3. Thus we choose εmer = 0.4kBT to describe the solvent quality for uncharged and charged polymers close to the critical conditions, with the exception of the strongly charged (ξ = 0.10) anionic polymer where the value εmer = 0.5kBT is used instead. Note that the critical value of εmer depends on the actual chain size and the charge fraction. The value approaches 0.3kBT for an infinitely long uncharged chain.
4.2 Salt interaction with an uncharged polymer
First, we investigate an uncharged polymer and relate qualitatively the simulation results to the known experimental data of ELP. Two different regimes, determined by the salt type, can be observed when the mean radius of gyration of the uncharged 200-mer is plotted as a function of the salt concentration, Fig. 4(a). The repulsive salts (εanion = 0.1kBT and 0.3kBT) induce a collapse through depletion as the salt concentration increases. The salts with an attractive anion (εanion = 0.7kBT and 0.9kBT) cause swelling of the polymer coil by attraction. Both regimes are described in detail for non-ionic cosolutes in our previous work,27 with the typical conformations of the polymer chain illustrated in Fig. 5(a and d), respectively.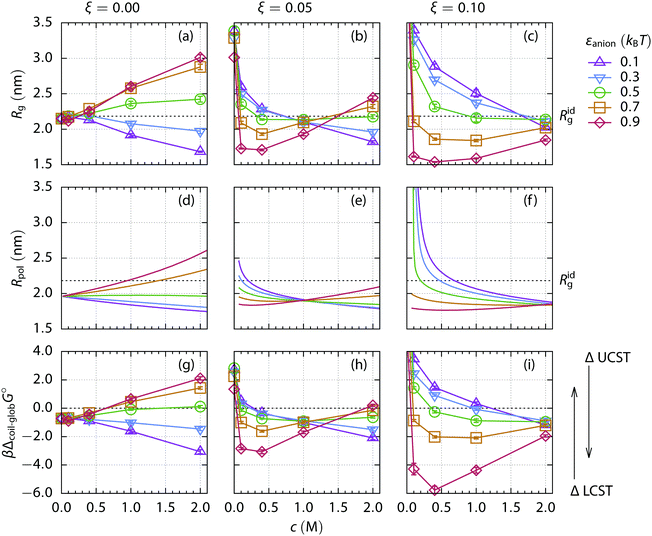 | ||
| Fig. 4 (a–c) Mean radius of gyration Rg obtained from simulations of a 200-mer as a function of salt concentration. The polymer bears various charge fractions ξ of positively charged monomers: (a) 0.00, (b) 0.05, and (c) 0.10. Symbols and colors in the plots indicate the various strengths of the interaction between the anions and the monomers, εanion. Lines serve as a guide for the eye. Error bars are of the order of the symbol size. The mean radius of gyration of an ideal chain Ridg is indicated. (d–f) The effective radius of the polymer Rpol computed using the mean-field theory for the very same systems (column-wise). The same color code is used for the strength of the anion–polymer interaction. (g–i) The standard free energy of the coil-to-globule transition, Δcoil–globG°, computed from the simulations. Lines serve as a guide for the eye. Error bars are about the symbol size. An increase in the energy of the transition corresponds to the elevation of the LCST, and the depression of the UCST, respectively, cf.Fig. 1. | ||
The change in the radius of gyration can be also interpreted as a change of the standard free energy of the coil-to-globule transition
 | (13) |
Note, though our simulation model is directly applicable to simple UCST polymers, it may be also used for qualitative predictions on LCST polymers if the following consideration is taken into account: the solvent quality for LCST polymers worsens as the temperature increases. To capture this phenomenon in an implicit solvent model, the nonbonded potential between monomers—as the only means for controlling the solvent quality—has to be explicitly temperature dependent to overcome the chain conformational entropy.72 (Temperature dependent nonbonded potentials are sometimes also introduced in force fields with an explicit, yet coarse grained, solvent to describe interactions between water and hydrophobic groups.73)
The standard free energy of the coil-to-globule transition of the uncharged polymer obtained from simulation Fig. 4(g) can be qualitatively compared with the experimental LCST data of the uncharged ELP, as shown in Fig. 1(a). The anion quality transitions from repulsive (rather strongly hydrated with little polymer affinity) to attractive (rather weakly hydrated with large polymer affinity) as the value of εanion increases. Comparing to the charged polymer discussed later, only ion-specific effects can be observed both in the simulation and in the experiment.
To relate our model to experiments, a qualitative mapping between model anions and anions used in experiments has to be established. Such a mapping can be directly provided by size exclusion chromatography performed for various salts.74,75 Here, a greater retention factor corresponds to a stronger interaction of the respective anion with a polymeric stationary phase, and vice versa. The retention factor follows the Hofmeister series and increases from strongly hydrated towards weakly hydrated ions. The same results can be concluded from atomistic simulations,36 by comparing potentials of mean force between anions and the rather apolar group in NIPAM monomers.
Thiocyanate SCN− is a highly adsorbing anion in the mapping thus a relatively high εanion ∼ 0.9kBT is its appropriate parametrization in our simple model. The simulations predict a shift towards the swollen state of the uncharged polymer as the concentration of the salt increases, which agrees with the LCST elevation in the experimental results. Iodide I− is another adsorbing anion (from the observed behavior εanion ∼ 0.5kBT to 0.7kBT) having the same but weaker effect on the uncharged ELP both in simulations and experiments. Bromide has the slightest effect of the salts experimentally studied and the anion with εanion ∼ 0.3kBT exhibits similar effects in the simulation. Moving towards the strongly hydrated anions in the Hofmeister series, chloride Cl− and fluoride F−, the LCST drops significantly in the experiments. The same transition is observed in the simulations containing anions with εanion ∼ 0.1kBT to 0.3kBT. It can thus be concluded from the simulations and the experimental data that the salting-out (globule stabilization) power of anions follows the direct Hofmeister series for the uncharged ELP.
4.3 Salt interaction with a positively charged polymer
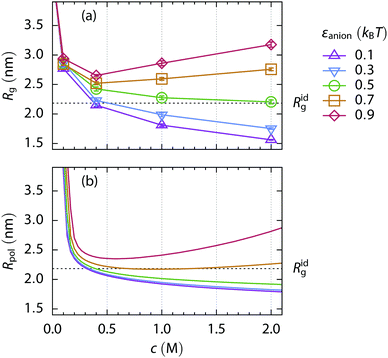
Now we turn to a cationic polymer. For this, a polymer chain containing 200 monomers, of which 20 are positively charged (a charge fraction ξ = 0.10), is simulated. Its radius of gyration Rg and the standard free energy of the coil-to-globule transition as a function of salt concentration are shown in Fig. 4(c and i). Two distinct phenomena can be observed, depending on salt concentration. Screening of the electrostatic repulsion between the charged monomers by the ions starts at low salt concentration (≲0.1 M). The polymer rapidly collapses from an extended coil (Rg ≃ 4.7 nm) to a more compact conformation as the salt is added and the Debye length, κ−1 = (8πlBNAI)−1/2, decreases. Here, NA is the Avogadro number and I is molar ionic strength. This screening strengthens with the increasing salt concentration in the polymer phase. Weakly hydrated ions with large polymer affinity, that is, having greater εanion, are more attracted to the polymer and cause stronger screening.However, the collapse of the polymer chain beyond the size of the uncharged polymer in a salt-free solution, as in the case of εanion = 0.9kBT, cannot be explained by the charge screening alone and another effect has to be taken into account. As the electroneutrality condition is fulfilled inside the polymer volume, the concentration of the strongly attractive anions is significantly higher than the concentration of the repulsive cations. The average B2 of the ion–mer interactions is thus shifted towards more negative, i.e., attractive, values, entering the bridging adhesion regime.27 The radial distribution functions of anions and cations in Fig. 6(c) prove the greater abundance of strongly attractive anions compared to cations at low salt concentrations. Typical conformations of the polymer chain are shown in Fig. 5(c and f) for the repulsive and attractive salt, respectively. As the salt concentration increases (≲1 M), the salt specific effects begin to contribute to the interactions, resembling the case of the uncharged polymer, however with a notably different polymer size, cf.Fig. 5(a, b, d and e).
When the standard free energy of the coil-to-globule transition is treated as a function of salt concentration, it monotonically decreases for more repulsive ions with little affinity to the polymer. A different behavior is observed for the attractive ions: after an initial depression caused by the screening and bridging effects at low salt concentrations, the function rises because the swelling by attraction mechanism starts to operate at high salt concentration. However, in the case of the highly charged polymer chain (ξ = 0.10), the screening–bridging mechanism dominates in the whole investigated concentration range (up to 2 M). Thus the salting-out power of ions is reversed when compared to the uncharged polymer.
The same simulation set is performed for a 200-mer bearing a lower charge fraction, ξ = 0.05. Two salt concentration ranges can be distinguished based on the radius of gyration and the free energy of the coil-to-globule transition, Fig. 4(b and h). When the salt concentration is less than 1 M, the screening and bridging mechanism dominates and the anions follow the reverse series regarding the salting-out power. At concentrations higher than 1 M, the specific ion effects are the driving force and the direct Hofmeister series of anions is obeyed.
The dividing point which separates the concentration ranges can be called the isospheric point as the radius of gyration of the polymer chain is the same regardless of the anion type. The isospheric point moves to higher salt concentrations as the charge fraction of the polymer chain increases. For the uncharged polymer (ξ = 0.00) it is trivially located at zero salt concentration, while for the highly charged polymer (ξ = 0.10) at 2 M salt concentration. The Rg at the isospheric point corresponds approximately to the Rg of the uncharged polymer in a salt free solvent in our setup, i.e., close to its radius of gyration under the critical conditions.
Though the size of the polymer at the isospheric point is the same, the concentration of the salt inside the polymer volume varies greatly depending on the salt type. Radial distribution functions of cations and anions around the polymer's center of mass at the isospheric point of the weakly charged polymer are shown in Fig. 6(a). The concentration of the anions—and synergetically also of the cations—increases inside the effective polymer volume as the affinity of the anions to the polymer increases. The attractive anions even make the concentration of the highly repulsive cation higher around the polymer compared to the bulk solution. Note, the salts with a highly attractive anion, however, do not intersect the isospheric point and the corresponding radius of gyration is achieved at a higher salt concentration, see Fig. S1 (ESI†). Very weakly hydrated ions, such as perchlorate ClO4−, are experimentally known to deviate in a similar manner.14
When we compare the data from simulation, Fig. 4(e), to the experiments, Fig. 1(b), a very good qualitative agreement can be found. When a small amount of salt is added, the LCST of the ELP decreases rapidly and the order of anions follows the reverse series at low salt concentration, in accordance with the simulation predictions. Crossing the isospheric point at ∼0.45 M, the anion order inverts and the direct Hofmeister series is recovered.
Experimental data available for PAU, Fig. 1(c), also confirm the results from our model. When salt is added in a small amount the UCST significantly increases, i.e., the collapsed state of the polymer is preferred. The magnitude of the effect corresponds to the anion location in the reverse Hofmeister series. When the salt concentration further increases, the salt effects equalize at the isospheric point (∼0.5 M) and the direct Hofmeister series is followed afterwards.
4.4 Theoretical predictions
For better interpretation and categorization of the simulation results, we apply the mean-field theory (Section 3) for the very same systems. Minimization of the Gibbs free energy of the system provides the effective volume of the polymer in the thermodynamic equilibrium with the salt reservoir, or equivalently the effective radius Rpol if a spherical geometry is assumed. The polymers' effective radii in the thermodynamic equilibrium are depicted in Fig. 4(d–f) for an uncharged, weakly charged, and highly charged polymer chain, respectively. The results will not change significantly if a mean volume is used instead of the equilibrium volume.The theory matches the simulation results almost quantitatively when the effective radius (Fig. 4 (d–f)) and the radius of gyration (Fig. 4(a–c)) are compared. The theory correctly predicts the salting-out power of anions and its concentration dependence for the uncharged polymer. In the cases of weakly and highly charged polymer chains, the location of the isospheric points matches the simulation data very well. Below the isospheric point, the salting-out power of anions forms the reverse series, while above the direct series is obeyed, which is in agreement with both the simulations and the experimental data.
The osmotic pressure of the salt inside the effective volume of the polymer at the isospheric point is the same, regardless of the salt type, as can be deduced from the mechanical (pressure) equilibrium. The osmotic pressure of the reservoir depends only on the salt concentration in our model. The counter pressure originates from the polymer chain and the osmotic pressure of ions. The pressure of the polymer chain is determined by its spatial extension, thus it does not differ at the isospheric point. Hence the osmotic pressure of the ions inside the effective polymer volume has to be the same, independent of the salt type. Note, however, the net salt-effect is a sum of two large contributions (see eqn (7)), namely of an ideal gas and of an excess interaction, which significantly vary with the salt type (i.e., with εanion).
The salt concentration at the isospheric point ciso scales linearly with the polymer's charge fraction ξ, provided the charge fraction is low (ξ ≲ 0.05), see Fig. 7. As the polymer's charge fraction increases, the isospheric point weakly deviates from the original linear trend and it is also gradually smeared out to a concentration range, as discussed in detail in the ESI.† Very weakly hydrated ions, e.g., perchlorate ClO4−, do not exhibit the isospheric point in experiments.14 Our theoretical model predicts such behavior for salts having εanion ≳ 1.1kBT.
The fluctuation of the radius of gyration of a polymer chain is maximized under the critical conditions.70 The amount of fluctuations can be accessed from the theory using the Boltzmann distribution of the chain's states, eqn (12). The dependence of the fluctuations on the solvent quality is depicted in Fig. 8 for the uncharged and weakly charged polymer chains. With increasing concentration of repulsive salt (panels a and d), the maximum in fluctuations (i.e., the critical conditions) is shifted to a better solvent quality (lower εmer). The opposite trend is observed for the attractive salt (panels c and f) where the solvent quality has to worsen to keep the critical conditions as the salt concentration increases. The relative shift of the critical solvent quality for the uncharged (c) and weakly charged (f) polymer is consistent with the difference in the standard free energy of the coil-to-globule transition obtained by simulations, Fig. 4(g and h).
Let us stress again that the theory assumes a spherical geometry of the polymer and electroneutrality within this effective polymer volume. These assumptions are well fulfilled close to the critical conditions at ≳0.1 M salt concentration. For example, our mean-field theory cannot predict the radius of gyration of a charged polymer without salt as no explicit electrostatic interaction between charged monomers is included. Also at low salt concentrations, the effective radius predicted by the theory deviates significantly from the radius of gyration. In such cases, different approaches have to be used.44,56,76
4.5 Mean-field theory predictions for a negatively charged polymer
Having verified the descriptive power of the mean-field theory, we use it now to predict the effects of salts on a negatively charged polymer. The set of salts remains the same, i.e., the cation is highly repulsive while the type of the anion varies. The solvent quality has to worsen to εmer = 0.5kBT to retain the critical conditions. The theory prediction is depicted in Fig. 9(b), while the simulation results which we use for verification are shown in panel (a) of the same figure. To the best of our knowledge, no systematic experimental data are yet available for such a setup.The simulation and theory results are in very good mutual agreement. When the salt is added the collapse of the polymer chain is observed at first. The extent of the collapse is determined mainly by the (same) very repulsive cation and only mildly modulated by the anion type. Both electrostatic screening in the polymer and build-up of the osmotic pressure in the bulk solution contribute to the collapse. As the concentration of the salt increases, the anion-specific effects further drive the collapse or swelling, similarly to the case of an uncharged polymer. Contrary to the cationic polymer, neither does the extent of the initial collapse depend on the salt (anion) type, nor does the isospheric point occur. Consequently, the salting-out power of anions follows the direct Hofmeister series in the whole concentration range.
5 Conclusions
We have developed a generic implicit-solvent/explicit-salt coarse grained (CG) simulation model to describe ion-specific effects on uncharged polymers and weakly charged polyelectrolytes. For that, we have conveniently employed a Lennard-Jones parametrization of an effective nonbonded potential between ions and monomers. In contrast to the commonly used Weeks–Chandler–Andersen (WCA) potential,50,77,78 the interaction strength between ions and polymer can be gradually changed from repulsive to attractive, which enables then a qualitative mapping of anions in the Hofmeister series to our simple model.Using further simplifying assumptions, we have developed a mean-field model which provides a quantitative agreement with the CG computer simulations. Here, the quality of ions with respect to their affinity and preferential interaction with the polymer is represented by an effective second virial coefficient B2.
We have demonstrated that our model qualitatively captures the critical solution temperature response (and corresponding swelling and collapse) of polymers to the addition of salts observed in experiments. Namely, we have compared our model to the UCST and LCST changes in ureido copolymers (PAU),9 and elastin-like polypeptides (ELPs),13,14 respectively. The same rich behavior of CST response to the salt addition, stemming from a combination of ion-specific screening of these weakly charged polyelectrolytes and direct ion–polymer interactions, has been observed in our model.
We made an important theory-grounded observation of an isospheric point, i.e., a salt concentration at which ion-specific effects vanish and the Hofmeister series inverts. That is, the salting-out power of ions follows a reverse series below the isospheric point and a direct one above. We have shown how the salt concentration at the isospheric point depends on the polymer charge fraction. Our observation of the isospheric point is supported by experimental data for thermoresponsive polymers,9,13,14 as well as for positively charged proteins.4
Our work demonstrates the sensitivity of the structural behavior of weakly charged polymers to the addition of specific salts. Ion-specific effects can enhance or diminish non-specific screening, depending on the salt type and concentration. Our mean-field model shall be useful for further interpretation and guidance of related experiments.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank Won Kyu Kim for a valuable discussion about the mean-field theory. R. C. and J. D. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG grant DZ-74/6), Germany, for this project. J. H. thanks the Czech Science Foundation (grant 16-24321Y) for support.References
- D. S. Ken, A. Dill and S. Bromberg, Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology, Garland Science, Taylor & Francis Group, 2003 Search PubMed.
- F. Hofmeister, Arch. für Exp. Pathol. und Pharmakologie, 1888, 25, 1–30 CrossRef.
- W. Kunz, J. Henle and B. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37 CrossRef CAS.
- Y. Zhang and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249–15253 CrossRef CAS PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2013, 29, 2602–2614 CrossRef CAS PubMed.
- P. Jungwirth and P. S. Cremer, Nat. Chem., 2014, 6, 261–263 CrossRef CAS PubMed.
- R. Kou, J. Zhang, T. Wang and G. Liu, Langmuir, 2015, 31, 10461–10468 CrossRef CAS PubMed.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed.
- N. Shimada, H. Ino, K. Maie, M. Nakayama, A. Kano and A. Maruyama, Biomacromolecules, 2011, 12, 3418–3422 CrossRef CAS PubMed.
- J. Kherb, S. C. Flores and P. S. Cremer, J. Phys. Chem. B, 2012, 116, 7389–7397 CrossRef CAS PubMed.
- K. Suwa, K. Yamamoto, M. Akashi, K. Takano, N. Tanaka and S. Kunugi, Colloid Polym. Sci., 1998, 276, 529–533 CrossRef CAS.
- P. Kujawa and F. M. Winnik, Macromolecules, 2001, 34, 4130–4135 CrossRef CAS.
- Y. Cho, Y. Zhang, T. Christensen, L. B. Sagle, A. Chilkoti and P. S. Cremer, J. Phys. Chem. B, 2008, 112, 13765–13771 CrossRef CAS PubMed.
- Y. Cho, PhD Dissertation, Texas A&M University, USA, 2009.
- H. Kawasaki, S. Sasaki and H. Maeda, J. Phys. Chem. B, 1997, 101, 5089–5093 CrossRef CAS.
- S. Sasaki, H. Kawasaki and H. Maeda, Langmuir, 1999, 15, 4266–4269 CrossRef CAS.
- H. Kawasaki, S. Sasaki, H. Maeda and K. Nishinari, Langmuir, 2000, 16, 3195–3199 CrossRef CAS.
- D. E. Meyer and A. Chilkoti, Biomacromolecules, 2002, 3, 357–367 CrossRef CAS PubMed.
- D. E. Meyer and A. Chilkoti, Biomacromolecules, 2004, 5, 846–851 CrossRef CAS PubMed.
- J. R. McDaniel, D. C. Radford and A. Chilkoti, Biomacromolecules, 2013, 14, 2866–2872 CrossRef CAS PubMed.
- D. W. Urry, C. H. Luan, T. M. Parker, D. C. Gowda, K. U. Prasad, M. C. Reid and A. Safavy, J. Am. Chem. Soc., 1991, 113, 4346–4348 CrossRef CAS.
- D. W. Urry, J. Phys. Chem. B, 1997, 101, 11007–11028 CrossRef CAS.
- B. Zhao, N. K. Li, Y. G. Yingling and C. K. Hall, Biomacromolecules, 2016, 17, 111–118 CrossRef CAS PubMed.
- K. B. Rembert, J. Paterová, J. Heyda, C. Hilty, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2012, 134, 10039–10046 CrossRef CAS PubMed.
- J. Heyda, H. I. Okur, J. Hladílková, K. B. Rembert, W. Hunn, T. Yang, J. Dzubiella, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2017, 139, 863–870 CrossRef CAS PubMed.
- Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, J. Am. Chem. Soc., 2005, 127, 14505–14510 CrossRef CAS PubMed.
- J. Heyda, A. Muzdalo and J. Dzubiella, Macromolecules, 2013, 46, 1231–1238 CrossRef CAS.
- Y. A. Budkov and M. G. Kiselev, J. Phys.: Condens. Matter, 2018, 30, 043001 CrossRef PubMed.
- R. Winkler, M. Gold and P. Reineker, Phys. Rev. Lett., 1998, 80, 3731–3734 CrossRef CAS.
- U. Micka, C. Holm and K. Kremer, Langmuir, 1999, 15, 4033–4044 CrossRef CAS.
- S. Liu and M. Muthukumar, J. Chem. Phys., 2002, 116, 9975–9982 CrossRef CAS.
- S. Liu, K. Ghosh and M. Muthukumar, J. Chem. Phys., 2003, 119, 1813–1823 CrossRef CAS.
- H. J. Limbach and C. Holm, J. Phys. Chem. B, 2003, 107, 8041–8055 CrossRef CAS.
- J. Jeon and A. V. Dobrynin, Macromolecules, 2007, 40, 7695–7706 CrossRef CAS.
- Q.-l. Lei, K. Hadinoto and R. Ni, Langmuir, 2017, 33, 3900–3909 CrossRef CAS PubMed.
- E. A. Algaer and N. F. A. van der Vegt, J. Phys. Chem. B, 2011, 115, 13781–13787 CrossRef CAS PubMed.
- S. Backes, P. Krause, W. Tabaka, M. U. Witt, D. Mukherji, K. Kremer and R. von Klitzing, ACS Macro Lett., 2017, 6, 1042–1046 CrossRef CAS.
- D. Mukherji, C. M. Marques and K. Kremer, J. Phys.: Condens. Matter, 2018, 30, 024002 CrossRef PubMed.
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- H. Schiessel and P. Pincus, Macromolecules, 1998, 31, 7953–7959 CrossRef CAS.
- H. Schiessel, Macromolecules, 1999, 32, 5673–5680 CrossRef CAS.
- F. J. Solis and M. O. de la Cruz, J. Chem. Phys., 2000, 112, 2030–2035 CrossRef CAS.
- P. Loh, G. R. Deen, D. Vollmer, K. Fischer, M. Schmidt, A. Kundagrami and M. Muthukumar, Macromolecules, 2008, 41, 9352–9358 CrossRef CAS.
- A. Kundagrami and M. Muthukumar, Macromolecules, 2010, 43, 2574–2581 CrossRef CAS PubMed.
- A. Moncho-Jordá, J. A. Anta and J. Callejas-Fernández, J. Chem. Phys., 2013, 138, 134902 CrossRef PubMed.
- A. Moncho-Jordá, J. Chem. Phys., 2013, 139, 064906 CrossRef PubMed.
- A. Moncho-Jordá and I. Adroher-Benítez, Soft Matter, 2014, 10, 5810 RSC.
- T. Colla, C. N. Likos and Y. Levin, J. Chem. Phys., 2014, 141, 234902 CrossRef PubMed.
- I. Adroher-Benítez, S. Ahualli, A. Martín-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Macromolecules, 2015, 48, 4645–4656 CrossRef.
- P. Košovan, T. Richter and C. Holm, Macromolecules, 2015, 48, 7698–7708 CrossRef.
- J. Heyda and J. Dzubiella, Soft Matter, 2012, 8, 9338 RSC.
- A. N. Krishnamoorthy, C. Holm and J. Smiatek, Soft Matter, 2018, 14, 6243–6255 RSC.
- Y. A. Budkov, A. L. Kolesnikov, N. Georgi and M. G. Kiselev, J. Chem. Phys., 2014, 141, 014902 CrossRef PubMed.
- Y. A. Budkov, I. I. Vyalov, A. L. Kolesnikov, N. Georgi, G. N. Chuev and M. G. Kiselev, J. Chem. Phys., 2014, 141, 204904 CrossRef PubMed.
- B. Schulz, R. Chudoba, J. Heyda and J. Dzubiella, J. Chem. Phys., 2015, 143, 243119 CrossRef PubMed.
- Y. A. Budkov, A. L. Kolesnikov, N. Georgi, E. A. Nogovitsyn and M. G. Kiselev, J. Chem. Phys., 2015, 142, 174901 CrossRef PubMed.
- Y. A. Budkov and A. L. Kolesnikov, J. Stat. Mech.: Theory Exp., 2016, 103211 CrossRef.
- Y. A. Budkov and A. L. Kolesnikov, Soft Matter, 2017, 13, 8362–8367 RSC.
- J. Heyda and J. Dzubiella, J. Phys. Chem. B, 2014, 118, 10979–10988 CrossRef CAS PubMed.
- M. Senske, D. Constantinescu-Aruxandei, M. Havenith, C. Herrmann, H. Weingärtner and S. Ebbinghaus, Phys. Chem. Chem. Phys., 2016, 18, 29698–29708 RSC.
- J. Heyda, S. Soll, J. Yuan and J. Dzubiella, Macromolecules, 2014, 47, 2096–2102 CrossRef CAS.
- A. Moncho-Jordá and J. Dzubiella, Phys. Chem. Chem. Phys., 2016, 18, 5372–5385 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- R Core Team, R: A Language and Environment for Statistical Computing, 2015, https://www.r-project.org/.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids: with Applications to Soft Matter, Academic Press, 4th edn, 2013, p. 636 Search PubMed.
- M. Thol, G. Rutkai, A. Köster, R. Lustig, R. Span and J. Vrabec, J. Phys. Chem. Ref. Data, 2016, 45, 023101 CrossRef.
- T. Sun and A. S. Teja, J. Phys. Chem., 1996, 100, 17365–17372 CrossRef CAS.
- M. Fixman, J. Chem. Phys., 1962, 36, 306–310 CrossRef CAS.
- V. A. Ivanov, W. Paul and K. Binder, J. Chem. Phys., 1998, 109, 5659–5669 CrossRef CAS.
- Mathematica, Wolfram Research Inc., 2017 Search PubMed.
- R. Chudoba, J. Heyda and J. Dzubiella, J. Chem. Theory Comput., 2017, 13, 6317–6327 CrossRef CAS PubMed.
- L. J. Abbott and M. J. Stevens, J. Chem. Phys., 2015, 143, 244901 CrossRef PubMed.
- M. W. Washabaugh and K. D. Collins, J. Biol. Chem., 1986, 261, 12477–12485 CAS.
- V. Mazzini, G. Liu and V. S. J. Craig, J. Chem. Phys., 2018, 148, 222805 CrossRef PubMed.
- A. R. Khokhlov, J. Phys. A: Math. Gen., 1980, 13, 979–987 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- I. Adroher-Benítez, A. Martín-Molina, S. Ahualli, M. Quesada-Pérez, G. Odriozola and A. Moncho-Jordá, Phys. Chem. Chem. Phys., 2017, 19, 6838–6848 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematica notebook implementing the mean-field theory; simulation setup details; trajectories and distributions of the radius of gyration; the isospheric point/highly attractive anions; and evaluation of the Donnan potential. See DOI: 10.1039/c8sm01646a |
| This journal is © The Royal Society of Chemistry 2018 |