Charge polarization, local electroneutrality breakdown and eddy formation due to electroosmosis in varying-section channels

Abstract

We characterize the dynamics of an electrolyte embedded in a varying-section channel under the action of a constant external electrostatic field. By means of molecular dynamics simulations we determine the stationary density, charge and velocity profiles of the electrolyte. Our results show that when the Debye length is comparable to the width of the channel bottlenecks a concentration polarization along with two eddies sets inside the channel. Interestingly, upon increasing the external field, local electroneutrality breaks down and charge polarization sets leading to the onset of net dipolar field. This novel scenario, that cannot be captured by the standard approaches based on local electroneutrality, opens the route for the realization of novel micro and nano-fluidic devices.

---

The transport of ions, molecules and polymers across constrictions such as pores, membranes or varying-section micro- nano-channels is crucial for several biological as well as synthetic systems. For example, in biological cells ion channels control the uptake of ions from the environment¹ whereas, in resistive pulse sensing techniques, the interactions of colloidal particles² or macromolecules^3–7 with the nano- or micro-pore are measured from the variation of the electric conductance of the pore induced by the presence of the particle. Moreover, electro-osmotic flux can play a crucial role in molecule capturing in nanopores.^8–10 Recent studies have shown that ionic transport and electro-osmotic flow in micro- and nano-fluidic circuitry can be controlled by tuning the geometry of the micro–nano-channel.^11–13 Indeed, conical^14–16 or heterogeneously charged¹⁷ pores have been used to realize nano-fluidic diodes and to rectify electro-osmotic flows.^18,19 Moreover, periodic varying-section channels have been used to realize nanofluidic transistors.²⁰ Similarly, recent contributions have shown that the shape of the confining vessel and the boundary conditions therein imposed can be exploited to control the flow. Indeed, electro-osmotic transport can be strongly enhanced by grafting charged brushes on the channel walls²¹ and by hydrophobic surfaces.²²

In this contribution, we study, via molecular dynamics simulations the electro-osmotic flow of an electrolyte embedded in a varying-section channel. The advantage of our approach, as compared to others based on the solution of some continuum models,^23–27 is that the ionic densities are left free to relax according to the interactions among ions and between ions and the channel walls. Therefore our approach allows us to critically discuss, for example, the local electroneutrality assumption and its possible breakdown. Our results show that when the systems is driven by a constant electrostatic field acting along the longitudinal axis of the channel, inhomogeneous ionic and charge densities are induced due to the variations of local channel section. This phenomenon is similar to concentration polarization (CP) reported for electrolytes transported across ionic-selective membranes^23,25,28 (see also ref. 29 and 30 for recent reviews) i.e., in open circuit conditions and under severe modulations of channel section.^25,27,28 Interestingly, our results show that CP can be obtained also for close circuit conditions and for smooth variations of channel section. In particular, we observe CP when the Debye length is comparable with the channel bottlenecks, i.e., in the entropic electrokinetic regime.³¹ Concerning local electroneutrality, our numerical results confirm that even in the entropic electrokinetic regime, the local electroneutrality assumed by previous works^26,27,30,32 is fulfilled for mild values of the external field. However, upon increasing the external field our numerical simulations show that local electroneutrality breaks down and charge polarization (QP) sets, leading to the onset of a net dipolar contribution to the electrostatic field. Interestingly, a similar phenomenon has been recently observed for pressure-driven flows across conical pores.³³

Results

We study the electro-osmotic flow (see ESI† for the details) of a KCl water solution across a channel with half section

h(x) = h₀ + h₁ cos(2πx/L_x) (1)

with average section h₀ = 38.5 Å and modulation h₁ = 32.5 Å and periodicity L_x = 836.6 Å, see Fig. 1. Channel section is constant along the y direction, with thickness L_y = 60.37 Å, and periodic boundary conditions are applied along x and y. Both channel walls are covered with a constant charge density σ = 0.15 C m⁻². The system is globally electroneutral since we compensated the wall charge with additional Cl⁻ ions. After equilibration, a homogeneous and constant external electric field E = (E_x, 0, 0) is applied to the whole system.

Fig. 1 System set-up. (A) Sketch of the system. The electrolyte solution (light blue) is confined between two curved charged walls. Half section is . Periodic boundary conditions are applied in the x and y direction. (B) Snapshot of molecular dynamics set-up. The solid walls (gray) are constituted by Lennard-Jones atoms. The atoms of the layer exposed to the liquid are charged (blue). Water molecules are not reported while blue and red spheres represent K⁺ and Cl⁻ ions. An external electrical field parallel to the x-axes in applied.

We begin our analysis by focusing on the case of larger ionic concentration ρ₀ ≃ 3 M. The density profile of both Cl⁻ and K⁺ is expected to decay over a length scale comparable to the Debye length, , where e is the elementary charge, z is the valence of the ions (z = 1, in our case), β = (k_BT)⁻¹ with k_B the Boltzmann constant and T the absolute temperature and ε = 80·ε₀ is the dielectric constant with ε₀ the vacuum dielectric constant. For 3 M ionic solution we estimate a Debye length of λ_D ≃ 1.8 Å and therefore λ_D ≪ h_min being h_min = h₀ − h₁ = 6 Å the half-section calculated at channel bottlenecks. In such a case, since there is only a small overlap between the Debye layers of the two facing walls, we do not expect the onset of any entropic electrokinetic effects.³¹ As expected, the accumulation of Cl⁻ ions at the positively charged solid wall induces and electro-osmotic flow, opposed to the direction of the external electrostatic field, that is almost symmetric with respect to the z-axis (see panels (a and b) of Fig. 2).

Fig. 2 Net concentration of Cl⁻ and velocity profile (arrows) for external fields corresponding to potential drop ΔV = 0.6 (left) and ΔV = 2.4 V, (right). Panels (a and b) (first row) refer to ion concentration ρ₀ = 3 M, panels (c and d) (central row) refer to ρ₀ = 1 M and panels (e and f) (bottom row) refer to ρ₀ = 0.3 M. The labels in the color bar refer to the concentration expressed in mol L⁻¹. For clarity sake, the arrows of the velocity profile are rescaled in each panel. The upper and bottom grey solid lines indicates the channel walls.

We have then increased the Debye length by reducing the ionic concentration ρ₀. For ρ₀ ∼ 1 M we have λ_D ≃ 3.1 Å. Hence, the Debye layers of the facing walls overlaps in the narrower sections (λ_D/h_min ∼ 1, h_min = 6 Å) highlighting that the system is within the entropic electrokinetic regime.³¹ Panel (d) of Fig. 2 shows that, for ΔV = 2.4 V, the ionic densities are quite affected by the flow. In particular, Cl⁻ concentration largely increases in the channel bottleneck, see e.g. the region x/L_x ∈ (0.45, 0.5) in Fig. 2d. This increase in Cl⁻ concentration is associated to K⁺ depletion, that will be discussed more in details in next paragraphs. This feature is associated to the onset of eddies in the electro-osmotic velocity profile, as shown in panels (c and d) of Fig. 2. These eddies form for sufficiently large driving forces. Indeed, while for ΔV = 0.6 V we do not observe major discrepancies with the previous case, for ΔV = 2.4 V two eddies form inside the channel. Interestingly, such eddies break down the left-right symmetry of the channel, for instance, Fig. 2d, shows that the eddies are shifted in the direction of the volumetric fluid flow, i.e. negative x in our reference frame. This occurrence is in contrast to the prediction obtained in linear regime³¹ for which the eddies center is in the channel center, x/L_x = 0. Then we further increase the Debye length by setting ρ₀ ∼ 0.3 M, for which λ_D ≃ 5.6 Å. In such a regime panels (e and f) of Fig. 2 show that the zone in which K⁺ are depleted is enhanced as compared to the previous cases. Moreover, comparing panels (e and f) to (c and d) in Fig. 2 we notice that, for ρ₀ ∼ 0.3 M, the onset of the eddies occurs for smaller values of the external force as compared to ρ₀ ∼ 1 M.

In order to quantitatively capture the accumulation of ions density, we have analyzed the dependence of the ionic densities averaged over the channel section as a function of the longitudinal position. Fig. 3 shows that the dependence of normalized densities profiles [small rho, Greek, macron]^±(x) defined as

on the longitudinal position strongly depends on the value of the Debye length as compared to the channel section at the bottleneck. Indeed, when λ_D/h_min ≪ 1, i.e. for ρ₀ = 3 M, panel (a) of Fig. 3 shows that the density profiles are almost constant along the channel for all the values of the external force we have tested. The only relevant difference occur close to the narrowest sections x/L_x ≃ ±0.5. In contrast, when λ_D/h_min ∼ 1, i.e. for ρ₀ = 1 M and ρ₀ = 0.3 M panels (b and c) of Fig. 3 show the onset of a region where the coions (K⁺) are depleted and the left-right symmetry is broken. Once we have analyzed the density of Cl⁻ and K⁺ separately we move to the local total charge and local ionic densities defined as:

q(x) ≡ 2h(x)[[small rho, Greek, macron]₊(x) − [small rho, Greek, macron]₋(x)] (3)

[small rho, Greek, macron](x) ≡ [small rho, Greek, macron]₊(x) + [small rho, Greek, macron]₋(x) (4)

We stress that we choose a different normalization for q(x) and [small rho, Greek, macron](x) so that in a plane channel |q(x)| always match the total surface charge of channel walls 2|σ| whereas [small rho, Greek, macron](x) is the average density that, in the Debye–Hückel regime, determines the local value of the Debye length.‡ Interestingly, Fig. 4a shows that in the limit of small Debye lengths, λ_D/h_min < 1, local electroneutrality is recovered, i.e. q(x) ≃ 2σ, and the ionic density profile is almost constant along the channel. Only at very high voltages a small deviation is present at x/L_x ≃ 0.4.

Fig. 3 [small rho, Greek, macron] ⁺(x) (blue) and [small rho, Greek, macron]⁻(x) (red) curves as a function of the longitudinal position for ρ = 3 M (panel a), ρ = 1 M (panel b) and ρ = 0.3 M (panel c). [small rho, Greek, macron]⁺(x) and [small rho, Greek, macron]⁻(x) are calculated viaeqn (2).

Fig. 4 [small rho, Greek, macron](x) (red curves) and q(x) (blue curves), defined respectively in eqn (3) and (4), as a function of the longitudinal position for ρ = 3 M (panel a), ρ = 1 M (panel b) and ρ = 0.3 M (panel c). Lighter color stand for large values of the potential drop ΔV, see legend.

In contrast, for larger values of the Debye length, λ_D/h_min ≃ 1, neither q(x) nor [small rho, Greek, macron](x) are constant. Such inhomogeneities trigger the onset of modulations in the magnitude of the local electrostatic potential. In particular, an accurate inspection of panels (b and c) of Fig. 4 reveals that weaker values of the external field triggers solely an inhomogeneity in the ionic density but do not affect the local electroneutrality. Interestingly, upon increasing the strength of external electric field local electroneutrality breaks down and on the top of the well-known concentration polarization (CP),^{26,27,30,32,34} a charge polarization (QP) appears. We remark that charge polarization sets for smaller values of the external force for smaller values of the Debye length. This can be due to finite liquid slippage at solid wall that cannot be disregarded in the regime under study. Indeed, slippage is commonly described in term of the Navier boundary condition that, for a plane channel, reads u_t|_wall = L_s∂u_t/∂n with u_t the component of the velocity field tangent to the wall, n the normal to the wall and L_s the slip length.³⁵ Atomistic simulation showed that for smooth hydrophilic and slightly hydrophobic (contact angle <120°) surfaces L_s, hardly exceeds a nanometer.^36–38 In addition, the presence of a strong surface charge, further reduces the slip length for hydrophobic surfaces.³⁹ When comparing simulations performed with different ionic concentrations it should be taken into account that the slip length L_s in the three setups may be slightly different. Indeed, the relevant parameter ruling the effect of slippage on the electroosmotic flow is the ratio L_s/λ_D.⁴⁰ This feature is emphasized by Fig. S1 in ESI† that shows that the mismatch between the prediction of the analytical model (see ref. 31) and the numerical results increases upon decreasing λ_D.

In conclusion, we have reported on numerical simulations concerning a KCl solution embedded in a varying-section channel under the action of a constant electrostatic field. Our simulations show that, when the Debye length is comparable to the width of the channel bottlenecks, the system is in the entropic electrokinetic regime that is characterized by the onset of eddies.³¹ In this perspective we observe, in agreement with what has been reported in the literature, the onset of a concentration polarization and local recirculation of the fluid velocity that comes along with the onset of a standing shock in the ionic concentration. Surprisingly, for stronger external fields the local electroneutrality breaks down and an additional charge polarization (QP) sets in. Such a novel phenomena has been observed thanks to our microscopic approach based on Molecular Dynamics simulations in which the ionic densities are not constrained. In this perspective, our results show that for mild external fields local electroneutrality is recovered. This can justify a posteriori the assumption of local electroneutrality in these regimes. However, for larger external fields, local electroneutrality does not hold and a net electric dipole sets in inside the channel.

Conflicts of interest

There are no conflicts to declare

Acknowledgements

PM acknowledges Dr Mathijs Janssen for useful discussions. This research used the computational resource from CINECA (NATWE project), and the Swiss National Super-computing Centre (CSCS), project ID sm11. Open Access funding provided by the Max Planck Society.

References

1. B. Hille, Ion channels of excitable membranes, Sinauer, Sunderland, MA, 2001, vol. 507.
2. E. Weatherall and G. R. Willmott, Analyst, 2015, 140, 3318.
3. H. Bayley, O. Braha and L.-Q. Gu, Adv. Mater., 2000, 12, 139.
4. G. Celaya, J. Perales-Calvo, A. Muga, F. Moro and D. Rodriguez-Larrea, ACS Nano, 2017, 11, 5815–5825.
5. E. L. Bonome, R. Lepore, D. Raimondo, F. Cecconi, A. Tramontano and M. Chinappi, J. Phys. Chem. B, 2015, 119, 5815.
6. A. Asandei, A. Ciuca, A. Apetrei, I. Schiopu, L. Mereuta, C. H. Seo, Y. Park and T. Luchian, Sci. Rep., 2017, 7, 6167.
7. M. Chinappi and F. Cecconi, J. Phys.: Condens. Matter, 2018, 30 DOI:10.1088/1361-648X/aababe.
8. A. Asandei, I. Schiopu, M. Chinappi, C. H. Seo, Y. Park and T. Luchian, ACS Appl. Mater. Interfaces, 2016, 8, 13166.
9. M. Boukhet, F. Piguet, H. Ouldali, M. Pastoriza-Gallego, J. Pelta and A. Oukhaled, Nanoscale, 2016, 8, 18352–18359.
10. G. Huang, K. Willems, M. Soskine, C. Wloka and G. Maglia, Nat. Commun., 2017, 8, 935.
11. P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Macromol. Symp., 2015, 357, 178.
12. P. Malgaretti, I. Pagonabarraga and J. M. Rubi, J. Chem. Phys., 2016, 144, 034901.
13. A. Bolet, G. Linga and J. Mathiesen, Phys. Rev. E, 2018, 97, 043114.
14. W. Guo, Y. Tian and L. Jiang, Acc. Chem. Res., 2013, 46, 2834.
15. S. Balme, T. Ma, E. Balanzat and J.-M. Janot, J. Membr. Sci., 2017, 544, 18.
16. J. Experton, X. Wu and C. R. Martin, Nanomaterials, 2017, 7, 445.
17. C. B. Picallo, S. Gravelle, L. Joly, E. Charlaix and L. Bocquet, Phys. Rev. Lett., 2013, 111, 244501.
18. N. Laohakunakorn and U. F. Keyser, Nanotechnology, 2015, 26, 275202.
19. P. Bacchin, Membranes, 2018, 8, 10.
20. E. Kalman, I. Vlassiouk and Z. Siwy, Adv. Mater., 2008, 20, 293.
21. G. Chen and S. Das, J. Phys. Chem. B, 2017, 121, 3130.
22. S. R. Maduar, A. V. Belyaev, V. Lobaskin and O. I. Vinogradova, Phys. Rev. Lett., 2015, 114, 118301.
23. I. Rubinstein and B. Zaltzman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2238.
24. S. Y. Park, C. J. Russo, D. Branton and H. A. Stone, J. Colloid Interface Sci., 2006, 297, 832.
25. A. Mani, T. A. Zangle and J. G. Santiago, Langmuir, 2009, 25, 3898.
26. A. Mani and M. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061504.
27. Y. Green, S. Shloush and G. Yossifon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 043015.
28. T. A. Zangle, A. Mani and J. G. Santiago, Langmuir, 2009, 25, 3909.
29. H.-C. Chang, G. Yossifon and E. A. Demekhin, Annu. Rev. Fluid Mech., 2012, 44, 401.
30. V. V. Nikonenko, A. V. Kovalenko, M. K. Urtenov, N. D. Pismenskaya, J. Han, P. Sistat and G. Pourcelly, Desalination, 2014, 342, 85.
31. P. Malgaretti, I. Pagonabarraga and J. M. Rubi, Phys. Rev. Lett., 2014, 113, 128301.
32. H. Leese and D. Mattia, Microfluid. Nanofluid., 2014, 16, 711.
33. L. Jubin, A. Poggioli, A. Siria and L. Bocquet, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4063.
34. M. Andersen, K. Wang, J. Schiffbauer and A. Mani, Electrophoresis, 2017, 38, 702.
35. E. Lauga, M. Brenner and H. Stone, Springer handbook of experimental fluid mechanics, Springer, 2007, pp. 1219–1240.
36. M. Chinappi and C. Casciola, Phys. Fluids, 2010, 22, 042003.
37. D. M. Huang, C. Sendner, D. Horinek, R. R. Netz and L. Bocquet, Phys. Rev. Lett., 2008, 101, 226101.
38. M. Sega, M. Sbragaglia, L. Biferale and S. Succi, Soft Matter, 2013, 9, 8526–8531.
39. D. M. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Langmuir, 2008, 24, 1442–1450.
40. L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm01298a

‡ We stress that according to eqn (4) we have that where 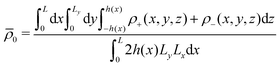is the density averaged over the full volume.

---