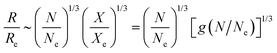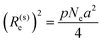DOI:
10.1039/C8SM00968F
(Paper)
Soft Matter, 2018,
14, 7507-7515
Topological free volume and quasi-glassy dynamics in the melt of ring polymers
Received
11th May 2018
, Accepted 2nd August 2018
First published on 17th August 2018
Abstract
Motivated by recent observations that non-concatenated ring polymers in their dense solution exhibit a glass-like dynamics, we propose a free volume description of the motion of such rings based on the notion of topological volume. We first construct a phenomenological free energy which enables one to quantify the degree of topological crowding measured by the coordination number. Then we pinpoint a key role of the cooperative dynamics of neighboring rings, which is responsible for an anomalous dependence of the global structural relaxation (diffusion) time on ring length. Predictions on molecular weight dependence of both static (ring size, coordination number) and dynamic (relaxation time, diffusion coefficient) quantities are in very good agreement with reported numerical simulations. Throughout the discussion, the entanglement length Ne is assumed to be a unique characteristic length for the topological constraint, and hence, all the physical quantities are universally described in terms of the rescaled chain length N/Ne. Finally, we discuss how the dense solution of rings is analogous to yet different from ordinary glassy systems.
1 Introduction
Despite their ubiquity in biology and potential applicability in materials science, the behavior of ring polymers remains largely mysterious in many respects, understanding of which lags far behind that of the linear polymer counterpart.1,2 The main source of difficulty arises from the inevitable constraint that a topological state on inter-ring concatenation and intra-ring knotting has to be rigorously conserved at any later stage unless bond breakage occurs. Recent experiments and simulations have raised several puzzles in the dynamics of a dense solution of non-concatenated rings,3–5 hinting at some analogy to the glass transition.6,7 The conceived state, dubbed as topological glass, however, seems to be very different from ordinary glass in that the large scale dynamical anomaly entails essentially no motional restriction at the scale of constituents (monomers). Here, we propose a viewpoint that qualifies rings as ultra-soft particles, whose effective volume arises from the topological constraint (TC). In dilute solution, two rings in unlinked topology feel an entropic repulsion upon close approach, since the unlinking (non-concatenation) TC reduces the number of available conformations (Fig. 1(a)). In a dense solution of unlinked rings, we are naturally led to think of the free volume of the effective volume of topological origin; as we shall see this topological free volume is intimately connected to the coordination number of rings. Bringing these concepts together, we set up a stage for statistical mechanical analysis, which yields various predictions in remarkable agreement with reported observations. It unveils a rational scenario through which the large scale cooperative dynamics of rings emerges; the physical picture indeed bears some similarity with ordinary glassy dynamics, but with a cardinal difference originating from the ultra soft nature of rings.
 |
| | Fig. 1 Schematics of the system of non-concatenated rings. (a) For two rings close to each other (bottom), the number of their possible configurations is reduced from the free state (top) due to the non-concatenation TC. This produces an entropic repulsion between them.10 (b) Length scales in the system. The central dot is the center of mass (COM) of a reference ring, whose spatial size R is indicated by a dotted circle. Other black dots inside the dotted circle denote the COMs of rings overlapping with the reference ring, which defines the number of overlapping rings X, i.e., coordination number. A shaded circle represents the effective size ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) of a ring due to the TC. In a particle picture, the average distance r between COMs of neighboring rings is a key quantity to control the global structural relaxation. In contrast to (c) the short ring case N < Ne, (d) the TC for a longer ring N > Ne imposes severe crowding (larger X, thus, higher topological volume fraction Ψ) in such a way that any ring is caged by its surroundings. As in ordinary crowded systems, the global structural relaxation requires cage breaking realized by the passage of a ring through its “gate”, but the solitary motion of any single ring is ineffective. However, the gate opening could be achieved by a cooperative motion of M(N) neighboring rings. of a ring due to the TC. In a particle picture, the average distance r between COMs of neighboring rings is a key quantity to control the global structural relaxation. In contrast to (c) the short ring case N < Ne, (d) the TC for a longer ring N > Ne imposes severe crowding (larger X, thus, higher topological volume fraction Ψ) in such a way that any ring is caged by its surroundings. As in ordinary crowded systems, the global structural relaxation requires cage breaking realized by the passage of a ring through its “gate”, but the solitary motion of any single ring is ineffective. However, the gate opening could be achieved by a cooperative motion of M(N) neighboring rings. | |
2 Topological constraint in linear vs. ring polymers
To make the nature of the TC in the ring polymer system clear, let us recall the phenomenon of entanglement in a linear polymer melt, which is also a consequence of the TC. Consider a melt of flexible polymers, each of which consists of N monomers of size a. Because of the screening of excluded-volume interactions, the size of individual linear polymers is R ∼ aN1/2, and hence the number of overlapping polymers with any reference polymer defined asis evaluated as X ∼ N1/2.8 A consequence is that the entanglement is inevitable in a dense solution of long polymers. The modern development of rheology of entangled polymers is based on the geometrical picture, where a polymer is confined in a virtual tube made up of the surrounding polymers. The reptation model describes the motion of the polymer in the tube, where the chain ends play a pivotal role, emphasizing the transient (though long-lived) nature of the TC.8,9
In the ring polymer counterpart, there are now a large number of indications that the size is much more compact characterized by the smaller exponent; R ∼ Nν with ν = 1/3 for large N, but with a prefactor substantially larger than a, i.e., R/(aN1/3) ≫ 1.11–17 This results in X ∼ const.(≫1) indicative of a qualitatively different TC from the classical entanglement picture of heavily overlapping threads. Rather it implies a soft particle-like behavior, which allows some degree of overlapping. Indeed, as might be intuitively clear, the TC endows any reference ring with entropic repulsion against surrounding rings which are unlinked to it10 (Fig. 1(a)). One can then define the length
which measures the average distance between the neighboring rings (
Fig. 1(b)). This is analogous to the inter-particle distance
r ∝
b/
ψ1/3 in the system of rigid particles (with size
b and particle volume fraction
ψ). Such a consideration suggests an interesting possibility to investigate the problem of dense ring polymers under the TC with the concepts developed in the liquid and glass transition physics.
6,7 Unlike the rigid particle case
r >
b, however, one admits here a strong overlapping
r <
R reflecting the ultra-soft nature of the ring (
Fig. 1). Note that numerical and experimental observations suggest that the exponent
ν = 1/3 is realized only for very long rings, and many of the practical cases may fall into a broad crossover characterized by some effective exponent bounded as 1/3 <
νeff < 1/2.
3 Free energy in terms of the topological volume fraction
The primal control parameter in the problem is the ring length N, which plays a similar role to the temperature T in the ordinary glass transition phenomenology. For a systematic study, one therefore needs a framework, which describes how R and X depend on N. Here, we utilize the phenomenological free energy, which is constructed based on the following two observations; (i) as rings behave like soft particles due to the TC, there should be an associated topological volume, and (ii) the TC in rings becomes relevant above some characteristic length scale Ne,18,19 which implies the ideal chain statistics on a smaller scale, thus| | | Xe ≡ X(N = Ne) ∼ Re3/(Nea3) ∼ Ne1/2, | (3) |
where Re ∼ aNe1/2 is the spatial extent of the Ne-strand. Note that the second observation is akin to an empirical fact admitted in the entanglement effect in linear polymers,8,9 which is the reason we employed the symbol Ne for the characteristic chain length. The simplest free energy in accordance with the above observations is14,15,20| |  | (4) |
where Xc represents the maximum number of overlapping rings achieved in the large N limit, and ν0 ≃ 0.588 is a critical exponent describing the size of the self-avoiding chain (see the Appendix for more discussion on the proposed free energy). The quantity Ψ ≡ X/Xc may be regarded as a topological volume fraction. To motivate such a usage, let us rewrite eqn (2) for the inter-ring distance as| |  | (5) |
Now Ψ is bounded as Ψ ≤ 1 by definition, and the comparison with the rigid particle case qualifies ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = RXc−1/3 and Ψ as the effective size and the corresponding volume fraction associated with the TC. The first term in eqn (4) takes a form from the celebrated van der Waals theory, which represents the reduction in the free volume, in the present context, reflecting the entropic repulsion due to the non-concatenation TC. This term favors a smaller Ψ, and thus leads to ring shrinkage. Contrary to this is the second term, which represents an entropic penalty associated with squeezing a ring while maintaining the unknotting constraint, and can be derived from the standard scaling argument (see the Appendix).
= RXc−1/3 and Ψ as the effective size and the corresponding volume fraction associated with the TC. The first term in eqn (4) takes a form from the celebrated van der Waals theory, which represents the reduction in the free volume, in the present context, reflecting the entropic repulsion due to the non-concatenation TC. This term favors a smaller Ψ, and thus leads to ring shrinkage. Contrary to this is the second term, which represents an entropic penalty associated with squeezing a ring while maintaining the unknotting constraint, and can be derived from the standard scaling argument (see the Appendix).
Free energy (4) has a desired property F ∼ kBT at N = Ne with a supplement Ψe ≡ Xe/Xc ≃ 0.5, ensuring the onset of the TC at this length scale in accordance with the above observation (ii). For longer rings, the optimum X as a function of N can be derived by minimizing eqn (4). We are thus led to a generic form X(N) = Xe![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne) with a function
(N/Ne) with a function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) → 1 at x = 1 and
(x) → 1 at x = 1 and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) → Xc/Xe at x ≫ 1. From this, the ring size follows as R(N) ≃ Re(N/Ne)1/3[
(x) → Xc/Xe at x ≫ 1. From this, the ring size follows as R(N) ≃ Re(N/Ne)1/3[![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne)]1/3. In Fig. 2, we compare predictions from our free energy (with Ψe = 0.5) with three sets of numerical simulation data. Here we adopt the spanning distance R(s) (root mean-square distance between monomers N/2 apart) as a measure of the spatial size of rings, so that X is the average number of surrounding rings, whose centers of mass (COMs) are located within the distance R(s) from the COM of the reference ring. Note that the Re and Xe values are evaluated from the numerical data in ref. 4, 11 and 12 (see Table 1), which play the role of rescaling factors in the master plot. While the resultant Re values reasonably accord with the theoretical expectation (Appendix), it is striking that all the data sets point to almost the same value for Xe ≃ 8 despite different simulation models and conditions employed. The same conclusion is reached if we measure the ring size with the radius of gyration R(g), in which case Xe ≃ 1.4 is found (Appendix, Fig. 4). Hence, besides the quantitative predictability of the proposed free energy, we find that the coordination number serves as a robust measure for the TC. In particular, the onset of the TC can be identified by Xe, whose precise value is independent of the system details. The crossover towards the compact statistic regime for longer rings is quantified by the function
(N/Ne)]1/3. In Fig. 2, we compare predictions from our free energy (with Ψe = 0.5) with three sets of numerical simulation data. Here we adopt the spanning distance R(s) (root mean-square distance between monomers N/2 apart) as a measure of the spatial size of rings, so that X is the average number of surrounding rings, whose centers of mass (COMs) are located within the distance R(s) from the COM of the reference ring. Note that the Re and Xe values are evaluated from the numerical data in ref. 4, 11 and 12 (see Table 1), which play the role of rescaling factors in the master plot. While the resultant Re values reasonably accord with the theoretical expectation (Appendix), it is striking that all the data sets point to almost the same value for Xe ≃ 8 despite different simulation models and conditions employed. The same conclusion is reached if we measure the ring size with the radius of gyration R(g), in which case Xe ≃ 1.4 is found (Appendix, Fig. 4). Hence, besides the quantitative predictability of the proposed free energy, we find that the coordination number serves as a robust measure for the TC. In particular, the onset of the TC can be identified by Xe, whose precise value is independent of the system details. The crossover towards the compact statistic regime for longer rings is quantified by the function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x), which describes a gradual increase of the coordination number from Xe towards Xc.
(x), which describes a gradual increase of the coordination number from Xe towards Xc.
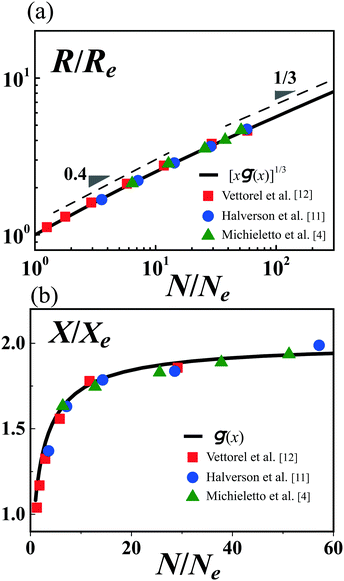 |
| | Fig. 2 Comparison of free energy prediction (solid line) with numerical simulation data for spatial size R and coordination number X of rings in their non-concatenated melt of dense solution. As a measure of the ring size, we adopt here the spanning distance R ≡ R(s). Numerical data are obtained from the literature (squares,11 circles,12 triangles4) (a) plot of R/Re as a function of N/Ne. Before reaching the asymptotic compact scaling with ν = 1/3, there exists a broad crossover up to N/Ne → Nc/Ne ∼ 30 (see the Appendix for the estimation of Nc). (b) Plot of X/Xe as a function of N/Ne. See Table 1 for details of simulation models and the estimated values of Re and Xe. | |
Table 1 A summary of methods and numerical values employed in or extracted from simulations (lp: persistence length). The values Re2 and Xe are obtained by inter-(or extra-)polating the data in references. All lengths are measured in units of lattice size (MC) or bead diameter (MD)
|
|
Vettorel11 |
Halverson12 |
Michieletto4 |
| Method |
MC on cubic lattice |
MD |
MD |
| Stiffness |
No angle potential |
l
p ≃ 1.5–2 |
l
p ≃ 5 |
| Volume fraction |
0.5 |
0.85 |
0.1 |
|
N
e
|
175 |
28 |
40 |
| (R(s)e)2 |
75 |
18 |
88 |
|
X
e|R=R(s) |
7.7 |
8.4 |
7.8 |
| (R(g)e)2 |
26 |
6.1 |
30 |
|
X
e|R=R(g) |
n/a |
1.4 |
1.3 |
Here it is instructive to draw a connection of the particle-like behavior of non-concatenated rings in their dense solution with the argument based on random packing. For the assembly of particles to be mechanically stable, Maxwell's criterion claims that the minimum coordination number Xiso = 2df is required, where df is the number of degrees of freedom determined by the symmetry of the constituent particles.7 With df = 6 for a generally shaped particle in 3 dimensions, we see an impressive consonance of Xiso with Xe and Xc = Xe/Ψe when we adopt the spanning distance R(s) as a measure of the ring size. Note also that the range of the value X ∈ (Xe,Xc) in this case corresponds to the so-called Kavassalis–Noolandi number to mark the onset of the entanglement effect in dense linear polymer solutions.8,21 This suggests the fundamental role of X in describing the TC in polymer systems. We also emphasize that the function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) is universal in the sense that it does not depend on the system parameters (Appendix).
(x) is universal in the sense that it does not depend on the system parameters (Appendix).
4 Cooperative mechanism for global structural relaxation
To discuss the consequences of topological volume on ring dynamics in dense solution, let us recall a topological length N = Ne. It indicates Rouse dynamics for a shorter scale, thus introducing a time scale τe ∼ τ0Ne2 for the relaxation of the Ne-strand (with τ0 being a monomeric time scale), which plays the role of an elementary time scale for larger scale dynamics, where the TC matters. Here, while recent rheological measurements have evidenced a self-similar stress relaxation process without the sign of a rubber plateau,22,23 the neutron spin-echo experiment detected glassy dynamics of rings' COM.3 A connection between these two observations remains unsolved. A hint comes from a detailed analysis of numerical simulation data, which indicates that while the stress relaxation is correlated with the internal conformational reorganization, whose characteristic time scales as τ(1) ≃ τe(N/Ne)z1 with z1 ≃ 2.2, the diffusion would be much slower, that is to say, τ ≫ τ(1) for large N, where τ is the time scale for global structural relaxation during which the ring travels its own size.24 It is likely that a reason for such a self-diffusion slower than expected lies in a cooperative dynamics, which is necessary for the global structural relaxation.
As a prototype, we begin with reviewing a minimal description of cooperative dynamics in glass transition.26 Consider an assembly of particles of radius b with volume fraction ψ such that the average interparticle distance r ∝ bψ−1/3. The mechanism for structural relaxation would depend on the average size Δ ∼ r − 2b of the gate, through which each particle escapes from its cage. Two characteristic interparticle distances rc and rv can be conceived; while the latter corresponds to the kinetic arrest point rv ≃ 2b, the former rc(>rv) signals the onset of the crowding effect so that, at higher concentration (r < rc), cage breaking requires the cooperative motion of adjacent particles. Since the missing space for gate opening is rc − r, and the space created by the cooperative motion of M − 1 neighboring particles is (M − 1)Δ, it follows
| |  | (6) |
where
ψc ∝ (
b/
rc)
3 and
ψv ∝ (
b/
rv)
3 are volume fractions corresponding, respectively, to
rc and
rv. From this, the structural relaxation time
τ (in units of molecular time scale
τm) is
| |  | (7) |
where
τliq is a typical liquid-like relaxation time at
ψ =
ψc, indicating a drastic slowing down of dynamics due to the crowding at
ψ >
ψc towards a sharp divergence of
τ at
ψ =
ψv. To recast
eqn (7) in the form of temperature dependence, one usually invokes the thermal expansion of materials, which is assumed to be described by
ψ(
T) ≃
ψv[1 +
α(
Tv −
T)] in the range (
ψc,
Tc) to (
ψv,
Tv). Combining this with
eqn (6) and (7), one obtains the Vogel–Fulcher–Tammann (VFT) relation
| |  | (8) |
with
A = (
Tc −
Tv)ln(
τliq/
τm).
Applying the above picture of the cooperative dynamics to the slow diffusion of rings under the TC, the notion of topological volume invites a correspondence ψ → Ψ. The cooperative onset ψc then naturally corresponds to the TC onset Ψe at Ne with the replacement of characteristic time scales τm → τe and τliq → τ(1). We then set rv → 0, which amounts to saying that there is no spontaneous kinetic arrest due to the ultra-softness of rings, i.e., their COMs can indeed overlap in space. Such a translation leads to the growing cooperativity M(N) ∼ (Ψ(N)/Ψe)1/3 = [![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne)]1/3 with N, hence, the global structural relaxation time
(N/Ne)]1/3 with N, hence, the global structural relaxation time
| |  | (9) |
where the exponent
zeff =
z1 × [
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif)
(
N/
Ne)]
1/3 increases from
z1 at
Ne towards
z∞ =
z1[
Xc/
Xe]
1/3 ∼ 3 in the long chain asymptote (Appendix,
Fig. 5). Notice that the
Ψ–
N relation (or equivalently
X–
N relation shown in
Fig. 2(b)) determined by our free energy plays an analogous role to the
ψ–
T relation (thermal expansibility) in the context of the derivation of the VFT relation in particle systems.
As demonstrated in Fig. 3, eqn (9) captures all the essential features observed in numerical simulations. In addition to the semi-quantitative prediction for τ and its departure from τ(1), it provides the diffusion coefficient D(N) ∼ R(N)2/τ(N), whose scaling with N remarkably agrees with numerical observations4,24 (Fig. 3 (inset); see also Appendix, Fig. 5). Compared to previous predictions based on the conventional estimation D(1) ∼ R(N)2/τ(1)(N),19,27 this improvement on D once again sets forth the notion of slow diffusion due to the cooperative structural relaxation. Yet noticeable is the absence of VFT-like divergence in τ despite invoking mandatory cooperative motion for cage breaking. In our description, this traces back to the ultra-soft nature of rings rv → 0, thus no divergence in the cooperativity M. Still, there is a small build up in M at N > Ne, and combined with the slowing down of single ring dynamics τ(1), it acts as a multiplicative factor in the exponent, leading to an unconventional, i.e., faster than power-law, increase in τ with N.
 |
| | Fig. 3 Internal (τ(1)) and global (τ) structural relaxation times as a function of N/Ne compared with MD simulation data24 with τe = 120τ0. Also plotted is the stress relaxation time τsr (multiplied by a factor c = 0.4) evaluated in ref. 19 using the data in ref. 24. Here, we adopted z1 = 7/3 suggested in ref. 19. (inset) Diffusion coefficient. Here the line with [R(s)]2/τ is compared with the diffusion coefficient measured in MD simulations.24 See also ref. 25 for very similar numerical data on the separation between τ(1) and τ. | |
5 Conclusions
To summarize, we have proposed a cooperativity scenario for slow dynamics in a dense solution of non-concatenated ring polymers motivated by some analogy between soft colloids and rings. While we have shown that many of the puzzling observations could be resolved by introducing the notion of topological volume, it should be recognized as a minimal description in the sense that we only look at the COM degrees of freedom of the rings to evaluate the cooperativity M, which is mirrored in a small Mc = (Xc/Xe)1/3 ∼ 1.3 in the large N limit. A more realistic picture would be that a larger number of neighboring rings behave collectively not only by the COM translation but also by internal deformation modes to create a gate for structural relaxation. Our discussion yields several challenges and future directions. (i) Quantifying the degree and the nature of the cooperativity in ring solutions – it should help with a possible refinement of our current description. (ii) Clarifying the relation with the threading picture4,28 – there seems to be some correspondence between our structural relaxation time τ and the ring dethreading time possibly responsible for the slow mode in stress relaxation.28 (iii) Elucidating the analogy with soft colloids – they are known to be strong glass formers,29 and rings could be viewed as the softest “particle” ever known. Compared, for instance, to star polymers,30 the energy scale of the effective repulsive pair potential is much lower (on the order of kBT), and the COMs of different rings can spatially overlap rather easily. A quantitative comparison with a dense solution of the soft core (such as the Gaussian core) model may yield useful insights.31 (iv) An apparently similar soft colloidal picture (with comparable energy scale) is known to describe the linear polymer systems as well.32 Unlike the ring polymer systems, however, it has nothing to do with the conformation of individual chains, and the correlation hole (or effective repulsion) becomes weaker with the chain length. Nonetheless, some anomalous feature in the diffusive dynamics of COMs,3,4,24 which is not captured by the reptation theory, may be described by the cooperative mechanism scenario proposed here. (v) Building a microscopic foundation for the proposed description should be a fundamental problem. Some attempts for coarse-graining of ring polymer systems indicate the crucial effect of the TC.33,34 (vi) Exploring a novel depletion effect35 – the notion of topological volume indicates an associated depletion effect. This would be related to the recent prediction on the promotion of phase separation in the blend of ring polymers with dissimilar molecular weights,20,36 and may have non-trivial effects in confined spaces, e.g. in the cell nucleus.
Conflicts of interest
There are no conflicts to declare.
Appendix
Some discussion on free energy associated with the TC
Entropic penalty due to the non-concatenation constraint.
A unique feature in the system of unlinked rings compared to the standard particle system is that constituents have freedom to adjust their spatial size to reduce the repulsive interaction (here originated from the non-concatenation TC among neighboring rings). In the free energy (4), it is accounted for through the van der Waals term Funlink/kBT = −ln(1 − Ψ) based on the free volume concept.
Let c denote the number concentration of rings in the melt. From free energy Funlink per ring, we obtain the free energy density funlink = cFunlink as
| |  | (10) |
where we have used the relation
c ≡
Nring/
Ω =
ϕ/(
Na3) (
Nring is the total number of rings in the system volume
Ω, and the monomer volume fraction
ϕ ∼ 1 in the melt state), and the definition of the coordination number
X given as
eqn (1). The final expression is obtained by the expansion into a virial series, which identifies the virial coefficients
B2 ≃
R3/
Xc,
B3 ≃
R6/2
Xc2,
etc. Note that the second virial coefficient is in line with the effective ring size
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif)
invoked in
eqn (5),
i.e.,
B2 ≃
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 3
3, that is, the soft nature of the ring is linked with
Xc =
Xe/
Ψe, hence with
Ne. It is instructive to compare our free energy
Funlink with that conjectured by Cates and Deutsch long ago. They suggested the form
Funlink/
kBT ∼
R3/(
Na3) ∼
X.
37 In light of the present discussion, their free energy corresponds to the second virial approximation (which amounts to setting
Bn = 0 for integer
n > 2) neglecting the softness factor
Xc (thus
B2 ∼
R3). Therefore, it fails to capture the many-body effect responsible for the compact statistics (
ν = 1/3) in the long
N limit, and lacks
Ne as a unique characteristic length in the problem.
Entropic penalty due to the unknotting constraint.
The free energy Funlink(Ψ) due to the non-concatenation constraint favors a smaller Ψ, and hence the ring shrinkage. With more shrinkage, however, another TC associated with unknotting within individual rings becomes more relevant. Here we briefly outline the derivation of the entropic penalty due to the unknotting TC (second term in eqn (4)) following the discussion in ref. 20.†
According to the standard scaling argument, the entropic cost of squeezing a polymer into the size R is evaluated as
| | 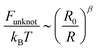 | (11) |
where
R0 is the size of a ring in the reference state.
9 In the present problem, a ring in the reference state can be prepared by hypothetically switching off the non-concatenation TC among different rings,
i.e., it is free from the ordinary excluded-volume effect (
i.e., screened in melt), and not perturbed by the non-concatenation TC, but constrained to maintain the unknot topology. Such a ring is essentially identical to an ideal, but non-phantom unknot ring in dilute solution, whose size is given by
| |  | (12) |
where
N0 (∼300 for a flexible ring) is a characteristic length beyond which the ring (without excluded volume) swells due to the unknotting TC.
38 It has been shown that this topological swelling is characterized by the excluded volume exponent
ν0.
To determine the exponent β in eqn (11), we require the squeezing free energy to be an extensive quantity; Funknot(kN,kR3) = kFunknot(N,R3) for an arbitrary positive number k. This leads to β = 6 for N < N0 or β = 3/(3ν0 − 1) for N ≫ N0.39 With this exponent and the definition of X (eqn (1)) and Xe (eqn (3)), the free energy (11) is rewritten as
| |  | (13) |
where a factor
c0 = (
N0/
Ne)
3(1–2ν0)/[2(3ν0)−1] of order unity arises since the two characteristic topological lengths
N0 and
Ne are generally different (though their relation is not well understood yet). In all the calculation in the main text, we adopted the free energy form for
N ≫
N0 with
c0 = 1. It would be more accurate to interpolate the two expressions for
Funknot as a function of
N, but we have carefully checked that this does not cause any essential change in the results presented in the main text.
‡ As long as
Funknot is written in the form ∼(
N/
Ne)(
Xe/
X)
1/(3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −1)
−1), the result of free energy minimization is insensitive to the value of
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
(either
ν0 or 1/2; the latter case corresponds to the first line of
eqn (13), that is
Funknot with
N <
N0).
§
Dependence of the coordination number on the measure of the ring size
The coordination number X ∼ R3/N has an arbitrariness in its quantitative evaluation depending on how we measure the ring size R. In the main text, we adopt R ≡ R(s), where R(s) is the spanning distance between monomers N/2 apart along the ring. Here, we repeat the same analysis by adopting the gyration radius as a measure, i.e., R ≡ R(g). The dependence of R(g) on N is measured in simulations.4,11,12 These data are plotted in Fig. 4(a) along with the theoretical prediction given in the main text. Similarly, the dependence of the R(g)-based coordination number X|R=R(g) on N is measured in simulations,4,12 and compared with the theoretical master curve in Fig. 4(b). The plot of Fig. 4(a) is virtually indistinguishable from that of Fig. 2(a) in the main text. The plot of X measured in simulations in Fig. 4(b) is slightly off from the free energy prediction compared with the excellent match seen in Fig. 2(b) in the main text. The latter point may be related to the smallness of the numerical value X|R=R(g), i.e., Xe|R=R(g) ∼ 1.3–1.4 (see Table 1 in the main text), indicating the sensitivity to sampling fluctuation. Yet, the deviation is at most on the order of 10 percent, and the general agreement on the N dependence is still remarkable. Therefore, we conclude that as expected from theory, the results are insensitive to the size measure upon appropriate rescaling. This highlights the importance of the notion of topological length scale Ne and associated coordination number Xe in the problem. We also note that the estimated numerical values for the rescaling factors Re and Xe listed in Table 1 in the main text are consistent with the assumption on the onset of the TC, i.e., the ideal chain statistics applies up to the chain length Ne (see the discussion in the Section Effect of chain stiffness and concentration in this Appendix).
 |
| | Fig. 4 Comparison of free energy prediction (solid line) with numerical simulation data for spatial size R and coordination number X of rings in their non-concatenated melt. Unlike in Fig. 2 in the main text, here the measure of the ring size is the gyration radius R = R(g). Numerical data are obtained from the literature (squares,11 circles,12 triangles4). (a) Plot of R/Re as a function of N/Ne. (b) Plot of X/Xe as a function of N/Ne. See Table 1 in the main text for details of simulation models and the estimated values of Re and Xe. | |
The comparison done here indicates that, for most practical purposes (numerical or theoretical analysis), it would be more useful to adopt the definition of X in terms of R(s) rather than R(g); the numerical value is more robust against the sampling fluctuation, and fits in well with that expected from the general packing problem as discussed in the main text.
Onset of compact statistics
In the main text, we have shown that the effective exponent νeff(N) for the size R ∼ Nνeff of the ring continuously decreases before reaching the asymptotic compact statistics regime with ν = 1/3 (Fig. 2 in the main text). Here we give a rough estimate for the ring length Nc, which signals the onset of the compact statistics regime. For convenience, we rewrite the free energy given as eqn (1) in the main text as F = Funlink(Ψ) + Funknot(Ψ;N), where Funlink(Ψ)/kBT = −ln[1 − Ψ] and Funknot(Ψ;N)/kBT = (N/Ne)(Ψe/Ψ)1/(3ν0−1).
First, we note that the limit Ψ(≡X/Xc) → Ψc ≃ 1 signals the onset of the compact statistics. In other words, Xc is the maximum coordination number, which can be achieved in dense ring polymer solutions. To deal with this limit, let us introduce a number S ≫ 1 such that Funlink(Ψc)/kBT = S, thus Ψc = 1 − e−S. The free energy balance indicates Funknot(Ψc;Nc)/kBT ≃ S, which leads to Nc/Ne ≃ [(1 − e−S)/Ψe]1/(3ν0−1)S ≃ Ψe1/(1−3ν0)S.
We determine the value S from the following observation. If we count the number of the pair of overlapping rings at N = Nc, it is evaluated as Xc/2 per ring. Given that kBT is the natural energy scale, it would be plausible to say that the energetic penalty of kBT for each overlap at the maximum coordination provides an appropriate energetic measure for the Ψ → 1 limit, which yields S ≃ Xc/2.
We thus find  . With Ψe ≃ 0.5 and Xc = 15–20, the above argument provides the estimate Nc/Ne ∼ 30. Here, from the consonance with the packing picture discussed in the main text (last part of Section 3), we adopt the coordination number defined in terms of the spanning distance as the measure of the ring size. Although crude, this discussion indicates a broad range for the crossover Nc/Ne ∼ 30 (between ideal and compact statistics regimes) in agreement with the numerical simulation results.
. With Ψe ≃ 0.5 and Xc = 15–20, the above argument provides the estimate Nc/Ne ∼ 30. Here, from the consonance with the packing picture discussed in the main text (last part of Section 3), we adopt the coordination number defined in terms of the spanning distance as the measure of the ring size. Although crude, this discussion indicates a broad range for the crossover Nc/Ne ∼ 30 (between ideal and compact statistics regimes) in agreement with the numerical simulation results.
In Fig. 5, we plot the prediction on the evolution of various effective exponents with the increase in N during the crossover regime.
 |
| | Fig. 5 (a) Effective size exponent νeff defined as R(N) ∼ Nνeff. (b) Effective exponents of global relaxation time zeff and diffusion coefficient γeff defined, respectively, as τ(N) ∼ Nzeff and D(N) ∼ N−γeff. | |
Note that while ideally νeff → 1/2 for N → Ne + 0 is expected, Fig. 5(a) shows a slightly smaller value. This may be associated with the mean-field nature of the theory. In fact, around the onset of the TC N ∼ Ne, the free energy due to TC is comparable to the thermal energy, and therefore, the value determined by free energy minimization does not necessarily correspond to the actual value.
Finally we mention that although most of recent works admit the asymptotic size exponent ν = 1/3, there is another claim against it.40 If ν > 1/3 in the long chain limit, it implies that the coordination number M grows with N without saturation, and hence the dynamical and diffusion exponents z and γ keep increasing with N.
Effect of chain stiffness and concentration
Topological length scale Ne.
Consider a dense solution of rings with segment volume fraction ϕ, in which individual rings are composed of N beads of size a. There is a bending potential introducing the directional persistence of bonds such that the segment length l > a. For short rings with N < Ne, the ideal chain statistics implies the ring size R ∼ lM1/2 = ap1/2N1/2, where M = aN/l is the number of segments and p = l/a is the segment aspect ratio. The coordination number is X ∼ R3ϕ/(Mvseg) ∼ R3ϕ/(Na3), where vseg ∼ a2l is the segment volume. At the onset of the TC, we have Xe ∼ Re3ϕ/(Nea3) with Re ∼ ap1/2Ne1/2, which is converted to| |  | (14) |
where the proportionality constant depends on the definition of the measure of the ring size (R(s) or R(g)etc.). This is very similar to the entanglement criterion in a dense solution of linear polymers due to Kavassalis–Noolandi.8,21 The observation of constant Xe (see the main text) indicates the concentration and stiffness dependence of the topological length scale Ne ∼ ϕ−2p−3, the systematic investigation of which in dense solution of ring polymers would be very interesting. Note that in the “genuine” semidilute regime ϕ ≲ p−3, the correlation effect will alter the dependence as Ne ∼ ϕ1/(1−3ν0)p3(2–3ν0)/(1–3ν0) ∼ ϕ−5/4p−3/4 with the SAW exponent ν0, where the final expression is obtained by the Flory approximation ν0 ≃ 3/5.
Ring size.
From the definition of the coordination number, the ring size is written as R ∼ a(NX/ϕ)1/3. For long rings, N ≫ Ne, the equilibrium X is determined by the free energy discussed in the main text. Since the free energy is constructed based on the coordination number, it is independent of ϕ and p. Bearing this point in mind, let us rescale the ring size in units of Re ∼ ap1/2N1/2. After some arrangement, we find| | 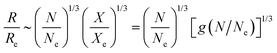 | (15) |
where the function g(x) follows from the free energy, and thus, is independent of ϕ and p, too, with the asymptotic behaviors discussed in the main text. Therefore, the dependence on ϕ and p is absorbed in rescaling factors Re and Ne, and one can collapse various data sets with different system parameters onto the master curve as demonstrated in the main text.
In the long chain limit N ≫ Ne, the ring size is
| |  | (16) |
where
eqn (14) is used in the last relation.
Quantitative evaluation of Re.
Since the ideal chain statistics without the TC applies for short rings with N < Ne, it is possible to provide a quantitative estimate for Re. In terms of mean square size, we find| | 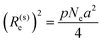 | (17) |
| |  | (18) |
for spanning size R(s) and the gyration radius R(g), respectively, at the onset of the TC. With p ≃ 2lp/a expected for a worm-like chain, one can see that the values used in Fig. 2(a) in the main text and Fig. 4(a), which are summarized in Table 1 in the main text, are indeed reasonable. In addition, the relation (R(s)e)2/(R(g)e)2 = 3 indicates the ratio Xe|R=R(s)/Xe|R=R(g) ≃ 33/2 ≃ 5.2 between the coordination numbers based on two different measures for the ring size. As seen in Table 1 in the main text, this is almost the case within statistical accuracy.
Acknowledgements
This work was supported by KAKENHI (No. JP16H00804, “Fluctuation and Structure”) from MEXT, Japan, and JST, PRESTO (JPMJPR16N5). T. S. thanks D. Michieletto for the enlightening discussion and providing numerical data in ref. 4.
References
- T. McLeish, Science, 2002, 297, 2005–2006 CrossRef PubMed.
- T. McLeish, Nat. Mater., 2008, 7, 933–935 CrossRef PubMed.
- A. R. Bras, S. Gooßen, M. Krutyeva, A. Radulescu, B. Farago, J. Allgaier, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, Soft Matter, 2014, 10, 3649–3655 RSC.
- D. Michieletto and M. Turner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5195–5200 CrossRef PubMed.
- D. Michieletto, N. Nahali and A. Rosa, Phys. Rev. Lett., 2017, 119, 197801 CrossRef PubMed.
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587–645 CrossRef.
- A. Liu and S. Nagel, Annu. Rev. Condens. Matter Phys., 2010, 1, 347–369 CrossRef.
-
M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed.
-
P.-G. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca [u.a.], 1979, p. 324 S Search PubMed.
- M. D. Frank-Kamenetskii, A. V. Lukashin and A. V. Vologodskii, Nature, 1975, 258, 398–402 CrossRef PubMed.
- T. Vettorel, A. Grosberg and K. Kremer, Phys. Biol., 2009, 6, 025013 CrossRef PubMed.
- J. Halverson, W. Lee, G. Grest, A. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904 CrossRef PubMed.
- J. Suzuki, A. Takano, T. Deguchi and Y. Matsushita, J. Chem. Phys., 2009, 131, 144902 CrossRef PubMed.
- T. Sakaue, Phys. Rev. Lett., 2011, 106, 167802 CrossRef PubMed.
- T. Sakaue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021806 CrossRef PubMed.
- A. Rosa and R. Everaers, Phys. Rev. Lett., 2014, 112, 118302 CrossRef PubMed.
- S. Obukhov, A. Johner, J. Baschnagel, H. Meyer and J. P. Wittmer, Europhys. Lett., 2014, 105, 48005 CrossRef.
- J. D. Halverson, J. Smrek, K. Kremer and A. Grosberg, Rep. Prog. Phys., 2014, 77, 022601 CrossRef PubMed.
- T. Ge, S. Panyukov and M. Rubinstein, Macromolecules, 2016, 49, 708–722 CrossRef PubMed.
- T. Sakaue and C. Nakajima, Phys. Rev. E, 2016, 93, 042502 CrossRef PubMed.
- T. A. Kavassalis and J. Noolandi, Phys. Rev. Lett., 1987, 59, 2674–2677 CrossRef PubMed.
- M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Nat. Mater., 2008, 7, 997–1002 CrossRef PubMed.
- Y. Doi, K. Matsubara, Y. Ohta, T. Nakano, D. Kawaguchi, Y. Takahashi, A. Takano and Y. Matsushita, Macromolecules, 2015, 48, 3140–3147 CrossRef.
- J. Halverson, W. Lee, G. Grest, A. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204905 CrossRef PubMed.
- E. Lee, S. Kim and Y. Jung, Macromol. Rapid Commun., 2015, 36, 1115–1121 CrossRef PubMed.
- T. Salez, J. Salez, K. Dalnoki-Veress, E. Raphaël and J. Forrest, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8227–8231 CrossRef PubMed.
- J. Smrek and A. Y. Grosberg, J. Phys.: Condens. Matter, 2015, 27, 064117 CrossRef PubMed.
- D. G. Tsalikis, V. G. Mavrantzas and D. Vlassopoulos, ACS Macro Lett., 2016, 5, 755–760 CrossRef.
- J. Mattsson, H. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. Reichman and D. Weitz, Nature, 2009, 462, 83–86 CrossRef PubMed.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef.
- A. Ikeda and K. Miyazaki, Phys. Rev. Lett., 2011, 106, 015701 CrossRef PubMed.
- A. A. Louis, P. G. Bolhuis, J. P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef PubMed.
- A. Narros, A. J. Moreno and C. N. Likos, Soft Matter, 2010, 6, 2435–2441 RSC.
- A. Narros, C. N. Likos, A. J. Moreno and B. Capone, Soft Matter, 2014, 10, 9601–9614 RSC.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef.
- Y. Kobayashi, Y. Doi, S. S. Abdul Rahman, E. Kim, T.-H. Kim, A. Takano and Y. Matsushita, Macromolecules, 2018, 51, 1885–1893 CrossRef.
- M. Cates and J. M. Deutsch, J. Phys., 1986, 47, 2121–2128 CrossRef.
- A. Y. Grosberg, Phys. Rev. Lett., 2000, 85, 3858–3861 CrossRef PubMed.
- T. Sakaue and E. Raphaël, Macromolecules, 2006, 39, 2621–2628 CrossRef.
- M. Lang, J. Fischer and J.-U. Sommer, Macromolecules, 2012, 45, 7642–7648 CrossRef.
Footnotes |
| † In ref. 14 and 15, this term has the form (N/Ne)(Xe/X)2, which amounts to setting ν0 = 1/2, but it was corrected later to account for the swelling of the unknotted ring due to the TC;20 see the discussion below. |
| ‡ Even if we use the first line of eqn (13) instead of the second in the free energy minimization calculation, the results basically agree with those in Fig. 2 with the deviation being smaller than the symbol size there. |
| § In Cates and Deutsch's argument, they adopted as a competing term with Funlink the free energy of squeezing an ideal chain into a narrow space of size R (which may be regarded as a proxy of Funknot here).37 This amounts to setting β = 2 in eqn (11), which is not compatible with the extensivity requirement discussed in the text; see ref. 39 for the scaling structure of confining a (non-ideal) chain in a closed space. |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab
ab

![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) of a ring due to the TC. In a particle picture, the average distance r between COMs of neighboring rings is a key quantity to control the global structural relaxation. In contrast to (c) the short ring case N < Ne, (d) the TC for a longer ring N > Ne imposes severe crowding (larger X, thus, higher topological volume fraction Ψ) in such a way that any ring is caged by its surroundings. As in ordinary crowded systems, the global structural relaxation requires cage breaking realized by the passage of a ring through its “gate”, but the solitary motion of any single ring is ineffective. However, the gate opening could be achieved by a cooperative motion of M(N) neighboring rings.
of a ring due to the TC. In a particle picture, the average distance r between COMs of neighboring rings is a key quantity to control the global structural relaxation. In contrast to (c) the short ring case N < Ne, (d) the TC for a longer ring N > Ne imposes severe crowding (larger X, thus, higher topological volume fraction Ψ) in such a way that any ring is caged by its surroundings. As in ordinary crowded systems, the global structural relaxation requires cage breaking realized by the passage of a ring through its “gate”, but the solitary motion of any single ring is ineffective. However, the gate opening could be achieved by a cooperative motion of M(N) neighboring rings.

![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = RXc−1/3 and Ψ as the effective size and the corresponding volume fraction associated with the TC. The first term in eqn (4) takes a form from the celebrated van der Waals theory, which represents the reduction in the free volume, in the present context, reflecting the entropic repulsion due to the non-concatenation TC. This term favors a smaller Ψ, and thus leads to ring shrinkage. Contrary to this is the second term, which represents an entropic penalty associated with squeezing a ring while maintaining the unknotting constraint, and can be derived from the standard scaling argument (see the Appendix).
= RXc−1/3 and Ψ as the effective size and the corresponding volume fraction associated with the TC. The first term in eqn (4) takes a form from the celebrated van der Waals theory, which represents the reduction in the free volume, in the present context, reflecting the entropic repulsion due to the non-concatenation TC. This term favors a smaller Ψ, and thus leads to ring shrinkage. Contrary to this is the second term, which represents an entropic penalty associated with squeezing a ring while maintaining the unknotting constraint, and can be derived from the standard scaling argument (see the Appendix).
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne) with a function
(N/Ne) with a function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) → 1 at x = 1 and
(x) → 1 at x = 1 and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) → Xc/Xe at x ≫ 1. From this, the ring size follows as R(N) ≃ Re(N/Ne)1/3[
(x) → Xc/Xe at x ≫ 1. From this, the ring size follows as R(N) ≃ Re(N/Ne)1/3[![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne)]1/3. In Fig. 2, we compare predictions from our free energy (with Ψe = 0.5) with three sets of numerical simulation data. Here we adopt the spanning distance R(s) (root mean-square distance between monomers N/2 apart) as a measure of the spatial size of rings, so that X is the average number of surrounding rings, whose centers of mass (COMs) are located within the distance R(s) from the COM of the reference ring. Note that the Re and Xe values are evaluated from the numerical data in ref. 4, 11 and 12 (see Table 1), which play the role of rescaling factors in the master plot. While the resultant Re values reasonably accord with the theoretical expectation (Appendix), it is striking that all the data sets point to almost the same value for Xe ≃ 8 despite different simulation models and conditions employed. The same conclusion is reached if we measure the ring size with the radius of gyration R(g), in which case Xe ≃ 1.4 is found (Appendix, Fig. 4). Hence, besides the quantitative predictability of the proposed free energy, we find that the coordination number serves as a robust measure for the TC. In particular, the onset of the TC can be identified by Xe, whose precise value is independent of the system details. The crossover towards the compact statistic regime for longer rings is quantified by the function
(N/Ne)]1/3. In Fig. 2, we compare predictions from our free energy (with Ψe = 0.5) with three sets of numerical simulation data. Here we adopt the spanning distance R(s) (root mean-square distance between monomers N/2 apart) as a measure of the spatial size of rings, so that X is the average number of surrounding rings, whose centers of mass (COMs) are located within the distance R(s) from the COM of the reference ring. Note that the Re and Xe values are evaluated from the numerical data in ref. 4, 11 and 12 (see Table 1), which play the role of rescaling factors in the master plot. While the resultant Re values reasonably accord with the theoretical expectation (Appendix), it is striking that all the data sets point to almost the same value for Xe ≃ 8 despite different simulation models and conditions employed. The same conclusion is reached if we measure the ring size with the radius of gyration R(g), in which case Xe ≃ 1.4 is found (Appendix, Fig. 4). Hence, besides the quantitative predictability of the proposed free energy, we find that the coordination number serves as a robust measure for the TC. In particular, the onset of the TC can be identified by Xe, whose precise value is independent of the system details. The crossover towards the compact statistic regime for longer rings is quantified by the function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x), which describes a gradual increase of the coordination number from Xe towards Xc.
(x), which describes a gradual increase of the coordination number from Xe towards Xc.
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (x) is universal in the sense that it does not depend on the system parameters (Appendix).
(x) is universal in the sense that it does not depend on the system parameters (Appendix).


![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne)]1/3 with N, hence, the global structural relaxation time
(N/Ne)]1/3 with N, hence, the global structural relaxation time
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (N/Ne)]1/3 increases from z1 at Ne towards z∞ = z1[Xc/Xe]1/3 ∼ 3 in the long chain asymptote (Appendix, Fig. 5). Notice that the Ψ–N relation (or equivalently X–N relation shown in Fig. 2(b)) determined by our free energy plays an analogous role to the ψ–T relation (thermal expansibility) in the context of the derivation of the VFT relation in particle systems.
(N/Ne)]1/3 increases from z1 at Ne towards z∞ = z1[Xc/Xe]1/3 ∼ 3 in the long chain asymptote (Appendix, Fig. 5). Notice that the Ψ–N relation (or equivalently X–N relation shown in Fig. 2(b)) determined by our free energy plays an analogous role to the ψ–T relation (thermal expansibility) in the context of the derivation of the VFT relation in particle systems.


![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) invoked in eqn (5), i.e., B2 ≃
invoked in eqn (5), i.e., B2 ≃ ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 3, that is, the soft nature of the ring is linked with Xc = Xe/Ψe, hence with Ne. It is instructive to compare our free energy Funlink with that conjectured by Cates and Deutsch long ago. They suggested the form Funlink/kBT ∼ R3/(Na3) ∼ X.37 In light of the present discussion, their free energy corresponds to the second virial approximation (which amounts to setting Bn = 0 for integer n > 2) neglecting the softness factor Xc (thus B2 ∼ R3). Therefore, it fails to capture the many-body effect responsible for the compact statistics (ν = 1/3) in the long N limit, and lacks Ne as a unique characteristic length in the problem.
3, that is, the soft nature of the ring is linked with Xc = Xe/Ψe, hence with Ne. It is instructive to compare our free energy Funlink with that conjectured by Cates and Deutsch long ago. They suggested the form Funlink/kBT ∼ R3/(Na3) ∼ X.37 In light of the present discussion, their free energy corresponds to the second virial approximation (which amounts to setting Bn = 0 for integer n > 2) neglecting the softness factor Xc (thus B2 ∼ R3). Therefore, it fails to capture the many-body effect responsible for the compact statistics (ν = 1/3) in the long N limit, and lacks Ne as a unique characteristic length in the problem.
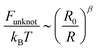


![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −1), the result of free energy minimization is insensitive to the value of
−1), the result of free energy minimization is insensitive to the value of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) (either ν0 or 1/2; the latter case corresponds to the first line of eqn (13), that is Funknot with N < N0).§
(either ν0 or 1/2; the latter case corresponds to the first line of eqn (13), that is Funknot with N < N0).§

 . With Ψe ≃ 0.5 and Xc = 15–20, the above argument provides the estimate Nc/Ne ∼ 30. Here, from the consonance with the packing picture discussed in the main text (last part of Section 3), we adopt the coordination number defined in terms of the spanning distance as the measure of the ring size. Although crude, this discussion indicates a broad range for the crossover Nc/Ne ∼ 30 (between ideal and compact statistics regimes) in agreement with the numerical simulation results.
. With Ψe ≃ 0.5 and Xc = 15–20, the above argument provides the estimate Nc/Ne ∼ 30. Here, from the consonance with the packing picture discussed in the main text (last part of Section 3), we adopt the coordination number defined in terms of the spanning distance as the measure of the ring size. Although crude, this discussion indicates a broad range for the crossover Nc/Ne ∼ 30 (between ideal and compact statistics regimes) in agreement with the numerical simulation results.