DOI:
10.1039/C8SM00495A
(Paper)
Soft Matter, 2018,
14, 4577-4590
Shear-density coupling for a compressible single-component yield-stress fluid
Received
9th March 2018
, Accepted 1st May 2018
First published on 7th May 2018
Abstract
Flow behavior of a single-component yield stress fluid is addressed on the hydrodynamic level. A basic ingredient of the model is a coupling between fluctuations of density and velocity gradient via a Herschel–Bulkley-type constitutive model. Focusing on the limit of low shear rates and high densities, the model approximates well—but is not limited to—gently sheared hard sphere colloidal glasses, where solvent effects are negligible. A detailed analysis of the linearized hydrodynamic equations for fluctuations and the resulting cubic dispersion relation reveals the existence of a range of densities and shear rates with growing flow heterogeneity. In this regime, after an initial transient, the velocity and density fields monotonically reach a spatially inhomogeneous stationary profile, where regions of high shear rate and low density coexist with regions of low shear rate and high density. The steady state is thus maintained by a competition between shear-induced enhancement of density inhomogeneities and relaxation via overdamped sound waves. An analysis of the mechanical equilibrium condition provides a criterion for the existence of steady state solutions. The dynamical evolution of the system is discussed in detail for various boundary conditions, imposing either a constant velocity, shear rate, or stress at the walls.
I. Introduction
Heterogeneous flow and shear banding are ubiquitous phenomena, commonly occurring in a variety of complex fluids such as polymer solutions and worm-like micelles,1–3 colloidal gels,4 hard sphere colloidal glasses5,6 and granular media.7 In line with this diversity of the physical systems, one encounters different underlying mechanisms as being responsible for localized flow. Classically, shear banding occurs in systems with a strongly shear-thinning flow curve (stress versus imposed shear rate).8 Alternatively, banding can result for a non-monotonic flow curve stemming from a shear-induced phase transformation. In this case, an instability occurs if the globally imposed shear rate lies between the two solutions corresponding to homogeneous steady flow. The system divides into two regions, each flowing with one of the stable shear rates.1 For colloidal gels, on the other hand, the mechanism of shear localization is attributed to a competition between formation and growth of fractal-like clusters and its shear-induced breakage.4
An interesting case occurs in dense suspensions of hard sphere colloidal particles and granular materials, where the underlying flow curve is monotonic, yet the flow can develop spatio-temporal heterogeneities.5,7 In these “soft glassy materials”,9 shear-induced rejuvenation competes with the sluggish relaxation (aging) kinetics and may lead to a heterogeneous flow in the glassy state.10–12
Flow localization in dense hard-sphere suspensions has been recently rationalized in terms of the so-called shear–concentration coupling (SCC),5,6 a hydrodynamic model, first proposed in ref. 13, which couples the local flow to the concentration field. This coupling is encoded in a non-Newtonian stress and in a shear-rate dependent osmotic pressure.
Within SCC, one considers a background fluid which transports—and is influenced by—a concentration field. While this picture emerges naturally in the case of polymer solutions, the role of the background fluid is less obvious in hard sphere colloidal glasses. Indeed, there is a common consensus that the effect of hydrodynamic interactions can be neglected in colloidal hard-sphere systems close to the glass transition in the low shear rate limit, which is of primary interest to the present study.14,15 Accepting this standpoint, it is tempting to fully neglect the background fluid and investigate the issue of flow heterogeneity within hydrodynamic equations of a single-component non-Newtonian fluid. This paper presents such a study.
In ref. 5, 13 and 16, the instability of a sheared colloidal suspension has been investigated based on an advection–diffusion equation for the colloid concentration ρ, embedded in a solvent of velocity u,
| |  | (1) |
where
j denotes the total particle flux,
ζ is a friction coefficient, and
μ is a (shear-rate dependent) generalized chemical potential.
17Eqn (1) asserts that the total flow velocity
j/
ρ of the colloidal particles consists of an imposed “background” flow
u, onto which a contribution −(1/
ζ)∇
μ due to the diffusive motion of the particles is superimposed. The flow velocity
u is assumed to be governed by the Stokes equation,
where
σ is the viscous stress tensor, which is typically given in terms of an expansion in gradients of
u. The Greek symbols stand for spatial directions (
α,
β ∈ {
x,
y} in the present 2D study) and Einstein's sum rule over repeated indices is used.
In ref. 6, the possibility of a coupling between shear and concentration has been investigated in a system of hard spheres. A constant kinetic temperature has been imposed by continuously rescaling the particle velocity during the simulations. Notably, there is no background fluid in the system investigated in ref. 6. Thus, it can be considered as an isothermal compressible single-component fluid, described by a continuity equation for the particle density ρ and a transport equation for the fluid momentum ρu:
| | | ∂t(ρuα) = −∂βΠαβ + ∂βσαβ. | (3b) |
As in
ref. 6,
Π and
σ denote the reversible and the irreversible (viscous) stress tensors. In close analogy to shear concentration coupling, one postulates a coupling between fluid density and local shear rate, which we shall call “shear-density coupling” (SDC) in the following. As shown in Section II, this coupling is generated by reversible and viscous stresses being functions of the shear rate and density, respectively. In equilibrium, the divergence of the reversible stress tensor can be related to a chemical potential
via ∂
βΠαβ =
ρ∂
αμ. Beyond equilibrium, this relation serves as a definition of a shear-rate dependent chemical potential.
Before proceeding further with our analysis, a comment on the above equations is at order here. The advection–diffusion eqn (1) is central to dynamic density functional theory and widely used for the description of driven colloidal suspensions.18–20 In these approaches, u represents the velocity of the background fluid, which consists of an externally imposed component (e.g., shear flow) and a contribution arising from the hydrodynamic inter-particle interactions. Notably, the dynamics of a subset of tagged particles in a single-component fluid flowing with velocity u is formally also described by eqn (1) and (2).21,22 In this case, the chemical potential and the viscosity would react only to the fluctuations of the tagged particles. However, the viscosity and the pressure are actually sensitive to the total density, since this quantity describes the caging and trapping responsible for the dynamic slowing down near the glass transition.
In view of these arguments on the single-component fluid nature of the problem, it appears more appropriate to analyze the hard-sphere system of ref. 6 in terms of the isothermal compressible fluid equations in eqn (3), rather than an advection–diffusion equation. In passing, we remark that the different nature of the two models is also crucial in the case of critical phenomena: here, the advection–diffusion and momentum transport equations define the universality class of “model H”, which primarily describes a binary fluid mixture.23 The isothermal single-component fluid, instead, is described in terms of a continuity equation and a momentum equation, giving rise to a critical behavior distinct from model H.24
II. Model
We consider a fluid described by eqn (3), bounded by walls at y = 0 and y = L (see Fig. 1). The flow is assumed to be homogeneous along the vorticity direction (z) as well as along the flow direction (x), such that generally ∂x(⋯) = ∂z(⋯) = 0. The local shear rate is defined as| | ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t) = ∂yux(y,t). (y,t) = ∂yux(y,t). | (4) |
In this and the following section, we focus on bulk dynamics, such that specification of the boundary conditions at the walls is not necessary. We shall therefore merely assume the presence of a constant steady background shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. (We return to the effect of boundary conditions in Section IV, where we numerically solve the Navier–Stokes equations in a finite domain.) The pressure tensor Π is isotropic, Παβ = Πδαβ, where Π denotes the scalar pressure. Consequently, eqn (3) reduces to
0. (We return to the effect of boundary conditions in Section IV, where we numerically solve the Navier–Stokes equations in a finite domain.) The pressure tensor Π is isotropic, Παβ = Πδαβ, where Π denotes the scalar pressure. Consequently, eqn (3) reduces to| | | ∂t(ρuy) = −∂yΠ + ∂yσyy. | (5c) |
Analogously to ref. 16, 25 and 26, we take the following form for the viscous stress tensor σ:| |  | (6) |
which corresponds to an expansion in gradients of the flow field u respecting certain symmetry properties of the stress.27 Here, η and ζ denote the shear and bulk viscosity, respectively, which are generally functions of the density and the shear rate (see below). The parameter κ denotes the shear–curvature viscosity, and the stress contribution associated with it serves to stabilize the flow field against large gradients. Analogously, the parameter κ′ controls the corresponding contribution stabilizing the bulk viscous stress. The yield stress σyield is independent of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and is nonzero only in the glassy phase (ρ > ρg). In contrast to the shear viscosity η (see below), detailed data for the bulk viscosity ζ and the curvature viscosities κ and κ′ in a hard-sphere fluid near the glass transition are not available. Following ref. 16, we shall therefore assume these viscosities to have the same functional form as η, i.e.,
and is nonzero only in the glassy phase (ρ > ρg). In contrast to the shear viscosity η (see below), detailed data for the bulk viscosity ζ and the curvature viscosities κ and κ′ in a hard-sphere fluid near the glass transition are not available. Following ref. 16, we shall therefore assume these viscosities to have the same functional form as η, i.e.,| |  | (7a) |
| | ζ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = b′η(ρ, ) = b′η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) ) | (7b) |
| | κ′(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = b′κ(ρ, ) = b′κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). ). | (7c) |
Here, η0 and κ0 are the shear (curvature) viscosities in the zero-shear rate (Newtonian) limit [see eqn (13b)], and b′ is a free dimensionless parameter. Typically, we set b′ = 1 and κ0/η0 ≃ (10 − 100)a2, where a is a microscopic length scale, e.g., the average particle diameter in a colloidal glass. This choice gives rise to an effective interface width,  , of the shear band of a few particle diameters a.16 Using eqn (4), the relevant components of the viscous stress tensor follow as
, of the shear band of a few particle diameters a.16 Using eqn (4), the relevant components of the viscous stress tensor follow as| | σxy = σyieldxy(ρ) + η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) )![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ(ρ, − κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )∂y2 )∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , , | (8) |
| |  | (9) |
with b ≡ b′ + 4/3 = 7/3. In order to track the influence of the bulk viscosity, we shall carry along the parameter b in our calculations. Summarizing, eqn (5) reduces to| | ∂t(ρux) = σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂yρ − κ∂y3 + σρ∂yρ − κ∂y3![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − [(∂ρκ)(∂yρ) + (∂ − [(∂ρκ)(∂yρ) + (∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) κ)(∂y κ)(∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )](∂y2 )](∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), ), | (10b) |
| | ∂t(ρuy) = −Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) − Πρ∂yρ + b(η − κ∂y2)∂y2uy, − Πρ∂yρ + b(η − κ∂y2)∂y2uy, | (10c) |
where we defined| | Πρ ≡ ∂(Π − σyieldyy)/∂ρ, Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂Π/∂ ≡ ∂Π/∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , , | (11a) |
| | σρ ≡ ∂(σyieldxy + η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/∂ρ, σ )/∂ρ, σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂(η ≡ ∂(η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/∂ )/∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , , | (11b) |
which are generally functions of ρ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
 |
| | Fig. 1 Slit geometry considered in the present study. The fluid is subjected to a steady shear flow in lateral direction (x) with a spatially constant (background) shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, but can develop arbitrarily large deviations described by a local shear rate 0, but can develop arbitrarily large deviations described by a local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t). We assume the fluid to be homogeneous both in the lateral and the vorticity direction (z, pointing normal to the figure plane). (y,t). We assume the fluid to be homogeneous both in the lateral and the vorticity direction (z, pointing normal to the figure plane). | |
It seems reasonable to assume
| | | σyieldyy ≃ σyieldxy = σyield, | (12) |
where
σyield is a common yield stress function. In the liquid phase (
ρ <
ρg), the yield stress vanishes and the shear viscosity is well described by a Krieger–Dougherty relationship (
cf.ref. 16):
Here and in the following,
Φ ≡
ρ/
ρm, where
ρm = 0.67 (in appropriate units, see below) is the packing fraction corresponding to random close packing of (polydisperse) hard spheres.
In the glassy phase (ρ > ρg), instead, MD simulations of a hard-sphere system indicate6
| |  | (14a) |
| | η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = σyield(ρ)A(1 − Φ)n ) = σyield(ρ)A(1 − Φ)n![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1, n−1, | (14b) |
where the parameters
σ0 ≃ 0.0119
kBT/
a3,
A = 34.5(
η0a3/(
kBT))
n,
p ≃ 2.355,
n ≃ 0.4 result from a fit.
kBT denotes the thermal energy and
ρg = 0.585 is the density of the glass transition. The pressure is given, for any
ρ, by
6| |  | (15) |
with
Π0 ≃ 8.4
kBT/
a3,
B = 0.07(
η0a3/(
kBT))
m,
n =
m ≃ 0.4,
r = 4.1. The shear-rate dependence of
Π is a manifestation of the flow-induced distortion of the pair-correlation function. We remark that the parameters in
eqn (14) and (15) have been obtained in
ref. 6 from a fit to the global flow curves, taking
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
≡
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0, but are assumed here to apply also locally in the system. We shall henceforth fix the units of mass, length and time by setting
kBT =
a =
η0 = 1. With these choices, the fundamental “microscopic” time scale
t0 ≡
η0a3/
kBT = 1. Using the fact that
η0 is the fluid viscosity in the dilute limit [see
eqn (13b)] and invoking the Stokes–Einstein relation, one obtains
t0 ∼
a2/
D with the self-diffusion coefficient
D. In other words,
t0 is the time needed for a particle to explore, in the dilute limit, a distance comparable to its own size. Noteworthy, this is also a measure of the structural relaxation time. Accordingly, the microscopic time scale
t0 determines, together with thermal energy and particle size, the viscosity and stress scale. In the context of macroscopic fluid dynamics, however, a more natural dimensionless measure of time, which we shall use in the discussion of our results, is instead given by the strain
t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
.
III. Linear stability analysis
A. Linearization of the dynamics
We consider small fluctuations of the density and the shear-rate, i.e., ρ(y,t) = ρ0 + δρ(y,t), ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t) =
(y,t) = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 + δ
0 + δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t), where ρ0 and
(y,t), where ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 denote the uniform background values. In linear order in the fluctuations and derivatives, eqn (10) becomes
0 denote the uniform background values. In linear order in the fluctuations and derivatives, eqn (10) becomes| | ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0∂tδρ + ρ0∂tδ 0∂tδρ + ρ0∂tδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = σ = σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y2δ ∂y2δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂y2δρ − κ∂y4δ + σρ∂y2δρ − κ∂y4δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , , | (16b) |
| | ρ0∂tuy = −Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂yδ ∂yδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − Πρ∂yδρ + bη∂y2uy − bκ∂y4uy, − Πρ∂yδρ + bη∂y2uy − bκ∂y4uy, | (16c) |
where now the coefficients σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,ρ, Π
,ρ, Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,ρ, η, and κ are understood to be evaluated for the background values ρ0 and
,ρ, η, and κ are understood to be evaluated for the background values ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.
0.
In order to develop a basic understanding of the transport mechanisms in the compressible fluid, note that, inserting eqn (16a) into eqn (16b), the latter becomes a generalized diffusion equation for the shear rate fluctuation δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,
| | ρ0∂tδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = σ = σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y2δ ∂y2δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ∂y4δ − κ∂y4δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂y2δρ + + σρ∂y2δρ + ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0ρ0∂yuy. 0ρ0∂yuy. | (17) |
While the last term on the r.h.s. is typically negligible, the first and the second term induce a smoothing of shear rate inhomogeneities. However, due to the third term, which is not present in a Newtonian fluid, a positive density fluctuation can effectively lower the local shear rate. Such a negative shear rate fluctuation drives,
via the first term on the r.h.s. of
eqn (16c), a flow which [
viaeqn (16a)] further enhances the density in that region. This gives rise to a feedback mechanism, which is further analyzed in Section IIIB. In passing, we note that
eqn (16a) and (16c) can be combined into a generalized “sound-wave” equation
| |  | (18) |
The dynamics induced by the above compressible fluid equations is further discussed and contrasted to a diffusive transport model in Appendix A.
In order to investigate the linear stability, we solve eqn (16)via the ansatz
| | 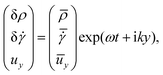 | (19) |
where
ω and
k represent the growth rate and wavenumber of a fluctuation, respectively, and the bared quantities denote the fluctuation amplitudes. This ansatz transforms
eqn (16) into
| | ω![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = −ikρ0ūy, = −ikρ0ūy, | (20a) |
| |  | (20b) |
| |  | (20c) |
which can be written in matrix form as
| | 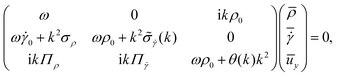 | (21) |
with the abbreviations
and
A nontrivial solution of
eqn (21) requires the coefficient matrix to be singular and, correspondingly, the determinant to vanish:
| |  | (24) |
Note that, in order to obtain a purely real solution, the ansatz in
eqn (19) must be linearly combined with an expression of the same form but where
k is replaced by −
k. The three roots
w1,2,3 of the cubic
eqn (24) are independent of the sign of ±
k. Accordingly, we can write the general solution to the linearized hydrodynamic
eqn (16) as
| | 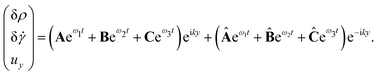 | (25) |
The coefficient vectors
A,
B,… are obtained by inserting each root
ωj into
eqn (21) and determining the null-space of the resulting linear mapping.
B. Boundary of stability and growth dynamics
Before turning to the discussion of the cubic eqn (24) in the full parameter space, we first focus on the region near the boundary of stability, where the analysis is simplified by the fact that the real part of at least one ωj must be small. We proceed by discussing the two possible cases admitted by the solutions to a cubic equation with real coefficients, like eqn (24).
Case 1: all the three roots are purely real (but not necessarily distinct). The general solution given in eqn (25) consists in this case only of exponentially growing, decaying or constant contributions. In the stable region, ωj ≤ 0 for all j. Directly at the boundary to the unstable region, one must have ωj = 0 for at least one mode index, say j = 1. Setting ω1 = 0 in eqn (24) readily yields
| |  | (26) |
As is shown below, the quantity

defined here determines the boundary of stability. Inserting
eqn (26) into
eqn (24), the other two decay rates result as
| |  | (27) |
For typical systems, one has
| | ρ0Πρ ≥ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0Π 0Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . . | (28) |
In fact, for the constitutive relations reported in
eqn (14) and (15), this inequality is violated only for unrealistically small shear rates
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
≲ 10
−12 and extreme densities
ρ ≃
ρm, where the hydrodynamic model considered here is doubtful. Since generally
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
≥ 0 and
θ(
k) > 0, it follows that
ω2,3 ≤ 0—still assuming purely real
ωj. Accordingly, provided that
eqn (28) holds, none of the frequencies
ω2 and
ω3 vanishes and, consequently, the boundary of stability is solely defined by the condition
ω1 = 0 in this case. Close to the boundary of stability, nonlinear terms in
ω1 can be neglected in
eqn (24), such that one readily obtains the growth rate
| |  | (29) |
We thus infer that, under the condition in
eqn (28), the system is linearly stable if
| |  | (30) |
This inequality is consistent with the stability of the Navier–Stokes equations for a purely Newtonian fluid, since
σρ =
Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
= 0 and thus

in that case. As discussed below,
eqn (30) in fact describes the boundary of stability of the whole relevant parameter space for the compressible single-component fluid.
In order for eqn (25) to be real, one must have Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Â = Re
 = Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, Im
A, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Â = −Im
 = −Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, with analogous conditions applying for B and C. These conditions are indeed fulfilled by the solution in eqn (25), which can be seen by writing eqn (21) as
A, with analogous conditions applying for B and C. These conditions are indeed fulfilled by the solution in eqn (25), which can be seen by writing eqn (21) as
| | | [M′(k) + iM′′(k)]A = 0, | (31) |
where
M′ and
M′′ denote the real and imaginary parts of the matrix in
eqn (21). Now let
A =
A′ + i
A′′ be a solution to
eqn (31). Comparison of the real and imaginary parts of the resulting expression in
eqn (31) shows that
 =
A′ − i
A′′ is a solution to the equation [
M′(−
k) + i
M′′(−
k)]
 = [
M′(
k) − i
M′′(
k)]
 = 0, as required.
Case 2: one root is real and the other two are complex conjugates. Let ω1 denote the purely real and ω2,3 = Ω′ + iΩ′′ the complex conjugate solutions to eqn (24). For the imaginary part of eqn (25) vanish, B and C must be complex conjugates of one another, while A must be purely real. Taking B = C* = B′ + iB′′ allows one to write the general solution as
| | (ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,uy)Te−iky = Aeω1t + 2eΩ′t(B′cos ,uy)Te−iky = Aeω1t + 2eΩ′t(B′cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω′′t − B′′sin Ω′′t − B′′sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω′′t). Ω′′t). | (32) |
Analogously to case 1, at least either
ω1 or
Ω′ must vanish at the boundary of stability. If
ω1 = 0, we recover
eqn (26) as a necessary consequence and
eqn (27) shows that
Ω′ ≤ 0. Thus, in this case, the growing mode will be a monotonic function as in case 1 with a growth rate given by
eqn (29). In contrast, the oscillatory modes will in general be decaying functions of time and will not give rise to any linear instability.
In order to analyze the case Ω′ = 0, we consider Vieta's formulas28 for the solutions to the cubic eqn (24) in case 2:
| |  | (33a) |
| |  | (33b) |
| |  | (33c) |
If
Ω′ = 0,
eqn (33a) immediately implies
ω1 < 0,
i.e., the purely real mode is stable. Moreover, combining the relations in
eqn (33a) to
eqn (33c) results in
| |  | (34) |
In order to determine the stability boundary for the complex conjugate pair of solution, we consider in
eqn (24) small variations around
Ω′ = 0. Accordingly, we insert
ω = δ
Ω′ + i
Ω′′ into
eqn (24), where
Ω′′ is determined by
eqn (33b). Neglecting terms of
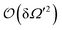
and higher in
eqn (24) (keeping, however, all orders in
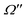
, as this quantity is not necessarily small), yields
| |  | (35) |
with
| | 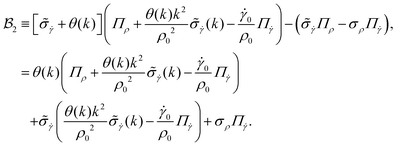 | (36) |
Under the condition (28), the denominator on the r.h.s. in
eqn (35) is positive for all
k, allowing one to conclude that the system is linearly stable for
| |  | (37) |
As expected, the condition

coincides with
eqn (34). Note furthermore that

for
k → ∞ and, generally,

. A numerical analysis reveals that the condition

and thus

is fulfilled for all physically relevant
ρ0 and
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0 of the present model.
The main result of the above analysis is that the cubic equation eqn (24) admits instability only through a single monotonically growing mode, the two other modes being decaying functions of time, either in a monotonic (case 1) or an oscillatory (case 2) fashion.
C. Stability diagram and discussion
As shown above, within the present linear stability analysis of the hydrodynamic equations for a compressible single component yield-stress fluid, the instability occurs uniquely via a monotonic (and thus non-oscillatory) mode, which grows exponentially with a rate given by eqn (29). In fact, an extensive numerical evaluation of the solutions of the dispersion relation in eqn (24) indicates that, over the whole relevant parameter space, all unstable modes have a non-oscillatory character. Owing to eqn (28) and the fact that  in the limit k → ∞, the growth rate in eqn (29) becomes negative for sufficiently large k, as is necessary for a physically reasonable model. In particular, asymptotically for k → ∞ one obtains
in the limit k → ∞, the growth rate in eqn (29) becomes negative for sufficiently large k, as is necessary for a physically reasonable model. In particular, asymptotically for k → ∞ one obtains| |  | (38) |
Note, however, that the continuum model in eqn (3) is not expected to be valid at arbitrarily small scales. We remark that, in the absence of the shear- and bulk-curvature viscosities κ and κ′, one has  . On the other hand, neglecting all contributions related to bulk viscosity, yields
. On the other hand, neglecting all contributions related to bulk viscosity, yields  . From these results one infers that the stability of the system for large k is indeed due to the shear–curvature viscosity.
. From these results one infers that the stability of the system for large k is indeed due to the shear–curvature viscosity.
Since ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is a growing function of k, the boundary of stability of the whole phase diagram of a bulk system is determined by eqn (30) for k = 0. Specifically, if
is a growing function of k, the boundary of stability of the whole phase diagram of a bulk system is determined by eqn (30) for k = 0. Specifically, if  , the system is unstable for all wavenumbers, satisfying
, the system is unstable for all wavenumbers, satisfying  (cf.eqn (29)). In other words, all wavenumbers 0 < k < kc are unstable, where the critical wavenumber kc is defined via
(cf.eqn (29)). In other words, all wavenumbers 0 < k < kc are unstable, where the critical wavenumber kc is defined via
| | 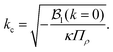 | (39) |
Remarkably, this expression as well as the condition for stability threshold,

, are identical to the corresponding expressions obtained in
ref. 16 for the advection–diffusion model described by
eqn (1) and (2).
29 However, as can be inferred from
eqn (29), owing to the presence of bulk viscosity, the fastest growing mode behaves differently as a function of
k for the compressible fluid. Such a finite bulk viscosity is to be expected, since colloidal suspensions exhibit a certain degree of local compressibility even in the highly concentrated regime.
Fig. 2 shows the stability diagram obtained for
k = 0. For illustrative purposes, it is more convenient to consider instead of

[
eqn (26)] the (dimensionless) stability parameter
| |  | (40) |
according to which the system is unstable for values

. As seen in
Fig. 2, the instability occurs only in the glassy phase (
ρ >
ρg).
 |
| | Fig. 2 Stability diagram for a liquid (a) below (ρ < ρg) and (b) above (ρ > ρg) the glass transition. The glass transition occurs at a density of ρg/ρm ≃ 0.873, where ρm = 0.67 denotes the density of random close packing (in dimensionless units, see Section II). The SDC instability occurs for values of the parameter  [eqn (40)] or, equivalently, for [eqn (40)] or, equivalently, for  [eqn (30)]. The boundary of stability is indicated by the solid curve in (b), corresponding to [eqn (30)]. The boundary of stability is indicated by the solid curve in (b), corresponding to  . For comparison, the dashed curve in (b) represents the boundary of stability computed with σyieldyy = 0 in Πρ [eqn (11a)]. . For comparison, the dashed curve in (b) represents the boundary of stability computed with σyieldyy = 0 in Πρ [eqn (11a)]. | |
The wavenumber km and the growth rate ωm of the fastest growing mode has to be determined numerically from eqn (24) in the general case. Fig. 3 shows km and ωm as functions of the background density ρ0 and shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. When expressed in terms of the fundamental time and length scales t0 and a (which are unity for our choice of units), ωm and km reach a maximum for intermediate shear rates and generally grow upon increasing the density. When taking instead the inverse shear rate as the fundamental time scale, ωm/
0. When expressed in terms of the fundamental time and length scales t0 and a (which are unity for our choice of units), ωm and km reach a maximum for intermediate shear rates and generally grow upon increasing the density. When taking instead the inverse shear rate as the fundamental time scale, ωm/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 grows with increasing distance from the boundary of stability [see main plot of Fig. 3(c)]. At intermediate shear rates, an effective algebraic behavior ωm/
0 grows with increasing distance from the boundary of stability [see main plot of Fig. 3(c)]. At intermediate shear rates, an effective algebraic behavior ωm/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ∼
0 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0−0.5 can be inferred from the numerics. As illustrated in Fig. 3(c) and (d), changing the value of the shear–curvature parameter κ0 [eqn (7)] has only a moderate effect on km and ωm.
0−0.5 can be inferred from the numerics. As illustrated in Fig. 3(c) and (d), changing the value of the shear–curvature parameter κ0 [eqn (7)] has only a moderate effect on km and ωm.
 |
| | Fig. 3 (a and b) Maximum growth rate ωm (a) and associated wavenumber km (b) of the unstable modes. In the white region, the system is stable (ω < 0). A value of κ0 = 100 is used for the calculation. (c and d) Growth rate ωm (c) and wavenumber km (d) of the maximally unstable mode as a function of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for ρ0/ρm = 0.93, κ0 = 100 (solid curve), ρ0/ρm = 0.91, κ0 = 100 (dashed curve), and ρ0/ρm = 0.93, κ0 = 1000 (dot-dashed curve). The dotted line in (c) represents a power-law ∝ for ρ0/ρm = 0.93, κ0 = 100 (solid curve), ρ0/ρm = 0.91, κ0 = 100 (dashed curve), and ρ0/ρm = 0.93, κ0 = 1000 (dot-dashed curve). The dotted line in (c) represents a power-law ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −0.5. The main plot and the inset in (c) shows ωm expressed in terms of the inverse shear rate 1/ −0.5. The main plot and the inset in (c) shows ωm expressed in terms of the inverse shear rate 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 and the microscopic time scale t0, respectively (see Section II). 0 and the microscopic time scale t0, respectively (see Section II). | |
Close to the stability boundary, 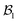 [eqn (26)] and therefore kc are small, such that a Taylor expansion of the growth rate in eqn (29) to
[eqn (26)] and therefore kc are small, such that a Taylor expansion of the growth rate in eqn (29) to  is sufficient to determine km. (The leading term of the expansion of ω is of
is sufficient to determine km. (The leading term of the expansion of ω is of  .) Within this approximation, the wavenumber of the fastest growing mode follows by evaluating the condition dω/dk = 0 as
.) Within this approximation, the wavenumber of the fastest growing mode follows by evaluating the condition dω/dk = 0 as
| |  | (41) |
with

. In the last expression, the fact that

close to the stability boundary has been used. Notably, due to bulk viscous effects,
eqn (41) is generally different from the corresponding result obtained in
ref. 16. In
Fig. 4, the typical behavior of the growth rate
ω as a function of the wavenumber
k is illustrated. We have chosen here values of the parameters
ρ0 and
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0 near the stability boundary, where
eqn (41) provides an accurate approximation to the actual maximum wavenumber. While
ω ∝
k2 for small
k [
eqn (29)],
ω eventually becomes negative for sufficiently large
k [see
eqn (38)], as required for reasons of stability.
 |
| | Fig. 4 Typical behavior of the growth rate ω [eqn (24)] as a function of the wavenumber k in the unstable region of the parameter space. For wavenumbers k with 0 < k < kc, the system is unstable. The dotted line indicates the location of the critical wavenumber kc [eqn (39)]. Near the boundary of stability, the wavenumber km of the fastest growth mode is estimated by eqn (41) (dash-dotted line). Near the boundary of stability and for small k, the growth rate ω is well approximated by eqn (29), implying ω ∝ k2. The values ρ0 = 0.91ρm, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 3.5 × 10−4, and κ0 = 100 are used for the calculation. 0 ≃ 3.5 × 10−4, and κ0 = 100 are used for the calculation. | |
Fig. 5 illustrates the direction of growth and the magnitude of the most unstable mode (having wavenumber km). In order to obtain the amplitude vector v(ρ0,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0), the nullspace solution
0), the nullspace solution  of eqn (21) is determined and normalized, v0/||v0||, and then projected onto the space spanned by ρ0 and
of eqn (21) is determined and normalized, v0/||v0||, and then projected onto the space spanned by ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, additionally normalizing the components by ρ0 and
0, additionally normalizing the components by ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, respectively. As illustrated in Fig. 5, in general,
0, respectively. As illustrated in Fig. 5, in general, ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) and
and  have opposite signs in the unstable region, as expected for the SDC instability. A similar anti-correlation has been reported in molecular dynamics studies of heterogeneous flow in a hard sphere glass.6 Note that, with v, also −v is a valid solution of eqn (21); in the plot, we have chosen the positive sign of
have opposite signs in the unstable region, as expected for the SDC instability. A similar anti-correlation has been reported in molecular dynamics studies of heterogeneous flow in a hard sphere glass.6 Note that, with v, also −v is a valid solution of eqn (21); in the plot, we have chosen the positive sign of ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . One notes that the development of the instability is dominated by a strong relative change of the shear rate, while the growth of the density is rather weak. This feature of the linear regime will also prevail in the nonlinear case discussed below. Comparing with Fig. 3(a) and (b), one infers that the growth amplitude ||v|| is largest in those regions of the phase diagram where the growth rate ωm and the wavenumber km are relatively small.
. One notes that the development of the instability is dominated by a strong relative change of the shear rate, while the growth of the density is rather weak. This feature of the linear regime will also prevail in the nonlinear case discussed below. Comparing with Fig. 3(a) and (b), one infers that the growth amplitude ||v|| is largest in those regions of the phase diagram where the growth rate ωm and the wavenumber km are relatively small.
 |
| | Fig. 5 Growth direction and magnitude of the fluctuation amplitude  (up to a normalization factor, see text) of the most unstable mode km, as determined by the nullspace solution of eqn (19). The coloring indicates the magnitude of v in a logarithmic scale, while the arrows indicate the growth direction (non-logarithmic scale along both axes), which is determined up to a sign. Accordingly, in the unstable region, fluctuations grow indefinitely by reducing the shear rate and increasing the density (or vice versa), providing a nonlinear feedback mechanism for the SDC-instability. (up to a normalization factor, see text) of the most unstable mode km, as determined by the nullspace solution of eqn (19). The coloring indicates the magnitude of v in a logarithmic scale, while the arrows indicate the growth direction (non-logarithmic scale along both axes), which is determined up to a sign. Accordingly, in the unstable region, fluctuations grow indefinitely by reducing the shear rate and increasing the density (or vice versa), providing a nonlinear feedback mechanism for the SDC-instability. | |
IV. Nonlinear dynamics and steady states
A. Dynamics
The one-dimensional Navier–Stokes equations for a compressible fluid given in eqn (5) are numerically solved in a slit geometry (see Fig. 1) in the following way: the flux j = ρu is introduced and the partial differential equations are converted to ordinary ones by spatial discretization on a grid of L/Δh nodes.30,31 Specifically, we use second-order accurate central differences for the approximation of the spatial derivatives. The grid spacing is taken as Δh = a, which is thus unity in our choice of units. A vanishing normal flux jy is assumed at the boundaries. The lateral flux jx at the boundaries is determined by imposing, at both walls, either a constant wall velocity uw, a constant wall shear rate γw, or a constant wall stress σw. Values of jx exterior to the computational domain (“ghost nodes”) are calculated via linear interpolation from the adjacent bulk nodes.32 Exterior values of ρ are determined by assuming a vanishing gradient of ρ at the boundary. We have checked that the total density,  , remains practically constant during the time evolution.
, remains practically constant during the time evolution.
As initial configuration we use a density and shear rate profile with a weak sinusoidal modulation (barely visible in the plots) in order to trigger the SDC instability. In the case of fixed wall stress, we initialize the shear rate with the constant value ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 calculated from eqn (43) below. The dynamical evolution is, however, not significantly altered if instead a different value for the initial shear rate is used, except for a short transient at early times. After this transient, the evolution of the shear rate is found to be essentially enslaved to the density dynamics. In all cases, the wavelength of the maximally unstable mode predicted by the dispersion relation [eqn (24), see also Fig. 3(d)] is somewhat larger than the system size. Accordingly, the instability is realized here with the largest wavelength that fits in the system (cf.Fig. 4), provided that π/kc ≲ L, i.e., the system size exceeds half of the critical wavelength [eqn (39)]. This condition constrains, inter alia, also the value of the curvature parameter κ0 [eqn (7)], which sets the width of the shear band interface. Simulations with π/km ≪ L are typically found to be unstable at late times since the nonlinear feedback mechanism leads to a singularity in the integration of the Navier–Stokes equations (see the discussion below eqn (44)). This singularity manifests itself in a diverging viscosity and vanishing shear rate. For sufficiently large interface widths, global mass conservation stabilizes the stationary state before the singularity is reached.
0 calculated from eqn (43) below. The dynamical evolution is, however, not significantly altered if instead a different value for the initial shear rate is used, except for a short transient at early times. After this transient, the evolution of the shear rate is found to be essentially enslaved to the density dynamics. In all cases, the wavelength of the maximally unstable mode predicted by the dispersion relation [eqn (24), see also Fig. 3(d)] is somewhat larger than the system size. Accordingly, the instability is realized here with the largest wavelength that fits in the system (cf.Fig. 4), provided that π/kc ≲ L, i.e., the system size exceeds half of the critical wavelength [eqn (39)]. This condition constrains, inter alia, also the value of the curvature parameter κ0 [eqn (7)], which sets the width of the shear band interface. Simulations with π/km ≪ L are typically found to be unstable at late times since the nonlinear feedback mechanism leads to a singularity in the integration of the Navier–Stokes equations (see the discussion below eqn (44)). This singularity manifests itself in a diverging viscosity and vanishing shear rate. For sufficiently large interface widths, global mass conservation stabilizes the stationary state before the singularity is reached.
Fig. 6–8 illustrate the time evolution of the density ρ, flow velocity ux, and local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = ∂yux across the slit in the unstable region for various boundary conditions. One observes that, in all cases, the system evolves from an essentially homogeneous initial state towards a steady state with inhomogeneous density and shear-rate profiles. The steady state of ux (or, correspondingly, the shear rate) is typically reached within a time scale 1/
= ∂yux across the slit in the unstable region for various boundary conditions. One observes that, in all cases, the system evolves from an essentially homogeneous initial state towards a steady state with inhomogeneous density and shear-rate profiles. The steady state of ux (or, correspondingly, the shear rate) is typically reached within a time scale 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 determined by the average shear rate
0 determined by the average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. The latter is given by (ux(L) − ux(0))/L =
0. The latter is given by (ux(L) − ux(0))/L = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av in the case where a fixed wall velocity is imposed and by
av in the case where a fixed wall velocity is imposed and by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w in the case where a fixed wall shear rate is used.
w in the case where a fixed wall shear rate is used.
 |
| | Fig. 6 Time evolution of (a) the density, (b) the velocity, and (c) the shear rate resulting from eqn (5) for a fixed wall velocity uw = ux(L) − ux(0) corresponding to an average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 2 × 10−4. The profiles shown are obtained at times t av = 2 × 10−4. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 0, 0.20, 0.28, ∞, where t = ∞ corresponds to the steady state reached for t av = 0, 0.20, 0.28, ∞, where t = ∞ corresponds to the steady state reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 103 (thick black curve). In the steady state, the local shear rate at the left and the right boundary are found to be γ ≃ 1.7 × 10−8 and 3.7 × 10−4, respectively. The initial growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100 and ρ0 = 0.91ρm are used. av ≳ 103 (thick black curve). In the steady state, the local shear rate at the left and the right boundary are found to be γ ≃ 1.7 × 10−8 and 3.7 × 10−4, respectively. The initial growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100 and ρ0 = 0.91ρm are used. | |
 |
| | Fig. 7 Time evolution of (a) the density, (b) the velocity, and (c) the shear rate resulting from eqn (5) for a fixed shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 10−4 at both walls. The profiles shown are obtained at times t w = 10−4 at both walls. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 0, 2.2 × 10−2, 4.0 × 10−2, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t w = 0, 2.2 × 10−2, 4.0 × 10−2, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≳ 0.4. In the steady-state, the local shear rate at each of the walls results as w ≳ 0.4. In the steady-state, the local shear rate at each of the walls results as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 1.0 × 10−4. The initial growth rate of the maximally unstable mode is given by ωm ≃ 0.078 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, and ρ0 = 0.93ρm are used. ≃ 1.0 × 10−4. The initial growth rate of the maximally unstable mode is given by ωm ≃ 0.078 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, and ρ0 = 0.93ρm are used. | |
 |
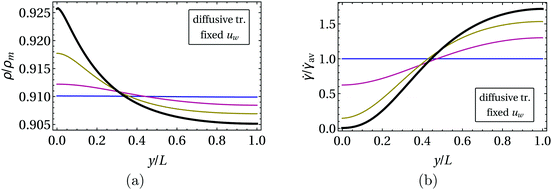
| | Fig. 8 Time evolution of (a) the density, (b) the velocity, and (c) the shear rate resulting from eqn (5) for a fixed wall stress σw. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 0.07, 0.42, 0.48, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t 0 = 0.07, 0.42, 0.48, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≳ 10. An effective shear rate 0 ≳ 10. An effective shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 10−3 is obtained from eqn (43) based in the initial density ρ0. In the steady state, the local shear rate at the boundary at y = 0 is obtained as 0 ≃ 10−3 is obtained from eqn (43) based in the initial density ρ0. In the steady state, the local shear rate at the boundary at y = 0 is obtained as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 3.3 × 10−5. The initial growth rate (corresponding to the above ≃ 3.3 × 10−5. The initial growth rate (corresponding to the above ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0) of the maximally unstable mode is given by ωm ≃ 0.012 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, ρ0 = 0.93ρm, and σw = 11 are used. 0) of the maximally unstable mode is given by ωm ≃ 0.012 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, ρ0 = 0.93ρm, and σw = 11 are used. | |
At late times, the evolution slows down due to the slow transport of mass towards the boundaries. This effect is particularly pronounced in the case of a fixed wall velocity (Fig. 6), where the shear rate profile is essentially fully developed at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 1, while the density at the left wall reaches the steady state only for times
av ≳ 1, while the density at the left wall reaches the steady state only for times  . One observes that the time evolution is fastest if a fixed wall-shear rate is imposed. The broken left-right symmetry with respect to the walls in Fig. 6 and 8 is a direct consequence of the asymmetry of the initial configuration. In fact, using an initial sinusoidal density profile with a maximum in the right half of the system leads to spatially mirrored evolution.
. One observes that the time evolution is fastest if a fixed wall-shear rate is imposed. The broken left-right symmetry with respect to the walls in Fig. 6 and 8 is a direct consequence of the asymmetry of the initial configuration. In fact, using an initial sinusoidal density profile with a maximum in the right half of the system leads to spatially mirrored evolution.
The density dynamics is generally overdamped, which is expected based on an analysis of the linear equations in eqn (16): for typical values ρ0, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 of the density and shear rate in the unstable regime and for wavenumbers
0 of the density and shear rate in the unstable regime and for wavenumbers  (in units of a), one finds for the present constitutive model [eqn (14)] that the viscous term η∂y2 dominates over the restoring force Πρ∂y2 in the sound-wave equation [eqn (18)].
(in units of a), one finds for the present constitutive model [eqn (14)] that the viscous term η∂y2 dominates over the restoring force Πρ∂y2 in the sound-wave equation [eqn (18)].
An interesting question here regards the existence of multiple shear bands. In order to obtain such a structure, we decrease the shear–curvature viscosity κ, whereby, as stated above [eqn (7)], the width of the interface between regions of low and high shear rates is reduced. As shown in Fig. 9, where we used a value of κ0 = 2 (in dimensionless units), multiple shear bands are indeed observed in our model. The figure also highlights the important role of the initial perturbations for the formation of a multi-banded structure, since the number of nodes of the band directly depends on the period of the initial sinusoidal profile. The shear-curvature viscosity κ, in contrast, plays a subordinate role for detailed band structure. We emphasize that the profiles in Fig. 9 are not in the steady state but correspond to times  . In fact, the presently used constitutive model does not allow us to reach the steady state in these cases due to the occurrence of an intrinsic singularity [see eqn (44) below].
. In fact, the presently used constitutive model does not allow us to reach the steady state in these cases due to the occurrence of an intrinsic singularity [see eqn (44) below].
 |
| | Fig. 9 Multiple shear bands occur for sufficiently small values of the shear–curvature viscosity κ0, which determines the effective interface width [see eqn (7)]. Panel (a) shows the density profile and panel (b) the shear rate profile at times  in the case of a fixed wall-velocity corresponding to an average shear rate in the case of a fixed wall-velocity corresponding to an average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≃ 2 × 10−4. The initial density profile is given by ρ(y,0) ∝ cos(nπy/L), with n = 4, 2, 1 for the solid, dashed, and dotted curve, respectively. A value κ0 = 2 is used, while all other parameters are the same as in Fig. 6. We emphasize here that, regardless of the initial structure, multiple bands are not observed for larger values of κ, such as those used in Fig. 6 and 8. av ≃ 2 × 10−4. The initial density profile is given by ρ(y,0) ∝ cos(nπy/L), with n = 4, 2, 1 for the solid, dashed, and dotted curve, respectively. A value κ0 = 2 is used, while all other parameters are the same as in Fig. 6. We emphasize here that, regardless of the initial structure, multiple bands are not observed for larger values of κ, such as those used in Fig. 6 and 8. | |
B. Steady states
In the steady state, the wall normal velocity must vanish, i.e., uy = 0. It thus follows from eqn (5) and (8) that the density ρ and the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in the steady state are determined by the equations
in the steady state are determined by the equations| | 0 = ∂y[σyield(ρ) − Π(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )], )], | (42a) |
| | 0 = ∂yσxy(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = ∂y[σyield(ρ) + η(ρ, ) = ∂y[σyield(ρ) + η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) )![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ(ρ, − κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )∂y2 )∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ]. ]. | (42b) |
Upon discretizing this boundary value problem using finite differences, the resulting system of nonlinear equations can be solved via Newton's method. In order for this scheme to converge, good initial guesses for ρ(y) and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y) are required, which can be obtained from the dynamical eqn (5), as discussed above. Alternatively, the steady state profiles may also be directly obtained by integrating the PDEs in eqn (5) over a sufficiently large time, as is done in Fig. 6–8.
(y) are required, which can be obtained from the dynamical eqn (5), as discussed above. Alternatively, the steady state profiles may also be directly obtained by integrating the PDEs in eqn (5) over a sufficiently large time, as is done in Fig. 6–8.
According to eqn (42), in the steady state, the effective pressure Π − σyield as well as the viscous stress σxy must be constant throughout the system. The resulting profiles realizing these constraints are illustrated in Fig. 6–8 (thick black curves). For a fixed wall velocity uw or a fixed wall stress σw, we obtain here spatially asymmetric steady state profiles for which the maximum density and minimum shear rate is attained close to the walls. These profiles are qualitatively similar to the ones observed in ref. 16, where a fixed wall stress was considered (see also Appendix B). The spatial symmetry of the steady profile in Fig. 7 is a consequence of the fact that the same shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w is imposed at both walls. Profile shapes similar to the ones in Fig. 6 and 8 result when the values of
w is imposed at both walls. Profile shapes similar to the ones in Fig. 6 and 8 result when the values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w at each wall are set accordingly (data not shown).
w at each wall are set accordingly (data not shown).
In the unstable region of the phase diagram, a necessary condition (which, however, is not sufficient; see below) for the development of an inhomogeneous steady state profile is the presence an initial perturbation in the system and a system size large enough such that at least one unstable mode can be accommodated. However, eqn (42) also admits constant solutions, i.e., ρ = ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. In this case, eqn (42b) with ∂y
0. In this case, eqn (42b) with ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 readily yields a relation between ρ0,
= 0 readily yields a relation between ρ0, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, and the stress in the system σw (which arises as an integration constant and typically corresponds to the wall stress):
0, and the stress in the system σw (which arises as an integration constant and typically corresponds to the wall stress):
| |  | (43) |
where
Φ =
ρ0/
ρm and we used
eqn (14). Alternatively,
eqn (42a) provides a relation between
ρ0,
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0, and the system (wall) pressure. If, instead of
σw, the wall shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w
w =
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0 or the wall velocity
uw (implying
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0
0 =
uw/
L) are prescribed,
eqn (43) represents a family of solutions for
ρ0 with the integration constant
σw as adjustable parameter.
Eqn (43) is illustrated in Fig. 10. A solution of eqn (43) exists provided that the numerator on the r.h.s. is positive, i.e., for
or, equivalently, if the yield stress remains below the system stress,
For
σyield >
σw, instead, the system becomes increasingly more rigid and thus ceases to flow. This singular behavior is indeed reflected in the solution of the fluid dynamical equations [
eqn (5)] in the SDC-unstable region. In order to gain a heuristic understanding of this singularity, let us assume that, close to the inhomogeneous steady state, the density and shear rate profiles in the fluid consists of large nearly flat portions. In each of these regions then
eqn (43) and thus
eqn (44) approximately hold, with
σw being the corresponding local stress. In order to trigger the SDC instability, here typical values of

are required,
33 for which
eqn (44) implies

as an upper limit for the density (see
Fig. 10). As indicated in
Fig. 5, once the system is unstable, some part of it evolves towards smaller shear rates and larger densities. In small systems, this growth is eventually limited by global mass conservation and the fact that the interface between low and high density regions must keep a certain width [see discussion after eqn (7)]. In contrast, for systems much larger than the interface width, the limit for
Φ implied by
eqn (44) can be easily exceeded by means of mass transport, leading to
σyield >
σw and thus causing the solution of
eqn (5) to become singular. The singularity, in particular, makes an observation of stationary inhomogeneous profiles with multiple shear bands rather difficult. Nevertheless, as shown in
Fig. 9, we do observe a multi-band structure up to the instant of the numerical singularity. Based on these findings and the above detailed analysis, we anticipate that a slightly modified version of the present constitutive model with a tamed singularity would exhibit stable multiple shear bands.
 |
| | Fig. 10 Relation between shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 and density ρ0 in a homogeneous system, as provided by eqn (43), for various values of the system stress σw (increasing in the direction of the arrow from σw = 8 to 12 in steps of 1). Eqn (43) is well-defined only if condition (44) holds, i.e., for sufficiently small densities. The maximum possible density corresponds in the plot to the (σw-dependent) location where 0 and density ρ0 in a homogeneous system, as provided by eqn (43), for various values of the system stress σw (increasing in the direction of the arrow from σw = 8 to 12 in steps of 1). Eqn (43) is well-defined only if condition (44) holds, i.e., for sufficiently small densities. The maximum possible density corresponds in the plot to the (σw-dependent) location where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 → 0. The dashed black curve represents the threshold of the SDC instability, 0 → 0. The dashed black curve represents the threshold of the SDC instability,  [see eqn (26) as well as Fig. 2]. [see eqn (26) as well as Fig. 2]. | |
Physically, the singularity can be understood as “freezing”—a behavior which is a hallmark of yield stress fluids upon increasing the density or decreasing the shear rate. Accordingly, a possibility to avoid this singularity would be to limit the growth of the yield stress and the viscosities in the constitutive eqn (14) and (25). An adequate study of this issue is an interesting topic for future work.
V. Summary
This study addresses the issue of flow heterogeneity, often observed in the glassy state of matter under externally imposed shear. We focus on the limit of gently sheared dense single-component fluids, such as colloidal hard sphere glasses, where hydrodynamic interactions are negligible. Therefore, the effect of solvent is ignored in this study. Instead of a coupling to the concentration field as in the original theory of shear–concentration coupling,13 in the present case, fluctuations of the velocity field are coupled to fluctuations of the fluid density. Analogously to a standard density-dependent thermodynamic pressure, here, a shear-rate dependent pressure drives a transverse flow away from regions of high shear rate, thus further lowering the viscosity in that region. Together with a strongly non-Newtonian viscous stress, this gives rise to a feed-back mechanism which ultimately determines the borders of flow stability. A detailed analysis of the resulting cubic dispersion relation reveals that the instability can occur only via a monotonic growth of fluctuations, thus excluding the possibility of an oscillatory growth mode. Notably, after an initial transient, the velocity and density fields reach a stationary profile. In this stationary state, regions of high shear rate exhibit low density and vise versa. For systems much larger than the characteristic width of the shear-band interface, the fluid model considered here generally develops a singularity in the unstable regime, accompanied by a vanishing shear rate and thus a divergent viscosity. The steady states obtained here in fact all occur for system sizes comparable to the interface width, in which case they are stabilized by means of global mass conservation.
Interestingly, the expression for the stability threshold and the range of unstable wavenumbers are identical to those obtained from an analysis of the advection–diffusion equation based on the original theory of shear–concentration coupling.16 The difference between the present compressible single-component fluid model and the one incorporating the coupling of flow to a concentration field is exhibited in the specific dynamics and underlying timescales, such as the expression for the fastest growing mode. In the compressible fluid, the density relaxes via overdamped sound waves—a transport mechanism which, in contrast to diffusion, leads to wavenumber-independent exponential relaxation in the limit of small frequencies and large wavenumbers. The use of a compressible fluid model is supported by molecular dynamics simulations,6 which show that variations of the density are a typically observed response to fluctuations of the shear rate in single-component hard-sphere colloidal glasses.
The existence of a stationary solution seems, at first sight, to be in conflict with the time dependent behavior of the shear band observed in molecular dynamics simulations.6 A plausible interpretation here would be to invoke the coupling between velocity fluctuations and structural heterogeneity in the glassy state. As also discussed in ref. 5, this may lead to the formation of a locally depleted zone with a density in the stable regime and a denser packing in the remaining part of the system with enhanced instability and a corresponding temporal evolution. This is also in-line with recent reports on the strong influence of structural heterogeneity on plastic deformation in the amorphous solid state.34–36 Notably, the time scale of the shear band dynamics in MD simulations is of the order of the inverse shear rate.6 This is also the time associated with structural fluctuations, since during this time a particle moves a distance comparable to its size and the cage of nearest neighbors around it relaxes to a large extent. This stochastic effect is not included in the present deterministic model. A way to account for this would be to add a noise term into hydrodynamic equations, which is left for future work.
Conflicts of interest
There are no conflicts to declare.
Appendix A: transport mechanism
Here, we provide further insights into the transport mechanism of the compressible fluid model, as compared to the diffusive transport model studied in the original SCC theory.13,16 In order to focus on the essential aspects, we consider linearized dynamics. In both models, shear rate fluctuations are governed by eqn (17), i.e., a diffusion equation with a coupling to density fluctuations. (The last term in eqn (17) is typically small in our case and absent in the model of ref. 16.) However, instead of following a diffusion equation as in ref. 13 and 16, density fluctuations δρ in the compressible fluid are governed by the generalized sound-wave eqn (18). In the glassy state, the viscosities are large and the dynamics is thus strongly overdamped, such that the term ∂t2δρ can be neglected in eqn (18), resulting in| |  | (A1) |
Noting that the kinetic coefficients are constants here and focusing on large wavelengths, where the term involving κ can be disregarded, eqn (A1) reduces, after two integrations over y, to| | ∂tδρ = −Aδρ − Bδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + c + dy, + c + dy, | (A2) |
with A ≡ ρ0Πρ/bη, B ≡ ρ0Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /bη, and integration constants c and d. In order to have δρ ≃ 0 at the boundaries of the domain, we set d = 0, such that the solution of eqn (A2) with initial condition ρ(y,0) = ρin(y) is obtained as
/bη, and integration constants c and d. In order to have δρ ≃ 0 at the boundaries of the domain, we set d = 0, such that the solution of eqn (A2) with initial condition ρ(y,0) = ρin(y) is obtained as| |  | (A3) |
Due to the neglect of the term ∂t2δρ, eqn (A2) does not conserve mass. The effect of global mass conservation can be mimicked in eqn (A3) by setting  , which follows from requiring
, which follows from requiring  . Eqn (A3) shows that, in the overdamped limit and for large wavelengths and small frequencies, density fluctuations essentially relax exponentially in the compressible fluid (cf.ref. 24). However, in contrast to diffusive relaxation, which is also exponential at late times, the relaxation rate is here independent of the wavenumber. Furthermore, according to eqn (A3), a positive shear rate fluctuation gives rise to a reduction of the local density. This behavior is an essential mechanism of the SDC instability.
. Eqn (A3) shows that, in the overdamped limit and for large wavelengths and small frequencies, density fluctuations essentially relax exponentially in the compressible fluid (cf.ref. 24). However, in contrast to diffusive relaxation, which is also exponential at late times, the relaxation rate is here independent of the wavenumber. Furthermore, according to eqn (A3), a positive shear rate fluctuation gives rise to a reduction of the local density. This behavior is an essential mechanism of the SDC instability.
Appendix B: diffusive transport model
Here, we compare our results obtained in Section IV to the SCC model studied in ref. 16, which is based on the advection–diffusion equation for the concentration given in eqn (1). The flow velocity u is assumed to relax much faster than the density, such that the shear-rate is essentially enslaved to the density evolution. Furthermore, also advective transport is neglected, such that the SCC model as considered in ref. 16 effective reduces to a purely diffusive transport model:| | ∂tρ = ∂y2Π(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), ), | (B1a) |
| | 0 = ∂yσxy(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), ), | (B1b) |
where σxy is given by eqn (8). In writing eqn (B1a), we used the fact that, for the constitutive model in eqn (15), the effective diffusivity Deff and the shear-gradient coefficient ξ defined in ref. 16 derive from the pressure Π(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) via Deff ≡ ∂ρΠ and ξ ≡ ∂
) via Deff ≡ ∂ρΠ and ξ ≡ ∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Π, such that ∂y2Π = ∂y[Deff∂yρ + ξ∂y
Π, such that ∂y2Π = ∂y[Deff∂yρ + ξ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ].
].
Instead of the Couette geometry considered in ref. 16, we study here the time evolution of eqn (B1) for a planar shear flow (see Fig. 1). As in the main text, we impose either a fixed wall velocity uw, a fixed wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w, or a fixed wall stress σw at the boundaries. For the first two cases, instead of eqn (B1b), we solve the full time-dependent equation eqn (5b) for the velocity ux,
w, or a fixed wall stress σw at the boundaries. For the first two cases, instead of eqn (B1b), we solve the full time-dependent equation eqn (5b) for the velocity ux,
| | ∂t(ρux) = ∂yσxy(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), ), | (B2) |
with
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
= ∂
yux. We generally impose a vanishing pressure gradient ∂
yΠ = 0 at the boundaries, which ensures global mass conservation for the dynamics described by
eqn (B1a).
Fig. 11–13 illustrate the time evolution of the density and the shear rate in an unstable system for various boundary conditions. In all cases, the density profile is initialized with a sinusoidal modulation in order to trigger the initial instability. In general, the steady state is reached significantly faster for diffusive dynamics than for the compressible fluid model described by eqn (5). Both for fixed uw and σw, the steady state is typically reached for strains  , respectively, while, for fixed
, respectively, while, for fixed ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w, instead, the growth rate of the maximally unstable mode ωm provides a better estimate of the dynamical time scale than the strain. (The value of the time scale inferred from simulation depends somewhat on the chosen initial configuration.) The larger steady-state time scale in the compressible fluid model is predominantly caused by the slow transport of mass towards the wall at the late stages of the evolution. In fact, apart from this difference, the spatio-temporal evolution in both the compressible and the diffusive transport model are qualitatively similar (cf.Fig. 6–8).
w, instead, the growth rate of the maximally unstable mode ωm provides a better estimate of the dynamical time scale than the strain. (The value of the time scale inferred from simulation depends somewhat on the chosen initial configuration.) The larger steady-state time scale in the compressible fluid model is predominantly caused by the slow transport of mass towards the wall at the late stages of the evolution. In fact, apart from this difference, the spatio-temporal evolution in both the compressible and the diffusive transport model are qualitatively similar (cf.Fig. 6–8).
 |
| | Fig. 11 Diffusive transport model [eqn (B1a) and (B2)]: time evolution of (a) the density and (b) the shear rate for a fixed wall velocity uw = ux(L) − ux(0) corresponding to an average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = uw/L = 2 × 10−4. The profiles shown are obtained at times t av = uw/L = 2 × 10−4. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 0, 0.38, 0.4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t av = 0, 0.38, 0.4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 0.8. The shear rate at the wall is obtained as av ≳ 0.8. The shear rate at the wall is obtained as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 1.1 × 10−6. The growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3. Parameters L = 200Δh, κ0 = 100, and ρav = 0.91ρm are used. ≃ 1.1 × 10−6. The growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3. Parameters L = 200Δh, κ0 = 100, and ρav = 0.91ρm are used. | |
 |
| | Fig. 12 Diffusive transport model [eqn (B1a) and (B2)]: time evolution of (a) the density and (b) the shear rate resulting from eqn (B1) for a fixed shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 10−4 at both walls. The profiles shown are obtained at times t w = 10−4 at both walls. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 0, 3.5 × 10−4, 5.9 × 10−4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t w = 0, 3.5 × 10−4, 5.9 × 10−4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≳ 10−2. The growth rate of the maximally unstable mode is given by ωm ≃ 0.078. Parameters L = 200Δh, κ0 = 100, and ρav = 0.93ρm are used. w ≳ 10−2. The growth rate of the maximally unstable mode is given by ωm ≃ 0.078. Parameters L = 200Δh, κ0 = 100, and ρav = 0.93ρm are used. | |
 |
| | Fig. 13 Diffusive transport model [eqn (B1)]: time evolution of (a) the density and (b) the shear rate resulting from eqn (B1) for a fixed wall stress σw. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 0, 0.06, 0.07, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t 0 = 0, 0.06, 0.07, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≳ 0.1. The effective shear rate 0 ≳ 0.1. The effective shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 8 × 10−4 is identified from eqn (43) using the initial density ρ0. The growth rate of the maximally unstable mode is given by ωm ≃ 0.028. Parameters L = 200Δh, κ0 = 100, ρav = 0.93ρm, and σw = 10.6 are used. 0 ≃ 8 × 10−4 is identified from eqn (43) using the initial density ρ0. The growth rate of the maximally unstable mode is given by ωm ≃ 0.028. Parameters L = 200Δh, κ0 = 100, ρav = 0.93ρm, and σw = 10.6 are used. | |
Since we impose a vanishing pressure gradient at the boundaries when solving eqn (B1a), the steady states resulting from eqn (42) and (B1) are characterized by Π and σxy being constant throughout the system. Thus the only difference between the steady states of two models stems from the presence of the yield stress in eqn (42a). Accordingly, the steady state-profiles obtained from eqn (42) and (B1) are very similar, which is illustrated in Fig. 14 for the case of fixed wall stress boundary conditions. It is therefore not surprising that the time evolution, when starting from the same initial conditions, is similar in the two models.
 |
| | Fig. 14 Comparison of the typical steady states obtained from eqn (42) (solid lines) and eqn (B1) (dashed lines) for a fixed wall stress σw. Parameters σw = 10.8, L = 200Δh, κ0 = 100, and ρav = 0.93ρm are used. | |
Acknowledgements
This work is supported by the German Research Foundation (DFG) under the project number VA 205/18-1. ICAMS acknowledges funding from its industrial sponsors, the state of North-Rhine Westphalia and the European Commission in the framework of the European Regional Development Fund (ERDF).
References
- S. Fielding and P. Olmsted, Flow phase diagrams for concentration-coupled shear banding, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 65 CrossRef PubMed.
- M. Cromer, M. C. Villet, G. H. Fredrickson and L. G. Leal, Shear banding in polymer solutions, Phys. Fluids, 2013, 25, 051703 Search PubMed.
- R. L. Moorcroft and S. M. Fielding, Shear banding in time-dependent flows of polymers and wormlike micelles, J. Rheol., 2014, 58, 103 CrossRef.
- P. C. F. Møller, S. Rodts, M. A. J. Michels and D. Bonn, Shear banding and yield stress in soft glassy materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041507 CrossRef PubMed.
- R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Shear Banding and Flow-Concentration Coupling in Colloidal Glasses, Phys. Rev. Lett., 2010, 105, 268301 CrossRef PubMed.
- S. Mandal, M. Gross, D. Raabe and F. Varnik, Heterogeneous Shear in Hard Sphere Glasses, Phys. Rev. Lett., 2012, 108, 098301 CrossRef PubMed.
- W. Losert, L. Bocquet, T. C. Lubensky and J. P. Gollub, Particle dynamics in sheared granular matter, Phys. Rev. Lett., 2000, 85, 1428 CrossRef PubMed.
- J. K. G. Dhont, K. Kang, H. Kriegs, O. Danko, J. Marakis and D. Vlassopoulos, Nonuniform flow in soft glasses of colloidal rods, Phys. Rev. Fluids, 2017, 2, 043301 CrossRef.
- P. Sollich, Rheological constitutive equation for a model of soft glassy materials, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 738 CrossRef.
- F. Varnik, L. Bocquet, J.-L. Barrat and L. Berthier, Shear localization in a model glass, Phys. Rev. Lett., 2003, 90, 095702 CrossRef PubMed.
- F. Varnik, L. Bocquet and J.-L. Barrat, A study of the static yield stress in a binary Lennard-Jones glass, J. Chem. Phys., 2004, 120, 2788 CrossRef PubMed.
- F. Varnik and D. Raabe, Profile blunting and flow blockage in a yield-stress fluid: a molecular dynamics study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011504 CrossRef PubMed.
- V. Schmitt, C. M. Marques and F. Lequeux, Shear-induced phase separation of complex fluids: the role of flow-concentration coupling, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 4009 CrossRef.
- T. N. Phung, J. F. Brady and G. Bossis, Stokesian Dynamics simulation of Brownian suspensions, J. Fluid Mech., 1996, 313, 181 CrossRef.
- M. Fuchs and M. E. Cates, Schematic models for dynamic yielding of sheared colloidal glasses, Faraday Discuss., 2003, 123, 267 RSC.
- H. Jin, K. Kang, K. H. Ahn and J. K. G. Dhont, Flow instability due to coupling of shear-gradients with concentration: non-uniform flow of (hard-sphere) glasses, Soft Matter, 2014, 10, 9470 RSC.
- Note that μ is, in fact, not a proper chemical potential since the shear rate is a non-conservative external field. In ref. 16 and here, the actual theoretical development does not rely on this notion but instead on a (well-defined) shear-rate dependent pressure.
-
J. K. G. Dhont, An Introduction to Dynamics of Colloids, Elsevier, 1996 Search PubMed.
- M. Rauscher, A. Domínguez, M. Krüger and F. Penna, A dynamic density functional theory for particles in a flowing solvent, J. Chem. Phys., 2007, 127, 244906 CrossRef PubMed.
- A. Scacchi, M. Krüger and J. M. Brader, Driven colloidal fluids: construction of dynamical density functional theories from exactly solvable limits, J. Phys.: Condens. Matter, 2016, 28, 244023 CrossRef PubMed.
-
R. L. Liboff, Kinetic Theory, Springer, 3rd edn, 2003 Search PubMed.
-
L. E. Reichl, A Modern Course in Statistical Physics, Wiley, 2nd edn, 1998 Search PubMed.
- Model H applies to a non-isothermal single-component fluid upon identifying the order-parameter as a certain combination of the fluid and the energy density37,38.
- M. Gross and F. Varnik, Critical dynamics
of an isothermal compressible nonideal fluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061119 CrossRef PubMed.
- J. K. G. Dhont, A constitutive relation describing the shear-banding transition, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4534 CrossRef.
- P. D. Olmsted and C.-Y. D. Lu, Phase coexistence of complex fluids in shear flow, Faraday Discuss., 1999, 112, 183 RSC.
- The stress should remain invariant under coordinate inversion and change its sign whenever the spatial derivatives of the velocity field, i.e., the shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the compression rate ∇·u, change sign.
and the compression rate ∇·u, change sign.
-
I. N. Bronstein, K. A. Semendyayev, G. Musiol and H. Mühlig, Handbook of Mathematics, Springer, Berlin, New York, 5th edn, 2007 Search PubMed.
- The actual shape of the boundary of stability is different in ref. 16 owing to the use of different constitutive equations.
-
P. Moin, Fundamentals of Engineering Numerical Analysis, Cambridge University Press, 2nd edn, 2010 Search PubMed.
-
S. Mazumder, Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods, Academic Press, 1st edn, 2015 Search PubMed.
- The resulting steady state profiles depend sensitively on the boundary conditions. If, in the case of a fixed wall velocity, one, e.g., imposes a constant velocity in the exterior nodes (implying a vanishing wall shear rate), a symmetric steady state shear-rate profile is found, cf.Fig. 6.
- For fixed wall velocity or fixed wall shear rate boundary conditions, the value of σw is found to change only weakly during the time evolution. Accordingly, σw is essentially set by the chosen initial density and shear rate profiles.
- H. Rösner, M. Peterlechner, C. Kübel, V. Schmidt and G. Wilde, Density changes in shear bands of a metallic glass determined by correlative analytical transmission electron microscopy, Ultramicroscopy, 2014, 142, 1 CrossRef PubMed.
- V. Schmidt, H. Rösner, M. Peterlechner, G. Wilde and P. M. Voyles, Quantitative Measurement of Density in a Shear Band of Metallic Glass Monitored Along its Propagation Direction, Phys. Rev. Lett., 2015, 115, 035501 CrossRef PubMed.
- M. Hassani, P. Engels, D. Raabe and F. Varnik, Localized plastic deformation in a model metallic glass: a survey of free volume and local force distributions, J. Stat. Mech.: Theory Exp., 2016, 2016, 084006 CrossRef.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic, Amsterdam, 3rd edn, 2006 Search PubMed.
-
A. Onuki, Phase Transition Dynamics, Cambridge University Press, 2002 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Fathollah
Varnik
ab and
Fathollah
Varnik
 c
c

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t) = ∂yux(y,t).
(y,t) = ∂yux(y,t).![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. (We return to the effect of boundary conditions in Section IV, where we numerically solve the Navier–Stokes equations in a finite domain.) The pressure tensor Π is isotropic, Παβ = Πδαβ, where Π denotes the scalar pressure. Consequently, eqn (3) reduces to
0. (We return to the effect of boundary conditions in Section IV, where we numerically solve the Navier–Stokes equations in a finite domain.) The pressure tensor Π is isotropic, Παβ = Πδαβ, where Π denotes the scalar pressure. Consequently, eqn (3) reduces to
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and is nonzero only in the glassy phase (ρ > ρg). In contrast to the shear viscosity η (see below), detailed data for the bulk viscosity ζ and the curvature viscosities κ and κ′ in a hard-sphere fluid near the glass transition are not available. Following ref. 16, we shall therefore assume these viscosities to have the same functional form as η, i.e.,
and is nonzero only in the glassy phase (ρ > ρg). In contrast to the shear viscosity η (see below), detailed data for the bulk viscosity ζ and the curvature viscosities κ and κ′ in a hard-sphere fluid near the glass transition are not available. Following ref. 16, we shall therefore assume these viscosities to have the same functional form as η, i.e.,
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = b′η(ρ,
) = b′η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )
)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = b′κ(ρ,
) = b′κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ).
). , of the shear band of a few particle diameters a.16 Using eqn (4), the relevant components of the viscous stress tensor follow as
, of the shear band of a few particle diameters a.16 Using eqn (4), the relevant components of the viscous stress tensor follow as![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )
)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ(ρ,
− κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )∂y2
)∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y
∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂yρ − κ∂y3
+ σρ∂yρ − κ∂y3![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − [(∂ρκ)(∂yρ) + (∂
− [(∂ρκ)(∂yρ) + (∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) κ)(∂y
κ)(∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )](∂y2
)](∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ),
),![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y
∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) − Πρ∂yρ + b(η − κ∂y2)∂y2uy,
− Πρ∂yρ + b(η − κ∂y2)∂y2uy,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂Π/∂
≡ ∂Π/∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/∂ρ, σ
)/∂ρ, σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂(η
≡ ∂(η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/∂
)/∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = σyield(ρ)A(1 − Φ)n
) = σyield(ρ)A(1 − Φ)n![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1,
n−1,
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡
≡ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, but are assumed here to apply also locally in the system. We shall henceforth fix the units of mass, length and time by setting kBT = a = η0 = 1. With these choices, the fundamental “microscopic” time scale t0 ≡ η0a3/kBT = 1. Using the fact that η0 is the fluid viscosity in the dilute limit [see eqn (13b)] and invoking the Stokes–Einstein relation, one obtains t0 ∼ a2/D with the self-diffusion coefficient D. In other words, t0 is the time needed for a particle to explore, in the dilute limit, a distance comparable to its own size. Noteworthy, this is also a measure of the structural relaxation time. Accordingly, the microscopic time scale t0 determines, together with thermal energy and particle size, the viscosity and stress scale. In the context of macroscopic fluid dynamics, however, a more natural dimensionless measure of time, which we shall use in the discussion of our results, is instead given by the strain t
0, but are assumed here to apply also locally in the system. We shall henceforth fix the units of mass, length and time by setting kBT = a = η0 = 1. With these choices, the fundamental “microscopic” time scale t0 ≡ η0a3/kBT = 1. Using the fact that η0 is the fluid viscosity in the dilute limit [see eqn (13b)] and invoking the Stokes–Einstein relation, one obtains t0 ∼ a2/D with the self-diffusion coefficient D. In other words, t0 is the time needed for a particle to explore, in the dilute limit, a distance comparable to its own size. Noteworthy, this is also a measure of the structural relaxation time. Accordingly, the microscopic time scale t0 determines, together with thermal energy and particle size, the viscosity and stress scale. In the context of macroscopic fluid dynamics, however, a more natural dimensionless measure of time, which we shall use in the discussion of our results, is instead given by the strain t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t) =
(y,t) = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 + δ
0 + δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y,t), where ρ0 and
(y,t), where ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 denote the uniform background values. In linear order in the fluctuations and derivatives, eqn (10) becomes
0 denote the uniform background values. In linear order in the fluctuations and derivatives, eqn (10) becomes![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0∂tδρ + ρ0∂tδ
0∂tδρ + ρ0∂tδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = σ
= σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y2δ
∂y2δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂y2δρ − κ∂y4δ
+ σρ∂y2δρ − κ∂y4δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂yδ
∂yδ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − Πρ∂yδρ + bη∂y2uy − bκ∂y4uy,
− Πρ∂yδρ + bη∂y2uy − bκ∂y4uy,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,ρ, Π
,ρ, Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,ρ, η, and κ are understood to be evaluated for the background values ρ0 and
,ρ, η, and κ are understood to be evaluated for the background values ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.
0.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,
,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = σ
= σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∂y2δ
∂y2δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ∂y4δ
− κ∂y4δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + σρ∂y2δρ +
+ σρ∂y2δρ + ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0ρ0∂yuy.
0ρ0∂yuy.
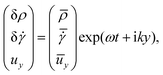
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = −ikρ0ūy,
= −ikρ0ūy,

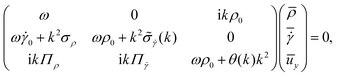
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (k) ≡ σ
(k) ≡ σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + κk2
+ κk2
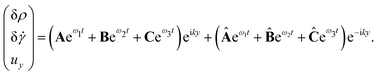

 defined here determines the boundary of stability. Inserting eqn (26) into eqn (24), the other two decay rates result as
defined here determines the boundary of stability. Inserting eqn (26) into eqn (24), the other two decay rates result as
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0Π
0Π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≲ 10−12 and extreme densities ρ ≃ ρm, where the hydrodynamic model considered here is doubtful. Since generally
≲ 10−12 and extreme densities ρ ≃ ρm, where the hydrodynamic model considered here is doubtful. Since generally ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≥ 0 and θ(k) > 0, it follows that ω2,3 ≤ 0—still assuming purely real ωj. Accordingly, provided that eqn (28) holds, none of the frequencies ω2 and ω3 vanishes and, consequently, the boundary of stability is solely defined by the condition ω1 = 0 in this case. Close to the boundary of stability, nonlinear terms in ω1 can be neglected in eqn (24), such that one readily obtains the growth rate
≥ 0 and θ(k) > 0, it follows that ω2,3 ≤ 0—still assuming purely real ωj. Accordingly, provided that eqn (28) holds, none of the frequencies ω2 and ω3 vanishes and, consequently, the boundary of stability is solely defined by the condition ω1 = 0 in this case. Close to the boundary of stability, nonlinear terms in ω1 can be neglected in eqn (24), such that one readily obtains the growth rate

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 and thus
= 0 and thus  in that case. As discussed below, eqn (30) in fact describes the boundary of stability of the whole relevant parameter space for the compressible single-component fluid.
in that case. As discussed below, eqn (30) in fact describes the boundary of stability of the whole relevant parameter space for the compressible single-component fluid.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Â = Re
 = Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, Im
A, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Â = −Im
 = −Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, with analogous conditions applying for B and C. These conditions are indeed fulfilled by the solution in eqn (25), which can be seen by writing eqn (21) as
A, with analogous conditions applying for B and C. These conditions are indeed fulfilled by the solution in eqn (25), which can be seen by writing eqn (21) as![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,uy)Te−iky = Aeω1t + 2eΩ′t(B′cos
,uy)Te−iky = Aeω1t + 2eΩ′t(B′cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω′′t − B′′sin
Ω′′t − B′′sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω′′t).
Ω′′t).



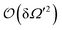 and higher in eqn (24) (keeping, however, all orders in
and higher in eqn (24) (keeping, however, all orders in  , as this quantity is not necessarily small), yields
, as this quantity is not necessarily small), yields
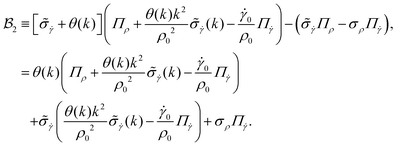

 coincides with eqn (34). Note furthermore that
coincides with eqn (34). Note furthermore that  for k → ∞ and, generally,
for k → ∞ and, generally,  . A numerical analysis reveals that the condition
. A numerical analysis reveals that the condition  and thus
and thus  is fulfilled for all physically relevant ρ0 and
is fulfilled for all physically relevant ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 of the present model.
0 of the present model.
 in the limit k → ∞, the growth rate in eqn (29) becomes negative for sufficiently large k, as is necessary for a physically reasonable model. In particular, asymptotically for k → ∞ one obtains
in the limit k → ∞, the growth rate in eqn (29) becomes negative for sufficiently large k, as is necessary for a physically reasonable model. In particular, asymptotically for k → ∞ one obtains
 . On the other hand, neglecting all contributions related to bulk viscosity, yields
. On the other hand, neglecting all contributions related to bulk viscosity, yields  . From these results one infers that the stability of the system for large k is indeed due to the shear–curvature viscosity.
. From these results one infers that the stability of the system for large k is indeed due to the shear–curvature viscosity.
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is a growing function of k, the boundary of stability of the whole phase diagram of a bulk system is determined by eqn (30) for k = 0. Specifically, if
is a growing function of k, the boundary of stability of the whole phase diagram of a bulk system is determined by eqn (30) for k = 0. Specifically, if  , the system is unstable for all wavenumbers, satisfying
, the system is unstable for all wavenumbers, satisfying  (cf.eqn (29)). In other words, all wavenumbers 0 < k < kc are unstable, where the critical wavenumber kc is defined via
(cf.eqn (29)). In other words, all wavenumbers 0 < k < kc are unstable, where the critical wavenumber kc is defined via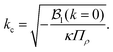
 , are identical to the corresponding expressions obtained in ref. 16 for the advection–diffusion model described by eqn (1) and (2).29 However, as can be inferred from eqn (29), owing to the presence of bulk viscosity, the fastest growing mode behaves differently as a function of k for the compressible fluid. Such a finite bulk viscosity is to be expected, since colloidal suspensions exhibit a certain degree of local compressibility even in the highly concentrated regime. Fig. 2 shows the stability diagram obtained for k = 0. For illustrative purposes, it is more convenient to consider instead of
, are identical to the corresponding expressions obtained in ref. 16 for the advection–diffusion model described by eqn (1) and (2).29 However, as can be inferred from eqn (29), owing to the presence of bulk viscosity, the fastest growing mode behaves differently as a function of k for the compressible fluid. Such a finite bulk viscosity is to be expected, since colloidal suspensions exhibit a certain degree of local compressibility even in the highly concentrated regime. Fig. 2 shows the stability diagram obtained for k = 0. For illustrative purposes, it is more convenient to consider instead of  [eqn (26)] the (dimensionless) stability parameter
[eqn (26)] the (dimensionless) stability parameter
 . As seen in Fig. 2, the instability occurs only in the glassy phase (ρ > ρg).
. As seen in Fig. 2, the instability occurs only in the glassy phase (ρ > ρg).

 [eqn (40)] or, equivalently, for
[eqn (40)] or, equivalently, for  [eqn (30)]. The boundary of stability is indicated by the solid curve in (b), corresponding to
[eqn (30)]. The boundary of stability is indicated by the solid curve in (b), corresponding to  . For comparison, the dashed curve in (b) represents the boundary of stability computed with σyieldyy = 0 in Πρ [eqn (11a)].
. For comparison, the dashed curve in (b) represents the boundary of stability computed with σyieldyy = 0 in Πρ [eqn (11a)].![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. When expressed in terms of the fundamental time and length scales t0 and a (which are unity for our choice of units), ωm and km reach a maximum for intermediate shear rates and generally grow upon increasing the density. When taking instead the inverse shear rate as the fundamental time scale, ωm/
0. When expressed in terms of the fundamental time and length scales t0 and a (which are unity for our choice of units), ωm and km reach a maximum for intermediate shear rates and generally grow upon increasing the density. When taking instead the inverse shear rate as the fundamental time scale, ωm/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 grows with increasing distance from the boundary of stability [see main plot of Fig. 3(c)]. At intermediate shear rates, an effective algebraic behavior ωm/
0 grows with increasing distance from the boundary of stability [see main plot of Fig. 3(c)]. At intermediate shear rates, an effective algebraic behavior ωm/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ∼
0 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0−0.5 can be inferred from the numerics. As illustrated in Fig. 3(c) and (d), changing the value of the shear–curvature parameter κ0 [eqn (7)] has only a moderate effect on km and ωm.
0−0.5 can be inferred from the numerics. As illustrated in Fig. 3(c) and (d), changing the value of the shear–curvature parameter κ0 [eqn (7)] has only a moderate effect on km and ωm.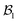 [eqn (26)] and therefore kc are small, such that a Taylor expansion of the growth rate in eqn (29) to
[eqn (26)] and therefore kc are small, such that a Taylor expansion of the growth rate in eqn (29) to  is sufficient to determine km. (The leading term of the expansion of ω is of
is sufficient to determine km. (The leading term of the expansion of ω is of  .) Within this approximation, the wavenumber of the fastest growing mode follows by evaluating the condition dω/dk = 0 as
.) Within this approximation, the wavenumber of the fastest growing mode follows by evaluating the condition dω/dk = 0 as
 . In the last expression, the fact that
. In the last expression, the fact that  close to the stability boundary has been used. Notably, due to bulk viscous effects, eqn (41) is generally different from the corresponding result obtained in ref. 16. In Fig. 4, the typical behavior of the growth rate ω as a function of the wavenumber k is illustrated. We have chosen here values of the parameters ρ0 and
close to the stability boundary has been used. Notably, due to bulk viscous effects, eqn (41) is generally different from the corresponding result obtained in ref. 16. In Fig. 4, the typical behavior of the growth rate ω as a function of the wavenumber k is illustrated. We have chosen here values of the parameters ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 near the stability boundary, where eqn (41) provides an accurate approximation to the actual maximum wavenumber. While ω ∝ k2 for small k [eqn (29)], ω eventually becomes negative for sufficiently large k [see eqn (38)], as required for reasons of stability.
0 near the stability boundary, where eqn (41) provides an accurate approximation to the actual maximum wavenumber. While ω ∝ k2 for small k [eqn (29)], ω eventually becomes negative for sufficiently large k [see eqn (38)], as required for reasons of stability.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 3.5 × 10−4, and κ0 = 100 are used for the calculation.
0 ≃ 3.5 × 10−4, and κ0 = 100 are used for the calculation.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0), the nullspace solution
0), the nullspace solution  of eqn (21) is determined and normalized, v0/||v0||, and then projected onto the space spanned by ρ0 and
of eqn (21) is determined and normalized, v0/||v0||, and then projected onto the space spanned by ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, additionally normalizing the components by ρ0 and
0, additionally normalizing the components by ρ0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, respectively. As illustrated in Fig. 5, in general,
0, respectively. As illustrated in Fig. 5, in general, ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) and
and  have opposite signs in the unstable region, as expected for the SDC instability. A similar anti-correlation has been reported in molecular dynamics studies of heterogeneous flow in a hard sphere glass.6 Note that, with v, also −v is a valid solution of eqn (21); in the plot, we have chosen the positive sign of
have opposite signs in the unstable region, as expected for the SDC instability. A similar anti-correlation has been reported in molecular dynamics studies of heterogeneous flow in a hard sphere glass.6 Note that, with v, also −v is a valid solution of eqn (21); in the plot, we have chosen the positive sign of ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . One notes that the development of the instability is dominated by a strong relative change of the shear rate, while the growth of the density is rather weak. This feature of the linear regime will also prevail in the nonlinear case discussed below. Comparing with Fig. 3(a) and (b), one infers that the growth amplitude ||v|| is largest in those regions of the phase diagram where the growth rate ωm and the wavenumber km are relatively small.
. One notes that the development of the instability is dominated by a strong relative change of the shear rate, while the growth of the density is rather weak. This feature of the linear regime will also prevail in the nonlinear case discussed below. Comparing with Fig. 3(a) and (b), one infers that the growth amplitude ||v|| is largest in those regions of the phase diagram where the growth rate ωm and the wavenumber km are relatively small.
 (up to a normalization factor, see text) of the most unstable mode km, as determined by the nullspace solution of eqn (19). The coloring indicates the magnitude of v in a logarithmic scale, while the arrows indicate the growth direction (non-logarithmic scale along both axes), which is determined up to a sign. Accordingly, in the unstable region, fluctuations grow indefinitely by reducing the shear rate and increasing the density (or vice versa), providing a nonlinear feedback mechanism for the SDC-instability.
(up to a normalization factor, see text) of the most unstable mode km, as determined by the nullspace solution of eqn (19). The coloring indicates the magnitude of v in a logarithmic scale, while the arrows indicate the growth direction (non-logarithmic scale along both axes), which is determined up to a sign. Accordingly, in the unstable region, fluctuations grow indefinitely by reducing the shear rate and increasing the density (or vice versa), providing a nonlinear feedback mechanism for the SDC-instability. , remains practically constant during the time evolution.
, remains practically constant during the time evolution.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 calculated from eqn (43) below. The dynamical evolution is, however, not significantly altered if instead a different value for the initial shear rate is used, except for a short transient at early times. After this transient, the evolution of the shear rate is found to be essentially enslaved to the density dynamics. In all cases, the wavelength of the maximally unstable mode predicted by the dispersion relation [eqn (24), see also Fig. 3(d)] is somewhat larger than the system size. Accordingly, the instability is realized here with the largest wavelength that fits in the system (cf.Fig. 4), provided that π/kc ≲ L, i.e., the system size exceeds half of the critical wavelength [eqn (39)]. This condition constrains, inter alia, also the value of the curvature parameter κ0 [eqn (7)], which sets the width of the shear band interface. Simulations with π/km ≪ L are typically found to be unstable at late times since the nonlinear feedback mechanism leads to a singularity in the integration of the Navier–Stokes equations (see the discussion below eqn (44)). This singularity manifests itself in a diverging viscosity and vanishing shear rate. For sufficiently large interface widths, global mass conservation stabilizes the stationary state before the singularity is reached.
0 calculated from eqn (43) below. The dynamical evolution is, however, not significantly altered if instead a different value for the initial shear rate is used, except for a short transient at early times. After this transient, the evolution of the shear rate is found to be essentially enslaved to the density dynamics. In all cases, the wavelength of the maximally unstable mode predicted by the dispersion relation [eqn (24), see also Fig. 3(d)] is somewhat larger than the system size. Accordingly, the instability is realized here with the largest wavelength that fits in the system (cf.Fig. 4), provided that π/kc ≲ L, i.e., the system size exceeds half of the critical wavelength [eqn (39)]. This condition constrains, inter alia, also the value of the curvature parameter κ0 [eqn (7)], which sets the width of the shear band interface. Simulations with π/km ≪ L are typically found to be unstable at late times since the nonlinear feedback mechanism leads to a singularity in the integration of the Navier–Stokes equations (see the discussion below eqn (44)). This singularity manifests itself in a diverging viscosity and vanishing shear rate. For sufficiently large interface widths, global mass conservation stabilizes the stationary state before the singularity is reached.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = ∂yux across the slit in the unstable region for various boundary conditions. One observes that, in all cases, the system evolves from an essentially homogeneous initial state towards a steady state with inhomogeneous density and shear-rate profiles. The steady state of ux (or, correspondingly, the shear rate) is typically reached within a time scale 1/
= ∂yux across the slit in the unstable region for various boundary conditions. One observes that, in all cases, the system evolves from an essentially homogeneous initial state towards a steady state with inhomogeneous density and shear-rate profiles. The steady state of ux (or, correspondingly, the shear rate) is typically reached within a time scale 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 determined by the average shear rate
0 determined by the average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. The latter is given by (ux(L) − ux(0))/L =
0. The latter is given by (ux(L) − ux(0))/L = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av in the case where a fixed wall velocity is imposed and by
av in the case where a fixed wall velocity is imposed and by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w in the case where a fixed wall shear rate is used.
w in the case where a fixed wall shear rate is used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 2 × 10−4. The profiles shown are obtained at times t
av = 2 × 10−4. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 0, 0.20, 0.28, ∞, where t = ∞ corresponds to the steady state reached for t
av = 0, 0.20, 0.28, ∞, where t = ∞ corresponds to the steady state reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 103 (thick black curve). In the steady state, the local shear rate at the left and the right boundary are found to be γ ≃ 1.7 × 10−8 and 3.7 × 10−4, respectively. The initial growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100 and ρ0 = 0.91ρm are used.
av ≳ 103 (thick black curve). In the steady state, the local shear rate at the left and the right boundary are found to be γ ≃ 1.7 × 10−8 and 3.7 × 10−4, respectively. The initial growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100 and ρ0 = 0.91ρm are used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 10−4 at both walls. The profiles shown are obtained at times t
w = 10−4 at both walls. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 0, 2.2 × 10−2, 4.0 × 10−2, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t
w = 0, 2.2 × 10−2, 4.0 × 10−2, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≳ 0.4. In the steady-state, the local shear rate at each of the walls results as
w ≳ 0.4. In the steady-state, the local shear rate at each of the walls results as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 1.0 × 10−4. The initial growth rate of the maximally unstable mode is given by ωm ≃ 0.078 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, and ρ0 = 0.93ρm are used.
≃ 1.0 × 10−4. The initial growth rate of the maximally unstable mode is given by ωm ≃ 0.078 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, and ρ0 = 0.93ρm are used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 0.07, 0.42, 0.48, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t
0 = 0.07, 0.42, 0.48, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≳ 10. An effective shear rate
0 ≳ 10. An effective shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 10−3 is obtained from eqn (43) based in the initial density ρ0. In the steady state, the local shear rate at the boundary at y = 0 is obtained as
0 ≃ 10−3 is obtained from eqn (43) based in the initial density ρ0. In the steady state, the local shear rate at the boundary at y = 0 is obtained as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 3.3 × 10−5. The initial growth rate (corresponding to the above
≃ 3.3 × 10−5. The initial growth rate (corresponding to the above ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0) of the maximally unstable mode is given by ωm ≃ 0.012 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, ρ0 = 0.93ρm, and σw = 11 are used.
0) of the maximally unstable mode is given by ωm ≃ 0.012 [see eqn (24)]. Parameters L = 200Δh, κ0 = 100, ρ0 = 0.93ρm, and σw = 11 are used.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 1, while the density at the left wall reaches the steady state only for times
av ≳ 1, while the density at the left wall reaches the steady state only for times  . One observes that the time evolution is fastest if a fixed wall-shear rate is imposed. The broken left-right symmetry with respect to the walls in Fig. 6 and 8 is a direct consequence of the asymmetry of the initial configuration. In fact, using an initial sinusoidal density profile with a maximum in the right half of the system leads to spatially mirrored evolution.
. One observes that the time evolution is fastest if a fixed wall-shear rate is imposed. The broken left-right symmetry with respect to the walls in Fig. 6 and 8 is a direct consequence of the asymmetry of the initial configuration. In fact, using an initial sinusoidal density profile with a maximum in the right half of the system leads to spatially mirrored evolution.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 of the density and shear rate in the unstable regime and for wavenumbers
0 of the density and shear rate in the unstable regime and for wavenumbers  (in units of a), one finds for the present constitutive model [eqn (14)] that the viscous term η∂y2 dominates over the restoring force Πρ∂y2 in the sound-wave equation [eqn (18)].
(in units of a), one finds for the present constitutive model [eqn (14)] that the viscous term η∂y2 dominates over the restoring force Πρ∂y2 in the sound-wave equation [eqn (18)]. . In fact, the presently used constitutive model does not allow us to reach the steady state in these cases due to the occurrence of an intrinsic singularity [see eqn (44) below].
. In fact, the presently used constitutive model does not allow us to reach the steady state in these cases due to the occurrence of an intrinsic singularity [see eqn (44) below].
 in the case of a fixed wall-velocity corresponding to an average shear rate
in the case of a fixed wall-velocity corresponding to an average shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≃ 2 × 10−4. The initial density profile is given by ρ(y,0) ∝ cos(nπy/L), with n = 4, 2, 1 for the solid, dashed, and dotted curve, respectively. A value κ0 = 2 is used, while all other parameters are the same as in Fig. 6. We emphasize here that, regardless of the initial structure, multiple bands are not observed for larger values of κ, such as those used in Fig. 6 and 8.
av ≃ 2 × 10−4. The initial density profile is given by ρ(y,0) ∝ cos(nπy/L), with n = 4, 2, 1 for the solid, dashed, and dotted curve, respectively. A value κ0 = 2 is used, while all other parameters are the same as in Fig. 6. We emphasize here that, regardless of the initial structure, multiple bands are not observed for larger values of κ, such as those used in Fig. 6 and 8.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in the steady state are determined by the equations
in the steady state are determined by the equations![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )],
)],![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = ∂y[σyield(ρ) + η(ρ,
) = ∂y[σyield(ρ) + η(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )
)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) − κ(ρ,
− κ(ρ,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )∂y2
)∂y2![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ].
].![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (y) are required, which can be obtained from the dynamical eqn (5), as discussed above. Alternatively, the steady state profiles may also be directly obtained by integrating the PDEs in eqn (5) over a sufficiently large time, as is done in Fig. 6–8.
(y) are required, which can be obtained from the dynamical eqn (5), as discussed above. Alternatively, the steady state profiles may also be directly obtained by integrating the PDEs in eqn (5) over a sufficiently large time, as is done in Fig. 6–8.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w is imposed at both walls. Profile shapes similar to the ones in Fig. 6 and 8 result when the values of
w is imposed at both walls. Profile shapes similar to the ones in Fig. 6 and 8 result when the values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w at each wall are set accordingly (data not shown).
w at each wall are set accordingly (data not shown).![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. In this case, eqn (42b) with ∂y
0. In this case, eqn (42b) with ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 readily yields a relation between ρ0,
= 0 readily yields a relation between ρ0, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, and the stress in the system σw (which arises as an integration constant and typically corresponds to the wall stress):
0, and the stress in the system σw (which arises as an integration constant and typically corresponds to the wall stress):
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, and the system (wall) pressure. If, instead of σw, the wall shear rate
0, and the system (wall) pressure. If, instead of σw, the wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w =
w = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 or the wall velocity uw (implying
0 or the wall velocity uw (implying ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = uw/L) are prescribed, eqn (43) represents a family of solutions for ρ0 with the integration constant σw as adjustable parameter.
0 = uw/L) are prescribed, eqn (43) represents a family of solutions for ρ0 with the integration constant σw as adjustable parameter.
 are required,33 for which eqn (44) implies
are required,33 for which eqn (44) implies  as an upper limit for the density (see Fig. 10). As indicated in Fig. 5, once the system is unstable, some part of it evolves towards smaller shear rates and larger densities. In small systems, this growth is eventually limited by global mass conservation and the fact that the interface between low and high density regions must keep a certain width [see discussion after eqn (7)]. In contrast, for systems much larger than the interface width, the limit for Φ implied by eqn (44) can be easily exceeded by means of mass transport, leading to σyield > σw and thus causing the solution of eqn (5) to become singular. The singularity, in particular, makes an observation of stationary inhomogeneous profiles with multiple shear bands rather difficult. Nevertheless, as shown in Fig. 9, we do observe a multi-band structure up to the instant of the numerical singularity. Based on these findings and the above detailed analysis, we anticipate that a slightly modified version of the present constitutive model with a tamed singularity would exhibit stable multiple shear bands.
as an upper limit for the density (see Fig. 10). As indicated in Fig. 5, once the system is unstable, some part of it evolves towards smaller shear rates and larger densities. In small systems, this growth is eventually limited by global mass conservation and the fact that the interface between low and high density regions must keep a certain width [see discussion after eqn (7)]. In contrast, for systems much larger than the interface width, the limit for Φ implied by eqn (44) can be easily exceeded by means of mass transport, leading to σyield > σw and thus causing the solution of eqn (5) to become singular. The singularity, in particular, makes an observation of stationary inhomogeneous profiles with multiple shear bands rather difficult. Nevertheless, as shown in Fig. 9, we do observe a multi-band structure up to the instant of the numerical singularity. Based on these findings and the above detailed analysis, we anticipate that a slightly modified version of the present constitutive model with a tamed singularity would exhibit stable multiple shear bands.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 and density ρ0 in a homogeneous system, as provided by eqn (43), for various values of the system stress σw (increasing in the direction of the arrow from σw = 8 to 12 in steps of 1). Eqn (43) is well-defined only if condition (44) holds, i.e., for sufficiently small densities. The maximum possible density corresponds in the plot to the (σw-dependent) location where
0 and density ρ0 in a homogeneous system, as provided by eqn (43), for various values of the system stress σw (increasing in the direction of the arrow from σw = 8 to 12 in steps of 1). Eqn (43) is well-defined only if condition (44) holds, i.e., for sufficiently small densities. The maximum possible density corresponds in the plot to the (σw-dependent) location where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 → 0. The dashed black curve represents the threshold of the SDC instability,
0 → 0. The dashed black curve represents the threshold of the SDC instability,  [see eqn (26) as well as Fig. 2].
[see eqn (26) as well as Fig. 2].
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) + c + dy,
+ c + dy,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /bη, and integration constants c and d. In order to have δρ ≃ 0 at the boundaries of the domain, we set d = 0, such that the solution of eqn (A2) with initial condition ρ(y,0) = ρin(y) is obtained as
/bη, and integration constants c and d. In order to have δρ ≃ 0 at the boundaries of the domain, we set d = 0, such that the solution of eqn (A2) with initial condition ρ(y,0) = ρin(y) is obtained as
 , which follows from requiring
, which follows from requiring  . Eqn (A3) shows that, in the overdamped limit and for large wavelengths and small frequencies, density fluctuations essentially relax exponentially in the compressible fluid (cf.ref. 24). However, in contrast to diffusive relaxation, which is also exponential at late times, the relaxation rate is here independent of the wavenumber. Furthermore, according to eqn (A3), a positive shear rate fluctuation gives rise to a reduction of the local density. This behavior is an essential mechanism of the SDC instability.
. Eqn (A3) shows that, in the overdamped limit and for large wavelengths and small frequencies, density fluctuations essentially relax exponentially in the compressible fluid (cf.ref. 24). However, in contrast to diffusive relaxation, which is also exponential at late times, the relaxation rate is here independent of the wavenumber. Furthermore, according to eqn (A3), a positive shear rate fluctuation gives rise to a reduction of the local density. This behavior is an essential mechanism of the SDC instability.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ),
),![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ),
),![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) via Deff ≡ ∂ρΠ and ξ ≡ ∂
) via Deff ≡ ∂ρΠ and ξ ≡ ∂![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Π, such that ∂y2Π = ∂y[Deff∂yρ + ξ∂y
Π, such that ∂y2Π = ∂y[Deff∂yρ + ξ∂y![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ].
].
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w, or a fixed wall stress σw at the boundaries. For the first two cases, instead of eqn (B1b), we solve the full time-dependent equation eqn (5b) for the velocity ux,
w, or a fixed wall stress σw at the boundaries. For the first two cases, instead of eqn (B1b), we solve the full time-dependent equation eqn (5b) for the velocity ux,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ),
),![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = ∂yux. We generally impose a vanishing pressure gradient ∂yΠ = 0 at the boundaries, which ensures global mass conservation for the dynamics described by eqn (B1a).
= ∂yux. We generally impose a vanishing pressure gradient ∂yΠ = 0 at the boundaries, which ensures global mass conservation for the dynamics described by eqn (B1a).
 , respectively, while, for fixed
, respectively, while, for fixed ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w, instead, the growth rate of the maximally unstable mode ωm provides a better estimate of the dynamical time scale than the strain. (The value of the time scale inferred from simulation depends somewhat on the chosen initial configuration.) The larger steady-state time scale in the compressible fluid model is predominantly caused by the slow transport of mass towards the wall at the late stages of the evolution. In fact, apart from this difference, the spatio-temporal evolution in both the compressible and the diffusive transport model are qualitatively similar (cf.Fig. 6–8).
w, instead, the growth rate of the maximally unstable mode ωm provides a better estimate of the dynamical time scale than the strain. (The value of the time scale inferred from simulation depends somewhat on the chosen initial configuration.) The larger steady-state time scale in the compressible fluid model is predominantly caused by the slow transport of mass towards the wall at the late stages of the evolution. In fact, apart from this difference, the spatio-temporal evolution in both the compressible and the diffusive transport model are qualitatively similar (cf.Fig. 6–8).
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = uw/L = 2 × 10−4. The profiles shown are obtained at times t
av = uw/L = 2 × 10−4. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av = 0, 0.38, 0.4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t
av = 0, 0.38, 0.4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) av ≳ 0.8. The shear rate at the wall is obtained as
av ≳ 0.8. The shear rate at the wall is obtained as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 1.1 × 10−6. The growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3. Parameters L = 200Δh, κ0 = 100, and ρav = 0.91ρm are used.
≃ 1.1 × 10−6. The growth rate of the maximally unstable mode is given by ωm ≃ 7.8 × 10−3. Parameters L = 200Δh, κ0 = 100, and ρav = 0.91ρm are used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 10−4 at both walls. The profiles shown are obtained at times t
w = 10−4 at both walls. The profiles shown are obtained at times t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 0, 3.5 × 10−4, 5.9 × 10−4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t
w = 0, 3.5 × 10−4, 5.9 × 10−4, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w ≳ 10−2. The growth rate of the maximally unstable mode is given by ωm ≃ 0.078. Parameters L = 200Δh, κ0 = 100, and ρav = 0.93ρm are used.
w ≳ 10−2. The growth rate of the maximally unstable mode is given by ωm ≃ 0.078. Parameters L = 200Δh, κ0 = 100, and ρav = 0.93ρm are used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 0, 0.06, 0.07, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t
0 = 0, 0.06, 0.07, ∞, where t = ∞ corresponds to the steady state (thick black curve) reached for t![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≳ 0.1. The effective shear rate
0 ≳ 0.1. The effective shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 ≃ 8 × 10−4 is identified from eqn (43) using the initial density ρ0. The growth rate of the maximally unstable mode is given by ωm ≃ 0.028. Parameters L = 200Δh, κ0 = 100, ρav = 0.93ρm, and σw = 10.6 are used.
0 ≃ 8 × 10−4 is identified from eqn (43) using the initial density ρ0. The growth rate of the maximally unstable mode is given by ωm ≃ 0.028. Parameters L = 200Δh, κ0 = 100, ρav = 0.93ρm, and σw = 10.6 are used.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the compression rate ∇·u, change sign.
and the compression rate ∇·u, change sign.

