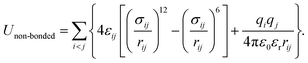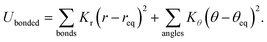Open Access Article
Open Access ArticleElectrostatic interactions in soft particle systems: mesoscale simulations of ionic liquids†
Yong-Lei
Wang
 *ab,
You-Liang
Zhu
c,
Zhong-Yuan
Lu
*ab,
You-Liang
Zhu
c,
Zhong-Yuan
Lu
 d and
Aatto
Laaksonen
d and
Aatto
Laaksonen
 *ae
*ae
aDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, SE-10691 Stockholm, Sweden. E-mail: wangyonl@gmail.com; aatto@mmk.su.se
bDepartment of Chemistry, Stanford University, Stanford, California 94305, USA
cState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, China. E-mail: youliangzhu@ciac.ac.cn
dState Key Laboratory of Supramolecular Structure and Materials, Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130021, China. E-mail: luzhy@jlu.edu.cn
eDepartment of Chemistry-Ångström Laboratory, Uppsala University, Box 538, SE-75121 Uppsala, Sweden
First published on 25th April 2018
Abstract
Computer simulations provide a unique insight into the microscopic details, molecular interactions and dynamic behavior responsible for many distinct physicochemical properties of ionic liquids. Due to the sluggish and heterogeneous dynamics and the long-ranged nanostructured nature of ionic liquids, coarse-grained meso-scale simulations provide an indispensable complement to detailed first-principles calculations and atomistic simulations allowing studies over extended length and time scales with a modest computational cost. Here, we present extensive coarse-grained simulations on a series of ionic liquids of the 1-alkyl-3-methylimidazolium (alkyl = butyl, heptyl-, and decyl-) family with Cl, [BF4], and [PF6] counterions. Liquid densities, microstructures, translational diffusion coefficients, and re-orientational motion of these model ionic liquid systems have been systematically studied over a wide temperature range. The addition of neutral beads in cationic models leads to a transition of liquid morphologies from dispersed apolar beads in a polar framework to that characterized by bi-continuous sponge-like interpenetrating networks in liquid matrices. Translational diffusion coefficients of both cations and anions decrease upon lengthening of the neutral chains in the cationic models and by enlarging molecular sizes of the anionic groups. Similar features are observed in re-orientational motion and time scales of different cationic models within the studied temperature range. The comparison of the liquid properties of the ionic systems with their neutral counterparts indicates that the distinctive microstructures and dynamical quantities of the model ionic liquid systems are intrinsically related to Coulombic interactions. Finally, we compared the computational efficiencies of three linearly scaling O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) Ewald summation methods, the particle–particle particle–mesh method, the particle–mesh Ewald summation method, and the Ewald summation method based on a non-uniform fast Fourier transform technique, to calculate electrostatic interactions. Coarse-grained simulations were performed using the GALAMOST and the GROMACS packages and hardware efficiently utilizing graphics processing units on a set of extended [1-decyl-3-methylimidazolium][BF4] ionic liquid systems of up to 131
N) Ewald summation methods, the particle–particle particle–mesh method, the particle–mesh Ewald summation method, and the Ewald summation method based on a non-uniform fast Fourier transform technique, to calculate electrostatic interactions. Coarse-grained simulations were performed using the GALAMOST and the GROMACS packages and hardware efficiently utilizing graphics processing units on a set of extended [1-decyl-3-methylimidazolium][BF4] ionic liquid systems of up to 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 ion pairs.
072 ion pairs.
1. Introduction
Mesoscale condensed, aggregated or assembled matter is typically mechanically soft and particularly prone to thermal stresses and fluctuations.1–3 Synthetic and biological macromolecules, colloidal suspensions, and granular materials, for example, are classified under a general term of soft condensed matter, in which the ionic soft matter systems hold special and particular significance.2,4,5 The electrostatic interactions between charged groups constitute a prominent factor in determining the structures and functions of ionic soft matter systems, leading to many industrial and biological applications.6–9 In the food emulsion and paint industries, a peculiar way of stabilizing a colloidal suspension against coagulation or flocculation is to generate long-range repulsive interactions between the constituent colloidal particles by imparting permanent like-charges onto these particles, or by grafting charged polymeric chains (polyelectrolytes) onto their surfaces to form hairy particles.5,10 In biological applications, the electrostatic interactions play a critical role in many vital processes, such as the packaging of DNA molecules in a cell nucleus.4,7 A tightly wrapped conformation of DNA molecules is stable only in intermediate and physiological salt concentrations, where an optimal balance between the self-repulsion of DNA segments and the electrostatic attractions of DNA–protein complexes is achieved.11 A biological membrane is another complex and heterogeneous object, of which the membrane structural properties, e.g., rigidity, structural stability, phase transition and dynamic behavior, depend substantially on electrostatic interactions.12Among all categories of ionic soft matter systems, a fascinating class of high-concentration electrolytes is the ionic liquids (ILs), which are liquid salts under ambient conditions, being solely composed of sterically mismatched molecular ions.13–16 ILs have remarkable and multifaceted physicochemical characteristics, and additionally, their properties and microstructural organization can be widely tuned in a controllable fashion through a judicious combination of different cation–anion moieties and by mutating specific atoms in the constituent ionic species.14,16,17 These fascinating characteristics make ILs exceptionally attractive and reliable candidates as reaction media, working fluids, promising electrolytes, suitable lubricants, and as an environmentally benign alternative to conventional toxic organic molecular solvents in many envisioned applications.13,15,18–20 Therefore, immediate scientific research on the synthesis, characterization, and applications of ILs has shown a rapid upswing in academic and industrial communities.19–21
Compared with traditional molten salts, like sodium chloride, one fascinating feature of ILs is that they exhibit distinct heterogeneously ordered structures in the bulk region and in confined environments.15,16,21–25 The nanoscopic liquid organization of ILs is characterized by either sponge-like interpenetrating polar and apolar networks or segregated polar (apolar) domains within an apolar (polar) framework depending on the number of hydrophobic alkyl units in the ionic species.23,26–29 Both experimental characterizations and computational investigations revealed that the characteristic size of nanoscopic structural heterogeneity scales linearly with the aliphatic chain length in imidazolium and pyrrolidinium based ILs.27–31 In typical IL matrices, the liquid structural heterogeneity spans over a few nanometers, and it is beyond the intermolecular distance of close contacted ions. Typically, the size of a simulation system should be several times larger than the characteristic length of the nanostructural organization of ILs, and the simulations should be performed over a long time scale to properly sample the populated molecular conformations of the ionic species in this highly heterogeneous IL organization. The latter, in particular, should be especially long due to the slow relaxation processes of ionic groups in IL matrices. Additionally, lengthening aliphatic chains or increasing the number of hydrophobic alkyl units in ionic species leads to changes in their voluminous characteristics, further slowing down their re-orientational relaxation in heterogeneous environments. This immediately imposes severe fundamental challenges for atomistic simulations to accurately predict dynamics and transport properties of ILs.21,32–34
In this regard, coarse-grained (CG) models become a natural choice and can provide extensive simulations over large length and long time scales with a modest computational cost. The coarse-graining strategy starts with a choice of length scale for coarsening, and then subsumes all atoms within the specific length scale into one bead. Some CG beads are connected by “bonds” to reproduce an overall architecture of the reference atomistic model. Based on the construction of CG models, the next challenge is to determine the effective interaction potentials between these CG beads. Several CG approaches have been developed and applied to representative chemical and biological systems.22,33–43
In a previous work, we proposed a CG model for 1-butyl-3-methylimidazolium hexafluorophosphate ([BMIM][PF6]) IL.44 Three sets of pair potentials between CG beads were derived from two iteration procedures, i.e., the Newton Inversion (NI)35,36 and Iterative Boltzmann Inversion (IBI)33,37 methods, respectively, with different treatments of electrostatic interactions, based on reference radial distribution functions (RDFs) calculated from underlying detailed atomistic simulations. Through systematic evaluation of the obtained computational results and comparison with available experimental data, it was verified that long-range electrostatic interactions should be explicitly treated in order to improve the reliability of CG Molecular Dynamics (MD) simulation results, rather than having them embedded in the overall effective potentials. However, for the same atomistic system, the obtained effective potentials between CG beads should in principle be re-calibrated/calculated at temperatures differing from that used in underlying reference atomistic simulations from which the effective CG potentials are constructed. In addition, the transferability of interaction potentials between CG beads within the same IL family is difficult since a small structural change in the polar and apolar moieties in constituent ions can result in distinct variation in the local ionic structures and even the destruction of liquid organization.
In the current work, we extend the previously constructed CG model to be a generic idealized ionic model that can capture essential physical and structural features of ILs while being simple enough to be computationally economical (Section 2). The liquid densities, microstructures, and dynamical properties of representative model IL systems are discussed in Section 3. In parallel, we have performed CGMD simulations on the equivalent neutral model systems to address the effect of electrostatic interactions between charged beads on representative structural and dynamical properties. These computational results are discussed in Section 4. The Coulombic interactions, as identified by us both in previous and in the present studies, play a critical role in maintaining the peculiar ionic structures and the distinct physical properties of ionic fluids. In particle-based simulations of ionic soft matter systems, a demanding computational task is the efficiency in calculating long-range electrostatic energies and forces between ions, especially for large simulation systems. These aspects are also discussed in Section 4. The summary and concluding remarks are provided in Section 5.
2. Ionic models and computational methods
2.1 Coarse-grained models for ionic liquids
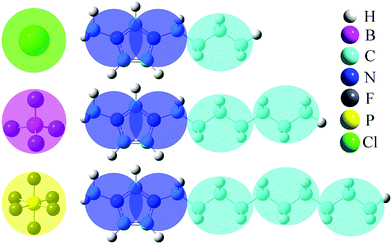
The generic ionic model is consistent with the one we constructed in a prior work for imidazolium cations. The two charged head beads (blue) represent the imidazolium ring and two closest methyl (methylene) groups. Three methylene units in the aliphatic chains are CG into a single bead. The detailed mapping schemes of the cationic models for describing the imidazolium cations with butyl-, heptyl-, and decyl- side chains are illustrated in Fig. 1. The three CG cationic models are labelled as [BMIM], [HMIM], and [DMIM], respectively, in following subsections for the convenience of data analysis and discussion. The anionic groups used in this work are chloride (Cl), tetrafluoroborate ([BF4]), and [PF6], all of which are represented by single beads.The interactions between CG beads in the constructed ionic models are described by non-bonded and bonded interaction terms. The non-bonded potential contains short-range van der Waals interactions and long-range Coulombic interactions between CG beads, and it is described by:
The non-bonded and bonded interaction parameters have their usual meaning as described in most force fields.23,34,42,45–48 The sizes of these CG beads are determined from their corresponding atomistic details and are listed in Table 1. The partial charge on all three anionic models is set to −1.0e, and the partial charges on the two (blue) beads representing imidazolium ring structures are descried by +0.5e to keep the model ion pair neutral. The bond length between connected CG beads and a bending angle of 180° are chosen to reflect the average disposition of these CG groups in their atomistic models. In the present CGMD simulations, each simulation system consists of 1024 pairs of model IL molecules in a cubic simulation box. Additionally, we have also performed CGMD simulations for the model [DMIM][BF4] IL systems consisting of 2048, 4096, and 8192 ion pairs at 400 K. No significant finite size effects beyond statistical uncertainties on liquid densities, microstructural quantities, and translational and re-orientational dynamical properties were observed for all these model IL systems.
| CG beads | σ ii (nm) | ε ii (kJ mol−1) | q i (e) | Mass (amu) |
|---|---|---|---|---|
| Ring | 0.4800 | 1.9500 | +0.5 | 48.0665 |
| Alkane | 0.4800 | 1.6200 | 0.0 | 43.0890 |
| Cl | 0.3755 | 0.6849 | −1.0 | 35.4530 |
| [BF4] | 0.4510 | 3.2400 | −1.0 | 96.8100 |
| [PF6] | 0.5060 | 4.7100 | −1.0 | 144.9620 |
2.2 Computational details
The CGMD simulations of all model IL systems were performed using the GROMACS 5.0.4 package.49 The equations of motion were integrated using a leap-frog integration scheme with a time step of 2.0 femtoseconds. A cut-off distance of 1.6 nm was set for short-range van der Waals interactions and real space electrostatic interactions between atom-centered point charges. The particle mesh Ewald (PME) summation method with an interpolation order of 5 and a Fourier grid spacing of 0.12 nm was used to handle long-range electrostatic interactions in reciprocal space. All model IL systems were first energetically minimized using a steepest descent algorithm, and thereafter annealed gradually from 1000 K to 500 K within 20 nanoseconds and thereafter equilibrated for 20 nanoseconds. For each model IL system, ensembles at other temperatures ranging from 500 to 300 K with an interval of 25 K were derived from this system and were annealed for 20 nanoseconds to target temperatures. All annealed simulation systems were equilibrated in an isothermal–isobaric (NPT) ensemble for 100 nanoseconds maintained using a Nosé–Hoover thermostat and a Parrinello–Rahman barostat with time coupling constants of 0.5 and 1.0 picoseconds, respectively, to control temperature and pressure at 1 atm. The CGMD simulations of all studied model IL systems were further performed in the NPT ensemble for at least 200 nanoseconds, and simulation trajectories were recorded at an interval of 400 femtoseconds for further structural and dynamical analysis.Using the GALAMOST (GPU (graphics processing unit)-accelerated large-scale molecular simulation toolkit) package,50,51 we have further benchmarked the computational efficiencies of two Ewald summation based methods for handling Coulombic interactions, the particle–particle particle–mesh (PPPM) Ewald summation method52,53 and the Ewald summation method based on a Non-Uniform fast Fourier transform (ENUF) technique.54–56 In the comparison, we also include the PME method57,58 as implemented in a hybrid CPU/GPU version of the GROMACS package.49 Considering the ENUF method, it utilizes the GPU and the Compute Unified Device Architecture (CUDA) technology with a combined CPU-GPU parallelization strategy.59,60 In the Appendix, we briefly describe the implementation of the ENUF method in the GALAMOST package.50 In Section 4, we discuss the efficiency of the ENUF method in handling electrostatic interactions in a model IL system and compare it with that of the PPPM and PME methods, where the time/time step results obtained from CG Molecular Dynamics (MD) simulations of the model [DMIM][BF4] IL systems consisting of various number of ion pairs are gathered and compared. The PPPM and ENUF simulations were performed using the GALAMOST package running on the Kebnekaise cluster at the High Performance Computing Center North (HPC2N), Umeå University (Sweden), and on a custom-built workstation at Jilin University (China). For the Kebnekaise cluster, a NVIDIA Tesla K80 GPU with Intel Xeon E5-2690v4 CPU cores is installed in an Ubuntu Xenial (16.04 LTS) operating system. A single NVIDIA GeForce GTX 1080 GPU is combined with the Intel Xeon E5-2630v3 CPU processors in a custom-built workstation. Since the GALAMOST package adopts the reduced interaction parameters, we rescale the CG force field parameters for the proposed ionic models with σii* = 1 = 0.48 nm and εii* = 1 = 2.50 kJ mol−1, and the corresponding CGMD simulations were performed at a reduced temperature of T* = 1 = 300 K.
3 Results and discussion
3.1 Liquid densities
Liquid densities of the model IL systems are the preliminary and most frequently used references as these data are easily accessible in both experimental measurements and molecular simulations. Additionally, the imidazolium based ILs provide a large amount of experimental density data, which can be directly adopted to validate the generic IL models. It is noteworthy that in many cases, different experimental measurements can give somewhat different liquid densities with a relative deviation of approximately 3% depending on the trace amount of unidentified impurities in IL samples.61–64 It is shown in Fig. 2 that the constructed CG models can essentially reproduce the liquid densities of all studied model IL systems at a wide temperature range. The largest discrepancy between these computational results and the experimental measurements is around 5%, which should be acceptable in CGMD simulations. It should be noted that an exact agreement between experimental measurements and CG simulation results is not expected because of the simplified ionic models, which are not capable of accurately reproducing all thermodynamic, microstructural and dynamical quantities of the real IL systems.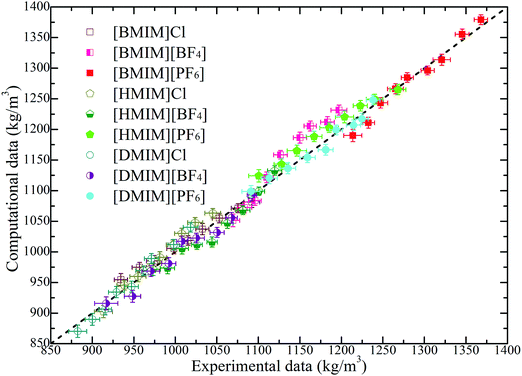 | ||
| Fig. 2 Comparison of liquid densities of the model IL systems obtained from coarse-grained simulations with the experimental data of the real IL systems over a wide temperature range of 300–500 K. These experimental data are obtained, extrapolated, and interpolated from the related IL systems from ref. 61–64. The dashed line provides a guide for the eye. | ||
The computational liquid densities of all model IL systems exhibit linear variations as temperature changes within the range of 300–500 K. The liquid densities of the investigated model ILs decrease with an increase in the number of neutral beads in the cationic models, which is consistent with the experimental and computational observations of imidazolium based ILs.61–64 In addition, a decrease in the sizes of anionic groups from [PF6] to Cl corresponds to a decrease of molecular mass and van der Waals interaction parameters, and thus, the liquid densities of the corresponding IL systems are consistently decreased at given temperatures.
3.2 Liquid structures
Representative snapshots of three simulation systems consisting of the same Cl anionic model coupled with different cationic models are presented in Fig. 3, in which the color codes of these CG beads are the same as those shown in Fig. 1. In the model [BMIM]Cl IL system, the anions and the charged head portion of the cationic models are distributed homogeneously in the simulation system. These charged moieties form a continuous tridimensional framework of ionic channels, in which the neutral (cyan) beads are dispersed. This observation is qualitatively consistent with the liquid morphologies and ionic organization of [BMIM] based ILs, in which there is no distinct apolar segregations in the IL matrices, as verified in the experimental characterizations and atomistic simulations.27,30,34,42,46,65–67 | ||
| Fig. 3 Representative snapshots of three model IL systems consisting of the same Cl anions coupled with different cationic models. (A) [BMIM]Cl, (B) [HMIM]Cl, and (C) [DMIM]Cl ILs. The color codes of these coarse-grained beads are the same as those shown in Fig. 1. | ||
Lengthening the neutral chains in imidazolium based cationic models results in an aggregation of neutral beads and the formation of apolar domains due to the collective solvophobic interactions between the neutral beads. Meanwhile, the polar framework becomes more permeated by apolar domains but, nevertheless, manages to preserve its continuity. This is analogous to a polymeric gel, where, despite the eventual swelling of the system, the interconnectivity of the cross-linked phase remains intact.68–71 The liquid organization of these model IL systems is characterized by sponge-like morphologies with interpenetrating polar and apolar networks, as shown in the representative snapshots of the model [HMIM]Cl and [DMIM]Cl IL matrices in panels B and C of Fig. 3, respectively. In a prior work, Lopes and Padua72 performed extensive atomistic simulations on a series of ILs consisting of [PF6] anions coupled with imidazolium cations with various aliphatic chains. It was found that lengthening the aliphatic chains in the imidazolium cations leads to the percolation of apolar domains within the entire simulation box. The current CGMD simulation results obtained from simplified ionic models are in qualitative agreement with experimental observations30,65–67 and computational studies23,29,34,72 in characterizing the evolution of microscopic liquid structures and ionic organization of imidazolium based ILs.
The detailed analysis on the microscopic ionic structures of these model IL systems, which is intrinsically related to the delicate trade-off between long-range electrostatic forces and local van der Waals and disperse interactions among the charged and neutral beads in the ionic models, can be obtained through calculations of site–site RDFs, 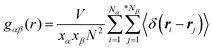 , and partial static structural factors,
, and partial static structural factors, 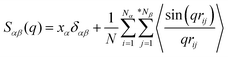 , where q is the wave vector magnitude, xα = Nα/N is the concentration of species α, δ(r) is the Dirac delta function, δαβ is the Kronecker delta function, the star on the sum implies the exclusion of self-interactions, and the angular brackets represent an ensemble average over all ionic species in the model IL simulation systems.72–75 A scaled static structural factor for the same type of ionic species is given as
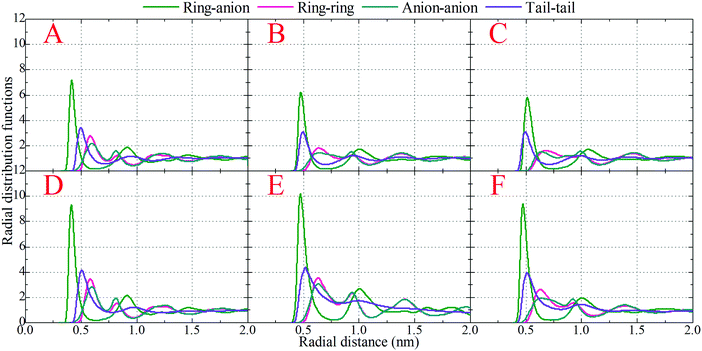
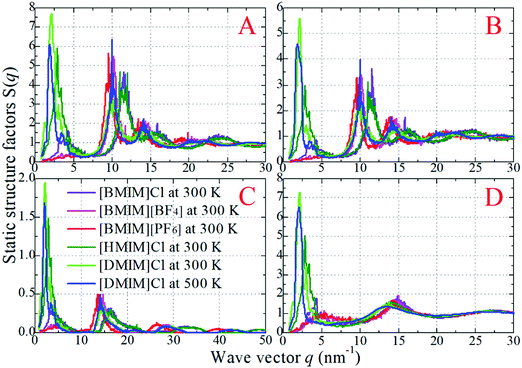
, where q is the wave vector magnitude, xα = Nα/N is the concentration of species α, δ(r) is the Dirac delta function, δαβ is the Kronecker delta function, the star on the sum implies the exclusion of self-interactions, and the angular brackets represent an ensemble average over all ionic species in the model IL simulation systems.72–75 A scaled static structural factor for the same type of ionic species is given as 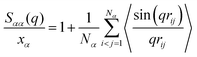 , which is convenient for a comparison of the same ionic groups in different model IL systems. In the constructed cationic models, the imidazolium ring and two closest methyl (methylene) groups are symmetrically split into two CG beads, as shown in Fig. 1. Therefore, we designate the center of these two positively charged (blue) beads as the “ring”, and the terminal neutral bead in each cationic model as the “tail”, respectively, which are used as reference sites to calculate the corresponding RDFs. Fig. 4 presents the representative RDFs for ring–ring, ring–anion, and anion–anion pairs, as well as the spatial correlations between terminal neutral beads in the cationic models, for the selected model IL systems. Accordingly, the calculated static structural factors for these representative model IL systems are provided in Fig. 5.
, which is convenient for a comparison of the same ionic groups in different model IL systems. In the constructed cationic models, the imidazolium ring and two closest methyl (methylene) groups are symmetrically split into two CG beads, as shown in Fig. 1. Therefore, we designate the center of these two positively charged (blue) beads as the “ring”, and the terminal neutral bead in each cationic model as the “tail”, respectively, which are used as reference sites to calculate the corresponding RDFs. Fig. 4 presents the representative RDFs for ring–ring, ring–anion, and anion–anion pairs, as well as the spatial correlations between terminal neutral beads in the cationic models, for the selected model IL systems. Accordingly, the calculated static structural factors for these representative model IL systems are provided in Fig. 5.
It is demonstrated that in all studied model IL systems, the ring–anion pair RDFs exhibit distinct maxima and minima at short distances (<0.75 nm), indicating the formation of well-defined solvation shells with anions around the charged beads in the cationic models, and vice versa. The existence of the second and the third peaks in the ring–anion RDFs indicates that the structural correlation is long ranged and these charged beads are strongly coupled together by means of Coulombic interactions. In addition, the distinct oscillations in spatial correlations between charged beads span beyond 2.0 nm. Such a charge-ordering phenomenon is an intrinsic characteristic of a system dominated by long-range electrostatic interactions.5,7,16,21–23,34,42,45,46,72,76
In panels A, B, and C of Fig. 4 of the model IL systems consisting of the same [BMIM] cationic model coupled with three anionic groups, it is shown that the radial distances of the first maxima in the ring–anion RDF plots are shifted toward larger values with decreased peak intensities with an increase in the size of anionic group from Cl to [PF6]. The most conspicuous feature in the partial structural factors for the ring–anion pair is the preferential peaks at around 15 nm−1, as shown in panel C of Fig. 5. These peak positions are associated with the characteristic intermolecular alternation distance d in real space via d = 2π/q. The peak positions in the partial structural factor functions for the ring–anion pair are located at 16.09 and 14.69 and 13.70 nm−1 in the model [BMIM]Cl, [BMIM][BF4], and [BMIM][PF6] IL systems at 300 K, respectively, and the corresponding characteristic distances between successive ring–anion neighbor shells are 0.39, 0.43, and 0.46 nm, respectively. These values are consistent with the peak positions in the ring–anion RDFs shown in Fig. 4. Similar microstructural changes are also observed in the ring–ring, anion–anion, and tail–tail pair RDF plots shown in Fig. 4 and the corresponding scaled partial static structural factors presented in Fig. 5.
In panels A, D, and E of Fig. 4 for systems consisting of a Cl anionic group coupled with three cationic models, lengthening the neutral chains in the cationic models leads to enhanced peak intensities in the ring–anion RDF plots. The radial distance of the first maxima in these RDFs shows negligible changes in the first two systems and is shifted to a larger value in panel E due to the formation of distinct apolar segregations in the polar framework. In addition to the changes in peak intensities and peak positions shown at q ≈ 15.0 nm−1 for the ring–anion pair in panel C of Fig. 5, significant variations are observed at lower q values at around 2.0 nm−1, indicating enhanced intermolecular correlations at intermediate radial distances with lengthened neutral chains in the cationic models. The preferential peak positions in the partial structural factors for the ring–anion pair are located at 4.23 and 2.86 and 2.18 nm−1 for the model [BMIM]Cl, [HMIM]Cl, and [DMIM]Cl IL systems at 300 K, respectively. The corresponding characteristic lengths for the ring–anion pair are 1.48, 2.19, and 2.88 nm, respectively. These values are consistent and compatible with those determined from atomistic simulations72,74 and estimated from coarse-grained simulations44,75 in prior studies. The enhanced intermolecular correlations are also embedded in the scaled partial structural factor functions for the ring–ring, anion–anion, and tail–tail pairs, which are corroborated by their respective RDF plots shown in Fig. 4 and are qualitatively visualized in Fig. 3.
The panels E and F of Fig. 4 present the RDF plots for the model [DMIM]Cl IL systems at 300 and 500 K, respectively. The peak intensities in all the pair RDF plots consistently decrease with an increase in temperature. This is clearly manifested in the static structural factors shown in Fig. 5 with decreased peak heights, and the corresponding peak positions are slightly shifted to short wave vectors. The elevated temperature promotes the thermal motions of the CG beads in the local IL matrices, preferring to loosen the microstructures and thus considerably decreasing the structural heterogeneity and the screening length in the model IL matrices.22,33,42,44
3.3 Translational dynamics
After exploring the microstructural feature, we seek to investigate the dynamical behavior of these model IL systems at different temperatures. A quantitative description of translational dynamics of the ionic groups in the IL matrices is characterized by their diffusion coefficients determined from the mean square displacements (MSDs) using the Einstein relationship, which is expressed as: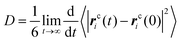 , where rci(t) denotes the center-of-mass (COM) vector coordinate of the ith ionic group at time t. The quantity 〈|rci(t) − rci(0)|2〉 represents an ensemble-averaged MSD over multiple time origins and all of the same type of ions in the simulation box to improve statistical precision.23,33,34,46,47,77,78
, where rci(t) denotes the center-of-mass (COM) vector coordinate of the ith ionic group at time t. The quantity 〈|rci(t) − rci(0)|2〉 represents an ensemble-averaged MSD over multiple time origins and all of the same type of ions in the simulation box to improve statistical precision.23,33,34,46,47,77,78
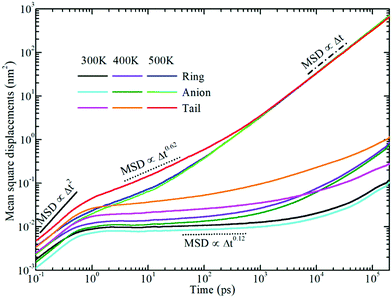
Fig. 6 displays the representative MSD plots of rings, anions, and neutral tail beads in model [BMIM]Cl IL systems at varied temperatures. All these MSD curves exhibit three distinct dynamical regimes: the ballistic, the sub-diffusive, and the true diffusive regimes. The translational motion of CG beads at short times is a fast and ballistic process due to their inertial motion in local ionic environments and the corresponding MSD plot is characterized by 〈|Δr(t)|2〉 ∝ Δt2. For these model IL systems, the ballistic diffusion of the CG beads occurs in the initial few picoseconds since the ionic groups have not interacted with their neighboring ions. An increase in temperature will shorten the time for the ballistic diffusion of these CG beads in local ionic environments.
After a long time, the motion of the CG beads becomes diffusive, and the time dependent MSD plot will change to 〈|Δr(t)|2〉 ∝ Δt. It is shown in Fig. 6 that the diffusive regime occurs at timescales of nanoseconds for the neutral terminal beads. However, the true diffusive regime for the charged beads in the cationic and anionic models is not achieved until a time scale larger than tens of nanoseconds due to strong Coulombic coordinations among them.
Between the ballistic and the diffusive regimes, there is a sub-diffusive regime, where the CG beads experience an intermediate terrain arising from the basin hopping and rattling motion of these CG beads trapped in a cage formed by the counterions for a significant duration of time without producing appreciable displacements. Such a sub-diffusive behavior is described by 〈|Δr(t)|2〉 ∝ Δtα with 0 < α < 1, and it is usually found in colloidal glasses and IL systems.77–83 This sub-diffusive feature is associated with dynamical heterogeneity in ILs due to the inconsistent relaxations of different moieties in the ionic models. The time window of the sub-diffusive plateau for the charged beads in the cationic models and anionic groups is of several nanoseconds, which is much larger than those for the neutral terminal beads in the cationic models. Additionally, the extent of the intermediate regime for the charged beads increases upon lengthening the neutral chains in the cationic models, reflecting the phase separation-induced cage hardening effect in all studied model IL systems.
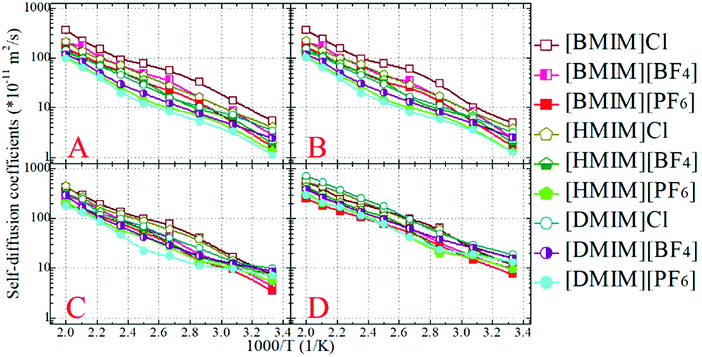
The diffusion coefficients of the COMs of the cationic and anionic models, and those of the representative beads in the cationic groups like the positively charged beads and the neutral terminal beads, are obtained from the diffusive regimes in the MSD plots and are presented in Fig. 7. The diffusion coefficients of the cationic and anionic models in all the model IL systems fall within an order of 10−11 m2 s−1 at 300 K. These CGMD simulation results are consistent with those for detailed imidazolium based IL systems determined from atomistic simulations and obtained from experimental measurements.34,46,47,77,84,85
At given temperatures, the translational diffusion of the positively charged ring beads is comparable with that of the corresponding anionic models. Such a dynamical similarity indicates a preferential association of these charged beads in the local ionic framework because of electrostatic interactions. In all cationic models, the neutral terminal beads exhibit the fastest translational diffusivities compared to the other CG beads within the cationic framework and the anionic models. This observation is even more distinct in the model IL systems with long neutral chains in the cationic models, like in the three [DMIM] based model IL systems, which can be rationalized by the librational motion of the neutral terminal beads in apolar domains. It is the fast diffusion of the neutral terminal beads and the relatively slow mobility of the positively charged beads that lead to the intermediate diffusivity of the whole cationic models in the IL matrices. This compromise contributes to the higher ionic displacement of the cationic models than that of the corresponding anionic models in all simulation systems, which is consistent with the experimental measurements and atomistic simulation results of real imidazolium based IL systems.22,33,42,44,84,85 It should be noted that in atomistic simulations, the larger diffusivity of imidazolium cations than their coupled anions is mainly attributed to the preferential translational diffusion of cations along the imidazolium ring plane.42,86 However, in the current CGMD simulations, it is difficult to observe such a tendency due to the adoption of the simplified cationic models.
The lengthening of neutral chains in the cationic models and the enlarging of anionic group size leads to a similar tendency for the cationic models with decreased translational diffusivities. The former can be rationalized by the distinct heterogeneous structures formed in the IL matrices with the gradual addition of neutral beads in the cationic models. As we addressed in the previous subsection, the polar framework consisting of charged beads manages to preserve its continuity due to strong electrostatic interactions, despite the lengthening of neutral chains in the cationic models. The addition of neutral beads to the cationic models enhances van der Waals interactions between the neutral beads. This increases the translational diffusivity of neutral terminal beads in the cationic models, which, however, in turn, compresses the translational dynamics of the charged beads due to their preferential coordination in the ionic channels. In the present CGMD simulations, these two effects synergistically contribute to the decreased diffusion of cationic models in the heterogeneous ionic matrices with the addition of neutral beads. The latter can be attributed to the molecular sizes and van der Waals interactions of the three anionic models. Both these two features are in qualitative agreement with the experimental characterizations of dynamical quantities of imidazolium based ILs.84,85
The translational diffusion coefficients of all CG beads and ionic models exhibit an exponential increase, and span three orders within the temperature range of 300–500 K. This observation indicates that the temperature dependence of translational diffusion coefficients can be depicted by the classical Arrhenius equation D = D0eEa/RT, where Ea is the activation energy. By fitting these diffusion coefficients to the given Arrhenius expression, it is found that the activation energies lie within a range of 20–35 kJ mol−1 depending on the constituent cationic and anionic groups in the model IL systems. The activation energies for charged beads in the cationic and anionic models are similar, and these values are considerably larger than those for neutral terminal beads in the corresponding cationic models. These activation energies represent the energies required to break and reform the local intermolecular structures at the nanoscopic level. As such, the structures of the charged beads are more difficult to break in “stiff” ionic channels, in contrast to the neutral terminal beads in “soft” apolar domains.
3.4 Re-orientational dynamics
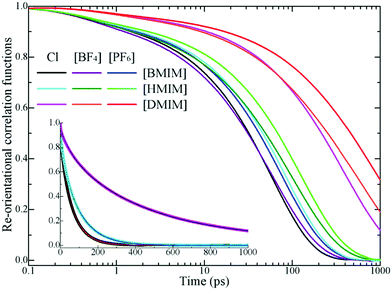
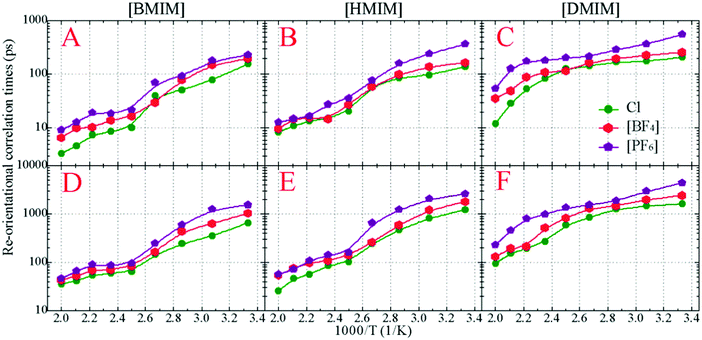
In addition to translational diffusion, the re-orientational dynamics of the cationic models have been investigated by examining the re-orientation of representative vectors ê fixed in their respective molecular frameworks.46,78,87,88 The re-orientational correlation function is defined as C(L)i(t) = 〈PL[êi(0)·êi(t)]〉, where PL is the Legendre polynomial of order L, and êi(t) is the orientation vector of the ith cationic group at time t. In the current work, we consider the first-order Legendre polynomial P1 of a unitary vector connecting two terminal beads (one is charged and the other one is neutral) in the cationic framework as this vector represents the longest geometrical axis in the cationic models and thus is expected to have the longest re-orientational relaxation time.46,87,88Fig. 8 presents the representative first-order re-orientational correlation functions of the cationic models in various IL matrices at 400 K. The decay of the re-orientational correlation functions of the three cationic models follows the order [DMIM] < [HMIM] < [BMIM], which can be rationalized by their molecular sizes. The larger the cationic model, the slower the re-orientational relaxation in local ionic environments. This observation is consistent with the translational dynamics of these cationic models in the IL matrices, as shown in panel C of Fig. 7. For IL systems consisting of the same cationic model, the effect of three anions on the re-orientational decay of the corresponding cationic models is described by [PF6] > [BF4] > Cl. Such an order is intrinsically related to their van der Waals interaction parameters. The [PF6] anions have the largest anionic size and strongest interaction parameters of the three anionic models, which promote their tight and preferential coordination with the positively charged beads in the neighboring cationic models. This, in turn, leads to the constrained translational and re-orientational dynamics of the corresponding cationic models in the heterogeneous IL matrices.
The asymptotic decay of these re-orientational correlation functions can be approximated by stretched exponential functions. It is found that the best fit of these re-orientational correlation functions is a bi-exponential function with the form of C(t) = c0 + c1e−t/τ1 + c2e−t/τ2. The accessible fitting correlation times τ1 and τ2 for all three cationic models in different model IL systems and at various temperatures are shown in Fig. 9. The fast decay mode corresponds to the free swing of neutral moieties in the cationic models in local environments and the time scale is of a hundred picoseconds. The slow re-orientational motion indicates that the backbone vectors in the cationic models lose their correlation from the original orientation, and the time scale is of nanoseconds. The decay of these two correlation modes is significantly temperature dependent. For the [BMIM] and [HMIM] cationic models, the correlation times for these two correlation modes exhibit a significant decrease within the temperature range of 300–400 K, and present negligible changes at temperatures larger than 400 K, respectively. However, the correlation times for these two correlation modes for the [DMIM] cationic models are described by a stepwise decrease as temperature increases, possibly due to their large cationic size in comparison with the [BMIM] and [HMIM] cationic models.
These two magnitudes of correlation times manifest the re-orientational heterogeneities of the charged and neutral moieties in the cationic models in microscopic environments. For cationic models with less neutral beads, such as the [BMIM] cationic model, the strong charge association cage effect is the only barrier for the cationic models to overcome before their re-orientational randomization in the IL matrices. The neutral terminal beads show a free-orientation motion due to their dispersed distribution in local ionic environments, and their influence on the re-orientational dynamics of the [BMIM] cationic model is negligible. The addition of neutral beads to the cationic models leads to the aggregation of neutral beads in apolar domains, as shown in the representative snapshots of the model [HMIM] and [DMIM] IL systems in Fig. 3. In these simulation systems, the total re-orientational relaxation of the cationic models is complicated and heterogeneous and is influenced by both polar and apolar associations. The charged moieties of the cationic models are locally liberated in the ion cages in the polar region while the neutral moieties freely swing in the segregated hydrophobic domains in the heterogeneous ionic matrices.33,42,46,77,87,89–93
The temperature dependence of these re-orientational correlation times shown in Fig. 9 is generally characterized by an Arrhenius-like feature. The obtained reorientation activation energies fall within the range of 11–23 kJ mol−1 depending on the constituent ions in the model IL systems, which are smaller than those of their translational dynamics in heterogeneous environments. Such a striking observation indicates that the dynamical quantities of the cationic models in various model IL systems are essentially determined by their translational motion. On the one hand, the charged moieties in the cationic models are essentially coordinated with the anionic groups via strong Coulombic interactions, and on the other hand, the neutral moieties in the cationic models are preferentially associated together due to their collective solvophobic intermolecular interactions. Such a two-fold spatial constraint on the cationic models leads to their constrained translational and re-orientational dynamics in the heterogeneous matrices. The marginal discrepancy between the current CGMD simulations of the bulk model IL systems and atomistic simulations of the [BMIM][BF4] IL/water mixtures89 may be attributed to the simplicity of molecular structures of the constituent ions and the reduction of the degrees of freedom in imidazolium cations and in the three anionic groups.22,33,34,44,75
4 Coulombic interactions – some considerations
In this section, we have studied the effect of Coulombic interactions on the computational results discussed above. We have also studied the efficiency of the calculation of Coulombic interactions using the representative Ewald summation methods when extending the length and time scales far beyond what has been used in previous CGMD simulations of model IL systems. These simulations were performed using GPU facilities offering substantial speed-ups on economically affordable computers. It is of particular interest to compare the performance of a cheap graphics card with a more expensive card designed for scientific computations.4.1 Effect of electrostatic interactions on structural and dynamical properties
In order to gain a better physical insight into the effect of Coulombic interactions on correlations between the liquid structures and dynamics in the model IL systems, we have performed CGMD simulations on the neutral analogues of the model IL systems in which only the van der Waals interaction parameters of the CG beads were kept but all electrostatic interactions between partial charges were switched off. The artificially neutral model systems clearly show considerable variations in their thermodynamics in comparison with those of their ionic counterparts. In all studied neutral systems, the lack of electrostatic interactions between the CG beads decreases the density of neutral mixtures by approximately 25% and the corresponding liquid compressibility by a factor of 3.1 at 400 K. This observation is consistent with the coarse-grained computational results of the [BMIM][PF6] IL system with a similar treatment of electrostatic interactions conducted by Roy and Maroncelli.46 It is noteworthy from the additional NPT simulations at 300 K that the decrease in liquid densities for the neutral mixtures falls within the range of 15–21%, which is comparable with the change of approximately 19% reported in the experimental measurements of pyrrolidinium based ILs and their neutral counterparts.94 It is likely that these thermodynamic properties might be exaggerated in the present model IL systems in comparison with the real IL systems due to the adoption of simplified ionic models. In addition, we performed canonical (NVT) simulations on the neutral model systems at the same densities as those of the corresponding ionic systems at 400 K, from which we can make a direct evaluation of the effect of electrostatic interactions on the liquid structures and dynamics of the model systems. Fig. 10 presents the site–site RDFs and MSDs of the representative beads in the model [DMIM][BF4] IL system and its neutral counterpart at 400 K, as well as the representative snapshots of these two systems.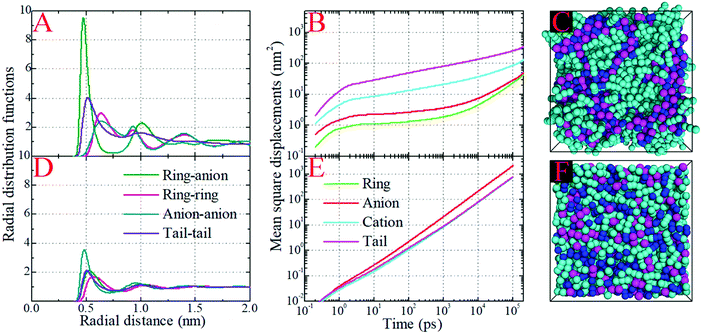 | ||
| Fig. 10 Comparison of radial distribution functions and mean square displacements of representative beads in the model [DMIM][BF4] IL system and its neutral counterpart at 400 K, and the representative snapshots of these two systems. The color codes of these coarse-grained beads are the same as those shown in Fig. 1. | ||
The first and most distinct difference is the decrease in the peak intensities of the ring–anion and tail–tail RDFs obtained from the neutral model system in comparison with its ionic counterpart. The second notable change is that the first peak in the anion–anion RDF plot is intensified and the corresponding radial distance shifts to a short distance in the neutral model system. These two observations can be related to the removal of electrostatic interactions between CG beads, which will loosen the liquid structures leading to an almost homogeneous distribution of neutral models in the simulation box. Additionally, the neutral model system has less “charge” ordering structures than the ionic model system at large radial distance. These computational results can be visually corroborated by the representative snapshots of the ionic and neutral model systems shown in panels C and F of Fig. 10, respectively. The charged beads in the ionic model system present distinct ordering structures and form a continuous tridimensional framework of interpenetrating ionic channels throughout the entire simulation box, whereas these CG beads exhibit a sort of random fluctuation in the neutral model system. This visualization suggests that the ionic model system can be considered as a distorted lattice structure of interleaved cation and anion arrays. The strong electrostatic interactions between the charged beads demanding a high penalty for improper charge balance, and the preferential solvophobic interactions between neutral beads in the model cationic groups, dictate the local ionic structures in the bulk IL matrices. However, in the neutral model system, the repulsive (packing) and entropic forces between neutral CG beads dominate the liquid structures, which are characterized by a uniform and loose distribution of neutral beads in liquid environments.46,87,93
The MSD analysis provides a comprehensive difference between the dynamical quantities of CG beads in the ionic and neutral systems. The detailed analysis of the MSD plots of the ionic systems is described in Fig. 6 and in Section 3.3. However, the MSD plots of the representative groups in the neutral model system exhibit distinct characteristics. For all CG beads and neutral models, the on-set times for the ballistic and diffusive regimes are greatly shifted to short time scales. The absence of electrostatic interactions between CG beads makes their intermolecular interactions very much softer. It is easier for these neutral beads to escape from the local cage formed by the surrounding neutral beads, and the corresponding time scale is shortened to tens of picoseconds. Also, the removal of electrostatic interactions between CG bead leads to their increased translational diffusivities. Neutral anionic groups exhibit the fastest translational mobility in the liquid matrices. The translational diffusivities of representative beads in the “cationic” models and the whole “cationic” models are characterized by uniform translational dynamics due to their “covalently bonded” molecular structures.
4.2 Efficiency in calculations of Coulombic interactions using Ewald summation-based methods
In the past few decades, a large variety of computational schemes have been proposed to handle electrostatic interactions in ionic systems under partial or full periodic boundary conditions.52,53,57,58,76,95–101 The Ewald summation method is believed to give the most realistic representation of electrostatic interactions in ionic systems under periodic boundary conditions.95 However, the traditional Ewald summation method suffers from drawbacks as the number of charged ions grows due to its intrinsic computational inefficiency, and thus the calculation of electrostatic interactions becomes the major bottleneck in molecular simulations of ionic systems.102 The particle mesh based methods, including the PPPM Ewald summation method proposed by Hockney and Eastwood in 1970s,52,53 the PME method,57,58 and later the smooth PME method,76,97,99 hold particular significance in dealing with electrostatic interactions with varied computational efficiencies. The essential idea of these particle mesh based methods is to adopt the fast Fourier transform (FFT) technique, which can drastically reduce the computational complexity in treating ionic systems.In prior studies, we suggested a novel approach, the Ewald summation method based on the Non-Uniform FFT technique called ENUF, to calculate electrostatic energies and forces between charged ions.54 The ENUF method was implemented in classical MD simulations and the dissipative particle dynamics (DPD) method.54–56 By using ENUF in MD and DPD simulations, both the electrostatic energy and momentum are conserved to floating point accuracy. With a judicious selection of the related physical parameters, the ENUF method behaves as the direct Ewald summation method with a desired accuracy while it presents a remarkable O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) linearly scaling computational efficiency. In subsequent studies, the ENUF method was implemented using the GPU and CUDA technology with a combined CPU–GPU parallelization strategy in the GALAMOST package.51,59,60 In this subsection, we present a preliminary test on the computational efficiency of the ENUF method in comparison with the PPPM Ewald summation method in the same GALAMOST framework, and with the PME method implemented in the GROMACS package.
N) linearly scaling computational efficiency. In subsequent studies, the ENUF method was implemented using the GPU and CUDA technology with a combined CPU–GPU parallelization strategy in the GALAMOST package.51,59,60 In this subsection, we present a preliminary test on the computational efficiency of the ENUF method in comparison with the PPPM Ewald summation method in the same GALAMOST framework, and with the PME method implemented in the GROMACS package.
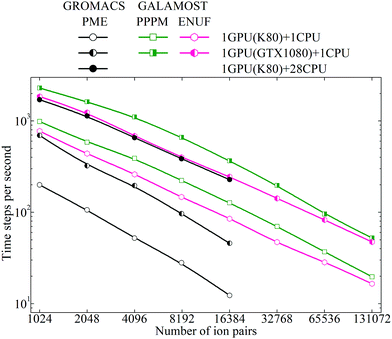
The CGMD simulations starting from an equilibrated initial configuration of the model [DMIM][BF4] IL system were performed in the NVT ensemble, using a leapfrog integrator, at single precision and dynamic load balancing, and similar simulation parameters unless stated otherwise. The buffer size (skin length) was set to 0.5 (approximately 0.25 nm in atomic unit), and the neighbor lists were heuristically updated every 10 time steps. These parameters were determined as the value that can yield the highest number of time steps per second (TPS) in a preliminary tuning run, and the distance check criterion was applied with the minimum frequency at which no dangerous builds were observed. Additional CGMD simulations on the model [DMIM][BF4] IL systems were performed using the GROMACS package for a comparison. The performance of these CGMD simulations quantified as TPS is given in Fig. 11.
Both for the PPPM Ewald summation method and for the ENUF method, the performance of the GTX 1080 is much faster than that of the K80 GPUs, which is inherent to the underlying architecture in these two GPU cards. For both GPU cards, the performance of the PPPM Ewald summation method appears better than that of the ENUF method by roughly 50% on small and intermediate simulation system sizes. However, the performance of these two methods becomes comparable for larger simulation systems and roughly equal with the number of ions exceeding 0.2 million. In principle, the computational efficiency of these two methods should be comparable, as seen in our previous investigations.54–56 However, in the practical use and implementation of the ENUF method, there are more physical parameters to be set and optimized than for the PPPM Ewald summation method. This is described in the Appendix “Implementation of the ENUF method in the GALAMOST package” below. Setting up these parameters will affect the computational efficiency of the ENUF method when applied to calculate electrostatic energies and forces for a complex charged system such as ILs. We expect to considerably improve the computational efficiency of the ENUF method by exploiting multiple parallelism at various levels in the new version of GALAMOST, which was recently released.51 The CGMD simulations of complex IL systems will gain from the optimized parallelization strategy of the multiple GPU GALAMOST together with the improved performance offered by the GPU cards in comparison with CPUs.
In each time step calculation, the GALAMOST package maximizes the amount of computations on the GPU cards and eliminates the need for any significant amount of communication between the GPU and the main memory or CPU, except when it is necessary to perform disk input/output. By avoiding both serial code bottlenecks and slow memory transfers between the host and device, the GALAMOST package reaches the maximum performance using a single GPU card.
The CGMD simulations of the model [DMIM][BF4] IL systems running on the K80 GPU using the GROMACS package exhibit excellent scaling properties up to 28 Intel Xeon E5-2690v4 CPU processors due to the optimum use of cache and the extremely high intra-node MPI (message passing interface) bandwidth. For smaller system sizes, the performance of the ENUF method in the GALAMOST package is better than the PME method in the GROMACS package on the same device. However, it is difficult to accurately quantify the computational performance of GALAMOST and GROMACS for the model [DMIM][BF4] IL systems at the current stage since these two packages support different features with different computational demands, and the parameter settings for optimal performance can differ between these two packages.
5. Summary and concluding remarks
ILs represent an intriguing class of molten salts with melting points below 100 °C. Compared with traditional molten salts, one fascinating feature of ILs is that they exhibit distinct heterogeneous microstructures and dynamics spanning multiple length and time scales. This requires that the size of the simulation system should be larger than the characteristic length of nanostructures in ILs, and long time simulations should be performed to improve the reliability of computational results because of the sluggish dynamics of the ionic groups in heterogeneous IL matrices. The CG models provide a valuable and preferred procedure to perform extensive simulations at a modest computational cost. In the current work, we have modified our previously constructed model to become a generic IL model representing imidazolium cations with varied aliphatic chains. The anionic groups including Cl, [BF4], and [PF6] are represented by single beads with various interaction parameters, which are derived from the corresponding atomistic analogues.CGMD simulations were performed on representative model IL systems to address the influence of neutral chain length in the cationic models, molecular size of anionic groups, and temperature on the microstructural and dynamical heterogeneities of ionic groups in the liquid matrices. The liquid densities obtained using the generic CG IL models are all in reasonable agreement with those measured experimentally for real IL systems. Lengthening the neutral alkyl chains in the cationic models leads to an aggregation of neutral beads and promotes the formation of spatially heterogeneous apolar domains dispersed in ionic channels. Accordingly, the liquid morphologies of the model IL systems are transformed from the one described by dispersed neutral (apolar) beads in a tridimensional framework of ionic channels throughout the entire simulation box to that characterized by bi-continuous sponge-like interpenetrating polar and apolar networks in liquid matrices. This microstructural evolution in the model IL matrices can be rationalized by a competition of short-range collective interactions between the neutral beads and long-range Coulombic interactions between the charged head groups in the cationic models and anions.
The translational diffusion coefficients of the model ionic groups present a gradual decrease upon lengthening of the neutral chains in the cationic models and enlarging the molecular size of the anionic groups. The neutral terminal beads exhibit faster translational mobility than their charged counterparts. Such a feature is even more distinct in the cationic models with long neutral chains, which is rationalized by the librational motion of neutral terminal beads in apolar domains. The temperature dependence of diffusion coefficients of all the representative beads in the ionic models is described by a classical Arrhenius relationship. The re-orientational dynamics of the cationic models in various IL matrices are characterized by a bi-exponential structural relaxation behavior. The larger the cationic model, the slower its re-orientational relaxation in local ionic environments. Re-orientational correlation times for the two re-orientational modes are significantly temperature dependent, and strongly related to cationic structures, indicating the re-orientational heterogeneities of the charged and neutral moieties in the cationic models in microscopic environments.
It should be mentioned that although these three coarse-grained imidazolium cations ([BMIM], [HMIM], and [DMIM]) and three simple spherical anions (Cl, [BF4], and [PF6]) were used as prototype ions in the current work giving reasonable results, it is not expected that such simple ionic models can reproduce all physical properties of the corresponding real IL systems. Therefore, no rigorous optimization was attempted in force field parameters and no direct comparison of the obtained microstructural and dynamical quantities was made with real IL systems obtained from experimental measurements except for liquid densities. Instead, we believe that a reasonable choice of force field parameters can lead to generic ionic models whose physical properties will fall within the range that is available in real IL systems. Indeed, both the microstructures and dynamical properties of the model IL systems are consistent with the available experimental data, indicating that the constructed ionic models can qualitatively describe representative physical and structural properties of real IL systems.
Additional CGMD simulations were carried out on the neutral analogues of model [DMIM][BF4] IL systems in which all partial charges were removed from these models. The removal of electrostatic interactions in the ionic models tends to loosen liquid structures leading to an almost homogeneous and interleaved distribution of neutral “ionic” models resembling a distorted ionic lattice in the entire simulation box. This visual microstructural change is manifested in detailed characterizations, such as the liquid densities, radial distribution functions, and translational dynamics of representative beads in neutral and ionic models. This observation highlights the critical role of electrostatic interactions in describing distinctive structural and dynamical heterogeneities of model IL systems.
Concerning the critical role of electrostatic interactions in describing the physicochemical properties of model ILs, we incorporated the ENUF method in the GALAMOST package to handle electrostatic interactions in atomistic and coarse-grained simulations. In the current work, we performed a set of preliminary tests on the model [DMIM][BF4] IL systems using different GPUs to explore the efficiency of the ENUF method in comparison with the PPPM Ewald summation method. The ENUF method presents distinct efficiency within the GALAMOST framework in treating long-range electrostatic interactions. A further improvement on the computational efficiency of this method by exploiting multiple parallelism at various levels will be the focus of our future work.
In the not so far future, we expect that the high-throughput trend will become increasingly accentuated: despite massively increased computational power, researchers have been reluctant to merely push long time simulations. Instead of extending a single simulation of the model system to the microsecond or even the second level, many researchers may rather use the same amount of computing time for a set of “short” time simulations to provide reliable computational statistics. This is similar to the ad hoc topics on deep and machine learning techniques in designing novel materials for specific applications. Fundamentally, we hope that this tendency is a scientifically sound development, and one that is likely to move molecular simulations and modeling from compute-centric to data-centric approaches more similar to other methods used in bioinformatics and the materials genome initiative.
Summing up, the constructed cationic and anionic models are intended to be idealized ionic models representing cations with a polar head group and simple spherical anions, respectively. These generic ionic models should be suitable for investigating the solute-based dynamics of model IL systems and other phenomena occurring at long time scales, which are not feasible with first-principles calculations or ab initio and atomistic simulations.
Conflicts of interest
There are no conflicts to declare.Appendix
Overview of the implementation of the ENUF method in the GALAMOST package
Herein, we give a simple description of the implementation of the ENUF method in the GALAMOST package.50,51 The detailed formulation of the ENUF method and its implementation in classical MD simulations and in the DPD framework are available in ref. 54–56.We consider a simulation system composed of N charged beads, each one carrying a partial charge qi at position ri in a cubic cell with the volume of V = L3. Herein, we only consider the charge–charge interaction for simplicity. The interactions between instantaneous dipoles, induced dipoles, quadrupoles, and multipoles are omitted in the current scheme. An overall charge neutrality is assumed in the simulation system. Charges interact with each other according to the Coulomb's law, and the total electrostatic energy of the simulation system can be written as
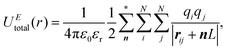 | (1) |
In the Ewald summation method, the electrostatic energy in eqn (1) is decomposed into real (UEreal(r)) and reciprocal (UEreciprocal(r)) space contributions, and a self-interaction term (UEself(r)) as
| UEtotal(r) = UEreal(r) + UEreciprocal(r) + UEself(r), | (2) |
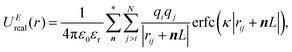 | (3) |
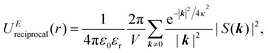 | (4) |
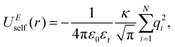 | (5) |
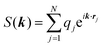 and
and 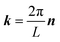 . κ is the Ewald convergence parameter and determines the relative convergence rate between the real and reciprocal space summations. k is the rescaled magnitude of the reciprocal vector n. With such a decomposition, both the real and reciprocal space contributions are short ranged and can be properly handled in their respective space.57,58,96–99
. κ is the Ewald convergence parameter and determines the relative convergence rate between the real and reciprocal space summations. k is the rescaled magnitude of the reciprocal vector n. With such a decomposition, both the real and reciprocal space contributions are short ranged and can be properly handled in their respective space.57,58,96–99
The ENUF method combines the traditional Ewald summation method with the non-uniform FFT technique to calculate electrostatic interactions between point charges.54–56 For a fixed vector k, the structure factor S(k) is a complex number. With the normalized locations of charged beads, xj = rj/L, the structure factor S(k) can be expressed with 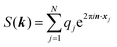 , which has the same structural format as the three-dimensional case of transposed FFT. By viewing the structure factor S(k) as a trigonometric polynomial
, which has the same structural format as the three-dimensional case of transposed FFT. By viewing the structure factor S(k) as a trigonometric polynomial ![[f with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0066_0302.gif) k, the reciprocal space electrostatic energy is recast and described by
k, the reciprocal space electrostatic energy is recast and described by
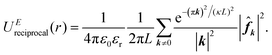 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) with distinct accuracy and efficiency in handling electrostatic interactions between point charges in classical MD simulations.54,56
N) with distinct accuracy and efficiency in handling electrostatic interactions between point charges in classical MD simulations.54,56
In the GALAMOST package, the real space contribution to the total electrostatic energy is available in the Ewald force module and is calculated together with non-bonded van der Waals interactions within the same cut-off distance. The related physical parameters in the Ewald force module are specific cut-off radius and κ. The reciprocal space contribution to the total electrostatic energy is labelled as ENUF force module and is calculated using the non-uniform FFT technique. The parameters in the ENUF force module are κ, hyper sampling factor σ, precision factor P and the number of grid points nx, ny, and nz in three dimensions. The ENUF force module provides three CUDA kernel functions, a forward and three inverse FFT procedures. The detailed computational algorithm is provided in Table 2.
| 0: Require |
N
ions – the number of charged particles in the simulation system. Ngrid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) points = nx × ny × nz – the number of grid points in the reciprocal space. points = nx × ny × nz – the number of grid points in the reciprocal space. |
| cuFFT – the NVIDIA CUDA fast Fourier transform library. | |
| 1: Spreading | The kernel function of charges spreads with Nions CUDA threads. The order of spreading is P × 2 + 2. |
| 2: FFT | One time forward fast Fourier transform using the cuFFT library. |
| 3: Subdividing | The kernel functions of dividing grid cells into smaller ones for oversampling with Ngrid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) points CUDA threads. points CUDA threads. |
| The numbers of divided cells are σ × nx, σ × ny and σ × nz in three dimensions. | |
| 4: Inverse FFT | Three times inverse fast Fourier transforms using the cuFFT library. |
| 5: Interpolating | The kernel functions of force calculation by interpolating Nions CUDA threads. |
| The order of interpolation is P × 2 + 2. |
Acknowledgements
Y.-L. Wang gratefully acknowledges financial support from the Knut and Alice Wallenberg Foundation. A. Laaksonen acknowledges the Swedish Science Council for financial support. This work was partially supported by the National Science Foundation of China (21534004). All molecular simulations were performed using computational resources provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N) in Umeå University.References
- P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, 2000 Search PubMed.
- T. A. Witten, Rev. Mod. Phys., 1999, 71, S367 CrossRef.
- P.-G. De Gennes, Rev. Mod. Phys., 1992, 64, 645 CrossRef.
- W. C. Poon and D. Andelman, Soft Condensed Matter Physics in Molecular and Cell Biology, CRC Press, 2006 Search PubMed.
- A. Naji, S. Jungblut, A. G. Moreira and R. R. Netz, Physica A, 2005, 352, 131–170 CrossRef.
- R. Messina, J. Phys.: Condens. Matter, 2009, 21, 113102 CrossRef PubMed.
- K. A. Sharp and B. Honig, Annu. Rev. Biophys. Biophys. Chem., 1990, 19, 301–332 CrossRef PubMed.
- C. Holm, P. Kékicheff and R. Podgornik, Electrostatic Effects in Soft Matter and Biophysics: Proceedings of the NATO Advanced Research Workshop on Electrostatic Effects in Soft Matter and Biophysics Les Houches, France, Springer Science & Business Media, 2012.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef.
- G. S. Manning, Annu. Rev. Phys. Chem., 1972, 23, 117–140 CrossRef.
- T. D. Yager, C. T. McMurray and K. Van Holde, Biochemistry, 1989, 28, 2271–2281 CrossRef PubMed.
- S. McLaughlin, Annu. Rev. Biophys. Biophys. Chem., 1989, 18, 113–136 CrossRef PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef PubMed.
- E. W. Castner Jr, C. J. Margulis, M. Maroncelli and J. F. Wishart, Annu. Rev. Phys. Chem., 2011, 62, 85–105 CrossRef PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef PubMed.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621 CrossRef PubMed.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150 RSC.
- F. Zhou, Y. Liang and W. Liu, Chem. Soc. Rev., 2009, 38, 2590–2599 RSC.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- Y. Wang, S. Izvekov, T. Yan and G. A. Voth, J. Phys. Chem. B, 2006, 110, 3564–3575 CrossRef PubMed.
- Y.-L. Wang, B. Li, S. Sarman and A. Laaksonen, J. Chem. Phys., 2017, 147, 224502 CrossRef PubMed.
- Y.-L. Wang, M. Golets, B. Li, S. Sarman and A. Laaksonen, ACS Appl. Mater. Interfaces, 2017, 9, 4976–4987 Search PubMed.
- Y.-L. Wang, A. Laaksonen and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2013, 15, 13559–13569 RSC.
- B. Wu, Y. Yamashita, T. Endo, K. Takahashi and E. W. Castner Jr, J. Chem. Phys., 2016, 145, 244506 CrossRef PubMed.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef PubMed.
- K. Fujii, R. Kanzaki, T. Takamuku, Y. Kameda, S. Kohara, M. Kanakubo, M. Shibayama, S.-I. Ishiguro and Y. Umebayashi, J. Chem. Phys., 2011, 135, 244502 CrossRef PubMed.
- K. Shimizu, C. E. Bernardes and J. N. Canongia Lopes, J. Phys. Chem. B, 2014, 118, 567–576 CrossRef PubMed.
- A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641–4644 CrossRef PubMed.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, T. G. Youngs and D. T. Bowron, J. Chem. Phys., 2010, 133, 074510 CrossRef PubMed.
- S. Gabl, C. Schröder and O. Steinhauser, J. Chem. Phys., 2012, 137, 094501 CrossRef PubMed.
- H. Karimi-Varzaneh, F. Müller-Plathe, S. Balasubramanian and P. Carbone, Phys. Chem. Chem. Phys., 2010, 12, 4714–4724 RSC.
- Y. Wang, S. Feng and G. A. Voth, J. Chem. Theory Comput., 2009, 5, 1091–1098 CrossRef PubMed.
- A. Lyubartsev, A. Mirzoev, L. Chen and A. Laaksonen, Faraday Discuss., 2010, 144, 43–56 RSC.
- A. Lyubartsev, A. Naômé, D. Vercauteren and A. Laaksonen, J. Chem. Phys., 2015, 143, 243120 CrossRef PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef PubMed.
- M. G. Saunders and G. A. Voth, Annu. Rev. Biophys., 2013, 42, 73–93 CrossRef PubMed.
- C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357–4366 RSC.
- Y.-L. Wang, S. Sarman, B. Li and A. Laaksonen, Phys. Chem. Chem. Phys., 2015, 17, 22125–22135 RSC.
- B. Li, K. Ma, Y.-L. Wang, M. Turesson, C. E. Woodward and J. Forsman, Phys. Chem. Chem. Phys., 2016, 18, 8165–8173 RSC.
- M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 1744–1752 CrossRef.
- S. Izvekov and G. A. Voth, J. Chem. Phys., 2005, 123, 134105 CrossRef PubMed.
- Y.-L. Wang, A. Lyubartsev, Z.-Y. Lu and A. Laaksonen, Phys. Chem. Chem. Phys., 2013, 15, 7701–7712 RSC.
- Y.-L. Wang, F. U. Shah, S. Glavatskih, O. N. Antzutkin and A. Laaksonen, J. Phys. Chem. B, 2014, 118, 8711–8723 CrossRef PubMed.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef PubMed.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 12629–12631 CrossRef PubMed.
- C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687–7693 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- Y.-L. Zhu, H. Liu, Z.-W. Li, H.-J. Qian, G. Milano and Z.-Y. Lu, J. Comput. Chem., 2013, 34, 2197–2211 CrossRef PubMed.
- Y.-L. Zhu, D. Pan, Z.-W. Li, H. Liu, H.-J. Qian, Y. Zhao, Z.-Y. Lu and Z.-Y. Sun, Mol. Phys., 2018, 116, 1065–1077 CrossRef.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, 1988, CRC Press Search PubMed.
- J. Eastwood, R. Hockney and D. Lawrence, Comput. Phys. Commun., 1984, 35, C618–C619 CrossRef.
- F. Hedman and A. Laaksonen, Chem. Phys. Lett., 2006, 425, 142–147 CrossRef.
- Y.-L. Wang, A. Laaksonen and Z.-Y. Lu, J. Comput. Phys., 2013, 235, 666–682 CrossRef.
- Y.-L. Wang, F. Hedman, M. Porcu, F. Mocci and A. Laaksonen, Appl. Math., 2014, 5, 520–541 Search PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef.
- H. G. Petersen, J. Chem. Phys., 1995, 103, 3668–3679 CrossRef.
- S.-C. Yang, Y.-L. Wang, G.-S. Jiao, H.-J. Qian and Z.-Y. Lu, J. Comput. Chem., 2016, 37, 378–387 CrossRef PubMed.
- S.-C. Yang, Z.-Y. Lu, H.-J. Qian, Y.-L. Wang and J.-P. Han, Comput. Phys. Commun., 2017, 220, 376–389 CrossRef.
- H. Machida, Y. Sato and R. L. Smith, Fluid Phase Equilib., 2008, 264, 147–155 CrossRef.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2007, 52, 1080–1085 CrossRef.
- M. Iguchi, Y. Hiraga, Y. Sato, T. M. Aida, M. Watanabe and R. L. Smith Jr, J. Chem. Eng. Data, 2014, 59, 709–717 CrossRef.
- S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517 CrossRef.
- D. Xiao, L. G. Hines Jr, S. Li, R. A. Bartsch, E. L. Quitevis, O. Russina and A. Triolo, J. Phys. Chem. B, 2009, 113, 6426–6433 CrossRef PubMed.
- A. Triolo, O. Russina, B. Fazio, G. B. Appetecchi, M. Carewska and S. Passerini, J. Chem. Phys., 2009, 130, 164521 CrossRef PubMed.
- O. Russina, A. Triolo, L. Gontrani, R. Caminiti, D. Xiao, L. G. Hines Jr, R. A. Bartsch, E. L. Quitevis, N. Plechkova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121 CrossRef.
- S. Schneider and P. Linse, Macromolecules, 2004, 37, 3850–3856 CrossRef.
- S. Edgecombe and P. Linse, Langmuir, 2006, 22, 3836–3843 CrossRef PubMed.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC.
- B. A. Mann, C. Holm and K. Kremer, J. Chem. Phys., 2005, 122, 154903 CrossRef PubMed.
- J. N. Canongia Lopes and A. A. Padua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef PubMed.
- B. M. Weight and A. R. Denton, J. Chem. Phys., 2018, 148, 114904 CrossRef PubMed.
- S. M. Urahata and M. C. Ribeiro, J. Chem. Phys., 2004, 120, 1855–1863 CrossRef PubMed.
- B. L. Bhargava, R. Devane, M. L. Klein and S. Balasubramanian, Soft Matter, 2007, 3, 1395–1400 RSC.
- T. Darden, A. Toukmaji and L. Pedersen, J. Chim. Phys. Phys.-Chim. Biol., 1997, 94, 1346–1364 CrossRef.
- Y.-L. Wang, Z.-Y. Lu and A. Laaksonen, Phys. Chem. Chem. Phys., 2014, 16, 20731–20740 RSC.
- Y.-L. Wang, M. R. Shimpi, S. Sarman, O. N. Antzutkin, S. Glavatskih, L. Kloo and A. Laaksonen, J. Phys. Chem. B, 2016, 120, 7446–7455 CrossRef PubMed.
- M. Sánchez-Miranda, B. Bonilla-Capilla, E. Sarmiento-Gómez, E. Lázaro-Lázaro, A. Ramírez-Saito, M. Medina-Noyola and J. Arauz-Lara, Soft Matter, 2015, 11, 655–658 RSC.
- E. R. Weeks and D. Weitz, Chem. Phys., 2002, 284, 361–367 CrossRef.
- C. Gutsche, U. Keyser, K. Kegler, F. Kremer and P. Linse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031403 CrossRef PubMed.
- Z. Hu and C. J. Margulis, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 831–836 CrossRef PubMed.
- Z. Hu and C. J. Margulis, Acc. Chem. Res., 2007, 40, 1097–1105 CrossRef PubMed.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110 CrossRef PubMed.
- H. Liu and E. Maginn, J. Chem. Phys., 2011, 135, 124507 CrossRef PubMed.
- S.-W. Park, S. Kim and Y. Jung, Phys. Chem. Chem. Phys., 2015, 17, 29281–29292 RSC.
- S. Zahn, K. Wendler, L. Delle Site and B. Kirchner, Phys. Chem. Chem. Phys., 2011, 13, 15083–15093 RSC.
- M. Sha, Y. Liu, H. Dong, F. Luo, F. Jiang, Z. Tang, G. Zhu and G. Wu, Soft Matter, 2016, 12, 8942–8949 RSC.
- B. Aoun, M. A. González, J. Ollivier, M. Russina, Z. Izaola, D. L. Price and M.-L. Saboungi, J. Phys. Chem. Lett., 2010, 1, 2503–2507 CrossRef.
- K. Nakamura and T. Shikata, ChemPhysChem, 2010, 11, 285–294 CrossRef PubMed.
- V. V. Matveev, D. A. Markelov, E. A. Brui, V. I. Chizhik, P. Ingman and E. Lähderanta, Phys. Chem. Chem. Phys., 2014, 16, 10480–10484 RSC.
- S. Kim, S.-W. Park and Y. Jung, Phys. Chem. Chem. Phys., 2016, 18, 6486–6497 RSC.
- H. Shirota and E. W. Castner, J. Phys. Chem. A, 2005, 109, 9388–9392 CrossRef PubMed.
- P. P. Ewald, Ann. Phys., 1921, 64, 253–287 CrossRef.
- D. York and W. Yang, J. Chem. Phys., 1994, 101, 3298–3300 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef.
- Y. Shan, J. L. Klepeis, M. P. Eastwood, R. O. Dror and D. E. Shaw, J. Chem. Phys., 2005, 122, 054101 CrossRef PubMed.
- B. Linse and P. Linse, J. Chem. Phys., 2014, 141, 184114 CrossRef PubMed.
- A. Arnold and C. Holm, Chem. Phys. Lett., 2002, 354, 324–330 CrossRef.
- P. Linse and H. C. Andersen, J. Chem. Phys., 1986, 85, 3027–3041 CrossRef.
- F. Hedman and A. Laaksonen, Mol. Simul., 1995, 14, 235–244 CrossRef.
Footnote |
| † In warm memory of our close colleague and dear friend, Per Linse. |
| This journal is © The Royal Society of Chemistry 2018 |