Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing nano-scale viscoelastic response in air and in liquid with dynamic atomic force microscopy
Federica
Crippa
 a,
Per-Anders
Thorén
a,
Per-Anders
Thorén
 b,
Daniel
Forchheimer
b,
Daniel
Forchheimer
 b,
Riccardo
Borgani
b,
Riccardo
Borgani
 b,
Barbara
Rothen-Rutishauser
b,
Barbara
Rothen-Rutishauser
 a,
Alke
Petri-Fink
a,
Alke
Petri-Fink
 ac and
David B.
Haviland
ac and
David B.
Haviland
 *b
*b
aAdolphe Merkle Institute, University of Fribourg, BioNanomaterials Group, Chemin des Verdiers 4, CH-1700 Fribourg, Switzerland. E-mail: federica.crippa@unifr.ch
bKTH Royal Institute of Technology, Nanostructure Physics, Albanova, SE-10791 Stockholm, Sweden. E-mail: pathoren@kth.se
cUniversity of Fribourg, Department of Chemistry, Chemin du Musée 8, CH-1700 Fribourg, Switzerland
First published on 17th April 2018
Abstract
We perform a comparative study of dynamic force measurements using an Atomic Force Microscope (AFM) on the same soft polymer blend samples in both air and liquid environments. Our quantitative analysis starts with calibration of the same cantilever in both environments. Intermodulation AFM (ImAFM) is used to measure dynamic force quadratures on the same sample. We validate the accuracy of the reconstructed dynamic force quadratures by numerical simulation of a realistic model of the cantilever in liquid. In spite of the very low quality factor of this resonance, we find excellent agreement between experiment and simulation. A recently developed moving surface model explains the measured force quadrature curves on the soft polymer, in both air and liquid.
I. Introduction
Applications in biology such as stiffness measurements on cancer cells or characterization of extremely soft gels1–5 require an understanding of interfacial properties in an aqueous environment. Not only the surface topography but also the viscoelasticity of biomimetic scaffolds affects the interaction between cells and their environment, in phenomena such as cellular adhesion, differentiation and migration.6–8 An atomic force microscope (AFM)9 is well suited to study such viscoelastic responses, and various methods have been used to investigate single cells10,11 and intracellular compartments such as cytoskeleton and nucleus12,13 and to compare physiological and pathological conditions.1,14The AFM is a versatile tool for the micro- and nano-scale characterization of surfaces, with applications from mapping of topography15 to the quantitative measurements of contact, electrostatic or magnetic forces between the tip and the surface.16–19 The AFM is frequently performed in air and in the vacuum where the cantilever's mechanical resonance has a high quality factor, but there are many applications of quantitative AFM in liquid environments where the quality factor is relatively low.20–23 A liquid environment is challenging for quantitative AFM due to the large inertial and viscous forces acting on the cantilever body, which complicate calibration and call into question the standard model of transduction between the tip–surface force and beam deflection – the starting points for quantitative surface analysis with the AFM.
Elastic response, or the tip–surface force resulting from static deformation of a cell or a substrate, is typically inferred from the quasi-static force–distance curve. Such curves are measured under the assumption that the tip–surface force is linearly dependent on cantilever deflection (Hooke's law) when the probe is moved toward and away from the surface at sufficiently low (and constant) velocity.24 Viscous response, or the tip–surface force that depends on velocity, requires a dynamic method of measurement.25–27 With dynamic methods, care must be taken to understand and calibrate the frequency-dependent relationship between the tip–surface and cantilever deflection, which changes radically from an air to liquid environment.
The dynamic method used in this study is called Intermodulation AFM (ImAFM).25 A special multi-frequency lockin amplifier captures many Fourier coefficients of the motion (i.e. both amplitude and phase at many frequencies) which are the result of frequency mixing (intermodulation) of two or more discrete frequency components in the drive waveform. Our work reports the first experimental results and the analysis of ImAFM in liquid. In spite of the low quality factor and significant hydrodynamic load of the liquid, we find that ImAFM can reconstruct both the viscous and elastic forces due to the interaction between the tip and the surface. We show that force reconstruction using the so-called dynamic force quadrature curves28 works remarkably well in liquid. We verify its accuracy by reconstructing the known force quadrature curves from simulated data using a realistic model for the cantilever oscillating in liquid. We further demonstrate the reconstruction of the unknown force quadrature curves from experimental data with a well-known test sample in liquid. Our study serves as a validation of the ImAFM method in liquid, setting the stage for future investigations of liquid-to-soft-solid interfaces more relevant to polymeric or biological applications.
II. Experiment
ImAFM has been thoroughly explained in our previous publications.28–31Fig. 1 and its caption describe the basic idea behind the technique. ImAFM can be performed with almost any AFM, using a hardware and software kit commercially available from Intermodulation Products AB.32,43 The AFM used here is the NanoWizard®3 from JPK instruments33 which is well suited to work in liquid. The cantilever is acoustically actuated with a small piezo shaker mounted below the cantilever base (JPK, direct drive module). We used a standard gold coated tapping mode cantilever (PPP-NCHAuD Nanosensors™, NanoWorld AG).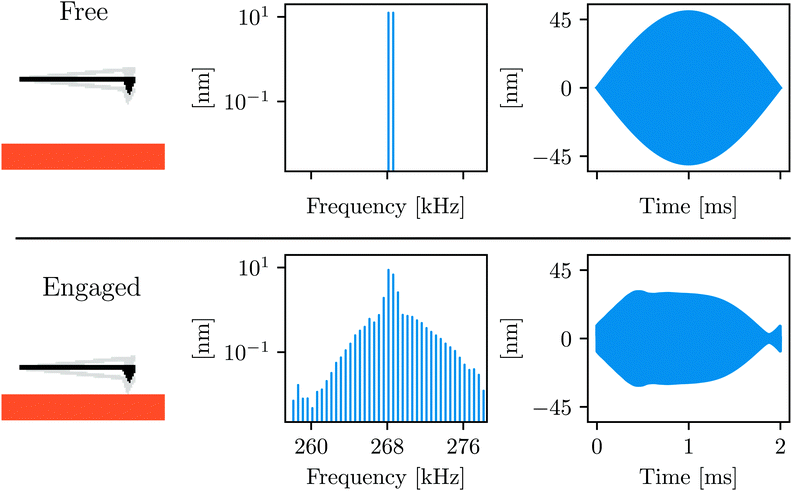 | ||
| Fig. 1 Schematic illustrating the working principle of ImAFM: the cantilever is acoustically excited with two frequencies around its first flexural resonance. In the time domain, driving at two closely spaced frequencies gives a beating waveform, or slow modulation of a rapid oscillation. When engaging the sample surface many intermodulation products of the two drive tones are created around resonance, describing the distortion of the slow modulation. Conservative and dissipative force quadratures are reconstructed from the analysis of this distortion.28–30 | ||
A. Calibration
We first calibrate the cantilever's dynamic stiffness in air using the Sader method with the analytical expression for the hydrodynamic damping as a function of the Reynolds number,34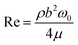 | (1) |
After performing our measurements in air, we calibrate the cantilever in liquid. We completely submerge the cantilever in a 100 μL drop of liquid buffer solution and leave it to equilibrate for a few minutes. We then re-calibrated using the same procedure (ρliquid = 998.2 [kg m−3], μliquid = 0.001 [kgm s−1] and Reliquid = 186). The resonance frequency decreases by a factor of about 2, f0,liquid = 132 kHz, and the quality factor is drastically lowered to Qliquid = 8. The stiffness found by using the Sader method in liquid, kliquid = 26.8 N m−1, differs from that in air by about 13%. The inverse responsivity is invOLRliquid = 23.3 [nm V−1].
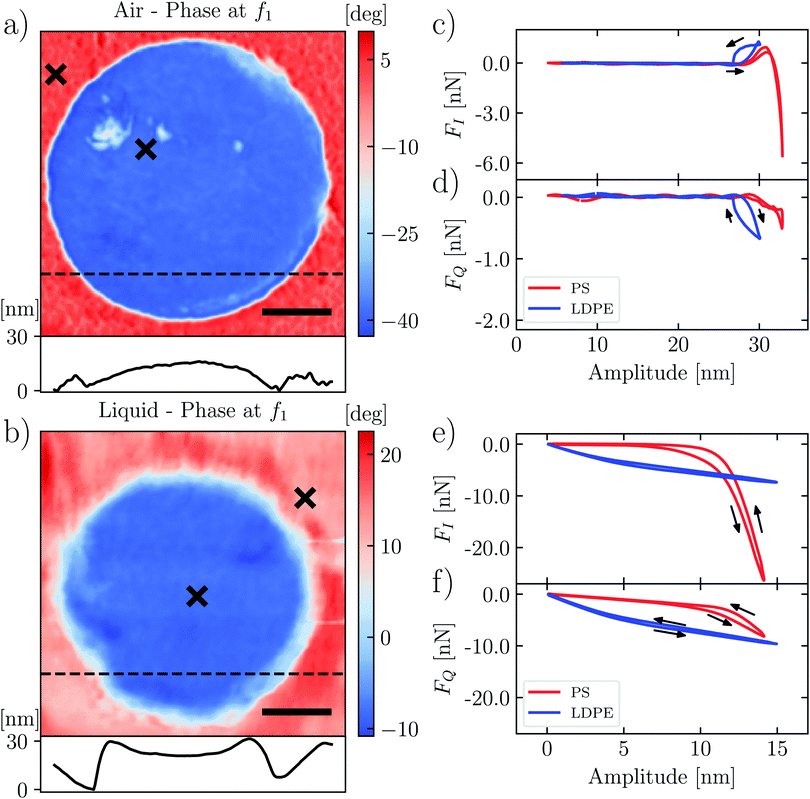
As a test-sample we used a well-studied polymer blend of polystrene and low-density polyethylene (PS-LDPE, Bruker's HarmoniX sample). The polymers are well-separated in two domains, with PS forming a homogeneous background and LDPE forming circular domains scattered around the sample. A significantly different mechanical response is expected in the two domains, as the bulk Young's moduli for PS and LDPE are EPSnom ≈ 2–4 GPa and ELDPEnom ≈ 0.3 GPa respectively. Indeed the phase images in both air and liquid show a sharp contrast when scanning an area around a LDPE domain (see Fig. 2).
In the following, we examine the interaction force between the tip and the liquid–solid interface, comparing the measurements at the individual position in each domain, marked with an × in Fig. 2. In order to isolate and examine only the tip–surface force, it is first necessary to subtract background forces due to squeezing of the dense and viscous liquid films between the cantilever body and the sample surface. We used the method of Borgani et al.36
B. Force quadrature curves
At different positions we characterize the interaction between the tip and the surface by measuring dynamic force quadratures. This method was introduced by Platz et al. and it has been well described in previous publications.28,29 We measure two force curves at each pixel of the image: the curve FI(A) shows the conservative part of the tip–surface interaction and the curve FQ(A) shows the dissipative part. These curves are determined independent of any assumed model of the interaction, but unlike the more familiar force–distance curves, they do not display the instantaneous force at some tip positions. Rather, they are the weighted integrals of force over a single oscillation cycle having a particular amplitude A. The force curve FI(A) shows the integrated force that is in-phase with the cantilever oscillation, and the curve FQ(A) shows the integrated force which is a quadrature to the motion or in-phase with the velocity.Fig. 2(c)–(f) show the force quadratures FI(A) and FQ(A) measured at one point on the stiffer PS region (red) and at one point on the softer LDPE region (blue), in both air and liquid. In air (Fig. 2(c) and (d)) we see the curves with typical shapes: the stiffer PS shows FI(A) reaching a large negative value, indicating that the force was dominantly repulsive for oscillation cycles with the largest amplitude. In contrast, FI(A) on the softer LDPE is always positive up to the largest amplitude, corresponding to a dominantly attractive force. We also see hysteresis in the FI(A) and FQ(A) curves, and a larger negative value of FQ(A) corresponding to a greater energy loss in the oscillation cycle. In the next section, we explain these features as resulting from adhesion and viscous damping, giving rise to slow relaxation of an up-lifted surface.
The shapes of FI(A) and FQ(A) in liquid (Fig. 2(e) and (f)) are distinctly different from those in air. In liquid we do not see attractive force (adhesion) at any amplitude, consistent with quasi-static force measurements. For the stiffer PS surface (red curves), we see that FI(A) = 0 for A < 7 nm, which we interpret as the tip not yet touching the surface when the oscillation amplitude is low. However, in contrast to air, we now see significant FQ(A) in this low amplitude regime. We may explain this observation as additional damping force when the liquid is compressed between the tip and the surface, as opposed to that when the liquid is compressed between the cantilever body and the surface. The squeeze-film damping by the cantilever body has been compensated for by subtracting off linear background forces.36 We also see hysteresis in both FI(A) and FQ(A) measured in liquid, which we explain in the next section using a moving surface model.
In comparison to liquid, the cantilever oscillation is larger in air (Fig. 2(c) and (d) and Fig. 2(e), (f)) and the probe works further from the surface. Hence we see a larger region of amplitude A, where the force quadratures are zero. This region of zero force could be reduced by decreasing the cantilever drive force, so that the free amplitude is smaller. However, it is not always possible to achieve stable imaging with lower drive, because the stored energy in the cantilever oscillation can be insufficient to break free of the adhesion experienced by the tip when it touches the soft surface.
For the stiffer PS surface, we can compare elastic response in air and liquid by simply comparing the slopes of FI(A) in the high amplitude regime, where we find 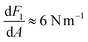 in both cases. To relate this stiffness to a modulus, we use the method of Forchheimer et al. and fit the parameters of the Derjaguin–Müller–Toporov (DMT) model to the measured intermodulation spectrum.30 Assuming a tip radius of 10 nm, we obtain the reduced moduli (i.e. the geometric mean of indenter modulus and surface modulus) EPS,air* = 8.1 ± 3 GPa and EPS,liquid* = 6.4 ± 2 GPa. For the softer LDPE region, this type of analysis is not appropriate. We explain both the shape and magnitude of FI(A) and FQ(A) on this soft surface in the next section.
in both cases. To relate this stiffness to a modulus, we use the method of Forchheimer et al. and fit the parameters of the Derjaguin–Müller–Toporov (DMT) model to the measured intermodulation spectrum.30 Assuming a tip radius of 10 nm, we obtain the reduced moduli (i.e. the geometric mean of indenter modulus and surface modulus) EPS,air* = 8.1 ± 3 GPa and EPS,liquid* = 6.4 ± 2 GPa. For the softer LDPE region, this type of analysis is not appropriate. We explain both the shape and magnitude of FI(A) and FQ(A) on this soft surface in the next section.
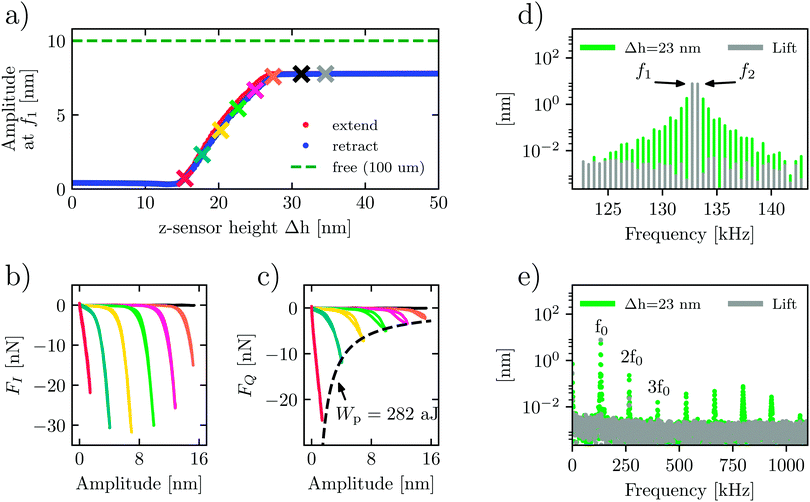
The force quadrature curves in Fig. 2 are shown at one position, but they are measured at every pixel while scanning. We can study the surface and liquid forces in more detail by measuring force quadrature curves while slowly approaching and retracting the probe at one point on the surface. Fig. 3 shows such a measurement in liquid when the free oscillation amplitude at drive frequency f1 was 10 nm. The other drive frequency f2 had the same amplitude, resulting in a beating waveform with a maximum amplitude of 20 nm, or 40 nm peak-to-peak. Fig. 3a plots the response amplitude at f1versus the change in probe height Δh, where the latter is measured with the internal z-sensor of the AFM scanner. We see that close to the surface, but well before touching, the amplitude at f1 has dropped to about 8 nm, due to squeeze-film forces acting on the cantilever body.
When the tip begins to touch the surface around Δh = 28 nm, the reconstructed force quadratures (orange curves in Fig. 3(b) and (c) reveal the onset of the tip–surface force). As expected, moving the probe closer to the surface shifts this onset to a lower amplitude. The evolution of these curves shows that the repulsive conservative force at full amplitude (the largest negative FI(A)) goes through the maximum and begins to decrease as we move very close to the surface. At small oscillation amplitudes, the tip is most likely never breaking free from the surface. Therefore, the non-monotonic behaviour of FI(A) may be associated with changing from the intermittent contact to the constant contact regimes of measurement. In contrast, the magnitude of the dissipative force is always increasing. However, the dissipated energy at the maximum amplitude Wpeak = 2πAmaxFQ,max ≈ −282 aJ does not change with probe height Δh (see the dashed line in Fig. 3c). This measurement demonstrates that, contrary to intuition, the work done by the cantilever on the sample surface in tapping mode AFM does not depend on how heavily the probe is engaged (oscillation amplitude).
The force quadrature curves are reconstructed from intermodulation spectra taken at the probe heights marked with an × of the corresponding color in Fig. 3(a). Two examples of such spectra are shown in Fig. 3(d). Here we see the spectrum at the ‘lift’ height Δh = 35 nm (gray) with no distinguishable intermodulation above the noise level, verifying that the response is highly linear. In contrast, at an engaged height Δh = 23 nm (green), we see strong intermodulation near resonance, well above the noise level. In Fig. 3(e) we see the same two spectra plotted over a much wider frequency range to display all nonlinear responses appearing near the integer multiples of the center frequency, nf0, where 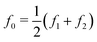 .
.
For the engaged case (green spectrum, Δh = 23 nm), one can see significant response at these higher harmonics and intermodulation products. We note that the response at higher frequencies around 5f0 to 7f0 is enhanced as a result of excitation of the second flexural eigenmode.21 While this higher-frequency nonlinear response is clearly observed above the detector noise due to the large dynamic range of the measurement, it is still a factor of 100 below the dominant response near f0. At the lift height none of this high-frequency nonlinear response is observed, apart from a small remnant near 2f0.
III. Theory and simulation
To validate our experimental methods and to better understand the nature of soft visco-elastic interfaces in liquid, we performed numerical simulations of the cantilever dynamics. We first simulate the cantilever dynamics assuming a particular model for the tip–surface interaction. From this simulated data we can verify the reconstruction of actual force quadrature curves using only the intermodulation spectrum near the resonance. In the second set of simulations, we apply a more realistic moving surface model to explain in detail the shape and hysteresis seen in the experimental force quadrature curves as resulting from the viscoelastic nature of the sample and liquid surroundings.A. Force quadrature reconstruction with low Q
Force quadrature reconstruction is based on the idea that the dominant response is located in a narrow frequency band around resonance. The data given in Fig. 3(e) show significant response at higher frequencies well above f0, clearly bringing this assumption into question. Nevertheless, the simulations described below show that reasonable reconstruction accuracy can be achieved when neglecting the high-frequency nonlinear response.We simulate the dynamics of a model cantilever with two flexural eigenmodes,37,38 where the total deflection from its equilibrium is d = d1 + d2. The equations of motion read,
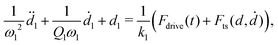 | (2) |
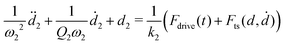 | (3) |
| Fts(d,ḋ) = Fce−d/lc + ḋFde−d/ld. | (4) |
We apply the two-frequency drive force used in ImAFM
Fdrive(t) = F1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf1t) + F2 cos(2πf1t) + F2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf2t) cos(2πf2t) | (5) |
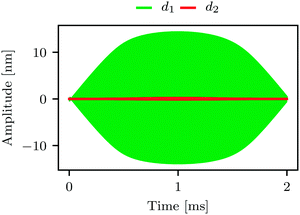 | ||
| Fig. 4 Simulated motion of the first eigenmode d1(t) (green) and second eigenmode d2(t) (red). At this timescale, corresponding to one pixel in an AFM image, one cannot see the rapid oscillations, only the smooth envelope of the motion. The influence of d2(t) appears to be weak using this linear vertical scale, but the Fourier transforms shown in Fig. 5(c) and (d) show significant response around the integer multiples of f0. | ||
The force quadratures reconstructed from this simulation are shown in Fig. 5(a) and (b) (red curves) where they can be compared with the actual force quadratures (black curves). We emphasize that the actual curves are calculated directly from the force model, not from the simulated dynamics. The reconstructed force quadratures determined from the simulated dynamics using only the Fourier coefficients of the total deflection ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) (ω) near f0 (i.e. response at 2 drives and 38 intermodulation products). Fig. 5(c) shows an expanded view of the 20 center peaks located at the shaded region in Fig. 5(d). As with the experiment, the simulation shows significant response at higher frequencies which is enhanced near the second eigenmode (compare Fig. 3(e) and 5(d)).
(ω) near f0 (i.e. response at 2 drives and 38 intermodulation products). Fig. 5(c) shows an expanded view of the 20 center peaks located at the shaded region in Fig. 5(d). As with the experiment, the simulation shows significant response at higher frequencies which is enhanced near the second eigenmode (compare Fig. 3(e) and 5(d)).
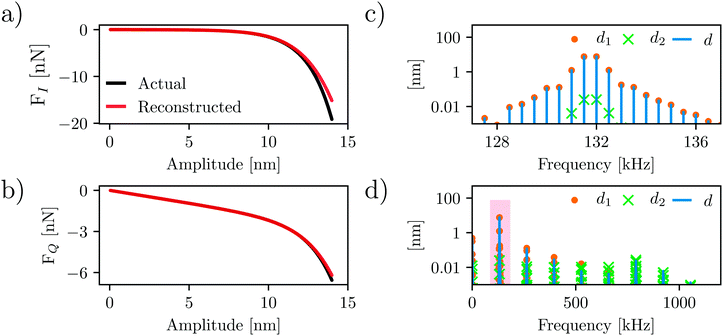 | ||
| Fig. 5 Comparison of the actual and reconstructed force quadrature curves. (a and b) show the force quadrature curves FI(A) shown in (a) and FQ(A) respectively. The actual curves (black) are calculated directly from the force model such as eqn (4), whereas the reconstructed curves (red) are determined from the simulated nonlinear dynamics, using only frequency components of the motion near resonance. (c) shows the spectral content of the tip motion for each eigenmode near resonance, and (d) shows the same over a wider frequency range. | ||
Comparing the actual and reconstructed force quadratures (red vs. black curves in Fig. 5(a) and (b)), it is clear that the reconstruction works quite well. The good agreement is due to the fact that the higher frequency spectral components are relatively small, with most of the spectral power contained in the components near f0. One can imagine alternative methods of force reconstruction using the higher frequency response. However, any such method would require an additional calibration of the second eigenmode parameters including its invOLR, where the latter calibration depends strongly on the position of the laser spot on the cantilever.
B. Viscoelastic response of a soft surface
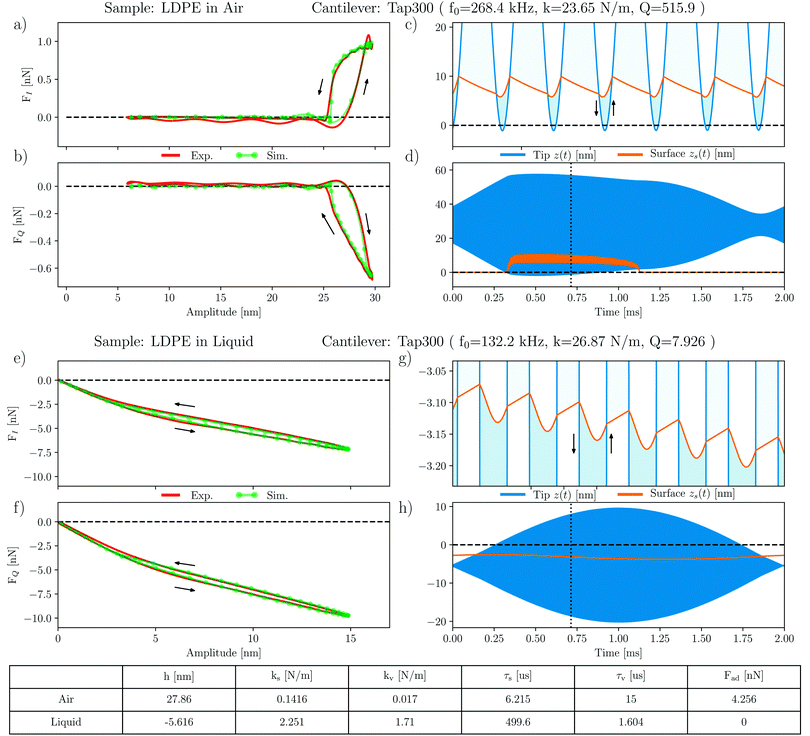
The force quadrature curves on very soft materials cannot be explained in terms of simple force models such as eqn (4) which treat the interaction as a function of tip position and velocity only. In our previous publications31,41 we described a simple model which accounts for the motion of the viscoelastic surface, and we demonstrated that it explains the force quadrature curves on many different soft materials measured in air. The total force needed to deform the soft surface is modeled with two stiffnesses ks and kv, and two viscous relaxation times τs and τv, resulting from interfacial and volumetric contributions respectively. In Fig. 6 we show that this model also works exceptionally well for LDPE, both in air and in liquid.The force quadratures in air are shown in Fig. 6(a) and (b) where we see excellent agreement between experiment and simulation of the moving surface model. All model parameters are given in the table and described in the caption of Fig. 6. The simulated tip motion and surface motion are shown in Fig. 6(c) and (d) where one sees that with each tip, the adhesion force lifts the surface, which does not fully relax before the next tip. The result is a time-average lifting of the surface, giving rise to the hysteresis observed in the force quadrature curves.
Excellent agreement between the measured and modeled force quadratures is also found in liquid, as shown in Fig. 6(e) and (f). Here the curves show a very different shape, but also observe hysteresis. Fig. 6(g) and (h) show that in liquid the cantilever is oscillating much closer to the surface, such that its equilibrium position of the tip h = −5.6 nm is actually below the equilibrium position of the surface. At low amplitude, the tip does not separate from the surface, with intermittent contact starting when the amplitude exceeds some 4 nm. We also see that, as expected, the adhesion force Fad = 0 nN in liquid. Hence the absence of surface lifting in liquid.
A comparison of the moving surface model parameters in air and liquid shows that LDPE is much stiffer in liquid, both interfacial and bulk contributions. We also see that the relaxation time of the free surface τs in liquid is much longer, but the volumetric relaxation time τv becomes shorter. These observations can be explained by the increased Laplace pressure in liquid: in air the topography of the LDPE domain has a convex curvature, forming a dome-like protrusion above the flat PS surface. When submerged in the liquid, an increase in interfacial energy results in an increase in Laplace pressure across this curved interface, which causes the dome to deform and crumple (see the height profiles in Fig. 2(a) and (b)). This deformation is associated with the stiffening of LDPE, causing the parameter kv to increase by two orders of magnitude. The viscous force constant η = τk also increases, but the relaxation time becomes shorter.
IV. Conclusion
We have demonstrated that ImAFM works extremely well in liquid environments where the cantilever's fundamental flexural resonance has the quality factor of order Q ≃ 10. We performed experiments capturing the full nonlinear response including Fourier components up to frequencies many times the resonant frequency. Numerical simulation of a realistic model of the cantilever in liquid, including two eigenmodes, showed that the ImAFM force reconstruction methodology works very well using only the response in a narrow frequency band near resonance. This reconstruction method applied to experimental data shows hysteresis in the force quadrature curves, typical of soft viscoelastic materials. In both air and liquid, these experimental results were well explained by a moving surface model, which takes into account both the viscous and elastic nature of the sample.Other fields such as biology and bioengineering can possibly take the advantage of measuring interfacial properties with ImAFM in environments relevant for cells, i.e. in liquid. Biological materials have widely varying mechanical properties. Bulk Young's moduli between E ≈ 103 Pa and E ≈ 109 Pa have been reported.42 In the case of extremely soft materials (E ≤ 106 Pa), typical AFM measurements are dominated by surface forces. AFM work has largely ignored viscosity but, in our experience with dynamic AFM on soft polymers, it plays a dominant role. It will be necessary to adapt the measurement conditions, i.e. cantilever resonance frequency, stiffness and drive amplitude, on a case-to-case basis. However for ImAFM, under damped dynamics, Q ≳ 10 is desirable. If Q becomes too small, force reconstruction using harmonics may be more appropriate.20
Conflicts of interest
Two of the authors, DBH and DF, are part owners in the company Intermodulation Products AB.Acknowledgements
PAT, DF, RB and DBH gratefully acknowledge financial support by the Swedish Vetenskapsrådet (VR), Stiftelsen Olle Engkvist Byggmästare and Knut och Alice Wallenbergs Stiftelse. FC, BRR and AF gratefully acknowledge financial support by the Swiss National Center of Competence in Research Bio-Inspired Materials and the Swiss National Science Foundation.References
- S. E. Cross, Y.-S. Jin, J. Tondre, R. Wong, J. Rao and J. K. Gimzewski, AFM-based analysis of human metastatic cancer cells, Nanotechnology, 2008, 19(38), 384003 CrossRef PubMed.
- M. Li, L. Liu, X. Xiao, N. Xi and Y. Wang, Viscoelastic Properties Measurement of Human Lymphocytes by Atomic Force Microscopy Based on Magnetic Beads Cell Isolation, IEEE Trans. Nanobioscience, 2016, 15(5), 398–411 CrossRef PubMed.
- A. B. Mathur, A. M. Collinsworth, W. M. Reichert, W. E. Kraus and G. A. Truskey, Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy, J. Biomech., 2001, 34(12), 1545–1553 CrossRef CAS PubMed.
- S. Tripathy and E. J. Berger, Measuring Viscoelasticity of Soft Samples Using Atomic Force Microscopy, J. Biomech. Eng., 2009, 131(9), 094507 CrossRef CAS PubMed.
- T. R. Matzelle, G. Geuskens and N. Kruse, Elastic properties of poly(N-isopropylacrylamide) and poly(acrylamide) hydrogels studied by scanning force microscopy, Macromolecules, 2003, 36(8), 2926–2931 CrossRef CAS.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Matrix Elasticity Directs Stem Cell Lineage Specification, Cell, 2006, 126(4), 677–689 CrossRef CAS PubMed.
- D. E. Discher, Tissue Cells Feel and Respond to the Stiffness of Their Substrate, Science, 2005, 310(5751), 1139–1143 CrossRef CAS PubMed.
- E. Martinez, A. Lagunas, C. A. Mills, S. Rodriguez-Segui, M. Estevez, S. Oberhansl, J. Comelles and J. Samitier, Stem cell differentiation by functionalized micro- and nanostructured surfaces, Nanomedicine, 2009, 4(1), 65–82 CrossRef CAS PubMed.
- G. C. Binnig, C. F. Quate and Ch. Gerber, Atomic Force Microscope, Phys. Rev. Lett., 1986, 56(9), 930 CrossRef PubMed.
- A. Cartagena and A. Raman, Local viscoelastic properties of live cells investigated using dynamic and quasi-static atomic force microscopy methods, Biophys. J., 2014, 106(5), 1033–1043 CrossRef CAS PubMed.
- H. Schillers, M. Wälte, K. Urbanova and H. Oberleithner, Real-time monitoring of cell elasticity reveals oscillating myosin activity, Biophys. J., 2010, 99(11), 3639–3646 CrossRef CAS PubMed.
- H. Babahosseini, B. Carmichael, J. S. Strobl, S. N. Mahmoodi and M. Agah, Sub-cellular force microscopy in single normal and cancer cells, Biochem. Biophys. Res. Commun., 2015, 463(4), 587–592 CrossRef CAS PubMed.
- B. Fallqvist, M. L. Fielden, T. Pettersson, N. Nordgren, M. Kroon and A. K. B. Gad, Experimental and computational assessment of F-actin influence in regulating cellular stiffness and relaxation behaviour of fibroblasts, J. Mech. Behav. Biomed. Mater., 2016, 59, 168–184 CrossRef CAS PubMed.
- S. Iyer, R. M. Gaikwad, V. Subba-Rao, C. D. Woodworth and I. Sokolov, AFM Detects Differences in the surface Brush of normal and cancerous cervical cells, Nat. Nanotechnol., 2011, 4(6), 389–393 CrossRef PubMed.
- L. Hamon, D. Pastré, P. Dupaigne, C. L. Breton, E. L. Cam and O. Piétrement, High-resolution AFM imaging of single-stranded DNA-binding (SSB) protein–DNA complexes, Nucleic Acids Res., 2007, 35(8), 1–7 CrossRef PubMed.
- M. B. Viani, T. E. Schäffer, A. Chand, M. Rief, H. E. Gaub and P. K. Hansma, Small cantilevers for force spectroscopy of single molecules, J. Appl. Phys., 1999, 86(4), 2258–2262 CrossRef CAS.
- R. Borgani, D. Forchheimer, J. Bergqvist, P.-A. Thorén, O. Inganäs and D. B. Haviland, Intermodulation electrostatic force microscopy for imaging surface photo-voltage, Appl. Phys. Lett., 2014, 105(14), 143113 CrossRef.
- W. Melitz, J. Shen, A. C. Kummel and S. Lee, Kelvin probe force microscopy and its application, Surf. Sci. Rep., 2011, 66(1), 1–27 CrossRef CAS.
- X. Zhao, J. Schwenk, A. O. Mandru, M. G. Penedo, M. Bacani, M. A. Marioni and H. J. Hug, Magnetic force microscopy with frequency-modulated capacitive tip-sample distance control, New J. Phys., 2018, 013018 CrossRef.
- J. Legleiter, M. Park, B. Cusick and T. Kowalewski, Scanning probe acceleration microscopy (SPAM) in fluids: mapping mechanical properties of surfaces at the nanoscale, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(13), 4813–4818 CrossRef CAS PubMed.
- X. Xu, J. Melcher and A. Raman, Accurate force spectroscopy in tapping mode atomic force microscopy in liquids, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(3), 1–7 CrossRef.
- T. Fukuma, M. J. Higgins and S. P. Jarvis, Direct imaging of individual intrinsic hydration layers on lipid bilayers at Ångstrom resolution, Biophys. J., 2007, 92(10), 3603–3609 CrossRef CAS PubMed.
- J. I. Kilpatrick, S. H. Loh and S. P. Jarvis, Directly probing the effects of ions on hydration forces at interfaces, J. Am. Chem. Soc., 2013, 135(7), 2628–2634 CrossRef CAS PubMed.
- J. P. K. Instruments AG. QI™ mode – Quantitative Imaging with the Nanowizard® 3 AFM. Technical report.
- D. Platz, E. A. Tholén, D. Pesen and D. B. Haviland, Intermodulation atomic force microscopy, Appl. Phys. Lett., 2008, 92(15), 153106 CrossRef.
- S. Jesse, S. V. Kalinin, R. Proksch, A. P. Baddorf and B. J. Rodriguez, The band excitation method in scanning probe microscopy for rapid mapping of energy dissipation on the nanoscale, Nanotechnology, 2007, 18(43), 435503 CrossRef.
- J. P. Killgore, D. G. Yablon, A. H. Tsou, A. Gannepalli, P. A. Yuya, J. A. Turner, R. Proksch and D. C. Hurley, Viscoelastic property mapping with contact resonance force microscopy, Langmuir, 2011, 27(23), 13983–13987 CrossRef CAS PubMed.
- D. B. Haviland, Quantitative force microscopy from a dynamic point of view, Curr. Opin. Colloid Interface Sci., 2017, 27, 74–81 CrossRef CAS.
- D. Platz, D. Forchheimer, E. A. Tholén and D. B. Haviland, Interaction imaging with amplitude-dependence force spectroscopy, Nat. Commun., 2013, 4, 1360 CrossRef PubMed.
- D. Forchheimer, D. Platz, E. A. Tholén and D. B. Haviland, Model-based extraction of material properties in multifrequency atomic force microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(19), 195449 CrossRef.
- P.-A. Thorén, R. Borgani, D. Forchheimer, I. Dobryden, P. M. Claesson, H. G. Kassa, P. Leclère, Y. W. Heinrich, M. Jaeger and D. B. Haviland, On modeling and measuring viscoelasticity with dynamic Atomic Force Microscopy, 2017, arXiv:1711.09024.
- http://www.intermodulation-products.com/ .
- http://www.jpk.com .
- J. E. Sader, Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope, J. Appl. Phys., 1998, 84(1), 64–76 CrossRef CAS.
- M. J. Higgins, R. Proksch, J. E. Sader, M. Polcik, S. M. Endoo, J. P. Cleveland and S. P. Jarvis, Noninvasive determination of optical lever sensitivity in atomic force microscopy, Rev. Sci. Instrum., 2006, 77(1), 13701 CrossRef.
- R. Borgani, P.-A. Thorén, D. Forchheimer, I. Dobryden, S. M. Sah, P. M. Claesson and D. B. Haviland, Background-force compensation in dynamic atomic force microscopy, Phys. Rev. Appl., 2017, 7, 064018 CrossRef.
- D. Forchheimer, S. S. Borysov, D. Platz and D. B. Haviland, Determining surface properties with bimodal and multimodal AFM, Nanotechnology, 2014, 25(48), 485708 CrossRef CAS PubMed.
- S. S. Borysov, D. Platz, A. S. de Wijn, D. Forchheimer, E. A. Tholén, A. V. Balatsky and D. B. Haviland, Reconstruction of tip–surface interactions with multimodal intermodulation atomic force microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(11), 115405 CrossRef.
- R. Garcia and E. T. Herruzo, The emergence of multifrequency force microscopy, Nat. Nanotechnol., 2012, 7(4), 217–226 CrossRef CAS PubMed.
- E. Jones, T. Oliphant and P. Peterson, et al., SciPy: Open source scientific tools for Python, 2001, [SciPy version 0.19.1].
- D. B. Haviland, C. A. van Eysden, D. Forchheimer, D. Platz, H. G. Kassa and P. Leclère, Probing viscoelastic response of soft material surfaces at the nanoscale, Soft Matter, 2016, 12(2), 619–624 RSC.
- E. Moeendarbary and A. R. Harris, Cell mechanics: principles, practices, and prospects, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2014, 6, 371 CrossRef.
- In the interest of full disclosure, we hereby declare that two of the authors, DBH and DF, are part owners in the company Intermodulation Products AB.
| This journal is © The Royal Society of Chemistry 2018 |