Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Maximum in density heterogeneities of active swimmers†
Fabian Jan
Schwarzendahl
ab and
Marco G.
Mazza
 *a
*a
aMax-Planck-Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077 Göttingen, Germany. E-mail: marco.mazza@ds.mpg.de
bGeorg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
First published on 1st May 2018
Abstract
Suspensions of unicellular microswimmers such as flagellated bacteria or motile algae can exhibit spontaneous density heterogeneities at large enough concentrations. We introduce a novel model for biological microswimmers that creates the flow field of the corresponding microswimmers, and takes into account the shape anisotropy of the swimmer's body and stroke-averaged flagella. By employing multiparticle collision dynamics, we directly couple the swimmer's dynamics to the fluid's. We characterize the nonequilibrium phase diagram, as the filling fraction and Péclet number are varied, and find density heterogeneities in the distribution of both pullers and pushers, due to hydrodynamic instabilities. We find a maximum degree of clustering at intermediate filling fractions and at large Péclet numbers resulting from a competition of hydrodynamic and steric interactions between the swimmers. We develop an analytical theory that supports these results. This maximum might represent an optimum for the microorganisms' colonization of their environment.
I. Introduction
Physical interactions in suspensions of microswimmers consisting of bacteria or algae have been recognized to play an important role in the swimmers' collective behavior.1–3 The nonequilibrium character of active suspensions, where the energy injection takes place at the scale of the microorganisms, produces myriad mesmerizing phenomena, such as complex interaction with solid surfaces,4–6 the spontaneous formation of spiral vortices,7 directed motion,8 swarming,9 bacterial turbulence,10 and self-concentration.11Almost invariably, motile microorganisms move in an aqueous environment, where, because of their size, viscous forces dominate, and inertial forces are completely negligible. In fact, consideration of the Navier–Stokes equations identifies that the nature of the dynamics is dictated by the ratio of viscous to inertial forces, known as the Reynolds number ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) = σvρ/η, where σ is the typical size of the microorganism, v its mean velocity, and ρ, η are the fluid's density and viscosity, respectively. For Escherichia coli, e.g., σ ≈ 10 μm, v ≈ 30 μm s−1, and for water ρ ≈ 103 kg m−3, η ≈ 10−3 Pa s, which result in
= σvρ/η, where σ is the typical size of the microorganism, v its mean velocity, and ρ, η are the fluid's density and viscosity, respectively. For Escherichia coli, e.g., σ ≈ 10 μm, v ≈ 30 μm s−1, and for water ρ ≈ 103 kg m−3, η ≈ 10−3 Pa s, which result in ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ≈ 10−5. As noted by Purcell,12 this means that if the propulsion of a swimmer were to suddenly disappear, it would only coast for 0.1 Å. Thus, the state of motion is only determined by the forces acting at that very moment, and inertia is negligible.
≈ 10−5. As noted by Purcell,12 this means that if the propulsion of a swimmer were to suddenly disappear, it would only coast for 0.1 Å. Thus, the state of motion is only determined by the forces acting at that very moment, and inertia is negligible.
Due to the microswimmers' low Reynolds numbers, the sum of viscous drag and thrust balances out to zero, in most situations. A direct consequence of force-free motion is that the leading term of the solution of the Stokes equation for a microswimmer is a symmetric force dipole (or stresslet).
Biological microswimmers are complex systems because of the combination of biological, biochemical and physical processes all taking place at the same time. It is thus of great scientific value to develop theoretical models that isolate the relevant degrees of freedom and interactions. Considerable work has been done in recent years, and various models have been introduced, like the squirmer model,13–31 the shape anisotropic raspberry swimmer,32–34 the force–counterforce model,35–38 the catalytic dimers,39 or other hydrodynamic models.40–43 Experiments have confirmed that the flow field of flagellated bacteria like E. coli is to very good approximation modeled by a simple force dipole,44 whereas Chlamydomonas reinhardtii are modeled by three Stokeslets.45 Furthermore, as cell shapes vary greatly in the natural world, and realistic steric interactions are important in dense suspensions, a model that allows for flexibility in the shape of a microswimmer is a highly desirable feature. In this article we fill this lacuna. We derive a model for a flexible-shape microswimmer that produces self-propulsion by means of a force dipole for pusher-like microswimmers, or three Stokeslets for puller-like microswimmers.
An efficient method to simulate fluids at mesoscopic scales, and their hydrodynamics is the multiparticle collision dynamics (MPCD) technique.46 MPCD is a particle-based simulation method that correctly produces hydrodynamic modes. Due to its particle nature MPCD naturally includes thermal fluctuations, and can be easily coupled to molecular dynamics methods of solutes, colloids,47 and active swimmers.20,24,26 The MPCD technique in fact proves to be ideal for our purposes.
The nonequilibrium phase diagram of microswimmers has been subject to considerable interest, especially with regard to the emergence of density heterogeneities in the swimmers' distribution.2 We explore the phase diagram of active swimmers and describe the presence of heterogeneities in the spatial distribution of both pushers and pullers. These heterogeneities arise due to the hydrodynamic interactions between the swimmers and relate to existing hydrodynamic theories.2,48–50 Interestingly, we find a maximum in the heterogeneities as filling fraction and Péclet number are varied. By using both computer simulations and analytical theory, we demonstrate that this maximum results from a competition between hydrodynamic and steric interactions, where the latter temper the hydrodynamic instability at higher filling fractions. This optimum might have important biological implications on the ability of motile bacteria and algae to form colonies or biofilms.
The remainder of this article is organized as follows. In Section II we introduce the model for the microswimmer. Section III describes the physical properties of the fluid and the microswimmer's flow field. In Section IV we present the nonequilibrium phase diagram of our model microswimmers, and specifically we characterize the density heterogeneities emerging from their hydrodynamic interactions and show that these are tempered by steric interactions at higher filling fractions. In Section V we present an analytical theory and show that we also find a maximum in heterogeneity, which is mediated by the interplay of hydrodynamic and steric interactions. Finally, in Section VI we discuss our main results and summarize our conclusions.
II. Model
We employ a stroke-averaged model of biological microswimmers, similarly to,1,10,51 taking into account the asymmetric shape of biological microswimmers due to the cell's body and the flagella. The swimmer is thus modeled as an asymmetric dumbbell, as depicted in Fig. 1, that mimics a C. reinhardtii or an E. coli cell. The smaller sphere models the swimmer's body and the larger sphere is a stroke average of the region spanned by flagellar motion. The rigid body dynamics of the dumbbells is simulated using Newton's equations and quaternion dynamics (for details see Appendix A1 and A2).In addition to the rigid body dynamics, we simulate the fluid surrounding the swimmers using MPCD (see Appendix A3), which is a mesoscopic, particle based method, that reproduces hydrodynamics at the Navier–Stokes level.47 Precise measurements44 show that the flow field of pusher-type microswimmers is well modeled by a force dipole. The pullers flow field, on the other hand, is well represented by a three-Stokeslet solution of the Stokes equation.45 These two flow-field models are included in our simulations by adding force regions to the fluid, as depicted by the red regions (3) in Fig. 1. Furthermore, we couple the fluid and swimmers' dynamics by imposing a no-slip boundary condition on the swimmers' surface (for details see Appendix A4).
It should be noted that the dumbbell model introduced here has an anisotropic rigid shape that can be easily modified to more complex shapes. Squirmer models have so far been described for spherical or ellipsoidal shapes.25 Our hydrodynamic flow field is very similar to the three-bead-spring model.52 However, the rigid body dynamics differ in the fact that in the three-bead-spring model the beads are connected by springs, whereas ours is a rigid model.
In the following, we express all physical quantities in terms of the MPCD particle mass m, the size of an MPCD grid cell a, and the temperature T of the fluid. We simulate (see Section IV) N = 300–1560 active swimmers in a cubic domain with side length of 100a, which is approximately 20 times the size of an individual swimmer, and with periodic boundary conditions. The resulting filling fraction ranges between ϕ = 0.05 and ϕ = 0.29. The average number of MPCD particles per cell is 〈NC〉 = 20 such that the total number of MPCD particles in a simulation is 2 × 107. The Reynolds number considered here ranges from ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ∼ 0.01 to
∼ 0.01 to ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ∼ 0.1 and the Péclet number reaches from 2.2 × 102 to 2.6 × 103.
∼ 0.1 and the Péclet number reaches from 2.2 × 102 to 2.6 × 103.
The full details of our numerical implementation are given in Appendix A.
III. Characterization of the fluid and active hydrodynamics
In the following we describe calculations aimed at characterizing the thermal (equilibrium) properties of our model in the passive case, and also the flow field generated by the active motion.We first consider a passive colloid (with the same geometry described above, and in Fig. 1) immersed in the MPCD fluid, that is, we carried out equilibrium simulations without activity. The equipartition theorem applied to the passive colloid for the translational motion predicts that the average of each velocity component squared is 〈Uα2〉 = kBT/M, where M is the colloid's mass, kB is the Boltzmann constant, and α = x, y, z. For our system, we find a theoretical value of the translational motion 〈Utheory2〉 = 2.7 × 10−4kBT/m and the simulations give 〈Ux2〉 = 〈Uy2〉 = 〈Uz2〉 = 2.3 × 10−4kBT/m. In case of the rotational motion, the equipartition theorem predicts for the angular velocity 〈(Ωbα)2〉 = kBT/Imα, where Imα is the moment of inertia tensor. Considering our swimmer, whose long axis is aligned with the z axis of a Cartesian reference frame, the theoretical prediction for the angular motion in x and y direction yields 〈(Ωbx,y)2〉 = 1.3 × 10−3kBT/ma2 while the simulations yield 〈(Ωbx)2〉 = 〈(Ωby)2〉 = 1.1 × 10−3kBT/ma2. In the z direction, the theory predicts 〈(Ωbz)2〉 = 1.4 × 10−3kBT/ma2 and the simulations give 〈(Ωbz)2〉 = 1.2 × 10−3kBT/ma2.
We now consider the active motion at ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ≪ 1. Hydrodynamics at low Reynolds numbers (relevant for micron-sized objects) allow a great simplification of the Navier–Stokes equations: the nonlinear, inertial effects can be neglected, and the governing equations are the Stokes equations
≪ 1. Hydrodynamics at low Reynolds numbers (relevant for micron-sized objects) allow a great simplification of the Navier–Stokes equations: the nonlinear, inertial effects can be neglected, and the governing equations are the Stokes equations
| η∇2u = ∇p − fext, ∇·u = 0, | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53,54
53,54 | (2) |
In free, three-dimensional space, the Green's function is found by considering a point force fext = feδ(r) acting on an infinite, quiescent fluid, where e is the unit vector representing the direction of the force, and δ(r) is the Dirac distribution. A straightforward calculation55 gives the Oseen tensor  where
where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ≡ r/r, r = |r|, and the resulting flow field
≡ r/r, r = |r|, and the resulting flow field  , which is termed a ‘Stokeslet’ and decays with distance as r−1.
, which is termed a ‘Stokeslet’ and decays with distance as r−1.
A theoretical prediction for the puller flow field is constructed from three Stokeslets, and for the pusher we use two Stokeslets. The Stokeslets positions are placed at the midpoints of the respective force regions in the swimmer model (see Fig. 1).
We now consider the flow field generated by the active motion of our model microswimmer. We switch on the active motion with a force f0 = 50kBT/a and carry out the full dynamics as described in Section II (see also Appendix A for a full definition of f0). Fig. 2 shows the flow fields of a pusher and a puller in the lab frame. As expected, the flow field of the puller is contractile, as fluid is drawn in from the front and the back, while fluid is pushed away normal to the swimming direction [Fig. 2(a)]. The situation is reversed in the pusher case [Fig. 2(c)] where fluid is pushed out at the front and back of the swimmer. The theoretical predictions for both the puller [Fig. 2(b)] and the pusher [Fig. 2(d)] show a good quantitative agreement with the simulated flow fields. For the Stokesian algebraic decay of u(r), the reader is referred to Section I in the ESI.†
The effective velocity veff ≡ |〈e·U〉| of an isolated swimmer in the steady state depends linearly on the active force f0.1 Here, e is the swimmer's orientation and U is the swimmer's velocity. From our simulations, we calculate veff for a pusher [see Fig. 3]. The linear fit has a slope of  . The analogous results for pullers are also shown in Fig. 3, where the slope of the linear fit is
. The analogous results for pullers are also shown in Fig. 3, where the slope of the linear fit is 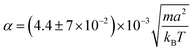 . The linear dependence of veff on f0 shows that our simulations correspond to the Stokes flow regime.
. The linear dependence of veff on f0 shows that our simulations correspond to the Stokes flow regime.
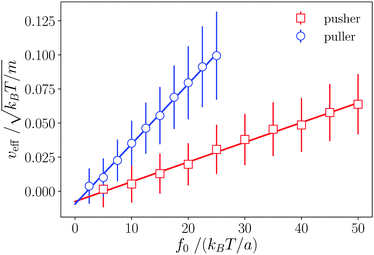 | ||
| Fig. 3 Dependence of the pusher and puller velocity veff on the active force f0. Lines are linear fits to the simulated data. The observed linear dependence is evidence of the Stokes flow regime. | ||
Further simulations on the two particle interaction statistics and two particle flow fields can be found in Section I (ESI†).
IV. Density heterogeneities
In the following we will study the nonequilibrium phase behavior of our active swimmer model. The filling fraction we employ here is computed using the volume of the swimmer's body VB, as well as the volume that is spanned by the flagella sphere VF, while taking into account their overlap volume VOl | (3) |
 | (4) |
 .
.
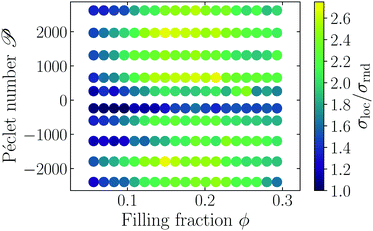
We analyze the system's density using a Voronoi tessellation56 and compute the local volume for each swimmer. A global measure for the heterogeneity of a configuration of swimmers is given by the standard deviation of the distribution of local Voronoi volumes σloc. In order to remove trivial scaling factors, we compare σloc to the standard deviation σrnd of local Voronoi volumes for random homogeneous configurations of nonoverlapping, passive dumbbells (as in Fig. 1) with the same filling fraction. Fig. 4 shows the resulting phase diagram, with the dependence of σloc/σrnd on Péclet number and filling fraction. Here, positive values of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) correspond to pusher-type swimmers, whereas negative values are puller-type swimmers.
correspond to pusher-type swimmers, whereas negative values are puller-type swimmers.
The phase diagram shows that for both pullers and pushers, initially σloc/σrnd grows with ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) and filling fraction, then it reaches a maximum and drops to lower values. The initial increase is related to an instability that is mediated by the hydrodynamic interactions of the microswimmers which has also been found in ref. 1, 2 and 48–50. Intuitively this can be understood in the following way: the hydrodynamic flow field from the swimmers creates heterogeneities in the fluid's velocity, which couple back to the swimmers and produce heterogeneities in the density. It should be noted that the Péclet number of the system has to be rather large, such that the hydrodynamic interaction between the swimmers is strong enough to produce heterogeneous structures. As the filling fraction increases, steric interactions grow in importance and compete with the hydrodynamic instability. Thus, we ascribe the presence of the maximum in σloc/σrnd to a tapering effect of the steric interactions on the hydrodynamic instability. This tapering effect becomes visible only when steric interactions are fully accounted for.
and filling fraction, then it reaches a maximum and drops to lower values. The initial increase is related to an instability that is mediated by the hydrodynamic interactions of the microswimmers which has also been found in ref. 1, 2 and 48–50. Intuitively this can be understood in the following way: the hydrodynamic flow field from the swimmers creates heterogeneities in the fluid's velocity, which couple back to the swimmers and produce heterogeneities in the density. It should be noted that the Péclet number of the system has to be rather large, such that the hydrodynamic interaction between the swimmers is strong enough to produce heterogeneous structures. As the filling fraction increases, steric interactions grow in importance and compete with the hydrodynamic instability. Thus, we ascribe the presence of the maximum in σloc/σrnd to a tapering effect of the steric interactions on the hydrodynamic instability. This tapering effect becomes visible only when steric interactions are fully accounted for.
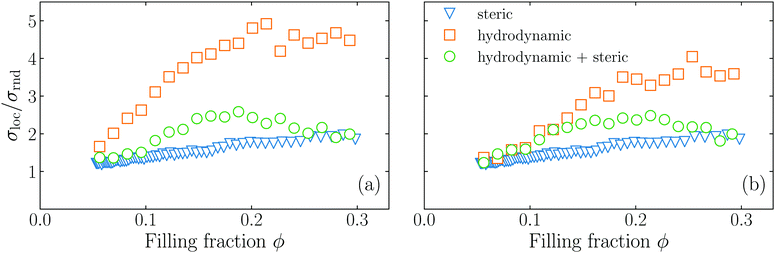
To test the hypothesis that steric interactions stabilize the hydrodynamic instability, we carry out two more types of simulations: first, we exclude the steric effects by setting the hard-core repulsion [eqn (A6)] to zero, thus only hydrodynamic effects are included. Second, we carry out Brownian dynamics simulations, which completely neglect hydrodynamic interactions. More details about the Brownian dynamics simulations are given in Section III of the ESI.†
In Fig. 5 we show our original simulations that fully account for hydrodynamic and steric interactions, the simulations without steric interactions, and the active Brownian simulations. The simulations with hydrodynamics alone give rise to a strong increase of σloc/σrnd, but no maximum occurs, while the active Brownian simulations show a monotonic increase of σloc/σrnd, which is much less pronounced. Our original simulations (with both hydrodynamics and steric effects) exhibit intermediate values of σloc/σrnd. Thus, we conclude that the maximum which we see is mediated by an interplay of the hydrodynamic interactions and the steric interactions, confirming our hypothesis.
V. Theoretical analysis
To bolster our numerical results, we develop an analytical theory of microswimmers that explicitly includes hydrodynamic and steric interactions. As in our numerical model (see Section II), we consider the dynamics of an asymmetric dumbbell, which is described by the following effective Langevin equations | (5) |
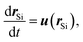 | (6) |
| η∇2u = ∇p − factive + fnoise. | (7) |
 | (8) |
 | (9) |
 | (10) |
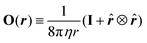 , which is regularized by using O(|r| ≤ aL,S) ≡ I/ΓL,S. Given the solution (10), the flow velocity can be eliminated from eqn (5) and (6). Using the hydrodynamic center
, which is regularized by using O(|r| ≤ aL,S) ≡ I/ΓL,S. Given the solution (10), the flow velocity can be eliminated from eqn (5) and (6). Using the hydrodynamic center  , we can simplify eqn (5) and (6) to
, we can simplify eqn (5) and (6) to | (11) |
 | (12) |
| 〈ξi,α(t)ξj,β(t′)〉 = 2Dδijδαβδ(t − t′), | (13) |
| 〈ξRi,α(t)ξRj,β(t′)〉 = 2DRδijδαβδ(t − t′), | (14) |
Following,1 we derive the one-body Smoluchowski equation from eqn (11) and (12). As we have seen in Section IV steric interactions among swimmers may play a crucial role in their dynamics. Thus, we explicitly include the effect of steric interactions by means of the Ansatz57,58
| v(c) = v0 − cζ. | (15) |
 | (16) |
 | (17) |
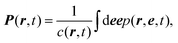 | (18) |
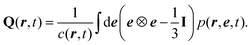 | (19) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (k), δ
(k), δ![[P with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0050_0303.gif) (k), and δ
(k), and δ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) (k). To first order in the fluctuations the equations governing the temporal evolution read
(k). To first order in the fluctuations the equations governing the temporal evolution read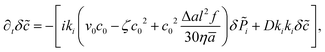 | (20) |
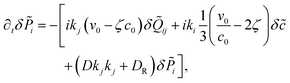 | (21) |
 | (22) |
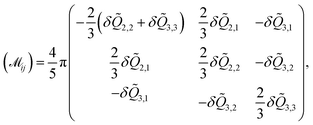 | (23) |
For pullers (f < 0) the concentration fluctuations δ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are dominant. To analyze the fluctuations in the concentration we use a large length-scale and long time-scale (DRt ≫ 1) approximation for the longitudinal polarization δ
are dominant. To analyze the fluctuations in the concentration we use a large length-scale and long time-scale (DRt ≫ 1) approximation for the longitudinal polarization δ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ‖ =
‖ = ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) iδ
iδ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) i,
i, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) i ≡ ki/k, which reads
i ≡ ki/k, which reads
 | (24) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ij are of higher order in k, when terms of order k2 in eqn (20) are kept. Inserting the quasi-stationary solution eqn (24) into the eqn (20) yields
ij are of higher order in k, when terms of order k2 in eqn (20) are kept. Inserting the quasi-stationary solution eqn (24) into the eqn (20) yields | (25) |
 introduces an instability at low concentrations c0, which are counteracted by the term
introduces an instability at low concentrations c0, which are counteracted by the term  , that stabilizes the system at higher concentrations. Since the first term is dominated by the hydrodynamic interactions and the second term by the steric interactions, we can draw the same conclusion as from the simulations: the hydrodynamic interactions cause heterogeneities in the system which are suppressed by the steric effects at larger c0. Moreover, inspection of the fastest-growing eigenvalue reveals a maximum of instability as a function of c0 and, hence, a maximum degree of heterogeneity. The position of the maximum of the filling fraction can be estimated from microscopic information extracted from scattering events between two swimmers; we find ϕmax = 0.12, which is consistent with the simulation in Fig. 5(b) (for details see Appendix B).
, that stabilizes the system at higher concentrations. Since the first term is dominated by the hydrodynamic interactions and the second term by the steric interactions, we can draw the same conclusion as from the simulations: the hydrodynamic interactions cause heterogeneities in the system which are suppressed by the steric effects at larger c0. Moreover, inspection of the fastest-growing eigenvalue reveals a maximum of instability as a function of c0 and, hence, a maximum degree of heterogeneity. The position of the maximum of the filling fraction can be estimated from microscopic information extracted from scattering events between two swimmers; we find ϕmax = 0.12, which is consistent with the simulation in Fig. 5(b) (for details see Appendix B).
We also find an instability in the splay fluctuations of the nematic tensor δ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ‖‖ =
‖‖ = ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) ·
·![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) ·
·![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) . Here, the approximation of the polarization fluctuations [eqn (21)] is different, since we need to consider eqn (22) for the counting of powers of k. In the large length and time scale limit we arrive at
. Here, the approximation of the polarization fluctuations [eqn (21)] is different, since we need to consider eqn (22) for the counting of powers of k. In the large length and time scale limit we arrive at
 | (26) |
 | (27) |
 | (28) |
For pushers (f > 0) the bend component of the nematic tensor fluctuations δ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0051_0303.gif) ‖⊥ =
‖⊥ = ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) ·δ
·δ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_char_0051_0303.gif) ·(I −
·(I − ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) ⊗
⊗ ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) ) become unstable, since here ki
) become unstable, since here ki![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ij(δjl − kjkl) < 0, ∀l = x, y, z. For the polarization we use the large length and time scale limit in eqn (26). Inserting eqn (26) into the term [kiδ
ij(δjl − kjkl) < 0, ∀l = x, y, z. For the polarization we use the large length and time scale limit in eqn (26). Inserting eqn (26) into the term [kiδ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) j]ST of eqn (22), and projecting onto the bend part gives
j]ST of eqn (22), and projecting onto the bend part gives
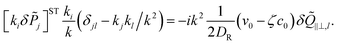 | (29) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0051_0303.gif) ‖⊥, which is given by
‖⊥, which is given by | (30) |
 destabilizes the system at low concentrations c0 through nematic fluctuations, which are counteracted by the term
destabilizes the system at low concentrations c0 through nematic fluctuations, which are counteracted by the term  , that stabilizes the system for higher concentrations. Again, the first term, which destabilizes the system, is dominated by the hydrodynamic interactions, whereas the second, stabilizing term comes from the steric interactions. Additionally from microscopic information extracted from scattering events between two swimmers we can estimate the filling fraction of the maximum heterogeneities, with the result ϕmax = 0.23, which is in accordance with the simulation from Fig. 5(a) (for details see Appendix B).
, that stabilizes the system for higher concentrations. Again, the first term, which destabilizes the system, is dominated by the hydrodynamic interactions, whereas the second, stabilizing term comes from the steric interactions. Additionally from microscopic information extracted from scattering events between two swimmers we can estimate the filling fraction of the maximum heterogeneities, with the result ϕmax = 0.23, which is in accordance with the simulation from Fig. 5(a) (for details see Appendix B).
VI. Conclusions
We have presented a new model for biological microswimmers that is based on Stokeslets and the stroke averaged motion of their flagella. The Stokeslets were distributed to model the flow fields of C. reinhardtii or E. coli cells. Furthermore, our model takes into account the anisotropic shape of a microswimmer. Typical for this is the shape of a C. reinhardtii cell, which is well modeled by an asymmetric dumbbell.10 Self-propulsion is generated through a symmetry breaking due to the asymmetric shape and force-free motion. The fluid and the hydrodynamic interactions are explicitly included with MPCD.We show that the flow fields produced in our simulations can be predicted using simple formulae from the literature. These formulae also correspond to the experimentally measured flow fields.44,45 Additionally, we test the effective velocity of the microswimmer model, and find that it depends linearly on the applied force, in agreement with the Stokes flow regime.
We study the phase diagram in terms of filling fraction and Péclet number. We find that both pullers and pushers exhibit density heterogeneities. The density heterogeneities show a maximum at intermediate filling fractions and high Péclet number. To determine the mechanism underpinning this phenomenon, we perform additional simulations, in which either the steric interactions or the hydrodynamic interactions were switched off. Simulations with active Brownian particles showed a small linear increase in the density heterogeneities, while simulations without the steric interactions show strong density heterogeneities. This is an instability caused only by the hydrodynamic interactions, which is known from the literature.1,2,48–50 However, no maximum arises in the simulations with only hydrodynamic or only steric interactions, which shows that the maximum in the density heterogeneities is mediated by an interplay of the hydrodynamic and the steric interactions. The hydrodynamic interactions destabilize the system, whereas the steric interactions stabilize the system as the filling fraction grows and thus a maximum in density heterogeneity arises.
We have also developed an analytical theory based on a Smoluchowski equation which includes steric as well as hydrodynamic interactions. We computed the hydrodynamic moments of this equation and performed a linear stability analysis of the moment equations around the homogeneous state. For both puller and pusher-type swimmers, we found that at low concentration the system is destabilized by hydrodynamic interactions. At higher concentrations, however, the instabilities are counteracted by the steric interaction. This interplay gives rise to a maximum in the instability of the homogeneous state, and thus a maximum heterogeneity in the concentration of swimmers. The position of the maxima calculated from the analytics is in accordance with the simulations. Our continuum theory does not explicitly account for steric effects at the microscopic level, which induce short range correlations, and lubrication forces, and influence the short range hydrodynamics. These effects, however, are captured by the numerical simulations. The agreement between our theory and simulations gives us confidence that our assumptions effectively includes the dominant physical effects.
The physical pictures from both simulations and analytical theory fit together: both show that the homogeneous state is not stable and there is a maximum of instability. Also, both analyses show that the instability arises from hydrodynamic interactions and is suppressed by the steric interactions.
The maximum in the density heterogeneities might have important biological implications: it points to a possible, optimal filling fraction and Péclet number for the formation of heterogeneous distributions of motile microorganisms. Bacteria or microalgae exhibiting these optimal parameters are more likely to form colonies or biofilms.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: model details
The microswimmer is characterized by its mass M, center of mass position R and orientation q. In the following we describe the equations governing the motion of the microswimmer, the fluid dynamics implemented through the MPCD, and their coupling.1. Rigid body dynamics of swimmers
As we do not consider shape deformable swimmers, we are only concerned with rigid-body dynamics. The most general motion of a rigid body is the combination of a translation along an axis (the Mozzi axis) and a rotation around the same axis, as per the Mozzi–Chasles theorem.59 Any orientation in space can be described using three numbers, that are commonly represented with the Euler angles, which correspond to three elementary rotations. However, there are a number of issues with the choice of the Euler angles. For instance, the composition of rotations with Euler angles or rotation matrices is rather complex, and involves trigonometric functions which lead to an accumulation of rounding-off errors. Eventually the matrices representing the rotations may become not orthogonal. Importantly, for some values of the Euler angles there are discontinuous jumps in the representation. More fundamentally, the Euler angles do not generate a covering map of the rotation group SO(3), that is, the map from Euler angles to SO(3) is not always a local homeomorphism. Fortunately, the topology of SO(3) is diffeomorphic to the real projective space![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) 3(
3(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) ) which admits a universal cover represented by the group of unit quaternions q = (q0,q1,q2,q3)T, where the superscript T indicates the matrix transposition.
) which admits a universal cover represented by the group of unit quaternions q = (q0,q1,q2,q3)T, where the superscript T indicates the matrix transposition.
The equations of motion for the rigid body dynamics in three dimensions and in terms of quaternions read60
 | (A1) |
 | (A2) |
 | (A3) |
 | (A4) |
 | (A5) |
 | (A6) |
Given a vector in the laboratory frame f the transformation to the body frame vector fb is given by
| fb = Df, | (A7) |
Quaternions are represented as q = q0 + q1i + q2j + q3k, with q0,…,q3 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) , and i2 = j2 = k2 = ijk = −1.
, and i2 = j2 = k2 = ijk = −1.
The unitary matrix D that transforms vectors from the lab to the body frame is (see also ref. 61)
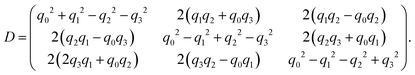 | (A8) |
Thus, the orientation of the swimmer at any given time is found from D−1(q(t))(0,0,1)T.
Note that all quantities that do not carry an index b are calculated in the laboratory frame.
2. Center of mass and moment of inertia
Fig. 6 shows the detailed geometry and dimensions of our model microswimmers (both pullers and pushers). In the body frame, the swimmer is aligned with the z direction and the coordinates of the centers of the B and F spheres are z1 and z2, respectively. Given a homogeneous mass distribution the center of mass of the swimmer is given by | (A9) |
 | (A10) |
 | (A11) |
 | (A12) |
 | (A13) |
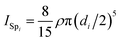 and with the use of the parallel axis theorem, we compute the moments of inertia of the swimmer as
and with the use of the parallel axis theorem, we compute the moments of inertia of the swimmer as| I(x,y) = ISp1,(x,y) − ISc1,(x,y) + ρ(V1 − VSc1)x12, | (A14) |
| Iz = ISp1,z + ISp2,z − ISc1,z − ISc2,z. | (A15) |
3. Multiparticle collision dynamics
To simulate a fluid at fixed density ρ and temperature T surrounding the swimmers, we use the MPCD algorithm, which is a mesoscopic, particle based method46 to simulate a fluid at the Navier–Stokes level of description. We include the Andersen thermostat and the conservation of angular momentum into the MPCD dynamics; the resulting algorithm is usually denoted as MPC-AT+a.47,64,65 The fluid is modeled using Nfl point-like particles of mass m, whose dynamics are executed through two steps: the streaming step and the collision step. In the streaming step the fluid particles' positions ri, i ∈ [1,Nfl] are updated according to| ri(t + δt) = ri(t) + vi(t)δt, | (A16) |
The collision step mediates the interactions between the particles. Here, the system is divided into Nc collision cells with a regular grid of lattice constant a. The center of mass velocity in each cell  is calculated and remains constant during the collision step, whereas the fluctuating part of the velocity of every fluid particle i is randomized, which mimics the collision between particles. Hence, the velocity of particle i is updated as follows64
is calculated and remains constant during the collision step, whereas the fluctuating part of the velocity of every fluid particle i is randomized, which mimics the collision between particles. Hence, the velocity of particle i is updated as follows64
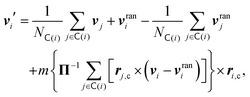 | (A17) |
 ,
,  is the number of fluid and ghost particles (see Section A4) in cell
is the number of fluid and ghost particles (see Section A4) in cell  . The vector rj,c is the position of the neighboring particle j relative to the center of mass of the cell
. The vector rj,c is the position of the neighboring particle j relative to the center of mass of the cell  . In eqn (A17), Π−1 is the inverse of the moment of inertia tensor
. In eqn (A17), Π−1 is the inverse of the moment of inertia tensor  for the fluid particles in cell
for the fluid particles in cell  . Note that Π−1 is a dynamical quantity that has to be updated at every timestep, and it also includes the ghost particles within the swimmer (see Section A4).
. Note that Π−1 is a dynamical quantity that has to be updated at every timestep, and it also includes the ghost particles within the swimmer (see Section A4).
To ensure Galilean invariance and avoid the build-up of spurious correlations in the velocities,66 the usual grid shift is performed at each timestep, that is, the grid is shifted by a random vector, whose components are uniformly distributed in the interval [−a/2,a/2].
4. Coupling of the swimmer's and fluid's dynamics
No velocity field is prescribed in our model of microswimmers. Locomotion is achieved by obeying the conservation of momentum in the collisions between the fluid particles and the swimmers; the shape asymmetry then induces self-propulsion. Two physical effects need to be included: we impose no-slip boundary conditions on the model swimmer's surface, and the force poles are explicitly included (see Fig. 1). Both effects induce modifications of the streaming and collision steps of the MPCD algorithm that we explain in the following.Ji = 2m[vi − U − Ω × (![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) i − R)], i − R)], | (A18) |
![[r with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0072_0303.gif) i is the position of the fluid particle upon collision with the sphere. The updated fluid particle velocity reads
i is the position of the fluid particle upon collision with the sphere. The updated fluid particle velocity reads| vi′ = vi − Ji/m. | (A19) |
 | (A20) |
 | (A21) |
The force poles are added as external force regions69 in the streaming step for each swimmer. This is done by modifying the streaming step inside the force regions to
 | (A22) |
| vi(t + δt) = vi(t) + flabacδt, | (A23) |
| flabac ≡ fac − [U + Ω × (ri − R)]/δt, | (A24) |
Pullers. The flow field is modeled by three Stokeslets, and the active force flabac is applied to Rpl,1, Rpl,2 and Rpl,2′ [see Fig. 6(a)]. The region Rpl,1 with diameter dpl,1 is located at the rear of the swimmer and its force points into the direction of the swimmer's orientation. The other two regions Rpl,2 and Rpl,2′ are placed on the side of the swimmer and have the opposite orientation. The angle αpl between the orientation of the puller and the line connecting the center of mass C and the midpoint of the region Rpl,2 (or Rpl,2′) defines their position on the boundary of the swimmer. The diameter of both Rpl,2 and Rpl,2′ is dpl,2 = dpl,1/(2)1/3, such that they have half the volume of Rpl,1, making the fluid force free. The total force in the region Rpl,1 is
 and in the regions Rpl,2, Rpl,2′ is
and in the regions Rpl,2, Rpl,2′ is 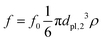 .
.
Pushers. The flow field is modeled by a force dipole. We apply the force flabac to all fluid particles located within spherical regions [see Fig. 6(b)]. The regions Rps,1 and Rps,2 where flabac is applied are equally sized spheres with diameter dps and the two forces fac are equal and opposite, to ensure that the fluid is overall force free. To generate a smooth flow on the boundary of the swimmer the direction of the applied force in regions Rps,1 and Rps,2 is modeled as follows. For fluid particles ri ∈ Rps,1 or Rps,2 we apply the force
 | (A25) |
 . This takes into account the redirection of the force on the boundary of the swimmer and the density ρ of the fluid.
. This takes into account the redirection of the force on the boundary of the swimmer and the density ρ of the fluid.
| vgi = U + Ω × (rgi − R) + vrani, | (A26) |
 . The resulting change in linear momentum due to the ghost particles is
. The resulting change in linear momentum due to the ghost particles is  and the change in angular momentum is Lgi = (rgi − R) × Jgi. These changes are then transferred to the swimmer17
and the change in angular momentum is Lgi = (rgi − R) × Jgi. These changes are then transferred to the swimmer17 | (A27) |
 | (A28) |
5. Algorithm implementation
In this section we explain how the present algorithm is implemented. First, note that the MPCD algorithm scales as![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N), and thus is particularly prone to an efficient implementation with parallel programming. We therefore implemented the entire dynamics (both swimmer and MPCD) on graphics processing unit (GPU) cards using the Nvidia CUDA language. Parallelization of the MPCD algorithm is rather straightforward. The streaming step is performed for each fluid particle independently in a separate CUDA kernel, whereas ghost particles are simply translated together with the corresponding swimmer. Then, a kernel for each particle is started to carry out the bounce-back rule and afterwards a kernel for each particle is started to apply the periodic boundary conditions. The collision step eqn (A17) is implemented with the following kernels:
(N), and thus is particularly prone to an efficient implementation with parallel programming. We therefore implemented the entire dynamics (both swimmer and MPCD) on graphics processing unit (GPU) cards using the Nvidia CUDA language. Parallelization of the MPCD algorithm is rather straightforward. The streaming step is performed for each fluid particle independently in a separate CUDA kernel, whereas ghost particles are simply translated together with the corresponding swimmer. Then, a kernel for each particle is started to carry out the bounce-back rule and afterwards a kernel for each particle is started to apply the periodic boundary conditions. The collision step eqn (A17) is implemented with the following kernels:
1. the cell of each particle is found and the center of mass for each cell is found by starting a kernel for each particle;
2. the two sums over the velocities in eqn (A17) are computed, where a kernel for each velocity component of each particle is started;
3. a kernel for each particle is started to compute the number of particles in each cell;
4. a kernel for each cell is started to normalize the velocities and compute the center of mass;
5. a kernel for each particle is started to compute its position with respect to the center of mass;
6. a kernel for each particle is started to compute the cross product in eqn (A17) and the contributions in each cell are summed;
7. six kernels for each particle are started to compute the contribution to the six components of the inertia tensor in the corresponding cell;
8. a kernel for each cell is started to compute the inverse of the respective inertia tensors;
9. for each cell a kernel is started to compute the curly bracket in eqn (A17);
10. a kernel for each particle is started to add all contributions of eqn (A17) and finish the collision step, while considering the rule for ghost particles eqn (A26);
11. a kernel for each ghost particle is started, which computes the momentum and angular momentum transfer [eqn (A27) and (A28)] to the swimmers.
Some of these computations could be combined into single kernels, but it is computationally more efficient to start many kernels with small computations, which we have opted for in this algorithm. After the MPCD steps the rigid body dynamics part (see also Section A1) of the code is executed. It consists of the following kernels, one for each swimmer:
1. the velocity and angular velocity stemming from the fluid interaction are added to the swimmers;
2. the positions and quaternions are updated;
3. periodic boundary conditions are applied;
4. the neighbor list between swimmers is updated (here we use a linked list);
5. the steric forces and torques are computed;
6. the velocities and angular velocities are updated.
This concludes the algorithm, which now goes back to the streaming step of the MPCD part.
6. Computational details
We carried out three-dimensional simulations with an average of 〈NC〉 = 20 fluid particles per cell. The timestep of the MPCD algorithm is fixed to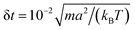 , whereas the MD timestep is
, whereas the MD timestep is  . The resulting kinematic viscosity ν = η/ρ of the fluid for the MPC-AT+a algorithm (including both kinetic and collisional contribution) can be calculated exactly as
. The resulting kinematic viscosity ν = η/ρ of the fluid for the MPC-AT+a algorithm (including both kinetic and collisional contribution) can be calculated exactly as 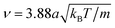 .47,65,70 Simulations using a forced flow (for details see ref. 69) produced a viscosity of
.47,65,70 Simulations using a forced flow (for details see ref. 69) produced a viscosity of  .
.
The large sphere F associated to the stroke-averaged flagella of the swimmer has a diameter of df = 7a, while the small sphere B associated to the body of the swimmer has db = 3a, and the distance between the spheres centers is l = 7a. The choice of the geometrical parameters is dictated by a combination of factors. First, it is computationally convenient to make the swimmers' linear size a few times the grid spacing a. Second, inspired by the geometric properties of C. reinhardtii a ratio df/db ≳ 2 is advisable.10 For the sake of clarity in the comparison of our results, we maintain the same geometry also for pushers. The energy scale of the steric interactions is set to ε = 10kBT. For pushers we fix the diameter of the force dipole regions Rps,1 and Rps,2 to dps = 3a. The region Rpl,1 of the pullers has the same diameter dpl,1 = 3a and accordingly the regions Rpl,2 and Rpl,2′ have the diameter dpl,2 = 3a/(2)1/3. The angle between the swimmers orientation and the line connecting the center of mass of the pullers C to the midpoint of the regions Rpl,2 and Rpl,2′ is αpl = 107°.
To initialize the simulations, we distribute the swimmers homogeneously (and without overlaps) across a cubic box with periodic boundary conditions.
Appendix B: estimate of maximum from theoretical prediction
To estimate the maximum predicted from the analytical treatment, we computed the maximum of the eigenvalues in eqn (30) for pushers and eqn (25) for pullers. As a first step, we have to find estimates for both the wavenumber k and the constant quantifying the steric interactions ζ. Since we expect the hydrodynamic interactions to be relevant on the size of the swimmer, we chose the distance between the force poles l to determine the characteristic wavenumber k = 2π/l. The constant ζ quantifying the steric interactions can be estimated from ref. 58| ζ = v02σsτc | (A29) |
 and for pushers
and for pushers  . The propulsion speed is extracted from Fig. 3 and the geometrical cross section is σs = 4πσ2. Here, σ = l/2 = 7.5a is the effective steric radius of the swimmer also estimated from the distance of the force poles. To finally obtain a filling fraction we use ϕ = c0(VB + VF − VOl) [see eqn (3)].
. The propulsion speed is extracted from Fig. 3 and the geometrical cross section is σs = 4πσ2. Here, σ = l/2 = 7.5a is the effective steric radius of the swimmer also estimated from the distance of the force poles. To finally obtain a filling fraction we use ϕ = c0(VB + VF − VOl) [see eqn (3)].
Acknowledgements
We gratefully acknowledge insightful conversations with Johannes Blaschke, Jens ElgetiStephan Herminghaus, Sebastian Mair, and Kuang-Wu Lee. We also gratefully acknowledge support from the Deutsche Forschungsgemeinschaft (SFB 937, project A20). Open Access funding provided by the Max Planck Society.References
- A. Baskaran and M. C. Marchetti, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15567–15572 CrossRef CAS PubMed.
- B. Ezhilan, M. J. Shelley and D. Saintillan, Phys. Fluids, 2013, 25, 070607 Search PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- T. Ostapenko, F. J. Schwarzendahl, T. J. Böddeker, C. T. Kreis, J. Cammann, M. G. Mazza and O. Bäumchen, Phys. Rev. Lett., 2018, 120, 068002 CrossRef PubMed.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 268102 CrossRef PubMed.
- H. Wioland, E. Lushi and R. E. Goldstein, New J. Phys., 2016, 18, 075002 CrossRef.
- M. F. Copeland and D. B. Weibel, Soft Matter, 2009, 5, 1174–1187 RSC.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- M. J. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- T. Ishikawa and T. J. Pedley, Phys. Rev. Lett., 2008, 100, 088103 CrossRef PubMed.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- I. Llopis and I. Pagonabarraga, J. Non-Newtonian Fluid Mech., 2010, 165, 946–952 CrossRef CAS.
- A. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef PubMed.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef.
- K. Ishimoto and E. A. Gaffney, Phys. Rev. E, 2013, 88, 062702 CrossRef PubMed.
- J. J. Molina, Y. Nakayama and R. Yamamoto, Soft Matter, 2013, 9, 4923–4936 RSC.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- M. Theers, E. Westphal, G. Gompper and R. G. Winkler, Soft Matter, 2016, 12, 7372–7385 RSC.
- J. Blaschke, M. Maurer, K. Menon, A. Zöttl and H. Stark, Soft Matter, 2016, 12, 9821–9831 RSC.
- F. Alarcon, C. Valeriani and I. Pagonabarraga, Soft Matter, 2017, 13, 814–826 RSC.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021408 CrossRef PubMed.
- G.-J. Li and A. M. Ardekani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013010 CrossRef PubMed.
- I. Pagonabarraga and I. Llopis, Soft Matter, 2013, 9, 7174–7184 RSC.
- R. Matas-Navarro, R. Golestanian, T. B. Liverpool and S. M. Fielding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032304 CrossRef PubMed.
- J. de Graaf, H. Menke, A. J. T. M. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- L. P. Fischer, T. Peter, C. Holm and J. de Graaf, J. Chem. Phys., 2015, 143, 084107 CrossRef PubMed.
- J. de Graaf, T. Peter, L. P. Fischer and C. Holm, J. Chem. Phys., 2015, 143, 084108 CrossRef PubMed.
- R. W. Nash, R. Adhikari, J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2010, 104, 258101 CrossRef CAS PubMed.
- R. W. Nash, R. Adhikari and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 026709 CrossRef CAS PubMed.
- J. P. Hernandez-Ortiz, C. G. Stoltz and M. D. Graham, Phys. Rev. Lett., 2005, 95, 204501 CrossRef PubMed.
- J. Stenhammar, C. Nardini, R. W. Nash, D. Marenduzzo and A. Morozov, Phys. Rev. Lett., 2017, 119, 028005 CrossRef PubMed.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS PubMed.
- D. Saintillan and M. J. Shelley, Phys. Rev. Lett., 2007, 99, 058102 CrossRef PubMed.
- R. Singh, S. Ghose and R. Adhikari, J. Stat. Mech.: Theory Exp., 2015, 2015, P06017 CrossRef.
- J. W. Swan, J. F. Brady, R. S. Moore and C. 174, Phys. Fluids, 2011, 23, 071901 CrossRef.
- D. Saintillan and M. J. Shelley, J. R. Soc., Interface, 2011 DOI:10.1098/rsif.2011.0355.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- K. Drescher, R. E. Goldstein, N. Michel, M. Polin and I. Tuval, Phys. Rev. Lett., 2010, 105, 168101 CrossRef PubMed.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Multi-particle collision dynamics: a particle-based mesoscale simulation approach to the hydrodynamics of complex fluids, Springer, 2009, vol. Advanced computer simulation approaches for soft matter sciences III, pp. 1–87 Search PubMed.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, J. Fluid Mech., 2008, 615, 401–431 CrossRef.
- D. Saintillan and M. J. Shelley, Phys. Rev. Lett., 2008, 100, 178103 CrossRef PubMed.
- P. T. Underhill, J. P. Hernandez-Ortiz and M. D. Graham, Phys. Rev. Lett., 2008, 100, 248101 CrossRef PubMed.
- A. Wysocki, J. Elgeti and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 050302 CrossRef PubMed.
- E. Lushi, V. Kantsler and R. E. Goldstein, Phys. Rev. E, 2017, 96, 023102 CrossRef PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- J. K. G. Dhont, An introduction to dynamics of colloids, Elsevier, 1996 Search PubMed.
- C. H. Rycroft, Chaos, 2009, 19, 041111 CrossRef PubMed.
- J. Bialké, H. Löwen and T. Speck, EPL, 2013, 103, 30008 CrossRef.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- H. Goldstein, C. P. Poole and J. L. Safko, Classical Mechanics, Addison-Wesley, 3rd edn, 2001 Search PubMed.
- I. P. Omelyan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 1169–1172 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- I. N. Bronstein and K. A. Semendjajew, Taschenbuch der Mathematik, BSB B. G. Teubner Verlagsgesellschaft, Nauka-Verlag, Leipzig, Moskau, 19th edn, 1979 Search PubMed.
- H. Noguchi, N. Kikuchi and G. Gompper, Europhys. Lett., 2007, 78, 10005 CrossRef.
- I. O. Götze, H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 046705 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, Europhys. Lett., 2001, 56, 319 CrossRef CAS.
- J. T. Padding and A. A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031402 CrossRef CAS PubMed.
- D. S. Bolintineanu, J. B. Lechman, S. J. Plimpton and G. S. Grest, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 066703 CrossRef PubMed.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016706 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm02301d |
| ‡ We recommend to fill the swimmer with multiple ghost particles, rather than using a single ghost particle of large mass, as this would result in a wrong value of the torque. |
| This journal is © The Royal Society of Chemistry 2018 |