Conversion/alloying lithium-ion anodes – enhancing the energy density by transition metal doping

Abstract

The development of alternative anodes is crucial for next generation lithium-ion batteries that can charge rapidly while maintaining high lithium storage capacity. Among the most promising candidates are conversion/alloying metal oxides like SnO₂, for which, however, the irreversibility of the conversion reaction provides a great hurdle – not least with respect to the substantial charge loss and, thus, limited energy density. Herein, we report on the improved reversibility of the conversion reaction by incorporating a transition metal dopant like iron, cobalt, or manganese. While all these dopants provide substantially enhanced capacities due to their beneficial effect on the alloying and conversion reaction, a detailed comparison concerning the achievable capacity at lower voltages, i.e., less than 2.0 V, reveals that the careful selection of the dopant plays a decisive role for the achievable energy density on the full-cell level. In fact, the highest energy density is obtained when doping SnO₂ with manganese rather than cobalt or iron because of its relatively lower redox potential and when setting the anodic cut-off to 1.5 V – despite the lower capacity. These results may serve as a general guideline when designing and evaluating alternatives for graphite – in particular, those including a conversion step.

---

Lithium-ion batteries (LIBs) are the power source of choice for a large variety of applications, covering, e.g., small-scale devices like portable electronics and large-scale applications like electric vehicles.^1–3 Particularly for the latter, however, there is a strong need for enhanced energy and power densities to meet the market and consumer demands.^3,4 Especially the realization of quickly rechargeable LIBs appears of great importance, as this will allow to compete with combustion-engine-powered vehicles also when traveling long distances – largely independent of the eventual driving range, i.e., the energy density of the battery.³ Nonetheless, the fast charging of LIBs is hampered by the state-of-the-art anode, graphite, as a result of the hazardous deposition of metallic lithium at the anode surface, the potential formation of lithium dendrites, and the occurrence of severe exothermic reactions, resulting in worst case in a thermal runaway.^5,6 Hence, to eventually enable a safe and rapid charging of LIBs, alternative anode materials, which can reversibly host lithium by conversion or alloying, are considered to be the key,⁷ while allowing for, at least, comparable gravimetric and volumetric energy densities.^8–11 One of the most investigated active materials in this regard is SnO₂, which theoretically provides specific capacities of about 1494 mA h g⁻¹, if both reactions, i.e., alloying and conversion are considered fully reversible (SnO₂ + 8.4 Li⁺ + 8.4 e⁻ ↔ 2 Li₂O + Li_4.4Sn). The reversible conversion reaction, however, is hindered by the increasing grain size of the tin particles formed upon reduction.^12,13 Thus, even if the alloying reaction can be stabilized, the theoretical capacity decreases to ca. 782 mA h g⁻¹, accompanied by a large irreversible capacity loss in the initial cycles. In recent years, there have been essentially three different approaches to render the conversion reaction reversible. The first one is based on the design of advanced SnO₂/transition metal oxide nanostructures.^14–19 Interestingly, only those composites reveal high reversible capacities, i.e., capacities exceeding the alloying contribution, for which two requirements are fulfilled: (i) an “intermixing” of the two different compounds on the nanocrystalline level and (ii) the incorporation of a metal oxide, which is reduced prior to tin oxide, such as iron, nickel, molybdenum, or cobalt. Both requirements underline the necessity of a high electronic conductivity within the active material composite to enable the reversibility of the conversion reaction.¹¹ The second approach is based on a composite of SnO₂, a metallic transition metal (e.g., iron, cobalt, or manganese), and graphite.^20,21 Also in this case, the intimate contact between the metallic transition metal and SnO₂ appears to be the key to enable the reversible conversion reaction, though requiring rather large fractions of the metal, i.e., about 30 wt% with respect to SnO₂. The third approach is based on the incorporation of transition metal cations into the SnO₂ lattice as, for instance, in Fe-,^22–24 W-,²⁵ or Co-doped^26–28 doped SnO₂. This approach provides the great advantage of an intrinsic mixing of the different cations on the atomic level, a combined reduction of the different cations, and the need for reduced amounts of the transition metal, as a doping concentration of 10% (TM to Sn) appears to be sufficient.²⁸

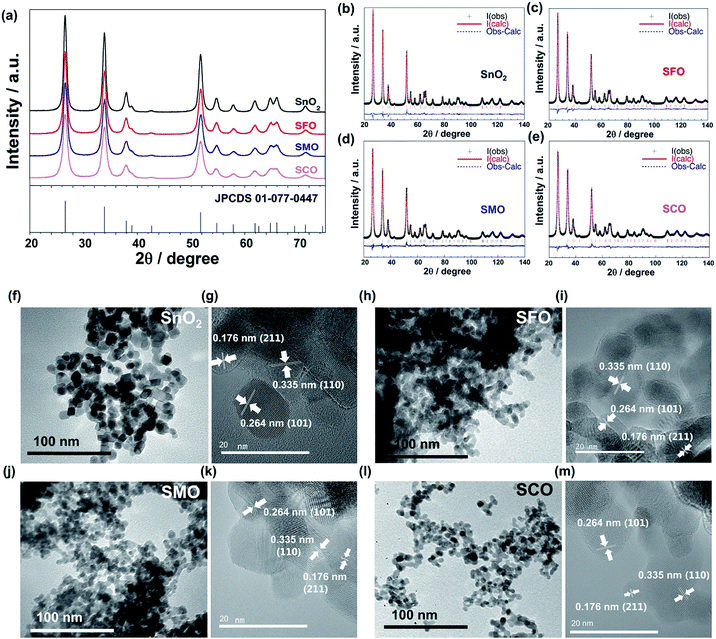
In this work, we will show that the careful selection of the transition metal cation, moreover, results in significantly enhanced energy densities on the full-cell level as well as an improved cycling stability and rate capability. For this purpose, we synthesized pure SnO₂ and TM-doped SnO₂ – with the TM being either Fe (SFO), Co (SCO), or Mn (SMO). The corresponding X-ray diffraction (XRD) patterns are presented in Fig. 1a, all revealing a tetragonal structure with the P4₂/mnm space group, matching well with the JCPDS 01-077-0447. The patterns show relatively pronounced, rather broad reflections, suggesting the formation of nano-crystalline samples. A closer examination of the diffractograms confirms that there are no additional reflections present, indicating the absence of secondary phases down to a level of well below 0.5 wt%.²⁹ The subsequently conducted Rietveld refinement (Fig. 1b–e) provides an accurate determination of the unit cell parameters and atomic positions, which are summarized in Table S1.† According to this in-depth structural analysis the partial substitution of tin by iron, manganese, or cobalt results in a small, but appreciable variation of the unit cell volume, increasing in the order SCO > SFO > SMO compared to pure SnO₂, which is supported by the excellent agreement indices of the performed fit. In fact, these appreciable variations of the unit cell volume indicate the incorporation of the dopant into the rutile crystalline lattice and its absence in interstitial sites. The FWHM (full width at half maximum) of the XRD reflections increases in the order SnO₂ < SMO < SFO < SCO, meaning that the crystallite size, calculated using the Scherrer formula based on the intercepts of the W–H. plots,³⁰ decreases in the same order, i.e., SnO₂ (30 nm) > SMO (16 nm) > SFO (15 nm) > SCO (11 nm).

Fig. 1 (a) XRD patterns of as-synthesized, pure SnO₂ (in black), Fe-doped SnO₂ (SFO; in red), Mn-doped SnO₂ (SMO; in blue), and Co-doped SnO₂ (SCO; in pink); as reference given in the bottom is JCPDS card no. 01-077-0447 for cassiterite SnO₂. (b–e) Rietveld refined diffractograms of (b) SnO₂, (c) SFO, (d) SMO, (e) and SCO. (f–m) TEM/HRTEM micrographs of (f and g) SnO₂, (h and i) SFO, (j and k) SMO, and (l and m) SCO, including the characteristic cassiterite lattice fringes for all four samples in the given HRTEM micrographs.

These results are supported by the subsequent (high-resolution) transmission electron microscopy ((HR)TEM) analysis (Fig. 1f–m), revealing the synthesis of well-crystallized, roughly spherical particles for all four samples with the characteristic lattice fringes of 0.335, 0.264, and 0.176 nm for the (110), (101), and (211) planes, respectively, in cassiterite-structured (TM-doped) SnO₂ without any apparent lattice defects.

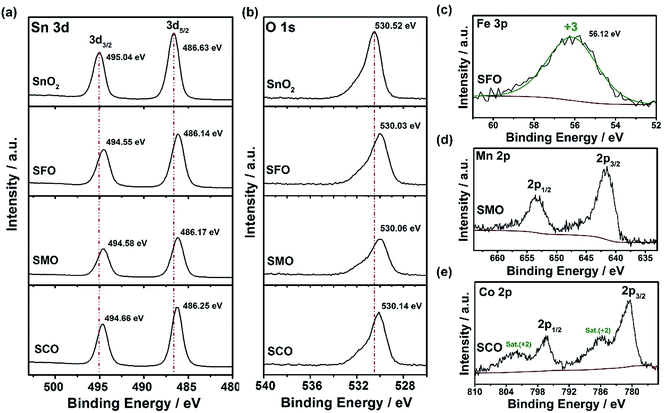
Further corroboration of the successful doping is provided by X-ray photoelectron spectroscopy (XPS). The corresponding survey spectra are presented in Fig. S1,† while a detailed comparison of the four samples is provided in Fig. 2. In Fig. 2a, the Sn 3d spectra are depicted, revealing two major peaks for all samples, related to Sn 3d_5/2 and Sn 3d_3/2 and located at 486.6 and 495.0 eV, respectively, in case of pure SnO₂, confirming its tetravalent oxidation state.^31,32 The spectra for the three TM-doped SnO₂ samples show essentially the same features, but the two peaks are slightly shifted to lower binding energies, i.e., by about 0.4–0.5 eV. Likewise, the O 1s transition peak (Fig. 2b) is slightly shifted to lower binding energies for the TM-doped samples by the same offset. Such decrease in binding energy is assigned to the presence of oxygen vacancies^33,34 as a result of the aliovalent TM doping to ensure charge neutrality. This assignment is further supported by the increasing asymmetry of this peak in presence of the transition metal dopants, which can be deconvoluted in a low binding energy component (LBEC) at around 530 eV and a high binding energy component (HBEC) at around 531.4 eV.^35,36 An increasing contribution of the HBEC, which is responsible for this increasing asymmetry, indicates an increasing presence of oxygen vacancies,^35,36 which is in excellent agreement with the Raman and UV-vis spectra depicted in Fig. S2 and S3,† respectively (see also the corresponding discussion in the ESI†). In fact, the oxidation state of iron was determined to be purely trivalent, as indicated by the single peak at 56.1 eV in the Fe 3p spectrum (Fig. 2c).^37,38 This value is slightly higher than for classic iron oxides (e.g., 55.8 eV for Fe₂O₃, 54.9 eV for FeO, and 53.9 eV for Fe₃O₄), which is attributed to the different atomic environment in Sn_0.9Fe_0.1O₂, compatible with the proposed incorporation into the rutile lattice.^39–41 For SMO, the maximum of the Mn 2p_3/2 peak is located at 641.86 eV (Fig. 2d), indicating an average Mn oxidation state slightly above +3 in consideration of the mean values in the NIST XPS database for MnO (641.2 eV), Mn₂O₃ (641.7 eV), and MnO₂ (642.3 eV). The lowest oxidation state is recorded for cobalt, for which the Co 2p spectra (Fig. 2e) show very prominent satellite peaks at ∼786 and 802 eV, which are a characteristic feature of Co²⁺.⁴² Nonetheless, the presence of a fraction of trivalent cobalt appears plausible based on a tentative fit, using the reference binding energies of the pure TM oxides (not shown herein). This tentative fit and the resulting estimation of the average TM cationic radius (low spin), which is about 0.69 Å for tetravalent tin, 0.66 Å for cobalt (average oxidation state of <3), 0.65 Å for trivalent iron, and 0.64 Å for manganese (average oxidation state of >3) provides also an explanation for the decrease of the unit cell volume earlier observed (see Table S1†). This means that the smaller the TM cation the smaller is the unit cell volume, which nicely illustrates the conformity of the obtained data. In contrast, the crystal growth is apparently kinetically hindered, the less similar the oxidation state of the dopant to the oxidation state of the tin cation.

Fig. 2 XPS analysis of pure SnO₂, SFO, SMO, and SCO: comparison of the (a) Sn 3d and (b) O 1s detail spectra for the four samples (top to bottom: SnO₂, SFO, SMO, SCO); (c) fitted Fe 3p spectrum for SFO – the Fe 3p spectrum is shown instead of the Fe 2p, as the latter overlaps with the strong Sn 3p peaks; (d) Mn 2p spectrum for SMO; and (e) Co 2p spectrum for SCO.

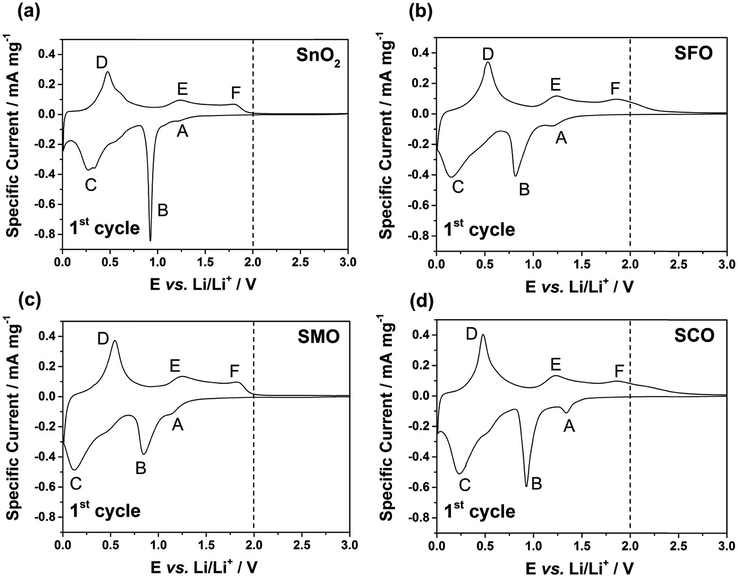
After this careful physicochemical characterization, confirming the successful doping in all three cases, we focused on the investigation of the impact of the TM dopant on the electrochemical behavior. For this purpose, we subjected electrodes comprising the different active materials to cyclic voltammetry (CV) tests in a first step (Fig. 3). Pure SnO₂ reveals essentially three reduction features in the first cathodic sweep, precisely at 1.22 V (A), 0.92 V (B), and around 0.31 V (C); the latter one being composed of several peaks (Fig. 3a). Peak (A) is commonly assigned to the formation of the solid electrolyte interphase (SEI) as a result of the occurring electrolyte decomposition.^43,44 The most intense peak (B) is attributed to the reductive conversion of SnO₂ to metallic tin and lithium oxide, and feature (C) is related to the alloying of metallic tin and lithium.^45,46 For the subsequent anodic sweep, feature (D) at around 0.47 V corresponds to the dealloying process, while the peaks (E) at 1.23 V and (F) at 1.81 V are generally assigned to the re-oxidation of tin and backformation of Li₂O.^43,44

Fig. 3 Cyclic voltammograms (1^st cyclic sweep) for electrodes based on (a) SnO₂, (b) SFO, (c) SMO, and (d) SCO (sweep rate: 0.05 mV s⁻¹; reversing voltages: 0.01 and 3.0 V vs. Li/Li⁺). A vertical dashed line at 2.0 V is included to guide the reader's eye in light of the corresponding discussion in the text on the impact of the dopant nature, highlighting the current flow above this voltage in case of Fe and Co.

For TM-doped SnO₂, the general CV features do not differ substantially (Fig. 3b–d), indicating that the presence of the dopant does not alter the reaction mechanism, while substantially enhancing the reversibility of the alloying and, in particular, the conversion reaction. In addition, the tin particle aggregation upon continuous cycling is hindered (see Fig. S4† for the subsequent CV sweeps and Fig. S5† for a comparative in situ XRD analysis). Nonetheless, there are three remarkable differences. First, all TM-doped samples (Fig. 3b–d) show a more pronounced peak (A), which is assigned to the higher surface area (84 m² g⁻¹ for SFO, 93 m² g⁻¹ for SMO, and 95 m² g⁻¹ for SCO compared to 36 m² g⁻¹ for SnO₂) because of the smaller particle size and the incorporation of the TM dopant into the rutile lattice. Moreover, the intensity maximum for peak (A) varies as a function of the transition metal. For SFO (Fig. 3b), it appears at 1.21 V, i.e., similar to SnO₂, while it is shifted upwards for SCO (Fig. 3d) to 1.34 V and downwards for SMO (Fig. 3c) to 1.15 V. These variations highlight that the elemental nature has a significant impact on the onset of the electrolyte decomposition. Second, features (B) and (C) are broader and less distinct which may be ascribed as well to the relatively smaller particle size, the presence of anionic vacancies, and the formation of presumably smaller domains of metallic tin and TM. Third, and most important for the following considerations, after peak (F), i.e., for E > 2.0 V there is essentially no current flow in case of SMO (Fig. 3c), while there is still a significant current flowing for SFO (Fig. 3b) and SCO (Fig. 3d). These observations can be explained by the re-oxidation of the corresponding TM, since the redox potential of Fe and, in particular, of Co is substantially higher than that of Mn.

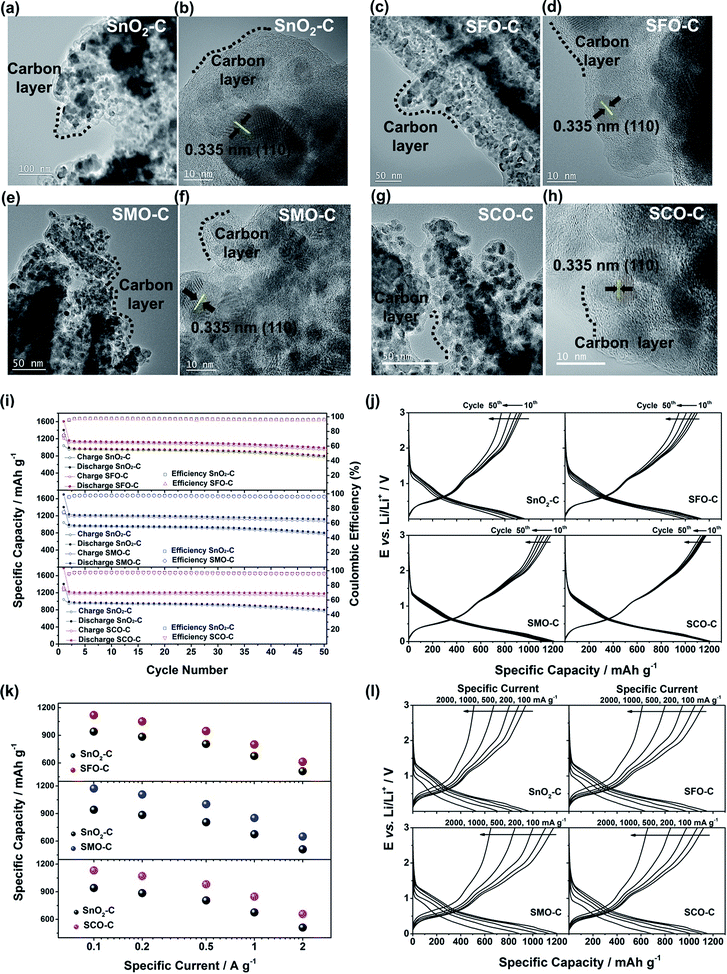
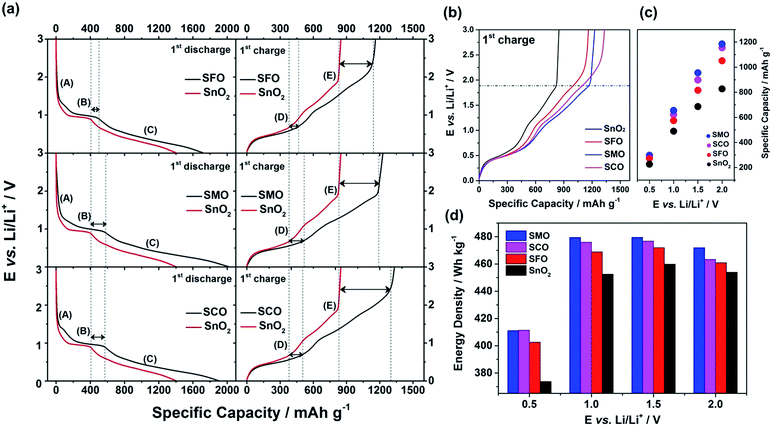
To quantify this effect in terms of capacity as a function of the anodic cut-off voltage, we conducted galvanostatic cycling (Fig. 4). A comparison for the first dis-/charge cycle of SFO, SMO, and SCO – each with pure SnO₂ – is provided in Fig. 4a. Electrodes based on pure SnO₂ reveal the characteristic potential profile⁴⁷ with a rapid potential drop to about 1.5 V, followed by a weakly defined feature at about 1.2–1.3 V, which is in excellent agreement with the CV data – just like the general impact of the TM doping on the electrochemical response. The incorporation of cobalt results in the highest reversible capacity, when charging up to 3.0 V, i.e., 1340 mA h g⁻¹, compared to 1230 mA h g⁻¹ for SMO, 1170 mA h g⁻¹ for SFO, and only 850 mA h g⁻¹ for pure SnO₂. While the choice of such a high anodic cut-off voltage is certainly valuable to determine the maximum capacity of an electrode material in context of the corresponding scientific literature, it is, nevertheless, of limited insight with regard to the potential application of the potential anode material candidates in (commercially viable) lithium-ion full-cells. Thus, we have carefully analyzed the achievable capacity at lower anodic cut-offs, which moreover provide the great advantage of enhanced cycling stabilities.^12,48 In fact, beside the incorporation of a TM dopant in general, the choice of the dopant nature plays a decisive role. The incorporation of manganese rather than iron or cobalt results in a superior reversible capacity at lower potentials up to ca. 1.9 V (Fig. 4b), which is assigned to the substantially lower redox potential of 1.87 V vs. Li/Li⁺ for Mn/Mn²⁺ compared to 2.60 V and 2.76 V for Fe/Fe²⁺ and Co/Co²⁺, respectively.⁴⁹ A plot of the specific capacity at a certain anodic cut-off voltage (Fig. 4c, see also Table S2†) underlines this finding, showing that the order in specific capacity for all these cut-offs is SMO > SCO > SFO > SnO₂. The capacity for SMO at 1.5 V, for instance, is 955 mA h g⁻¹, which is 57 mA h g⁻¹ higher than for SCO and 139 mA h g⁻¹ higher compared to SFO. Translating these capacity values into gravimetric energy densities with a theoretical LiNi_0.5Mn_1.5O₄ cathode (Fig. 4d, see also Table S3†) further highlights the advantageous effect of carefully selecting the TM dopant. For a cut-off voltage of 2.0 V, for instance, the estimated specific energy is 454 W h kg⁻¹ for SnO₂, 461 W h kg⁻¹ for SFO, 463 W h kg⁻¹ for SCO, and 472 W h kg⁻¹ for SMO, i.e., about 10 W h kg⁻¹ more compared to SCO and SFO and almost 20 W h kg⁻¹ more with respect to SnO₂. When selecting a lower cut-off of 1.5 V, the gravimetric energy density is even further enhanced, e.g., 480 W h kg⁻¹ for SMO, since theoretically less cathode material is required to balance the anode capacity, while the cell voltage is greater. Considering the same theoretical setup for a graphite anode results in an estimated energy density of 454 W h kg⁻¹, which is about 25 W h kg⁻¹ less. Critical for this estimation, of course, is the development of suitable strategies to reduce and/or balance the initial charge loss – e.g., by decreasing the surface area by forming advanced secondary particle architectures, stabilizing the electrode/electrolyte interface, and/or including viable pre-lithiation strategies.^11,50,51 A rather simple, though effective strategy is the application of suitable carbonaceous coatings.²⁸ A comprehensive physicochemical characterization of the coated samples by means of thermogravimetric analysis (TGA), Raman spectroscopy, and XRD is presented and discussed in Fig. S6.† The resulting (HR)TEM micrographs are presented in Fig. 5a–h, confirming the preservation of the particle size and morphology as well as the crystalline structure. Furthermore, the micrographs show that the derived carbon is forming a thin (ca. 5 nm), but continuous layer on the secondary particle surface, as highlighted by dashed black lines in all micrographs. Simultaneously, the carbon acts as an electronically conductive “glue”, interconnecting the single primary particles to larger secondary particle structures and by this enabling a percolating network for the electron conduction.

Fig. 4 Galvanostatic cycling of electrodes based on SnO₂, SFO, SMO, and SCO: (a) 1^st cycle discharge (left) and charge (right) profiles for SFO, SMO, and SCO (from top to bottom) always in direct comparison with the 1^st cycle dis-/charge profile of pure SnO₂ (given in red; applied specific current: 20 mA g⁻¹); (b) direct comparison of the 1^st cycle charge profiles for all four samples; (c) comparative analysis of the specific capacity as a function of the half-cell voltage at selected points of 0.5, 1.0, 1.5, and 2.0 V; (d) direct comparison of the resulting gravimetric energy density, when assuming a theoretical LiNi_0.5Mn_1.5O₄ cathode with a (constant) discharge potential of 4.7 V and a specific capacity of 140 mA h g⁻¹ (anode/cathode ratio of 1 : 1 in specific capacity).

Fig. 5 (a to h) (HR)TEM characterization of the carbon-coated samples: (a and b) SnO₂-C, (c and d) SFO-C, (e and f) SMO-C, and (g and h) SCO-C. (i to l) Galvanostatic cycling of electrodes based on carbon-coated SnO₂, SFO, SMO, and SCO: (i) plot of the specific dis-/charge capacity and coulombic efficiency vs. the cycle number for SFO-C, SMO-C, and SCO-C (from top to bottom) – always in direct comparison to SnO₂-C, serving as reference (1^st cycle: 20 mA g⁻¹, following cycles: 100 mA g⁻¹); (j) the corresponding potential profiles for selected cycles (10^th, 20^th, 30^th, 40^th, and 50^th) for SnO₂-C, SFO-C, SMO-C, and SCO-C (from top left to bottom right); (k) application of elevated specific currents to electrodes based on SFO-C, SMO-C, and SCO-C (from top to bottom) – always in direct comparison to SnO₂-C (the given capacity values are averaged over 10 cycles); (l) the corresponding potential profiles for the fifth cycle at each dis-/charge current for SnO₂-C, SFO-C, SMO-C, and SCO-C (from top left to bottom right).

The formation of such secondary structures, indeed, has a beneficial effect on the first cycle coulombic efficiency: while it is only 59.9% (SnO₂), 61.7% (SMO), 68.5% (SFO), and 70.8% (SCO) for the non-coated samples, it greatly increased to 74.1% (SnO₂), 75.2% (SMO), 75.0% (SFO), and 75.3% (SCO) after applying the carbonaceous coating. We anticipate that the first cycle coulombic efficiency can be further improved for optimized secondary particle structures with a reduced surface area and further stabilized electrode/electrolyte interface, both leading to a decreased electrolyte decomposition for the initial cycles. In addition, the carbon coating has also an advantageous effect on the cycling stability and rate capability as revealed by comparing the electrochemical performance before (Fig. S7†) and after the carbon coating (Fig. 5i–l). Especially in case of SMO-C and SCO-C no significant fading is observed for 50 constant current cycles, different from SnO₂-C and SFO-C, which slightly fade after about 35 and 40 cycles, respectively (Fig. 5i – see also Fig. S8† for the corresponding CV data). For the first cycle (at 20 mA g⁻¹) the cells provide a reversible capacity of 1041 mA h g⁻¹ for SnO₂-C, 1207 mA h g⁻¹ for SFO-C, 1276 mA h g⁻¹ for SMO-C, and 1336 mA h g⁻¹ for SCO-C. At the 50th cycle, a capacity of 772, 949, 1075, and 1130 mA h g⁻¹ is retained at a constant current density of 100 mA g⁻¹ for SnO₂-C, SFO-C, SMO-C, and SCO-C, respectively. Additionally, the rate capability is substantially improved for the carbon-coated samples and, once more, the TM-doped samples clearly outperform pure SnO₂-C (Fig. 5k). Remarkably, at very high specific currents of 2 A g⁻¹, the reversible capacity is still 511 mA h g⁻¹ for SnO₂-C, 613 mA h g⁻¹ for SFO-C, 651 mA h g⁻¹ for SMO-C, and 657 mA h g⁻¹ for SCO-C. This is up to almost twice the theoretical capacity of graphite (372 mA h g⁻¹), while such a high current would correspond to a dis-/charge rate of 5.3C for the latter.

In conclusion, we have shown that the incorporation of a transition metal dopant like Fe, Co, or Mn into the SnO₂ crystalline lattice generally results in substantially enhanced capacities due to an improved reversibility of the alloying and conversion reactions. This beneficial effect is assigned to the hindered tin particle aggregation and improved electronic conductivity within the primary active material particles. The careful choice of the transition metal dopant, however, plays a decisive role concerning the achievable energy density on the full-cell level. In fact, when comparing the transition metal dopants studied herein it turns out that the relatively lower redox potential of manganese allows for the highest energy densities – even though the capacity is lower than for cobalt when cycling the anode in a rather wide voltage range. We may anticipate that these results will serve as guideline for the development of new alternative anodes based on a combined alloying and conversion reaction and, thus, contribute to the realization of next generation high-energy, fast-chargeable lithium-ion batteries.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

Financial support from the Chinese Scholarship Council (CSC; Y.-J. M. and Y. M.), the Vector Foundation within the framework of the NEW E² project, and the Helmholtz Association is kindly acknowledged. Furthermore, the authors want to thank Yuanchun Ji for performing the TEM analysis as well as Oliver Mendoza Reyes and Ruihao Gong for conducting the UV-vis experiments including the very valuable discussion.

References

1. B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430.
2. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
3. D. Bresser, K. Hosoi, D. Howell, H. Li, H. Zeisel, K. Amine and S. Passerini, J. Power Sources, 2018, 382, 176–178.
4. B. G. Pollet, I. Staffell and J. L. Shang, Electrochim. Acta, 2012, 84, 235–249.
5. C. Uhlmann, J. Illig, M. Ender, R. Schuster and E. Ivers-Tiffée, J. Power Sources, 2015, 279, 428–438.
6. T. Waldmann, B.-I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124.
7. J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
8. J. Cabana, L. Monconduit, D. Larcher and M. R. Palacín, Adv. Mater., 2010, 22, E170–E192.
9. N. Nitta and G. Yushin, Part. Part. Syst. Charact., 2014, 31, 317–336.
10. M. N. Obrovac and V. L. Chevrier, Chem. Rev., 2014, 114, 11444–11502.
11. D. Bresser, S. Passerini and B. Scrosati, Energy Environ. Sci., 2016, 9, 3348–3367.
12. I. A. Courtney and J. R. Dahn, J. Electrochem. Soc., 1997, 144, 2943–2948.
13. R. Hu, H. Zhang, Z. Lu, J. Liu, M. Zeng, L. Yang, B. Yuan and M. Zhu, Nano Energy, 2018, 45, 255–265.
14. H. Guo, L. Liu, T. Li, W. Chen, Y. Wang and W. Wang, Chem. Commun., 2014, 50, 673–675.
15. C. Hua, X. Fang, Z. Wang and L. Chen, Chem.–Eur. J., 2014, 20, 5487–5491.
16. Y. Jiang, Y. Li, W. Sun, W. Huang, J. Liu, B. Xu, C. Jin, T. Ma, C. Wu and M. Yan, Energy Environ. Sci., 2015, 8, 1471–1479.
17. X.-Y. Xue, Z.-H. Chen, L.-L. Xing, S. Yuan and Y.-J. Chen, Chem. Commun., 2011, 47, 5205–5207.
18. W.-S. Kim, Y. Hwa, H.-C. Kim, J.-H. Choi, H.-J. Sohn and S.-H. Hong, Nano Res., 2014, 7, 1128–1136.
19. L. Zhang, H. B. Wu and X. W. Lou, J. Am. Chem. Soc., 2013, 135, 10664–10672.
20. R. Hu, Y. Ouyang, T. Liang, X. Tang, B. Yuan, J. Liu, L. Zhang, L. Yang and M. Zhu, Energy Environ. Sci., 2017, 10, 2017–2029.
21. R. Hu, Y. Ouyang, T. Liang, H. Wang, J. Liu, J. Chen, C. Yang, L. Yang and M. Zhu, Adv. Mater., 2017, 29, 1605006.
22. F. Mueller, D. Bresser, V. S. K. Chakravadhanula and S. Passerini, J. Power Sources, 2015, 299, 398–402.
23. Y. Yan, F. Du, X. Shen, Z. Ji, X. Sheng, H. Zhou and G. Zhu, J. Mater. Chem. A, 2014, 2, 15875–15882.
24. J. Wang, L. Wang, S. Zhang, S. Liang, X. Liang, H. Huang, W. Zhou and J. Guo, J. Alloys Compd., 2018, 748, 1013–1021.
25. S. Wang, L. Shi, G. Chen, C. Ba, Z. Wang, J. Zhu, Y. Zhao, M. Zhang and S. Yuan, ACS Appl. Mater. Interfaces, 2017, 9, 17163–17171.
26. M. Lübke, D. Ning, C. F. Armer, D. Howard, D. J. L. Brett, Z. Liu and J. A. Darr, Electrochim. Acta, 2017, 242, 400–407.
27. P. Nithyadharseni, K. P. Abhilash, S. Petnikota, M. R. Anilkumar, R. Jose, K. I. Ozoemena, R. Vijayaraghavan, P. Kulkarni, G. Balakrishna, B. V. R. Chowdari, S. Adams and M. V. Reddy, Electrochim. Acta, 2017, 247, 358–370.
28. Y. Ma, Y. Ma, U. Ulissi, Y. Ji, C. Streb, D. Bresser and S. Passerini, Electrochim. Acta, 2018, 277, 100–109.
29. G. Giuli, A. Trapananti, F. Mueller, D. Bresser, F. d'Acapito and S. Passerini, Inorg. Chem., 2015, 54, 9393–9400.
30. V. D. Mote, Y. Purushotham and B. N. Dole, J. Theor. Appl. Phys., 2012, 6, 6.
31. H. Ma, K. Teng, Y. Fu, Y. Song, Y. Wang and X. Dong, Energy Environ. Sci., 2011, 4, 3067.
32. S. Wu, S. Yuan, L. Shi, Y. Zhao and J. Fang, J. Colloid Interface Sci., 2010, 346, 12–16.
33. X. Dou, D. Sabba, N. Mathews, L. H. Wong, Y. M. Lam and S. Mhaisalkar, Chem. Mater., 2011, 23, 3938–3945.
34. E. Ramasamy and J. Lee, Energy Environ. Sci., 2011, 4, 2529–2536.
35. M. Naeem, S. K. Hasanain, M. Kobayashi, Y. Ishida, A. Fujimori, S. Buzby and S. I. Shah, Nanotechnology, 2006, 17, 2675–2680.
36. K. A. Bogle, M. N. Bachhav, M. S. Deo, N. Valanoor and S. B. Ogale, Appl. Phys. Lett., 2009, 95, 203502.
37. L. P. Kazansky, Y. I. Kuznetsov, N. P. Andreeva and Y. G. Bober, Appl. Surf. Sci., 2010, 257, 1166–1174.
38. T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441–2449.
39. D. Brion, Appl. Surf. Sci., 1980, 5, 133–152.
40. A. Punnoose, J. Hays, A. Thurber, M. H. Engelhard, R. K. Kukkadapu, C. Wang, V. Shutthanandan and S. Thevuthasan, Phys. Rev. B, 2005, 72, 054402.
41. A. Punnoose, K. Dodge, J. J. Beltrán, K. M. Reddy, N. Franco, J. Chess, J. Eixenberger and C. A. Barrero, J. Appl. Phys., 2014, 115, 17B534.
42. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
43. X. W. Lou, C. M. Li and L. A. Archer, Adv. Mater., 2009, 21, 2536–2539.
44. D. Bresser, F. Mueller, D. Buchholz, E. Paillard and S. Passerini, Electrochim. Acta, 2014, 128, 163–171.
45. I. A. Courtney and J. R. Dahn, J. Electrochem. Soc., 1997, 144, 2045–2052.
46. T. Brousse, R. Retoux, U. Herterich and D. M. Schleich, J. Electrochem. Soc., 1998, 145, 1–4.
47. R. Demir-Cakan, Y.-S. Hu, M. Antonietti, J. Maier and M.-M. Titirici, Chem. Mater., 2008, 20, 1227–1229.
48. F. Mueller, D. Bresser, V. S. K. Chakrayadhanula and S. Passerini, J. Power Sources, 2015, 299, 398–402.
49. A. J. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, CRC Press, 1985.
50. V. Aravindan, Y.-S. Lee and S. Madhavi, Adv. Energy Mater., 2017, 7, 1602607.
51. Y. Zhao, L. P. Wang, M. T. Sougrati, Z. Feng, Y. Leconte, A. Fisher, M. Srinivasan and Z. Xu, Adv. Energy Mater., 2017, 7, 1601424.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8se00424b

---