Evaluating microstructure evolution in an SOFC electrode using digital volume correlation

Abstract

Degradation mechanisms within solid oxide fuel cells (SOFC) during thermal cycling limit operational start-up times and cell lifetime, and must therefore be better understood and mitigated. This work explores such mechanisms using digital volume correlation (DVC) techniques applied to lab-based X-ray tomograms where the microstructural evolution is evaluated during the operational cycling of a Ni–YSZ/YSZ cell. To emulate reduced start-up times, five tomograms were collected over four operational thermal cycles to 750 °C at various ramp-rates: 3, 10, 20 and 30 °C min⁻¹. Two key features are observed in the 3D strain profiles. Firstly, during low ramp-rates the material produces microscopic channels towards cluster-points. This is thought to be caused by the ceramic skeleton inhibiting the effects of sintering. Secondly, previously unseen macroscopic ‘waves’ developed after high-rate cycling, consisting of linear regions of compression and tension throughout the sample. These wave features decay away from a heterogeneous defect which is thought to be responsible for the non-uniform strain profile. This work demonstrates the first use of sub-micron DVC computations applied to an SOFC exposed to operationally relevant temperatures. These findings will assist in the development of new electrode materials from their fabrication to operation, ultimately supporting commercial viability of SOFCs.

---

1. Introduction

The search for improved energy efficiencies while reducing the production of harmful pollutants has propelled the development of electrochemical devices. Fuel cells offer promising opportunities for many applications, particularly high-temperature devices, such as the solid oxide fuel cell (SOFC), which are able to operate with high net efficiencies on a variety of fuel gases without the requirement of expensive metal catalysts.^1,2 However, the degradation of cell components continues to impede electrochemical performance, limiting the lifetime of the device. Research has been aimed at improving our understanding of these degradation mechanisms, refining mitigation strategies which produce advanced cell designs that are competitive with existing technologies.

In its most simple form, the SOFC is composed of two porous electrodes, an anode and a cathode, which are separated by a dense ceramic electrolyte. Yttria-stabilised zirconia (YSZ) is a ceramic that is often used for the electrolyte material, the anode is commonly fabricated as a cermet material, whereby nickel oxide (NiO) is deposited with 8YSZ, in the form of NiO–YSZ, reduced to nickel during operational start-up.³ Perovskite-based compounds such as lanthanum strontium manganite (LSM) or lanthanum strontium cobalt ferrite (LSCF) are commonly employed as SOFC cathodes, again often combined with the electrolyte materials to form composite electrodes. Within the SOFC electrodes, the reaction site is defined as the location where the metallic, ceramic, and pore phases meet, which is termed the triple-phase boundary (TPB). The volumetric density of the TPB reaction sites (ρ_TPB) is calculated to compare different electrodes and to quantify electrode degradation.

SOFC electrodes can degrade through several mechanisms that are typically dependent on the operational thermal profile^4,5 and the composition of the fuel gas.⁶ Much research has focused on the mechanisms responsible for the degradation of the anode and the interactions at the anode/electrolyte interface as these locations are thought to trigger the most prominent performance losses.⁷ Two notable degradation processes are thermal shock and thermal ageing which are each comprised of several complex mechanisms. The former is generally attributed to the thermal cycling to/from operating temperature, and the latter predominantly while at operating temperature, where dwelling times are often on the order of hundreds or thousands of hours. One degradation mechanism is thermal shock resulting from the mismatch in the thermal expansion coefficients (TECs) of the constituent materials during thermal cycling; Ni and YSZ have average TEC values of approximately 16 and 10 × 10⁻⁶ °C⁻¹ through the temperature ranges typical of SOFC operation (100–800 °C). Thermal strain can be expected between the two materials within the complex electrode microstructure because of this mismatch, giving rise to degradation as a result of thermal shock. Whereas when at operating temperature, the Ni is significantly closer to its melting temperature (ca. 1455 °C) compared to the ceramic YSZ (ca. 2700 °C). Therefore while operating, or even dwelling at operating temperature, the Ni metal can be expected to agglomerate most substantially, giving rise to thermal ageing. Efforts to mitigate degradation have resulted in the use of cermet materials (e.g. Ni–YSZ), which provide several advantages but most noteworthy are: the maximisation of the reaction site density,⁸ and the provision of a ceramic-backbone which reduces the macroscopic mismatch in TECs⁹ aiding in thermal shock and inhibits metal sintering during thermal ageing.¹⁰

Characterisation of the TPB locations has become a prominent method in gaining understanding of degradation mechanisms, and has been used to develop advanced cell microstructures.¹¹ Initially TPB characterisation was accomplished via 2D studies using techniques such as scanning electron microscopes,¹² however, 2D information lacks statistical representation and may produce perspective-induced errors, and cannot account for percolation effects. Techniques therefore moved towards 3D characterisation with the use of focused ion beams techniques (FIB-SEM) to mill away the surface material exposing the fresh structure to be imaged using the SEM.¹³ Although FIB-SEM provides 3D data, it also requires the destruction of the sample, preventing 4D (3 spatial dimensions plus time) studies on the same region of interest (ROI). Consequently, X-ray computed tomography (CT) became widely utilised due to its non-destructive capabilities although, early use of X-ray CT involving three-phase segmentation required the use of specialist synchrotron facilities.^14,15 Use of such facilities can be limited and has resulted in few extended-duration experiments being conducted.^16–18 Lab-based CT instruments have made significant advancements in recent years, achieving comparable resolutions to cutting-edge synchrotron beamlines.¹⁹ Such techniques have recently established lab-based three-phase segmentation.²⁰ Moreover, the development of robust sample preparation techniques now allows 4D studies to be conducted using entirely lab-based facilities.^21,22

The use of 4D characterisation techniques are essential in performing accurate longitudinal studies of phenomena that develop with time: for instance, observing different samples from an electrode's microstructure before and after degradation does not permit a direct comparison, which is essential in order to truly understand how these complex mechanisms progress. This is uniquely possible using techniques such as those described here. A major advantage of 4D imaging lies in the correlative computations which can be applied to the structural data sets. Digital volume correlation (DVC)^23–25 compares two data sets from the exact same ROI before and after deformation. Correlation techniques²⁶ determine the displacement of features within the ROI after deformation producing 3D displacement and strain fields. Electrochemical devices have previously been explored with this technique^27–29 however, application has thus far been dominated by battery materials at coarser resolution.

To the authors' knowledge, this is the first report of DVC conducted on a solid oxide fuel cell using sub-micron resolution data obtained from material exposed to high temperatures. This work examines the evolution associated with various thermal ramp-rates and the resulting start-up times in an aim to elucidate the mechanisms responsible for SOFC degradation.

2. Experimental

2.1 Materials and sample preparation

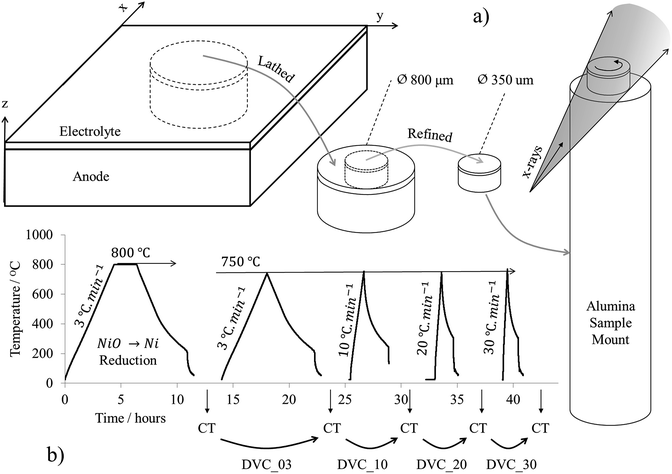
An anode-supported anode/electrolyte solid oxide half-cell comprising of a nickel oxide-8 mol% yttria stabilised zirconia (NiO–8YSZ) anode and an 8YSZ electrolyte is inspected through several operational thermal cycles. To conduct correlative computation, multiple tomograms of a sufficient resolution were required. To accomplish this, a sub-sample was removed from the cell using an A Series/Compact Class 4 532 nm Laser Micromachining System (Oxford Lasers, Oxford, UK).²¹ Initially, an 800 μm diameter pillar encompassing the full depth of the cell (500 μm of anode and 10 μm of electrolyte) was machined from the cell bulk and mounted to a pin using a technique developed for high-temperature studies.²² The pillar was then refined using the micromachining system to a diameter sufficient for high-resolution X-ray micro-CT, approximately 350 μm.

2.2 Lab-based X-ray micro-CT

Five tomograms were collected in total from the same sample in the same region of interest using a lab-based micro-CT X-ray instrument (Zeiss Xradia 520 Versa, Carl Zeiss., CA, USA), all under the same scanning parameters. During each tomography, 2401 radiograph projections were collected at an exposure time of 30 seconds per projection with the source operating with a voltage and current of 80 kV and 88 μA with a characteristic tungsten emission. The radiographs comprised isotropic pixels 395 nm in length. The 2401 radiographs were then reconstructed using commercial software (‘Reconstructor Scout-and-Scan’, Zeiss, Carl Zeiss., CA, U.S.A.) based on cone-beam filtered back projection algorithms producing a tomogram ca. 2 × 10⁷ μm³ in volume. The sample preparation and procedure for tomography can be seen in Fig. 1a. Structural properties such as particle size, contact area and tortuosity-factor have been assessed extensively and reported previously.^30,31

Fig. 1 Experimental set-up for the correlation of lab-based X-ray tomograms using digital volume correlation: (a) sample refinement and geometric set-up for X-ray characterisation and (b) thermal profile with indication of the time at which the five tomograms and four DVC computations were conducted.

2.3 Thermal cycling

Prior to thermal cycling, the furnace tube was purged with nitrogen in order to remove any air from the environment. All purging was conducted at room temperature for a duration of 2 hours. Each thermal cycle was conducted in a tubular furnace with an internal forming gas atmosphere (4% H₂, 96% N₂). The forming gas was run from a 5 bar line-pressure of bottled H₂ and a 5 bar line-pressure of bottled N₂ to two rotameters that regulated the volumetric flowrate of H₂ and N₂ to 4 cm³ min⁻¹ and 96 cm³ min⁻¹, respectively. Subsequent to the rotameters the gases were merged at a T-junction producing a forming gas mixture: the gases were then delivered to the tubular furnace with the furnace exhaust extracted via a suction pump. The length of the exhaust was long relative to the diameter and the flowrate of the gasses were high enough to ensure negligible back diffusion of air into the tube. In this arrangement the forming gas flow equated to ca. 0.09 standard litre per minute (SLPM). Five thermal cycles were conducted in total. The first thermal cycle was applied to reduce the anode from nickel oxide to nickel. To accomplish this, the sample was inserted into the furnace and a thermal ramp-rate of 3 °C min⁻¹ was applied to bring the furnace to an isothermal 800 °C, where it was held for a 2 hour dwell-time before being allowed to cool via natural convection. This is defined as the reduction cycle. After reduction, the first tomogram, XCT_00, was collected.

The sample was then exposed to four subsequent ‘operational’ thermal cycles with profiles typical of SOFC start-up and shut-down with pre- and post-cycle tomograms collected throughout. These are referred to as the operational cycles. To conduct the first operational cycle the sample was re-inserted into the furnace and a thermal ramp-rate of 3 °C min⁻¹ was applied to bring the furnace to 750 °C and was not held for any dwell-time. Tomogram XCT_03 was then collected. This process was repeated three more times with the same peak temperature but with an increasing ramp-rate for each cycle of 10, 20 and 30 °C min⁻¹, with tomograms XCT_10, XCT_20 and XCT_30 collected respectively after each thermal cycle. For all five thermal cycles, the system was allowed to cool via natural convection. The thermal profile and sequence of tomogram collection can be seen in Fig. 1b.

2.4 Digital volume correlation

Digital volume correlation (DVC) was computed and mapped using ‘TomoWarp2’, a Python-based open source software developed by Tudisco et al.²³ TomoWarp2 utilises correlation techniques such as those employed by Gates et al.,²⁴ whereby the movement of each feature within a material is tracked and quantified. To track movements, two tomograms are required from the exact same region of interest containing the ‘initial’ and ‘deformed’ structure. By locating the same feature within the initial and deformed structures the displacement of said feature can be quantified. To do this, a local sub-volume is drawn which encloses the feature within the initial structure, a similar sub-volume is then drawn within the deformed structure and rastered throughout the volume until the feature is found.

To find the feature within the deformed volume, the brightness distribution functions of the initial and deformed volumes are compared and their difference is minimised. The degree of confidence in the location of the feature within the deformed volume is quantified in the form of a correlation coefficient (CC), whereby an optimum match in the brightness distribution functions would result in a CC value of 1. The various methods of calculating the CC values have been discussed and compared by Tong²⁶ although, confidence is typically only placed in displacement data which has obtained CC values above 0.97.²⁸

DVC can be computationally intensive; therefore a sub-volume of the full diameter of the sample but half of the depth into the electrode, 350 μm × 350 μm × 100 μm, was removed from the same ROI within each tomogram for analysis. This halved the computation time (compared with the full tomographic volume) while maintaining a statistically representative volume that included information from both the anode/electrolyte interface and anode bulk. To conduct the DVC computations, first a regular grid of 3D nodes has to be defined according to the ‘node spacing’ over each tomogram. A ‘correlation window’ is then centred over each node for the correlation analysis and a ‘search window’ is defined to constrict the search for the displaced material within a local volume. The DVC computations within this work were performed with a node spacing of five, with search and correlation windows of fifteen and three, respectively. Previous analysis of these tomograms found the average Ni, YSZ and pore particle diameters to be 1.1 μm, 2.6 μm and 2.5 μm respectively.³⁰ The DVC parameters were therefore chosen to sufficiently reflect these feature sizes.

2.5 Correlation quality

The minimum (CC_Min), average (CC_Avg) and maximum (CC_Max) correlation values for each of the four DVC computations are presented in Table 1. The CC_Avg value decreases after each thermal cycle, possibly due to the increased deformation to which the cell is subject, however the values remain sufficiently high throughout. Although CC_Avg provides an indication of the correlation quality as a bulk, the CC_Min and CC_Max are also presented so that the worst and best regions of displacement correlation can also be inspected. The lowest CC values were always found at the cell walls, which have previously been reported to deform substantially during thermal cycling,³¹ making correlation more challenging. All values away from the cell walls produced CC values above 0.97 therefore only the cell walls are omitted from the analysis.

Table 1 Minimum, average and maximum correlation coefficient values for the four DVC computations conducted on the tomograms obtained from a solid oxide fuel cell throughout operational thermal cycling, all presented to 2 d.p.

	CCmin	CCavg	CCmax
DVC_03	0.97	1.00	1.00
DVC_10	0.93	0.99	1.00
DVC_20	0.97	0.98	0.98
DVC_30	0.93	0.97	0.97

---

2.6 Data analysis

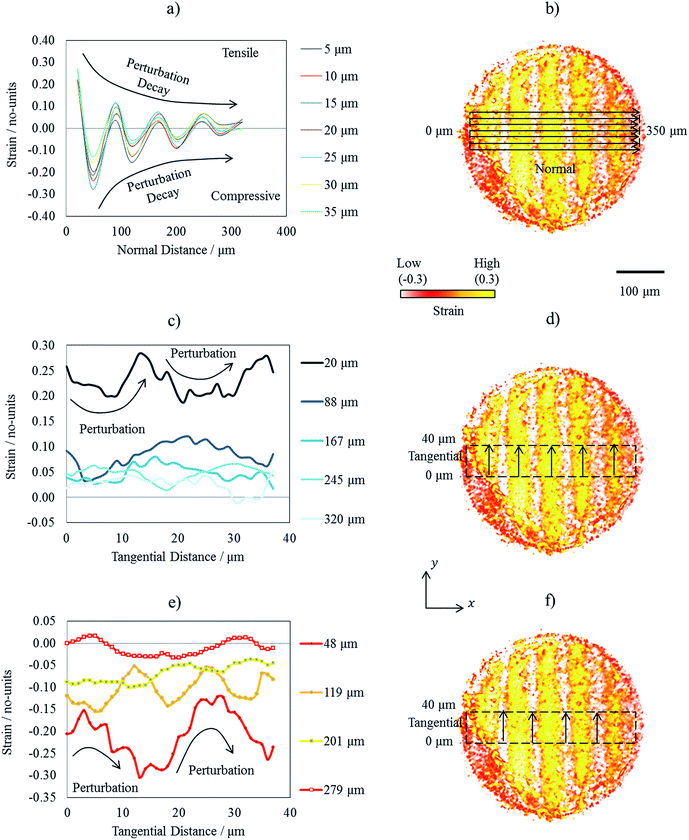
To visualise the displacement and strain data obtained from the DVC computations, Avizo Fire software (Avizo, Thermo Fisher Scientific, Waltham, Massachusetts, U.S.) was employed to generate 3D displacement vector fields and strain volume renderings. Quantifications were achieved with use the of ImageJ (ImageJ, National Institute of Health, U.S.A).³² Due to the periodic nature of the high ramp-rate strain map, the variation in strain is investigated across both the tangential and normal paths with respect to the strain wave propagation. To accomplish this, a strain map was extracted from the volume 350 μm in the normal length (x), 40 μm in the tangential length (y) and 5 μm in thickness (z), see Fig. 1 for a geometric reference. The strain was then averaged vertically in z to reduce noise. The result was a single 2D map of strain whereby the strain variation in x and y could be decoupled and compared; seven line scans spaced evenly in parallel were collected across the normal and nine line scans again evenly spaced in parallel were collected across the wave tangent.

3. Results

3.1 Thermally induced strain and displacement

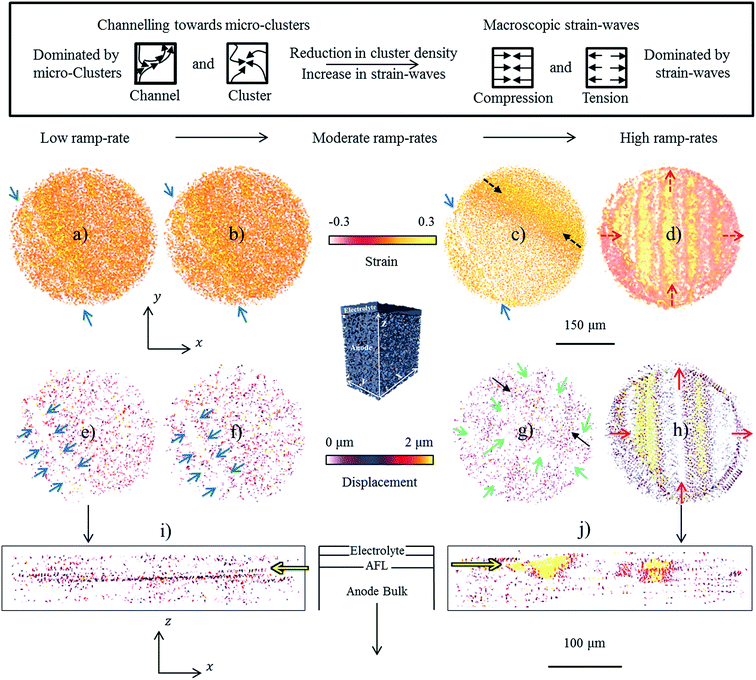
Volume renderings and vector fields were employed to visualise the structural alterations that were tracked using DVC. Four strain and four displacement maps in the x–y view, are accompanied by two x–z views of the displacement at low and high ramp-rates in Fig. 2. The only visible reference point between all data-sets in the x–y orientation was the existence of a large heterogeneous region, indicated by blue arrows, where minimal evolution appeared throughout thermal cycling. Apart from this heterogeneous region, two distinct features were observed: microscopic clusters and macroscopic waves. By inspecting the volume perpendicular to the interface, via the x–z views, it is possible to assess the evolution near the interface and into the anode bulk. It is seen that, regardless of thermal ramp-rate, the largest evolutions were consistently seen within the anode functional layer towards the anode/electrolyte interface, indicated by the yellow arrows (Fig. 2i and j).

Fig. 2 An overview of the workflow for data collection and analysis in the framework of the expected mechanisms of thermally induced degradation presented as strain and displacement results from the four DVC computations conducted on an interfacial anode/electrolyte volume from an SOFC: x–y strain maps for (a) 3 °C min⁻¹, (b) 10 °C min⁻¹, (c) 20 °C min⁻¹ and (d) 30 °C min⁻¹, x–y displacement maps for (e) 3 °C min⁻¹, (f) 10 °C min⁻¹, (g) 20 °C min⁻¹ and (h) 30 °C min⁻¹, and x–z displacement maps for (i) 3 °C min⁻¹, and (j) 30 °C min⁻¹.

Low ramp-rates were dominated by cluster formations where material appeared to channel from different sources towards a common destination. The cluster density was seen to decrease with increasing ramp-rate (Fig. 2a–c) accompanied by the introduction of a single strain-wave at moderate ramp-rates, indicated by dashed black arrows (Fig. 2c). At moderate ramp rates it was also observed that the clusters became significantly more sparse and were scattered around large voids, as indicated by green arrows (Fig. 2g). At the highest thermal ramp-rate strain-waves completely dominated the structure and minimal clustering was observed, indicated by dashed red arrows (Fig. 2d). Unlike the cluster formations which displayed localised microscopic features, the strain waves displayed macroscopic features that spanned the entire length of the sample. Moreover, hundreds of individual clusters were observed within the volume during low ramp-rates whereas, only nine distinct strain waves were observed after high-rate heating.

It is concluded that evolutions at low and high ramp-rates are dominated by the formation of microscopic clusters and macroscopic strain-waves respectively, with the greatest evolution occurring within the anode functional layer regardless of thermal ramp-rate. The channelling and wave propagation will now be investigated in closer detail.

3.2 Low and high ramp-rate evolution

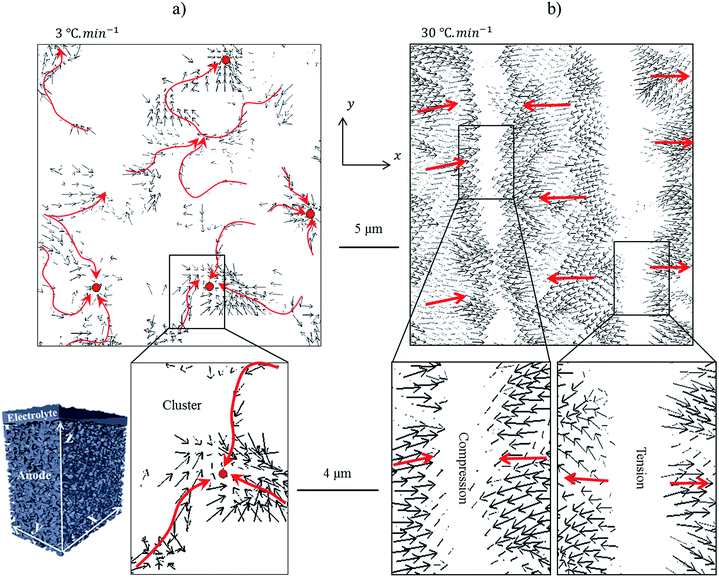
Through inspection of the displacement maps for the low- and high ramp-rates under high magnification detail of the microscopic and macroscopic mechanisms was revealed. The low ramp-rate evolution which was dominated by micro-mechanisms such as channelling and clustering are displayed in Fig. 3a and, the high ramp-rate evolution which was dominated by the macro-mechanisms such as the compression and tension strain-waves are displayed in Fig. 3b.

Fig. 3 Displacements during high and low ramp-rates: (a) x–y displacements displaying the micro-channelling towards micro-clusters during low ramp rates (3 °C min⁻¹), and (b) x–y displacements displaying tensile and compressive macroscopic strain-waves during high thermal ramp-rates (30 °C min⁻¹).

Within Fig. 3, red arrows have been added, on top of the black arrows which were generated by the DVC computation, to indicate the net movement of material. The low ramp-rate clusters were dispersed throughout the volume and were relatively homogenous in size; channels are ca. 1 μm in diameter and meander to lengths of 5–15 μm with the cluster region encompassed by a ca. 3 μm diameter (Fig. 3a). Unlike the clusters which were dispersed and meander in all directions, the strain-waves presented greater periodicity forming well-defined parallel waves throughout the structure. Regions of minimal displacement occurred within the centre of both the compression and tension bands. This stationary region was typically larger within the tensile band, approximately 4–5 μm, whereas the stationary regions within the compression bands were typically thinner, approx. 1–3 μm. The waves which connected the two bands are in the region of 5–8 μm in thickness. Although macroscopic in feature size, the waves were composed of many small displacements which were similar in magnitude to the individual displacements that were responsible for the channel and cluster formations.

It is concluded that the two features observed previously, microscopic clusters and macroscopic waves, formed and propagated through distinct mechanisms. The microscopic clusters were formed through the channelling of material from various locations to a common destination whereas the macroscopic waves propagated through compression and tension bands comprised of many small displacements aligned in the same orientation. These two mechanisms will now be investigated further in an effort to correlate the two distinct evolution mechanisms to degradation processes.

3.3 Microscopic cluster formations during low ramp-rates

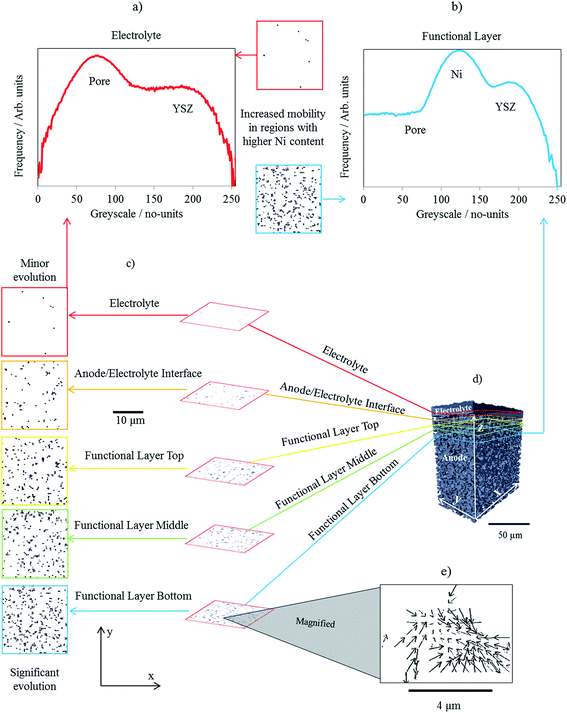
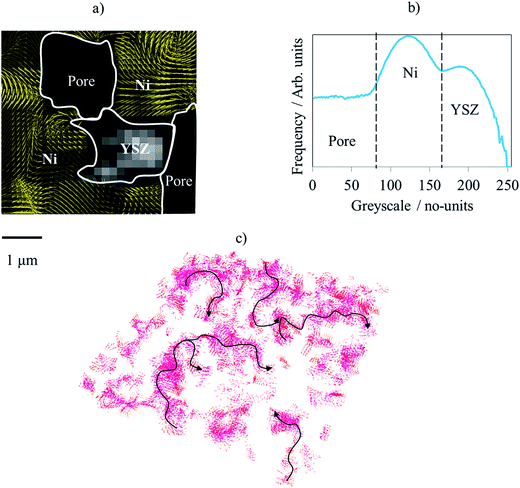
To better understand the processes responsible for the micro-channelling and the subsequent cluster formations, the cluster density was inspected at a macroscopic scale throughout the sample. Fig. 4 displays five x–y vector slices obtained from the low ramp-rate displacement field. Using a lower magnification, the macroscopic trends can be observed i.e. higher or lower densities of clusters. At the high resolution, each cluster displayed very similar characteristics, as discussed in the previous section, see Fig. 3 for finer detail. The macroscopic slices were extracted from the electrolyte through to the anode bulk in 5 μm increments. For simplicity, only the x and y components of the individual vectors are considered within each of the five slices but a 3D volume where the x, y and z components are all considered is presented for consideration in Fig. 5.

Fig. 4 Correlating displacement through throughout the cell to the constituent materials: (a) greyscale histograms for the ceramic and pore, and (b) ceramic, pore and nickel from the electrolyte/pore interface and anode functional layer respectively, (c) displacement vector slice raster from the electrolyte into the anode, with (d) a geometric reference, and (e) a magnified vector slice.

Fig. 5 Correlating the displacement of Ni through micro-channelling and cluster formations through greyscale segmentation: (a) magnified vector slice overlaid on top of the raw greyscale slice, with (b) accompanying histogram outlined with greyscale thresholds for the three materials: pore, Ni and YSZ, and (c) a 3D vector field from the anode with calculated vectors in red and annotated arrows in black.

Inspecting the vector slices, it is clear that the cluster density increases as the raster moves away from the electrolyte into the anode; there was a substantially higher evolution of material within the anode than the electrolyte. Unlike the electrolyte which was purely ceramic, the anode contains nickel metal which is known to undergo sintering/coarsening processes at elevated temperatures¹⁰ although; the structural changes associated with sintering during thermal cycling are thought to be subtle.³⁰ To determine whether nickel sintering may be responsible for the channel and cluster formations, the greyscale values responsible for the displacements were inspected to decouple the displacements of the constituent materials.

To distinguish which displacements are responsible for which material, the greyscale values must first be assigned to each of the three phases: metal, ceramic and pore. To do this, two sub-volumes were extracted from the same ROI to accompany the five slices, one from the electrolyte/pore interface and one from the anode bulk. The former was positioned to ensure that only ceramic and pore phases were within the sub-volume whereas, the latter was positioned within the anode where all three phases were present. Greyscale histograms were then calculated for both sub-volumes and their profiles compared (Fig. 4a and b). The top sub-volume, containing ceramic and pore, produced a profile with only two shoulders/peaks, as expected due to only two phases being present. The bottom sub-volume, containing ceramic, pore and metal, produced a histogram profile with three distinct shoulders/peaks, two of which overlapped with the peaks from the top profile. These two peaks were then assumed to cover greyscale values for pore (dark greys/black) and ceramic (bright greys/white). The third peak positioned between the pore and ceramic was assumed to be associated with the nickel metal. The authors have previously published work using this greyscale fiducial technique to segment and map the electrochemical reaction sites within SOFC anodes.^30,33

Now that the greyscale values could be associated with particular materials, vector slices were overlaid on top of the raw greyscale data in order to decouple the displacement of the constituent materials, as displayed in a highly magnified image within Fig. 5a. From the overlaid images the displacement was directly correlated to greyscale values associated with the metal phase, greyscale values of approx. 100–160 from a 0–255 range in Fig. 5b. Moreover, the greyscale values associated with the ceramic were also inspected; negligible overlap was observed between the displacement vectors and the greyscale values associated with the ceramic concluding that insignificant displacement is attributed to the ceramic. Furthermore, the displacement trajectories were consistently affected by the border between the greyscale values associated with the metal and ceramic, suggesting that the ceramic may be responsible for the channelling mechanism (Fig. 5c).

In conclusion, the correlation of the greyscale values associated with the metal phase with the majority of the displacements observed during low ramp-rate cycling corroborates that the microscopic channelling and cluster formations may be due to the mobility of the nickel metal while at elevated temperatures.

3.4 Macroscopic strain-wave propagation during high ramp-rates

To gain an understanding of the strain-wave propagation, the strain magnitude was inspected through both the normal and tangent of each strain wave, i.e. the normal inspects the variation between each wave and the tangent inspects the variation within each individual wave. Fig. 6 displays the high ramp-rate strain field with the addition of seven line scans across the cell normal to the strain-wave propagation and nine line scans across the cell tangential to each of the individual waves. The tangential line scans were also separated into tension and compression fronts for analysis.

Fig. 6 Strain-wave propagation in a solid oxide fuel cell exposed to high thermal ramp-rates: (a) tensile and compressive strain decay across the cell observed from, (b) seven line scans obtained normally to the wave propagation, (c) perturbations across the five tensile wave fronts taken (d) tangentially to each wave, (e) perturbations across the four compression wave fronts taken (f) normally to each wave.

All seven line scans which were collected normal to the wave propagation, i.e. comparing each wave in turn, displayed very similar profiles; strain values undulated from peaks of tension to peaks of compression which decayed in magnitude from one cell-wall to the other, spanning approximately 350 μm (Fig. 6a). The tension and compression data are displayed separately in Tables 2 and 3, respectively. An order of magnitude reduction in both the tension and compression peaks was observed across the cell; the tension peaks decayed from 0.283 to 0.053 and compression peaks decayed from −0.304 to −0.033.

Table 2 The maximum, average, minimum, range, and standard deviation of tension strain measurements obtained across the wave normal for each of the five wave fronts propagating in an SOFC sample after thermal cycling at high ramp-rates

Location along normal	20 μm	88 μm	167 μm	245 μm	320 μm
Maximum tension along tangent	0.283	0.119	0.080	0.066	0.053
Average tension along tangent	0.230	0.083	0.047	0.048	0.026
Minimum tension along tangent	0.187	0.031	0.017	0.014	−0.010
Tension range along tangent	0.096	0.088	0.063	0.052	0.063
Standard deviation along tangent	0.092	0.055	0.031	0.027	0.027

---

Table 3 The minimum, average, maximum, range, and standard deviation of compression strain measurements obtained across the wave normal for each of the five wave fronts propagating in an SOFC sample after thermal cycling at high ramp-rates

Location along normal	48 μm	119 μm	201 μm	279 μm
Minimum compression along tangent	−0.121	−0.052	−0.036	0.017
Average compression along tangent	−0.208	−0.105	−0.068	−0.010
Maximum compression along tangent	−0.304	−0.154	−0.100	−0.033
Compression range along tangent	0.183	0.102	0.064	0.050
Standard deviation along tangent	0.076	0.044	0.031	0.021

---

Within the tables, the minimum, average, maximum, range, and standard deviation strain values calculated from the tangent, i.e. across each individual wave, are also presented. Undulation was observed across the wave tangents but far less than what was seen along the wave normal. For example, the tension ranged by a maximum of 0.01 across the tangent whereas the tension ranged by a maximum of 0.24 across the normal. Consequently, the undulation across the tangent resulted in variation from high-compression to low-compression or high-tension to low-tension, as opposed to high-compression to high-tension across the normal. Furthermore, no decay profile was observed across the tangent, unlike the normal which decayed with a very similar profile for both the compression and tension peaks. This is visualised in Fig. 6c and e.

From the sixteen line scans taken across the strain waves which appeared during high thermal ramping, insight has been gained into the propagation profiles responsible for the strain variation throughout the cell. It is concluded that variations were observed within each of the strain waves in the form of minor undulations but the variation between waves was most considerable and decayed from one cell-wall to the other eventually reducing by an order of magnitude. However, unlike the microscopic channelling and cluster formations which are thought to be attributed to the sintering of the nickel metal, an extensively investigated mechanism,¹⁰ the mechanism responsible for the initiation of these strain waves is more elusive as no greyscale variation could be correlated to the compression–tension undulations. Nevertheless, non-linear strain distributions have been previously reported by the authors.^34,35 Previously, the strain was produced through thermal gradients which induced the ‘nearest-neighbour’ effect whereby contraction of the nickel units in a single direction enhanced strain. Unlike previous experiments, the thermal cycles explored in this work were conducted in highly isothermal environments; therefore, thermal gradients are not thought to be responsible for the strain waves observed here although, as mentioned in the previous section, a large heterogeneous region was observed where minimal mobility occurred throughout thermal cycling. This region of the anode also contained a higher ceramic content which may have been responsible for exacerbating or even initiating the strain wave propagation. The presence of the constraining electrolyte layer is thought to preferentially distribute strain, inducing gradients analogous to work discussed by Clague et al.,³⁶ but at a cell-level, as well as between individual particles. Cell walls were previously observed to deform during thermal cycling;³¹ a combination of the constriction during the wall deformation, the constraining electrolyte layer, and the existence of a large heterogeneous defect may have caused the rippling of strain throughout the anode. These mechanisms likely influence the probability of degradation and it has been previously reported that cell delamination³¹ and loss of reaction sites can be expected.³⁰

Conclusions

The microstructure evolution within an SOFC has been tracked and quantified throughout operational thermal cycling using digital volume correlation techniques for the first time. The microstructural data was obtained from an anode/electrolyte interface using entirely lab-based X-ray CT instruments, achieving sub-micron resolutions. Each operational cycle was conducted at an increased thermal ramp-rate to emulate successively faster start-up times, a known cause of degradation in planar cells. The pre- and post-cycle structural data was then compared to track the movements of material within the ROI. Two distinct features were observed, the formation of clusters and waves.

Low ramp-rates were dominated by the formation of microscopic clusters which dispersed throughout the entire volume showing no unified orientation. The cluster density decreased considerably on increasing ramp-rate, their decline was accompanied by the introduction of macroscopic waves. At high ramp-rates macroscopic waves dominated the cell, propagating periodically throughout the cell in a well-organised pattern. After high-resolution inspection, the microscopic clusters were determined to form through the micro-channelling of material from various locations to a common destination. These channels and clusters were then correlated to the greyscale values attributed to the Ni metal, which is known to undergo sintering mechanisms at elevated temperatures. By inspecting the boundaries between the metal and ceramic greyscale values, it was seen that the ceramic backbone appears to cause the channelling of the metal; nickel gains its mobility from the high temperature and its propensity to minimise its surface/interfacial energy and was channelled by the ceramic skeleton, likely inhibiting mobility effects. It is also suspected that the decrease in the cluster density that accompanied the increased ramp rate was likely due to the reduced time at temperature i.e. the degree of sintering is a function of the amount of time at a certain temp, rising to temperature faster results in less time at elevated temperatures and therefore less sintering. The high-resolution inspection of the macroscopic waves found that the propagation occurred through the formation of tension and compression fronts which decayed in magnitude across the cell. The waves were composed of many small displacements all aligned in the same orientation either pulling towards or away from one another, respectively causing the compressive and tensile strains. The waves and accompanying decay profiles are thought to be triggered by a combination of the cell-wall deformation and the existence of a large heterogeneous defect.

The two mechanisms observed here: micro-channelling with cluster formation and strain wave propagation, are also expected to affect the electrochemical performance as well as the mechanical properties of the cell. Ni mobility during channelling and cluster formation can improve percolation; however, it may also reduce the amount of reaction sites due to loss of Ni–YSZ contact area triggered by metal sintering and expansion mismatch. Strain waves may result in cracking and delamination of the constituent layers, such as the anode from the electrolyte. Tomography-based analysis which has been reported prior to this work supports both of these hypotheses.^30,31

Considering the wider application and future of the field of SOFC research, 4D techniques will enable microstructural design and tailored operational profiles. For instance, one microstructural design may electrochemically outperform another, at the expense of mechanical integrity or long term durability. If applied correctly, the techniques such as those that are discussed will enable enhanced cell microstructures to be fabricated, and improved operational profiles to be employed, ultimately leading to extended cell lifetimes.

This work is the first report of DVC computations applied to a solid oxide fuel cell exposed to high temperatures achieving sub-micron resolutions using entirely lab-based X-ray CT instruments. Furthermore, thermally driven degradation is not limited to electrochemical devices therefore this work will provide as an example of the advanced characterisation studies which are now possible using lab-based X-ray CT.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the EPSRC (EP/M014045/1, EP/P009050/1), the Centre for Doctoral Training (EP/L015749/1) and the Royal Academy for Engineering for financial support, access to the VERSA instrument was supported by EPSRC (EP/N032888/1).

Notes and references

1. N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337.
2. A. Choudhury, H. Chandra and A. Arora, Renewable Sustainable Energy Rev., 2013, 20, 430–442.
3. B. S. Prakash, S. S. Kumar and S. T. Aruna, Renewable Sustainable Energy Rev., 2014, 36, 149–179.
4. Y. H. Lee, H. Muroyama, T. Matsui and K. Eguchi, J. Power Sources, 2014, 262, 451–456.
5. K. Sasaki, K. Haga, T. Yoshizumi, D. Minematsu, E. Yuki, R. Liu, C. Uryu, T. Oshima, T. Ogura, Y. Shiratori and K. Ito, J. Power Sources, 2011, 196(22), 9130–9140.
6. K. Haga, S. Adachi, Y. Shiratori, K. Itoh and K. Sasaki, Solid State Ionics, 2008, 179(27), 1427–1431.
7. M. S. Khan, S. B. Lee, R. H. Song, J. W. Lee, T. H. Lim and S. J. Park, Ceram. Int., 2016, 42(1), 35–48.
8. X. Lu, T. M. Heenan, J. J. Bailey, T. Li, K. Li, D. J. Brett and P. R. Shearing, J. Power Sources, 2017, 365, 210–219.
9. M. Mori, T. Yamamoto, H. Itoh, H. Inaba and H. Tagawa, J. Electrochem. Soc., 1998, 145(4), 1374–1381.
10. S. P. Jiang, J. Mater. Sci., 2003, 38(18), 3775–3782.
11. F. S. Silva and T. M. de Souza, Int. J. Hydrogen Energy, 2017, 42, 26020–26036.
12. H. Fukunaga, M. Ihara, K. Sakaki and K. Yamada, Solid State Ionics, 1996, 86, 1179–1185.
13. J. R. Wilson, W. Kobsiriphat, R. Mendoza, H. Y. Chen, J. M. Hiller, D. J. Miller, K. Thornton, P. W. Voorhees, S. B. Adler and S. A. Barnett, Nat. Mater., 2006, 5(7), 541–544.
14. P. R. Shearing, J. Gelb, J. Yi, W. K. Lee, M. Drakopolous and N. P. Brandon, Electrochem. Commun., 2010, 12(8), 1021–1024.
15. Y. Guan, W. Li, Y. Gong, G. Liu, X. Zhang, J. Chen, J. Gelb, W. Yun, Y. Xiong, Y. Tian and H. Wang, J. Power Sources, 2011, 196(4), 1915–1919.
16. A. Zekri, K. Herbrig, M. Knipper, J. Parisi and T. Plaggenborg, Fuel Cells, 2017, 17(3), 359–366.
17. Y. Guan, Y. Gong, W. Li, J. Gelb, L. Zhang, G. Liu, X. Zhang, X. Song, C. Xia, Y. Xiong and H. Wang, J. Power Sources, 2011, 196(24), 10601–10605.
18. W. M. Harris, J. J. Lombardo, G. J. Nelson, B. Lai, S. Wang, J. Vila-Comamala, M. Liu, M. Liu and W. K. Chiu, Sci. Rep., 2014, 4, 5246.
19. J. R. Izzo, A. S. Joshi, K. N. Grew, W. K. Chiu, A. Tkachuk, S. H. Wang and W. Yun, J. Electrochem. Soc., 2008, 155(5), B504–B508.
20. T. M. M. Heenan, J. J. Bailey, X. Lu, J. B. Robinson, F. Iacoviello, D. P. Finegan, D. J. L. Brett and P. R. Shearing, Fuel Cells, 2017, 17(1), 75–82.
21. J. J. Bailey, T. M. M. Heenan, D. P. Finegan, X. Lu, S. R. Daemi, F. Iacoviello, N. R. Backeberg, O. O. Taiwo, D. J. L. Brett, A. Atkinson and P. R. Shearing, J. Microsc., 2017, 267 DOI:10.1111/jmi.12577.
22. T. M. M. Heenan, D. P. Finegan, B. Tjaden, X. Lu, F. Iacoviello, J. Millichamp, D. J. Brett and P. R. Shearing, Nano Energy, 2018, 47, 556–565.
23. E. Tudisco, E. Andò, R. Cailletaud and S. A. Hall, SoftwareX, 2017, 6, 267–270.
24. M. Gates, J. Lambros and M. T. Heath, Exp. Mech., 2011, 51(4), 491–507.
25. B. K. Bay, T. S. Smith, D. P. Fyhrie and M. Saad, Exp. Mech., 1999, 39(3), 217–226.
26. W. Tong, Strain, 2005, 41(4), 167–175.
27. D. S. Eastwood, V. Yufit, J. Gelb, A. Gu, R. S. Bradley, S. J. Harris, D. J. Brett, N. P. Brandon, P. D. Lee, P. J. Withers and P. R. Shearing, Adv. Energy Mater., 2014, 4(4) DOI:10.1002/aenm.201300506.
28. D. P. Finegan, E. Tudisco, M. Scheel, J. B. Robinson, O. O. Taiwo, D. S. Eastwood, P. D. Lee, M. Di Michiel, B. Bay, S. A. Hall and G. Hinds, Adv. Sci., 2016, 3(3) DOI:10.1002/advs.201700369.
29. J. M. Paz-Garcia, O. O. Taiwo, E. Tudisco, D. P. Finegan, P. R. Shearing, D. J. L. Brett and S. A. Hall, J. Power Sources, 2016, 320, 196–203.
30. T. M. M. Heenan, X. Lu, F. Iacoviello, J. Robinson, J. L. B. Brett and P. R. Shearing, J. Electrochem. Soc., 2018, 165(11), F921–F931.
31. T. M. M. Heenan, X. Lu, J. Robinson, F. Iacoviello, J. L. B. Brett and P. R. Shearing, J. Electrochem. Soc., 2018, 165(11), F932–F941.
32. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9(7), 671–675.
33. T. M. M. Heenan, D. J. L. Brett and P. R. Shearing, J. Phys.: Conf. Ser., 2017, 849, 012017.
34. J. B. Robinson, L. D. Brown, R. Jervis, O. O. Taiwo, T. M. Heenan, J. Millichamp, T. J. Mason, T. P. Neville, R. Clague, D. S. Eastwood and C. Reinhard, J. Power Sources, 2015, 288, 473–481.
35. T. M. M. Heenan, J. B. Robinson, X. Lu, B. Tjaden, A. Cervellino, J. J. Bailey, D. J. L. Brett and P. R. Shearing, Solid State Ionics, 2018, 314, 156–164.
36. R. Clague, P. R. Shearing, P. D. Lee, Z. Zhang, D. J. L. Brett, A. J. Marquis and N. P. Brandon, J. Power Sources, 2011, 196(21), 9018–9021.

---