Atomically precise Au₁₄₄(SR)₆₀ nanoclusters (R = Et, Pr) are capped by 12 distinct ligand types of 5-fold equivalence and display gigantic diastereotopic effects

Abstract

For two decades, Au₁₄₄(SR)₆₀ has been one of the most studied and used thiolate (SR) protected gold nanoclusters. In many ways, however, it proved to be a challenging and elusive case, also because of the difficulties in solving its structure by single-crystal X-ray crystallography. We used very short thiols and could prepare Au₁₄₄(SC₂H₅)₆₀ and Au₁₄₄(SC₃H₇)₆₀ in a very pure form, which was confirmed by UV-vis absorption spectroscopy and very regular electrochemistry patterns. Inductively coupled plasma and electrospray ionization mass spectrometries gave definite proof of the Au₁₄₄(SR)₆₀ stoichiometry. High-resolution 1D and 2D NMR spectroscopy in the solution phase provided the result of assessing the presence of 12 ligand types in exactly the same amount (5-fold equivalence). Equally important, we found that the two protons belonging to each methylene group along the thiolate chain are diastereotopic. For the α-CH₂ protons, the diastereotopic effect can be indeed gigantic, as it reaches chemical-shift differences of 2.9 ppm. DFT calculations provided insights into the relationship between structure and NMR results. In particular, the 12 ligand types and corresponding diastereotopic effects may be explained by considering the presence of C–H⋯S hydrogen bonds. These results thus provide fundamental insights into the structure of the thiolate layer capping this long-studied gold nanocluster.

---

Introduction

The study of the structural and physicochemical properties of stable thiolate-protected gold clusters prepared with atomic precision has been instrumental to develop new synthetic and purification procedures, prepare new clusters, perfect characterization methodologies, and devise applications.^1–3 When the number of gold atoms is small, quantum confinement makes these clusters display properties that cannot be seen in larger gold nanoparticle systems. For fewer than ca. 130 atoms, the clusters are sufficiently small to exhibit distinct molecular properties, such as a HOMO–LUMO gap clearly detectable (by electrochemistry⁴ or UV-vis absorption spectroscopy⁵), and quite featureful optical and, especially, NMR behaviors,^5–10 Although several, mostly molecular, thiolate-protected metal clusters have been prepared, only very few reached the status of benchmark system, in the sense that they played an especially important role to extend our knowledge and direct this ever-expanding area of research. For molecular clusters, this is the case of the very popular Au₂₅(SR)₁₈ and Au₃₈(SR)₂₄ nanoclusters.^1–4,7–17 Another reference system is undoubtedly Au₁₄₄(SR)₆₀, which was prepared long time ago¹⁸ and is special for several reasons; one of them is its exceptional stability. As opposed to some other clusters, Au₁₄₄(SR)₆₀ is very stable upon ligand-exchange reactions.^19–21 For example, we have shown that the monolayer of this cluster can be modified and linear polymers can be grown to form clusters that are extremely stable toward a number of aggressive reaction conditions.²² Au₁₄₄(SR)₆₀ is the first thiolate-protected gold nanocluster found to display evident size-related electronic features, especially by marking the transition between molecular systems and clusters displaying quantized double-layer charging behavior, i.e., clusters that exhibit a complex sequence of quite regular charging peaks in voltammetry.^4,20 Indeed, Au₁₄₄(SR)₆₀ was the cluster that appeared to be as the dominant form in the first reported differential pulse voltammetry (DPV) of this class of systems,²³ and whose spectacular DPV behavior was later assessed beyond doubts by using purer samples.^24–26 Au₁₄₄(SR)₆₀ is also important because it marks the transition between molecular clusters and clusters that start showing traces of a plasmon-resonance band.^27–30 Last but not least, whereas it is one of the most studied clusters, its structure had remained elusive for two decades. This problem has been addressed both experimentally and theoretically. The first step was to assess its stoichiometry. Over the years, the hunt for its formula progressed from initial reports of a cluster having a core mass of 29 kDa³¹ or compositions such as Au₁₄₀(SR)₅₆.^20,32 A stoichiometry of Au₁₄₄(SR)₅₉ was inferred from electrospray ionization mass-spectrometry (ESI-MS) measurements.³³ Further experimental work based on ESI-MS results described this cluster as Au₁₄₆(SR)_59-60 and Au₁₄₄(SR)₆₀,³⁴ and further proof of the Au₁₄₄(SR)₆₀ formula was provided.³⁵

This cluster is indeed featuring one of the magic numbers associated with thiolate-protected gold clusters, and unsurprisingly, it is a recurrent presence in several preparations, particularly those based on the two-phase Brust–Schiffrin approach³⁶ (but not exclusively, as we will show here) aimed at preparing the smaller Au₂₅(SR)₁₈ cluster,^12,37 formerly believed to have the formula Au₃₈(SR)₂₄.¹² For many years and especially following the impetus of the aforementioned mass-spectrometry results, several attempts to define its structure were carried out both experimentally and/or by density functional theory (DFT) calculations. Theoretical modeling,³⁸ based on the icosahedral Pd₁₄₅ structure³⁹ combined with the staple-motif concept, proposed that the stoichiometry Au₁₄₄(SR)₆₀, in which the ligands are arranged according to thirty −(SR)−Au−(SR)− staples, could account for available structural,³¹ optical,^31,33 and electrochemical information.^24–26 Further calculations took into account new evidence, especially regarding symmetry. In particular, in a recent study the ¹H NMR spectroscopy behavior of a cluster described as Au₁₄₄(SR)₆₀ (HSR = para-mercaptobenzoic acid) pointed to the presence of only one type of ligand,⁴⁰ as opposed to the rich NMR pattern exhibited by Au₂₅(SR)₁₈ (ref. 8–10) and Au₃₈(SCH₂CH₂Ph)₂₄.^7,41 This result was taken as the proof of the 60-fold symmetry equivalence of the capping ligands. The structure proposed by Lopez-Acevedo et al.³⁸ was thus modified by imposing the symmetry requirement and the resulting I-symmetrized structure computed.⁴² The latter was employed to analyze the optical spectrum of Au₁₄₄(SR)₆₀ as a function of temperature.²⁹ Despite the usual view of this cluster displaying a pretty much featureless spectrum, it was shown that at low temperature the UV-vis-near-IR spectrum shows individual peaks, thereby providing information on the energetic levels in the cluster. The capability of different theoretical treatments^27,38,42,43 in predicting the optical spectrum was analyzed, reaching the conclusion that the Au₁₄₄(SR)₆₀ cluster is not a homogeneous metal cluster, and that distortions in the orientation of the staples extend into the metallic Au core.⁴⁴ As to the actual structure, the outcome of scanning transmission electron microscopy experiments⁴² were consistent with the icosahedral core predicted by theory and shown in the related structure of icosahedral Pd₁₄₅.³⁹ The first structural determination of a Au₁₄₄ cluster has been published, though the cluster is protected by an alkynyl ligand, –C≡CAr (Ar = 2-F–C₆H₄–), rather than a thiolate.⁴⁵ This structure exhibits a metal-kernel core that is almost identical to the originally predicted structure.³⁸ After this work was completed, we have been made aware of the first single-crystal X-ray crystallographic determination of the structure of a thiolate-protected Au₁₄₄ cluster, Au₁₄₄(SCH₂Ph)₆₀.⁴⁶ This cluster is also similar to that originally proposed³⁸ in analogy with a Pd₁₄₅ monolayer-protected cluster.³⁹ Both structures show the presence of a pair of enantiomers.

It is, therefore, evident that the study of properties and structure of Au₁₄₄(SR)₆₀ provides an especially notable example of interplay between theory and experiments, whereby experimental results affect theoretical treatment and calculations are used to understand optical and electrochemical data. In fact, beside structure-determination attempts, other pieces of evidence are required to frame properly the properties and main structural features in solution, which do not necessarily match completely those in the solid state. Indeed, the monolayer capping smaller gold nanoclusters, such as Au₂₅(SR)₁₈, exhibits important dynamics in solution that affects very substantially the way these clusters exchange electrons or react.^9,47 As to Au₁₄₄(SR)₆₀ in solution and in the solid state, it has been shown that the infrared-spectroscopy spectra obtained for Au₁₄₄(SCH₂CH₂Ph)₆₀ are quite different, in that they point to ligands with more degrees of freedom when the cluster is in solution.⁴⁸

Here we describe a series of results obtained with highly purified samples of two new clusters, Au₁₄₄(SC₂H₅)₆₀ and Au₁₄₄(SC₃H₇)₆₀, hereafter indicated as Au₁₄₄(SCn)₆₀ (n = 2 and 3). The clusters' stoichiometry was confirmed by inductively coupled plasma (ICP) and electrospray ionization (ESI) mass spectrometries. 1D and 2D NMR analysis led to the discovery that these clusters are capped by 12 ligand types in exactly the same amount (5-fold equivalence). Furthermore, the methylene proton signals show diastereotopicity. For the α-CH₂ protons, the diastereotopic effect is indeed truly gigantic as it reaches chemical-shift differences as large as 2.9 ppm. DFT calculations were used to get insights into structural features that could explain the NMR results. Our analysis suggests that ligand type differences and diastereotopic effects could be caused by local asymmetries affecting the strength of inter-staple C–H⋯S hydrogen bonds involving one of the two α-CH₂ protons. These results thus provide an enriched new view for the actual monolayer structure of Au₁₄₄(SR)₆₀ in solution.

Results and discussion

Synthesis and characterization of Au₁₄₄(SR)₆₀

The synthesis of Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀ was carried out in tetrahydrofuran (THF) according to a strategy similar to that we usually employ to prepare Au₂₅(SCn)₁₈⁻,⁴⁹ as detailed in the ESI.† Briefly, 0.5 g HAuCl₄·3H₂O was dissolved in 40 mL THF in the presence of 1.2 equiv. tetra-n-octylammonium (Oct₄N⁺) bromide, and then 4 equiv. of the given alkanethiol was added dropwise. After ca. 45 min, 10 mL toluene was added, followed by addition of 10 mL of a freshly prepared icy-cold aqueous solution of 10 equiv. NaBH₄. After one day under aerobic conditions, the reaction mixture was filtered and THF was evaporated. The aqueous phase was removed and the resulting black-brownish oily solid was dissolved in toluene and washed with water a few times. After toluene was evaporated and the by-product, [Oct₄N⁺][Au₂₅(SCn)₁₈⁻], was removed by washing with acetonitrile, the solid residue was washed with methanol and then pentane. The purified Au₁₄₄(SCn)₆₀ clusters were obtained as crystalline black powders. The UV-vis spectra of the two clusters (Fig. S1†) display features that match but also enhance those shown for the same cluster capped by phenylethanethiolate ligands.³⁵ Details on a rich sequence of dips and shoulders are especially evident in the derivative spectra at 350–800 nm.

Definite proof for the molecular formula was obtained via mass spectrometry. ICP-MS analysis allows determining the S and Au content very precisely. For both Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀, we used a total amount of 40 mg, whose purity was carefully assessed ahead of the ICP-MS experiments by ¹H NMR spectroscopy, as detailed below. For gold and sulfur calibration, we relied on different multielement standard solutions. A suitable amount of sample (5 mg) was accurately weighed and digested. The resulting solution was diluted with the same solvent used for calibrations. Full details are described in the ESI.† For Au₁₄₄(SC2)₆₀, the theoretical weight percentages of Au and S are 88.55 and 6.006%, respectively. The average values of the 8 independent ICP-MS determinations were 88.2(0.5) and 5.99(0.07)% for Au and S, respectively, which correspond to a recovery of 99.6% and 99.7%, respectively. The same procedure was applied to Au₁₄₄(SC3)₆₀, for which we obtained Au, 86.3(0.4)% (theoretical 86.283%), recovery 100%; S, 5.86(0.06)% (theoretical 5.853%), recovery 100.1%. We note that a recovery very close to 100% indicates that the samples were purified extremely well. For both Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀ the experimental gold-to-sulfur weight ratios is 14.7(0.2), which is in excellent agreement with the theoretical value of 14.74 and allows us to conclude that the molecular formula is indeed Au₁₄₄(SR)₆₀.

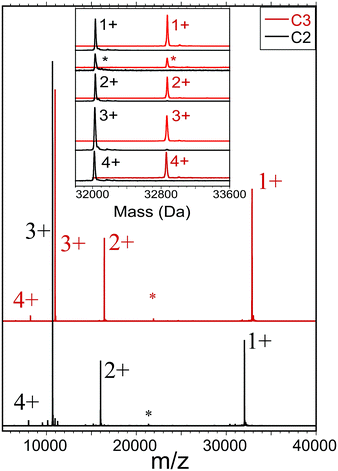
We also employed a second form of mass spectrometry to assess the sample purity and molecular mass of each compound (C2, C3). Fig. 1 shows ESI-MS results obtained by electrospraying dilute solutions (∼3 μM) of otherwise neat dichloromethane (DCM) under mild conditions, and detecting the ions by time-of-flight mass spectrometry (see ESI Section for detailed procedures and instrumental settings†). The obtained mass spectra (Fig. 1) show dominant features centered at masses that agree with those calculated from the molecular formulae, 32 032 and 32 873, to within the instrumental accuracy and calibration (see ESI†). In this case, we found no indication that the charging (z = 1+, 2+, 3+, and 4+ in Fig. 1) involved electrolyte adducts. Minor features in each region may be attributed to previously established fragmentation processes, e.g., RS-SR or (AuSR)₄ elimination, or adduct formation, as these features are enhanced by adjusting instrument voltages for in-source collision-induced dissociation (IS-CID results are included herein).

Fig. 1 Analysis of Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀ by electro-spray ionization mass spectrometry (ESI-MS). The main frame shows a complete mass spectrum for Au₁₄₄(SC2)₆₀ (in black) overlaid by a spectrum for Au₁₄₄(SC3)₆₀ (in red), spanning the mass-to-charge (m/z) range of 5000–40 000. Labels designate our assignments to charge states (z = 1+, 2+, 3+, and 4+) of the intact clusters or parent molecules, M^z+. The inset demonstrates the quantitative basis for these assignments by the alignment of all major features when the m/z-values are converted to mass (m) by multiplication of the respective portions of the spectrum by the assigned charge (z). For the minor features marked by the asterisk (*), the multiplier z = 3/2 is used, suggesting that these ions may arise from a dimer of the respective compounds in the z = 3+ charge-state, (2M)³⁺. The so-determined masses agree with those calculated from the molecular formulas, within the instrumental precision. The mass-differences separating respective C2 and C3 principal peaks, are all 840–841 Da, in agreement with the count of 60 ligands, i.e., the sixty additional methylene groups, ¹²C¹H_2, increment the mass by ∼60 × 14 = 840 Da.

The measured abundance of ions attributable to the common byproducts — Au-SR clusters of Au SR compositions (137,56), (130,50), (104,45), (38,24), (25,18), all of which are readily detected in this instrument — are very low, no more than ∼1% of the abundance of the main component. Note that instrumental separation (HPLC or trap-column insertion) was not used to remove small-molecule contaminants or to enhance the appearance of size-purity of the electrosprayed sample solution. The ESI-MS analyses thus clearly support the other evidence that new single compounds of definite molecular formula have been isolated as substances that are free of the most likely byproducts.

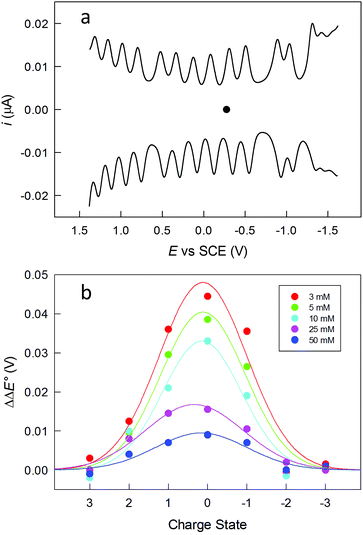
The clusters were also studied by electrochemistry. Fig. 2a shows the DPV patterns observed for Au₁₄₄(SC2)₆₀, in DCM containing 0.1 M tetra-n-butylammonium hexafluorophosphate (TBAH). DPV shows a very nice sequence of symmetrical peaks; a similar behavior is observed for Au₁₄₄(SC3)₆₀ (Fig. S2†). The peaks in the range from −1.2 to 1.3 V are fully reversible, as indicated by the unit ratio between the corresponding anodic and cathodic cyclic voltammetry peaks at low scan rates, which confirms that the corresponding electrogenerated species are stable. The separation between the formal potential (E°) values of successive DPV peaks (ΔE°) increases as the ligand length and thus the monolayer thickness increases. For example, the average ΔE° value for the peaks in the range from ca. −0.7 to 0.7 V is 0.207 ± 0.016 and 0.226 ± 0.018 V, for Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀, respectively (Fig. S2†). An increase of the ligand length causes a decrease of the average monolayer dielectric constant, as discussed for Au₂₅(SCn)₁₈,⁴⁷ with the consequence of making the charging processes more difficult. Instead, the two larger gaps centered at about −0.8 and −1.25 V have similar ΔE° values of ca. 0.38 and 0.28 V, respectively.

Fig. 2 (a) DPV of 0.048 mM Au₁₄₄(SC2)₆₀ in DCM/0.1 M TBAH at 25 °C on a microdisk glassy-carbon electrode. The black circle marks the equilibrium potential. The DPV was obtained with peak amplitude of 50 mV, pulse width of 0.05 s, increments per cycle of 2 mV, and pulse period of 0.1 s. (b) Plot of the separation between successive DPV peaks at different electrolyte concentrations (see legend) for 0.043 mM Au₁₄₄(SC2)₆₀ in DCM. The data are given as ΔΔE° = (ΔE°)_{[TBAH]=x mM} − (ΔE°)_{[TBAH]=100 mM}. The curves are the Gaussian best fits to the data.

One important aspect is assessing the actual charge possessed by the purified clusters. This is generally assumed to be zero. We studied the dependence of the DPV peaks as a function of the electrolyte concentration, which is a procedure similar to that previously described by Guo et al.⁵⁰ In Fig. 2b, the effect of the electrolyte concentration is shown for Au₁₄₄(SC2)₆₀. The ΔE° s of the peaks around the equilibrium potential (C2: −0.276 V; C3: −0.284 V) were measured at different TBAH concentrations and then referred to the corresponding values observed at 0.1 M TBAH. The data are plotted against the supposed cluster charge state. For example, the 0 state refers to the separation between the peaks related to the +1/0 and the 0/−1 redox couples. The graph resembles the behavior previously observed,⁵⁰i.e., a sizable increase of ΔE° as the TBAH concentration decreases for the peaks closer to the equilibrium potential. This behavior is indeed expected when the lower charged species (±1, ±2) are involved, whereas the electron-transfer steps involving more heavily charged states exhibit a general insensitivity toward the electrolyte concentration. This result thus points to the clusters in solution as being mostly in a neutral charge state. As to the magnetic state of Au₁₄₄(SCn)₆₀, we carried out some tests by performing continuous-wave electron paramagnetic resonance (cw-EPR) experiments with frozen solutions of 0.6 mM Au₁₄₄(SC2)₆₀ and Au₁₄₄(SC3)₆₀ in toluene. However, despite the different conditions employed (see ESI†) we could not detect any evident magnetic signal down to 5 K (Fig. S3†). This finding thus suggests that these clusters are diamagnetic, as opposed to that found for frozen solutions of the neutral, paramagnetic Au₂₅(SC2)₁₈ (ref. 49) and Au₂₅(SC3)₁₈ (ref. 10) clusters, which show detectable and progressively stronger signals upon decreasing the temperature from ca. 80 K. We should note, however, that the absence of evident signals could also be compatible with extreme line broadening due to faster relaxation and a higher number of hyperfine couplings, associated with the larger size of Au₁₄₄(SR)₆₀.

NMR spectroscopy

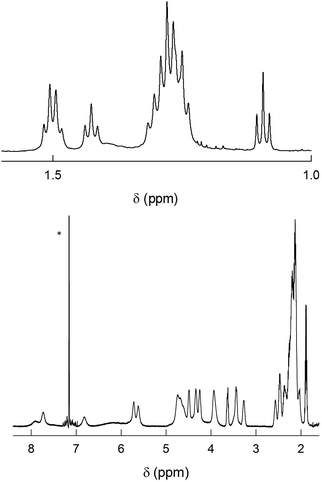
As already noted, previous findings regarding the NMR behavior of Au₁₄₄(SR)₆₀ pointed to a 60-fold symmetry equivalence of the ligands, i.e., the presence of only one ligand type.⁴⁰ This observation deeply affected subsequent research and especially theoretical refinement of the actual structure.⁴² Instead, the ¹H NMR spectra of Au₁₄₄(SCn)₆₀ in C₆D₆ exhibit an impressively large number of moderately to well-defined peaks from 0.95 to 8.25 ppm. In the following, we will address the NMR behavior of each cluster, starting from Au₁₄₄(SC2)₆₀, which has but a single methylene (alpha) group.

Fig. 3 shows the very detailed ¹H NMR spectrum of Au₁₄₄(SC2)₆₀ at 25 °C. Inspection of the spectral features shows that the spectrum can be decomposed into two regions: (i) a series of partially resolved triplets in the range of δ from ca. 1.2 to 2.5 ppm, which, on the basis of their position and multiplicity, are attributed to the methyl resonances (β-CH₃); (ii) the remaining of the spectrum is attributed to the α-CH₂ resonances and shows a series of typically broad signals that spread in the very wide δ range from 3.2 to 8 ppm. Stepwise increase of the solution temperature from 25 to 70 °C causes sharpening of the peaks, a general increase in resolution for all resonances (for examples, see Fig. S4†). The temperature effect is also useful to modify the position of the β-CH₃ peaks and thus the way by which they overlap, as well as to allow better integration of the signals. This allows understanding two important facts: (i) there are 12 types of clearly nonequivalent ligands; (ii) these ligands are present in the same amount (cf. integrals in Fig. S4†). Concerning the α-CH₂ resonances, increasing the temperature causes even more evident effects because the peaks both shift and sharpen. In particular, by following the T-dependent chemical shift of each resonance it is possible to count as many as 24 independent signals (Fig. S4†). As confirmed below, these numbers are thus in keeping with the molecular formula: 12 × 5 = 60 (total number of ligands); 24 × 5 = 120 (total number of methylene H-atoms).

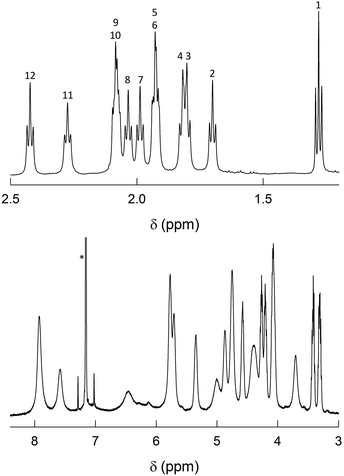Fig. 3 ¹H NMR spectrum of 1 mM Au₁₄₄(SC2)₆₀ in C₆D₆ at 25 °C. For convenience, the spectrum has been divided into two parts: β-CH₃ (top) and α-CH₂ (bottom). In the latter, the scale has been enlarged (9.3×). The numbers on the top plot label the 12 ligand types (cf. Fig. S4†). The asterisk marks the benzene signal.

2D-NMR homonuclear and heteronuclear measurements were carried out at 45 °C, which offers a good compromise between enhanced resolution and thermal stability of the cluster (for time-consuming experiments). ¹H,¹H-homonuclear correlation spectroscopy (COSY) evidences scalar interactions between each β-CH₃ triplet and two α-CH₂ signals (Fig. 4). Despite small differences between some of the β-CH₃ chemical-shift values, the ¹H,¹³C-heteronuclear multiple quantum coherence (HMQC) experiments allows determining a very well-resolved set of 12 ¹³C chemical-shift values that span a range of δ from 23 to 35 ppm (Fig. 5). For the α-CH₂ groups, HMQC data are affected by a higher uncertainty due to the lower signal-to-noise ratio arising from the broadening of the proton resonances. Nonetheless, the observed coherences, which fall in the region of 32.8–51.3 ppm, clearly show that in all cases two distinct proton resonances correlate with the same ¹³C resonance. This finding unequivocally confirms the nonequivalence of the protons belonging to the same α-CH₂. For symmetry reasons, only one correlation is observed for the β-CH₃ groups. Finally, the integrals of each proton, which for most of them could be determined by comparying the signals observed in the ¹H NMR spectra at different temperatures (Fig. S4†), are within experimental uncertainty identical to each other and correspond to 1/3 the integrals of the β-CH₃ triplets. All δ values are collected in Table S1.†

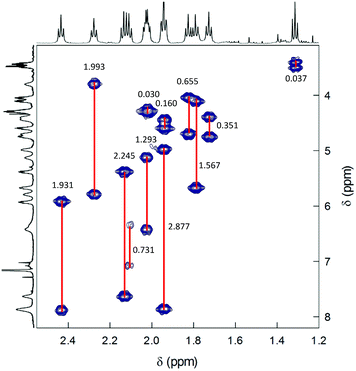Fig. 4 COSY spectrum of 0.5 mM Au₁₄₄(SC2)₆₀ in C₆D₆ at 45 °C. Correlations are evidenced and the Δδ values are indicated.

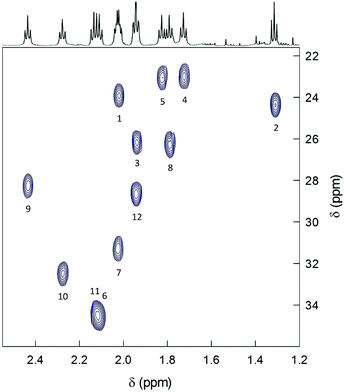Fig. 5 HMQC spectrum of 0.5 mM Au₁₄₄(SC2)₆₀ in C₆D₆ at 45 °C. The spectrum shows the correlations pertaining to the methyl groups. The numbers label the 12 ligand types according to increasing Δδ values (cf. Table S1† and Fig. 7).

The striking nonequivalence of the protons on the same carbon atom is worth noting. This phenomenon is referred to as diastereotopicity and is caused by different chemical environments experienced by the two otherwise identical methylene protons. In clusters protected by achiral thiolates, evidence for diastereotopic protons has been obtained for Au₃₈(SCH₂CH₂Ph)₂₄, which is characterized by a chiral arrangement of the protecting staples.⁵¹ In particular, Qian et al. found that the α-CH₂ signals can be separated by Δδ values as large as 0.76 ppm, whereas the effect on the β-CH₂ resonances is no larger than 0.17 ppm.⁷ Very recently, we studied Au₃₈(SCn)₂₄ capped by propanethiolates (n = 3) and butanethiolates (n = 4) and found that α-CH₂ signals split by up to 0.67 (C3) and 0.69 ppm (C4), the β-CH₂ by 0.023 (C3) and 0.085 ppm (C4), and the γ-CH₂ by 0.029 ppm (C4).⁴¹ These chirality-related diastereotopic effects are very large also in the context of many other molecular systems.^52–54 Comparatively, the effect observed for the α-CH₂ signals in Au₁₄₄(SC2)₆₀ can thus be easily defined as gigantic, being as large as 2.88 ppm and with a methylene proton resonance found at the very large downfield value of 7.87 ppm.

The ¹H NMR spectrum of Au₁₄₄(SC3)₆₀ shows three regions (Fig. 6): (i) at ca. 1.1 to 1.5 ppm there is a series of partially resolved triplets attributed to the γ-CH₃ protons; (ii) a group of overlapping sextets is then observed in the range from ca. 1.9 to 2.5 ppm, which for analogous reasons we attribute to the β-CH₂ groups; (iii) a series of quite broad signals from ca. 3.2 to 8.0 ppm, which pertain to the α-CH₂ protons. Again, stepwise increase of the solution temperature is expedient to shift and sharpen the peaks, and to make analysis of several integrals possible. For the sake of comparing the results with those of Au₁₄₄(SC2)₆₀, we selected 45 °C. For this cluster, we relied on total correlated spectroscopy (TOCSY). The spectrum exhibits scalar correlations (Fig. S5†) between each γ-CH₃ resonance with four methylene signals, two at the β-position and two at the α-position. In turn, the β-CH₂ and α-CH₂ protons exhibit vicinal and geminal scalar correlations.

Fig. 6 ¹H NMR spectrum of 1 mM Au₁₄₄(SC3)₆₀ in C₆D₆ at 25 °C. For convenience, the spectrum has been divided into two parts: γ-CH₃ (top) and α-CH₂ and β-CH₂ (bottom). In the latter, the scale has been enlarged (6.3×). The asterisk marks the benzene signal.

HMQC allows determining a set of 3 groups of signals each composed of 12 ¹³C resonances (not shown). The groups of the γ-CH₃ and β-CH₂ carbons are at 13.5–16.1 and 32–44 ppm, respectively. The ¹H,¹³C-methylene coherences for the α-CH₂ protons are affected by higher uncertainty due to the lower signal-to-noise ratio arising from the broadening of the proton resonances. Nonetheless, we find distinct coherences in the range from 35.3 to 58.5 ppm. Very importantly, the fact that two distinct proton signals correlate with the same ¹³C resonance confirms the nonequivalence of the protons in each α-CH₂ and β-CH₂ groups. For Au₁₄₄(SC3)₆₀, diastereotopicity causes maximum effects, Δδ, of 2.79 and 0.72 ppm for the α-CH₂ and the β-CH₂, respectively. All δ values are collected in Table S2.† Curiously, although β-CH₂ carbons generally resonate upfield with respect to the α-CH₂ carbons, the ¹³C resonances pertaining to the α-CH₂ and β-CH₂ carbons are found in very similar ranges. We observed a similar trend also in Au₃₈(SC3)₂₄ and Au₃₈(SC4)₂₄.⁴¹

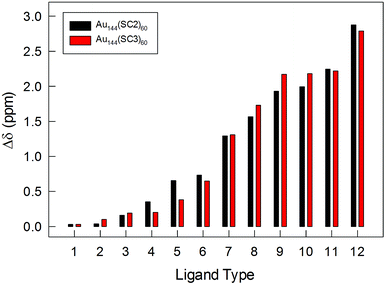
The NMR results obtained with very pure samples of Au₁₄₄(SCn)₆₀, as definitely assessed by ICP-MS and ESI-MS, show important features of the capping monolayer. (i) All clusters are characterized by self-consistent spectral patterns that indicate that only one structural form is present in solution. This is in contrast to a very recent study that concluded that two structures coexist in Au₁₄₄(SR)₆₀, though capped by longer thiolates. On the other hand, the DPV patterns provided in the same report exhibit charging features that are not quite as regular as those seen in Fig. 2 and S2,† and this suggests the presence of more than one species in solution, possibly related to the different synthetic protocol adopted.⁵⁵ (ii) The 12 ligand types are present in the same amount and, on the basis of the cluster stoichiometry, repeat themselves five times (12 × 5 = 60). The very fact that we consistently distinguish 12 ligand types indicates that none of the chemical environments experienced by each ligand type is the same. (iii) The diastereotopic effect on the α-CH₂ protons goes from very low to Δδ values as large as 2.8–2.9 ppm, resulting for the 12 ligand types in average Δδ values of 1.16 ppm (Tables S1 and S2†). Fig. 7 illustrates the impressive variety in maximum Δδ values displayed by the α-CH₂ protons for the 12 ligand types. The plot also shows that for these resonances there is no evident difference associated with a change in the ligand length.

Fig. 7 Plot of the maximum Δδ values displayed by the α-CH₂ protons for the 12 ligand types.

DFT calculations

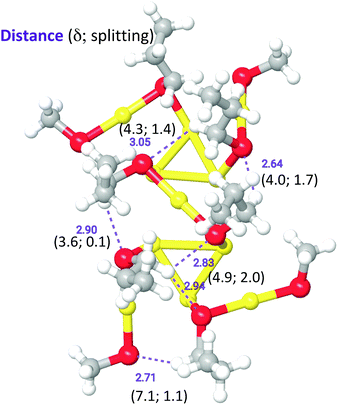
To shed some light onto the NMR evidence, we resorted to carry out DFT calculations. The structures here utilized are obtained by using a Au₁₄₄(SCH₃)₆₀ model in which the SH groups (employed earlier)⁴³ have been replaced by SCH₃. In the original Au₁₄₄(SH)₆₀ model, D₅ point-group symmetry was enforced and the coordinates of the Au atoms were constructed to reproduce the experimental structure factor of Au₁₄₄(SR)₆₀.³¹ This model, however, preserved the same arrangement proposed by Lopez-Acevedo et al.,³⁸ in which two of the six sets, of five staples each, equivalent by symmetry, namely two sets of staples between the poles and the equator of the cluster, exhibit SCH₃ ligands in cis-configuration, while the other four sets have ligands in trans-configuration (Fig. S6,† left panel). Here, instead, we turned each cis-configuration into trans (Fig. S6,† right panel), froze the coordinates of Au atoms, and performed a local geometry optimization enforcing D₅ point-group symmetry and charge of 2+, using the ADF program⁵⁶ with PBE xc-functional,⁵⁷ Double Zeta (DZ) basis set, Zero Order Regular Approximation (ZORA).⁵⁸ For details, see ESI.† For the sake of the ensuing discussion regarding the simulation of the NMR results, it is interesting to note that some of the methyl groups are found to approach the cluster surface to the point that some of the H atoms exhibit rather short H⋯S and H⋯Au distances (2.6–2.8 Å) from the S and Au atoms in neighboring staple units, as discussed in more detail in the ESI† and illustrated in Fig. S7† for a H⋯S close approach. Selected tests run with the uncharged species and/or with some cis-configurations produced analogous results. The resulting cluster model constitutes the structural basis for the simulation of NMR chemical shifts.

NMR calculations

We aimed at finding possible structural mechanisms that could explain the variety in ligand types and diastereotopic effects detected by NMR. Because a full NMR calculation considering the entire cluster with SC2-SC3 ligands is currently intractable, we resorted to a QM/MM calculation where a portion of the outer shell containing six SC3 ligands was treated quantum mechanically, whereas the rest of the outer-shell cluster was treated at the molecular mechanics level (Fig. S12†), following the parametrization of Guberman-Pfeffer et al.⁵⁹ Propyl groups were added to six ligands (two on the equator and four on the pole). Chemical shifts were calculated and recorded for all protons within the propyl groups (all values are in Table S3†).

While the purpose of these calculations was not to make a one-to-one comparison with the experimental NMR shifts, we were able to discover the origin of the diverse number of NMR peaks and the nature of the remarkable diastereotopicity. Note that the six ligands chosen represent only a subset of the 12 unique ligands that span from the north to the south pole. Yet, with this subset we observe a spectrum of methylene shifts and Δδ values. Fig. 8 shows the QM unit used in our QM/MM calculations, where C3 groups were added and optimized. In agreement with the experiment, calculations show a diverse set of chemical shifts (Fig. 8 and Table S3†) and Δδ values. The outcome of calculations (Table S3†) is indeed in excellent agreement with the experimental values, which show that the chemical shifts for α-CH₂ and β-CH₂ range from ca. 2 to 8 ppm. The experimental Δδ values range from 0 to 2.9 ppm, which is also in good agreement with the calculated range of Δδ values (0 to 2.0 ppm). More importantly, calculations reveal that the large downfield values of the α-CH₂ protons should originate from close C–H⋯S contacts. These contacts behave as hydrogen bonds. Large (δ, Δδ)-values fingerprints result from distances of < 3.0 Å and angles > 120 °.

Fig. 8 QM Unit used for the QM/MM NMR calculations. Characteristic distances involving prominent CH⋯S contacts are shown in purple (distances in Å). In parenthesis, the most downfield proton in α-CH₂ and the corresponding diastereotopic shift (in ppm) are also shown (Au: yellow; S: red; C: gray; H: white).

The two Au₁₄₄ structures solved very recently, Au₁₄₄(C≡CAr)₆₀ and Au₁₄₄(SCH₂Ph)₆₀,^45,46 will be referred to as Str-A and Str-B, respectively. Both Str-A and Str-B are qualitatively similar to the structure we have used in our work. It is worth noticing that the staples of Str-B are all in the trans-configuration, in accordance with our structure. This is different from the first theoretical work in which some of the ligands were in the cis-configuration.³⁸ The main differences of our structure with respect to Str-A and Str-B are: (1) a slightly outward protrusion of the Au and S atoms in our staples by 0.5 and 0.25 Å with respect to Str-A and Str-B, respectively (cf. Table S4†); (2) a slight rotation by 10–20° of the staples that in Str-A are along a high-symmetry line with respect to the underlying Au framework, whereas in Str-B are rotated by a lesser degree (around 5°); (3) the dihedral angles between the (CM,Au_staple,S) and (Au_staple,S, α-C) planes (where CM is the center of mass of the cluster) are larger in our structure (average 64°) with respect to, e.g., Str-B (average 47°). These differences are likely ascribable to the different, more rigid ligands used in these two works.^45,46 It cannot be excluded that other forms of inter-ligand interactions might weaken/contrast those inter-ligand interaction that conceivably give rise to the diastereotopic effect observed in our system. Indeed, we notice that the shortest H⋯S contact in Str-B is of 3.12 Å, which is larger than in our structure that shows distances as short as 2.64 Å and, therefore, should not give rise to any relevant inter-ligand interaction of this kind.

Conclusions

Highly pure samples of the two new clusters Au₁₄₄(SCn)₆₀, n = 2, 3, were prepared and fully characterized for their stoichiometry, optical behavior, and charging pattern. The NMR results showed that: (i) only one structural form is present in solution; (ii) the clusters are capped by 12 ligand types experiencing distinct chemical environments; (iii) each ligand type is present in the same amount and repeats itself five times on the cluster surface; (iv) the methylene protons show diastereotopic effects; (v) these effects are virtually independent of the thiolate length; (vi) for the α-CH₂ protons, the diastereotopic effect reaches unprecedented Δδ values.

The NMR data thus point to very significant local asymmetry. The latter induces a general asymmetry along the ligand chain, which makes the diastereotopic effect strong even at the β-CH₂ protons (average Δδ = 0.16 ppm). To get insights into these intriguing results, we used DFT calculations to generate a cluster model onto which simulations of the NMR chemical shifts were carried out. Calculations on representative patches of the surface staples could reproduce the experimental NMR shifts and Δδ values quite closely, and this led us to understand that the physical origin of the various ligand types and strong diastereotopic effects could be close C–H⋯S contacts affecting the α-CH₂ protons.

Evidence for local asymmetry is in contrast to a previous conclusion of the symmetry equivalent positions occupied by the para-mercaptobenzoic-acid ligands in a cluster described as Au₁₄₄(SR)₆₀.⁴⁰ This is indeed a very intriguing outcome because it suggests that the actual monolayer structure in solution is a function of the specific capping ligand and perhaps the solvent (the aforementioned NMR data were obtained in D₂O, which is a strong H-bond competitor). Evidence for different ligand environments and, for meta-mercaptobenzoic acid ligands, stabilization of the ligand–metal interface were indeed observed also for some clusters in D₂O.^60,61 In the case of aryl ligands, the monolayer structure might also be affected by inter-ligand interactions between the phenyl rings, as indeed noted in the structure solved very recently for Au₁₄₄(SCH₂Ph)₆₀.⁴⁶ which might have the consequence of making all chemical environments around the ligands equivalent. Instead, the short alkanethiolates could provide more “innocent” ligands, in the sense that they may let the surface structure of the gold core relax toward a virtually ligand-independent local symmetry, at least in solution. In this context, it is worth noticing that the ¹H NMR spectrum of Au₁₄₄(SCH₂CH₂Ph)₆₀ in CD₂Cl₂ also shows a large series of CH₂ signals, which points to different ligand types as well.⁶² In a non H-bonding solvent and even when the local structure does not show sufficiently short C–H⋯S contacts, as for Au₁₄₄(SCH₂Ph)₆₀,⁵⁹ or C–H⋯Au interactions,^63,64 it could be still possible to detect some diastereotopic effect associated with the chirality of the two experimentally determined Au₁₄₄ structures.^45,46 This diastereotopic contribution, however, should be small, probably no more than the minimum Δδ values that we observe for the α-CH₂ protons of Au₁₄₄(SCn)₆₀.

The unique capabilities of NMR in understanding the interface of hard–soft materials such as ligand-protected metal nanoparticles have been recently stressed and reviewed.⁶⁵ The results that we now describe provide an extension of this viewpoint by underscoring the wealth of information that can be obtained through accurate NMR studies of very pure samples, which in our specific case allowed obtaining compelling evidence for a complex surface structure of the ubiquitous Au₁₄₄ cluster in solution.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the University of Padova (P-DiSC-2017: Gold Nose). J. A. G. acknowledges support from NSF grants CHE-1359081 and CHE-1404998. Computational support from the CINECA Supercomputing Centre within the ISCRA Program is also gratefully acknowledged. We are indebted to Prof. Rongchao Jin and Prof. Zhikun Wu for providing us information from ref. 46 ahead of its publication.

Notes and references

1. Protected Metal Clusters: From Fundamentals to Applications, in Frontiers of Nanoscience, ed. T. Tsukuda and H. Häkkinen, Elsevier, Amsterdam, 2015, vol. 9.
2. R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413.
3. I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208–8271.
4. S. Antonello and F. Maran, Curr. Opin. Electrochem., 2017, 2, 18–25.
5. R. Jin, Nanoscale, 2015, 7, 1549–1565.
6. M. Zhu, W. T. Eckenhoff, T. Pintauer and R. Jin, J. Phys. Chem. C, 2008, 112, 14221–14224.
7. H. Qian, M. Zhu, C. Gayathri, R. R. Gil and R. Jin, ACS Nano, 2011, 5, 8935–8942.
8. A. Venzo, S. Antonello, J. A. Gascón, I. Guryanov, R. D. Leapman, N. V. Perera, A. Sousa, M. Zamuner, A. Zanella and F. Maran, Anal. Chem., 2011, 83, 6355–6362.
9. S. Antonello, G. Arrigoni, T. Dainese, M. De Nardi, G. Parisio, L. Perotti, A. René, A. Venzo and F. Maran, ACS Nano, 2014, 8, 2788–2795.
10. M. Agrachev, S. Antonello, T. Dainese, J. A. Gascón, F. Pan, K. Rissanen, M. Ruzzi, A. Venzo, A. Zoleo and F. Maran, Chem. Sci., 2016, 7, 6910–6918.
11. J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756–3757.
12. J. F. Parker, C. A. Fields-Zinna and R. W. Murray, Acc. Chem. Res., 2010, 43, 1289–1296.
13. S. Antonello, N. V. Perera, M. Ruzzi, J. A. Gascón and F. Maran, J. Am. Chem. Soc., 2013, 135, 15585–15594.
14. A. Tlahuice-Flores, R. L. Whetten and M. Jose-Yacaman, J. Phys. Chem. C, 2013, 117, 20867–20875.
15. M. Agrachev, S. Antonello, T. Dainese, M. Ruzzi, A. Zoleo, E. Aprà, N. Govind, A. Fortunelli, L. Sementa and F. Maran, ACS Omega, 2017, 2, 2607–2617.
16. O. Toikkanen, V. Ruiz, G. Ronnholm, N. Kalkkinen, P. Liljeroth and B. M. Quinn, J. Am. Chem. Soc., 2008, 130, 11049–11055.
17. H. Qian, Y. Zhu and R. Jin, ACS Nano, 2009, 3, 3795–3803.
18. T. G. Schaaff, M. N. Shafigullin, J. T. Khoury, I. Vezmar and R. L. Whetten, J. Phys. Chem. B, 2001, 105, 8785–8796.
19. R. L. Donkers, Y. Song and R. W. Murray, Langmuir, 2004, 20, 4703–4707.
20. R. W. Murray, Chem. Rev., 2008, 108, 2688–2720.
21. L. Becucci, R. Guidelli, F. Polo and F. Maran, Langmuir, 2014, 30, 8141–8151.
22. I. Guryanov, F. Polo, E. V. Ubyvovk, E. Korzhikova-Vlakh, T. Tennikova, A. T. Rad, M.-P. Nieh and F. Maran, Chem. Sci., 2017, 8, 3228–3238.
23. R. S. Ingram, M. J. Hostetler, R. W. Murray, T. G. Schaaff, J. Khoury, R. L. Whetten, T. P. Bigioni, D. K. Guthrie and P. N. First, J. Am. Chem. Soc., 1997, 119, 9279–9280.
24. J. F. Hicks, D. T. Miles and R. W. Murray, J. Am. Chem. Soc., 2002, 124, 13322–13328.
25. B. M. Quinn, P. Liljeroth, V. Ruiz, T. Laaksonen and K. Kontturi, J. Am. Chem. Soc., 2003, 125, 6644–6645.
26. A. H. Holm, M. Ceccato, R. L. Donkers, L. Fabris, G. Pace and F. Maran, Langmuir, 2006, 22, 10584–10589.
27. S. Malola, L. Lehtovaara, J. Enkovaara and H. Häkkinen, ACS Nano, 2013, 7, 10263–10270.
28. C. Yi, M. A. Tofanelli, C. J. Ackerson and K. L. Knappenberger Jr, J. Am. Chem. Soc., 2013, 135, 18222–18228.
29. H.-Ch. Weissker, H. B. Escobar, V. D. Thanthirige, K. Kwack, D. Lee, G. Ramakrishna, R. L. Whetten and X. Lopez-Lozano, Nat. Commun., 2014, 5, 1–8.
30. Y. Negishi, T. Nakazaki, S. Malola, S. Takano, Y. Niihori, W. Kurashige, S. Yamazoe, T. Tsukuda and H. Häkkinen, J. Am. Chem. Soc., 2015, 137, 1206–1212.
31. R. L. Whetten, J. T. Khoury, M. M. Alvarez, S. Murthy, I. Vezmar, Z. L. Wang, P. W. Stephens, C. L. Cleveland, W. D. Luedtke and U. Landman, Adv. Mater., 1996, 8, 428–433.
32. M. J. Hostetler, A. C. Templeton and R. W. Murray, Langmuir, 1999, 15, 3782–3789.
33. N. K. Chaki, Y. Negishi, H. Tsunoyama, Y. Shichibu and T. Tsukuda, J. Am. Chem. Soc., 2008, 130, 8608–8610.
34. C. A. Fields-Zinna, R. Sardar, C. A. Beasley and R. W. Murray, J. Am. Chem. Soc., 2009, 131, 16266–16271.
35. H. Qian and R. Jin, Nano Lett., 2009, 9, 4083–4087.
36. M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802.
37. R. L. Donkers, D. Lee and R. W. Murray, Langmuir, 2004, 20, 1945–1952.
38. O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Grönbeck and H. Häkkinen, J. Phys. Chem. C, 2009, 113, 5035–5038.
39. N. Tran, D. Powell and L. Dahl, Angew. Chem., Int. Ed., 2000, 39, 4121–4125.
40. O. A. Wong, C. L. Heinecke, A. R. Simone, R. L. Whetten and C. J. Ackerson, Nanoscale, 2012, 4, 4099–4102.
41. T. Dainese, S. Antonello, S. Bogialli, W. Fei, A. Venzo and F. Maran, ACS Nano, 2018, 12, 7057–7066.
42. D. Bahena, N. Bhattarai, U. Santiago, A. Tlahuice, A. Ponce, A. S. B. H. Bach, B. Yoon, R. L. Whetten, U. Landman and M. Jose-Yacaman, J. Phys. Chem. Lett., 2013, 4, 975–981.
43. G. Barcaro, L. Sementa, A. Fortunelli and M. Stener, Comment on “(Au–Ag)₁₄₄(SR)₆₀ Alloy Nanomolecules” by C. Kumara and A. Dass, Nanoscale, 2011, 3, 3064, Nanoscale, 2015, 7, 8166–8167.
44. H.-C. Weissker, O. Lopez-Acevedo, R. L. Whetten and X. López-Lozano, J. Phys. Chem. C, 2015, 119, 11250–11259.
45. Z. Lei, J.-J. Li, X.-K. Wan, W.-H. Zhang and Q.-M. Wang, Angew. Chem., Int. Ed., 2018, 57, 8639–8643.
46. N. Yan, N. Xia, L. Liao, M. Zhu, F. Jin, R. Jin and Z. Wu, Sci. Adv., 2018, 4, eaat7259.
47. S. Antonello, T. Dainese, M. De Nardi, L. Perotti and F. Maran, ChemElectroChem, 2016, 3, 1237–1244.
48. J. Koivisto, K. Salorinne, S. Mustalahti, T. Lahtinen, A. Malola, H. Häkkinen and M. Pettersson, J. Phys. Chem. Lett., 2014, 5, 387–392.
49. T. Dainese, S. Antonello, J. A. Gascón, F. Pan, N. V. Perera, M. Ruzzi, A. Venzo, A. Zoleo, K. Rissanen and F. Maran, ACS Nano, 2014, 8, 3904–3912.
50. R. Guo, D. Georganopoulou, S. W. Feldberg, R. L. Donkers and R. W. Murray, Anal. Chem., 2005, 77, 2662–2669.
51. H. Qian, T. Eckenhoff, Y. Zhu, T. Pintauerand and R. Jin, J. Am. Chem. Soc., 2010, 132, 8280–8281.
52. E. Petruzzella, N. Margiotta, G. Natileb and J. D. Hoeschele, Dalton Trans., 2014, 43, 12851–12859.
53. H. Amer, T. Nypelö, I. Sulaeva, M. Bacher, U. Henniges, A. Potthast and T. Rosenau, Biomacromolecules, 2016, 17, 2972–2980.
54. Y. Rondelez, G. Bertho and O. Reinaud, Angew. Chem., Int. Ed., 2002, 41, 144–146.
55. K. M. Ø. Jensen, P. Juhas, M. A. Tofanelli, C. L. Heinecke, G. Vaughan, C. J. Ackerson and S. J. L. Billinge, Nat. Commun., 2016, 7, 11859.
56. E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
58. E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
59. M. J. Guberman-Pfeffer, J. Ulcickas and J. A. Gascón, J. Phys. Chem. C, 2015, 119, 27804–27812.
60. K. Salorinne, S. Malola, O. A. Wong, C. D. Rithner, X. Chen, C. J. Ackerson and H. Häkkinen, Nat. Commun., 2016, 7, 10401.
61. T.-R. Tero, S. Malola, B. Koncz, E. Pohjolainen, S. Lautala, S. Mustalahti, P. Permi, G. Groenhof, M. Pettersson and H. Häkkinen, ACS Nano, 2017, 11, 11872–11879.
62. K. Salorinne, T. Lahtinen, J. Koivisto, E. Kalenius, M. Nissinen, M. Pettersson and H. Häkkinen, Anal. Chem., 2013, 85, 3489–3492.
63. H. Schmidbaur, H. G. Raubenheimer and L. Dobrzanska, Chem. Soc. Rev., 2014, 43, 345–380.
64. M. A. Bakr, M. Sugiuchi, M. Iwasaki, Y. Shichibu and K. Konishi, Nat. Commun., 2017, 8, 576.
65. L. E. Marbella and J. E. Millstone, Chem. Mater., 2015, 27, 2721–2739.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S12, Tables S1–S4, details on the synthesis of the clusters, ICP-MS, ESI-MS, NMR, electrochemistry, EPR, and DFT calculations. See DOI: 10.1039/c8sc04092c

---