Open Access Article
Open Access ArticleAtomic structure of boron resolved using machine learning and global sampling†
Si-Da
Huang
 ,
Cheng
Shang
,
Cheng
Shang
 ,
Pei-Lin
Kang
and
Zhi-Pan
Liu
,
Pei-Lin
Kang
and
Zhi-Pan
Liu
 *
*
Collaborative Innovation Center of Chemistry for Energy Materials, Key Laboratory of Computational Physical Science (Ministry of Education), Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Department of Chemistry, Fudan University, Shanghai 200433, China. E-mail: zpliu@fudan.edu.cn
First published on 11th September 2018
Abstract
Boron crystals, despite their simple composition, must rank top for complexity: even the atomic structure of the ground state of β-B remains uncertain after 60 years’ study. This makes it difficult to understand the many exotic photoelectric properties of boron. The presence of self-doping atoms in the crystal interstitial sites forms an astronomical configurational space, making the determination of the real configuration virtually impossible using current techniques. Here, by combining machine learning with the latest stochastic surface walking (SSW) global optimization, we explore for the first time the potential energy surface of β-B, revealing 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 distinct configurations out of the 2 × 105 minima visited, and reveal the key rules governing the filling of the interstitial sites. This advance is only allowed by the construction of an accurate and efficient neural network (NN) potential using a new series of structural descriptors that can sensitively discriminate the complex boron bonding environment. We show that, in contrast to the conventional views on the numerous energy-degenerate configurations, only 40 minima of β-B are identified to be within 7 meV per atom in energy above the global minimum of β-B, most of them having been discovered for the first time. These low energy structures are classified into three types of skeletons and six patterns of doping configurations, with a clear preference for a few characteristic interstitial sites. The observed β-B and its properties are influenced strongly by a particular doping site, the B19 site that neighbors the B18 site, which has an exceptionally large vibrational entropy. The configuration with this B19 occupancy, which ranks only 15th at 0 K, turns out to be dominant at high temperatures. Our results highlight the novel SSW-NN architecture as the leading problem solver for complex material phenomena, which would then expedite substantially the building of a material genome database.
293 distinct configurations out of the 2 × 105 minima visited, and reveal the key rules governing the filling of the interstitial sites. This advance is only allowed by the construction of an accurate and efficient neural network (NN) potential using a new series of structural descriptors that can sensitively discriminate the complex boron bonding environment. We show that, in contrast to the conventional views on the numerous energy-degenerate configurations, only 40 minima of β-B are identified to be within 7 meV per atom in energy above the global minimum of β-B, most of them having been discovered for the first time. These low energy structures are classified into three types of skeletons and six patterns of doping configurations, with a clear preference for a few characteristic interstitial sites. The observed β-B and its properties are influenced strongly by a particular doping site, the B19 site that neighbors the B18 site, which has an exceptionally large vibrational entropy. The configuration with this B19 occupancy, which ranks only 15th at 0 K, turns out to be dominant at high temperatures. Our results highlight the novel SSW-NN architecture as the leading problem solver for complex material phenomena, which would then expedite substantially the building of a material genome database.
1. Introduction
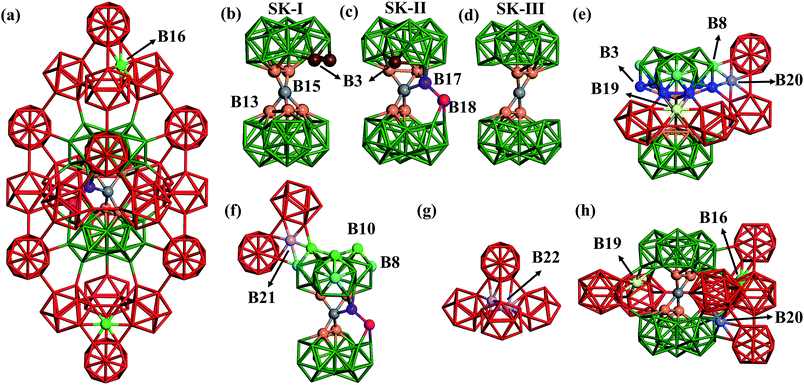
The mysteries of boron have persisted in chemistry since the discovery of the B2H6 molecule. To name a few, (i) unlike carbon with its typical bonding patterns (such as sp2 and sp3), the chemical bonding of boron is highly flexible and complex;1 (ii) the most stable structures of boron clusters, B80 as a famous example, are generally unknown; (iii) the ground state structure of boron crystals has not been conclusively determined in the sense that there are no conclusive experimental and theoretical results on the relative stability of α-B and β-B.2–4 The potential energy surface (PES) of boron is thus of general interest, but is highly challenging to rationalize by both experiments and theory. On the other hand, machine learning has emerged as a promising tool to solve complex physical problems that are “much too complicated to be soluble” using quantum mechanics. While state-of-the-art neural network (NN) techniques5–8 are now available to establish the link between molecular characteristics (e.g. geometry) and the observable properties, it remains an open question how far NN techniques can be applied to solve the top challenges in physical science, especially those involving the PES, for which a quantitative solution for energy is needed. The structure determination of β-B is a very hard problem.Among the 16 known boron allotropes, the rhombohedral form (β-B) was recently proven to be the most stable phase.4,9–12 The basic framework of β-B is considered as the layer by layer packing of B12 icosahedral cages and B28 triple-fused icosahedral cages along the [111] axis in a rhombohedral lattice (105 atoms in total, i.e. β-B105, #166, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), as shown in Fig. 1a. Recent work suggested that the stability of β-B might be related to the existence of numerous partially occupied sites (POSs). These POSs are located in or near the vacant spaces surrounded by B12 and B28 cages, and it is known from experiments that there are at least 107 likely arrangements for 42 POSs in a rhombohedral cell, without even considering the other unknown POSs. Traditionally, the simple “hand picking” strategy was utilized for searching for stable configurations of β-B based on the experimental XRD data.12,13 In 2009, an Ising model together with Monte Carlo sampling revealed that there were many energy-nearly-degenerate configurations for β-B.3,14,15 However, the Ising model fits the energetics of β-B minima structures containing the known dominant POSs. Therefore, the Ising model cannot go further to predict new structures with unknown POSs and importantly, cannot be used for geometry relaxation and global sampling. As an important consequence, current knowledge of the detailed occupancy of all possible POSs in β-B is still far from satisfactory. How to search the complete configurational space of β-B by taking into account all likely geometry relaxation remains a great challenge and thus requires highly efficient PES exploration techniques.
m), as shown in Fig. 1a. Recent work suggested that the stability of β-B might be related to the existence of numerous partially occupied sites (POSs). These POSs are located in or near the vacant spaces surrounded by B12 and B28 cages, and it is known from experiments that there are at least 107 likely arrangements for 42 POSs in a rhombohedral cell, without even considering the other unknown POSs. Traditionally, the simple “hand picking” strategy was utilized for searching for stable configurations of β-B based on the experimental XRD data.12,13 In 2009, an Ising model together with Monte Carlo sampling revealed that there were many energy-nearly-degenerate configurations for β-B.3,14,15 However, the Ising model fits the energetics of β-B minima structures containing the known dominant POSs. Therefore, the Ising model cannot go further to predict new structures with unknown POSs and importantly, cannot be used for geometry relaxation and global sampling. As an important consequence, current knowledge of the detailed occupancy of all possible POSs in β-B is still far from satisfactory. How to search the complete configurational space of β-B by taking into account all likely geometry relaxation remains a great challenge and thus requires highly efficient PES exploration techniques.
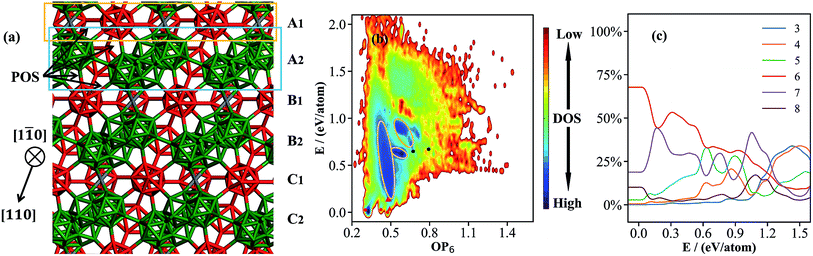 | ||
| Fig. 1 (a) Atomic structure of the basic framework of β-B, β-B105 (105 B atoms per rhombohedral lattice), highlighting the close packing of B12 cages (red) and B28 cages (green), and the connecting B15 sites (grey, detailed in Section 3). The cubic close packing pattern of β-B105 (A1A2B1B2C1C2A1A2…) together with the locations of possible partially occupied sites (POSs); (b) the OP6–E contour map of the global dataset from first principles. OP6 is the distance-weighted Steinhardt order parameter in eqn (1) with L = 6, and the density of states (DOS) is indicated by color. The energy of α-B is set as zero. The red dots represent α-B, β-B105 and γ-B, the red triangles represent #66 and honeycomb structures, and the black dots represent B40-ball and B40-flat. Their coordinates (E, OP6) in the map are as follows: α-B: (0.00, 0.48); β-B105: (0.03, 0.30); γ-B: (0.03, 0.42); #66: (0.04, 0.49); H-2: (0.14, 0.48); H-1: (0.14, 0.49); B40-ball: (0.65, 0.67); B40-flat: (0.67, 0.79); (c) the percentages of differently coordinated B for structures in the global dataset. | ||
The fast development of NN methods in recent years gives hope for the understanding of complex PES problems. The current NN methods generally involve the convolution of the 3-D atomic structure into numerical structure descriptors as input, and the subsequent learning against a big dataset, i.e. training the network parameters, for property prediction. Being the link between molecular/material structures and their properties, the structural descriptor plays key roles in the application type and predictive power of the NN. Apart from the straightforward Cartesian coordinates, many structural descriptors were proposed recently, e.g. extended-connectivity fingerprint,16 Coulomb matrix,17–19 graph convolution,20,21 SMILES strings22,23 and symmetry functions.24,25 For example, graph convolution has been utilized to encode organic molecules for reaction prediction and drug toxicity prediction.20,21 Based on the idea of local internal coordinates, e.g. bond distances and bond angles, to construct a classical force field, Behler and Parinello proposed a high dimensional neural network (HDNN) approach for describing the PES of complex materials, where the atomic distances and angles are assembled to form atom-centered structural descriptors (also known as symmetry functions).24,25 In this approach, the total energy of the system is decomposed into the sum of individual atomic energies that can be obtained by NN training. We recently proposed a global-to-global scheme to generate a NN potential for describing the global PES of a material, which opens the possibility of material discovery from large-scale global PES scanning.26
Here we aim to shed light on the global PES of boron by developing and applying machine learning methods. For this purpose, a large first principles calculation dataset is first constructed by using stochastic surface walking (SSW) global optimization27,28 to explore the global PES of boron. By developing new power-type structural descriptors, training the NN global potential and performing SSW global optimization on the boron NN potential, we are finally able to resolve the long-standing puzzles of the atomic structure of β-B. We reveal the general rules governing the stability of β-B configurations and resolve the physical origin of the strong temperature-dependence of the β-B structure, which has profound implications on the properties of boron.
This paper is organized as follows. In Section 2, we describe the boron global PES dataset generated by SSW PES exploration using first principles calculations, and develop a series of power-type structural descriptors for training such a complex dataset to obtain an accurate and transferable NN potential. In Section 3, we explore the PES of β-B using a SSW global search with NN potential, present all the low energy configurations of β-B and determine the occupancy rate for the interstitial sites, which is compared with experimental data in detail.
2. Construction of boron global NN PES
a First principles dataset for boron global PES
A dataset for boron based on quantum mechanics calculations lays the foundation for machine learning of the boron PES. To reach high predictive power and transferability, this dataset needs to include as many different boron allotropes as possible, including solids and clusters. It therefore requires efficient PES sampling techniques,29–31e.g. the SSW global optimization method27,28 utilized here, which can combine with quantum mechanics calculations to explore the PES. The SSW method has been applied for both structures and pathway searches of many complex systems, ranging from clusters (e.g. B40,32 carbon fullerene33), to surfaces,34 to solids (e.g. TiO2,35 ZrO2 (ref. 36)). Because the SSW simulation produces continuous trajectories when exploring the PES, it is an ideal tool to quickly generate a dataset with a variety of structural patterns, containing both minima and saddle points on the PES. More details on the SSW method and its recent combination with a HDNN for material discovery can be found in our previous work,26 and also briefly in the ESI.†In this work, the global dataset for boron is established via an iterative approach to incorporate as many boron bonding environments as possible. The first stage, being the most important and time-consuming step, was carried out using first-principles SSW global optimization in different systems with fewer than 40 atoms. Subsequently, a sample of structures from the first stage was taken as the training dataset for building a NN potential, which was then utilized to speed up the global optimization in large systems (up to 107 atoms). The HDNN architecture was utilized for the NN potential, and the network was trained by simultaneously matching the energy, force and stress (see ESI† and our previous work26 for details). It should be mentioned that the NN potential trained for the purpose of expanding the global dataset does not need to be accurate and hence the structure descriptors and the network size utilized at this stage are generally small (these are discussed in depth in the ESI†).
To be more specific, the first stage of sampling involves up to 100 SSW simulations, each starting from a different initial structure, namely bulk, cluster and layer structures with different numbers of atoms (12, 14, 28, 40 per cell). These initial structures include the known solid allotropes (e.g. α-,2 γ-B37), the reported B40 minima32 and randomly configured structures. All first-principles calculations were carried out using the plane-wave DFT code VASP38 with the GGA-PBE functional,39 and the details of the calculation setups are described in the ESI.†
Finally, we obtained a global dataset with 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 structures in total, containing 109
423 structures in total, containing 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 bulk, 4649 layer, and 50
881 bulk, 4649 layer, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 cluster structures with different numbers of atoms, as detailed in Table S1.† In the dataset, the number of atoms per cell is usually 12 or 14, each with around 40
893 cluster structures with different numbers of atoms, as detailed in Table S1.† In the dataset, the number of atoms per cell is usually 12 or 14, each with around 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures. These small systems prevail in the dataset because they can represent major atomic environments and are computationally more efficient for both first-principles calculations and subsequent NN training. To provide an overview of this dataset, we constructed an energy versus geometry contour plot, as shown in Fig. 1b. The x-axis in Fig. 1b is the distance-weighted Steinhardt-type order parameter40 (OP) defined by eqn (1) with the degree L = 6, as also utilized previously to distinguish the short–medium range ordering of solid structures.
000 structures. These small systems prevail in the dataset because they can represent major atomic environments and are computationally more efficient for both first-principles calculations and subsequent NN training. To provide an overview of this dataset, we constructed an energy versus geometry contour plot, as shown in Fig. 1b. The x-axis in Fig. 1b is the distance-weighted Steinhardt-type order parameter40 (OP) defined by eqn (1) with the degree L = 6, as also utilized previously to distinguish the short–medium range ordering of solid structures.
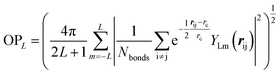 | (1) |
In eqn (1), YLm is the spherical harmonic function, i and j are atoms in the lattice, rij is the vector between atoms i and j, rij is the distance between them, rc is set as 60% of the typical single bond length between i and j atoms (1.7 Å here for boron–boron single bonds), and Nbonds is the number of bonds in the first bonding shell (2.05 Å). The y-axis is the energy per atom (eV per atom), where zero energy is set as the energy of α-B hereafter, since its crystal structure is well defined.
Fig. 1b shows that at the bottom of the PES there are three major funnels belonging to three stable crystal phases: from left to right, they are β-B105, γ-, and α-B (red dots in the figure) with OP6 values of 0.30, 0.42 and 0.48, respectively. Many new boron crystal forms that are not reported in the literature can also be identified in these regions. For example, a high symmetry structure (Cccm, #66, red triangle) shares the same icosahedral packing skeleton as α-B but with 4 extra doping atoms at the interstitial sites per 52-atom unit cell. The honeycomb structures (H-1 and H-2, red triangles) are also typical in less stable B crystal forms,41 and form by packing two-dimensional boron sheets with different connections between neighboring layers (also see ESI† for these crystals). Above 0.15 eV per atom, there are dark blue zones with high density of states (circled by yellow lines), which correspond to amorphous solids and cluster structures. The lowest energy B40 cluster (black dots) in the dataset is the B40 fullerene (OP6 = 0.67 in Fig. 1b), which is 0.65 eV per atom less stable than α-B.
It is of general interest to analyze the geometrical environment of boron in the global dataset. For this purpose, we have computed the B coordination number for all structures in the global set. The B–B distance of 2.05 Å is set as the criterion for B coordination, which takes into account the first nearest bonding neighboring atoms as indicated from the pair distribution function (see ESI†). In Fig. 1c, we plot the evolution of the B coordination number with increasing energy (x-axis). The y-axis is the percentage of different coordination numbers, which is calculated by counting and averaging the B coordination numbers for structures in the same energy interval, E to E + dE (dE = 1 meV per atom). As shown, six and seven are the major coordination environments for the low energy crystal phases. Five coordination becomes popular in the amorphous solid region (0.15–0.6 eV per atom), and three and four coordination are the dominant coordination patterns only in the very high energy region (>1.0 eV per atom).
Fig. 1b and c demonstrate clearly that the bonding patterns of boron in the global dataset are highly complex, with coordination numbers ranging from 2 to 8 with few similarities to common polyhedral bonding. This feature must be attributed to the unique electronic structure of the B atom, which, to reach octet saturation, often adopts multi-center delocalized bonding.2 This results in an extremely complex atomic environment for boron and thus leads to a great challenge in constructing either empirical or NN potentials for boron-containing materials.
b Structural descriptors with power radial function
Because the structure descriptor is the key to correlating a structure with its energetics in a HDNN, one would expect that a qualified structural descriptor needs to be sensitive enough to distinguish as many structures as possible on the PES. For the boron global dataset, which has great structural diversity, it is thus more difficult to identify the appropriate structural descriptors.Let’s first recall the structural descriptors originally proposed by Behler and Parrinello:24,25 the most used two-body G2 and three-body G4 functions are described in eqn (2)–(4):
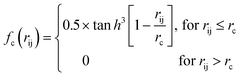 | (2) |
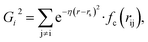 | (3) |
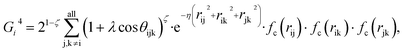 | (4) |
In fact, we initially tested the BTSDs for constructing the boron NN PES using the global dataset. However, it was unable to achieve a high accuracy (the root mean square (RMS) for energy was larger than 30 meV per atom). This implies that the global PES of boron, despite containing only a single element, is much too complex to describe using the BTSDs alone.
To solve this problem, we have designed a series of new structural descriptors, S1 to S6 (eqn (5)–(11)). Inspired by the Laguerre polynomials for atomic orbitals, all these structural descriptors utilize the power function as the radial function. We therefore named them power-type structural descriptors (PTSDs) to distinguish them from the BTSDs.
| Rn(rij) = rijn·fc(rij), | (5) |
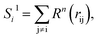 | (6) |
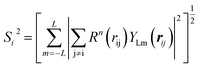 | (7) |
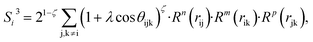 | (8) |
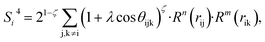 | (9) |
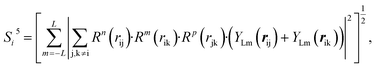 | (10) |
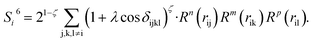 | (11) |
In the PTSDs, S1 and S2 are two-body functions, S3, S4 and S5 are three-body functions, and S6 is a four-body function. S1 and S3 mimic G2 and G4, respectively, except for the change in the radial function. S2 and S5 have a common component, i.e. the spherical function, as seen in the Steinhardt-type order parameter (eqn (1)), which has been found to be sensitive for distinguishing the local coordination of an atom.40,42S6 is a four-body term, designed to describe the torsion angle. The torsion angle δijkl in eqn (11) is the dihedral angle centered at the I and j atoms, with k and l being the neighboring atoms. In total, there are seven adjustable parameters, n, m, p, L, rc, ζ and λ in the PTSDs.
The replacement of the Gaussian function in the BTSDs by the power function in the PTSDs has several advantages: (i) the computational cost of the numerical calculations is reduced; (ii) the adjustable parameters are reduced from two (rs, η) to one (n) which simplifies the search for the optimal parameters for the two-body functions; (iii) the power function when combined with the decaying cutoff function can create radial distributions with flexible peak and shape, which fulfills the similar purpose of the Gaussian function; (iv) the introduction of different powers (n, m, p) in the three-body functions can conveniently couple different radial distributions. To illustrate point (iii), we plot in Fig. 2 the evolution of Rnversus rij for different n and the same cutoff radius rc = 3.2 Å. As shown, the peak of the Rn function shifts to larger rij and becomes narrower with increasing n. This enables us to portray the neighboring atoms within any circular shell by adjusting rc and n.
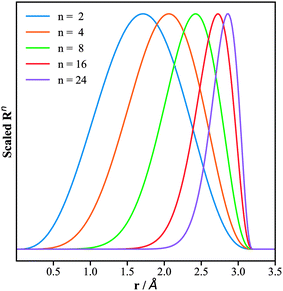 | ||
| Fig. 2 Plots of the radial part of the PTSDs, eqn (5), for the same cutoff radius of 3.2 Å but different power n. The x-axis is the distance r, while the y-axis is the function value scaled to (0, 1). | ||
Overall, the new PTSDs incorporate flexible radial functions, spherical functions and up to four-body functions. To assess the structure discrimination ability of the different types of structural descriptors (detailed in ESI†), we have performed principle component analysis (PCA) as detailed in the ESI,† which demonstrates that the new PTSDs outperform the BTSDs in describing the structures in the boron global dataset. In particular, it outlines the importance of the S2, S4 and S5 descriptors, which rank top out of the two-body and three-body functions. Apparently, the incorporation of the spherical harmonic function in the S2 and S5 PTSDs enhances substantially the structure discrimination ability.
c Boron NN potential
We are now ready to produce the boron NN potential using the global dataset. To achieve a high accuracy which is desirable for differentiating the energy-degenerate configuration isomers of β-B, we have adopted a large set of structural descriptors, which contains 173 PTSDs, i.e. 39 S1, 36 S2, 16 S3, 52 S4, 18 S5 and 12 S6, and compatibly, the network utilized is also large, involving two hidden layers each with 110 neurons, equivalent to 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461 network parameters in total. Our theoretical procedure to set up the structural descriptors and network size is discussed in detail in the ESI,† where we verify that the current structure descriptor set is complete and that the network size is the optimum to achieve a highly accurate NN potential. After training the network on the global dataset, we obtain the first boron global NN PES with RMS values for energy, force and stress of 12.4 meV per atom, 0.28 eV Å−1, and 3.00 GPa, respectively. The overall accuracy is quite standard for a global NN PES considering that the energies of the structures in the dataset span a large window from 0 to 4 eV per atom.
461 network parameters in total. Our theoretical procedure to set up the structural descriptors and network size is discussed in detail in the ESI,† where we verify that the current structure descriptor set is complete and that the network size is the optimum to achieve a highly accurate NN potential. After training the network on the global dataset, we obtain the first boron global NN PES with RMS values for energy, force and stress of 12.4 meV per atom, 0.28 eV Å−1, and 3.00 GPa, respectively. The overall accuracy is quite standard for a global NN PES considering that the energies of the structures in the dataset span a large window from 0 to 4 eV per atom.
We have examined the accuracy of the NN PES for the representative crystal/cluster boron structures and benchmarked it against DFT calculations, as listed in Table 1. These structures were fully optimized using the NN until the maximal force component was below 0.01 eV Å−1 and the stress was below 0.01 GPa, and then refined using DFT for comparison. As shown, the energy RMS error is 2.73 meV per atom for these typical low energy minima, while the volume RMS error is ∼0.45%. This accuracy is sufficient for a global structure and pathway search to identify the low energy candidates.
| Name | Z | E DFT | ΔE‡ | V DFT | ΔVc |
|---|---|---|---|---|---|
| a Crystal structures identified from global PES. b Z: number of atoms per unit cell. c ΔE = EDFT − ENN and ΔV is the percentage volume deviation between the NN and DFT. | |||||
| Important crystal structures | |||||
| α-B | 12 | 0 | 2.77 | 7.25 | 0.66 |
| β-B105 | 105 | 25.29 | 2.45 | 7.78 | 0.28 |
| γ-B | 28 | 27.31 | 0.88 | 6.99 | −0.88 |
| #66a | 52 | 39.52 | 2.74 | 7.62 | −0.02 |
| H-1a | 12 | 136.83 | −4.67 | 6.88 | 0.34 |
| H-2a | 19 | 143.01 | 4.25 | 6.88 | −0.47 |
| B40-ball | 40 | 649.40 | 0.29 | — | — |
| B40-flat | 40 | 671.33 | −3.74 | — | — |
| RMS | — | — | 2.73 | — | 0.45 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Structures of β-B | |||||
| β-II-1 | 107 | −0.75 | 0.81 | 7.64 | 0.03 |
| β-II-2 | 107 | −0.69 | 0.58 | 7.65 | −0.06 |
| β-II-3 | 107 | −0.09 | −0.93 | 7.65 | −0.08 |
| β-II-4 | 107 | 0.07 | −0.47 | 7.65 | −0.09 |
| β-II-5 | 107 | 1.18 | 1.37 | 7.65 | 0.19 |
| β-I-6 | 106 | 1.30 | 2.67 | 7.71 | −0.1 |
| β-I-7 | 106 | 1.42 | 2.86 | 7.72 | −0.24 |
| β-II-8 | 107 | 1.53 | 0.66 | 7.65 | 0.29 |
| β-II-9 | 107 | 1.71 | 0.79 | 7.65 | 0.3 |
| β-I-10 | 106 | 1.92 | 2.01 | 7.72 | −0.28 |
| β-II-11 | 107 | 2.51 | 0.41 | 7.65 | 0.05 |
| β-II-12 | 107 | 2.68 | 0.51 | 7.65 | 0.07 |
| β-II-13 | 107 | 2.89 | −1.87 | 7.65 | −0.04 |
| β-II-14 | 107 | 3.4 | −1.43 | 7.65 | −0.05 |
| β-I-15 | 106 | 4.03 | 0.85 | 7.72 | −0.13 |
| RMS | — | — | 1.44 | — | 0.17 |
3. Structure of β-B
a β-B PES from the SSW-NN
β-B was long believed to have numerous structural configurations as a “frustrated system”, similar to ice.14 Due to the electron deficiency of B12 icosahedra and the intrinsic instability of B28 triple-fused icosahedra,43 the crystal is self-doped with the doping atoms appearing in many likely interstitial sites in the lattice. These sites, commonly known as partially occupied sites (POSs), are only partly distinguishable from XRD experiments: the reported occupancy of the dominant POSs varies from experiment to experiment, and about 3% of POSs are even unassigned since their geometric positions are unknown.44 Unlike previous work14,15 that utilized the Ising model to establish the static interaction between the known POSs, we are now able to utilize the NN potential to explore all the likely structures on the boron global PES, where both the atom and the lattice can be fully optimized.Starting from the known β-B rhombohedral lattice, a SSW global optimization was utilized to explore all the possible low energy structures of β-B. More than 20 SSW runs were carried out independently, with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 minima to visit in each run. The structures contained either 105, 106 or 107 atoms per cell, since these are known as the most stable structures in the literature. By removing duplicated minima, we finally obtained 15
000 minima to visit in each run. The structures contained either 105, 106 or 107 atoms per cell, since these are known as the most stable structures in the literature. By removing duplicated minima, we finally obtained 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 distinct minima for β-B, and the OP6–energy PES contour plot for these minima is plotted in Fig. 3. The representative atomic structures of β-B are shown in Fig. 4.
293 distinct minima for β-B, and the OP6–energy PES contour plot for these minima is plotted in Fig. 3. The representative atomic structures of β-B are shown in Fig. 4.
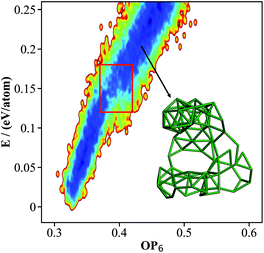 | ||
| Fig. 3 The contour map (E against OP6, also see Fig. 1 caption for explanation) for the β-B minima from the SSW global optimization using the boron NN PES. The red box indicates the boundary above which the B28 cages start to melt. The inset shows a typical structure with broken B28 cages. | ||
It should be emphasized that the SSW sampling of large systems (>100 atoms) is extremely computationally demanding using first principles calculations. We estimated that the NN calculations are at least 3 × 103 times faster than DFT calculations,26 and thus the SSW-NN allows more than 2 × 105 minima of β-B to be visited in a short time.
As shown in Fig. 3, there are two high density of states regions (deep blue zones) in the β-B PES, which are separated by a gap at ∼0.15 eV per atom (red box). We found that all structures below the gap have intact B12 (red units in Fig. 4a) and B28 cages (dark green units in Fig. 4a) as the skeleton, the same as the known β-B, and that these cages start to melt (crack) for high energy structures above the gap (a typical melting B28 cage is shown in the insert of Fig. 3).
To determine an accurate energy sequence for the β-B isomers, we selected the 366 most stable minima (25 meV per atom above the most stable minimum) predicted by the NN PES and refined them using DFT. The energy root mean square error (RMSE) between the NN and DFT for these minima is 3.85 meV per atom, suggesting that these selected minima from the NN PES should cover the most stable minima of β-B. Table 1 provides a comparison between DFT and the NN for the 15 most stable structures, based on energy and volume. Clearly, for these most stable structures, the RMSEs in energy and volume for the NN prediction are rather low, being 1.44 meV per atom and 0.17%, respectively. We emphasize that all results below are referenced to the DFT calculations for the high accuracy setups (see ESI†).
Structural patterns
Now we are in a position to inspect closely the atomic structures of the most stable β-B isomers. From our results, there are three different skeletons for β-B, namely SK-I, SK-II and SK-III, differing in the connecting blocks between neighboring B28 cages. SK-I and SK-II were known previously,3 and SK-III was newly found in this work. They are elaborated as follows.(i) SK-I. The SK-I structure (Fig. 4b) features five B13 (orange balls) and one B15 (grey ball) in the connecting unit. The five B13 are all apex atoms of two B28 units, which are connected by the five-coordinated B15. Since there is one missing apex site in one B28 unit, there are two least-coordinated B3 (brown balls) that are only four-coordinated to the skeleton.
(ii) SK-II. The SK-II structure (Fig. 4c) features four B13, one B15, one B17 (purple ball) and one B18 (magenta ball) in the connecting unit. B17 and B18 can be considered as the relocation of two B13 into the vacant region between two B28 cages. B17 is four-coordinated to B15, B18 and one B28 cage, while B18 links to B17, one B28 cage and also the neighboring two B12 cages. Obviously, only one least-coordinated B3 is present (brown ball) in SK-II.
(iii) SK-III. The SK-III structure (Fig. 4d) is similar to SK-I but with one B13 missing. Thus, only four B13 are left in SK-III. The connecting B15 has a planar four-coordination with the four B13.
In these skeletons, every four neighboring cages, either B12 or B28, form a tetrahedral void, which provides four possible doping sites in the hexagonal ring of the tetrahedral faces. B16, B19 and B20 are such doping sites, dominant in the most stable β-B structures and accounting for ∼30% of doping sites according to experiments (the other 70% are accounted for by the skeleton POSs B13, B17 and B18). B16 (light green balls) is the most frequently encountered, and resides in the ring connecting three B12 units. B19 (yellow ball in Fig. 4e) and B20 (light purple ball) are in the rings connecting two B12 units and one B28 unit. They link to B28 differently, via two B3 (blue balls) for B19, but via one B3 and one B8 (turquoise balls) for B20. By taking B13, B17 and B18 into account, there are 42 total POSs (six for B13, B16, B17, B18 and B19, and twelve for the B20 sites) in one rhombohedral unit cell and thus at least 107 possible configurations.
Interestingly, other unknown doping sites were also revealed by our global search. Two such sites, namely B21 and B22, are illustrated in Fig. 4f and g and are described as follows. B21 (light purple ball in Fig. 4f) is located in the ring connecting two B12 units and one B28 unit via one B8 and one B10 (green balls). B22 is located inside the tetrahedron surrounded by four B12 units, which can be occupied by a pair of atoms (light purple balls in Fig. 4g).
Energy spectrum
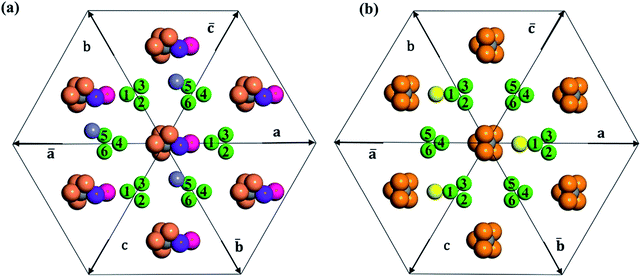
In Table 2, we list the key structural information for the important β-B isomers. From DFT, SK-II is the most stable skeleton, being present in the five most stable structures. The most stable β-B is β-II-1, which has two doping atoms in the B16 sites per rhombohedral cell. Hereafter the notation (β-II-1) follows this rule: the Roman number (II) represents the skeleton (SK-II) and the Arabic number (1) indicates the energy ranking. This global minimum (GM) from our SSW search is in accordance with the most stable structure reported in ref. 13. The second to the fourth most stable structures, i.e. β-II-2 to β-II-4 (<1 meV per atom), are structurally similar to the GM with the major difference being the B16 position. Due to symmetry breaking in SK-II, there are six distinct B16 sites, as shown in Fig. 5a, numbered from 1 to 6. In the figure, a, b, and c represent the three lattice axes in the close packing (111) plane in the rhombohedral lattice.12 Restricted by the three-fold symmetry, the three sites (a1, b1, c1) are equivalent, and so are (a2, b2, c2) and (a3, b3, c3). These four degenerate GM structures have the following B16 arrangements: β-II-1: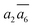 ; β-II-2:
; β-II-2: 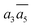 ; β-II-3:
; β-II-3: 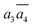 , β-II-4:
, β-II-4: 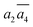 .
.
| Name | E DFT | B13 | B16 | B17 | B18 | B19 | B20 | B21 | B22 | Pattern | C% | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 1500 | 2000 | |||||||||||
| β-II-1 | −0.75 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 18.2 | 8.0 | 4.2 |
| β-II-2 | −0.69 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 17.1 | 7.7 | 4.1 |
| β-II-3 | −0.09 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 8.1 | 4.7 | 2.8 |
| β-II-4 | 0.07 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 6.6 | 4.1 | 2.5 |
| β-II-5 | 1.18 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 11.0 | 9.8 | 7.4 |
| β-I-6 | 1.29 | 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | P3 | 4.6 | 4.5 | 3.5 |
| β-I-7 | 1.42 | 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | P3 | 3.9 | 4.0 | 3.2 |
| β-II-8 | 1.53 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 7.1 | 7.3 | 5.9 |
| β-II-9 | 1.71 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 5.8 | 6.4 | 5.3 |
| β-I-10 | 1.92 | 5 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | P3 | 2.1 | 2.7 | 2.4 |
| β-II-11 | 2.51 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 2.1 | 3.3 | 3.2 |
| β-II-12 | 2.68 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 1.7 | 2.9 | 2.9 |
| β-II-13 | 2.89 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 0.2 | 0.4 | 0.4 |
| β-II-14 | 3.4 | 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | P1 | 0.1 | 0.3 | 0.3 |
| β-I-15 | 4.03 | 5 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | P4 | 7.6 | 18.3 | 23.2 |
| β-II-17 | 4.32 | 4 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | P5 | 0.2 | 0.8 | 1.1 |
| β-III-18 | 4.42 | 4 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | P5 | 0.1 | 0.3 | 0.5 |
| β-I-21 | 4.65 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | P5 | 0.0 | 0.1 | 0.2 |
| β-II-26 | 4.93 | 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | P6 | 0.0 | 0.1 | 0.1 |
| β-II-27 | 4.98 | 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | P2 | 0.1 | 0.4 | 0.7 |
| β-I-29 | 5.15 | 5 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | P4 | 1.9 | 7.3 | 11.7 |
| β-I-34 | 5.64 | 5 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | P6 | 0.0 | 0.1 | 0.2 |
It is interesting to further understand why only four energy-nearly-degenerate isomers are present out of C26= 30 possible configurations. This is due to the fact that the following three scenarios are energetically not favored, i.e. exclusion rules: (i) two atoms in one tetrahedral void. The structural configurations with two atoms (i.e. B22 site, β-II-22) are at least 5.4 meV per atom less stable than the GM; (ii) the filling of the a1 site in SK-II. This is due to the too short contact with the nearby B18 site. (Fig. 5a); and (iii) two occupied B16 in the same close packing plane, such as 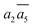 . The structure with the
. The structure with the 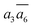 B16 arrangement, β-II-13, is 3.64 meV per atom above the GM. The poorer stability is obviously due to the large strain induced by the two neighboring doping B16 atoms in the same close packing plane.
B16 arrangement, β-II-13, is 3.64 meV per atom above the GM. The poorer stability is obviously due to the large strain induced by the two neighboring doping B16 atoms in the same close packing plane.
The fifth most stable structure, β-II-5, contains one B16 and one B20, and is 1.93 meV per atom above the GM. It also has two energy-nearly-degenerate isomers, β-II-8 and β-II-9. They share the same B20 site, which is 4.29 Å away from B17 as shown in Fig. 5a. This B20 site is coordinated to the least-coordinated B3 in the B28 cage. The B16 sites for these three structures are: (i) 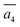 ; (ii) a2; (iii) a3. The other possibilities, a1,
; (ii) a2; (iii) a3. The other possibilities, a1, 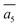 and
and 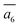 , are not favored due to the same exclusion rules as mentioned above for the four GM isomers.
, are not favored due to the same exclusion rules as mentioned above for the four GM isomers.
SK-I appears in the sixth most stable structure, β-I-6, which contains two B16 sites (the same as reported in ref. 12). It has only two energy-nearly-degenerate structures, β-I-7 and β-I-10, apparently because only four distinct B16 sites are present in SK-I and the same exclusion rules must be obeyed. Their B16 arrangements are as follows: β-I-6: 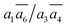 ; β-I-7:
; β-I-7: 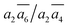 ; β-I-10:
; β-I-10: 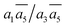 . Next, the 11th to 14th most stable structures contain either B16 or B20 doping atoms in the less favored configurations.
. Next, the 11th to 14th most stable structures contain either B16 or B20 doping atoms in the less favored configurations.
Importantly, the B19 site only starts to be occupied in β-I-15, which is 4.78 meV per atom above the GM. This B19 site, being 3.8 Å away from B15, is connected to two least-coordinated B3 and thus can be considered as a relocation of B18 by shifting only 0.83 Å towards the nearby B12 unit. The second stable structure with B19 is β-I-29, which is another 1.12 meV per atom above β-I-15. They contain the same B19 site, but with different B16 positions as shown in Fig. 5b: (i) 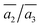 ; (ii)
; (ii) 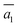 .
.
Overall, these low energy structures (top 40 structures, <7 meV per atom above the GM) can be summarized as six major patterns ordered by energy sequence:
P1: SK-II with 2 B16;
P2: SK-II with a B16 and a B20;
P3: SK-I with 2 B16;
P4: SK-I with a B16 and a B19;
P5: structures with B21/B22 doping sites or SK-III;
P6: SK-II with a B16 and a B19 or SK-I with a B16 and a B20.
With all these minima, most of them discovered for the first time, it is possible for us to assess current knowledge of the structure of β-B, which has been found to be either misleading or even incorrect.
(i) Only 91 structures are within 10 meV per atom and 40 are within 7 meV per atom above the GM, which is remarkably smaller than the >107 possible configurations from different arrangements of dominant POSs. Apparently, the energy degeneracy is much lower than expected. This is because (i) the exclusion rules are critical for pinning the position of B16; (ii) the filling of B19 strongly prefers only one position, i.e. that in β-I-15; (iii) the filling of B20 prefers five positions out of 12 possibilities in the top 40 structures. Ogitsu14et al. stated that the filling of B20 must occur simultaneously with a vacant B13, which is indeed true for the most preferable B20 position (β-II-5). But, we also found that the filling of B20 near an occupied B13 site (β-II-11) is only 1.33 meV per atom less stable than β-II-5.
(ii) The filling of a particular B20 site can be energetically rather stable, which rationalizes the experimental observation of B20 filling. From our results, occupation at the B20 site (β-II-5) is slightly more preferable than that at the B19 site (β-II-26). Apparently, occupation at the B20 site preferentially occurs in SK-II, while occupation at the B19 site preferentially occurs in SK-I. This corrects the view of Setten12et al., who suggested that the filling of an arbitrary B19 is more stable than the filling of a B20. Moreover, we found that the simultaneous filling of one B19 and one B20 in one rhombohedral cell can also be stable. For example, β-III-18 (Fig. 4h) contains three doping atoms at B16, B19 and B20 sites, which is only 5.17 meV per atom above the GM.
(iii) Unknown POSs are present and have low energies. This information was not available previously, but it is important for understanding the residual boron observed in experiments.44 The main newly identified POSs from our results are B21 and B22, occurring in β-II-17 (5.07 meV per atom above the GM, containing a B16 and a B21) and β-I-21 (5.4 meV per atom above the GM, containing a B–B pair in B22 sites).
b POS occupancy rates at different temperatures
With all these low energy minima, it is now possible to derive from theory the occupancy rates for POSs at different temperatures, which can be compared with the fitted data from XRD experiments. The data available from experiment,44i.e. the three examples MG57, MG179 and EP, as listed in Table 3, exhibit a variation in POS occupancy rate of up to 6.5%. Since the MG57 and MG179 samples were cooled from the melt at rates of ∼350 and 2.2 °C min−1, respectively, the variation in the data suggests that the occupancy rates of the POSs are sensitive to the sample preparation conditions, especially temperature. This suggests that one must take into account the free energy contribution in order to properly address the structure of β-B.| B13 | B16 | B17 | B18 | B19 | B20 | Resb | |
|---|---|---|---|---|---|---|---|
| a Experimental data from ref. 44. b Residual atoms with unknown location. | |||||||
| NN-1000 | 68.3 | 29.4 | 15.0 | 15.0 | 1.5 | 1.2 | 0.5 |
| NN-1500 | 71.8 | 23.3 | 11.6 | 11.5 | 4.6 | 2.3 | 2.0 |
| NN-2000 | 74.1 | 20.2 | 9.1 | 9.1 | 6.8 | 2.4 | 3.2 |
| DFT-1000 | 70.1 | 26.8 | 13.2 | 13.2 | 1.6 | 2.4 | 0.6 |
| DFT-1500 | 73.2 | 22.8 | 10.1 | 10.1 | 4.6 | 2.8 | 2.3 |
| DFT-2000 | 75.0 | 20.7 | 8.1 | 8.1 | 6.7 | 2.7 | 3.7 |
| MG179a | 73.0 | 28.4 | 9.7 | 7.4 | 7.0 | 2.5 | 3.2 |
| EPa | 74.5 | 27.2 | 8.5 | 6.6 | 6.8 | 3.2 | 2.1 |
| MG57a | 77.7 | 25.8 | 3.2 | 5.8 | 7.2 | 0 | 3.9 |
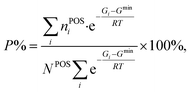
From theory, we can derive the occupancy rates of the POSs using eqn (12) and (13), assuming thermodynamic equilibrium at a given temperature T:
 | (12) |
| Gi = Ei + ZPEi − TSi. | (13) |
At a given temperature T, the free energy Gi for the i-th configuration is first determined by correcting the zero-point energy (ZPE) and vibrational entropy (S). These thermodynamic properties are calculated from the full phonon dispersion by using the numerical finite difference approach to diagonalize the Hessian matrix (more details in the ESI†). The one with the lowest free energy Gmin is then identified, and is utilized to establish the partition function and calculate the occupancy rate P. In the equation, NPOS is the total number of POSs (six for B13, B16, B17, B18, and B19; twelve for B20), and nPOSi is the number of occupied POSs in the structure.
In Table 3, we listed the calculated POS occupancies at three typical temperatures, 1000, 1500 and 2000 K, and compared them with the experimental data. It can be seen that the data predicted by the NN agrees well with that from DFT (within 3% deviation), and the theoretical occupancies are also consistent with the experimental observations, with the deviation generally within 5%. In particular, our results interestingly show that with an increase in temperature, the occupancy of B13 increases, while that of B16, B17 and B18 decreases monotonically. This temperature dependence of the POS occupation concurs with the variation of the data from three different experimental samples. Table 2 also lists the detailed POS contributions for selected important structures at different temperatures. These results are elaborated as follows.
In general, the B13 occupancy is around 75%, which is obviously an average value from the B13 occupancy in the two dominant skeletons, 83% in SK-I and 68% in SK-II. In addition, B17 and B18 have 17% occupancy in SK-II and zero occupancy in SK-I, which suggests that the occupancies of B17 and B18 are equivalent and around 8% on average. As for the B16 sites, one or two sites per rhombohedral cell are filled in the low energy structures (P1 to P4), resulting in a B16 occupancy of around 25%. On the other hand, the filling of B19 and B20 sites generally occurs in combination with the filling of B16 sites, suggesting that their occupancies are below 8%.
Taking the POS occupancy rates at 1500 K as an example, there are 73.2% B13, 22.8% B16, 10.1% B17 and B18, 4.6% B19 and 2.8% B20. At this high temperature, the top 20 structures with the lowest free energy, all belonging to P1 to P5, have obvious contributions (95.4%) to the overall POS occupancy rates. The most important configuration is β-I-15 (P4), which contributes 18.3% to the final occupancy. The structure with the lowest contribution among them, β-II-27 (P2), still contributes more than 0.4%. For the rest of the structures in the top 100 structures, their total contribution reaches up to ∼4.5%, and the top 100 to 300 structures only have very low contributions of <0.1%. Therefore, numerical convergence of the POS occupancies calculated from the boron global PES is achieved with the 100–300 lowest energy structures (see ESI† for details).
To understand the origin of the free energy difference, we plotted the phonon spectra of four structures, i.e., β-II-1, β-II-5, β-I-6 and β-I-15, corresponding to the lowest energy structures for P1 to P4, in Fig. 6a. There are three major peaks at low frequencies (350 cm−1, 580 cm−1 and 680 cm−1). Obviously, compared to the other isomers, β-I-15 shows the highest phonon density of states (DOS) for these three peaks; β-II-5 has a higher phonon DOS for the peaks at 580–700 cm−1 compared to β-II-1 and β-I-6; β-I-6 has a higher phonon DOS for the 350 cm−1 peak compared to β-II-1 and β-II-5.
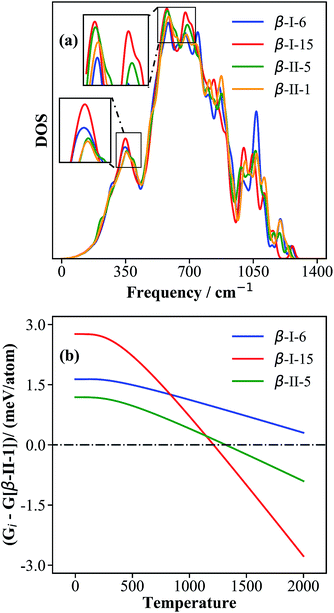 | ||
| Fig. 6 The phonon density of states (a) and the relative free energies (b) for the key configurations, β-I-6, β-I-15, β-II-5 and β-II-1. The relative free energy (Gi in eqn (13)) is with respect to that of β-II-1, G[β-II-1]. | ||
By examining the phonon displacement vectors, we found that the 350 cm−1 peak is mainly due to the vibrational motion of B13 atoms, and that the 580–700 cm−1 peaks correspond to the soft translational/rotational motion of skeleton B12 and B28 cages. The more intense peak of β-I-15 at ∼350 cm−1 can be attributed to the additional B19 vibrations due to the flat PES associated with the B19 atom (also see the next section for electronic structure analyses). For similar reasons, B17 and B18 doping (in β-II-1 and β-II-5) will restrict the motion of B13 atoms and reduce the phonon density at ∼350 cm−1. The more intense peaks of β-I-15 and β-II-5 at 580–700 cm−1 are related to their only singly-occupied B16 sites, the filling of which will hinder the collective motion of the B12 cages (c.f. the two B16 present in β-II-1 and β-I-6).
By plotting the relative free energy (Gi − G[β-II-1]) for β-II-5 (green), β-I-6 (blue), and β-I-15 (red) with respect to β-II-1 (Fig. 6b), one can see that at elevated temperatures, β-I-15 has the lowest free energy, followed by β-II-5 and then β-I-6. Above 1210 K and 1320 K respectively, the free energies of β-I-15 and β-II-5 are lower than that of the GM β-II-1. This provides clear evidence that at temperatures above ∼1200 K, the GM β-II-1 is no longer the thermodynamically favored configuration.
This dramatic free energy contribution, up to 5.5 meV per atom, leads to a change in POS occupancy at 1000 to 2000 K. β-II-1 and β-II-2, belonging to P1, contribute ∼30% of the total POS occupancy at 1000 K, while β-I-15 and β-I-29, belonging to P4, provide a slightly higher contribution (∼34%) at 2000 K. The change in preference from SK-II to SK-I rationalizes the monotonic increase in B13 occupancy, and the decrease in B16, B17 and B18 occupancies, as also observed in experiments.
It is also interesting to note that the B16 occupancy observed experimentally is in general higher than our theoretical results by ∼5%. This is equivalent to ∼1 additional B16 atom per hexagonal lattice (∼320 atoms per cell) in the experimental sample. A possible explanation is that our theoretical results are from bulk calculations and do not consider the surfaces and domain boundaries. Due to the electron deficient nature of surfaces, the filling of an extra B16 would provide additional electrons and thus stabilize the surface. Another difference between theory and experiment lies in the paired nature of B17 and B18: the B17 and B18 occupancies are the same from theory, but different by up to 3% from experiment. This peculiar phenomenon was also noticed previously and attributed to possible errors in the experimental measurements by Slack et al.44 From our work, considering that the filled B19 is only 0.8 Å away from the nearby B18 site in low energy configurations, we suggest that the lower occupancy of B18 from experiment may be correlated with the higher occupancy of B19, due to the incorrect assignment of these two close-lying sites. Assuming that B17 and B18 must have the same occupancy rate, the B18 and B19 occupancies need to be adjusted to 9.7% and 4.7%, respectively for MG179, which then agrees nicely with the theoretical results at 1500 K (B18: 10.1% and B19: 4.6%).
Finally, we note that the occupancy of B20 in all experimental samples is below 3%, which is similar to that of the residual boron atoms (2–4%), whose locations are difficult to assign44 (see Table 3). Indeed, our theoretical prediction for B20 is also below 3%, and the occupancies of the residual boron atoms, now assigned to the B21 and B22 positions, also range from 0–4% at different temperatures.
c Electronic structure of β-B
With the PES of β-B having been clarified, we are now in a position to discuss the electronic structure and bonding of β-B in the context of previous knowledge on boron chemistry. In fact, the instability of perfect (undoped) β-B105 has been addressed in many previous papers,3,43,45–47 and is attributed to the electron deficiency of the B12 cage45,46 and the electron abundance of the perfect B28 cage.43,47 Each doping B atom inside the hexagonal B ring can transfer its three electrons into the neighbouring B12 cage via multi-center bonding, which converts three two-center bonds into three three-center bonds14,48 (our wavefunction analyses of the doping B also confirm this picture, see ESI Fig. S5†). Naturally, this doping atom may directly come from the B13 site of the B28 cage. Both the B13 vacancy and the population of the B17 and B18 sites are beneficial for decreasing the electron abundance of the B28 cage.14,43 Indeed, the low energy minima found in this work are consistent with previous understanding: (i) the doping atom is located either in a hexagonal ring (B16, B19, B20 and B21) or in a void (B22) surrounded by B12 and B28 cages, and generally achieves multi-center bonding with its neighbors; and (ii) all three skeletons (SK-I to SK-III) of β-B contain B13 vacancies: one in SK-I; two in SK-II and SK-III. Thus, the low energy β-B106 structures prefer SK-I, while the low energy β-B107 structures adopt SK-II.Since the B19 and B16 doping sites play key roles in the temperature dependence of POS occupancy, we have further analyzed the electronic differences between them by taking β-I-15 as an example. For β-I-15, our Bader charge analyses show that the net charges of filled B16 and B19 are +0.35 and +0.26, respectively, which demonstrates that a filled B16 near three B12 cages can donate more electrons than a filled B19 near two B12 and one B28 cages. Consistent with this, the center of the B16 2p band occurs at −6.35 eV below the valence band maximum (VBM), while that of the B19 2p band is at −6.02 eV below the VBM (see ESI Fig. S5†). All this information suggests that B16 interacts more strongly with the nearby B12 cages and restricts the soft motion of the cages. This would in turn reduce the phonon density in the low frequency region (500–700 cm−1) and lead to smaller entropy due to the B16 doping. On the other hand, B19 has a flatter PES with weaker bonding to nearby cages, which results in a higher entropy.
4. Conclusions
The ground state structure of boron crystals has long been a fascinating but challenging topic in fundamental science. Here, with newly developed machine learning methods to exhaustively explore the PES of boron with the SSW global optimization method, we are now able to establish the energy spectrum of all low energy configurations within the huge configuration space of β-B, which allows us to resolve in fine detail the β-B atomic structure at different temperatures. The structure determination paves the way towards a deep understanding and an accurate prediction of the physicochemical properties of boron crystals.In total, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 unique β-B configurations are found, but only 40 structures are within ∼7 meV per atom above the global minimum. These low energy structures belong to three types of skeletons, namely SK-I, SK-II and SK-III, and can be further classified into six patterns, P1 to P6. The occupancy rates of different POSs are then derived and are found to be highly temperature dependent. It is the large vibrational entropy of the P4 configurations that matters: P4 becomes the dominant configuration at high temperatures. We demonstrate that, in contradiction to the long-held belief that β-B exhibits a huge energy degeneracy, only 20 configurations are of significance in the observed boron structures, and contribute the most (>95%) to the overall POS occupancies.
293 unique β-B configurations are found, but only 40 structures are within ∼7 meV per atom above the global minimum. These low energy structures belong to three types of skeletons, namely SK-I, SK-II and SK-III, and can be further classified into six patterns, P1 to P6. The occupancy rates of different POSs are then derived and are found to be highly temperature dependent. It is the large vibrational entropy of the P4 configurations that matters: P4 becomes the dominant configuration at high temperatures. We demonstrate that, in contradiction to the long-held belief that β-B exhibits a huge energy degeneracy, only 20 configurations are of significance in the observed boron structures, and contribute the most (>95%) to the overall POS occupancies.
In addition to new boron chemistry, this work also made great progress in methodology development for machine learning potentials. The great complexity of the boron global PES not only provides an excellent opportunity for developing sensitive structural descriptors, the key tool for correlating a structure with its quantitative properties (e.g. energy), but also enables us to identify the bottleneck and the key ingredients for generating high-dimensional NN potentials for complex materials. Major achievements are outlined below.
(i) This work reports a series of new structural descriptors, PTSDs, for describing the complex atomic bonding environment in boron. The PTSDs improve greatly the predictive power of the NN potential, which manages to reach an RMS accuracy of 12 meV per atom for energy and 0.28 eV Å−1 for force for the global dataset (>160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures spanning over 4 eV per atom in energy).
000 structures spanning over 4 eV per atom in energy).
(ii) The first principles boron dataset established here, as also provided in the ESI,† can be utilized as a standard dataset for sharing, benchmarking and improving machine learning methods for building PESs in future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2018YFA0208600), the National Science Foundation of China (21533001, 91745201, 91645201 and 21603035), the Science and Technology Commission of Shanghai Municipality (08DZ2270500) and the Shanghai Pujiang Program (16PJ1401200).Notes and references
- W. N. Lipscomb, Science, 1977, 196, 1047 CrossRef PubMed.
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef PubMed.
- T. Ogitsu, E. Schwegler and G. Galli, Chem. Rev., 2013, 113, 3425–3449 CrossRef PubMed.
- M. A. White, A. B. Cerqueira, C. A. Whitman, M. B. Johnson and T. Ogitsu, Angew. Chem., Int. Ed., 2015, 54, 3626–3629 CrossRef PubMed.
- M. H. S. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604 CrossRef PubMed.
- M. K. Nielsen, D. T. Ahneman, O. Riera and A. G. Doyle, J. Am. Chem. Soc., 2018, 140, 5004–5008 CrossRef PubMed.
- J. P. Janet and H. J. Kulik, Chem. Sci., 2017, 8, 5137–5152 RSC.
- K. Yao, J. E. Herr, D. Toth, R. McKintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- D. E. Sands and J. L. Hoard, J. Am. Chem. Soc., 1957, 79, 5582–5583 CrossRef.
- A. Masago, K. Shirai and H. Katayama-Yoshida, Phys. Rev. B, 2006, 73, 104102 CrossRef.
- S. Shang, Y. Wang, R. Arroyave and Z.-K. Liu, Phys. Rev. B, 2007, 75, 092101 CrossRef.
- M. J. van Setten, M. A. Uijttewaal, G. A. de Wijs and R. A. de Groot, J. Am. Chem. Soc., 2007, 129, 2458–2465 CrossRef PubMed.
- M. Widom and M. Mihalkovič, Phys. Rev. B, 2008, 77, 064113 CrossRef.
- T. Ogitsu, F. Gygi, J. Reed, Y. Motome, E. Schwegler and G. Galli, J. Am. Chem. Soc., 2009, 131, 1903–1909 CrossRef PubMed.
- T. Ogitsu, F. Gygi, J. Reed, M. Udagawa, Y. Motome, E. Schwegler and G. Galli, Phys. Rev. B, 2010, 81, 020102 CrossRef.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- T. B. Hughes, N. L. Dang, G. P. Miller and S. J. Swamidass, ACS Cent. Sci., 2016, 2, 529–537 CrossRef PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef PubMed.
- H. Altae-Tran, B. Ramsundar, A. S. Pappu and V. Pande, ACS Cent. Sci., 2017, 3, 283–293 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- S.-D. Huang, C. Shang, X.-J. Zhang and Z.-P. Liu, Chem. Sci., 2017, 8, 6327–6337 RSC.
- C. Shang, X.-J. Zhang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2014, 16, 17845–17856 RSC.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef PubMed.
- S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671 CrossRef PubMed.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368 CrossRef PubMed.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef PubMed.
- H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu, Y.-B. Wu, Y.-W. Mu, G.-F. Wei, Z.-P. Liu, J. Li, S.-D. Li and L.-S. Wang, Nat. Chem., 2014, 6, 727 CrossRef PubMed.
- X.-J. Zhang, C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 3252–3260 CrossRef PubMed.
- S.-C. Zhu, S.-H. Xie and Z.-P. Liu, J. Am. Chem. Soc., 2015, 137, 11532–11539 CrossRef PubMed.
- W.-N. Zhao, S.-C. Zhu, Y.-F. Li and Z.-P. Liu, Chem. Sci., 2015, 6, 3483–3494 RSC.
- S.-H. Guan, X.-J. Zhang and Z.-P. Liu, J. Am. Chem. Soc., 2015, 137, 8010–8013 CrossRef PubMed.
- A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef.
- X.-J. Zhang, C. Shang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2017, 19, 4725–4733 RSC.
- W. H. Han, Y. J. Oh, D.-H. Choe, S. Kim, I.-H. Lee and K. J. Chang, NPG Asia Mater., 2017, 9, e400 CrossRef.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B, 1983, 28, 784–805 CrossRef.
- E. D. Jemmis and M. M. Balakrishnarajan, J. Am. Chem. Soc., 2001, 123, 4324–4330 CrossRef PubMed.
- G. A. Slack, C. I. Hejna, M. F. Garbauskas and J. S. Kasper, J. Solid State Chem., 1988, 76, 52–63 CrossRef.
- W. H. Eberhardt, B. Crawford and W. N. Lipscomb, J. Chem. Phys., 1954, 22, 989–1001 CrossRef.
- H. C. Longuet-Higgins and M. D. Roberts, Proc. R. Soc. London, Ser. A, 1955, 230, 110 CrossRef.
- M. Tillard-Charbonnel, A. Manteghetti and C. Belin, Inorg. Chem., 2000, 39, 1684–1696 CrossRef PubMed.
- W. N. Lipscomb, Boron hydrides, Courier Corporation, 2012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SSW-NN methodology, including the HDNN architecture, the iterative dataset generation, statistical assessment of different structural descriptors, general guidelines for setting up the structural descriptors and network size; DFT calculation details; pair distribution function of α-B; parameters for the structural descriptors used in set-1 and final NN potential; phonon and free energy calculations; convergence of occupancy rates with respect to number of minima; electronic analyses of β-I-15; XYZ coordinates for low energy crystals of boron and the top 40 β-B structures; the 8000-dataset for benchmarking purposes. See DOI: 10.1039/c8sc03427c |
| This journal is © The Royal Society of Chemistry 2018 |