Cyclic tris-[5]helicenes with single and triple twisted Möbius topologies and Möbius aromaticity

Abstract

A number of singly (180°) twisted, largely single-stranded and thus conformationally rather fragile, Möbius molecules have been synthesized within the last 15 years, which are aromatic with 4n electrons, thus violating the Hückel rule. Annulenes with significantly higher twist (e.g. 540°) that retain a full cyclic conjugation path have been elusive, mainly because of the high strain and loss of orbital overlap. Recently, a topological strategy was devised to project the “twist” into “writhe”, thus reducing the strain. However, orbital overlap was still severely reduced within the flexible building blocks. We now present a single and a triple twisted annulene with fully conjugated peripheries. They are unique in their pronounced band shape and conformational robustness as they are made up of three fully kata-condensed [5]helicene fragments. The triple twisted molecule exhibits a strong diatropic ring current in the outer periphery, even though the π system includes 4n electrons. The diatropic current is counterbalanced by a paratropic current in the σ system, resulting in no net manifestation of macrocyclic aromaticity. The key step of the synthesis of both Möbius compounds is a Perkin condensation of complementary bifunctional bismaleates leading to a flexible macrocycle containing alternating benzene and biphenyl fragments. Subsequent photocyclization yields a separable mixture of rigid diastereomeric tris-helicene macrocycles of the above topologies.

---

Introduction

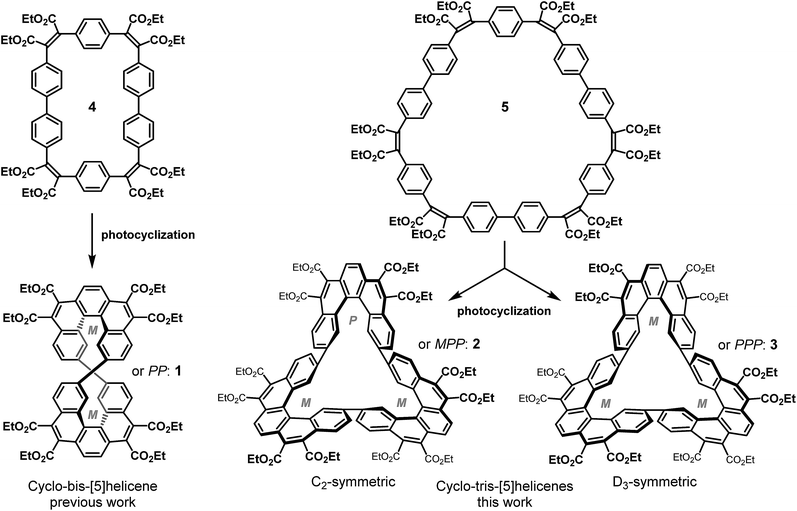
According to the Hückel rule, annulenes are aromatic with 4n + 2 electrons and antiaromatic with 4n electrons delocalized in a cyclic topology.^1,2 Heilbronner in 1964 predicted that the Hückel rule should be reversed in Möbius annulenes.³ The latter structures can be envisioned by formally cutting a bond in a “normal” annulene, giving one end a 180° twist, and rejoining both ends. Möbius annulenes were predicted to be aromatic with 4n electrons and antiaromatic with 4n + 2 electrons. Heilbronner further pointed out that the severe strain induced by the twist should decrease at ring sizes >20. It took 40 years until the first Möbius annulene was synthesized, and Heilbronners electron count rules were experimentally confirmed.^4–6 Within the last 15 years a number of 4n electron aromatic Möbius annulenes with a 180° twist were prepared. The majority of these systems are extended porphyrins.⁷ Heilbronner's electron count rules should also formally hold for higher twisted systems, or more precisely, for any annulene with an odd number of twists (n·180°, n = 1, 3, 5…). However, the severe strain induced by multiple twists is expected to prevent synthesis or at least should drastically reduce overlap between neighbouring p orbitals. We recently pointed out that there are strategies to overcome these problems.^6,8,9 The decisive topological parameter determining aromaticity is not the number of twists T_w, but the linking number L_k.¹⁰ Hückel systems have an even linking number (L_k = 0, 2, 4…) and Möbius objects exibit an odd linking number (L_k = 1, 3, 5…). T_w and L_k are connected by Calugareanu's theorem: L_k = T_w + W_r (W_r = writhe).¹¹ Besides the precise mathematical definition, Calugareanu's theorem can be demonstrated by an everyday life experiment. If a band e.g. a two-core power cord is twisted and both ends are joined, the band would wind around itself. Thus, the strain induced by the twists T_w is released, and projected into writhe W_r without changing the linking number L_k. Similar arguments hold for molecules. The topological transformation can be used as a strategy to reduce strain, while keeping the topological parameter L_k constant. We recently used this strategy to synthesize the first triply twisted Möbius annulene.⁸ Unfortunately, the building block diethynyl-binaphthalene is too flexible to provide a smooth distribution of dihedral angles along the periphery of the annulene and the conjugation was interrupted by torsional angles close to 90°. We now present the synthesis of a triple twisted annulene (540°) with small dihedral angles, and thus retaining full conjugation, and a diatropic ring current within the twisted π system in the periphery.

In the last five years, we have developed an efficient and versatile synthetic approach for the formation of large carboxy-substituted polycyclic arenes. It relies on Perkin reactions that yield flexible diarylmaleate-type precursors, followed by catalyst- or light-induced cyclization reactions.^12,13 This synthetic method has shown considerable potential for the construction of double helicenes^14,15 as well for as the formation of large conjugated macrocycles.^16,17 Recently, we have combined these two structural elements in a Perkin-assembled propeller-shaped macrocycle that incorporates two identical [5]helicene fragments.¹⁸ This dimeric cyclo-bis-[5]helicene 1 has been obtained as a racemic mixture of two enantiomers whose helicene fragments have identical helicity: PP or MM. The PM (meso) compound has not been observed, which is in line with the extreme distortion of its simulated structure.

This article presents the synthesis and study of trimeric homologs of macrocycle 1: the C₂-symmetric cyclo-tris-[5]helicenes 2 (MPP and PMM configurations), and the D₃-symmetric cyclo-tris-[5]helicenes 3 (PPP and MMM configurations) which are diastereomers and have been obtained as racemic mixtures (Scheme 1). In contrast to the dimeric case (the non-observed meso isomer of 1), three helicenes of different helicity can be cyclically linked without generating much distortion, thus both possible diastereomers are formed. In both of these two rigid conjugated macrocycles, the adjacent terminal benzene rings at the interhelicene bonds are essentially coplanar, leading to an overall Möbius band geometry of π electron systems of both macrocycles. The C₂-symmetric isomer has the geometry of a simple (singly twisted) Möbius band, whereas the D₃-symmetric isomer has the geometry of a triply twisted Möbius band.

Scheme 1 Cyclo-poly-[5]helicenes obtained by photocyclisation of flexible conjugated macrocycles.

Results and discussion

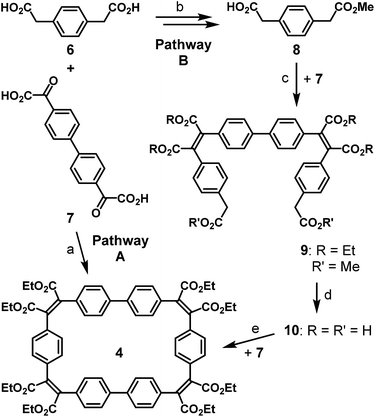
The Perkin condensation of bifunctional arylene–diglyoxylic acids with bifunctional arylene–diacetic acids leads with surprisingly good size-selectivities and yields to the 2 + 2 macrocyclic products, where four arylene moieties are connected by four maleic bridges. This approach has been used in the reported synthesis¹⁸ of the four-block flexible macrocycle 4 (Scheme 2, pathway A), with a moderate yield of 21%, precursor of the cyclic dimer of [5]helicene 1 (Scheme 1). Aiming at the formation of the trimeric counterparts 2 and 3 of the latter, the synthetic strategy based on the Perkin reaction involves one common macrocyclic intermediate 5 made of six building blocks: three 1,4-phenylenediacetic acid units 6 and three 4,4′-bis(phenylglyoxylic acid) units 7. The formation of a six-block macrocycle by Perkin reaction from bifunctional simple building blocks has been observed only once, as a minor side product of a four-block macrocycle composed exclusively of biphenyl units.¹⁸ A stepwise procedure is therefore necessary for the controlled synthesis of large six-block macrocycles by Perkin reaction. We focused on the combination of two complimentary linear bifunctional three-block intermediates (3 + 3 approach), which is more convergent than a 5 + 1 approach and synthetically simpler than a 4 + 2 approach due to the symmetry of the precursors.

Scheme 2 Synthesis of diacetic three-block precursor and its use in the synthesis of four-block macrocycle. (a) High dilution, Ac₂O, NEt₃, THF, reflux, 48 h, then EtOH, EtBr, DBU, reflux, 24 h, 21%; (b) SOCl₂, MeOH, reflux, 4 h, 85%, then KOH, 1,4-dioxane, reflux, 75 min, 47%; (c) Ac₂O, NEt₃, THF, reflux, 18 h, then EtOH, EtBr, DBU, reflux, 24 h, 65%; (d) KOH, H₂O, EtOH, reflux, 18 h, 100%; (e) high dilution, Ac₂O, NEt₃, THF, reflux, 48 h, then EtOH, EtBr, DBU, reflux, 24 h, 55%.

We have recently reported the synthesis of three-block linear intermediates, bearing two acetic acid functions at their extremities for the formation of long phenacenes.¹⁷ The same synthetic strategy has been applied to the diacetic and diglyoxylic building blocks 6 and 7 in the synthesis of the three-block diacetic precursor 10. 1,4-Phenylenediacetic acid 6 was first fully esterified in presence of methanol and SOCl₂ to give dimethyl 1,4-phenylenediacetic ester,¹⁹ which was then partially saponified with one equivalent of potassium hydroxide. The resulting mixture of remaining diester, diacetate and monoacetate monoester compounds was separated by selective pH-dependant solid–liquid extractions to finally give pure mono-protected phenylene diacetic acid 8. The yield of this mono-deprotection reaction is satisfying (47%) as it can be carried out on a large scale (10 g) without complicated purification and 48% of the starting compound is recovered separately as diacid or diester. Mono-protected phenylene diacetic acid 8 reacted twice with diglyoxylic acid 7 by Perkin reaction to afford the three-block hexaester 9 in good yield (65%), and then full saponification by treatment with potassium hydroxide quantitatively formed the three-block diacetic acid precursor 10. To verify its reactivity in the formation of macrocycles, it has been combined with the diglyoxylic building block 7 (Scheme 2, pathway B) by Perkin reaction in high dilution conditions to form the four-block macrocycle 4 with an improved yield of 55%, compared to 21% when single building blocks 6 and 7 are mixed under the same reaction conditions (Scheme 2, pathway A).¹⁸

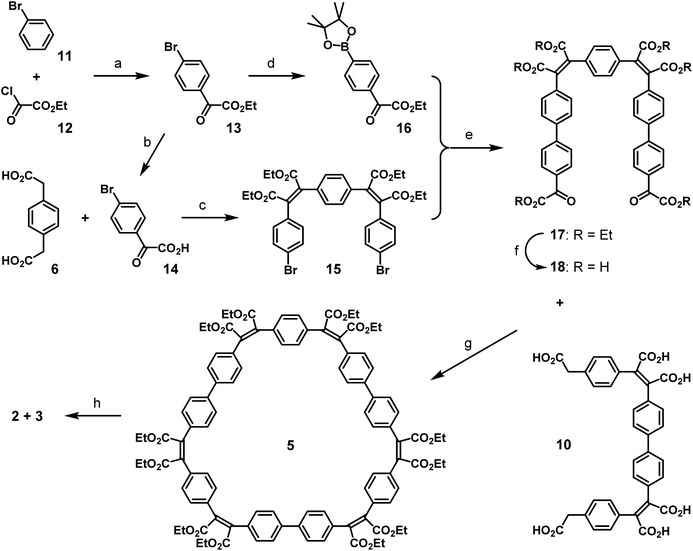
The mono-protection of arylene-diglyoxylic acids for the Perkin reaction not yet having been developed, a different synthetic approach was pursued for the complimentary three-block diglyoxylic precursor 18 (Scheme 3). In biphenyl-based species, the central sigma C–C bond can easily be formed by usual palladium-catalyzed coupling reactions between adequately functionalized aryl fragments. Thus bromobenzene 11 was first functionalized with one glyoxylic ester function by a Friedel–Crafts reaction with ethyl oxalyl chloride 12 as an electrophile in presence of AlCl₃ following a recently reported procedure.²⁰ The glyoxylic ester function of the resulting ester 13 was saponified efficiently by treatment with sodium hydrogen carbonate and the resulting para-brominated phenylglyoxylic acid 14 reacted then twice with 1,4-phenylenediacetic acid 6 in Perkin conditions to give the dibrominated bis-maleate precursor 15 with a very good yield (83%). In parallel, para-brominated phenylglyoxylic ester 13 was transformed into the corresponding boronic ester 16 by palladium-catalyzed substitution of the bromo-substituent in presence of bis(pinacolato)diboron. In spite of non-removable traces of pinacol in the latter, it was coupled twice to the dibrominated bis-maleate precursor 15 by a double Suzuki reaction with Pd(PPh₃)₄ as a catalyst. The resulting bis-maleate hexaester 17 was obtained with a modest yield (45%) for this usually efficient reaction, because of partial saponification of the product in basic conditions, even in the absence of water. Full saponification of the hexa-ester 17 quantitatively afforded the three-block diglyoxylic acid precursor 18.

Scheme 3 Synthesis of the second three-block precursor 18 and its combination with complimentary three-block precursor 10 to form the six-block macrocycle 5, precursor of cyclo-tris-[5]helicenes 2 and 3. (a) AlCl₃, CH₂Cl₂, −10 °C, 20 min, 71%; (b) NaHCO₃, H₂O, EtOH, reflux, 16 h, 93%; (c) Ac₂O, NEt₃, THF, reflux, 16 h, then EtOH, EtBr, DBU, reflux, 24 h, 83%; (d) (Bpin)₂, PdCl₂dppf, KOAc, 1,4-dioxane, 90 °C, 2.5 h, 87% with traces of pinacol; (e) Pd(PPh₃)₄, K₃PO₄, PhMe, reflux, 20 h, 45%; (f) NaHCO₃, H₂O, EtOH, reflux, 24 h, 100%; (g) Ac₂O, NEt₃, THF, reflux, 72 h, then EtOH, EtBr, DBU, reflux, 24 h, 29%; (h) I₂, AcOEt, UV-irradiation, rt, 48 h, 18% (2) and 18% (3).

The two three-block diacetic 10 and diglyoxylic 18 precursors were then coupled together by double Perkin reaction to form the six-block flexible conjugated macrocycle 5. High dilution conditions were not used, because of the low solubility of compound 18, but the cyclic product 5 was obtained with a very satisfying macrocyclization yield of 28%, after a difficult purification process. Irradiation of a 0.07 mM solution of 5 in ethyl acetate in the presence of iodine and oxygen for two days with pyrex-filtered light from a medium pressure mercury lamp afforded a mixture of the two cyclo-tris-[5]helicenes 2 and 3 with an average yield of 40%. ¹H-NMR analysis of this mixture revealed that these two rigid macrocycles are present in near-equal proportions. In spite of their structural differences, compounds 2 and 3 could not be separated by chromatography, but recrystallization of this mixture in a large amount of ethanol surprisingly afforded crystals of pure racemic C₂-symmetric cyclo-tris-[5]helicene 2, and further purification of the remaining product in the mother liquor gave pure racemic D₃-symmetric cyclo-tris-[5]helicene 3, in 18% yield each. Racemic crystals suitable for X-ray structure determination (Fig. 1) where obtained by slow diffusion of methanol into a chloroform solution in the case of 2, and by slow diffusion of cyclohexane into a toluene solution in the case of 3.

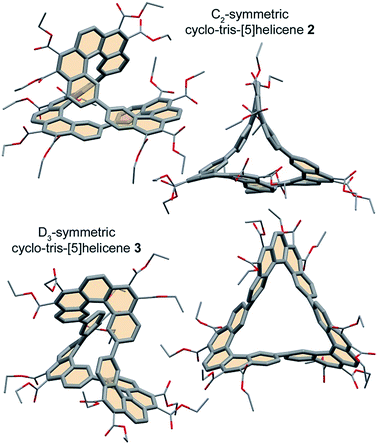Fig. 1 Crystal structures of cyclo-tris-[5]helicenes 2 and 3 (PMM and MMM represented respectively).

Whereas the dimeric homolog 1 did not show any evidence of coplanarity and thus of conjugation between the two helicenes, the crystal structures of the trimers show that the two linked benzene rings of adjacent helicenes are almost coplanar. In these conditions, the conjugated π electron systems of these rigid macrocycles have persistent shapes of cyclic twisted ribbons.

A first evidence of the conjugation between the three helicenes composing the cyclo-tris-[5]helicenes 2 and 3 has been obtained from their optical absorption. The cyclo-bis-[5]helicene 1 was expected not to exhibit any conjugation between its two parts due to a lack of coplanarity at the junctions between helicenes. This was confirmed by the absorption spectra, where this cyclic dimer of ester-substituted [5]helicenes behaved approximately like two independent ester-substituted [5]helicenes²¹ (Fig. 2). In contrast, trimeric cyclo-tris-[5]helicenes 2 and 3 show a significantly modified absorption profile compared to the single [5]helicene.

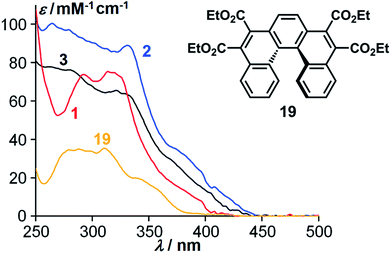Fig. 2 Absorption spectra of a single [5]helicene tetraester 19 (yellow) and of the corresponding cyclic dimer 1 (red) and trimers 2 (blue) and 3 (black).

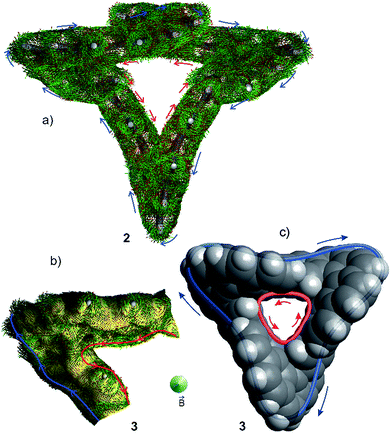
For a closer inspection of the topology of 2 and 3, we used our program ANEWWRITHM²² and determined the topological parameters L_k, T_w and W_r. Since both annulenes are not single stranded, there are different conjugation pathways that can be defined within the cyclic π system. We distinguish between the inner cyclic pathway with 24 π electrons (red line) and the outer pathway with 48 π electrons (blue line, Fig. 3). Thus, both conjugation pathways exhibit 4n π electrons. In Fig. 3cyclo-tris-[5]helicenes are represented as topologically stretched 2D projections (2′ and 3′), as well as with their native 3D geometry (2 and 3). The stretched representation is easier to conceive, and it reveals that 2 is singly twisted and 3 is triply twisted. Cyclo-helicene 2 is composed of two helicene units of like helicity, and one unit with opposite helicity. In terms of the stretched representation, the opposite twists cancel, and a singly twisted Möbius ribbon results. The helicities of the three helicene units in 3 are equal, and the twists add up to a triply twisted Möbius band. Note that the term “twist” has different meanings in the general English language and in topology. In the following we use the topological twist (as defined in the Calugeanou theorem: L_k = T_w + W_r) in combination with the symbol T_w. The topologically stretched geometries would be highly strained, and exhibit reduced overlap between neighbouring p orbitals. In the native geometry large part of the twist T_w is projected into writhe W_r by folding into a 3D geometry (Fig. 3). This topological transformation is obviously more efficient in 3 than in 2. Surprisingly, the triply twisted 3 is 5.8 kcal mol⁻¹ more stable than its singly twisted isomer 2. However, if dispersion is included (D3 method, see ESI†) the relative energies are reverse. Obviously, singly twisted 2 is more densely packed which leads to stabilization by an increased intramolecular dispersion interaction. The inner (red) and outer (blue) conjugation pathways in both cyclo-tris-[5]helicenes 2 and 3 exhibit odd linking numbers L_k (Möbius topology) however, they have different linking numbers L_k in the same molecule (Fig. 3).

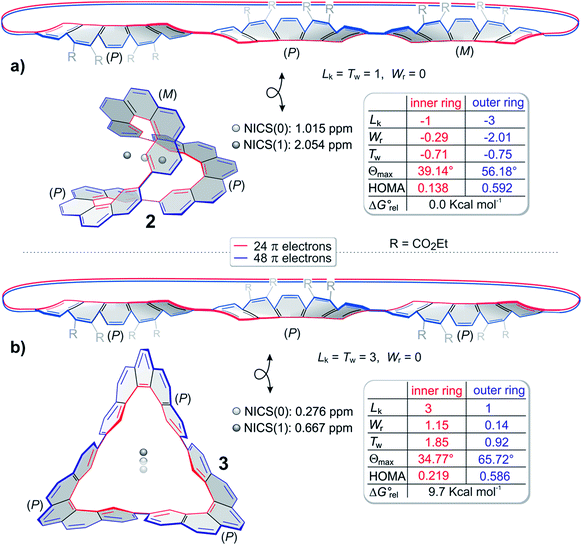Fig. 3 Topologies and aromaticity parameters of cyclo-tris-[5]helicenes 2 and 3. Geometries are optimized at the B3LYP/6-31G* level of density functional theory. The ester substituents are omitted for clarity. The topological parameters L_k, W_r and T_w are calculated with the program ANEWWRITHM.²² The looped double headed arrows define that both objects are topologically equivalent (homeomorphic). (a) top and (b) top: cyclo-tris-helicene 2 and 3 in topological stretched, writhe-free (W_r = 0) representations. In these forms the linking numbers L_k equal the twists T_w. (a) bottom and (b) bottom: 3D structures of 2 and 3. In these “relaxed” structures a considerable part of the twist T_w is projected into writhe W_r. The topological parameters are given for the inner (red) and the outer conjugation path (blue). θ_max is the largest dihedral angle between neighboring carbon atoms, and thus is a measure of the conjugation. Note that enantiomers have the same topological parameters, albeit with opposite algebraic sign, and inner and outer periphery exhibit different linking numbers L_k. E_rel are the relative energies of 2 and 3 at the B3LYP/6-31G* level of DFT. NICS values are calculated at the B3LYP/6-31G* level of DFT using the GIAO method.²³ NICS(0) was calculated at the center of gravity of molecules 2 and 3. NICS(1) was calculated in a distance of 1 Å on an axis dissecting the center of gravity. In structure 3 the axis is identical to the C₂ axis, and in 2 the axis is orthogonal to the largest enclosed area obtained by all conceivable 2D projections (relative orientation of the molecule and the magnetic field leading to the largest ring current). HOMA values were calculated for the inner and outer periphery according to the published method.²⁴

Since the conjugation pathways in 2 and 3 include 4n electrons, and exhibit odd linking numbers L_k, they should be Möbius aromatic. ACID (anisotropy of the induced current density)^25–27 calculations reveal that the situation is more complicated. Similar to the paragon of aromatic compounds benzene, Möbius compound 3 exhibits a diatropic ring current in the outer π system, and a paratropic current in the inner σ system.^26,28 In 3 these currents cancel, and almost no net ring current results (Fig. 4).²⁹ In benzene the paratropic current is located within the ring plane, and there are two maximum diatropic ring currents approximately 1 Å above and underneath the ring plane (along the two paths with the highest π electron density).^30,31 In the triply twisted Möbius molecule 3, however, the current follows a path mainly restricted to outer part of the molecule, changing the side of the π system three times.³² As a consequence of the inner paratropic ring current in the σ system, the six inner protons (8.88 ppm) are deshielded by 0.58 ppm as compared to the corresponding two protons in the [5]helicene building block 19. The diatropic ring current in the outer periphery (blue) does not induce a strong shift of the remaining 18 protons, because they are not located in the range of the induced magnetic field. Similar arguments hold for the singly twisted Möbius compound 2. There is a diatropic ring current in the periphery and a paratropic current in the σ system in the inner conjugation path (Fig. 3). NICS values²³ calculated for Möbius structures 2 and 3 are close to zero (Fig. 3) and corroborate the fact that diatropic and paratropic ring currents almost cancel. Also in agreement with our ACID analysis are the bond length analyses of 2 and 3 using the HOMA method.²⁴ For both Möbius compounds, the HOMA values are considerably larger in the periphery (diatropic, aromatic) than in the inner conjugation path (paratropic, antiaromatic) (see Fig. 3a and b). The C–C bonds connecting the [5]helicene units in 2 and 3 exhibit a bond length of 1.48–1.49 Å which is considerably longer than the bond length in the prototypic aromatic molecule benzene (∼1.40 Å). Upon distortion of D_6h benzene towards a D_3h 1,3,5-hexatriene structure with alternating C–C bond lengths of 1.553 Å and 1.337 Å, benzene retains 72% of its diatropic ring current.³³ We conclude that a corresponding bond length elongation by 0.01 Å in 2 and 3 does not significantly reduce the ring currents.

Fig. 4 Ring currents in cyclo-tris[5]helicene 2 and 3. The structures were optimized at the B3LYP/6-31G* level of density functional theory and the current density was determined with the CSGT method. The anisotropy of the induced current density was calculated using the ACID program at an isosurface value of 0.032. Current density vectors are plotted onto the ACID surface. The lengths of the green vectors with red arrowheads represent the current strengths. The magnetic field vector B (large green arrowhead) points towards the viewer. (a) Current density vectors on the ACID surface of 2. The ACID hypersurface is removed for clarity. Bold blue arrows indicate the diamagnetic and red arrows the paramagnetic current flow. (b) ACID plot including current density vectors of a section of 3. The bold lines represent the general direction of the ring currents in the inner (red) and outer (blue) periphery. (c) Schematic view of the outer (diatropic) and inner (paratropic) current, plotted onto the van der Waals surface of 3.

Conclusions

Highly twisted annulenes have been considered as very challenging targets because of the severe strain and weak π overlap induced by the twist. In contrast to this intuitive conclusion, we prove that even a triple twisted Möbius annulene with a 540° twist in its π system, is easily accessible by standard chemical synthesis. Within the inner and the outer conjugation path of the triply twisted system, no torsional angle between neighbouring p orbitals is larger than 35° and 66°. So, conjugation is still efficient. All conjugation pathways include 4n electrons and an odd linking number L_k. Hence, they should be Möbius aromatic. A detailed ring current analysis reveals that a paratropic current is induced in the inner σ system, and a diatropic current in the outer π periphery, which almost cancel. The surprisingly low strain and considerable π overlap is due to a topological transformation of twist into writhe by folding of the Möbius ring into a 3D structure, a process which is similar to the supercoiling of DNA.³⁴ Annulenes with chiral π systems are interesting from another point of view. Theoretical calculations predict that upon irradiation with a strong laser pulse (even in the absence of a magnetic field), ring currents should be induced which are orders of magnitude larger than the currents induced in a superconducting NMR magnet.^35,36 Moreover, peculiar nonlinear optical³⁷ and two photon absorption properties³⁸ have been predicted for Möbius annulenes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding by the Agence Nationale de la Recherche (13-JS07-0009-01) and the German Research Foundation (SFB677) are gratefully acknowledged.

Notes and references

1. E. Hückel, Z. Phys., 1931, 70, 204–286.
2. E. Hückel, Z. Phys., 1932, 76, 628–648.
3. E. Heilbronner and E. Hückel, Tetrahedron Lett., 1964, 29, 1923–1928.
4. D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821.
5. D. Ajami, K. Hess, F. Köhler, C. Näther, O. Oeckler, A. Simon, C. Yamamoto, Y. Okamoto and R. Herges, Chem.–Eur. J., 2006, 12, 5434–5445.
6. R. Herges, Chem. Rev., 2006, 106, 4820–4842.
7. T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640.
8. G. R. Schaller, F. Topić, K. Rissanen, Y. Okamoto, J. Shen and R. Herges, Nat. Chem., 2014, 6, 608–613.
9. S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2007, 130, 7613–7619.
10. P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777.
11. G. Calugareanu, Czech. Math. J., 1961, 11, 588–625.
12. P. Sarkar, F. Durola and H. Bock, Chem. Commun., 2013, 49, 7552–7554.
13. T. S. Moreira, M. Ferreira, A. Dall'armellina, R. Cristiano, H. Gallardo, E. A. Hillard, H. Bock and F. Durola, Eur. J. Org. Chem., 2017, 4548–4551.
14. H. Bock, S. Huet, P. Dechambenoit, E. A. Hillard and F. Durola, Eur. J. Org. Chem., 2015, 1033–1039.
15. M. Ferreira, G. Naulet, H. Gallardo, P. Dechambenoit, H. Bock and F. Durola, Angew. Chem., Int. Ed., 2017, 56, 3379–3382.
16. A. Robert, P. Dechambenoit, H. Bock and F. Durola, Can. J. Chem., 2017, 95, 450–453.
17. G. Naulet, A. Robert, P. Dechambenoit, H. Bock and F. Durola, Eur. J. Org. Chem., 2018, 619–626.
18. A. Robert, P. Dechambenoit, E. A. Hillard, H. Bock and F. Durola, Chem. Commun., 2017, 53, 11540–11543.
19. M. Neeb, C. Hohn, F. R. Ehrmann, A. Härtsch, A. Heine, F. Diederich and G. Klebe, Bioorg. Med. Chem., 2016, 24, 4900–4910.
20. M. Sasikumar, D. Bharath, G. S. Kumar, N. R. Chereddy, S. Chithiravel, K. Krishnamoorthy, B. Shanigaram, K. Bhanuprakash and V. J. Rao, Synth. Met., 2016, 220, 236–246.
21. M. G. Belarmino Cabral, D. Pereira de Oliveira Santos, R. Cristiano, H. Gallardo, A. Bentaleb, E. A. Hillard, F. Durola and H. Bock, ChemPlusChem, 2017, 82, 342–346.
22. F. Köhler, Dissertation, University of Kiel, 2008The algorithm is based is based on a method developed by K. Klenin and J. Langowski, Biopolymers, 2000, 54, 307–317.
23. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
24. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420.
25. R. Herges and D. Geuenich, J. Phys. Chem. A, 2001, 105, 3214–3220.
26. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
27. R. Herges, Magnetic Properties of aromatic compounds and aromatic transition states, in The Chemical Bond : Chemical Bonding Across the Periodic Table, ed. G. Frenking and S. Shaik, Wiley-VCH-Verlag, 2014.
28. E. Steiner and P. W. Fowler, Int. J. Quantum Chem., 1995, 60, 609–616.
29. A partial cancelling of the paratropic and diatropic ring current is also observed in benzene, explaining the rather small downfield shift of the protons in benzene as compared to hexatriene: S. Pelloni, A. Ligabue and P. Lazzaretti, Org. Lett., 2004, 6, 4451–4454.
30. J. S. Waugh and R. W. Fessenden, J. Am. Chem. Soc., 1957, 79, 846–849.
31. C. E. Johnson and F. A. Bovey, J. Chem. Phys., 1958, 29, 1012–1014.
32. Note that the ring currents don't exhibit a topology because they are not bands with two edges.
33. D. E. Bean and P. W. Fowler, J. Phys. Chem. A, 2011, 115, 13649–13656.
34. O. M. J. Lilley, Biochem. Soc. Trans., 1986, 14, 489–493.
35. I. Barth, J. Manz, Y. Shigeta and K. Yagi, J. Am. Chem. Soc., 2006, 128, 7043–7049.
36. H. Mineo and Y. Fujimura, J. Phys. Chem. Lett., 2017, 8, 2019–2025.
37. Z. S. Yoon, J. H. Kwon, M.-C. Yoon, M. K. Koh, S. B. Noh, J. L. Sessler, J. T. Lee, D. Seidel, A. Aguilar, S. Shimizu, M. Suzuki, A. Osuka and D. Kim, J. Am. Chem. Soc., 2006, 128, 14128–14134.
38. V. Kundi, M. M. Alam and P. P. Thankachan, Phys. Chem. Chem. Phys., 2015, 17, 6827–6833.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, NMR spectra, 2D NMR spectra, single crystal X-ray diffraction, ACID plots, orbital plots, cartesian coordinates of B3LYP/6-31G* optimized structures. CCDC 1826373 and 1826374. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc02877j

---