Open Access Article
Open Access ArticleThe hydrogen atom transfer reactivity of sulfinic acids†
Markus
Griesser
 ,
Jean-Philippe R.
Chauvin
,
Jean-Philippe R.
Chauvin
 and
Derek A.
Pratt
and
Derek A.
Pratt
 *
*
Department of Chemistry and Biomolecular Sciences, University of Ottawa, Ottawa, Ontario, Canada K1N 6N5. E-mail: dpratt@uottawa.ca
First published on 31st July 2018
Abstract
Sulfinic acids (RSO2H) have a reputation for being difficult reagents due to their facile autoxidation. Nevertheless, they have recently been employed as key reagents in a variety of useful radical chain reactions. To account for this paradox and enable further development of radical reactions employing sulfinic acids, we have characterized the thermodynamics and kinetics of their H-atom transfer reactions for the first time. The O–H bond dissociation enthalpy (BDE) of sulfinic acids was determined by radical equilibration to be ∼78 kcal mol−1; roughly halfway between the RS-H BDE in thiols (∼87 kcal mol−1) and RSO-H BDE in sulfenic acids (∼70 kcal mol−1). Regardless, RSH, RSOH and RSO2H have relatively similar inherent H-atom transfer reactivity to alkyl radicals (∼106 M−1 s−1). Counter-intuitively, the trend in rate constants with more reactive alkoxyl radicals follows the reaction energetics: ∼108 M−1 s−1 for RSO2H, midway between thiols (∼107 M−1 s−1) and sulfenic acids (∼109 M−1 s−1). Importantly, since sulfinic and sulfenic acids are very strong H-bond donors (αH2 ∼ 0.63 and 0.55, respectively), their reactivity is greatly attenuated in H-bond accepting solvents, whereas the reactivity of thiols is largely solvent-independent. Efforts to measure rate constants for the reactions of sulfinic acids with alkylperoxyl radicals were unsuccessful. Computations predict these reactions to be surprisingly slow; ∼1000-times slower than for thiols and ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-times slower than for sulfenic acids. On the other hand, the reaction of sulfinic acids with sulfonylperoxyl radicals – which propagate sulfinic acid autoxidation – is predicted to be almost diffusion-controlled. In fact, the rate-determining step in sulfinic acid autoxidation, and the reason they can be used for productive chemistry, is the relatively slow reaction of propagating sulfonyl radicals with O2 (∼106 M−1 s−1).
000-times slower than for sulfenic acids. On the other hand, the reaction of sulfinic acids with sulfonylperoxyl radicals – which propagate sulfinic acid autoxidation – is predicted to be almost diffusion-controlled. In fact, the rate-determining step in sulfinic acid autoxidation, and the reason they can be used for productive chemistry, is the relatively slow reaction of propagating sulfonyl radicals with O2 (∼106 M−1 s−1).
Introduction
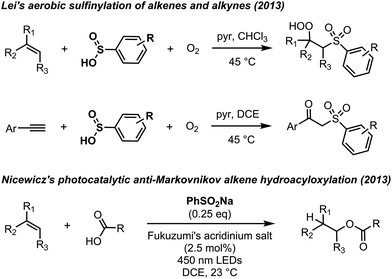
Sulfinic acids (RSO2H) are trivalent sulfur oxyacids isoelectronic with carboxylic acids. Although they are less prominent than the thiols from which they are derived, and the sulfonic acids to which they are oxidized, they are useful Brønsted acids and as precursors to various sulfonate derivatives. One-electron oxidation of sulfinic acids (or their conjugated bases) yields sulfonyl radicals,1,2 important intermediates in industrial processes (e.g. sulfoxidation to produce surfactants)3 and synthetic transformations where they often give way to sulfones via radical additions to double and triple bonds.4–11 Sulfonyl radicals are most commonly generated from sulfonyl halides,5 pseudohalides8 or azides9 by photolysis or atom/group transfer reactions as part of chain reactions.Despite the fact that sulfinic acids are widely considered to be difficult to work with due to their autoxidizability, the direct use of sulfinic acids in organic synthesis has recently gained popularity.12–21 Particularly noteworthy are Lei's reports of the use of sulfinic acids for sulfonylation of alkenes12 and alkynes,13 and Nicewicz's use of sulfinic acids as catalytic H-atom donors in photocatalytic anti-Markovnikov alkene functionalizations (e.g.Fig. 1).15 Central to these radical chain reactions are chain-propagating steps which involve H-atom transfer (HAT) from a sulfinic acid to a peroxyl radical (top, Fig. 1), to a peroxyl radical and alkoxyl radical (middle, Fig. 1) or alkyl radical (bottom, Fig. 1). Rate constants for these key reactions are unknown;22 data which would greatly enable further development of reactions utilizing sulfinic acids for organic synthesis.
 | ||
| Fig. 1 Examples of recently reported transformations employing sulfinic acids for group transfer/radical additions. | ||
Likewise, surprisingly little is known of the stability of sulfonyl radicals relative to radicals derived from other commonly utilized reagents for addition and/or H-atom transfer in organic synthesis, such as thiols. The stability of a given radical (e.g. X˙) relative to another (e.g. Y˙) is generally estimated by comparing the X–H bond dissociation enthalpy (BDE) to that of Y–H. No definitive sulfinic acid O–H BDE has been reported. To the best of our knowledge, the first suggestion was made in 1971 (111 kcal mol−1),23 but was shortly thereafter revised to be at most 104 kcal mol−1.24 Benson later estimated that the phenylsulfonyl radical should have a similar stability to the benzyl radical (and therefore a BDE of ca. 90 kcal mol−1).25 A subsequent estimate put the BDE at 73 kcal mol−1,26 and a recent calculation suggested 77 kcal mol−1.27 Given the central importance of the 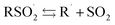 equilibrium to the chemistry of sulfonyl radicals, knowledge of the inherent stability of
equilibrium to the chemistry of sulfonyl radicals, knowledge of the inherent stability of  is highly desirable.
is highly desirable.
Herein we provide the first experimental determination of the O–H BDE in sulfinic acids, and report on the kinetics of their H-atom transfer reactions with alkyl, alkoxyl, and peroxyl radicals. We compare these results to corresponding data for the structurally-related sulfenic acids, which have among the weakest O–H bonds28 and some of the fastest HAT reactions29,30 ever reported. We also study the solvent effects on these reactions, and demonstrate that sulfinic (and sulfenic) acid(s) engage in strong H-bonding interactions that slow HAT.
Our results provide key information for the development of synthetic methodology employing sulfonyl radicals and/or sulfinic acids and offer unique insights on the role of secondary orbital interactions in the reactions of peroxyl radicals, which are quite significant for sulfenic acids and virtually non-existent for sulfinic acids.
Results
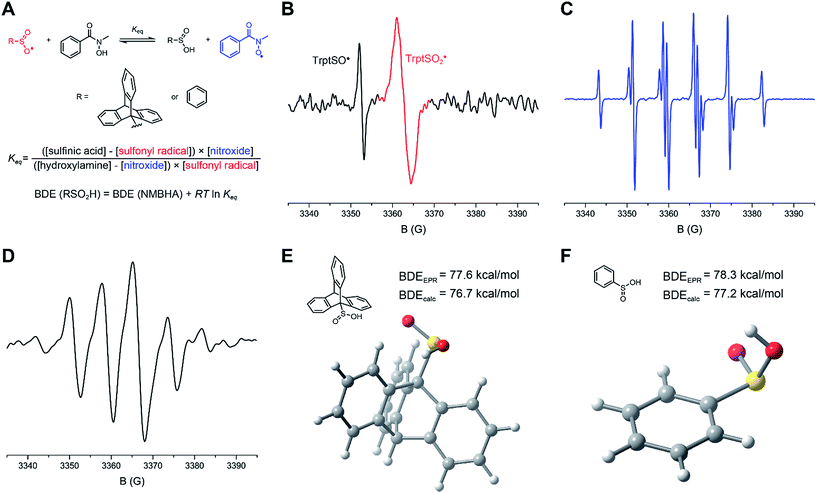
Kinetic and thermochemical experiments were carried out with phenylsulfinic acid (PhSO2H) (generated from its commercially-available sodium sulfinate salt) and/or 9-triptycenesulfinic acid (TrptSO2H), which enables direct comparison with the analogous 9-triptycenesulfenic acid (TrptSOH).28,31,74 The 9-triptycenesulfinic acid was prepared as described in the ESI,† in a manner similar to that we recently described for the synthesis of a fluorinated analog.32O–H bond dissociation enthalpies of sulfinic acids
The radical equilibration EPR (REqEPR) technique33 was employed to establish a reliable O–H BDE for sulfinic acids. The approach, depicted in Fig. 2A, relies on the equilibration of persistent radicals – one derived from a precursor whose X–H BDE is known (the reference compound) and one from the compound for which the Y–H BDE is desired. The difference in the X–H and Y–H BDEs can be estimated directly from the equilibrium constant determined by double integration of the EPR signals of the two equilibrated radicals X˙ and Y˙, assuming the entropy of the H-atom exchange is negligible.Previous EPR studies of sulfonyl radicals24,34,35 have been challenging owing to their rapid disproportionation (e.g. k = 8 × 108 M−1 s−1 for p-tosylsulfonyl)35 to sulfinyl and sulfonyloxyl radicals. As such, it was hoped that the triptycene substituent in TrptSO2H would impart sufficient persistence to the sulfonyl radical to enable the REqEPR experiment. Indeed, the room temperature photolysis of a solution of 9-triptycenesulfinic acid containing t-BuOOt-Bu yielded a broad signal which could be ascribed to the 9-triptycenesulfonyl radical (Fig. 2B). Within seconds, a significantly sharper signal appeared at slightly lower field. Assuming that the latter signal corresponded to the 9-triptycenesulfinyl radical, which we had previously characterized to have g = 2.0114,28 the former signal was centered at g = 2.0053 in good agreement with previously reported values for sulfonyl radicals.24,36
To identify an appropriate reference compound for the REqEPR experiment, CBS-QB3 calculations were carried out to predict the O–H BDEs of each of the phenylsulfinic acid (77.2 kcal mol−1) and 9-triptycenesulfinic acid (76.7 kcal mol−1).37 We also calculated an O–H BDE of 71.0 kcal mol−1 for 9-triptycenesulfenic acid using the same methodology, which is in excellent agreement with the experimental value of 71.9 kcal mol−1 we previously determined using the REqEPR technique,28,38 suggesting that oxidation of the sulfur atom has a relatively modest (∼5 kcal mol−1) effect on the O–H BDE. N-Methylbenzohydroxamic acid (NMBHA) was chosen as the reference compound since its O–H BDE (78 kcal mol−1)39 is similar to the predicted values for the sulfinic acids and the N-oxyl radical produced upon H-atom abstraction therefrom is persistent (Fig. 2C).
Photolysis of a solution of 9-triptycenesulfinic acid and NMBHA containing t-BuOOt-Bu yielded spectra consistent with the superposition of the sulfonyl and N-oxyl radical spectra (Fig. 2D). The equilibrium constant was readily determined from these data, but estimation of the sulfinic acid O–H BDE first required correction of the equilibrium constant for the H-bonding interactions between the sulfinic acid/NMBHA and the t-BuOH used to help solubilize them in benzene (10% v/v) – see ESI† for the details. The resultant value of 77.6 kcal mol−1 is in excellent agreement with the CBS-QB3 calculations, and confirms that oxidation of the sulfur atom in a sulfenic acid raises the O–H BDE by 5 to 6 kcal mol−1. Analogous experiments were carried out with phenylsulfinic acid in benzene, which yielded an O–H BDE of 78.3 kcal mol−1, again consistent with the predictions by CBS-QB3. By comparison, alkylthiols and arylthiols have S–H BDEs of 87 and 79 kcal mol−1, respectively.
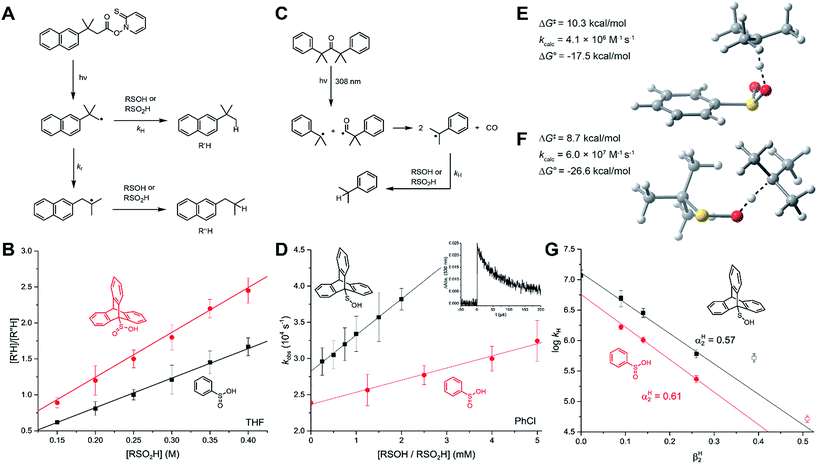
Reactions with alkyl radicals
The kinetics of H-atom transfer from PhSO2H and TrptSO2H to alkyl radicals were determined using the radical clock approach employing the 1,2-aryl migration in the (naphthyl)neophyl radical as the reference reaction (kr = 1.4 × 104 M−1 s−1 at 25 °C).40 The radicals were generated by photolysis of the corresponding Barton (PTOC) ester, and the reduced and rearranged products were quantified by GC/MS as a function of sulfinic acid concentration to yield the H-atom transfer rate constant (Fig. 3A). Initial experiments in THF yielded kH = (5.2 ± 0.7) × 104 and (8.7 ± 1.8) × 104 M−1 s−1 for PhSO2H and TrptSO2H, respectively (Fig. 3B) – the order of reactivity being consistent with the slightly weaker O–H bond in TrptSO2H compared to PhSO2H. Given the acidity of the O–H bond in sulfinic acids, we anticipated a significant solvent effect on the H-atom transfer kinetics and therefore sought to determine rate constants in a range of H-bond accepting solvents. Unfortunately, the limited solubility of the sulfinic acids at the concentrations necessary to afford reliable kinetics by the competition method precluded such an endeavor.Therefore, we also performed direct kinetic experiments by laser flash photolysis. Cumyl radicals were generated by the photolysis of dicumylketone with the 308 nm emission of a nanosecond-pulsed XeCl excimer laser. The rate of decay of the 330 nm absorption of the cumyl radicals was determined as a function of sulfinic acid concentration to yield the H-atom transfer rate constant (Fig. 3C). Initial experiments in benzene yielded a rate constant of (1.0 ± 0.2) × 106 M−1 s−1 for PhSO2H (Fig. 3D) – consistent with a substantial kinetic solvent effect when comparing to the data in THF. Additional experiments were carried out in chlorobenzene and anisole, which revealed a dramatic drop in the HAT rate constant with increasing hydrogen bond basicity (Fig. 3G). Plotting the data according to the Ingold–Abraham equation41 that relates H-atom transfer kinetics to solvent H-bond basicity (βH2),
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kSinh = −8.32αH2βH2 + log kSinh = −8.32αH2βH2 + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k0inh k0inh |
Corresponding experiments carried out with the sulfenic acid (in isooctane, chlorobenzene, benzene, and anisole) yielded rate constants that were systematically ca. 3-fold greater than those of the sulfinic acids (e.g. (2.9 ± 0.4) × 106 M−1 s−1 for TrptSOH in benzene). Plotting these data according to the Ingold–Abraham equation yields αH2 = 0.57 for the sulfenic acid, in excellent agreement with our previous report (αH2 = 0.54).31 The modest difference in the H-atom transfer kinetics of sulfinic and sulfenic acids is surprising given the ca. 5–6 kcal mol−1 difference in the experimental O–H BDEs, and may reflect a more favorable polarization of the H-atom transfer TS in the case of the sulfinic acid compared to the sulfenic acid (consistent with their pKas of ∼1.9 and 12.5, respectively).32
The HAT transition states (TS) for the reactions of representative sulfinic and sulfenic acids are shown in Fig. 3E and F. The results are fully consistent with the experimental trends. That is, CBS-QB3 predicts a barrier of ΔG‡ = 10.3 kcal mol−1 for PhSO2H (corresponding to k = 4.1 × 106 M−1 s−1) and ΔG‡ = 8.7 kcal mol−1 for t-BuSOH (corresponding to k = 6.0 × 107 M−1 s−1). Again, the difference in the kinetics (ca. 15-fold) is relatively modest given the significant difference in the driving force (ΔΔG° = 9.1 kcal mol−1).
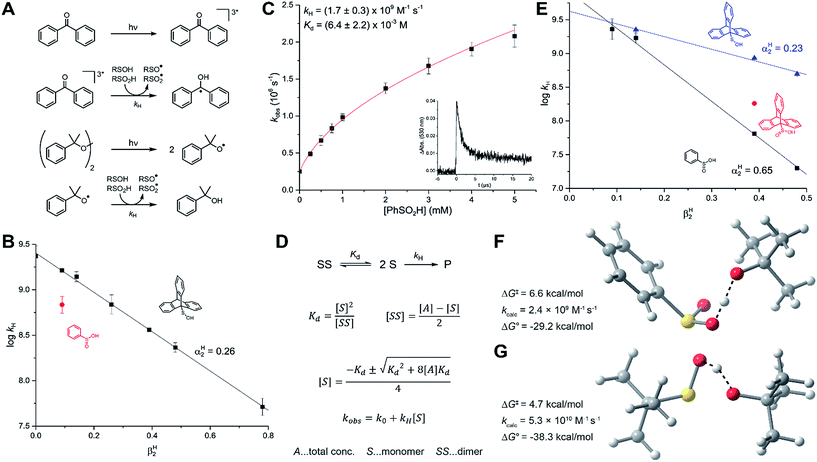
Reactions with alkoxyl radicals
The reaction of sulfinic acids with t-butoxyl radicals has been used to generate sulfonyl radicals for low-temperature EPR studies24 (as above for our REqEPR experiments), but the kinetics of this reaction have never been reported.42 To provide insight to this reactivity, we chose cumyloxyl radicals as model species since they possess an absorption at 485 nm. The cumyloxyl radicals were generated from dicumylperoxide via laser flash photolysis, and their decay monitored as a function of sulfinic acid concentration to obtain the desired rate constants. In addition, kinetics for the reactions of the sulfinic acids with the triplet state of benzophenone (monitored at 530 nm) were also determined (Fig. 4A). The benzophenone triplet state has a much higher extinction coefficient than the cumyloxyl radical, greatly improving the signal quality. The results are comparable to those obtained with cumyloxyl radicals since the n → π* state of the carbonyl has a similar electronic structure to alkoxyl radicals. Representative results from measurements of the reactivity of PhSO2H with the benzophenone triplet (3BP) are shown in Fig. 4C. Interestingly, the pseudo first order rate constants from the decay traces yielded a non-linear relationship with sulfinic acid concentration. This suggested that self-association of the sulfinic acid in H-bonded dimers may retard the rate by precluding access to the labile H-atom. Indeed, the data could be easily fit to a non-linear equation accounting for the contribution of the competing equilibrium that defines the amount of sulfinic acid available for reaction (Fig. 4D). Doing so for the data in Fig. 4C yielded kH = (1.7 ± 0.3) × 109 M−1 s−1 and Kd = (6.4 ± 2.2) × 10−3 M. Corresponding data obtained with cumyloxyl radicals under otherwise identical conditions was ca. 2-fold slower, yielding kH = (6.9 ± 1.3) × 108 M−1 s−1.Given the retardation of the H-atom transfer from PhSO2H to 3BP and cumyloxyl by self-association, and the foregoing results with alkyl radicals, it was expected that the H-atom transfer kinetics would again be highly solvent dependent. Therefore, our investigations were expanded to include more (CH3CN, EtOAc) and less (PhCl) H-bond accepting solvents, the results of which are summarized in Fig. 4E. Plotting these data according to the Ingold–Abraham equation yields αH2 = 0.65, in good agreement with the value of 0.61 derived from the alkyl radical kinetic data. The rate constant for the reaction of TrptSO2H with 3BP was also determined for comparison. In CH3CN, where self-association does not contribute, kH = (1.8 ± 0.1) × 108 M−1 s−1, a factor of ∼3 greater than that measured for PhSO2H (kH = 6.5 ± 0.2) × 107 M−1 s−1, consistent with its slightly lower O–H BDE, and implying that the triptycene moiety imparts little to no steric effect on its fast HAT activity.
For comparison, the kinetics of HAT from TrptSOH to 3BP and cumyloxyl were also determined. In benzene, kH = (2.3 ± 0.1) × 109 and (1.4 ± 0.2) × 109 M−1 s−1 for 3BP and cumyloxyl, respectively. Consistent with the foregoing observations with the sulfinic acids, and trends in HAT reactions, in general, the rate constant for HAT to 3BP is slightly greater than for cumyloxyl. These kinetics were also explored in different solvents, revealing a significantly smaller effect than for the sulfinic acids (see Fig. 4B and E as well as the ESI†) – a surprising result given the similarity in H-bond acidity of the sulfenic and sulfinic acids (vide supra). In fact, when the rate constants for reactions with 3BP and cumyloxyl are plotted against the solvent H-bond basicity, the Ingold–Abraham equation predicts αH2 = 0.23 and 0.26, respectively – less than half the value measured directly by IR spectroscopy (αH2 = 0.54)31 or determined above from the kinetics of reactions with alkyl radicals (αH2 = 0.57). We surmise that a competing electron transfer reaction is enabled by the more polar (H-bond accepting) solvents.43
The CBS-QB3-calculated TS structures for HAT from PhSO2H and t-BuSOH to a model alkoxyl radical (t-butyloxyl) are shown in Fig. 4F and G. Consistent with experiment, the calculated free energy barriers are very small; ΔG‡ = 6.6 and 4.7 kcal mol−1 for PhSO2H and t-BuSOH, respectively, corresponding to k = 2.4 × 109 and 5.3 × 1010 M−1 s−1, respectively. Obviously, the exergonicity of these reactions is so great (ΔG0 = −29.2 and −38.3 kcal mol−1, respectively) that the kinetics have converged to be essentially diffusion-controlled.
Reactions with peroxyl radicals
The reactivity of sulfinic acids to peroxyl radicals was explored via inhibited co-autoxidation of PBD-BODIPY (Fig. 5A).44 PBD-BODIPY reports on the reaction progress of the autoxidation and its consumption is conveniently monitored by conventional spectrophotometry. Since its reactivity toward peroxyl radicals has been independently determined (e.g. kPBD-BODIPY = 3790 M−1 s−1 in 1-hexadecene/chlorobenzene at 37 °C, see ESI†), the inhibition rate constant (kinh) of an added peroxyl radical-trapping antioxidant and the stoichiometry of the inhibition reactions (n) can be easily derived from the data as in Fig. 5B. | ||
| Fig. 5 (A and B) PBD-BODIPY serves as the signal carrier in hydrocarbon autoxidations, enabling determination of rate constants (kinh) and reaction stoichiometries (n) for reactions of inhibitors with chain-carrying peroxyl radicals. (C) Co-autoxidations of 1-hexadecene (2.8 M) and PBD-BODIPY (10 μM) initiated by AIBN (6 mM) at 37 °C (dashed black trace) and inhibited by 10 μM of TrptSOH (red), TrpSO2H (blue), and PhSO2H (green). (D) The inhibition rate constants for TrptSOH, plotted as a function of medium βH2. (E–H) Calculated (CBS-QB3) TS structures for HAT between model sulfenic and sulfinic acid and model peroxyl radical (MeOO˙) and associated free energy barriers and rate constants estimated using transition state theory, HOMO visualized. TS structures were confirmed to link H-bonded pre- and post-reaction complexes by intrinsic reaction coordinate calculations (see ESI†). | ||
Despite extensive experimentation under various conditions and co-substrates, such as 1-hexadecene and styrene, we were unable to observe any inhibition of autoxidation by the sulfinic acids, suggesting that they do not efficiently react with the chain-carrying peroxyl radicals. Representative data are shown in Fig. 5C, where co-autoxidations carried out in the presence of PhSO2H and TrptSO2H can be compared to TrptSOH, which has previously been shown to undergo very fast reactions with peroxyl radicals (k = 3.0 × 106 M−1 s−1).30 Since sulfonyl radicals are known to readily add to alkenes (e.g. k = 7 × 109 M−1 s−1 for 2-vinylnaphthalene),45 which would afford an alkyl radical that could carry the autoxidation chain, inhibited autoxidations of substrates lacking a double bond (THF and dioxane) were also carried out, but yielded similar results. As expected, the peroxyl radical-trapping kinetics of the sulfenic acid was highly solvent-dependent, yielding αH2 = 0.46 when the data was plotted according to the Ingold–Abraham relationship (Fig. 5D), consistent with our previous report.31
To provide insight on the lack of reactivity of the sulfinic acids to peroxyl radicals, we calculated the transition state structures for the reactions of t-BuSO2H and t-BuSOH with a model peroxyl radical (methylperoxyl). Two low energy structures were identified for each system (Fig. 5E–H), one wherein the substituents on the oxygen atoms between which the H-atom is transferred are oriented anti with respect to one another, and the other wherein they are syn. The syn TS structures were significantly lower in energy in both cases and, consistent with the experimental observations, the predicted barriers for the reaction of t-BuSO2H were much higher than those for t-BuSOH. These results suggest that the inhibition rate constants for sulfinic acids are roughly seven orders of magnitude lower than for corresponding sulfenic acids, and as such, consistent with our observations that the sulfinic acids are incapable of inhibiting the co-autoxidations that were carried out.
Insight to the stark contrast in reactivity of the sulfinic and sulfenic acids is provided upon consideration of the HOMO of the transition states which are shown in Fig. 5E and F for the preferred syn TS and in Fig. 5G and H for the anti TS. Although there is clearly overlap between the π* of the peroxyl radical and the lone pair of the sulfur atom that leads to the preference for the syn TS in the reactions of both the sulfinic and sulfenic acids, this interaction is smaller in the sulfinic acid (ΔΔG‡ = 2.7 kcal mol−1) compared to the sulfenic acid (ΔΔG‡ = 5.1 kcal mol−1), presumably due to the lower sulfur lone pair energy in the sulfinic acid. Indeed, natural bond orbital analyses indicate that the interaction energy of the sulfur lone pair and peroxyl radical π* drops from 3 kcal mol−1 in the syn TS of the sulfenic acid reaction to 0.4 kcal mol−1 in the syn TS of the sulfinic acid reaction.
In addition to the foregoing efforts, we performed transient absorption spectroscopic experiments to directly monitor the reaction of peroxyl radicals with sulfinic acids. The cumyl radicals generated from photolysis of dicumylketone (see above) were used to produce cumylperoxyl radicals simply by carrying out the photolysis under an atmosphere of O2. Although cumylperoxyl radicals do not exhibit a visible absorption – precluding observation of their decay in the presence of sulfinic acids – the product sulfonyl radicals absorb at 350 nm. Nevertheless, the data acquired over a wide range of concentrations (validated through comparing with the equivalent alkyl radicals – see ESI† for conditions), suggested no sulfonyl radical formation on the timescale of the experiment.
Discussion
Thiols, the precursors to both sulfenic and sulfinic acids,32,46,47 are eminently useful H-atom transfer agents,48 serving as terminal (stoichiometric) reductants in a number of transformations, including the thiol-ene coupling49,50 and its aerobic counterpart, the TOCO reaction.51,52 We recently showed that the oxidation of a thiol to a sulfenic acid32 renders it a better H-atom donor – on thermodynamic grounds (i.e. alkyl sulfenic acid SO–H BDE ∼70 kcal mol−1vs. alkyl thiol S–H BDE ∼87 kcal mol−1)31 and kinetic grounds (e.g. k ∼ 107 M−1 s−1 for reactions of alkyl sulfenic acids with peroxyl radicals vs. <103 M−1 s−1 for alkyl thiols).30 However, the greater stability of the sulfinyl radicals precludes useful chemistry. To the best of our knowledge, there is no equivalent of the thiol-ene coupling or TOCO reaction with a sulfenic acid, although these could be very useful reactions! In the preceding pages we have expanded our previous studies to show that, despite their significantly weaker bonds, sulfenic acids are only slightly more inherently reactive towards alkyl and alkoxyl radicals compared to thiols. Moreover, because sulfenic acids are such good H-bond donors (αH2 ∼ 0.55) they react more slowly than thiols (αH2 ∼ 0–0.1)53 in good H-bond accepting solvents.Further oxidation of the sulfenic acid to a sulfinic acid enables production of the more reactive sulfonyl radical that can be used for productive chemistry. Indeed, Lei and co-workers recently demonstrated the sulfinic acid equivalent of a TOCO reaction,12 another example that sulfinic acids are gaining in popularity. The foregoing results enable us to place the reactivity of sulfinic acids into proper context; the alkyl sulfinic S(O)O–H BDE ∼78 kcal mol−1 infers that the stability of the sulfonyl radical is roughly midway between that of thiyl and sulfinyl radicals. Nevertheless, sulfinic acids are similarly inherently reactive to both alkyl and alkoxyl radicals as sulfenic acids and thiols. Importantly, like sulfenic acids, sulfinic acids are excellent H-bond donors (αH2 ∼ 0.63), and as such, they are relatively poor H-atom donors compared to thiols in good H-bonding solvents. Thus, sulfinic acids are expected to be useful as H-atom transfer agents only in non-H-bonding solvents;54 otherwise, thiols are likely to be a much better choice. Indeed, Lei's TOCO-like reaction and Nicewicz's use of sulfinic acids as catalytic H-atom donors in photocatalytic alkene functionalizations are optimal in weak H-bond accepting chlorinated hydrocarbons (βH2 ∼0.15).55
To complete the sulfur oxyacid series, we used CBS-QB3 to predict the O–H BDE in a sulfonic acid. The computed result of 107.4 kcal mol−1 for t-BuSO3H underscores why these compounds are unreactive to any of the radicals we have investigated here. For ease of reference, a summary of our results is presented in Fig. 6.
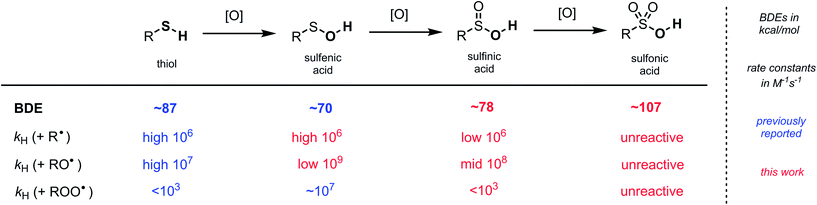 | ||
| Fig. 6 Comparison of H-atom transfer thermochemistry and kinetics for thiols and each of the thiol-derived sulfur oxyacids. | ||
In light of the similar inherent reactivity of thiols, sulfinic acids, and sulfenic acids to alkyl and alkoxyl radicals, the difference in the peroxyl radical reactivity between thiols and sulfenic acids (>4 orders of magnitude) is quite significant. In one sense, this is intuitive given that the reactions are far less exergonic (e.g. compare ΔG° ∼ −16 and ∼0 kcal mol−1 for reactions of sulfenic acids and thiols with peroxyl radicals versus ΔG° = −34 and −18 kcal mol−1 for reactions of sulfenic acids and thiols with primary alkyl or alkoxyl radicals). However, previous work from our group31,56,57 suggests that there is more to it; specifically, that HAT to peroxyl radicals is enabled by secondary orbital interactions, wherein filled π or non-bonding orbitals on the group attached to the atom from which the H-atom is being transferred interact with the proximal end of the peroxyl radical π* MO.73 Upon oxidation of the electron-rich sulfur atom in the sulfenic acid to a sulfinic acid, this secondary orbital interaction is expected to be significantly reduced. Indeed, our calculations predict that the sulfinic acid is not only less reactive to peroxyl radicals than the sulfenic acid, but is even less reactive than thiols, despite significantly more favourable reaction energetics (of ca. 10 kcal mol−1). Moreover, both PhSO2H and TrptSO2H were incapable of inhibiting the autoxidation of styrene and 1-hexadecene, substrates whose autoxidation is propagated by peroxyl radicals.58
At first glance, the poor HAT reactivity of sulfinic acids toward peroxyl radicals would seem to be the best evidence to date that secondary orbital interactions contribute to the reactivity of good peroxyl radical-trapping agents (i.e. antioxidants). However, it must be acknowledged that there is another explanation for the lack of inhibition of the autoxidation: the sulfinic acids themselves autoxidize. This has been noted to be particularly facile in water,59 where it is likely to be initiated and propagated by single electron transfer reactions, eventually producing a sulfonate:
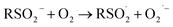 | (1) |
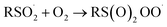 | (2) |
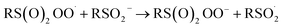 | (3) |
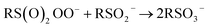 | (4) |
There is also precedence for sulfinic acid autoxidation in non-polar organic solvents,60 which presumably propagates via H-atom transfer in lieu of single electron transfer (In˙ is an arbitrary initiating radical):
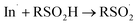 | (5) |
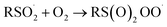 | (6) |
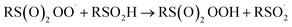 | (7) |
| RS(O)2OOH + RSO2H → 2RSO3H | (8) |
Presented in this way, sulfinic acid autoxidation is analogous to aldehyde autoxidation, which eventually yields carboxylic acids via Baeyer–Villiger oxidation of the aldehyde with the autoxidation product peracid.
The increasing popularity of sulfinic acids (and/or their corresponding sulfinate salts) to carry out sulfonylations of multiple bonds or serve as a terminal reducing agent is surprising in light of their purported facile autoxidation. The autoxidation depends on the rate and equilibrium position of eqn (6) as well as the follow-up H-atom transfer reaction (eqn (7)). The rate constant for the reaction of sulfonyl radicals with O2 has been reported to be 1 × 109 M−1 s−1 in water/MeOH.61 If the reaction were this fast in organic solvent, reactions involving sulfonyl radicals would be impossible under aerobic conditions.12,13,17 For example, under the reaction conditions developed by the Lei group for oxidative functionalization of alkynes,13 both the addition of sulfonyl radicals and the addition of oxygen would have effective rates of around 1 × 107 s−1. Therefore, yields of 80% would be impossible, since the sulfinic acid (present in excess) would simply autoxidize. Surprisingly, there is no data for the reaction of sulfonyl radicals with O2 in the non-aqueous solvents in which synthetic organic transformations are generally carried out. Moreover, there are no data on the position of the 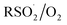 equilibrium and the H-atom abstraction from a sulfinic acid by a sulfonylperoxyl radical.
equilibrium and the H-atom abstraction from a sulfinic acid by a sulfonylperoxyl radical.
To provide some insight on the rate and equilibrium position of 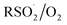 in organic solvents, we carried out additional CBS-QB3 calculations. The addition of oxygen to
in organic solvents, we carried out additional CBS-QB3 calculations. The addition of oxygen to 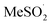 and
and 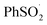 is predicted to be exergonic by 2.9 kcal mol−1, with barriers of ΔG‡ = 11.0 and 10.0 kcal mol−1, corresponding to rate constants of k = 2.8 × 106 and 1.4 × 107 M−1 s−1, respectively, at 37 °C.62 These results suggest that water and/or protic solvents accelerate the reaction and increase the driving force – perhaps due to stronger H-bonding interactions in the product sulfonylperoxyl than the starting sulfonyl.
is predicted to be exergonic by 2.9 kcal mol−1, with barriers of ΔG‡ = 11.0 and 10.0 kcal mol−1, corresponding to rate constants of k = 2.8 × 106 and 1.4 × 107 M−1 s−1, respectively, at 37 °C.62 These results suggest that water and/or protic solvents accelerate the reaction and increase the driving force – perhaps due to stronger H-bonding interactions in the product sulfonylperoxyl than the starting sulfonyl.
Interestingly, if the sulfonylperoxyl radical forms, it is predicted to be extremely reactive; the calculated barrier for H-atom abstraction from MeSO2H by MeS(O)2OO˙ is predicted be ΔG‡ = 7.0 kcal mol−1, corresponding to a rate constant of 1.9 × 109 M−1 s−1. This would lead to very fast consumption of sulfinic acid.63 Recall, the predicted barrier for H-atom abstraction from MeSO2H by MeOO˙ is nine orders of magnitude slower!
To corroborate these predictions, we photolyzed p-toluenesulfonyl iodide in benzene and monitored the decay of the p-toluenesulfonyl radical at 350 nm in the presence and absence of O2. Under an atmosphere of N2, the tosyl radicals decayed with k = (7.3 ± 0.5) × 108 M−1 s−1, consistent with the kinetics of their disproportionation to sulfinyl and sulfonyloxyl radicals obtained by EPR.35 The tosyl radicals decayed at a greater rate when analogous experiments were carried out under an air atmosphere, yielding an apparent rate constant of k = (1.0 ± 0.2) × 109 M−1 s−1. Assuming this rate constant is the superposition of the disproportionation and O2 addition reactions, a rate constant for the latter can be estimated to be k = (9 ± 4) × 105 M−1 s−1, in remarkably good agreement with the value predicted by CBS-QB3, and most importantly, >1000-fold slower than in aqueous solution.64 With a rate constant in this range, typical propagating reactions of sulfonyl radicals (e.g. addition to double and triple bonds, k = 107 to 109 M−1 s−1)45 can compete effectively with oxygen addition, which under typical synthetic conditions65 translates to a difference of 3–3.5 orders of magnitude in reaction rates.66 An indication that optimized synthetic procedures depend strongly on these kinetics is highlighted by the significant drop in yield (>50%) that is observed upon switching from an air atmosphere to exclusively O2.13
Conclusions
Sulfinic acids are very good H-atom donors which lead to highly reactive sulfonyl radicals having a wide range of synthetic applications. Their HAT reactivity is quite similar to that of sulfenic acids, however, because of their increased BDE of ∼78 (vs. 70) kcal mol−1 they are typically slightly slower with rate constants of at 2 × 106 M−1 s−1 with alkyl radicals and 5 × 108 M−1 s−1 with alkoxyl radicals. A surprising property is the slow reaction of sulfinic acids with peroxyl radicals, which could not be measured, and was calculated to take place with a rate constant of ∼1 M−1 s−1, which underscores the role of secondary orbital interactions in facilitating H-atom transfer to peroxyl radicals. Although sulfinic acids are known to readily autoxidize, this has not deterred recent synthetic endeavours. We have found that the key propagating reaction of the sulfonyl radical with O2 is greatly slowed in organic solvents relative to water to enable these reactions to proceed. Similar to sulfenic acids, the more oxidized sulfinic acids also show high H-bond acidity and therefore a very large modulation of their HAT activity in different solvents. This should be taken into account when employing them in catalytic and/or chain reactions.Experimental section
General
Reagents were obtained from commercial suppliers and used as received, unless indicated otherwise. Column chromatography was carried out with 40–63 μm, 230–400 mesh silica gel. 1H and 13C NMR spectra were recorded on a Bruker AVANCE spectrometer operating at 400 MHz and 101 MHz, respectively, unless indicated otherwise. High-resolution mass spectra were obtained on a Kratos Concept Tandem mass spectrometer (EI) and Micromass Q-TOF (ESI). TrptSO2H, PhSO2H and dicumylketone were synthesized as described in the ESI.† TrptSOH,28 PBD-BODIPY,31 STY-BODIPY,44 NMBHA,67 tosyl iodide,68 as well as the GC standards for the alkyl radical clock kinetics69 were synthesized following previously reported procedures. Chlorobenzene was dried over 3 Å molecular sieves before use. Solvents for kinetics experiments were of anhydrous or HPLC quality. UV-visible spectra were measured with a Cary 100 spectrophotometer equipped with a thermostatted 6 × 6 multi-cell holder.Radical equilibration EPR (REqEPR)
Electron paramagnetic resonance (EPR) spectra were recorded on a Bruker EMXplus (X-band) spectrometer equipped with an ER 4119HS cavity. The (composite) spectra were fitted and the radical concentration was determined using the quantitative EPR package of the Bruker Xenon software. The full procedure to determine thermodynamic data can be found in the ESI.† To generate the radicals, 5% (v/v) di-tert-butyl peroxide was added to the solutions in benzene (with or without 10% v/v t-BuOH) under nitrogen and the EPR cavity irradiated with a Hamamatsu LC5 Hg–Xe lamp (150 W) via a 3.5 mm quartz light guide. REqEPR experiments with sulfonyl radicals were performed under continuous irradiation.Laser flash photolysis
Nanosecond transient absorption experiments were performed on an LFP-112 spectrometer (Luzchem, Canada) using a EX10 (GAM Laser, USA) XeCl excimer laser (308 nm, ca. 10 mJ per pulse, ca. 12 ns pulse width). The transient absorption data were recorded in a quartz cuvette (1 cm × 1 cm) equipped with a septum. Sample concentrations were adjusted to yield an absorbance of 0.2–0.3 at 308 nm and the solutions were bubbled with nitrogen for 10 minutes before measurement. The rate constants for H-atom abstraction (kH) were determined under pseudo-first-order conditions and calculated according to kobs = k0 + kH[H-donor].Competition kinetics
Alkyl radical clock kinetics was determined using a previously reported procedure by Valgimigli and co-workers.40 The Barton (PTOC) ester synthesis is described in the ESI† and the standards were synthesized as described previously.69 Briefly, vials were loaded with the appropriate amount of sulfinic acid (150–400 mM) and capped with a septum. THF (950 μL) was added followed by 1 eq. of methanesulfonic acid and the vials were wrapped in aluminum foil before adding the PTOC ester (20 mM). The vials were purged with nitrogen and the aluminum foil was removed before the vials were exposed to a sodium lamp (400 W) at a distance of 40 cm for 1 h at room temperature (ca. 25 °C). Aliquots of 50 μL were taken from each vial and added to a GC vial containing hexylbenzene standard solution (50 μL, 40 mM). The solution was diluted with 900 μL of acetonitrile for a total volume of 1 mL per vial. The samples (4 μL splitless injections) were analyzed by GC-MS on an Agilent HP-5 ms column (30 m × 0.25 mm × 0.25 μm) with a constant He flow of 1.1 mL min−1 using the following temperature profile: (inlet temperature was set to 150 °C): 90 °C, hold 1 min, 2 °C min−1 to 120 °C, hold 1 min, 5 °C min−1 to 165 °C, hold 1 min, 20 °C min−1 to 300 °C, hold 5 min. The method yielded retention times of 10.9, 22.9, 23.4, and 25.4 min for hexylbenzene, 2-tert-butylnaphthalene, 2-isobutylnaphthalene, 2-(2-methylallyl)naphthalene and 2-(2-methylprop-1-en-1-yl)naphthalene, respectively.Inhibited autoxidations
Inhibited autoxidations were performed as previously described.56 The procedure for 1-hexadecene autoxidation in chlorobenzene is transcribed below. 1-Hexadecene (2.0 mL) was added to a 3.5 mL cuvette along with PhCl (0.44 mL). The cuvette was then placed in the thermostated sample holder of a UV-vis spectrophotometer and equilibrated to 37 °C for approximately 10 min. The PBD-BODIPY probe (12.5 μL, 2.0 mM solution in 1,2,4-trichlorobenzene) was added followed by AIBN (50 μL, 300 mM in chlorobenzene) and the solution was thoroughly mixed. The absorbance at 588 nm was monitored for 10 min after which 10 μL of a solution of the test antioxidant was added. The solution was then mixed and the absorbance readings resumed. The resulting data were processed as previously reported.44,56 PMC, which has an established stoichiometry of 2,70 was used as a standard to derive the rate of initiation (Ri = 1.3 × 10−9 M s−1) and propagation rate constant for the dye (kPBD-BODIPY = 3790 M−1 s−1).Calculations
Electronic structure calculations were carried out using the CBS-QB3 complete basis set method71 as implemented in the Gaussian 16 suite of programs.72 Stationary points were identified as minima or maxima by calculation of second derivatives. Maxima were verified to be transition states for the relevant H-atom transfer reactions by carrying out intrinsic reaction coordinate calculations in both the forward and reverse directions. Rate constants were calculated via transition state theory at 25 °C, except for reactions with peroxyl radicals (37 °C, for comparison with experiment).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grants from the Natural Sciences and Engineering Research Council of Canada and the Canada Foundation for Innovation and through generous access to the computational resources of the Centre for Advanced Computing (https://cac.queensu.ca). JPC acknowledges the support of the Ontario Graduate Scholarships program. We are grateful to Dr Marco Mazzonna and Prof. Osvaldo Lanzalunga (University of Rome, Sapienza) for their early efforts to understand the kinetics of the reactions of sulfenic acids with alkoxyl radicals.Notes and references
- C. Chatgilialoglu, M. P. Bertrand and C. Ferreri, in S-Centered Radicals, ed. Z. B. Alfassi, Wiley, 1999, pp. 311–354 Search PubMed.
- R. S. Glass, Top. Curr. Chem., 2018, 376, 1–42 CrossRef PubMed.
- Oxidation and Antioxidants in Organic Chemistry and Biology, ed. E. T. Denisov and I. B. Afanas'ev, CRC Press, 2005 Search PubMed.
- Y. Jiang and T.-P. Loh, Chem. Sci., 2014, 5, 4939–4943 RSC.
- A. Garcia-Dominguez, S. Mueller and C. Nevado, Angew. Chem., Int. Ed., 2017, 56, 9949–9952 CrossRef PubMed.
- C. S. Gloor, F. Denes and P. Renaud, Angew. Chem., Int. Ed., 2017, 56, 13329–13332 CrossRef PubMed.
- T. Taniguchi, A. Idota and H. Ishibashi, Org. Biomol. Chem., 2011, 9, 3151–3153 RSC.
- J. M. Fang and M. Y. Chen, Tetrahedron Lett., 1987, 28, 2853–2856 CrossRef.
- N. Mantrand and P. Renaud, Tetrahedron, 2008, 64, 11860–11864 CrossRef.
- E. Block, M. Aslam, V. Eswarakrishnan, K. Gebreyes, J. Hutchinson, R. Iyer, J. A. Laffitte and A. Wall, J. Am. Chem. Soc., 1986, 108, 4568–4580 CrossRef.
- They also figure prominently in polymer chemistry,11a–c and air pollution.11d (a) V. Percec, B. Barboiu and H. J. Kim, J. Am. Chem. Soc., 1998, 120, 305–316 CrossRef; (b) C. Gorsche, M. Griesser, G. Gescheidt, N. Moszner and R. Liska, Macromolecules, 2014, 47, 7327–7336 CrossRef; (c) G. Gryn'ova, T. Guliashvili, K. Matyjaszewski and M. L. Coote, Aust. J. Chem., 2013, 66, 308–313 CrossRef; (d) A. Mardyukov and P. R. Schreiner, Acc. Chem. Res., 2018, 51, 475–483 CrossRef PubMed.
- Q. Lu, J. Zhang, F. Wei, Y. Qi, H. Wang, Z. Liu and A. Lei, Angew. Chem., Int. Ed., 2013, 52, 7156–7159 CrossRef PubMed.
- Q. Lu, J. Zhang, G. Zhao, Y. Qi, H. Wang and A. Lei, J. Am. Chem. Soc., 2013, 135, 11481–11484 CrossRef PubMed.
- Z. Huang, Q. Lu, Y. Liu, D. Liu, J. Zhang and A. Lei, Org. Lett., 2016, 18, 3940–3943 CrossRef PubMed.
- A. J. Perkowski and D. A. Nicewicz, J. Am. Chem. Soc., 2013, 135, 10334–10337 CrossRef PubMed.
- Z. Yuan, H.-Y. Wang, X. Mu, P. Chen, Y.-L. Guo and G. Liu, J. Am. Chem. Soc., 2015, 137, 2468–2471 CrossRef PubMed.
- Y. Ning, Q. Ji, P. Liao, E. A. Anderson and X. Bi, Angew. Chem., Int. Ed., 2017, 56, 13805–13808 CrossRef PubMed.
- Y. Xi, B. Dong, E. J. McClain, Q. Wang, T. L. Gregg, N. G. Akhmedov, J. L. Petersen and X. Shi, Angew. Chem., Int. Ed., 2014, 53, 4657–4661 CrossRef PubMed.
- F. Chen, Q. Meng, S.-Q. Han and B. Han, Org. Lett., 2016, 18, 3330–3333 CrossRef PubMed.
- T. C. Johnson, B. L. Elbert, A. J. M. Farley, T. W. Gorman, C. Genicot, B. Lallemand, P. Pasau, J. Flasz, J. L. Castro, M. MacCoss, D. J. Dixon, R. S. Paton, C. J. Schofield, M. D. Smith and M. C. Willis, Chem. Sci., 2018, 9, 629–633 RSC.
- A. U. Meyer, K. Strakova, T. Slanina and B. Koenig, Chem.–Eur. J., 2016, 22, 8694–8699 CrossRef PubMed.
- Gilbert and co-workers have estimated k ∼ 106 M−1 s−1 for the reaction of methanesulfinic acid with methyl radicals, both of which are formed in the reaction of DMSO with hydroxyl radicals.36.
- J. G. Calvert, C. C. Badcock, H. W. Sidebottom, G. W. Reinhardt and E. K. Damon, J. Am. Chem. Soc., 1971, 93, 3115–3121 CrossRef.
- A. G. Davies, B. P. Roberts and B. R. Sanderson, J. Chem. Soc., Perkin Trans. 2, 1973, 626–630 RSC.
- S. W. Benson, Chem. Rev., 1978, 78, 23–35 CrossRef.
- F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, J. Org. Chem., 2008, 73, 9109–9120 CrossRef PubMed.
- A. Gunturu, R. Asatryan and J. W. Bozzelli, J. Phys. Org. Chem., 2011, 24, 366–377 CrossRef.
- A. J. McGrath, G. E. Garrett, L. Valgimigli and D. A. Pratt, J. Am. Chem. Soc., 2010, 132, 16759–16761 CrossRef PubMed.
- V. Vaidya, K. U. Ungold and D. A. Pratt, Angew. Chem., Int. Ed., 2009, 48, 157–160 CrossRef PubMed.
- R. Amorati, P. T. Lynett, L. Valgimigli and D. A. Pratt, Chem.–Eur. J., 2012, 18, 6370–6379 CrossRef PubMed.
- Z. Zielinski, N. Presseau, R. Amorati, L. Valgimigli and D. A. Pratt, J. Am. Chem. Soc., 2014, 136, 1570–1578 CrossRef PubMed.
- J.-P. R. Chauvin and D. A. Pratt, Angew. Chem., Int. Ed., 2017, 56, 6255–6259 CrossRef PubMed.
- M. Lucarini, P. Pedrielli, G. F. Pedulli, S. Cabiddu and C. Fattuoni, J. Org. Chem., 1996, 61, 9259–9263 CrossRef.
- C. Chatgilialoglu, B. C. Gilbert and R. O. C. Norman, J. Chem. Soc., Perkin Trans. 2, 1979, 770–775 RSC.
- J. E. Bennett, G. Brunton, B. C. Gilbert and P. E. Whittall, J. Chem. Soc., Perkin Trans. 2, 1988, 1359–1364 RSC.
- B. C. Gilbert, R. O. C. Norman and R. C. Sealy, J. Chem. Soc., Perkin Trans. 2, 1975, 303–308 RSC.
- The previously calculated value was 75.7 kcal mol−1 for t-butylsulfinic acid27 which shows a significant difference to TrptSO2H.
- Previous CBS-QB3 calculations on t-butylsulfenic acid yielded 68.6 kcal mol−1, indicating that the three aryl substituents bonded to the carbon which bears the sulfenic acid in TrptSOH clearly impart a slight electron-withdrawing effect, destabilizing the electron-poor sulfinyl radical and driving up the O–H BDE.
- R. Amorati, M. Lucarini, V. Mugnaini, G. F. Pedulli, F. Minisci, F. Recupero, F. Fontana, P. Astolfi and L. Greci, J. Org. Chem., 2003, 68, 1747–1754 CrossRef PubMed.
- R. Leardini, M. Lucarini, G. F. Pedulli and L. Valgimigli, J. Org. Chem., 1999, 64, 3726–3730 CrossRef PubMed.
- D. W. Snelgrove, J. Lusztyk, J. T. Banks, P. Mulder and K. U. Ingold, J. Am. Chem. Soc., 2001, 123, 469–477 CrossRef.
- A rate constant for the reaction of hydroxyl radicals with methanesulfinic acid has been reported (6.0 × 10−9 M−1 s−1).36.
- ET reactions are more facile in more polar solvents, and will therefore increase when moving to higher βH2 values in the solvent diagram. This will lower the slope of the overall rate constant k and therefore lead to a decrease in αH2. This effect correlates with the reduction potential of the involved radical and is therefore strongest with benzophenone (E° = 1.27 V)43a and alkoxyl radicals (E° = 0.9 V),43b but not present with alkyl radicals (E° = −1.73 V).43c (a) K. McNeill and S. Canonica, Environ. Sci.: Processes Impacts, 2016, 18, 1381–1399 RSC; (b) G. Merenyi, J. Lind and L. J. Engman, J. Chem. Soc., Perkin Trans. 2, 1994, 2551–2553 RSC; (c) D. D. M. Wayner, D. J. McPhee and D. Griller, J. Am. Chem. Soc., 1988, 110, 132–137 CrossRef.
- E. A. Haidasz, A. T. M. Van Kessel and D. A. Pratt, J. Org. Chem., 2016, 81, 737–744 CrossRef PubMed.
- C. Chatgilialoglu, O. Mozziconacci, M. Tamba, K. Bobrowski, G. Kciuk, M. P. Bertrand, S. Gastaldi and V. I. Timokhin, J. Phys. Chem. A, 2012, 116, 7623–7628 CrossRef PubMed.
- M. Hugo, L. Turell, B. Manta, H. Botti, G. Monteiro, L. E. S. Netto, B. Alvarez, R. Radi and M. Trujillo, Biochemistry, 2009, 48, 9416–9426 CrossRef PubMed.
- K. Goto, M. Holler and R. Okazaki, J. Am. Chem. Soc., 1997, 119, 1460–1461 CrossRef.
- F. Denes, M. Pichowicz, G. Povie and P. Renaud, Chem. Rev., 2014, 114, 2587–2693 CrossRef PubMed.
- M. J. Kade, D. J. Burke and C. J. Hawker, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 743–750 CrossRef.
- C. E. Hoyle, A. B. Lowe and C. N. Bowman, Chem. Soc. Rev., 2010, 39, 1355–1387 RSC.
- M. S. Kharasch, W. Nudenberg and G. J. Mantell, J. Org. Chem., 1951, 16, 524–532 CrossRef.
- H. H. Szmant, A. J. Mata, A. J. Namis and A. M. Panthananickal, Tetrahedron, 1976, 32, 2665–2680 CrossRef.
- M. H. Abraham, R. J. Abraham, J. Byrne and L. Griffiths, J. Org. Chem., 2006, 71, 3389–3394 CrossRef PubMed.
- At elevated concentrations in solvents of low H-bond accepting ability, the reactivity of sulfinic acids to highly reactive species (e.g. alkoxyl radicals) may, however, be diminished due to self-association (dimerization).
- M. H. Abraham, P. L. Grellier, D. V. Prior, J. J. Morris and P. J. Taylor, J. Chem. Soc., Perkin Trans. 2, 1990, 521–529 RSC.
- J.-P. R. Chauvin, M. Griesser and D. A. Pratt, J. Am. Chem. Soc., 2017, 139, 6484–6493 CrossRef PubMed.
- D. Hu and D. A. Pratt, Chem. Commun., 2010, 46, 3711–3713 RSC.
- During our investigations we found one further example of a significant difference in HAT reactivity between sulfinic and sulfenic acids: the phenylthiyl radical – for further details see the ESI.†.
- K. Sehested and J. Holcman, Radiat. Phys. Chem., 1996, 47, 357–360 CrossRef.
- L. Horner and O. H. Basedow, Justus Liebigs Ann. Chem., 1958, 612, 108–131 CrossRef.
- M. Tamba, K. Dajka, C. Ferreri, K.-D. Asmus and C. Chatgilialoglu, J. Am. Chem. Soc., 2007, 129, 8716–8723 CrossRef PubMed.
- The corresponding reaction of MeSO˙ is 12.2 kcal mol−1 endergonic.
- To test this assumption, we attempted to monitor the sulfinic acid during the autoxidation. To do so, we employed a 9-triptycenesulfinic acid featuring a fluorine atom at the other bridgehead position such that the reaction could be followed directly by 19F NMR. We recently showed that the sulfinic and sulfonic acids of this fluorinated triptycene have distinct chemical shifts.32 Although the concentration of the sulfinic acid was increased up to 10 mM in order to facilitate detection by NMR, the experiment revealed rapid consumption of the sulfinic acid on the time-scale of the experiment, which would prevent them to inhibit the autoxidation.
- This indicates that the formation of sulfonyl radicals should be visible in LFP experiments with cumyloxyl radicals if they would react at rates similar to sulfenic acid (107 M−1 s−1) or other comparable antioxidants (such as α-tocopherol, which has a comparable BDE and reacts at 106 M−1 s−1). Therefore, the LFP results strongly suggest that the reaction of alkylperoxyl radicals with sulfinic acids are as slow as predicted by calculations (<103 M−1 s−1).
- [Substrate (alkene or alkyne)] = 50 mM and [oxygen] = 2–7 mM.
- Of course, the additions must also compete with the disproportionation of sulfonyl radicals, but this is quite slow in comparison due to the very low concentrations of these transient intermediates compared to the alkene/alkyne substrate.
- G. X. Ortiz, B. N. Hemric and Q. Wang, Org. Lett., 2017, 19, 1314–1317 CrossRef PubMed.
- G. L. Edwards, C. A. Muldoon and D. J. Sinclair, Tetrahedron, 1996, 52, 7779–7788 CrossRef.
- J. J. Hanthorn, R. Amorati, L. Valgimigli and D. A. Pratt, J. Org. Chem., 2012, 77, 6895–6907 CrossRef PubMed.
- G. W. Burton, T. Doba, E. Gabe, L. Hughes, F. L. Lee, L. Prasad and K. U. Ingold, J. Am. Chem. Soc., 1985, 107, 7053–7065 CrossRef.
- J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03; Wallingford, CT, 2016 Search PubMed.
- It is very difficult to definitively tease out whether these types of reactions should be described as a HAT or proton-coupled electron transfer (PCET). However, simply considering the TS geometries in Fig. 5, the authors are inclined to describe them as HAT-like. Since both the sulfinyl/sulfonyl and peroxyl radicals are π radicals, a HAT TS would feature the H-atom moving along a coordinate that is orthogonal to the planes made up by the carbon, sulfur and oxygen of the sulfinyl/sulfonyl radical and the carbon, oxygen and oxygen of the peroxyl radical. In contrast, in a purely PCET process, the proton and electron are, by definition, transferred between different pairs of (nominally orthogonal) orbitals; the proton between the lone pairs on the terminal oxygen atoms of the sulfinyl/sulfonyl and peroxyl radicals and the unpaired electron is delocalized across both π* orbitals. The predicted structures are more consistent with the former description than the latter. This is perhaps easiest to see in the SOMOs, where there is a node on the H-atom (see ESI†).
- N. Nakamura, J. Am. Chem. Soc., 1983, 105, 7172–7173 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization data, further autoxidation data, LFP results, calculations of REqEPR and hydrogen bonding, optimized geometries and energies for computational results. See DOI: 10.1039/c8sc02400f |
| This journal is © The Royal Society of Chemistry 2018 |