Open Access Article
Open Access ArticleThinking outside the box: placing hydrophilic particles in an oil phase for the formation and stabilization of Pickering emulsions†
Paula
Facal Marina‡
 ,
Jie
Xu‡
,
Xuan
Wu
and
Haolan
Xu
,
Jie
Xu‡
,
Xuan
Wu
and
Haolan
Xu
 *
*
Future Industries Institute, University of South Australia, Mawson Lakes Campus, Adelaide, SA 5095, Australia. E-mail: haolan.xu@unisa.edu.au
First published on 27th April 2018
Abstract
Pickering emulsions, also known as particle stabilized emulsions, are one kind of extremely important emulsion for both fundamental research and practical applications. Many colloidal particles have been utilized as emulsifiers to stabilize Pickering emulsions. However, the most challenging issue is preparing Pickering emulsions with highly hydrophilic particles, because their adsorption onto oil–water interfaces is either thermodynamically or kinetically unfavorable. Although several strategies have been developed to overcome the poor ability of the hydrophilic particles to stabilize the emulsions, surface modification and functionalization of the hydrophilic particles or a change in solvent (i.e. water phase) conditions such as pH and ionic strength is required. Herein, we present an effective and not yet explored strategy to stabilize Pickering emulsions with unmodified highly hydrophilic particles, strikingly, without changing the solvent conditions. The innovative aspect of the strategy presented here is the unconventional dispersion of hydrophilic particles in an oil phase before emulsification, while the results experimentally demonstrate the theoretical calculations predicted more than a decade ago. This study will promote the diversity of Pickering emulsions and expand their real-world applications.
Introduction
Pickering or particle-stabilized emulsions are remarkably stable due to the unfavourable detachment of the emulsifier particles that are surrounding the emulsion droplets.1,2 Such a protective shell of the particle provides steric hindrance and effectively prevents the coalescence of emulsion droplets.3–5 Compared to traditional emulsions, Pickering emulsions possess superior stability, while avoiding the utilization of surfactants, which alleviates environmental issues since most of them end up being dispersed in different environmental compartments such as soil, water or sediment.6 Although Pickering emulsions were first reported about 100 years ago, the renewed interest and their further development were promoted in the 1990s by Velev and Binks in the form of application and fundamental studies.7–16 Soon thereafter the use of Pickering emulsions was extended and they became unique platforms used to synthesize advanced capsules, colloidosomes, supracolloidal materials and colloidal nano-composites.17–26 Recently, Pickering emulsions stabilized by catalytic particles have shown unique advantages in interfacial catalysis in terms of phase transfer and product separation.27–31 Particle-stabilized emulsions have also found a use in a myriad of industrial processes, such as food, crude-oil and mineral processing.32To meet this wide range of applications, it is highly desired to prepare Pickering emulsions with a wide spectrum of particles as emulsifiers. Indeed, the latest trends point towards the use of types of particle as yet unexplored, such as coloured organic pigment, core–shell, polymeric and highly hydrophilic particles.33–37 With regards to the latter, several attempts have been made to use hydrophilic silica particles to stabilize oil-in-water emulsions by either adjusting the solution pH, adding salt, adding a cationic surfactant or even by in situ modification of the particles’ surface.38–40 It seems reasonable that decreasing the effective anionic surface charge density on the silica particles causes the particles to be less hydrophilic.41–45 However, one matter that increasingly captures the interest of specialist researchers is the possibility of stabilizing Pickering emulsions with highly hydrophilic particles as emulsifiers, without changing the solvent conditions or the surface property and activity of such particles, which has been rarely realized so far.
Thermodynamically, the adsorption of particles onto oil–water interfaces to form Pickering emulsions is an energy favourable process. Upon mixing oil and water, the as-formed droplets dispersed throughout the continuous phase dramatically increase the overall oil–water interfacial area, and thus the free energy of the system. To counterbalance this effect, if particles are present in the system, they are prone to migrate to the interfaces to reduce the overall free energy of the system:
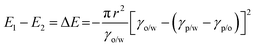 | (1) |
E = πr2γ(1 ± cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 θ)2 | (2) |
Therefore, the hydrophobicity of the particles (determined by θ) governs the free energy change of the system. From eqn (2), it can be calculated that attachment of colloidal particles of 0.01–10 μm in size and with an intermediate θ (30–60°) at oil–water interfaces reduces the free energy of 102–106kBT.46 Therefore, from a thermodynamic point of view, Pickering emulsions should be readily produced. In contrast, when the particle is super hydrophilic, the contact angle of the particle at oil–water interfaces may be close to 0 and little free energy change occurs as the particles migrate from the bulk water phase to interfaces. Consequently, the formation of a Pickering emulsion is not thermodynamically favourable.
Kinetically and from a practical viewpoint, the approach of colloidal particles to oil–water interfaces is also a key process for the formation of Pickering emulsions. Generally, hydrophilic particles carry charges due to the surface groups, likewise the pristine oil–water interfaces, which are also negatively charged in a wide pH range.47–52 Hence, when the hydrophilic particles and interfaces are both negatively charged, strong electrostatic repulsion between them could effectively hinder the adsorption of the colloidal particles onto the oil–water interfaces. Therefore the electrostatic and van der Waals interactions (DLVO theory) per se determine the magnitude of the energy barrier of the adsorption of colloidal particles.53,54 In most cases, the existence of such an adsorption barrier significantly reduces the probability of particle attachment to the interfaces and the formation of Pickering emulsions.39 In principle, to effectively eliminate the energy barrier it is necessary to screen the surface charge of either the oil–water interfaces or the particles, which is unrealistic under normal solvent conditions (e.g. neutral pH and low ionic strength). Adding salts and lowering the pH may eliminate the energy barrier and form the Pickering emulsions,38,39,55–57 however the solvent conditions will be changed. For many industries such as food processing, and drug and cosmetic production, in which the stabilization of emulsions is required to preserve the characteristics of the final product, it is not possible to adjust the pH or ionic strength to extreme values. In addition, commercial oil-in-water emulsions may be exposed to various environmental stresses during their manufacture, transport and storage, thus it is paramount that an emulsifier should be able to maintain emulsion stability under all of the possible conditions.58,59 Therefore, it is of great importance to develop new and effective strategies to realize the formation of Pickering emulsions with hydrophilic particles without changing solvent conditions.
Herein, by thinking outside the box, the hydrophilic emulsifier particles were initially placed in an oil phase, but not in an aqueous phase, before emulsification. This unconventional treatment successfully eliminated the energy barrier without modifying either the ionic strength or the pH value of the solvent. With this strategy bare hydrophilic silica (SiO2) particles synthesized by the Stöber method, as well as hydrophilic magnetite (Fe3O4) and polydopamine (PDA) particles, were successfully used to form and stabilize Pickering emulsions.
Finally, this novel and simple strategy not only proves that it is possible to eliminate the energy barrier of the adsorption of hydrophilic particles to oil–water interfaces, but it also promotes their entrapment at the interfaces by introducing a contact angle of ∼90° at the oil–water interfaces. This unorthodox way of stabilizing the emulsions does not require the use of exotic or complex experimental methods, and from the point of view of energy saving it is important to emphasize that strong mechanical agitation is not required to achieve it. It is interesting to note that the ability to stabilize emulsions in the manner proposed in this paper was predicted theoretically more than a decade ago by Danov and Kralchevsky et al.60 The results presented here will promote the diversity of Pickering emulsions and exponentially expand their real-world applications.
Materials
Tetraethyl orthosilicate (TEOS, ReagentPlus® ≥99%, product no. 236209), poly(acrylic acid) (PAA Mw ∼ 1800, product no. 323667), Nile red (NR, product no. 298395), hexadecane (HD, ReagentPlus®, 99%, product no. H67063) and dopamine hydrochloride (product no. H8502) were purchased from Sigma-Aldrich. Ammonia (30% solution AR, product number AA005), ethanol (EtOH undenatured 100% AR, glass bottle EA043), FeCl3·6H2O (Laboratory reagent FL023), ethanediol (AR, product no. EA007 glass bottle), NaOH pellet (AR, product no. SA178) and NaCl (AR, product no. SA046) were purchased from Chem-Supply. HCl (37% Reagent Grade) was purchased from Scharlau. Sodium acetate (anhydrous product no. 10236) was purchased from AnalaR.All of the chemicals were used without further purification. The water in all of the experiments was prepared in a three-stage Millipore Milli-Q Plus 185 purification system and had a resistivity of 18.2 MΩ cm−1.
Synthesis of SiO2 particles
Spherical SiO2 particles were prepared based on the Stöber method by hydrolyzing TEOS in a water–ethanol mixture containing ammonia.61 The detailed procedure for SiO2 particle synthesis is given in Table S1.† In brief, first ammonia, Milli-Q water and ethanol were mixed (final pH = 10). Then, TEOS was injected and allowed to react overnight while stirring at maximum speed. The temperature was kept constant at 30 °C. In order to purify the SiO2 particles, the dispersion was centrifuged at 3500 rpm for 30 minutes followed by redispersion in pure EtOH and sonication for 15 minutes (4 times). Half of the ethanolic dispersion was transferred to water by carrying out cycles of centrifugation at 3500 rpm for 30 minutes and redispersing in water until a neutral pH was reached. To transfer the SiO2 particles to HD, the ethanolic dispersion was centrifuged once at 3500 rpm for 30 minutes and redispersed in HD, followed by three steps of centrifugation at 3500 rpm for 5 minutes and redispersion in HD. To ensure that there was no trace of ethanol in the final SiO2 particle dispersion in HD, the process was repeated at least 4 times.Synthesis of magnetite particles (Fe3O4@PAA)
Fe3O4@PAA particles were synthesized according to a method reported by Liu et al.62 In brief, 0.864 g of FeCl3·6H2O was dissolved into 32 ml of ethylene glycol. After vigorous stirring, 0.0864 g of PAA was added into the mixture. After the FeCl3·6H2O completely dissolved in the ethylene glycol, 7.2 g of sodium acetate was then added and stirred until the mixture formed a homogeneous solution. Finally the solution was placed in a Teflon-lined stainless steel autoclave and kept in the oven at 200 °C for 12 h. After that, the dispersion was cooled down in the oven followed by steps of centrifugation to purify. Subsequently, the Fe3O4@PAA particles were transferred to HD by a process of centrifuging and redispersing, firstly in EtOH four times and then four times in HD.Synthesis of polydopamine particles (PDA)
PDA particles were synthesized by the self-polymerization of dopamine in alkaline solutions according to a procedure reported previously by our group.63 Briefly, 5 mg of dopamine was dissolved in 10 ml of NaOH (0.06 M) solution and then shaken for 18 h. The colour of the solution turned from colourless to black. The PDA particles were collected by centrifugation, and washed with water several times. The particles obtained were finally redispersed in 1 ml of water. Subsequently, the PDA particles were transferred to HD by steps of redispersing in EtOH and centrifuging 4 times. In the final step the particles were dispersed in HD followed by three more cycles of centrifugation and redispersion in HD.Characterization
Transmission electron microscopy (TEM) imaging was performed on an FEI Tecnai G2 Spirit Transmission Electron Microscope operating at an acceleration voltage of 120 kV, equipped with a FEG LaB6 emitter and BioTWIN lens design. Imaging was done via an in-column Olympus-SIS Veleta CCD camera. Five microliter droplets of each sample were dropped onto a piece of ultrathin Formvar-coated 200-mesh copper grid (GSCu200CH-100 Proscitech) and left to dry in air. To determine the diameter and diameter distribution of the resulting particles based on their TEM images, at least 100 particles were measured with the aid of the graphics editing program ImageJ®. Optical microscopy images were recorded by using a Nikon Eclipse Ti-U fluorescence microscope. Dynamic Light Scattering (DLS) and zeta potential studies were carried out on a Malvern Zetasizer Nano ZS (UK) at 25 °C. The measurements were conducted at a scattering angle of 173° at 25 °C using a He–Ne laser with a wavelength of 633 nm.64 The mean zeta potential was computed based on the electrophoretic mobility (i.e. the ratio of the velocity of the particles to the field strength) by applying the Smoluchowski theory.64,65Emulsification
Simple emulsions were prepared from equal volumes of HD as the non-polar phase and Milli-Q water. The particles were initially dispersed either in HD or water. Refer to the ESI for details of the composition of each emulsion system (Table S2 ESI†). After 30 seconds of shaking by hand, the resulting systems were tested for the type of emulsion and kept at room temperature to monitor their stability with time. More than two runs of the experiments were performed to test the reproducibility of the results obtained. Unless indicated elsewhere, the final pH of the emulsion system was neutral. However, when it was required, the pH of the system was adjusted to different values from low to high with sodium hydroxide (0.1 mol L−1) and HCl (0.1 mol L−1) added dropwise, using a 100 μL micropipette. The pH was recorded after a short time with a glass pH electrode which was previously calibrated using aqueous buffer solutions.Results and discussion
As a general rule of thumb, SiO2 particles prepared by the Stöber method without further functionalization to render them partially hydrophobic are inherently hydrophilic.61 FTIR and 29Si NMR spectroscopy and titration measurements were performed to investigate the hydrophilicity of the obtained SiO2 particles. The FTIR (Fig. S1†) and 29Si NMR spectra (Fig. S2†) prove the existence of a hydrophilic silanol group on the surface of the particles, while the titration quantitatively estimated that the density of silanol on the SiO2 particle surface is 4.1 OH per nm2, which is close to the theoretical maximum of 4.6 OH per nm2,66 confirming the hydrophilicity of the SiO2 particles.Determination of the zeta potential (ζ) indicated that the surfaces of the SiO2 particles were negatively charged when pH > 3, while at a neutral pH, the zeta potential of SiO2 fell to −30 mV (Fig. S3†). As expected, the zeta potential decreases with increasing pH. As common sense dictates, the SiO2 particles were dispersed in water (1.17% wt and 2.40 × 1012 particles per ml), and upon mixing with an immiscible oil phase and vigorous shaking by hand, no Pickering emulsion was formed. A fast and complete phase separation was observed (Fig. 1A right). Predictably, the existence of a significant energy barrier inhibited the approach of SiO2 to the oil–water interfaces, preventing the formation and stabilization of the emulsion.
Surprisingly, we found that these hydrophilic SiO2 particles could be transferred to hexadecane (HD) (1.42% wt and 1.99 × 1012 particles per ml) by stepwise centrifugation and redispersion as detailed in the Experimental section. The Tyndall effect of the SiO2 suspension in HD can be clearly observed (Fig. S4†). No particles floated on the surface of the HD. No obvious aggregation of the SiO2 particles was observed. Pickering emulsions were easily produced by shaking by hand a mixture of HD that contained the hydrophilic SiO2 particles and the same volume of Milli-Q water (Fig. 1A left). Optical microscopy images (Fig. 1C and D) show that oil droplets were nicely dispersed in a continuous water phase. The type of emulsion was oil-in-water as evidenced by the fluorescent oil phase (emulsion droplets) stained by Nile red. These results confirm that in addition to being “fanciful” to disperse hydrophilic particles in an oil phase, this significantly promotes the formability of Pickering emulsions with those hydrophilic particles. A Pickering emulsion was also achieved by mixing the aqueous phase with the particles dispersed in HD and emulsifying using an Ultra Turrax homogeniser (IKA®, Germany) fitted with an 8 mm head operating at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 1 min. The application of a significant shear force did not affect the formation and long-term stability of the Pickering emulsions.
000 rpm for 1 min. The application of a significant shear force did not affect the formation and long-term stability of the Pickering emulsions.
Commercial hydrophilic SiO2 particles with a size of about 160 nm (microParticles GmbH Monodisperse Particle for Research Purposes) and small SiO2 aggregates (50–86 nm) composed of 11 nm SiO2 nanoparticles (Aerosil® fumed silica) were also applied as emulsifiers. Both types of SiO2 particle could be transferred into HD and the Pickering emulsions were successfully formed by using the same strategy (Fig. S5†).
As a proof of concept, other types of hydrophilic particle, such as polydopamine (PDA) and Fe3O4@PAA (Fig. S6B and S7B†), were tested as emulsifiers for Pickering emulsions. Both types of particle are hydrophilic but can also be transferred to HD by steps of centrifugation and redispersion, and both dispersions showed no signs of obvious aggregation. As shown in Fig. S6A and S7A,† when the hydrophilic PDA and Fe3O4@PAA particles were initially dispersed in the organic phase, Pickering emulsions were steadily formed. All of the Pickering emulsions are oil-in-water type emulsions (Fig. S6(C and D) and S7(C and D)†). However, when the PDA and Fe3O4@PAA particles were initially dispersed in the water phase, no stable Pickering emulsion was obtained. The aim of using Fe3O4 particles functionalized with PAA was simply to corroborate the efficacy of the method with the use of particles that, although they are not pristine and the surface has been modified, still maintain their hydrophilic character.
It seems reasonable to conclude that these results confirm the generality and effectiveness of the proposed strategy for Pickering emulsion preparation and stabilization with hydrophilic particles.
The question that remains is: when the hydrophilic particles are initially dispersed in the oil phase, what happens during emulsification?
The fundamental difference between aqueous and oil phase emulsification lies in the fact that charged hydrophilic particles such as SiO2 dispersed in the aqueous phase need to overcome the energy barrier in order to approach the oil–water interfaces. It is well-documented that pristine oil–water interfaces spontaneously acquire a negative charge.47–51 Herein, the measured zeta potential of pristine HD droplets dispersed in water clearly showed that the surface of the HD droplets was negatively charged when pH > 3, and the surface became more negative with an increase in pH (Fig. S8†), which is in good agreement with previously reported results.47,50
Concurrently, the surface charge of the SiO2 particles was also negative and became more negative with an increase in pH (Fig. S3†). The numerical value of the energy barrier of adsorption as a function of the surface charge of both the SiO2 particles and the pristine HD droplets, can be estimated as the total interaction between two charged spheres approaching each other. According to DLVO theory, the overall interaction energy (Utotal) is described as the sum of the energy of electrostatic repulsion (Ues in kT) and the energy of the van der Waals attraction (UvdW in kT).53,54 The energy of electrostatic repulsion (Ues in kT) between two charged spheres of radius R1 and R2 (m), and surface charge γ1 and γ2, approaching at a distance of h (m), can be estimated using eqn (3).67 Suffix 1 corresponds to the particles and suffix 2 corresponds to the oil droplets.
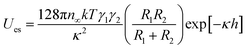 | (3) |
The inverse of the magnitude of the Debye length (κ−1 in nm) depends on the properties of the solution. For the case of a monovalent electrolyte (z = 1), and assuming n∞, the total ion concentration, is equal to 1 × 10−3 mol L−1 and at room temperature, the Debye length of the aqueous solution can be estimated as 9.61 nm. In addition, γ, the surface potential, can be calculated from the Stern potential, which approximates to ψ0 (mV), the measured zeta potential at each pH value.
The energy of the van der Waals attraction (UvdW in kT) between two approaching and dissimilar spheres of radius R1 and R2 separated at a distance of h (m) can be estimated using eqn (4):43
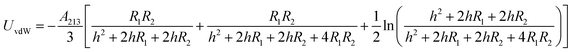 | (4) |
As depicted in Fig. 2, at a pH above 4, the energy barrier of adsorption is significant, mainly due to the contribution of the electrostatic repulsion between the two negatively charged spheres. At a neutral pH of 7, the calculated energy barrier between a 200 nm SiO2 particle and a 20 μm HD droplet is higher than 200 kT. At a pH of 11, the energy barrier is about 920 kT. This explains why the hydrophilic SiO2 particles cannot be utilized to form Pickering emulsions when they are initially dispersed in the water phase.
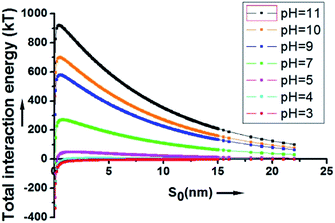 | ||
| Fig. 2 The overall interaction energy (Utotal) between a 200 nm SiO2 particle and a 20 μm HD droplet as a function of the surface to surface distance. | ||
However, if the hydrophilic SiO2 particles are originally dispersed in an organic phase such as HD, the electrostatic repulsion is supposed to be less significant, as is the magnitude of the energy barrier that the particles need to overcome to approach the oil–water interface. In fact, theoretical calculation indicates that there is an electrostatic attraction between the hydrophilic SiO2 particles (dispersed in the oil phase) and the oil–water interfaces which facilitates the migration of particles from the oil phase to the interfaces, and the consequent formation of Pickering emulsions. It has been proved that the hydrophilic SiO2 particles are also charged in a nonpolar solvent because of the existence of a thin water layer on the surfaces that can only be removed by extensively drying at temperatures higher than 100 °C.67,68 In the Experimental section it was clearly stated that the as-prepared SiO2 particles (without drying) were transferred to HD by steps of centrifugation and redispersion, therefore, it is not unrealistic to expect that a thin water layer remained on the surface of the particles. This was quantitatively studied by using AFM via measuring the repulsion forces between two hydrophilic SiO2 particles.69
The experimental results fit well with the theoretical calculations, proving a free ion concentration of 0.306 and a surface potential of −38 mV of the SiO2 particles in dodecane. It is reasonable that this surface potential leads to moderate repulsion between the SiO2 particles in HD, which explains why no aggregation of the particles was observed in such a non-polar solvent. In addition, an electrostatic attraction arises when the charged hydrophilic SiO2 particle approaches the oil–water interfaces from the HD phase. The theory developed by Danov and Kralchevsky et al. was then applied to calculate the particle-interface interactions across the nonpolar medium.60 It considers a spherical particle (phase 1) in an oil phase (phase 2), located at a distance to the interface between oil and water (phase 3). Herein in this work, the electrostatic energy of the interaction between the charged SiO2 particles (dispersed in HD) with a dielectric constant ε1 = 3.97 and the HD–water interfaces could be estimated as
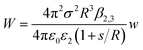 | (5) |
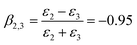 | (6) |
HD is a nonpolar solvent with a relative dielectric constant of approximately 2 (ε2 = 2) and ε3 is the relative dielectric constant of the third medium, water (ε3 = 78.2). The negative value of β2,3 is a clear indication that the interaction between the SiO2 particle (in the oil phase) and the oil–water interface is attractive.
The surface charge density σ of the SiO2 particles in HD could be estimated by a method reported by McNamee et al. based on the Grahame equation:69
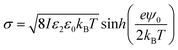 | (7) |
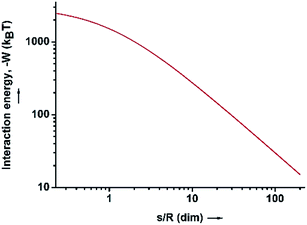 | ||
| Fig. 3 The interaction energy between the water–HD interface and the SiO2 particles in the HD phase, as a function of the dimensionless distance (s/R). | ||
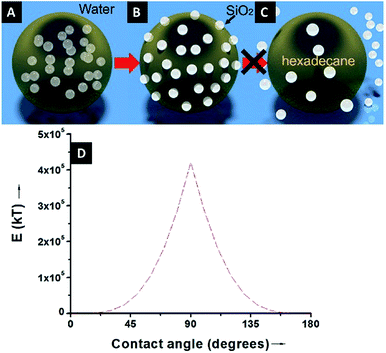
Because of the unequivocally hydrophilic character of SiO2 particles, once they reach the interfaces from the oil phase, they tend to cross the oil–water interfaces and transfer to the water phase. It can be suggested that during this process the contact angle of the SiO2 particles will gradually change from 0 degrees, when completely dispersed in the organic phase (Fig. 4A), to 90 degrees when the particles are straddled at the oil–water interfaces (Fig. 4B). The contact angle is measured from the solid surface of the particles through the oil phase, with a small angle indicating that a larger part of the particle is immersed in the oil phase and vice versa. The hydrophilic particles appear to be expelled into the aqueous phase, but somehow on their way across the interfaces they become trapped at the oil–water interfaces. This scenario can be addressed with the already well-known calculation for detachment energy of a particle from interfaces (eqn (2)). As showed in Fig. 4D, the detachment energy of the particle remarkably increases when the contact angle of the SiO2 particle changes from 0 to 90 degrees after approaching the interface from the HD phase, reaching its maximum at exactly 90 degrees. As calculated, the maximum detachment energy is around 4.2 × 105 kT. Thus, the particles are prevented from completely crossing the interfaces (Fig. 4C). They are locked at oil–water interfaces with a contact angle of ∼90°, which will never be reached if the hydrophilic particles are initially dispersed in the water phase. In fact, after the formation of Pickering emulsion, the water phase is clear, and few SiO2 particles crossed the interface and transferred to the water phase, which agrees well with the theoretical prediction.
A finding of great importance, determined with this new strategy, is that the critical concentration of emulsifier particles for Pickering emulsion stabilization is extremely low. As mentioned above, Pickering stabilization requires the formation of a protective particle layer around the oil droplets that prevents their coalescence.
Generally, for an oil-in-water Pickering emulsion stabilized by partially hydrophobic particles (30–60°), the surface coverage is required to be as high as 90% to effectively stabilize the emulsion droplets, otherwise coalescence or phase separation will take place. Herein, it is found that by using our strategy, the Pickering emulsion can be stabilized by hydrophilic particles in extremely low concentrations. A series of experiments were performed to compare the minimum amount of particles required to stabilize the emulsion when particles were dispersed either in the water phase or in the oil phase.
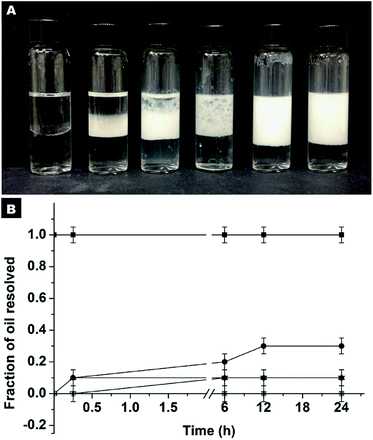
The first set of experiments were carried out using hydrophilic SiO2 particles dispersed in water as stabilizers at a pH of around 2.5. It should be mentioned that at neutral pH, the formation of Pickering emulsions cannot be realized due to the significant electrostatic repulsion between oil droplets and particles. Accordingly, the pH value was fixed at the isoelectric point (pH ≈ 2.5) to reduce the magnitude of the energy barrier of adsorption. As can be seen from Fig. S10A,† successful emulsification was only achieved at extremely high concentrations of SiO2 particles. In fact, at concentrations lower than 11.2% wt complete destabilization was observed within minutes, as evidenced by the amount of oil resolved (fast creaming of emulsions releases a fraction of pure oil)34 which is 100% (Fig. S10B†).
For comparison, another series of experiments were performed but in this case the hydrophilic SiO2 particles were originally dispersed in HD. It is noted that the Pickering emulsion can be formed in a wide pH range from 2.86–10.45 (Fig. S11†), which implies that the pH of the aqueous phase has no remarkable impact on the SiO2 particles in the oil phase and their approach to oil–water interfaces. At a neutral pH, the stabilization of the emulsion can be achieved at an extremely low particle concentration (Fig. 5). Even at a particle concentration of 0.25% wt, Pickering emulsion can be formed. The fraction of resolved oil is only ∼12% (Fig. 5A and B). When the particle concentration is 1% wt or higher, no resolved oil was observed, confirming the formation of stable Pickering emulsions. Therefore, this new strategy not only enhances the formability of Pickering emulsions with hydrophilic particles as an emulsifier, but also dramatically lowers the critical amount of particles needed for emulsion stabilization.
During emulsification, as described above, the hydrophilic SiO2 particles transfer from the oil phase to the oil–water interfaces with an equilibrium contact angle close to 90°. The hemispheres of the SiO2 particles in the water phase regain the surface charge, which gives rise to strong electrostatic repulsions between the particles. Concurrently, the difference in the electrical double layer structures between the two hemispheres induces dipoles and thus dipole–dipole repulsion between the particles.70–72 Such strong dipole–dipole and electrostatic repulsion between the particles at the oil–water interfaces gives rise to the remarkable inter-particle spaces (Fig. 4B). Therefore, the oil droplets can be stabilized with low surface particle coverage. This explains why the Pickering emulsion can be formed with an extremely low SiO2 particle concentration when they are initially dispersed in the oil phase.
Conclusions
In summary, a novel and effective approach for the preparation of Pickering emulsions with hydrophilic particles, inherently non-surface active, is presented.The novelty of the method relies on dispersing the hydrophilic emulsifier particles in the oil phase and not in the water phase as is conventional. This non-commonsense treatment successfully turns the significant repulsion between the particle and oil–water interfaces into a strong attraction, thus dramatically facilitating the migration of the hydrophilic particles to the oil–water interfaces and the formation of Pickering emulsions. Interestingly, theoretical calculation based on a theory reported a decade ago supports the experimental results. It is argued that hydrophilic particles are locked at the oil–water interfaces with a contact angle of ∼90° during their crossing of the interfaces, resulting in excellent long-term stability of the obtained Pickering emulsions. It is of great importance that a change in solvent conditions was not required for the formation of the Pickering emulsion, thus the process is pH-independent. Additionally, the emulsification can be easily achieved by shaking by hand and the critical particle concentration for the stabilization of Pickering emulsion is extremely low. Stable Pickering emulsions can be obtained when the particle concentration is as low as 0.25% wt. These three advantages, of great importance from a cost-effective emulsification method point of view, make this new strategy promising for the preparation of Pickering emulsions in various industrial processes. This will contribute to the mitigation of environmental issues caused by surfactants and nanoparticles. It is believed that the developed strategy will significantly broaden the diversity of Pickering emulsions and their applications.
Conflicts of interest
There is no conflicts to declare.Acknowledgements
This work was financially supported by the Future Industries Institute, University of South Australia. We would like to acknowledge the contribution of Prof Peter A. Kralchevsky for his valuable discussion.Notes and references
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164 CrossRef CAS.
- S. U. Pickering, J. Chem. Soc., Faraday Trans. 1, 1907, 91, 2001–2021 RSC.
- N. Yan, M. R. Gray and J. H. Masliyah, Colloids Surf., A, 2001, 193, 97–107 CrossRef CAS.
- R. Aveyard, J. H. Clint and T. S. Horozov, Prog. Colloid Polym. Sci., 2002, 121, 11–18 CAS.
- B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41 CrossRef CAS.
- E. Olkowska, Ż. Polkowska and J. Namieśnik, Chem. Rev., 2011, 111, 5667–5700 CrossRef CAS PubMed.
- B. P. Binks and S. O. Lumsdon, Phys. Chem. Chem. Phys., 1999, 1, 3007–3016 RSC.
- N. P. Ashby and B. P. Binks, Phys. Chem. Chem. Phys., 2000, 2, 5640–5646 RSC.
- B. P. Binks and S. O. Lumsdon, Phys. Chem. Chem. Phys., 2000, 2, 2959–2967 RSC.
- B. P. Binks and S. O. Lumsdon, Langmuir, 2000, 16, 8622–8631 CrossRef CAS.
- B. P. Binks and S. O. Lumsdon, Langmuir, 2001, 17, 4540–4547 CrossRef CAS.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- B. P. Binks and C. P. Whitby, Langmuir, 2004, 20, 1130–1137 CrossRef CAS PubMed.
- B. P. Binks, J. Philip and J. A. Rodrigues, Langmuir, 2005, 21, 3296–3302 CrossRef CAS PubMed.
- P. S. Clegg, E. M. Herzig, A. B. Schofield, T. S. Horozov, B. P. Binks, M. E. Cates and W. C. K. Poon, J. Phys.: Condens. Matter, 2005, 17, S3433–S3438 CrossRef CAS.
- B. P. Binks, R. Murakami, S. P. Armes and S. Fujii, Langmuir, 2006, 22, 2050–2057 CrossRef CAS PubMed.
- C. Zeng, H. Bissig and A. D. Dinsmore, Solid State Commun., 2006, 139, 547–556 CrossRef CAS.
- Y. Lin, H. Skaff, T. Emrick, A. D. Dinsmore and T. P. Russell, Science, 2003, 299, 226–229 CrossRef CAS PubMed.
- O. D. Velev and K. Nagayama, Langmuir, 1997, 13, 1856–1859 CrossRef CAS.
- O. D. Velev and S. Gupta, Adv. Mater., 2009, 21, 1897–1905 CrossRef CAS.
- O. D. Velev, K. Furusawa and K. Nagayama, Langmuir, 1996, 12, 2385–2391 CrossRef CAS.
- O. D. Velev, K. Furusawa and K. Nagayama, Langmuir, 1996, 12, 2374–2384 CrossRef CAS.
- O. D. Velev, Nat. Nanotechnol., 2013, 8, 620–621 CrossRef CAS PubMed.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- J. Xu, X. Li, X. Wu, W. Wang, R. Fan, X. Liu and H. Xu, J. Phys. Chem. C, 2016, 120, 12666–12672 CAS.
- J. Xu, A. Ma, Z. Xu, X. Liu, D. Chu and H. Xu, J. Phys. Chem. C, 2015, 119, 28055–28060 CAS.
- M. Pera-Titus, L. Leclercq, J.-M. Clacens, F. De Campo and V. Nardello-Rataj, Angew. Chem., 2015, 127, 2028–2044 CrossRef.
- M. Pera-Titus, L. Leclercq, J.-M. Clacens, F. De Campo and V. Nardello-Rataj, Angew. Chem., Int. Ed., 2015, 54, 2006–2021 CrossRef CAS PubMed.
- H. Yang, T. Zhou and W. Zhang, Angew. Chem., Int. Ed., 2013, 52, 7455–7459 CrossRef CAS PubMed.
- J. Huang, F. Cheng, B. P. Binks and H. Yang, J. Am. Chem. Soc., 2015, 137, 15015–15025 CrossRef CAS PubMed.
- H. Yang, L. Fu, L. Wei, J. Liang and B. P. Binks, J. Am. Chem. Soc., 2015, 137, 1362–1371 CrossRef CAS PubMed.
- T. Sharma, G. Suresh Kumar and J. S. Sangwai, Geosyst. Eng., 2014, 17, 195–205 CrossRef CAS.
- J. Wu and G.-H. Ma, Small, 2016, 12, 4633–4648 CrossRef CAS PubMed.
- B. P. Binks and S. O. Olusanya, Chem. Sci., 2017, 8, 708–723 RSC.
- J. Marto, A. Ascenso, S. Simoes, A. J. Almeida and H. M. Ribeiro, Expert Opin. Drug Delivery, 2016, 13, 1093–1107 CrossRef CAS PubMed.
- C. Linke and S. Drusch, Crit. Rev. Food Sci. Nutr., 2017 DOI:10.1080/10408398.2017.1290578.
- P. A. Facal Marina, I. Delcheva and D. A. Beattie, Colloids Surf., A, 2018, 538, 765–773 CrossRef.
- J. Frelichowska, M.-A. Bolzinger and Y. Chevalier, Colloids Surf., A, 2009, 343, 70–74 CrossRef CAS.
- L. Ridel, M.-A. Bolzinger, N. Gilon-Delepine, P.-Y. Dugas and Y. Chevalier, Soft Matter, 2016, 12, 7564–7576 RSC.
- B. P. Binks and D. Yin, Soft Matter, 2016, 12, 6858–6867 RSC.
- S. Schmidt, T. Liu, S. Rütten, K.-H. Phan, M. Möller and W. Richtering, Langmuir, 2011, 27, 9801–9806 CrossRef CAS PubMed.
- K. L. Thompson and S. P. Armes, Chem. Commun., 2010, 46, 5274 RSC.
- Z. Li and T. Ngai, Langmuir, 2010, 26, 5088–5092 CrossRef CAS PubMed.
- N. Saleh, T. Sarbu, K. Sirk, G. V. Lowry, K. Matyjaszewski and R. D. Tilton, Langmuir, 2005, 21, 9873–9878 CrossRef CAS PubMed.
- S. Fujii, E. S. Read, B. P. Binks and S. P. Armes, Adv. Mater., 2005, 17, 1014–1018 CrossRef CAS.
- S. Levine, B. D. Bowen and S. J. Partridge, Colloids Surf., 1989, 38, 325–343 CrossRef CAS.
- K. G. Marinova, R. G. Alargova, N. D. Denkov, O. D. Velev, D. N. Petsev, I. B. Ivanov and R. P. Borwankar, Langmuir, 1996, 12, 2045–2051 CrossRef CAS.
- P. Creux, J. Lachaise, A. Graciaa, J. K. Beattie and A. M. Djerdjev, J. Phys. Chem. B, 2009, 113, 14146–14150 CrossRef CAS PubMed.
- J. K. Beattie and A. M. Djerdjev, Angew. Chem., Int. Ed., 2004, 43, 3568–3571 CrossRef CAS PubMed.
- A. Ma, J. Xu and H. Xu, J. Phys. Chem. C, 2014, 118, 23175–23180 CAS.
- H. Xu, X. Liu and D. Wang, Chem. Mater., 2011, 23, 5105–5110 CrossRef CAS.
- S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS.
- B. L. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the stability of lyophobic colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- J. Y. Won, G. G. Gochev, V. Ulaganathan, J. Krägel, E. V. Aksenenko, V. B. Fainerman and R. Miller, Colloids Surf., A, 2017, 519, 161–167 CrossRef CAS.
- V. R. Dugyala, J. S. Muthukuru, E. Mani and M. G. Basavaraj, Phys. Chem. Chem. Phys., 2016, 18, 5499–5508 RSC.
- A. K. F. Dyab, Colloids Surf., A, 2012, 402, 2–12 CrossRef CAS.
- J. Djuris, D. Vasiljevic, S. Jokic and S. Ibric, Int. J. Cosmet. Sci., 2014, 36, 79–87 CrossRef CAS PubMed.
- B. Ozturk and D. J. McClements, Curr. Opin. Food Sci., 2016, 7, 1–6 CrossRef.
- K. D. Danov, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2005, 22, 106–115 CrossRef PubMed.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69 CrossRef.
- J. Liu, Z. Sun, Y. Deng, Y. Zou, C. Li, X. Guo, L. Xiong, Y. Gao, F. Li and D. Zhao, Angew. Chem., Int. Ed., 2009, 48, 5875–5879 CrossRef CAS PubMed.
- H. L. Xu, X. K. Liu, G. Su, B. Zhang and D. Y. Wang, Langmuir, 2012, 28, 13060–13065 CrossRef CAS PubMed.
- Zetasizer nano series User manual, Malvern Instruments Ltd., 2009 Search PubMed.
- R. J. Hunter, Zeta potential in colloid science: principles and applications, Academic press, 2013 Search PubMed.
- L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- R. Hogg, T. W. Healy and D. W. Fuerstenau, J. Chem. Soc., Faraday Trans. 1, 1966, 62, 1638–1651 RSC.
- R. K. Iler, The chemistry of silica : solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, New York, 1979 Search PubMed.
- C. E. McNamee, Y. Tsujii and M. Matsumoto, Langmuir, 2004, 20, 1791–1798 CrossRef CAS.
- G. V. Bossa, K. Bohinc, M. A. Brown and S. May, J. Phys. Chem. B, 2016, 120, 6278–6285 CrossRef CAS PubMed.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572 CrossRef CAS.
- T. S. Horozov, R. Aveyard, J. H. Clint and B. P. Binks, Langmuir, 2003, 19, 2822–2829 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00678d |
| ‡ J. X. and P. M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |