Open Access Article
Open Access ArticleUnexpected solvation-stabilisation of ions in a protic ionic liquid: insights disclosed by a bond energetic study†
Zhen
Wang
ac,
Feixiang
Gao
a,
Pengju
Ji
 *a and
Jin-Pei
Cheng
*a and
Jin-Pei
Cheng
 *ab
*ab
aCentre of Basic Molecular Science (CBMS), Department of Chemistry, Tsinghua University, Beijing, 100084, China. E-mail: jipengju@mail.tsinghua.edu.cn; jinpei_cheng@mail.tsinghua.edu.cn
bState Key Laboratory of Elemento-Organic Chemistry, Collaborative Innovation Centre of Chemical Science and Engineering, Nankai University, Tianjin, 300071, China
cSchool of Chemical and Environmental Engineering, Anyang Institute of Technology, Anyang 455000, China
First published on 5th March 2018
Abstract
Equilibrium acidities (pKas) of 42 organic acids were precisely determined in protic ionic liquid (PIL) [DBUH][OTf]. Surprisingly, the often seen homoassociation complication during the pKa measurement of O–H acids in DMSO was not detected in [DBUH][OTf], implying that the incipient oxanion should be better solvation-stabilized by the PIL, although its “apparent” dielectric constant is much lower than that of the conventional molecular solvent DMSO. Evidence showing that the solute ions in the PIL are also free from other specific ion associations like ion-pairing is further demonstrated by the identical pKas of protic amine salts bearing largely different counter-anions. Correlations between the RO–H, N–H, N+–H and RCOO–H bond acidities in [DBUH][OTf] and in water revealed different slopes and intercepts for each individual series, suggesting far superior properties of the DBUH+-based PIL for differentiating the solvation effect of various species in structural analysis to the well applied EAN that is known for leveling out differential solvation.
Introduction
Accurate acidity (pKa) scales1 are indispensable tools for understanding many fundamental relationships in chemistry.2 Consequently, various pKa scales have been established in conventional molecular solvents in the past,1 and also, in some aprotic ionic liquids (AILs) quite recently.3,4 The latter has been encouraged by the rapid increase of research activities in this rising mainstream solvent category, due to its amazing features and great potential for promoting new chemistry.5As an important subset, protic ILs are found to be superior to aprotic ILs in many aspects, such as higher hydrogen bond donicity and ionic conductivity, better proton conduction, etc.,6 and have been extensively applied in many frontier areas by virtue of their dissociable protons.7 Since Brønsted acidities of functional molecules play a vital role in dictating their unique properties and applications, the knowledge of acid and base equilibria in PILs is crucial to understanding the fundamental aspects of PILs such as ionicity degree and solvation behaviours, which may provide valuable insights into rational design of PILs as reaction media.6 However, compared to the present knowledge on the bonding features in molecular solvents and in AILs, the current understanding of heterolytic bond dissociation in PILs is surprisingly limited. As a result, rationales for observations or deductions made from experimental results in PILs were almost solely based on the available acidity data measured in molecular solvents, such as water and DMSO,8 which, as already realised, do not necessarily explain the acid–base behaviours in ILs satisfactorily.9
To the best of our knowledge, there was no study on pKas of organic substrates in neat PILs until the recent pioneering work of Kanzaki and Umebayashi et al., who used potentiometric titration to measure the acidity constants of ten O–H acids and two N+–H salts in pure EAN (ethylammonium nitrate, Fig. 1).10
In recent years, our group has conducted a study on the pKa scales of C–H, O–H, N–H, N+–H and S–H acid series in several standard AILs4a (Fig. 1) by spectroscopic titration with high precision.4 Naturally, we intend to employ this approach to systematically study the pKas of the relevant acid series in PILs so as to determine the specific solvation behaviours in this particular type of media.
DBU-based PILs, [DBUH][X] (DBU: 1,5-diazabicyclo[5.4.0]-5-undecene; X: conjugate anions of strong acids, such as OTf− or NTf2−), have been widely used as catalysts as well as reaction solvents in many synthetic and catalytic processes.11 To date, no equilibrium acidity in neat DBU-based PILs has been reported. More importantly, DBU-based PILs can serve as a model solvent for the majority of PILs that bear only one dissociable proton instead of two or three, and therefore, it should be more suitable to represent the normal type solvation characteristics of PILs in a general sense.
Results and discussion
The DBU-based PIL selected for this study is [DBUH][OTf] (Fig. 1). The equilibrium acidities for four types of bonds covering the C–H, O–H, N–H and N+–H acid series (1a–5g, altogether 42 acids) were measured in this PIL following the UV-vis indicator method employed in the AILs earlier,4 which is provided in detail in the ESI.† It is worth noting that [DBUH][OTf] prepared from direct equimolar neutralisation between DBU and HOTf was not suitable for the pKa measurement due to the persistent presence of a yellowish colour. Therefore, alternatively, ultrapure colourless [DBUH][OTf] that is suitable for spectroscopic experiments was prepared by an ion exchange method (see the ESI for details†).Unlike the acidic dissociation in the gas phase, free molecules and ions do not exist in solution, and therefore the pKa values are solvent dependent.1e,12 In molecular solvents, the acidic dissociation involves a proton transfer between a Brønsted acid (H–A) and solvent molecule S (Fig. 2).12 In ILs, however, this could be complicated by various entities, such as free ions, ion-pairs, etc., which coexist in the solution and potentially interact with the dissociated and undissociated species of H-A. In light of this, the acidic dissociation in [DBUH][OTf] can be expressed as depicted in Fig. 2. Due to the strong coulombic interactions, protons and anions (A−) from acidic dissociation are preferentially solvated by [OTf]− and [DBUH]+, respectively. However, it should be noted that currently the explicit solvent structures of ILs are still not very clear and subject to intense debate,13 and more in-depth research efforts in this respect are needed to achieve a better understanding of the solvation behaviour of ILs with respect to acidic dissociations.
The pKa scales, which are based on a carefully determined anchor pKa (ESI†), are summarised in Tables S1† and 1, with a precision ≤± 0.05 pK units. The solvation behaviours of the PIL with respect to acidic bond dissociation equilibria of these substrates are discussed and compared with those of conventional molecular solvents (such as water and DMSO), and of EAN and AILs. Important insights into specific solvation in the PIL are drawn from these bond energetic data that should benefit the future rational exploration of PIL chemistry.
| Organic acid (HA) | [DBUH][OTf]a | [BMIM][OTf]b | DMSOc | H2Oc |
|---|---|---|---|---|
| a SD ≤ ± 0.05 pK units. b [BMIM]+ = 1-butyl-3-methylimidazolium. c Ref. 1f. d 2-Hydroxy-2,4,6-cycloheptatrien-1-one. e Pyr = pyridine. f The counter-anion is OTf−. g Im = imidazole. h Mor = morpholine. | ||||
| 4-Chloro-2,6-dinitrophenol (1a) | 7.4 | 8.0 | 3.6 | 3.0 |
| 2,4-Dinitrophenol (1b) | 9.0 | 9.5 | 5.1 | 4.1 |
| (CF3)3COH (1c) | 10.5 | 10.7 | 5.1 | |
| 2-Chloro-4-nitrophenol (1d) | 10.8 | 5.4 | ||
| Tropolone (1e) | 12.4 | 14.7 | 6.7 | |
| 4-Nitrophenol (1f) | 12.8 | 11.0 | 7.1 | |
| 4-Cyanophenol (1g) | 13.8 | 13.3 | 8.0 | |
| PhNH3+ OTf−(2a) | 7.5 | 3.6 | 4.6 | |
| PhNH3+ NTf2−(2b) | 7.4 | |||
| PhNH3+ Cl−(2c) | 7.4 | |||
| PyrH+ OTf−(2d) | 8.2 | 3.4 | 5.2 | |
| PyrH+ NTf2− (2e) | 8.3 | |||
| PyrH+ Cl− (2f) | 8.3 | |||
| , ImH+ (2g) | 10.4 | 6.4 | 7.0 | |
| , MorH+ (2h) | 11.5 | 9.2 | 8.4 | |
| PhCH2NH(CH3)2+ (2i) | 12.4 | 12.2 | 7.6 | 9.0 |
| PhCH2NH3+ (2j) | 12.7 | 10.2 | 9.4 | |
| 5-Thiomethyltetrazoles (3a) | 10.4 | 6.1 | 4.3 | |
| Tetrazoles (3b) | 10.5 | 8.2 | 4.9 | |
| 5-Methyltetrazoles (3c) | 11.4 | 12.9 | 5.6 | |
| 5-Chlorobenzotriazole (3d) | 12.8 | 14.4 | 7.7 | |
| Benzotriazole (3e) | 13.6 | 15.6 | 11.9 | 8.6 |
| 5-Methylbenzotriazole (3f) | 13.9 | 8.9 | ||
| Trifluoroacetic acid (4a) | 5.6 | 3.6 | 0.23 | |
| CF3CH2COOH (4b) | 9.4 | 3.1 | ||
| 4-NO2C6H4CH2COOH (4c) | 10.3 | 3.9 | ||
| Benzoic acid (4d) | 11.0 | 13.3c | 11.0 | 4.2 |
| Acetic acid (4e) | 11.8 | 12.3 | 4.8 | |
| 4-NO2C6H4CH(CN)2 (5a) | 5.2 | 5.1c | −1.8 | 2.3 |
| 4-CNC6H4CH(CN)2 (5b) | 6.4 | 6.4c | ||
| 4-CF3C6H4CH(CN)2 (5c) | 7.4 | 7.5c | ||
| 4-ClC6H4CH(CN)2 (5d) | 8.85 | 8.9c | 3.1 | |
| PhCH(CN)2 (5e) | 9.8 | 9.8c | 4.2 | 5.8 |
| 4-MeOC6H4CH(CN)2 (5f) | 11.1 | 11.1c | 5.7 | |
| 9-Cyanofluorene (5g) | 13.8 | 13.8c | 8.3 | 10.7 |
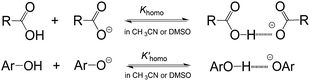
As is well known, the acidity scale in water provides the so-called “free-ion” pKas, as facilitated by the high polarity (ε = 78.4 (ref. 14)) and strong H-bonding ability of water. This feature allows cations and anions to be fully solvated, respectively, by solvent molecules to avoid the formation of ion-pairs or other specific ion associations, so as to warrant the measurement of the “true pKa” in water. Besides the scale in water, the only energetic scale showing a similar feature, but the most commonly used in current organic chemistry, is the pKa scale in DMSO,1d due also to its high polarity (ε = 46.5 (ref. 15)) and strong proton affinity.16 However, this is not without exception. As is well realised, acidic dissociation of phenols and benzoic acids is subject to a homoassociation complication (Fig. 3) in DMSO, because the solvent alone is unable to provide sufficient solvation-stabilisation for incipient oxanions.17 Similar phenomena were also found in our earlier pKa measurement of benzoic acids4b and phenols18 in AILs. The deviation caused by this homoassociation complication in the measured pKa values could be quite large (usually 0.5–1 pK units),4b,17,18 which could be serious enough to mislead the interpretations of experimental data. It should be remembered that this kind of perturbation in the derived pKa, if it occurred, could not be readily recognized by experimental approaches other than photometric titration.1c,17 Fortunately, all the data for O–H acids in Bordwell's pKa scale measured by the indicator-overlapping method have already been corrected for this deviation,17c and so, it would be safe to use those “ion-pair free” acidities as reported, as for our pKa data in AILs.4
Surprisingly, no sign of the homoassociation phenomenon was detected here in the pKa measurement of benzoic acids, phenols and other O–H acids in Table 1 in [DBUH][OTf] (ESI, Table S2†), although this phenomenon is generally observed between weak acids and bases even in solvents as strongly polar as DMSO. This implies that the involved oxanions can be fully solvation-stabilised by the PIL through solvation without invoking additional ion-interactions like homoassociation for further stabilisation under our experimental conditions (ESI†). This is unexpected, especially to most organic chemists, because when the solvation effect is compared, they usually use the conventional solvent polarity index ε to make a judgment, but the present observation clearly indicates the failure of such an index in the IL19 though it has been of general success in most cases in molecular media.
The absence of the homoassociation effect in [DBUH][OTf] also suggests that all the oxanions of this study can exist in the form of “free ions” (i.e., no specific ion association besides with solvent) at low concentrations, due to the unexpected strong solvation of the PIL. The “free” status of the dissociated ions in the PIL can also be realised by precise pKa measurement of organic salts. As shown in Table 1 (entries 2a–2c), the pKa values of PhNH3+X−, where X = Cl, OTf, or NTf2, are identical, regardless of the dramatic difference of their size and basicity.20 This is also true for the PyrH+X− salts (entries 2d–2f). This implies that the counter-anion of the salts cannot be in the vicinity of its cation counterpart (a prerequisite for forming an ion-pair12a,21), because, if it were the opposite, the positive charge on N+ would, at least, be partially neutralised, and as a consequence, the N+–H bond would have become less acidic. Obviously, this is not the case. Thus, the present findings, together with those reported earlier in AILs,4e suggest a perhaps universal phenomenon for both PILs and AILs of moderately low to high polarity, that is, there should be no serious specific ion association for ions in dilute IL solution.
Specific ion association is a widely accepted phenomenon for ions in ILs, though it is not without debate.13,22 As addressed above, homoassociation is a generally observed phenomenon for oxanions in aprotic molecular solvents as strongly polar as DMSO17c and also in weakly polar protic solvents,1c,12a due to the strong H-bond acceptability of oxanions towards their parents which are excellent H-bond donors. Hence, the absence of both these phenomena in the PIL used in the present study may be unintuitive, and must be related to an unexpected strong hydrogen donicity of [DBUH]+ whose solvation behaviour should be further understood. From our point of view, the enhanced solvability of this PIL must be mainly due to the even stronger H-bond stabilisation of oxanions by [DBUH]+, as judged by its much greater acidity in DMSO (pKa = 13.9 (ref. 1f)) than that for the cation of AIL [BMIM]+ (22.0 (ref. 1f)), where homoassociation was observed.
If as was addressed above the solvation stabilisation of solute ions by this PIL is indeed very strong, a question should be asked, that is, would the hydrogen donicity of [DBUH]+ be too strong to level out all the solvation differences of various species in the PIL as was reported for EAN.10 In this regard, regression analysis would be the most convenient and reliable tool for differentiating the role of solvation by the PIL in various substrate series. Accordingly, a linear free energy relationship (LFER) study was conducted, and the result is exhibited in Fig. 4.
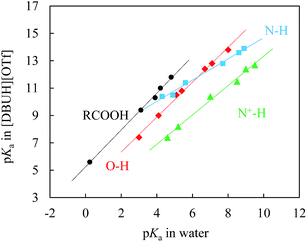 | ||
| Fig. 4 Correlations between pKas of N–H (■), N+–H (▲), O–H (◆), and carboxylic (RCOOH, ●) acids in [DBUH][OTf] and those in water; the linearity (R2) of each individual correlation is better than 0.991 (ESI†). The ESI provides further details of the acidity correlation equations between these two solvents (eqn S3–6†). | ||
Fig. 4 demonstrates the LFER lines for the pKas of benzoic acids, N–H acids, phenols, and N+-H acids in [DBUH][OTf] (Table 1, entries 1a–4e) against the corresponding values in water.1f The most noteworthy features of these lines are that they all show an excellent linearity (R2 ≥ 0.991, ESI†) and that each substrate series demonstrates its own characteristic line which is not overlapping with the LFERs of other substrate families. It is known that LFERs are separated for different families of acids with various electronic and structural features.23 In light of this, it is surprising that a recent study by Kanzaki et al. obviously showed only one straight line (ESI, Fig. S25†), though a bit rough, between the pKas in EAN and in water for the 12 acids bearing different charges (neutral, cationic and anionic).10b As explained there, that should be caused by the higher acidity of HNO3 in EAN than that of H3O+ in water, but not by the difference in the solvation state of the ions, which raises hope for the authors “to establish a pH scale that is universally applicable to protic solvents, both molecular and ionic”, regardless of the substantial difference of these two media categories in solvation. However, the precisely determined pKa data shown here in Table 1 clearly indicate an alternative possibility, that is, the so-stated universally applicable pH scale may be true for the type of PILs that bear more than one donative proton like EAN, but not for the majority of PILs as represented by [DBUH][OTf] that have one H-bond donor. The distinctive behaviour of solvation between these two typical types of PILs as shown by the single-line vs. multiline LFERs could be understood, however, by considering that, compared to [DBUH]+, the ethylammonium cation of EAN is small in size and has three potential H-bond donors instead of one. These structural features could cause EAN to behave in a way reminiscent of water to form highly cross-linked networks by virtue of its multi-H-bond donors.24 In other words, the solvent components in EAN could be more structured than in [DBUH][OTf], and thus, the solvation sensitivity towards structural variations of various series should not be as strong as that of [DBUH][OTf]. Actually, EAN may be considered as a special case with respect to solvation patterns for PILs. The present results indicate that the number of proton donors in PILs plays a subtle but crucial role in the solvation behaviour of PILs.
One may have noted that the carbon acid (C–H) series (Table 1, entries 5a–5g) is missing from the LFERs given in Fig. 4. This is due primarily to the consideration of the remarkable difference between carbanions and heteroatom anions in solvation, not just due to the lack of the corresponding data in water. It is well realised that compared to heteroatom anions, carbanions, especially those that have extensively delocalised charge and are large in size like 5a–5g, are poorly solvated by H-bonding even in protic solvent. As a consequence, their solvation should not be expected to resemble that of heteroatom anions (i.e., all the other entries in Table 1) in either water or PIL, but rather, it is likely to mimic the solvation observed in an aprotic solvent. Indeed, when the pKa values of 5a–5g in [DBUH][OTf] are plotted against those in DMSO and in the aprotic IL [BMIM][OTf], excellent linear correspondences were observed in both solvents (ESI, Fig. S20 and S23,†R2 = 0.992 and 0.999, respectively). This, again, indicates that there is no simple correlation pattern between solvation effects in protic molecular and protic ionic solvents for acid dissociation (ESI, Fig. S21 and S22†). Interestingly, one may also find that these C–H acids have essentially identical pKas in [DBUH][OTf] and in [BMIM][OTf] (Table 1 and Fig. S20,† compared with other acid series), despite their conceptual distinction and the tremendous difference between the PIL and the AIL in terms of H-bond donicity. Actually, this is not too hard to understand, because H-bonding, usually the most powerful tool for a PIL to play its role in solvation, is not applicable in the case of carbanions, which induced a changeover for [DBUH]+ from largely relying on the H-bond in solvation to a more general solvation pattern like that of its aprotic counterpart, the [BMIM]+ cation.
Conclusions
In summary, the equilibrium acidities of the O–H, N–H, N+–H and C–H acid series listed in Table 1 were systematically studied for the first time in a neat PIL with high precision. Unlike the acidity measurement of O–H acids in DMSO, no homoassociation was found in the acidic dissociation of all O–H acids examined in [DBUH][OTf], indicating a “super-dissociating” feature of this PIL and its similarity to the H-bond based solvation of water, where salts are free from all specific ion associations (homoassociation, ion-pairing, etc.) in dilute solution except with the solvent molecule. Regression analyses between the acidity in the PIL and in water showed excellent linearity for each individual heteroatom acid series with its own slope and intercept, but not for the C–H acid series. The latter, however, was found to correlate quite nicely with the corresponding data derived from either the aprotic molecular solvent DMSO or the aprotic ionic solvent [BMIM][OTf], as a result of the diminishing role of hydrogen bonding in the case of carbanions. These observations identify the DBUH+-based PIL as a superior probe to EAN in differentiating the solvation effect in the PIL, and imply that there is no simple solvation pattern for the PIL to stabilise the dissolved species of different structures and charges in general.Experimental section
The measurement procedures employed when using the UV-vis indicator spectroscopic method were similar to those reported previously.4 In brief, firstly the acidity of an anchor compound, i.e. 4-nitrophenylmalononitrile in this work, was obtained by self-dissociation in [DBUH][OTf], and then the pKas of a series of indicator acids (acidity ladder) were determined based on this anchor point. The pKa of other acids employed in this work was then measured by referencing to one or two of these indicator acids through titration. Taking a typical run as an example, the pKa measurement of other acids was commenced by degassing and weighing a specially made UV cell, followed by the adding of 1.5 ml of [DBUH][OTf] and 40 mg of base into the cell. An indicator acid of known pKa was added dropwise after the cell was weighed again and a baseline was recorded. Monitored by the UV machine, after the base, DBU, was fully consumed by normally 6–8 drops of the indicator acid, an excess amount of indicator solution was added. During the titration, the spectrum and weight upon each addition was recorded. Next the target acid of interest was added in several portions. The weight of the UV cell and the corresponding spectrum were also recorded upon each addition. The corresponding pKa was obtained with the data derived from the change of absorbance and the amount of acid added. See the ESI† for details of building up the acidity ladder, pKa measurement, the synthesis of ultrapure [DBUH][OTf] through ion exchange, and regression analyses.Conflicts of interest
The authors have declared no conflicts of interest.Acknowledgements
We are grateful for the financial grants from the National Natural Science Foundation of China (No. 21390401, 21672124, and 21702005); a part of this work was also supported by the Tsinghua University Initiative Scientific Research Program (No. 20131080083 and 20141081295). We also sincerely thank the referees for their invaluable suggestions and comments on the manuscript.Notes and references
- (a) E. J. King, Acid-Base Equilibria, Pergamon Press, New York, 1965 Search PubMed; (b) E. P. Serjeant and B. Dempsey, Ionisation Constants of Organic Acids in Aqueous Solution, Pergamon Press, New York, 1979 Search PubMed; (c) K. Izutsu, Acid-Base Dissociation Constants in Dipolar Aprotic Solvents, Blackwell Scientific Publications, Oxford, 1990 Search PubMed; (d) F. G. Bordwell, Acc. Chem. Res., 1988, 21, 456–463 CrossRef CAS and the references cited therein; (e) D. Himmel, S. K. Goll, I. Leito and I. Krossing, Angew. Chem., Int. Ed., 2010, 49, 6885–6888 CrossRef CAS PubMed; (f) Internet Bond-energy Databank (iBond), http://ibond.chem.tsinghua.edu.cn or ibond.nankai.edu.cn.
- (a) L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 2nd edn, 1970 Search PubMed; (b) N. Isaacs, Physical Organic Chemistry, Prentice Hall, London, 2nd edn, 1996 Search PubMed; (c) E. V. Anslyn and D. D. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, CA, 2006 Search PubMed.
- (a) R. Barhdadi, M. Troupel, C. Comminges, M. Laurent and A. Doherty, J. Phys. Chem. B, 2012, 116, 277–282 CrossRef CAS PubMed; (b) D. Millán, M. Rojas, J. G. Santos, J. Morales, M. Isaacs, C. Diaz and P. Pavez, J. Phys. Chem. B, 2014, 118, 4412–4418 CrossRef PubMed; (c) D. Himmel, S. K. Goll, F. Scholz, V. Radtke, I. Leito and I. Krossing, ChemPhysChem, 2015, 16, 1428–1439 CrossRef CAS PubMed.
- (a) H. Deng, X. Li, Y. Chu, J.-Q. He and J.-P. Cheng, J. Org. Chem., 2012, 77, 7291–7298 CrossRef CAS PubMed; (b) Z. Wang, H. Deng, X. Li, P. Ji and J.-P. Cheng, J. Org. Chem., 2013, 78, 12487–12493 CrossRef CAS PubMed; (c) Z. Wang, P. Ji, X. Li and J.-P. Cheng, Org. Lett., 2014, 16, 5744–5747 CrossRef CAS PubMed; (d) C. Mao, Z. Wang, P. Ji and J.-P. Cheng, J. Org. Chem., 2015, 80, 8384–8389 CrossRef CAS PubMed; (e) C. Mao, Z.-D. Wang, Z. Wang, P. Ji and J.-P. Cheng, J. Am. Chem. Soc., 2016, 138, 5523–6626 CrossRef CAS PubMed; (f) Z.-D. Wang, X. Li, P. Ji and J.-P. Cheng, J. Org. Chem., 2016, 81, 11195–11200 CrossRef CAS PubMed.
- (a) S. Tang, G. A. Baker and H. Zhao, Chem. Soc. Rev., 2012, 41, 4030–4066 RSC; (b) J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed; (c) J. E. Bara, D. E. Camper, D. L. Gin and R. D. Noble, Acc. Chem. Res., 2010, 43, 152–159 CrossRef CAS PubMed; (d) A. Pinkert, K. N. Marsh, S. Pang and M. P. Staiger, Chem. Rev., 2009, 109, 6712–6728 CrossRef CAS PubMed; (e) M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- (a) T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed; (b) T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef CAS PubMed.
- (a) E. Janus, I. Goc-Maciejewska, M. Lozynski and J. Pernak, Tetrahedron Lett., 2006, 47, 4079–4083 CrossRef CAS; (b) Y. Du and F. Tian, J. Chem. Res., 2006, 8, 486–489 CrossRef; (c) Z. Duan, Y. Gu, J. Zhang, L. Zhu and Y. Deng, J. Mol. Catal. A: Chem., 2006, 250, 163–168 CrossRef CAS; (d) A. Noda, M. A. B. H. Susan, K. Kudo, S. Mitsushima, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2003, 107, 4024–4033 CrossRef CAS; (e) T. Yasuda and M. Watanabe, MRS Bull., 2013, 38, 560–566 CrossRef CAS; (f) M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- (a) C.-M. Wang, H.-M. Luo, D.-E. Jiang, H.-R. Li and S. Dai, Angew. Chem., Int. Ed., 2010, 49, 5978–5981 CrossRef CAS PubMed; (b) K. Chen, G. Shi, W. Zhang, H. Li and C. Wang, J. Am. Chem. Soc., 2016, 138, 14198–14201 CrossRef CAS PubMed; (c) Q. Yang, Z. Wang, Z. Bao, Z. Zhang, Y. Yang, Q. Ren, H. Xing and S. Dai, ChemSusChem, 2016, 9, 806–812 CrossRef CAS PubMed; (d) M. Hulla, S. M. A. Chaman, G. Laurenczy, S. Das and P. J. Dyson, Angew. Chem., Int. Ed., 2017, 56, 10559–10563 CrossRef CAS PubMed.
- (a) L. M. Mihichuk, G. W. Driver and K. E. Johnson, ChemPhysChem, 2011, 12, 1622–1632 CrossRef CAS PubMed; (b) S. K. Shukla and A. Kumar, J. Phys. Chem. B, 2013, 117, 2456–2465 CrossRef CAS PubMed.
- (a) R. Kanzaki, H. Doi, X. Song, S. Hara, S. Ishiguro and Y. Umebayashi, J. Phys. Chem. B, 2012, 116, 14146–14152 CrossRef CAS PubMed; (b) R. Kanzaki, H. Kodamatani, T. Tomiyasu, H. Watanabe and Y. Umebayashi, Angew. Chem., Int. Ed., 2016, 55, 6266–6269 CrossRef CAS PubMed.
- (a) A. G. Ying, L. Liu, G. F. Wu, G. Chen, X. Z. Chen and W. D. Ye, Tetrahedron Lett., 2009, 50, 1653–1657 CrossRef CAS; (b) Z.-Z. Yang, L.-N. He, C.-X. Miao and S. Chanfreau, Adv. Synth. Catal., 2010, 352, 2233–2240 CrossRef CAS; (c) D. S. Patel, J. R. Avalani and D. K. Raval, J. Braz. Chem. Soc., 2012, 23, 1951–1954 CrossRef CAS; (d) B. Yu, H. Zhang, Y. Zhao, S. Chen, J. Xu, L. Hao and Z. Liu, ACS Catal., 2013, 3, 2076–2082 CrossRef CAS; (e) H. Singh, J. Sindhu, J. M. Khurana and C. Sharma, Eur. J. Med. Chem., 2014, 22, 145–154 CrossRef PubMed; (f) Y. Zhao, B. Yu, Z. Yang, H. Zhang, L. Hao, X. Gao and Z. Liu, Angew. Chem., Int. Ed., 2014, 53, 5922–5925 CrossRef CAS PubMed; (g) J. Hu, J. Ma, Q. Zhu, Z. Zhang, C. Wu and B. Han, Angew. Chem., Int. Ed., 2015, 54, 5399–5403 CrossRef CAS PubMed; (h) X.-D. Lang, Y.-C. Yu, Z.-M. Li and L.-N. He, J. CO2 Util., 2016, 15, 115–122 CrossRef CAS.
- (a) C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, Wiley-VCH, Weinheim, 4th edn, 2011 Search PubMed; (b) E. Paenurk, K. Kaupmees, D. Himmel, A. Kütt, I. Kaljurand, I. A. Koppel, I. Krossing and I. Leito, Chem. Sci., 2017, 8, 6964–6973 RSC.
- (a) M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed; (b) S. Perkin, M. Salanne, P. Madden and R. Lynden-Bell, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4121 CrossRef CAS PubMed; (c) A. A. Lee, D. Vella, S. Perkin and A. Goriely, J. Phys. Chem. Lett., 2015, 6, 159–163 CrossRef CAS PubMed; (d) H. Chen, X. Chen, J. Deng and J. Zheng, Chem. Sci., 2018, 9, 1464–1472 RSC.
- 298.2 K value, see: D. P. Fernandez, Y. Mulev, A. R. H. Goodwin and J. M. H. L. Sengers, J. Phys. Chem. Ref. Data, 1995, 24, 33–70 CrossRef CAS.
- 298.2 K value, see: J. F. Casteel and P. G. Sears, J. Chem. Eng. Data, 1974, 19, 196–200 CrossRef CAS.
- (a) E. P. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS; (b) C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422 CrossRef CAS PubMed.
- (a) I. M. Kolthoff, M. K. Chantooni Jr and S. Bhownik, J. Am. Chem. Soc., 1968, 90, 23–28 CrossRef CAS; (b) M. K. Chantooni Jr and I. M. Kolthoff, J. Phys. Chem., 1976, 80, 1306–1310 CrossRef; (c) F. G. Bordwell, R. McCallum and W. N. Olmstead, J. Org. Chem., 1984, 49, 1424–1427 CrossRef CAS.
- Unpublished results, phenol has a Khomo value of 2.75 × 104 L−1 mol−1 (log10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khomo = 4.44) in an aprotic ionic liquid [BMPY][NTf2], where [BMPY] = N-butyl-N-methylpyrrolidinium.
Khomo = 4.44) in an aprotic ionic liquid [BMPY][NTf2], where [BMPY] = N-butyl-N-methylpyrrolidinium. - ε [DBUH][OTf] of 23.6 < εDMSO of 46.5 (at 289.2 K). The dielectric constant of [DBUH][OTf] is calculated based on a group contribution method. For details, see: Y. Zhou, Z. Lin, K. Wu, G. Xu and C. He, Chin. J. Chem. Eng., 2014, 22, 79–88 CrossRef CAS . It should be noted, however, that because there were controversies on the suitability of the DC method for measuring the dielectric constant in ionic conducting solvent [cf. J. H. Ambrus, C. T. Moynihan and P. B. Macedo, J. Phys. Chem., 1972, 76, 3287–3295], care should be taken when values derived in such media are directly used without calibration.
- J. Bartosik and A. Mudring, Phys. Chem. Chem. Phys., 2010, 12, 4005–4011 RSC.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- For the ion pair issues in neat ILs, see a recent review: B. Kirchner, F. Malberg, D. S. Firaha and O. Hollóczki, J. Phys.: Condens. Matter, 2015, 27, 463002 CrossRef PubMed and the references cited therein.
- (a) M. Berthelot, C. Laurence, M. Safar and F. Besseau, J. Chem. Soc., Perkin Trans. 2, 1998, 283–290 RSC; (b) M. Berthelot and C. Laurence, Perspect. Drug Discovery Des., 2000, 18, 39–60 CrossRef.
- (a) D. F. Evans, S.-H. Chen, G. W. Schriver and E. M. Arnett, J. Am. Chem. Soc., 1981, 103, 481–482 CrossRef CAS; (b) K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2009, 48, 3184–3186 CrossRef CAS PubMed; (c) R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2012, 51, 1–5 CrossRef PubMed; (d) Z. Chen, T. L. Greaves, R. A. Caruso and C. J. Drummond, J. Phys. Chem. B, 2015, 119, 179–191 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed pKa measurement procedures, indicators used in this work and their corresponding pKas in the PIL; UV-vis spectra for the representative measurements; and synthesis and characterisation of the PIL and salts. See DOI: 10.1039/c7sc05227h |
| This journal is © The Royal Society of Chemistry 2018 |