Open Access Article
Open Access ArticleCation–π interactions in protein–ligand binding: theory and data-mining reveal different roles for lysine and arginine†
Kiran
Kumar‡
 a,
Shin M.
Woo‡
a,
Thomas
Siu
a,
Wilian A.
Cortopassi
a,
Fernanda
Duarte
a,
Shin M.
Woo‡
a,
Thomas
Siu
a,
Wilian A.
Cortopassi
a,
Fernanda
Duarte
 *b and
Robert S.
Paton
*b and
Robert S.
Paton
 *a
*a
aChemistry Research Laboratory, University of Oxford, 12 Mansfield Road, Oxford OX1 3TA, UK. E-mail: robert.paton@chem.ox.ac.uk
bEaStCHEM School of Chemistry, University of Edinburgh, Joseph Black Building, David Brewster Road, Edinburgh EH9 3FJ, UK. E-mail: fernanda.duarte@ed.ac.uk
First published on 31st January 2018
Abstract
We have studied the cation–π interactions of neutral aromatic ligands with the cationic amino acid residues arginine, histidine and lysine using ab initio calculations, symmetry adapted perturbation theory (SAPT), and a systematic meta-analysis of all available Protein Data Bank (PDB) X-ray structures. Quantum chemical potential energy surfaces (PES) for these interactions were obtained at the DLPNO-CCSD(T) level of theory and compared against the empirical distribution of 2012 unique protein–ligand cation–π interactions found in X-ray crystal structures. We created a workflow to extract these structures from the PDB, filtering by interaction type and residue pKa. The gas phase cation–π interaction of lysine is the strongest by more than 10 kcal mol−1, but the empirical distribution of 582 X-ray structures lies away from the minimum on the interaction PES. In contrast, 1381 structures involving arginine match the underlying calculated PES with good agreement. SAPT analysis revealed that underlying differences in the balance of electrostatic and dispersion contributions are responsible for this behavior in the context of the protein environment. The lysine–arene interaction, dominated by electrostatics, is greatly weakened by a surrounding dielectric medium and causes it to become essentially negligible in strength and without a well-defined equilibrium separation. The arginine–arene interaction involves a near equal mix of dispersion and electrostatic attraction, which is weakened to a much smaller degree by the surrounding medium. Our results account for the paucity of cation–π interactions involving lysine, even though this is a more common residue than arginine. Aromatic ligands are most likely to interact with cationic arginine residues as this interaction is stronger than for lysine in higher polarity surroundings.
Introduction
Cation–π interactions influence biological structures, molecular recognition and catalysis.1–5 They play an important role in determining protein structure and function. X-ray structural analyses and computational studies show that cation–π interactions are prevalent in protein–protein,6–9 protein–ligand,10–12 and protein–DNA complexes.13 It is estimated that a “typical” protein contains at least one cation–π interaction for every 77 amino acid residues.7a The existence of almost 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 X-ray crystal structures currently in the Protein Data Bank (PDB), with an average protein length of 802 residues, suggests more than 1
000 X-ray crystal structures currently in the Protein Data Bank (PDB), with an average protein length of 802 residues, suggests more than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cation–π interactions may be present in those structures.
000 cation–π interactions may be present in those structures.
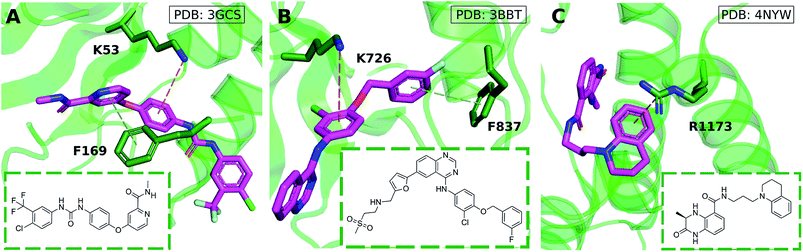
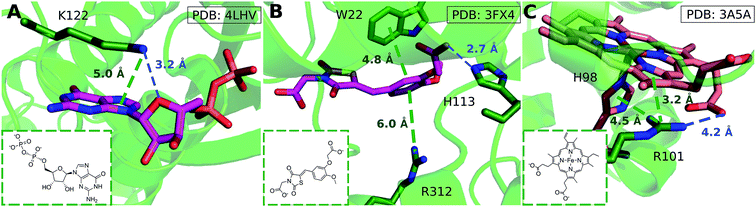
Cation–π interactions are vital for several physiological processes. Notable examples include acetylcholine binding,14–17 the recognition of post-translationally modified histones by epigenetic proteins18–21 and ion selectivity in K+ channels.22 These are examples of positively charged ligands interacting favorably with the aromatic sidechains of histidine, phenylalanine, tryptophan and tyrosine residues. On the other hand, the interaction of aromatic ligands with positively charged residues – arginine, histidine, lysine – can also occur. Given the abundance of aromatic and heteroaromatic rings in the structures of drug-like molecules, this type of cation–π interaction is the focus of this paper. For example, sorafenib, approved for the treatment of liver cancer, forms a cation–π interaction with a positively charged lysine residue of the human p38 MAP kinase (Fig. 1A).23 Lapatinib, approved for breast cancer treatment, forms a cation–π interaction with a lysine residue of ErbB4 kinase (Fig. 1B).24 Dihydroquinoxalinone derivatives selectively inhibit the CBP/p300 bromodomain over the closely-related BRD4 receptor, attributed to the formation of a cation–π interaction with a positively charged arginine residue close to the active site (Fig. 1C).25–27 Predictable structure–activity relationships were established according to the electrostatic interaction strength.27
Cation–π interactions are dominated by the electrostatic attraction between an electron-rich arene and electron-deficient cation.28,29 Houk30 and Wheeler31,32 showed that ring substituents augment this interaction strength with additional electrostatic interactions between the substituents and cation. Differences in binding strength can be explained quantitatively in terms of these additive, through-space electrostatic interactions, more so than by considering any polarizing effect on the π system. Nevertheless, non-electrostatic effects such as induction feature in accurate physical descriptions of cation–π interaction energies.33,34
Analyses of the structures deposited in the PDB provide information about the occurrence and geometric characteristics of cation–π interactions in biological systems, including protein–DNA complexes,35 protein–protein interactions,8,9 metal cation–π interactions36 and cation–π–cation interactions.37 Quantifying the nature and magnitude of these interactions remains a challenge. Combined studies employing both small models and crystal structure analyses have proven useful in understanding these interactions in naturally occurring systems. The aromatic–aromatic interactions of nitroarenes with amino acid side chains of histidine, phenylalanine, tryptophan, and tyrosine have been studied in this way. Wheeler constructed CCSD(T)/aug-cc-pVTZ//B97-D/TZV(2d,2p) theoretical models and compared the computed energies and geometries against nitroarene binding sites from the PDB.38 Chipot studied model systems of intra-residue cation–π interactions between lysine/arginine and phenylalanine/tyrosine/histidine complexes at the MP2/6-311++G**//MP2/6-31G** level of theory and compared them to results obtained with 1718 cation–π protein–protein complexes found in the PDB.8
Over 40% of small molecule drugs launched in clinical trials or under development in 2009 contained a (hetero)-aromatic ring.39 Given the prevalence of aromatic rings in drug-like molecules, we reasoned there should be many crystallographically characterized cation–π interactions in which aromatic rings of ligands interact with positively-charged amino acids of protein active sites. A large collection of structures provides a statistically significant empirical dataset against which to test the relevance of theoretical model complexes. The foci of previous studies exploring the presence of cation–π interactions in biomolecular databases3 have centered on cationic ligands interacting with aromatic residues8 and intra-residue cation–π interactions inside proteins40a or at protein–protein interfaces.9 Comparative studies on aromatic ligands are restricted to nucleic acid bases.40b To the best of our knowledge, a meta-analysis of the interactions between aromatic ligands and cationic residues has not been described previously. Herein, we study the occurrence, geometrical features and magnitude of cation–π interactions between positively charged amino acid sidechains: arginine (Arg), lysine (Lys), and histidine (His), and (non-protein) ligands featuring an aromatic ring. The distance and angular dependence of these interactions has been characterized at the DLPNO-CCSD(T) level of theory and interpreted with symmetry adapted perturbation theory (SAPT). These results are compared to naturally occurring interactions between ligands and proteins found through systematic data-mining of non-redundant protein structures from the PDB.
Methods
Model cation–π complexes
Positively-charged sidechains of lysine, arginine and histidine residues were abbreviated in our quantum chemical studies to ammonium [NH4]+, guanidinium [Gdm]+ and imidazolium [Imi]+ cations. We used benzene as the archetype aromatic ligand. We explicitly considered two conformations of each complex (Fig. 2). For complex [C6H6][NH4]+, these differ by the orientation of the N–H bonds above ring atoms (A) or bonds (B); similarly for [C6H6][Gdm]+ the NH2 groups are either above ring atoms (C) or bonds (D). For the [C6H6][Imi]+ complex, we considered two rotamers with a parallel alignment of the two rings (E and F); and two distinct perpendicular (T-shape) complexes (G and H).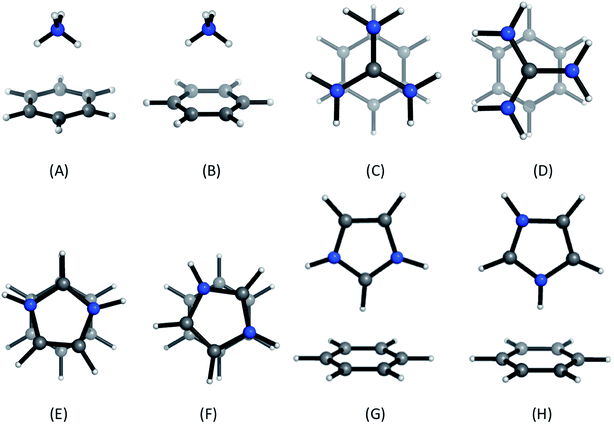 | ||
| Fig. 2 Cation–π complexes analyzed in this work. Models of (A)/(B) lysine; (C)/(D), arginine; and (E)–(H), histidine sidechains interacting with benzene. | ||
Based on gas phase ab initio calculations, a bidentate orientation of NH4+ above aromatic rings is favored over those with one or three N–H atoms facing the aromatic ring.41 This binding mode is most prevalent in protein inter-residue interactions.42 Guanidinium–benzene complexes can adopt at least two conformations: perpendicular (T-shaped) or parallel. While T-shaped geometries are preferred in gas-phase, parallel-complexes are preferred in solution and have been observed more frequently in protein structures.7,43 We studied the parallel configuration, based on its biological relevance.7,44 For [C6H6][Imi]+ complexes, both perpendicular and parallel arrangements are found in protein interactions.45 We included both interaction types in our analysis.
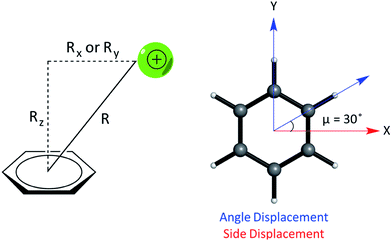
We studied the interaction energy (Eint) of each model cation–π complex as a function of intermolecular separation and of horizontal displacement parallel to the aromatic plane. Distances were calculated between the center of mass of both species in the complex. Cartesian (x,y) displacements are defined with respect to the benzene ring as shown (Fig. 3).
Potential energy curves (PECs) were generated at the domain-based local pair-natural orbital coupled cluster with perturbative triple excitations, DLPNO-CCSD(T),46 level of theory. An augmented, correlation consistent basis set, aug-cc-pVTZ, was used. The convergence of valence DZ, TZ, and QZ quality basis sets was examined for the [benzene][Na]+ complex (Fig. S1†). The aug-cc-pVTZ equilibrium separation closely matches that obtained with a larger aug-cc-pVQZ basis, with an interaction energy within 0.5 kcal mol−1. DLPNO-CCSD(T) energies achieve an accuracy of 1 kcal mol−1 or better compared to CCSD(T),47 while CCSD(T)/CBS values are generally considered benchmark values for intermolecular interaction energies.48 DLPNO-CCSD(T) thermochemistry of small organic molecules is accurate to within 3 kJ mol−1 against experimental data.49 For complexes (A), (C), (E), and (G) CCSD(T) calculations were also carried out using a dielectric constant of 4.2 (diethyl ether) and 78.4 (water).
In relation to the D6h symmetry of benzene, two vectors in the plane of the ring represent extreme scenarios of displacement – one towards a C–H bond (angle displacement) and the other towards a C–C bond (side displacement). These vectors are related by a rotation of μ = 30° about the C6 axis (Fig. 3). By plotting a potential energy curve (PEC) with vertical distance against displacement in each vector, behaviour for 12 planes (360°/30°) about the C6 axis of benzene can be achieved for a minimum of 12 geometries per complex. MP2/aug-cc-pVTZ optimized geometries of monomers were obtained imposing Td, D3h, C2v and D6h symmetry restraints for the NH4+, Gdm+, Imi+, and benzene monomers, respectively.
E int was then calculated as a difference between the energy of the complex and the sum of the energies of the optimized monomers (eqn (1)):
| Eint = Ecomplex − Ecation − Eπ | (1) |
MP2 optimizations were performed with Gaussian50 and DLPNO-CCSD(T) energy calculations with ORCA.51 Computed structures and absolute energies are available as ESI (Tables S2–S9†).
The DLPNO-CCSD(T) potential energy curves were interpolated (spline interpolation in 1-d with SciPy) to obtain minimum energy separations and corresponding geometries, on which symmetry adapted perturbation theory computations (SAPT)52 were performed with PSI4.53 The aug-cc-pVDZ-JKFIT basis set was used for these calculations. Briefly, SAPT provides a rigorous partitioning of the intermonomer interaction energy (Eint) into various physical contributions. These include short-range exchange–repulsion (Eee), electrostatics (Eele, e.g. charge–charge, charge–dipole, dipole–dipole, etc.), induction polarization (Eind, e.g. dipole/induced-dipole) and London dispersion forces (Edisp, e.g. instantaneous dipole/induced dipole). This approach has been used to analyze non-covalent interactions including π–π and cation–π interactions.54 SAPT (at orders above SAPT2) gives interaction energies close to benchmark CCSD(T)/CBS values.55,56 Our results are consistent with this (Table S1†), with all SAPT2+3 interaction energies lying within ±0.6 kcal mol−1 of corresponding DLPNO-CCSD(T) values (see Fig. S5† for full comparison).
Meta-analysis of cation–π interactions involving aromatic ligands
An empirical distribution of protein–ligand cation–π interactions was sought from the PDB.57 The following workflow was implemented in Python to select a high-resolution, non-redundant dataset:(i) X-ray crystal structures of proteins with non-covalent bound ligands at a resolution of ≤2.0 Å were retained for further analysis. This returned 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 structures.
053 structures.
(ii) The Protein–Ligand Interaction Profiler (PLIP)58 was used to identify cation–π interactions by imposing geometric criteria. OpenBabel was used to identify rings by Smallest Set of Smallest Rings (SSSR) perception and assign aromaticity.59 Based on previous works,7,8 two thresholds were applied: a 6.0 Å cut-off from the centroid of the aromatic ring and a 2.3 Å horizontal cut-off in the plane of the ring (Fig. S2†).
(iii) PROPKA 3.1 (ref. 60) was used to determine the protonation state of all residues at a physiological pH of 7.4. This considers the local environmental perturbation of sidechain intrinsic pKa values. This is most pertinent for histidine residues, whose protonation state is influenced by nearby residues, although instances of neutral lysine and arginine residues were also predicted. We removed all interactions where these sidechains were predicted to be neutral. Equally, we found instances initially characterized as a π–π interaction that were reassigned as cation–π interactions once the sidechain was predicted to be protonated.
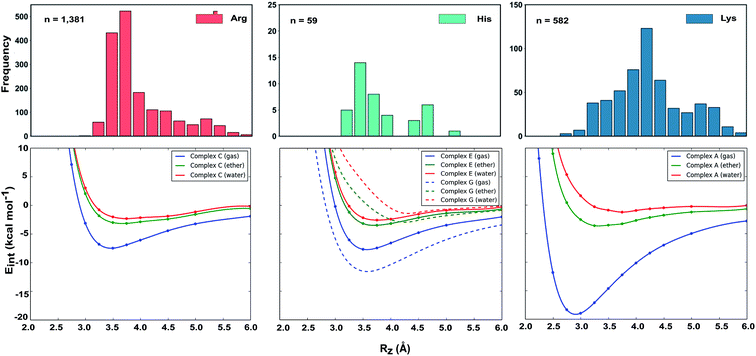
(iv) Two sources of duplicate records were considered and removed; homologous protein chains within the same protein structure, and polycyclic aromatic ligands that were initially counted as two or more distinct interactions by satisfaction of the geometric cutoffs. To address this, only the first homologous chain containing the cation–π interaction was retained. In the case of polycyclic aromatic ligand interactions, these were further classified as either ‘fused’, ‘sandwich’, or ‘bridge’ complexes (Fig. S3†). For fused complexes the shortest distance was used and described as one cation–π complex, while sandwich and bridge complexes containing n aromatic rings were treated as n occurrences. Following this automated workflow, we obtained a total of 1827 unique protein structures, with 2012 cation–π interactions (Table 1).
| Stage | Filter | PDBs | His | Arg | Lys | Total |
|---|---|---|---|---|---|---|
| a | 2.0 ≥ Å resolution, containing ligand | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
— | — | — | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
| b | Geometric thresholds | 3248 | 4959 | 3141 | 930 | 9030 |
| c | Residue pKa >7.4 | 1827 | 68 | 2954 | 848 | 3870 |
| d | Non-redundant chain and polycyclic ligand | 1827 | 49 | 1381 | 582 | 2012 |
Results and discussion
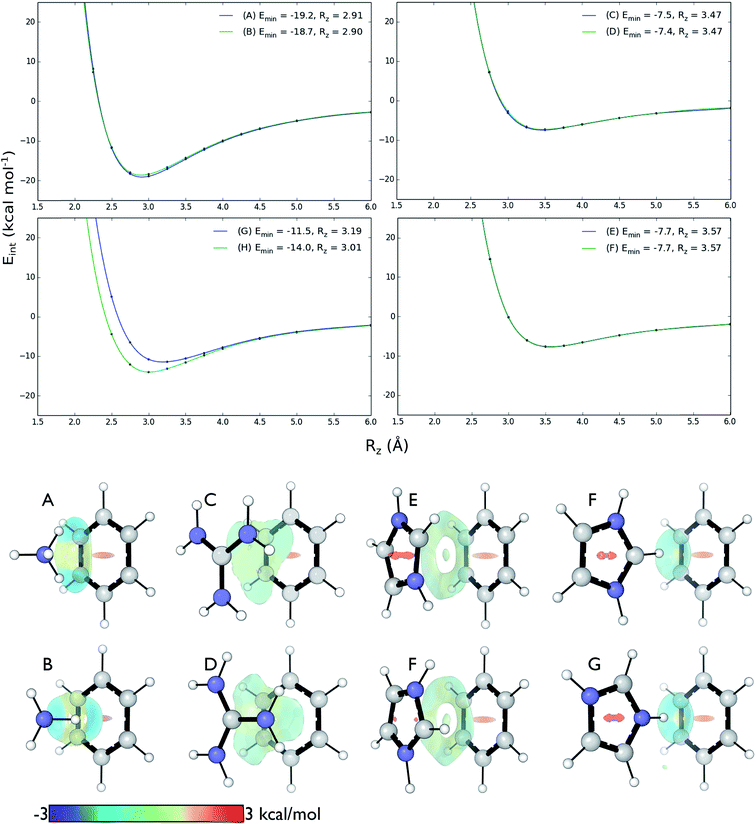
We computed DLPNO-CCSD(T)/aug-cc-pVTZ interaction energies for all eight complexes along an intermolecular axis perpendicular to the aromatic plane, as shown in Fig. 4.The strongest interaction energies occur for complexes in which N–H bonds are oriented towards the aromatic ring: for model complexes (A)/(B) of lysine (−19.2 & −18.7 kcal mol−1) and the T-shaped histidine complex G (−14.0 kcal mol−1). In the other T-shaped complex a C–H bond is oriented towards the ring, giving a smaller interaction energy of −11.5 kcal mol−1. Interaction energies for the stacked complexes, arginine (C)/(D) (−7.5 & −7.4 kcal mol−1) and parallel histidine (E)/(F) (−7.7 & −7.7 kcal mol−1) are weaker still. The more strongly interacting complexes ((A), (B), (G) and (H)) have shorter equilibrium intermolecular separations around 2.9–3.0 Å. Correspondingly, the Non-Covalent Interaction (NCI) isosurfaces61 (Fig. 4) show focused, strongly attractive regions due to the polar X–H–π contacts and more diffuse, weakly attractive regions associated with the stacked systems. Molecular van der Waals surfaces using Bondi radii (Fig. S4†) show that X–H⋯π contacts occur at distances less than the sum of atomic van der Waals radii, whereas the stacked complexes are separated by interatomic distances slightly longer than the sum of these radii.
These interactions depend negligibly on the orientation of each complex. Very similar interaction energy profiles (within 0.5 kcal mol−1) were obtained for the two rotamers of each of the lysine, arginine, and parallel histidine complexes. For the T-shaped [C6H6][Imi]+ complexes, there is a more pronounced difference, depending on whether an N–H or C–H bond is oriented towards the arene. An N–H⋯π interaction is 2.5 kcal mol−1 (complex (F)) is more stable than C–H⋯π interaction (complex (G)) and gives a shorter equilibrium separation by 0.25 Å. This is due to the increased polarity of the N–H bond.62
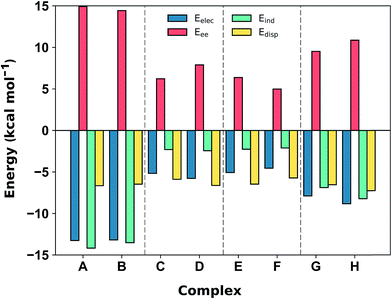
Comparison with the available gas-phase experimental thermochemistry is promising. Our DLPNO-CCSD(T) interaction energy for [C6H6][NH4]+ of −19.2 kcal mol−1 matches the experimental ΔH° (380 K) of −19.3 ± 1.0 kcal mol−1,41b as well as [C6H6][K]+, being −19 kcal mol−1.54 In order to further rationalize these quantitative results, SAPT2+3/aug-cc-pVDZ analysis was used to partition the interaction energy (Eint) into various physical contributions (exchange repulsion Eee, induction Eind, dispersion Edisp, and electrostatic Eele) (Fig. 5) at the equilibrium separation of each complex. In line with previous studies,56 the SAPT2+3 Eint methods gave values within ±0.6 kcal mol−1 of the DLPNO-CCSD(T) energies (Fig. S5†).
The SAPT2+3 decomposition shows that [C6H6][NH4]+ complexes (A)/(B) are very different from the others. The dominant favorable terms are electrostatic and induction (polarization). In the remaining complexes the terms are more evenly balanced: for T-shape [C6H6][Imi]+ complexes (G)/(H) the electrostatic term is the most favorable, whereas for [C6H6][Gdm]+ complexes (C)/(D) and parallel [C6H6][Imi]+ complexes (E)/(F) the dispersion term is most favorable. Hobza has proposed that noncovalent complexes can be classified based on the ratio of SAPT Edisp/Eelec terms.63 Empirical observation suggests that dispersion/electrostatics ratio less than 0.59 should be categorized as electrostatic; greater than 1.7 (1/0.59) as dispersion bound; between 0.59 and 1.7 as mixed. Adopting this convention, [C6H6][NH4]+ complexes (A) and (B) are electrostatics dominated (Edisp/Eelec = 0.49–0.50), whereas all others are mixed (Edisp/Eelec = 0.82–0.83 for complexes (G) and (H); Edisp/Eelec = 1.13–1.27 for complexes (C)–(F)).
Finally, the large energy difference between (H) and (G), with the former being 2.5 kcal mol−1 more stable, arises from favorable Eee, Eind, which operate cooperatively. In this case, the N–H bond closest to the ring is more polar, and therefore induces both a stronger electrostatic attraction and a greater polarization response from the π system. This brings [Imi]+ closer to the ring of the benzene by 0.18 Å, which increases both Eee and, to a lesser extent, Edisp. The favorable interactions from this closer contact negate the increase in repulsive Eee.
In addition to the magnitude of the interaction strengths, SAPT analysis illustrates a continuum of interaction type. The [C6H6][NH4]+ cation–π interactions are dominated by the favorable electrostatic attraction, whereas the other complexes feature a balanced mixture of electrostatic and dispersion interactions. Within this mixed category, the electrostatic term is the most favorable in the [C6H6][Gdm]+ T-shape complexed, and is 3–4 kcal mol−1 larger in magnitude than those experienced by [C6H6][Gdm]+ and [C6H6][Imi]+ stacked complexes. The stacked complexes have the smallest electrostatic terms and dispersion is the most favorable attractive term. The distinct nature of this interaction has been additionally classified as a π+–π interaction.64
Cation–π interaction in protein–ligand complexes
The prevalence of protein–ligand cation–π interactions was evaluated in a non-redundant set of PDB structures. An initial search returned 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 X-ray crystal structures with resolution ≤2 Å containing unique ligands (Table 1, stage A). Following an implementation of geometric rule-based criteria, 3248 structures were found to contain 9030 active sites with a Lys/Arg/His residue in proximity to an aromatic ligand (Table 1, stage B). Of the complexes identified, 4954 involved histidine, however, these results also contained π–π interactions involving a neutral residue. The protonation state of each of the residues at physiological pH was computed with PROPKA (Table 1, stage C), drastically reducing the number of interactions involving histidine acting as a cation. In contrast, Arg-ligand and Lys-ligand complexes retained 94% and 92% of their interactions from the previous stage. Finally, 40% of duplicate interactions were removed to yield a final data set of 2012 interactions dominated by Arg (69%), Lys (29%), and to a lesser extent His (2%) residues (Table 1, stage D).
053 X-ray crystal structures with resolution ≤2 Å containing unique ligands (Table 1, stage A). Following an implementation of geometric rule-based criteria, 3248 structures were found to contain 9030 active sites with a Lys/Arg/His residue in proximity to an aromatic ligand (Table 1, stage B). Of the complexes identified, 4954 involved histidine, however, these results also contained π–π interactions involving a neutral residue. The protonation state of each of the residues at physiological pH was computed with PROPKA (Table 1, stage C), drastically reducing the number of interactions involving histidine acting as a cation. In contrast, Arg-ligand and Lys-ligand complexes retained 94% and 92% of their interactions from the previous stage. Finally, 40% of duplicate interactions were removed to yield a final data set of 2012 interactions dominated by Arg (69%), Lys (29%), and to a lesser extent His (2%) residues (Table 1, stage D).
Empirical vs. calculated cation–π potential energy surface
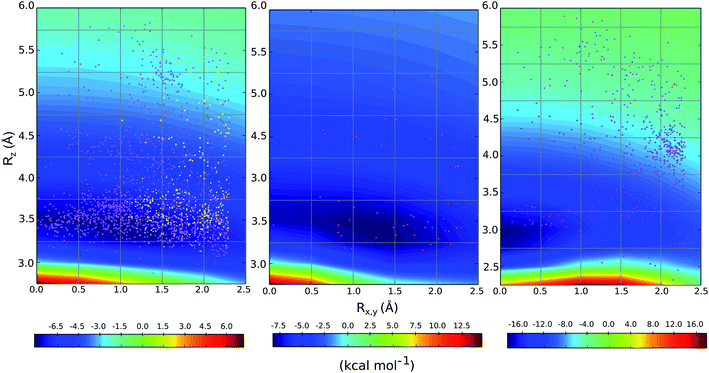
We compared the distribution of cation–π complexes extracted from crystal structures against the DLPNO-CCSD(T)/aug-cc-pVTZ PES. For each interaction the vertical displacement from the aromatic plane (Rz) is shown against horizontal displacement from the ring centroid (Rx,y) (Fig. 6). The underlying color reflects the calculated interaction energy of the model complex for arginine, histidine and lysine.For arginine, the empirical distribution from X-ray and computed PES agree well. The 1381 geometries are clustered empirically in the minimum energy well of the PES, with a vertical offset of 3.5 Å. Additionally, interplanar angles between the guanidium and aromatic group are predominantly clustered below 30° – i.e. closer to a parallel stacked geometry, as considered by our model calculations, than to a T-shaped conformation (Fig. S6†). The computed PES is relatively flat with respect to horizontal displacement and accordingly the interactions are evenly spread across this range. Additionally, most of the interactions with secondary rings of bicyclic aromatics are found within the potential well. Much fewer (59) X-ray structures were available for cationic His-aromatic complexes, making statistical inference more difficult. 70% of the complexes are found close to the minimum energy well centered at Rx,y = 1.25, Rz = 3.25. The computed well for lysine is deeper and narrower, however, the empirical distribution of these interactions is scattered widely (Fig. 6). Unlike arginine, the empirical distribution of lysine's cation–π interactions is more scattered than predicted by theory. A large cluster of interactions occurs at Rx,y = 2.0, Rz = 4.0, far from the PES minimum at (0.0, 3.0).
Why do the X-ray structures of cationic arginine–arene interactions match theory well, whereas cationic lysine–arene interactions do not? Recalling our SAPT results, dispersion interactions prevail for arginine while for lysine, electrostatics interactions dominate. This led us to consider how each interaction type is influenced by the surrounding medium. We compared the empirical distance dependence of each interaction type against the DLPNO-CCSD(T) energy profile calculated in the gas-phase, and with a surrounding conductor-like polarizable continuum model (CPCM)65 with dielectric constant of 4.2 and 78.4 (Fig. 7). These values reflect the average polarity of the relatively hydrophobic protein interior and that of bulk water.66 Solvation corrections were computed at the MP2/cc-pVTZ level of theory.
Each cation–π interaction is weakened by the presence of a surrounding dielectric medium. For lysine, the interaction strength decreases to 19% of its gas-phase value (to 3.6 kcal mol−1) for ε = 4.2, and 7% (1.3 kcal mol−1) for ε = 78.4. For arginine, the decrease is less pronounced at these values of dielectric constant, to 47% (3.2 kcal mol−1) and 34% (2.3 kcal mol−1) – in water this interaction is stronger than lysine's even though it is less favorable by 11.5 kcal mol−1 in the gas-phase. With the SMD solvation model,66 arginine's cation–π interaction is also stronger than lysine's in water, although the interaction strengths were greater. A previous computational estimate of the lysine–benzene interaction strength in water is larger (5.5 kcal mol−1 with SM5.42R/HF/6-31+G*)7b compared to the values of 1.3/2.8 kcal mol−1 (CPCM/SMD) we have obtained with correlated wavefunction theory and a larger basis set.
The scattered distribution of lysine–arene interactions found empirically is consistent with a small interaction strength. This also explains the relative paucity of this interaction type, in relation to the abundance of lysine residues in proteins. In contrast, the arginine–arene interaction strength is less strongly influenced by the presence of a surrounding polar medium and a clear minimum remains on the PEC. The high frequency of this interaction type and the empirical distribution is consistent with the position of this minimum energy separation. The distinct behavior of lysine's and arginine's interactions results from the predominantly electrostatic character of the former interaction and mixed character of the latter, as shown by SAPT analysis. The cation–π interactions of T-shaped histidine are weakened to 21% of the gas-phase value (3.0 kcal mol−1) for ε = 4.2 and 9% (1.3 kcal mol−1) for ε = 78.4. For stacked histidine the reduction is smaller, to 44% (3.4 kcal mol−1) and 32% (2.5 kcal mol−1) at these values of dielectric constant. Again, the interaction with a greater electrostatic character (by SAPT) is diminished more severely by the surrounding dielectric medium.
We considered as large a data set possible, but the interactions we found are still biased by the proteins and ligands studied experimentally and crystallized. Few lysine–arene interactions were found empirically above the center of the aromatic ring, although the PES minimum is found at Rx,y = 0. Fig. 8 illustrates how several intermolecular interactions influence ligand position, such that the cation–π interaction itself between lysine–arene ligands is not a determinant of this pose. For example, a high proportion (63%) of the lysine–arene interactions found around Rx,y, Rz ≈ (2.0, 4.0) involve GTP/ATP/NAD/FAD related ligands. In such cases, the ligand's binding position is also influenced by a hydrogen bond interaction involving the ribose ester and the interactions between the phosphate group and the surroundings (Fig. 8A). It is interesting to notice that even when the systems involving these cofactors are removed from the analysis (Fig. S7†), the scattered nature of Lys-aromatic complexes is still evident. This is more likely due to additional interactions, such as salt bridges or hydrogen bonds, that Lysine can establish with nearby residues and solvent molecules. In the case of arginine–arene complexes, some long distance (6 Å) cation–π interactions are observed as a result of a π–π interaction with another aromatic residue (Fig. 8B). Cation–π interactions may also be shortened due to cooperative effects, such as those which occur when an N–H aromatic interaction between Arg101 and His98A inductively enhances the positive charge on arginine, thereby strengthening the electrostatic components of the cation–π interaction and salt bridge (Fig. 8C).
Conclusions
We have studied the cation–π interactions of neutral aromatic ligands with the cationic amino acid residues arginine, histidine and lysine. Quantum chemical potential energy surfaces for these interactions were obtained at the DLPNO-CCSD(T) level of theory and compared against the empirical distribution of 2012 unique protein-ligand cation–π interactions found in X-ray crystal structures. We created a workflow to extract these structures from the PDB, filtering by interaction type and residue pKa.The gas phase cation–π interaction of lysine is significantly stronger than arginine by more than 10 kcal mol−1. However, the distribution of 582 empirical structures is scattered away from the minimum on the interaction PES, with a much longer intermolecular separation. In contrast, the 1381 structures involving arginine (69% of the total found) reflect the underlying calculated PES well. This reflects the different electrostatic contributions to each of these residues' interactions with an aromatic ring, which was established by SAPT analysis. The electrostatics dominated lysine–arene interaction is greatly diminished by a surrounding dielectric medium, such that it becomes essentially negligible in strength and without a well-defined equilibrium separation. The arginine–arene interaction involves a near equal mix of dispersion and electrostatic attraction, which is weakened to a much smaller degree by the surrounding medium.
Our results account for the relative paucity of cation–π interactions involving lysine, despite its prevalence in protein structures. Particularly in protein active sites of medium to high polarity, such as those which are solvent exposed, the lysine–arene interaction is predicted to be weakened to the point that it has a negligible effect on an aromatic ligand binding mode. In contrast, the cation–π interaction made by arginine residues with aromatic ligands is more robust to changes in the surrounding environment. This interaction is the most frequent found empirically and is also computed to be stronger than for lysine in higher polarity surroundings. There are relatively few cation–π interactions involving positively charged histidine residues, although the stacked π+–π interaction is predicted to be of similar magnitude to that of arginine.
Systematic analysis of crystal structures showed that other factors, such as competitive hydrogen bonding interactions and solvent accessibility, unconnected to the cation–π interaction may also affect the cation–π interaction geometry. This investigation has characterized the intrinsic properties of biologically relevant cation–π interactions and the effect of the protein environment in an average way using a surrounding polarizable dielectric medium. Future work will consider the inhomogeneous nature of the local environment on these interactions.67
Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. K. was supported by a World Bank Education Grant, W. A. C. by a Science Without Borders (CAPES) scholarship, and F. D. through a Royal Society Newton Fellowship. We acknowledge the EPSRC Centre for Doctoral Training in Theory and Modelling in Chemical Sciences (EP/L015722/1) and use of the Dirac cluster at Oxford.References
- D. A. Dougherty, Cation–π Interactions Involving Aromatic Amino Acids, J. Nutr., 2007, 137, 1504S–1508S CrossRef CAS PubMed.
- J. C. Ma and D. A. Dougherty, The Cation–π Interaction, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS PubMed.
- A. S. Mahadevi and G. N. Sastry, Cation–π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science, Chem. Rev., 2013, 113, 2100–2138 CrossRef CAS PubMed.
- E. A. Meyer, R. K. Castellano and F. Diederich, Interactions with Aromatic Rings in Chemical and Biological Recognition, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef CAS PubMed.
- (a) C. R. Kennedy, S. Lin and E. N. Jacobsen, The Cation–π Interaction in Small-Molecule Catalysis, Angew. Chem., Int. Ed., 2016, 55, 2–31 CrossRef; (b) C. P. Johnston, A. Kothari, T. Sergeieva, S. I. Okovytyy, K. E. Jackson, R. S. Paton and M. D. Smith, Catalytic Enantioselective Synthesis of Indanes by a Cation-Directed 5-endo-trig Cyclization, Nat. Chem., 2015, 7, 171–177 CrossRef CAS PubMed.
- M. M. Flocco and S. L. Mowbray, Planar Stacking Interactions of Arginine and Aromatic Side-Chains in Proteins, J. Mol. Biol., 1994, 235, 709–717 CrossRef CAS PubMed.
- (a) J. P. Gallivan and D. A. Dougherty, Cation–π Interactions in Structural Biology, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9459–9464 CrossRef CAS PubMed; (b) J. P. Gallivan and D. A. Dougherty, A Computational Study of Cation–π Interactions vs. Salt Bridges in Aqueous Media: Implications for Protein Engineering, J. Am. Chem. Soc., 2000, 122, 870–874 CrossRef CAS.
- H. Minoux and C. Chipot, Cation–π Interactions in Proteins: Can Simple Models Provide an Accurate Description?, J. Am. Chem. Soc., 1999, 121, 10366–10372 CrossRef CAS.
- P. B. Crowley and A. Golovin, Cation–π Interactions in Protein–Protein Interfaces, Proteins, 2005, 59, 231–239 CrossRef CAS PubMed.
- J. C. Ma and D. A. Dougherty, The Cation–π Interaction, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS PubMed.
- C. Biot, E. Buisine and M. Rooman, Free-energy Calculations of Protein–Ligand Cation–π and Amino–π Interactions: from Vacuum to Protein like Environments, J. Am. Chem. Soc., 2003, 125, 13988–13994 CrossRef CAS PubMed.
- N. Zacharias and D. A. Dougherty, Cation–π interactions in ligand recognition and catalysis, Trends Pharmacol. Sci., 2002, 23, 281–287 CrossRef CAS PubMed.
- R. Wintjens, J. Lievin, M. Rooman and E. Buisine, Contribution of cation–π interactions to the stability of protein–DNA complexes, J. Mol. Biol., 2000, 302, 395–410 CrossRef CAS PubMed.
- J. D. Schmitt, C. G. V. Sharples and W. S. Caldwell, Molecular Recognition in Nicotinic Acetylcholine Receptors: The Importance of π–Cation Interactions, J. Med. Chem., 1999, 42, 3066–3074 CrossRef CAS PubMed.
- D. A. Dougherty and D. A. Stauffer, Acetylcholine Binding by a Synthetic Receptor: Implications for Biological Recognition, Science, 1990, 250, 1558–1560 CrossRef CAS PubMed.
- M. M. Torrice, K. S. Bower, H. A. Lester and D. A. Dougherty, Probing the Role of the Cation–π Interaction in the Binding Sites of GPCRs using Unnatural Amino Acids, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11919–11924 CrossRef CAS PubMed.
- S. Salentin, V. J. Haupt, S. Daminelli and M. Schroeder, Polypharmacology Rescored: Protein–Ligand Interaction Profiles for Remote Binding Site Similarity Assessment, Prog. Biophys. Mol. Biol., 2014, 116, 174–186 CrossRef CAS PubMed.
- J. F. Flanagan, L. Z. Mi, M. Chruszcz, M. Cymborowski, K. L. Clines, Y. Kim, W. Minor, F. Rastinejad and S. Khorasanizadeh, Double Chromodomains Cooperate to Recognize the Methylated Histone H3 tail, Nature, 2005, 438, 1181–1185 CrossRef CAS PubMed.
- H. Li, S. Ilin, W. Wang, E. M. Duncan, J. Wysocka, C. D. Allis and D. J. Patel, Molecular Basis for Site-Specific Read-out of Histone H3K4me3 by the BPTF PHD Finger of NURF, Nature, 2006, 442, 91–95 CrossRef CAS PubMed.
- S. A. Jacobs and S. Khorasanizadeh, Structure of HP1 Chromodomain Bound to a Lysine 9-Methylated Histone H3 Tail, Science, 2002, 295, 2080–2083 CrossRef CAS PubMed.
- W. A. Cortopassi, K. Kumar, F. Duarte, A. S. Pimentel and R. S. Paton, Mechanisms of Histone Lysine-Modifying Enzymes: a Computational Perspective on the Role of the Protein Environment, J. Mol. Graphics Modell., 2016, 67, 69–84 CrossRef CAS PubMed.
- D. A. Dougherty, Cation–π Interactions in Chemistry and Biology: A New View of Benzene, Phe, Tyr, and Trp, Science, 1996, 271, 163–168 CAS.
- J. R. Simard, M. Getlik, C. Grutter, V. Pawar, S. Wulfert, M. Rabiller and D. Rauh, Development of a fluorescent-tagged kinase assay system for the detection and characterization of allosteric kinase inhibitors, J. Am. Chem. Soc., 2009, 131, 13286–13296 CrossRef CAS PubMed.
- C. Qiu, M. K. Tarrant, S. H. Choi, A. Sathyamurthy, R. Bose, S. Banjade, A. Pal, W. G. Bornmann, M. A. Lemmon, P. A. Cole and D. J. Leahy, Mechanism of activation and inhibition of the HER4/ErbB4 kinase, Structure, 2008, 16, 460–467 CrossRef CAS PubMed.
- T. P. C. Rooney, P. Filippakopoulos, O. Fedorov, S. Picaud, W. A. Cortopassi, D. A. Hay, S. Martin, A. Tumber, C. M. Rogers, M. Philpott, M. Wang, A. L. Thompson, T. D. Heightman, D. C. Pryde, A. Cook, R. S. Paton, S. Müller, S. Knapp, P. E. Brennan and S. J. Conway, A Series of Potent CREBBP Bromodomain Ligands Reveals an Induced-Fit Pocket Stabilized by a Cation–π Interaction, Angew. Chem., Int. Ed., 2014, 126, 6240–6244 CrossRef.
- D. A. Hay, O. Fedorov, S. Martin, D. C. Singleton, C. Tallant, C. Wells, S. Picaud, M. Philpott, O. P. Monteiro, C. M. Rogers, S. J. Conway, T. P. C. Rooney, A. Tumber, C. Yapp, P. Filippakopoulos, M. E. Bunnage, S. Müller, S. Knapp, C. J. Schofield and P. E. Brennan, Discovery and Optimization of Small-Molecule Ligands for the CBP/p300 Bromodomains, J. Am. Chem. Soc., 2014, 136, 9308–9319 CrossRef CAS PubMed.
- W. A. Cortopassi, K. Kumar and R. S. Paton, Cation–π interactions in CREBBP Bromodomain Inhibition: An Electrostatic Model for Small-Molecule Binding Affinity and Selectivity, Org. Biomol. Chem., 2016, 14, 10926–10938 CAS.
- S. Mecozzi, A. P. West and D. A. Dougherty, Cation–π Interactions in Aromatics of Biological and Medicinal Interest: Electrostatic Potential Surfaces as a Useful Qualitative Guide, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 10566–10571 CrossRef CAS.
- S. Mecozzi, A. P. West and D. A. Dougherty, Cation–π Interactions in Simple Aromatics: Electrostatics Provide a Predictive Tool, J. Am. Chem. Soc., 1996, 118, 2307–2308 CrossRef CAS.
- S. E. Wheeler and K. N. Houk, Substituent Effects in Cation/π Interactions and Electrostatic Potentials Above the Centers of Substituted Benzenes are Due Primarily to Through-Space Effects of the Substituents, J. Am. Chem. Soc., 2009, 131, 3126–3127 CrossRef CAS PubMed.
- R. K. Raju, J. W. Bloom, Y. An and S. E. Wheeler, Substituent Effects on Non-Covalent Interactions with Aromatic Rings: Insights from Computational Chemistry, ChemPhysChem, 2011, 12, 3116–3130 CrossRef CAS PubMed.
- S. E. Wheeler, Understanding Substituent Effects in Noncovalent Interactions Involving Aromatic Rings, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS PubMed.
- S. Tsuzuki, M. Yoshida, T. Uchimaru and M. Mikami, The Origin of the Cation/π Interaction: The Significant Importance of the Induction in Li+ and Na+ Complexes, J. Phys. Chem. A, 2001, 105, 769–773 CrossRef CAS.
- I. Soteras, M. Orozco and F. J. Luque, Induction Effects in Metal Cation–Benzene Complexes, Phys. Chem. Chem. Phys., 2008, 10, 2616–2624 RSC.
- R. Sathyapriya and S. Vishveshwara, Interaction of DNA with Clusters of Amino Acids in Proteins, Nucleic Acids Res., 2004, 32, 4109–4118 CrossRef CAS PubMed.
- A. S. Reddy, D. Vijay, G. M. Sastry and G. N. Sastry, From Subtle to Substantial: Role of Metal Ions on π–π Interactions, J. Phys. Chem. B, 2006, 110, 2479–2481 CrossRef CAS PubMed.
- S. Pinheiro, I. Soteras, J. L. Gelpi, F. Dehez, C. Chipot, F. J. Luque and C. Curutchet, Structural and Energetic Study of Cation–π–Cation Interactions in Proteins, Phys. Chem. Chem. Phys., 2017, 19, 1463–9076 Search PubMed.
- Y. An, J. W. G. Bloom and S. E. Wheeler, Quantifying the π-Stacking Interactions in Nitroarene Binding Sites of Proteins, J. Phys. Chem. B, 2015, 119, 14441–14450 CrossRef CAS PubMed.
- W. R. Pitt, D. M. Parry, B. G. Perry and C. R. Groom, Heteroaromatic Rings of the Future, J. Med. Chem., 2009, 52, 2952–2963 CrossRef CAS PubMed.
- (a) Y. Dehouck, C. Biot, D. Gilis, J. M. Kwasigroch and M. Rooman, Sequence-Structure Signals of 3D Domain Swapping in Proteins, J. Mol. Biol., 2003, 330, 1215–1225 CrossRef CAS PubMed; (b) R. Wintjens, J. Lievin, M. Rooman and E. Buisine, Contribution of Cation–π Interactions to the Stability of Protein-DNA Complexes, J. Mol. Biol., 2000, 302, 395–410 CrossRef CAS PubMed.
- (a) K. S. Kim, J. Y. Lee, S. J. Lee, T.-K. Ha and D. H. Kim, On Binding Forces between Aromatic Ring and Quaternary Ammonium Compound, J. Am. Chem. Soc., 1994, 116, 7399–7400 CrossRef CAS; (b) C. A. Deakyne and M. Meotner, Unconventional Ionic Hydrogen-Bonds 2. NH+/–π Complexes of Onium Ions with Olefins and Benzene-Derivatives, J. Am. Chem. Soc., 1985, 107, 474–479 CrossRef.
- D. A. Dougherty, The Cation–π Interaction, Acc. Chem. Res., 2013, 46, 885–893 CrossRef CAS PubMed.
- E. M. Duffy, P. J. Kowalczyk and W. L. Jorgensen, Do Denaturants Interact with Aromatic Hydrocarbons in Water?, J. Am. Chem. Soc., 1993, 115, 9271–9275 CrossRef CAS.
- J. B. O. Mitchell, C. L. Nandi, I. K. McDonald, J. M. Thornton and S. L. Price, Amino/Aromatic Interactions in Proteins: Is the Evidence Stacked Against Hydrogen Bonding?, J. Mol. Biol., 1994, 239, 315–331 CrossRef CAS PubMed.
- E. Cauët, M. Rooman, R. Wintjens, J. Liévin and C. Biot, Histidine–Aromatic Interactions in Proteins and Protein–Ligand Complexes: Quantum Chemical Study of X-ray and Model Structures, J. Chem. Theory Comput., 2005, 1, 472–483 CrossRef PubMed.
- C. Riplinger and F. Neese, An Efficient and Near Linear Scaling Pair Natural Orbital Based Local Coupled Cluster Method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- (a) P. Hobza, Calculations on Noncovalent Interactions and Databases of Benchmark Interaction Energies, Acc. Chem. Res., 2012, 45, 663–672 CrossRef CAS PubMed; (b) J. Pittner and P. Hobza, CCSDT and CCSD(T) calculations on model H-bonded and stacked complexes, Chem. Phys. Lett., 2004, 390, 496–499 CrossRef CAS.
- E. Paulechka and A. Kazakov, Efficient DLPNO–CCSD(T)-Based Estimation of Formation Enthalpies for C-, H-, O-, and N-Containing Closed-Shell Compounds Validated Against Critically Evaluated Experimental Data, J. Phys. Chem. A, 2017, 121, 4379–4387 CrossRef CAS PubMed.
- M. J. Frisch et al. , Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, Wavefunction Methods for Noncovalent Interactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 304–326 CrossRef CAS.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Psi4: An Open-Source ab initio Electronic Structure Program, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565 CrossRef CAS.
- C. D. Sherrill, Energy Component Analysis of π Interactions, Acc. Chem. Res., 2013, 46, 1020–1028 CrossRef CAS PubMed.
- K. E. Riley, M. Pitonak, P. Jurecka and P. Hobza, Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- A. Li, H. S. Muddana and M. K. Gilson, Quantum Mechanical Calculation of Noncovalent Interactions: A Large-Scale Evaluation of PMx, DFT, and SAPT Approaches, J. Chem. Theory Comput., 2014, 10, 1563–1575 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, The Protein Data Bank, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- S. Salentin, S. Schreiber, V. J. Haupt, M. F. Adasme and M. Schroeder, PLIP: Fully Automated Protein–Ligand Interaction Profiler, Nucleic Acids Res., 2015, 43, 443–447 CrossRef PubMed.
- In cases where no aromaticity is reported by OpenBabel, the ring is checked for planarity. The normals of each atom in the ring to its neighbors are calculated. The angle between each pair of normals has to be less than 5°. If this is true, the ring is also considered as aromatic.
- C. R. Sondergaard, M. H. Olsson, M. Rostkowski and J. H. Jensen, Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values, J. Chem. Theory Comput., 2011, 7, 2284–2295 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sańchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, Origin of the Attraction and Directionality of the NH/π Interaction: Comparison with OH/π and CH/π Interactions, J. Am. Chem. Soc., 2000, 122, 11450–11458 CrossRef CAS.
- J. Rezac, K. E. Riley and P. Hobza, S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef CAS PubMed.
- N. J. Singh, S. K. Min, D. Y. Kim and K. S. Kim, Comprehensive Energy Analysis for Various Types of π-Interaction, J. Chem. Theory Comput., 2009, 5, 515–529 CrossRef CAS PubMed.
- CPCM calculations were performed with UAKS radii. The use of atomic radii with either CPCM or SMD solvation models gave rise to a discontinuous PES due to abrupt changes in solute cavity shape along the profile. Nevertheless, the same trend in minimum energy values was found irrespective of the solvation model used: (a) A. Klamt and G. Schüürmann, COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient, J. Chem. Soc., 1993, 799 CAS; (b) J. Andzelm, C. Kölmel and A. Klamt, Incorporation of Solvent Effects into Density Functional Calculations of Molecular Energies and Geometries, J. Chem. Phys., 1995, 103, 9312–9320 CrossRef CAS; (c) V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS; (d) M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed; (e) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543 CrossRef CAS PubMed.
- The physical meaning of dielectric constant, a macroscopic observable, at the atomic scale is questionable: nonetheless, the representation of an active site as a homogeneous polarizable medium account describes its electrostatic effect in an average way: (a) D. J. Tantillo, J. Chen and K. N. Houk, Theozymes and Compuzymes: Theoretical Models for Biological Catalysis, Curr. Opin. Chem. Biol., 1998, 2, 743–750 CrossRef CAS PubMed; (b) K. Hotta, X. Chen, R. S. Paton, A. Minami, H. Li, K. Swaminathan, I. I. Mathews, K. Watanabe, H. Oikawa, K. N. Houk and C.-Y. Kim, Enzymatic Catalysis of Anti-Baldwin Ring Closure in Polyether Biosynthesis, Nature, 2012, 483, 355–358 CrossRef CAS PubMed; (c) F. Himo, Recent Trends in Quantum Chemical Modeling of Enzymatic Reactions, J. Am. Chem. Soc., 2017, 139, 6780–6786 CrossRef CAS PubMed.
- F. Duarte and R. S. Paton, Molecular Recognition in Asymmetric Counteranion Catalysis: Understanding Chiral Phosphate-Mediated Desymmetrization, J. Am. Chem. Soc., 2017, 139, 8886–8896 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: DLPNO-CCSD(T)/aug-cc-pVnZ benchmarks; PLIP geometric criteria; polycyclic aromatic ring visualizations; van der Waals surfaces of model complexes; absolute energies from DLPNO-CCSD(T)/aug-cc-pVTZ and SAPT2+3/aug-cc-pVDZ calculations; Cartesian coordinates; Table of PDB IDs and corresponding cation–π interactions identified (.xls). See DOI: 10.1039/c7sc04905f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |