Slow magnetic relaxation in octahedral low-spin Ni(III) complexes

Abstract

Herein we report the first examples of single-molecule magnet (SMM) behaviour in S = 1/2 Ni(III) complexes. We find that low-spin 3d⁷trans-[Ni^III(cyclam)(X)₂]Y complexes (cyclam = 1,4,8,11-tetraazacyclotetradecane; X and Y are singly charged anions) exhibit field-induced slow relaxation of magnetization for O-donor axial ligands (nitrate) but not for N-donor variants (isothiocyanate). Experimental and electronic structure computational investigations indicate that intrinsic spin polarisation of low-spin Ni(III) is modulated significantly by local coordination geometry and supramolecular interactions. Solid state dilution of Ni(III) with diamagnetic Co(III) ions forms a related complex salt, [Ni_xCo_1−x(cyclam)(NO₃)₂](NO₃)·2HNO₃ (0.1 < x < 1), which preserves slow magnetic dynamics, thus supporting a molecular component to slow relaxation. An initial analysis of magnetic relaxation lifetime fits best to a combination of Raman and direct relaxation processes.

---

Introduction

Single-molecule magnets (SMMs) are intrinsically promising to contribute to a wide range of nanoscale electronic applications, such as high-density information storage, spintronic devices, quantum computing and magnetic refrigeration.^1–12 Magnetic anisotropy governs the barrier height for magnetization switching in molecular magnets, therefore the understanding and optimisation of slow relaxation of magnetization has been an active area of research. Whereas mononuclear lanthanide-based complex examples are numerous,¹³ in comparison, the number of 3d mononuclear complexes exhibiting similar magnetic relaxation is smaller due to weaker orbital contributions, with the notable exception of Co(II), where plentiful examples of SMM behaviour in S = 3/2 3d⁷ complexes arise from large spin orbit coupling (SOC).¹⁰ We are interested in 3d⁷ Ni(III) complexes since the Ni(III) free ion has an even larger SOC parameter than Co(II) (725 cm⁻¹vs. 530 cm⁻¹, respectively),^14–16 therefore, we might expect significant influences on Ni(III) magnetic behaviour from the orbital contribution in less constrained coordination environments.

A clear limitation for employing Ni(III) ions in traditional SMMs is the requirement of a threshold high spin state (S > 1/2), which is challenged by the tendency for trivalent nickel to adopt doublet ground states. The source of magnetic anisotropy in mononuclear transition-metal systems is almost always zero field splitting (ZFS) of the ground state, as measured by the axial parameter D, which in turn requires S > 1/2 to obtain nonzero values. Notwithstanding, SMM-type behaviour in S = 1/2 systems has been reported recently. Examples found in f¹ complexes (Ce(III), U(V)) are rationalized by anisotropy for J > 1/2.^17–19 Only a few examples have been reported for the 3d transition metal series. A linear d⁹ Ni(I) complex exhibits slow relaxation of magnetization under applied dc fields: anisotropy is attributed to significant orbital degeneracy generated by the confined low-coordinate environment.²⁰ In the case of trigonal planar Ni(I) complexes, the SMM properties are controlled by direct and Raman relaxation processes.²¹ A four-coordinate S = 1/2 Mn(IV) complex shows SMM behaviour governed by Raman relaxation.²² The magnetic relaxation of five-coordinate vanadyl complexes are also exemplified to show spin lattice relaxation.^23,24 Finally, a recent example of Cu(II) exhibits field-induced slow relaxation of magnetization.²⁵ The mechanisms of slow relaxation of magnetization in these compounds are challenging to discern, and often attributed to a combination of different temperature-dependent relaxation processes, including Orbach (for J > 1/2), direct, phonon bottleneck, and Raman processes, which compete with each other under applied magnetic fields. The importance of vibrations on spin relaxation has been critically analysed recently.²⁶

In the present report, we explore the possibility of slow relaxation of magnetization in selected octahedral Ni(III) complex salts (Fig. 1). The low-spin d⁷trans-[Ni(cyclam)(X)₂]⁺ systems have been known for several decades to exhibit S = 1/2 ground states.^{14–16,27–29} Perhaps not surprisingly, given spin threshold requirements for nonzero anisotropy, no significant studies of their dynamic magnetic properties have been reported. Interestingly, we find that some [Ni(cyclam)(X)₂]⁺ complexes exhibit SMM-type properties that depend on the nature of X as well as intermolecular interactions.

Fig. 1 Left: low-spin Ni(III) cyclam complexes: the first coordination sphere has Ni–N₄O₂ and Ni–N₆ formulations, respectively, for compounds 1 and 2. Right: single crystal X-ray structures of the [Ni(cyclam)(NO₃)₂]⁺ (top) and [Ni(cyclam)(NCS)₂]⁺ (bottom) cations (excluding hydrogen atoms), where magenta, red, yellow blue and black ellipsoids represent Ni, O, S, N and C atoms, respectively.

Results and discussion

Preparations and structures of Ni(III) cyclam complex salts

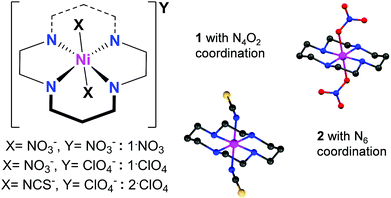
Slight modifications of literature procedures,^27,30 to reduce reaction temperatures to room temperature or below, have allowed us to isolate several Ni(III) cyclam complex salts in single crystal form. Oxidation of Ni(II) cyclam precursor complexes in aqueous solution, either with nitric acid (for 1·Y) or sodium dithionate (for 2·ClO₄), followed by standing for 24 hours, give complex salts [Ni(cyclam)(NO₃)₂](NO₃) (1·NO₃), [Ni(cyclam)(NO₃)₂](ClO₄) (1·ClO₄), and [Ni(cyclam)(NCS)₂](ClO₄) (2·ClO₄) in excellent yields. Details of synthetic preparations are provided in the ESI.† Structural characterizations for 1·NO₃ and 2·ClO₄ (Fig. S1 and Table S1) are also in the ESI,† whereas the same for 1·ClO₄ have been reported previously.³⁰ X-ray photoelectron spectroscopic measurements on solid samples of 1·NO₃ (Fig. S12†) show signals corresponding only to Ni in the 3+ oxidation state.

We note that minimal chemical changes generate a variety of coordination and packing possibilities. Complex 1 has a Ni–N₄O₂ first coordination sphere, whereas 2 displays Ni–N₆ coordination (Fig. 1), so that we can investigate the influence of ligand field on their properties. Likewise, different anions in 1·NO₃ and 1·ClO₄ may be expected to generate different supramolecular influences on the magnetic behaviour of 1.

In all three complexes, the cyclam ligand occupies the equatorial sites of the first coordination sphere, and is arranged in a trans-III (S,S,R,R) pattern. The local symmetry of the complex is C_2h overall, and approximately D_4h in the first coordination sphere. The structures of 1 and 2 reveal intermolecular hydrogen bonding interactions between the H atoms of the amine groups of cyclam and counter anions nitrate (in 1·NO₃), perchlorate (in 1·ClO₄) and isothiocyanato S atoms (in 2·ClO₄) (Fig. S2 and S3, Table S2†). In 1·NO₃, additional intramolecular contacts are found between the cyclam amines and coordinated nitrate groups. Overall, hydrogen bonding interactions between complexes are comparable to those within a complex. The minimum Ni–Ni distances are very similar in 1·NO₃, 1·ClO₄ and 2·ClO₄ (7.658(4) Å, 7.565(3) Å and 7.590(4) Å, respectively), therefore we might expect that the magnetic interactions between complexes in these salts should be similarly small in magnitude.

Initial observation of slow relaxation in Ni(III) cyclam complexes

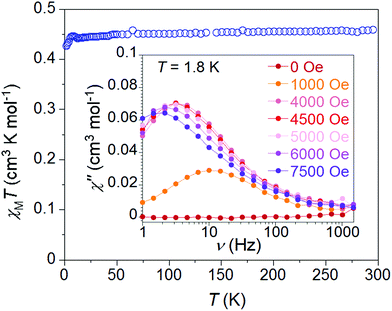
Testing the hypothesis that spin–orbit coupling considerations would be large enough to access J-state anisotropy, as demonstrated with Ni(I) complexes,²⁰ we explored the magnetic properties of 1·NO₃ (Fig. 2). At 300 K, the χ_MT value is 0.46 cm³ mol⁻¹ K for 1·NO₃, slightly higher than the theoretical Curie constant of 0.375 cm³ mol⁻¹ K for S = 1/2 and g = 2. As the temperature is decreased, χ_MT remains almost constant until 5 K, below which there is a very small decrease to ca. 0.42 cm³ mol⁻¹ K at 1.8 K, indicating a lack of significant intermolecular antiferromagnetic interactions or “standard” uniaxial magnetic anisotropy. Magnetization values saturate close to 1 μ_B at 2 K and 5 T (Fig. S10†) and support an S = 1/2 ground spin state. The reduced field (H/T) dependence of magnetization data exhibit superimposable isofield lines (Fig. S11†), consistent with the theoretical expectation of an absence of zero-field splitting. Fitting the static susceptibility data with the program PHI³² affords g_iso = 2.19(1) and negligible mean field antiferromagnetic interaction zJ/K = −0.05(2) K (Fig. S35†).

Fig. 2 Initial solid-state magnetic characterization of 1·NO₃. Temperature dependence of the χ_MT product, collected between 2 K and 300 K at 1000 Oe. Inset: dc field dependence of out-of-phase magnetic susceptibility signal, collected at 1.8 K.

Despite the inauspicious prospects provided by the static magnetic data, dynamic magnetic properties are observed in 1·NO₃. At zero applied field, the compound exhibits no out-of-phase magnetic susceptibility (χ′′) response. However, a non-zero χ′′ response is observed with applied dc fields as low as 500 Oe (Fig. 1 (inset) and S13†); this signal increases in magnitude with increasing applied field while the maxima gradually shift to the lower frequency, indicating that magnetic relaxation gradually becomes slower. The χ′′ value maximizes at 4500 Oe (3.5 Hz at 1.8 K), and further increases up to 7500 Oe shift the χ′′ maxima toward even lower frequencies, while the magnitude of χ′′ continues to decrease.

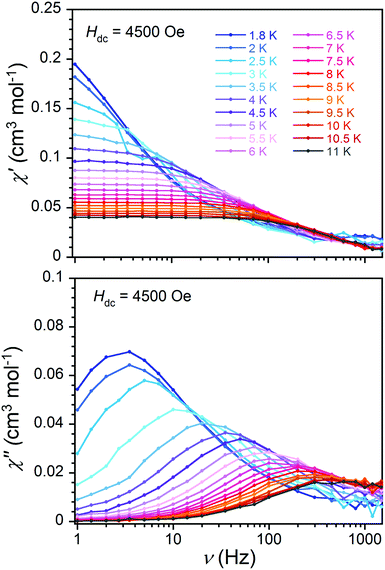
The frequency dependence of in- and out-of-phase susceptibility components are presented in Fig. 3 for 1·NO₃ in the temperature range 1.8–11 K. The temperature dependent relaxation lifetime τ(T) of 1·NO₃ can be obtained from corresponding frequencies of the maxima of χ′′(ν) curves at different temperatures (Fig. 3 (bottom) and S15†).

Fig. 3 Low temperature frequency dependence of in-phase (χ′, top) and out-of-phase (χ′′, bottom) ac magnetic susceptibility of 1·NO₃, collected between 1.8 K and 11 K at different temperatures under an applied dc field of 4500 Oe, with a 4 Oe oscillating ac field and frequency range 1–1500 Hz.

Comparison of magnetic and spectroscopic properties

As expected, the static magnetic properties of 1 and 2 are consistent with low-spin Ni(III) ions. The temperature dependence of χ_MT for 1·ClO₄ is similar in character to 1·NO₃ (Fig. S9†) but a little smaller in magnitude at all temperatures. The χ_MT values for 1·ClO₄ are 0.38 cm³ mol⁻¹ K and 0.34 cm³ mol⁻¹ K at 300 K and 1.8 K, respectively. The best fit of the χ_MT vs. T data (using PHI³²) affords g_iso = 2.04(2) and mean field antiferromagnetic interaction zJ/K = −0.09(1) K (Fig. S35†). Whereas χ_MT for 2·ClO₄ (0.43 cm³ mol⁻¹ K at 300 K) decreases below 20 K and reaches 0.21 cm³ mol⁻¹ K at 1.8 K (Fig. 4). This downturn is most likely associated with intermolecular antiferromagnetic interactions, even though the Ni–Ni distances are comparable in all three compounds. Anisotropic g values can potentially cause downturns in low temperature susceptibility data.³¹ Fitting the static susceptibility data of 2·ClO₄ with the program PHI³² affords g_iso = 2.19(2) and mean field antiferromagnetic interaction zJ/K = −0.91(1) K (Fig. S35†). The fit of the same data with anisotropic g parameters provides g_x = g_y = 2.36(3), g_z = 2.19(5) and zJ/K = −0.91(1) K, suggesting that the downturn is primarily due to antiferromagnetic interactions.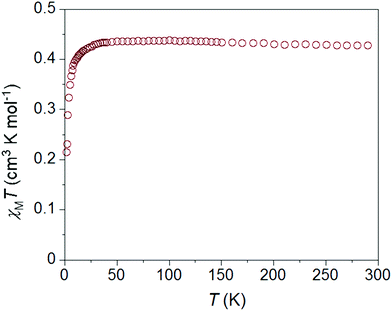

Fig. 4 Temperature dependence of the χ_MT product for compound 2·ClO₄, collected between 1.8 and 300 K at an applied dc field of 1000 Oe.

One other notable difference between the χ_MT vs. T plots for 1 and 2 is the presence of a small hump between 5 and 12 K for 1, which is absent in case of 2. This feature persists at higher fields, only disappearing at measuring fields of 3 T and above (Fig. S11†). We note that similar features are present in most reported examples of S = 1/2 SMMs^18,20 and a few Co(II) SMMs,^10–12 but no explanations have been offered.

Studies of the dynamic magnetic properties of both salts of 1 demonstrate field-induced slow magnetic relaxation behaviour in both nitrate and perchlorate salts (Fig. 1, 2 and S13–S17†). Both compounds show significant temperature-dependent χ′′(ν) signals below 10 K, where the magnitude of out-of-phase susceptibility data above 10 K is very small. The nature of the relaxation profile differs between the two salts, suggesting that dynamic magnetic properties are influenced by the environment beyond the first coordination sphere. In the remainder of this report, we will focus our discussion on the dynamic magnetic behaviour of compound 1·NO₃. A detailed description of the perchlorate salt 1·ClO₄ is provided in the ESI.†

In contrast to the results obtained with the nitrate-bound complex, the isothiocyanato-ligated 2·ClO₄ does not show any slow dynamics of magnetization, even under the applied dc field.

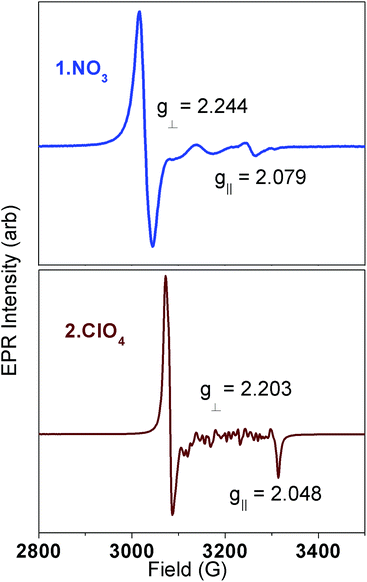
The very different dynamic magnetism results prompted more detailed spectroscopic investigations. EPR spectra of these compounds in the solid state (ground) and frozen aqueous solutions are all consistent with S = 1/2 ground states for the Ni(III) complexes.^14,27–29 Representative spectra for solid state samples of 1·NO₃ and 2·ClO₄ are shown in Fig. 5; data for 1·ClO₄ are shown in Fig. S6.† The sharp features at 3000–3100 G in Fig. 5 are strongly suggestive of g_⊥ in an axial system for both compounds. The broad features between 3100 and 3300 G in Fig. 5 (top) are consistent with weak scalar (A_∥) coupling to g_∥ involving several nuclei (cyclam N atoms); the sharpest feature at 3265 G is provisionally assigned to g_∥ for 1·NO₃. Meanwhile, the features between 3100 and 3300 G for 2·ClO₄ are possibly due to crystallites. The sharp feature around 3300 G in Fig. 5 (bottom) is consistent with g_∥ in an axial system. Computed g values for the three complexes, using B3LYP,³³ SORCI,³⁴ and NEVPT2 (ref. 35–37) in the ORCA software suite³⁸ (Table 1 and ESI†), are self-consistent and agree well with experimental values. All support the axial nature of the spectra observed.

Fig. 5 Solid state EPR spectra for 1·NO₃ (top) and 2·ClO₄ (bottom), collected at 100 K.

Table 1 Experimental and computed g values for 1·NO₃, 1·ClO₄, and 2·ClO₄^a

	g zz	g xx	g yy	g iso
a Experimental values given in bold typeface; g∥ = gxx = gyy.
1·NO3	2.079	2.244	2.244	2.189
B3LYP	2.030	2.129	2.139	2.099
SORCI	2.032	2.247	2.283	2.187
NEVPT2	2.008	2.185	2.203	2.132
1·ClO4	2.041	2.224	2.224	2.163
B3LYP	2.030	2.126	2.148	2.102
SORCI	2.032	2.241	2.291	2.188
NEVPT2	2.009	2.180	2.210	2.133
2·ClO4	2.048	2.224	2.224	2.165
B3LYP	2.032	2.107	2.116	2.085
SORCI	1.994	2.222	2.235	2.150
NEVPT2	1.994	2.207	2.212	2.137

---

Considering the nitrogen atoms from the cyclam are co-planar with the Ni(III) ion in 1 and 2, the unpaired electron should reside in the d_z2 orbital in idealized D_4h symmetry. For such a system, g_∥ is expected to be close to 2.0 and g_⊥ = g_e − 6ζ/Δ, where Δ is the energy differences between the singly-occupied orbital in the ground state (d¹_z2) and excited state (d¹_xz or d¹_yz, Fig. S40†).

To determine experimental ζ values for the powdered samples, we performed diffuse reflectance measurements (Fig. S7†). As expected, the 1·NO₃ and 1·ClO₄ solid state electronic absorption spectra are similar. The spectrum for 2·ClO₄ shows an additional broad feature at lower energy. B3LYP³³ TD-DFT³⁹ calculations in the g16 software suite,⁴⁰ ESI† were used to assist spectral assignments. The lowest energy features for 1·NO₃ and 1·ClO₄ are at 13 660 cm⁻¹ (15 700 cm⁻¹ computed) and 13 920 cm⁻¹ (15 600 cm⁻¹ computed), respectively. For 2·ClO₄ the transitions are much more mixed, owing to stronger NCS⁻ involvement. The lowest band is at 10 020 cm⁻¹ (11 000 cm⁻¹ computed), but the character of this transition is computed to be d_z2 to d_x2–y2, which does not contribute to changes in g due to orbital selection rules, see Fig. S40.† The lowest d_xz/d_yz to d_z2 transition is computed to be at 13 700, which is 2000 cm⁻¹ lower than calculated for 1·NO₃ or 1·ClO₄. This analysis was used to determine the Δ values as 13 660, 13 930 and 11 700 cm⁻¹, respectively, for compounds 1·NO₃, 1·ClO₄ and 2·ClO₄.

Combining the spectroscopically-determined g and Δ values, we obtain spin–orbit coupling parameters (ζ) as 550, 520 and 432 cm⁻¹, respectively. The lowered excitation energy, coupled with greater ligand character in the d_z2 orbital, results in a g_⊥ parameter nearly the same for 2·ClO₄ as for 1·NO₃. This analysis, along with the observation of relatively “spin-only” magnetic susceptibility behaviour, strongly suggests that spin–orbit coupling is not the key driver in the different dynamic properties.

Comparing EPR spectra acquired at the same temperature, 2·ClO₄ is significantly sharper than 1·NO₃. The extent to which this observation may be diagnostic for slow relaxation of magnetization requires further investigation. For 1·NO₃ and 2·ClO₄, we calculate weak couplings of the unpaired spin to cyclam N nuclei (0–3 MHz and 3–6 MHz, respectively, see Tables S8 and S9†). For 2·ClO₄, we also compute strong couplings to isothiocyanato N nuclei (50–60 MHz). This is consistent with literature spectra of 2·ClO₄ but not with sharp features in the spectrum (Fig. 5 bottom), implying that strong coupling between the thiocyanate nitrogens and the unpaired electron is not observed here: we speculate that the bent NCS⁻ ligand may be bending in the crystal lattice at the Ni–N–C arrangement, leading to vibrionic interactions/relaxation processes.

Based on the limited data set, we suspect that slow relaxation of magnetization for 1·NO₃ is correlated to the axial ligand not possessing active nuclear spin. For both salts of 1, the axial ligands are coordinated through oxygen. For 2·ClO₄ significant scalar coupling is observed. The degree of delocalization and/or coupling should be related to low energy vibrations of the axial ligands. Electronic structure computations for 2·ClO₄ show coupling between g/A and select vibrational modes for the NCS-ligated complex. For the lowest 21 vibrational modes, g and nitrogen A tensors are computed at geometries wherein the coordinates are displaced along the normal mode in the plus and minus directions. The differences between the equilibrium and displaced g and A are reported as Δ in Tables 2 and 3. Estimates for 1^st and 2^nd derivatives are obtained as average of and differences between Δ values, respectively. Data is collected in Tables 2, 3, S5, S10, 11, and Fig. S41.† For g (Table 2), a Ni-NCS bending mode (mode 13) contributes a first derivative coupling, while a cyclam ring breathing mode (mode 18) makes a second derivative contribution. We note that a cyclam ring breathing mode should also be present in 1, where slow relaxation is observed. For A (Table 3), the largest coupling is for a Ni-NCS bend involving the NCS nitrogen atoms (mode 17). It provides a first derivative coupling. The first derivative terms are relevant to anharmonic spin-phonon dynamics and the second derivatives are important for harmonic spin-vibrational coupling.^41,42

Table 2 Computed variation in g for select vibrational modes in 2·ClO₄

Mode	Disp.	g ∥	g ⊥	g ⊥	g iso
13	−	2.033	2.156	2.159	2.116
	Δg	0.001	−0.024	−0.023	−0.015
	+	2.035	2.108	2.113	2.085
	Δg	0	0.024	0.023	0.016
	1^st deriv.	−0.001	0.024	0.023
18	−	2.036	2.106	2.158	2.1
	Δg	−0.001	0.026	−0.022	0.001
	+	2.035	2.107	2.158	2.1
	Δg	−0.001	0.026	−0.022	0.001
	2^nd deriv.	−0.001	0.026	−0.022

---

Table 3 Computed variation in A for vibrational mode 17 in 2·ClO₄

N atom	Disp.	A xx	A yy	A zz	A iso
a Nitrogen atoms for axial (NCS^−) ligands.
3^a	−	73.6	74.4	83.3	77.1
	ΔA	19.4	19.3	21.2	20
	+	34.2	35.1	39.9	36.4
	ΔA	−19.9	−20	−22.2	−20.7
	1^st deriv.	−19.6	−19.6	−21.7
6^a	−	34.2	35.1	39.9	36.4
	ΔA	−19.9	−20	−22.2	−20.7
	+	73.6	74.4	83.3	77.1
	ΔA	19.4	19.2	21.2	19.9
	1^st deriv.	19.6	19.6	21.7

---

An interesting feature of the Ni(III) cyclam system is that both g and A are being modulated; and further, that the scalar coupling appears to be anisotropic. Theory papers in this area tend to focus only on perturbations of g.^41–44 In a future report, we seek to understand if the difference in magnetic behaviours can be attributed to spin-vibrational coupling involving g or A, or both.

Magnetic dilution studies

In efforts to isolate the intrinsic magnetic properties of the low-spin Ni(III) complexes and probe the origin of magnetic dynamics, we prepared mixed cation salts where Ni(III) was replaced with diamagnetic Co(III) ions. Control of Ni and Co stoichiometry is directly obtained by varying the ratios of metal precursors in aqueous solution before adding the cyclam solution. Interestingly, we find that any incorporation of Co(III) ions affords crystalline compounds where two equivalents of nitric acid are included per metal centre.⁴⁵ We thus rationally synthesized a dilution series with the general formula [Ni_xCo_1−x(cyclam)(NO₃)₂](NO₃)·2HNO₃, where x = 1 (3a), 0.5 (3b), 0.25 (3c), 0.1 (3d), and 0 (3e). The synthesis and characterization of a related [Co(cyclam)(NO₃)₂](NO₃)·HNO₃ have been reported,⁴⁵ where only one equivalent of nitric acid co-crystalizes. Note the only difference in the preparations of 1·NO₃ and 3a is heating the reaction mixture for the latter before adding nitric acid: the higher temperatures are required to dissolve green precipitates formed initially in the Co-containing reactions.

Comparison of the electronic absorption spectra obtained for 3a–e in water indicates successful control of Ni : Co ratios (Fig. S18†). Diffuse reflectance measurements performed on solid state samples (Fig. S19†) also support the formation of mixed metal compounds. The single crystal structures of 3a and 3d (Table S1 and Fig. S4†) and unit cell data for 3b, 3c and 3e indicate all these compounds are isostructural (Table S3 and Fig. S20†). Additional powder X-ray data collected for 3a–e also indicate the mixed metal systems are members of an isostructural solid solution, not an inhomogeneous mixture of two metal complex salts (Fig. S21 and S22†).

Like 1·NO₃, the Ni-containing members of solid solution 3 show slow relaxation of magnetization under applied fields, albeit at differing temperatures and frequencies (see ESI† for details). We focus here on the magnetic properties of 3d, as it contains the maximum dilution of Ni(III) ions. The EPR signal for 3d is noisy but comparable to 1 (Fig. S23†) and confirms the presence of low-spin Ni(III). The solid state magnetic measurements of 3d (Fig. S24†) exhibit χ_MT values corresponding to 10% of the low spin Ni(III) signal found in 1. The M vs. H data collected at 2 K between 0 and 50 kOe (inset of Fig. S24†) saturate at 0.1 μ_B, further supporting the expected dilution. Compound 3d also displays field-induced slow magnetic dynamics, albeit different in nature from both salts of 1. These observations indicate that slow magnetic relaxation properties are intrinsic to low-spin octahedral Ni(III), and are also influenced by small changes to its outer sphere coordination environment. For comparison with the magnetic dynamics of 1 (and 3a), the ac magnetic susceptibility of 3d is measured at 4500 Oe (Fig. S26†). It is important to note here that while compound 3a exhibits similar slow dynamics of magnetization (Fig. S27†), the co-crystallized nitric acids could be responsible for the slight differences in magnetic dynamics of 1·NO₃. At all temperatures probed, the χ′′(ν) value maximizes at lower frequencies for 3d (e.g. 1.0 Hz at 1.8 K) compared to 1·NO₃ (e.g. 3.5 Hz at 1.8 K, Fig. 2 and 4) and 3a (3.0 Hz at 1.8 K, 4000 Oe, Fig. S27†) which implies slower relaxation in the diluted sample.

As an alternative to solid-state dilution, ac magnetic measurements were also performed on flash-frozen aqueous solutions of 1·NO₃ (Fig. S29–31†). Slow dynamics are also observed (Fig. S31†), albeit a bit faster than in the solid state. We note the high likelihood of partial or total displacement of the axially coordinated nitrates (in 1·NO₃) by water, which should influence the observed magnetic behaviour of these compounds, but in those cases, a local axial N₄O₂ coordination sphere would be maintained. Qualitatively, the combined results are consistent with the notion that some aspect of the observed SMM properties is intrinsic to the Ni(III) complex.

Analysis of magnetic dynamic properties

In principle, several relaxation pathways may be involved in the magnetic dynamics. Spin–lattice relaxation rates exhibit temperature dependences proportional to T, T², exp(U_eff/k_BT), T⁷ or T⁹ for direct, phonon-bottlenecked direct (PB), Orbach, Raman, or Kramers–Raman processes, respectively. Theoretically, the Orbach relaxation is not possible for magnetic relaxation involving the S = 1/2 ground state. Related, the χ_MT values are only slightly higher than theoretically expected for octahedral S = 1/2 3d metal complexes (Fig. 1 and 3) and do not reflect what would be expected if orbital contributions of J = 11/2 or 9/2 states were operative.

The absence of significant nuclear spin in Ni isotopes voids the possibility of metal electro-nuclear microstates involved in the slow magnetic relaxation of Ni(III). Nickel has only one stable isotope with a nuclear spin of I = 3/2 (⁶¹Ni, 1.14% abundant) so we do not expect Ni-based hyperfine coupling to contribute significantly to the observed slow dynamics of magnetism. Such hyperfine coupling has been shown to affect magnetic dynamics in Co(II) complexes due to the 100% natural abundance of ⁵⁹Co (I = 7/2).^46,47 Magnetic property measurements on ⁶¹Ni isotopically enriched samples of 1 are planned to assess the effects, if any, of electronuclear spins on magnetic relaxation in this system.⁴⁸

To investigate if the relaxation processes are only related to a phonon bottleneck (PB)^49–52 mechanism, we performed additional measurements on diluted samples. Out-of-phase susceptibility (χ′′) values for 3b (1 : 1 Ni : Co) collected at different applied dc fields at 1.8 K show multiple relaxation modes below 6000 Oe (Fig. S33†). For PB processes, the dilution of paramagnetic centres is expected to promote faster relaxation at set temperatures and fields.⁴⁹ Instead, the relaxation pattern of 3b is very different from 3a and 3d at the same field (at 1.8 K): in fact, at 4500 Oe 3b relaxes faster than 3d and with multiple relaxation modes. In addition, at a specific field and temperature we do not expect phonons of multiple energies to control multiple relaxation modes of an S = 1/2 system. Therefore, we do not think the PB process explains the slow magnetic dynamics in these compounds.

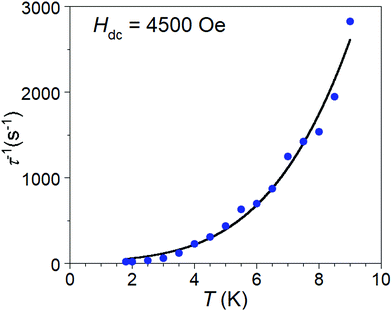
After disqualifying the possibility of Orbach and phonon bottleneck pathways, the remaining possibility is Raman relaxation. The temperature dependent relaxation times, τ(T), of 1·NO₃ are obtained from the frequencies corresponding to the maxima of χ′′(ν) curves below 10 K (Fig. 3 (bottom), and S15†) using the relation (τ(T) = 1/(2πν)). We found a best fit to the τ(T) vs. T data with a combination of Raman and direct processes, according to the relation τ⁻¹ = BTⁿ + AH²T (Fig. 6), which affords the coefficients B = 0.6817(8) and n = 3.71(4) for the Raman process, and coefficient A = 1.26 for the direct process, which is most significant at low temperatures. The value of the exponent n between 3 and 4 in the Raman process is unusual compared to the expected value of 9 or higher for a Kramers S = 1/2 ion, but not unreasonable based on the recent literature examples of V(IV) and Mn(IV) complexes, where Raman-like relaxation has been attributed to acoustic and optical vibrations.^22–24

Fig. 6 Temperature dependence of inverse magnetization lifetime for 1·NO₃. The line represents the best fit (goodness of fit R = 0.991) for a combination of direct and Raman relaxation modes, with the equation τ⁻¹ = AH²T + BTⁿ which provided exponent n = 3.71(4), A = 1.26 and B = 0.6817(8).

Similarly, the best fit to the τ(T) vs. T data for 1·ClO₄ provides exponent n = 3.16(3), A = 0.93(4) and B = 1.87(4) with a combination of Raman and direct processes (Fig. S38†). Because of the multiple relaxation modes in the compound 3b (1 : 1 Ni : Co) we have not performed the similar analysis, where the same is presented in Fig. S39† for compound 3d (1 : 9 Ni : Co).

We note that complex salts based on 1 show different relaxation behaviours with different charge balancing anions and dilution conditions. The multiple relaxation processes observed in 1·NO₃ and 3b suggest at least one relaxation pathway beyond a Raman process. Detailed analyses of the possible structural contributions to multiple relaxation pathways are underway which includes a comparative study of several similar compounds, and will be reported in due course. The influence of the intra and intermolecular H bonding interactions could be studied by replacing the N–H bonds of the cyclam ligand with N–Me bonds, which potentially will omit the close H-bonding interactions in the crystal structure.

Conclusions and outlook

The observation of slow relaxation of magnetization in hexacoordinate Ni(III) cyclam complexes challenges some aspects of our current understanding of the origins of SMM properties. The spectroscopic and magnetic properties of the complex salts reported here indicate both intrinsic and intermolecular interactions that modulate spin relaxation properties. Unlike most of the other S = 1/2 SMMs reported previously, this Ni(III) cyclam system offers many synthetically-tunable variables. Our current and future efforts are focused on teasing apart intra- and intermolecular effects by combining computational calculations with rational structural and chemical variations of [Ni(cyclam)]³⁺ complex salts, so as to understand electronic structures that drive magnetic relaxation in single-ion, single-spin systems. The current results suggest that differential couplings between spin and nuclear coordinates in complexes with geometric anisotropy may constitute a viable path for discovering SMM-like properties in other S = 1/2 3d metal complexes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by National Science Foundation, CHE-1058889 and CHE-1363274. We thank Prof. Melissa Reynolds and Ms Bella Neufeld for access to and assistance with diffuse reflectance measurements. We also thank Ms Leslie Kraynak for assistance with XPS measurements.

Notes and references

1. Molecular Magnets: Physics and Applications, ed. J. Bartolome, L. Fernando and J. F. Fernández, Springer Verlag, Berlin Heidelberg, 2014.
2. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179.
3. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194.
4. K. R. Dunbar, Editorial for the Virtual Issue on Quantum Molecular Magnets, Inorg. Chem., 2012, 51, 12055.
5. R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992.
6. G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537.
7. Y.-Z. Zeng, M. Evangelisti, F. Tuna and R. E. P. Winpenny, J. Am. Chem. Soc., 2012, 134, 1057.
8. J.-B. Peng, Q.-C. Zhang, X.-J. Kong, Y.-Z. Zheng, Y.-P. Ren, L.-S. Long, R.-B. Huang, L.-S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314.
9. Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and reactivity, ed. M. Swart and M. Costas, John Wiley & Sons, U.K., 2015.
10. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 and references therein.
11. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 and references therein.
12. S. Gomez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 2015, 289–290 , 379−392 and references therein.
13. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110.
14. D. Shamir, I. Zilbermann, E. Maimon, A. I. Shames, H. Cohen and D. Meyerstein, Inorg. Chim. Acta, 2010, 363, 2819.
15. J. Taraszewska, J. Sadlo, J. Michalik and B. Korybut-Daszkiewicz, Pol. J. Chem., 2000, 74, 813.
16. S. Anuradha and V. R. Vijayaraghavan, J. Chem. Sci., 2013, 125, 1123.
17. S. K. Singh, T. Gupta, L. Ungur and G. Rajaraman, Chem.–Eur. J., 2015, 21, 13812.
18. S. Hino, M. Maeda, K. Yamashita, Y. Kataoka, M. Nakano, T. Yamamura, H. Nojiri, M. Kofu, O. Yamamuro and T. Kajiwara, Dalton Trans., 2013, 42, 2683.
19. D. M. King, F. Tuna, J. McMaster, W. Lewis, A. J. Blake, E. J. L. McInnes and S. T. Liddle, Angew. Chem., Int. Ed., 2013, 52, 4921.
20. R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. Lopez, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640.
21. W. Lin, T. Bodenstein, V. Mereacre, K. Fink and A. Eichhöfer, Inorg. Chem., 2016, 55, 2091.
22. M. Ding, G. E. Cutsail, D. Aravena, M. Amoza, M. Rouzières, P. Dechambenoit, Y. Losovyj, M. Pink, E. Ruiz, R. Clérac and J. M. Smith, Chem. Sci., 2016, 7, 6132–6140.
23. L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074.
24. M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157.
25. R. Boča, C. Rajnák, J. Titiš and D. Valigura, Inorg. Chem., 2017, 56, 1478–1482.
26. L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275.
27. E. S. Gore and D. H. Busch, Inorg. Chem., 1973, 12, 1.
28. G. V. Koten and D. M. Grove, J. Am. Chem. Soc., 1983, 105, 1379.
29. D. E. Berry, S. Girard and A. McAuley, J. Chem. Educ., 1996, 73, 551.
30. A. McAuley, T. Palmer and T. W. Whitcombe, Can. J. Chem., 1993, 71, 1792.
31. O. Kahn, Molecular Magnetism, VCH Publishers, Inc., 1993, pp. 12, 32–38.
32. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
33. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
34. F. Neese, J. Chem. Phys., 2003, 119, 9428–9443.
35. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
36. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
37. C. Angeli, M. Pastore and R. Cimiraglia, Theor. Chem. Acc., 2007, 117, 743–754.
38. F. Neese, Wires Comput Mol Sci, 2012, vol. 2, pp. 73–78.
39. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
40. M. J. Frisch et al. , Gaussian 16, Revision A.03.
41. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2016, 8, 14620.
42. A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059.
43. L. Escalera-Moreno, N. Suaud, A. Gaita-Ariño and E. Coronado, J. Phys. Chem. Lett., 2017, 8, 1695–1700.
44. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341.
45. A. M. Funston, W. D. McFadyen and P. A. Tregloan, Aust. J. Chem., 2002, 55, 535.
46. S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 1.
47. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010.
48. J. Harmer, C. Finazzo, R. Piskorski, C. Bauer, B. Jaun, E. C. Duin, M. Goenrich, R. K.Thauer, S. Van Doorslaer and A. Schweiger, J. Am. Chem. Soc., 2005, 127, 17744.
49. J. C. Gill, J. Phys. C: Solid State Phys., 1973, 6, 109.
50. I. Chiorescu, W. Wernsdorfer, A. Müller, H. Bögge and B. Barbara, Phys. Rev. Lett., 2002, 84, 3454.
51. N. Lopez, A. V. Prosvirin, H. Zhao, W. Wernsdorfer and K. R. Dunbar, Chem.–Eur. J., 2009, 15, 11390.
52. R. Schenker, M. N. Leuenberger, G. Chaboussant, D. Loss and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184403.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of complex syntheses and spectroscopic characterizations, structural and magnetic data, and results of electronic structure calculations, including computed atomic coordinates and animations of key vibrational modes. CCDC 1579276, 1579279–1579281. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc04482h

‡ Current affiliation: Colorado State University, Pueblo.

---