Approach control. Stereoelectronic origin of geometric constraints on N-to-S and N-to-O acyl shifts in peptides

Abstract

Intramolecular N-to-S or N-to-O acyl shifts in peptides are of fundamental and practical importance, as they constitute the first step in protein splicing and can be used for the synthesis of thioester-modified peptides required for native chemical ligation. It has been stated that the nucleophile must be positioned anti to the carbonyl oxygen, as in a cis amide. Despite the importance of such reactions, an understanding of this geometric restriction remains obscure. Here we argue that the empirical requirement for positioning the nucleophile is a stereoelectronic effect arising from the ease of approach of the nucleophile to a carbonyl group, not ground-state destabilization. DFT calculations on model amides support our explanation and indicate a significant decrease in both the transition-state energy and the activation energy for a cis amide. However, the approach of the nucleophile must be anti not only to the carbonyl oxygen but also to the nitrogen. The direction of approach is expressed by a new, modified Bürgi–Dunitz angle. Our data shed light on the mechanisms of acyl shifts in peptides, and they explain why a cis peptide might be required for protein splicing. The further implications for acyl shits in homoserine and homocysteine peptides and for aldol condensations are also considered.

---

Introduction

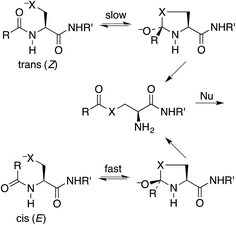
Protein splicing is the posttranslational excision of an internal polypeptide sequence, the intein, followed by ligation of the C-terminal and N-terminal segments, thereby generating the spliced extein.¹ For standard class I inteins (which have a nucleophilic amino acid as the N-terminal residue),² the initial step in this process utilizes an N-to-S or N-to-O acyl shift in a cysteine or serine residue, to produce a thioester or ester that is more reactive than the original amide toward nucleophilic attack.³ This process has been exploited for several important protein-engineering applications, such as expressed-protein ligation and recombinant-protein purification.⁴ The intramolecular N-to-S acyl shift reaction is also valuable for synthesizing peptide thioesters for native chemical ligation.⁵ This technique has become increasingly popular for such tasks as coupling to an alanyl or serinyl peptide by selective deselenization,⁶ synthesizing phospholipids,⁷ and generating a mixture of peptides in a dynamic exchange equilibrium.⁸

It has been stated that the nucleophilic S or O must be positioned anti to the carbonyl oxygen for the N-to-S or N-to-O acyl shift to take place.⁹ Thus the shift is faster for a cis (E) amide, even though the product ester is the same from either (Scheme 1). Structural studies on class I inteins have illuminated the details of the initial acyl shift in proteins.¹⁰ In many cases the scissile peptide bond is found to be distorted,¹¹ or in a cis conformation.¹² In synthetic peptides a nucleophile anti to the carbonyl oxygen can be achieved with the cis stereoisomer of a secondary amide, such as an N-alkyl cysteine or serine,¹³ or else a bis(mercaptoethyl)amide.¹⁴ It should be noted that the reverse reaction, an S-to-N acyl shift, is key to the synthesis of proteins by native chemical ligation.¹⁵ In this case there is no stereochemical constraint imposed by the thioester.

Scheme 1 Activation of an acylcysteine or acylserine residue of a peptide or protein by N-to-S (X = S) or N-to-O (X = O) acyl shift, which is faster for a cis peptide.

The issue we address is the requirement that the nucleophilic S or O must be anti to the carbonyl oxygen. Among the suggestions that we reject are the steric effect that destabilizes the cis amide and the more similar interconversion rate between cis and trans in an N-alkyl amide.¹⁶ These explanations violate the Curtin–Hammett principle,¹⁷ which states that the relative rates and the product distribution depend only on the relative energies of the two transition states and not on the equilibrium between the reactants. Also, although ground-state destabilization is well established for some enzyme catalysis,¹⁸ this cannot explain the greater reactivity of cis amides. The fallacy is the assumption that the transition state is the same for cis and trans amides, made implicitly,¹⁹ whereas the steric repulsion that destabilizes a cis amide is still present in its transition state for cyclization, the key first step in the acyl shift. Therefore the destabilization of a cis amide is irrelevant. Nor does invoking the power of the enzyme to twist the amide bond²⁰ or to N-protonate a twisted amide²¹ explain why a cis amide is more reactive.²²

These acyl shifts are classified as allowed 5-exo-trig in Baldwin's Rules (which may not apply to a sulfur nucleophile).²³ But for both O and S nucleophiles Baldwin's Rules offer no prohibition of either orientation of the C=O. The difference between cis and trans must be sought elsewhere.

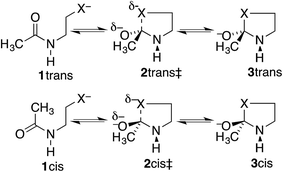
Our proposal is that the trans amide reacts more slowly because its geometry restricts the nucleophilic O or S from approaching the C=O from the preferred direction. To test this proposal, we have calculated structures and energies for the intramolecular reactions of cis and trans acetamides 1 with O, S, and Se anions (simplified from OH, SH, and SeH nucleophiles activated through general-base catalysis by an appropriate amino-acid residue), via transition states 2, leading to tetrahedral intermediates 3 (Scheme 2). Note that these amides are designated as the familiar cis and trans, rather than the E and Z recommended by IUPAC. Also, it may be noted that the two intermediates are of opposite configurations at the C undergoing addition, but the same configuration at NH, because the NH must remain either trans or cis to O. We claim that the calculated structures and energies provide a persuasive explanation for the geometric constraints required for the N-to-S or N-to-O acyl shift in cysteine and serine peptides.

Scheme 2 Cyclization of trans and cis N-CH₂CH₂X⁻-substituted acetamides (X = O or S).

Methodology

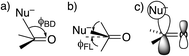
DFT(B3LYP)/6-311++G(d,p) calculations were performed with Gaussian 09 software Revision C.01.²⁴ Solvation by water was modeled with the polarized-continuum model.²⁵ Transition states were found by the QST3 procedure and characterized by one negative (imaginary) frequency, while reactant amides and tetrahedral intermediates properly had no such frequencies.²⁶

The approach of a nucleophile to a carbonyl group is often specified by two angles. The more familiar is the Bürgi–Dunitz angle ϕ_BD,²⁷ between the C–Nu and C=O directions (Fig. 1a). The other is the lateral-displacement angle ϕ_FL, between the C=O direction and the projection of the C–Nu direction onto the plane containing the C and the two attached groups (Fig. 1b). It is often called the Flippin–Lodge angle,²⁸ which can describe the steric hindrance by bulky groups on the carbonyl. Both of these angles affect the overlap between the orbital on the nucleophile and the π* molecular orbital of the carbonyl (Fig. 1c).²⁹ That overlap is maximized for ϕ_BD ∼107° and for ϕ_FL = 0, which thus specify the preferred direction of approach.

Fig. 1 Approach of a nucleophile to a ketone or aldehyde carbonyl. (a) Side view of Bürgi–Dunitz angle. (b) Top view of Flippin–Lodge angle. (c) Overlap between the orbital on Nu⁻ and the π* MO of C=O.

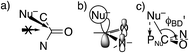
However, these angles are not appropriate for specifying the preferred direction of approach to an amide. Whereas the nucleophile approaches anti to the carbonyl O of an aldehyde or ketone, for amides the preferred approach is anti to both O and N, as suggested by the arrow in Fig. 2a and as has been rationalized in terms of the overlap between the orbital on the nucleophile and the π* molecular orbital of the amide (Fig. 2b).³⁰ Indeed, according to the calculated transition state for OH⁻ addition to trans-N-methylacetamide or for HS⁻ addition to trans-N-methylacetamide ·HCl, the preferred ϕ_FL is not 0° but 52° or 61°, respectively. The Bürgi–Dunitz angle must then be modified as the complement of the Nu–C–P_Nu angle (Fig. 2c, where P_Nu is the projection of the nucleophile onto the NCO plane), which we designate as ϕ′_BD.

Fig. 2 Approach of a nucleophile to an amide carbonyl. (a) Top view of approach anti to both O and N of an amide. (b) Overlap between the orbital on Nu⁻ and the amide π* MO. (c) Side view of modified Bürgi–Dunitz angle.

The modified Bürgi–Dunitz angle ϕ′_BD was calculated as follows: first X_normal, the normal to the OCN plane containing C, O, and N, was calculated as (X_O − X_C) × (X_N − X_C), the cross product between the C–O and C–N vectors. Next P_Nu, the projection of X_Nu onto the NCO plane, was calculated as X_Nu + X_normal(X_C·X_normal − X_Nu × X_normal)/X_normal × X_normal. Finally, cos(180° − ϕ′_BD) was evaluated as the normalized dot product (X_Nu − X_C)(P_Nu − X_C)/|X_Nu − X_C||P_Nu − X_C|.

Results

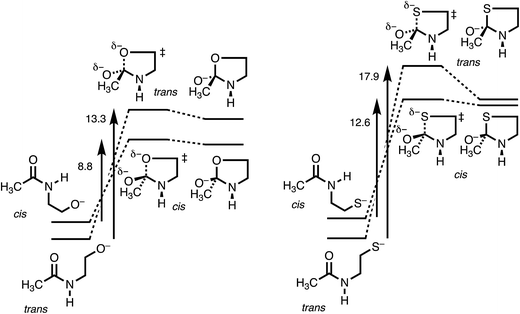
Table 1 lists calculated energies of cis and trans stereoisomers of extended-chain amide 1, tetrahedral intermediate 3, and transition state 2 connecting them, for X = O, S, and Se, along with the activation energies E_a = E(2) − E(1). For X = S and Se either HF or HCl, respectively, was coordinated to the carbonyl oxygen in order to converge addition to the amide, which otherwise is thermodynamically unfavorable because RS⁻ and RSe⁻ are such stable anions and because C–S and C–Se bonds are weak. Besides, the coordinated acid can mimic the “oxyanion hole”, which stabilizes the tetrahedral intermediate in some enzyme-catalyzed reactions.

Table 1 Calculated relative energies (kcal mol⁻¹) for N-to-X (X = O, S, Se) acyl transfer in 1

	X = O	X = S^a	X = Se^b
a HF. b HCl.
E(1cis)	1.7	2.0	1.9
E(1trans)	≡0.0	≡0.0	≡0.0
E(3cis)	10.1	14.1	4.6
E(3trans)	12.6	14.5	4.2
E(2‡cis)	10.5	14.6	6.7
E(2‡trans)	13.3	17.9	7.4
E a(cis)	8.8	13.6	4.8
E a(trans)	13.3	17.9	7.4

---

Because the coordination to HF or to HCl, the use of anionic nucleophiles, and the use of PCM are all devices to facilitate the calculations, the absolute energies in Table 1 cannot be compared to experimental energies. Nevertheless, the trans amides are a reasonable 2 kcal mol⁻¹ more stable than the cis, and the open-chain amides 1 are calculated to be more stable than the high-energy tetrahedral intermediates 3. Moreover, nearly the same results for X = O are obtained with the M06-2X method, which accounts for dispersion,³¹ as documented in Table S1,† and also with B3LYP/6-311++G(d,p) free energies, which include vibrational frequencies and zero-point energies, as documented in Table S2.†

Fig. 3 makes the energies in Table 1 graphic. The key result is the lower energy of the cis transition state for both X = O (without HF) and X = S (with HF), by ∼2.5 kcal mol⁻¹. The differences in activation energies are slightly larger, 4–5 kcal mol⁻¹. These differences thus reproduce the faster cyclization seen for cis amides. However, the faster cyclization is not merely because of the destabilization of a cis amide, but because of the lower energy of the cis transition state, consistent with the Curtin–Hammett Principle. The case of X = Se, omitted from Fig. 3, is discussed below.

Fig. 3 Energy diagram (kcal mol⁻¹) for N-to-X (X = O, S) acyl transfer in 1.

The details of the transition-state structures clarify these relative reactivities. Table 2 presents key distances and angles, and Fig. S1† shows views of these structures. The C–X bond that is being formed is properly longer in the transition state than when the bond is fully formed in intermediate 3. The lengthening is greater for 2trans, especially for X = O (as seen in the MOs in Fig. S2†), and this may reflect a better overlap for the cis stereoisomer, but it is not conclusive. The XCO angles in intermediates 3 are close to tetrahedral, as expected. The XCO angles in the transition states are also near tetrahedral, and deviate from the preferred Bürgi–Dunitz angle of 107°, but not by much.

Table 2 Calculated C–X distances (Å), Bürgi–Dunitz (XCO) angles (°), modified Bürgi–Dunitz angles ϕ′_BD (°) in transition states for acyl transfer

	d C–O	d C–S	d C–Se	θ OCO	θ SCO	θ SeCO	ϕ′BD(O)	ϕ′BD(S)^a	ϕ′BD(Se)^b
a HF. b HCl. c N-Methylacetamide.
NMA^c	1.92	2.36^b		106.9	103.4^b		118.6	118.3^b
2‡ cis	1.84	2.27^a	2.69	110.5	110.5^a	109.6	117.9	117.5^a	112.5
2‡ trans	1.86	2.30^a	2.70	107.4	105.7^a	100.3	113.4	111.2^a	101.7

---

The most informative parameter is the modified Bürgi–Dunitz angle ϕ′_BD (Fig. 2c). The values should be compared with the 118.6° or 118.3° calculated for unconstrained addition of OH⁻ or HS⁻ to N-methylacetamide (NMA) or N-methylacetamide HCl. The smaller angles in the cyclic transition states and especially in the trans transition states represent a greater displacement of the nucleophile from the π* MO of the amide group (Fig. 2b), and a correspondingly greater loss of overlap, which raises the energy of the cyclic transition states, and especially the trans. However, the displacements are small and cannot readily be detected in Fig. S1.†

Discussion

The data in Table 1 show that the DFT calculations reproduce the greater reactivity of the cis amides. The data in Table 2 show that the difference between cis and trans transition states lies in the ability of the nucleophile to approach the carbonyl group from the preferred direction. This is not simply a steric effect. Although the greater reactivity of a cis peptide (or of an N-alkylated peptide) is due to the greater proportion of a stereoisomer that cyclizes more rapidly, the reason for the faster cyclization is the ease of nucleophilic approach. Moreover, the approach is not simply anti to the carbonyl oxygen, but anti to both O and N.

Approach control has previously been recognized as arising from steric repulsions in the transition state, as in hydride reduction of cyclohexanones.³² Here it is a stereoelectronic effect, ³³ arising instead from orbital overlaps in the transition state, which are more favorable for one direction of approach over the other. The more difficult approach of the nucleophile in the trans amide is a consequence of a greater restriction on the ability of the nucleophile to reach the carbonyl carbon, as manifested by ϕ′_BD < optimum. This is a constraint of the five-membered ring being formed. It is an unusual example of angle strain that differs between cis and trans, even though they are both 5-exo-trig.

This difference in angle strain is recognizable even with a simple molecular-model kit. Therefore we expect that the order of relative energies in Table 1 is not an artifact of our particular computational model but will be obtained by any such calculation.

The N-to-Se acyl shift in a selenocysteine residue provides an instructive contrast. According to the calculated energies in Table 1, the activation energy for the trans is substantially higher than that for the cis. This is simply because of the ground-state steric destabilization of the cis, as originally proposed to explain its greater reactivity. However, the data also show that the transition-state energies for cis and trans differ by less than 1 kcal mol⁻¹, much less than the 4–5 kcal mol⁻¹ for N-to-O and N-to-S shifts. Those shifts of a trans amide are retarded by the inability of the nucleophile to reach the carbonyl carbon. However, because the C–Se bond is longer, the nucleophilic selenium has less difficulty in reaching the carbonyl carbon. However, according to the values in Table 2, the modified Bürgi–Dunitz angle ϕ′_BD is again significantly smaller in the trans transition state, just as for X = O or S, so that this parameter does not reflect the slight difference in transition-state energies. This may be a consequence of C–Se–C angles in both transition states that are constrained near 80°, thereby distorting the five-membered ring.

As a corollary, there may be no strong constraint on the approach of the selenium to the carbonyl carbon. Although a bis(selenylethyl) peptide readily undergoes a N-to-Se acyl shift,³⁴ the disubstitution may not be necessary. We suggest that a trans mono(selenylethyl) peptide might suffice, although it would be retarded by the lack of the ground-state steric destabilization of the cis isomer.

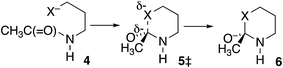
In further contrast, according to the data in Table 3, the transition-state energies for cyclization of homolog 4 (X = O) or 4 HF (X = S) are nearly equal for cis and trans amides Scheme 3). Moreover, for X = O the preferred ϕ_FL is calculated to be 55° for cis and 50° for trans, not far from the 52° for OH⁻ addition to N-methylacetamide. With a six-membered ring there is little restriction on the ability of the nucleophile to reach the carbonyl carbon. Indeed, the N-to-S acyl shift in a homocysteine residue is facile, without any necessity for N-alkylation or population of the cis amide.³⁵ Likewise, there is no such necessity with class 2 and 3 inteins, where a distant nucleophile adds to the carbonyl and forms a macrocycle.³⁶

Table 3 Calculated energies (kcal mol⁻¹, relative to 4trans) of transition states 5‡ for cyclization of 4

	X = O	X = S^a
a HF.
E(5‡cis)	11.39	15.84
E(5‡trans)	11.44	15.67

---

Scheme 3 Cyclization of homologous N-CH₂CH₂CH₂X⁻-substituted acetamides (X = O or S).

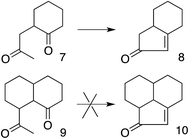
These results also have implications for aldol condensation (Scheme 4). Although many conversions of enolate 7 and its derivatives to the corresponding 8 are known,³⁷ we can find no report of the conversion of any derivative of 9 to the corresponding 10. This could be due simply to a lack of demand for 10, but it can also be explained by the difficulty for the enolate carbon of 9 to reach the carbonyl carbon, whereas 7 can twist to allow its enolate carbon to achieve the preferred approach to the carbonyl, as described by the Bürgi–Dunitz and Flippin–Lodge angles.

Scheme 4 Constraint on aldol condensation.

Conclusions

DFT calculations can reproduce the greater reactivity of a cis acylcysteine or acylserine toward N-to-S or N-to-O acyl shift. The reactivity difference between cis and trans can be attributed to the ease of approach to the carbonyl carbon by the nucleophile, not to ground-state destabilization. This represents an extension of Baldwin's rules to two distinguishable cases of 5-exo-trig ring closures. Moreover, there is no large reactivity difference in an N-to-Se acyl shift or in 6-exo-trig ring closures. We thus have provided a better understanding of the geometric constraints required for the N-to-S or N-to-O acyl shift in cysteine and serine peptides. We expect that this information will enable better design of peptides, especially ones containing homocysteine, that generate thioesters useful for chemical ligation techniques.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research was supported by U.S. Army Research Office MURI Award W911NF-13-1-0383 and by NSF grants CHE-1254611 and CHE11-48992.

References

1. (a) H. Paulus, Annu. Rev. Biochem., 2000, 69, 447–496; (b) N. H. Shah and T. W. Muir, Chem. Sci., 2014, 5, 446–461; (c) C. J. Minteer, et al. , Biochemistry, 2017, 56, 1042–1050.
2. K. Tori, et al. , J. Biol. Chem., 2010, 285, 2515–2526.
3. F. B. Perler, IUBMB Life, 2005, 57, 469–476.
4. (a) M. Vila-Perelló and T. W. Muir, Cell, 2010, 143, 191–200; (b) J. Liu, Q. Chen and S. Rozovsky, J. Am. Chem. Soc., 2017, 139, 3430–3437.
5. (a) J. Kang and D. Macmillan, Org. Biomol. Chem., 2010, 8, 1993–2002; (b) F. Burlina, G. Papageorgiou, C. Morris, P. D. White and J. Offer, Chem. Sci., 2014, 5, 766–770; (c) C. L. Lee, H. Liu, C. T. T. Wong, H. Y. Chow and X. Li, J. Am. Chem. Soc., 2016, 138, 10477–10484; (d) V. P. Terrier, H. Adihou, M. Arnould, A. F. Delmas and V. Aucagne, Chem. Sci., 2016, 7, 339–345; (e) C. Rao and C. Liu, Org. Biomol. Chem., 2017, 15, 2491–2496.
6. N. Metanis, E. Keinan and P. E. Dawson, Angew. Chem., Int. Ed. Engl., 2010, 49, 7049–7053.
7. R. J. Brea, C. M. Cole and N. K. Devaraj, Angew. Chem., Int. Ed. Engl., 2014, 53, 14102–14105.
8. Y. Ruff, V. Garavini and N. Giuseppone, J. Am. Chem. Soc., 2014, 136, 6333–6339.
9. T. Kawakami, Top. Curr. Chem., 2015, 362, 107–136.
10. L. Saleh and F. B. Perler, Chem. Rec., 2006, 6, 183–193.
11. A. Romanelli, A. Shekhtman, D. Cowburn and T. W. Muir, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 6397–6402.
12. T. Klabunde, S. Sharma, A. Telenti, W. R. Jacobs Jr and J. C. Sacchettini, Nat. Struct. Biol., 1998, 5, 31–36.
13. H. Hojo, Y. Onuma, Y. Akimoto, Y. Nakahara and Y. Nakahara, Tetrahedron Lett., 2007, 48, 25.
14. N. Ollivier, J. Dheur, R. Mhidia, A. Blanpain and O. Melnyk, Org. Lett., 2010, 12, 5238–5241.
15. (a) P. E. Dawson, T. W. Muir, I. Clark-Lewis and S. B. Kent, Science, 1994, 266, 776–778; (b) A. Roloff and O. Seitz, Chem. Sci., 2013, 4, 432–436.
16. J. Binschik and H. D. Mootz, Angew. Chem., Int. Ed. Engl., 2013, 52, 4260–4264.
17. J. I. Seeman, Chem. Rev., 1983, 83, 83–134.
18. (a) W. P. Jencks, Catalysis in Chemistry and EnzymologyMcGraw-Hill, New York, 1969, pp. 282–96; (b) F. M. Menger, Biochemistry, 1992, 31, 5368–5373; (c) V. E. Anderson, Encyclopedia of Life Sciences, 2001, John Wiley, http://www.els.net, pp. 1–5.
19. D. G. A. Johansson, B. Macao, A. Sandberg and T. Härd, J. Mol. Biol., 2008, 377, 1130–1143.
20. J. I. Mujika, J. M. Mercero and X. Lopez, J. Am. Chem. Soc., 2005, 127, 4445–4453.
21. D. G. A Johansson, G. Wallin, A. Sandberg, B. Macao, J. Åqvist and T. Härd, J. Am. Chem. Soc., 2009, 131, 9475–9477.
22. The application of the Curtin–Hammett Principle requires that reactants be in rapid equilibrium. For cis and trans amides this does not hold, but the twisting of the amide bond envisions such equilibration.
23. (a) J. E. Baldwin, J. Chem. Soc., Chem. Commun., 1976, 734; (b) I. V. Alabugin and K. Gilmore, Chem. Commun., 2013, 49, 11246–11250; (c) K. Gilmore, R. K. Mohamed and I. V. Alabugin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 487–514.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2010.
25. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
26. No attempt was made to carry out a state-of-the-art computation, because our goal is to understand the stereochemical requirement. The chosen basis set is identical to or slightly larger than the basis sets that were adequate for modeling alkaline hydrolysis of amides,²⁶ which also proceeds via an anionic transition state. Nevertheless, to verify that these results are not merely an artifact of the B3LYP method and of the 6-31++G(d,p) basis set, the same calculation was performed for 1, 2 and 3, X = O, with M06-2X/6-311++G(d,p) and also by calculating B3LYP/6-311++G(d,p) free energies, which corrects for zero-point energy. Results of all of these comparisons are tabulated in ESI.†.
27. H. B. Bürgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Tetrahedron, 1974, 30, 1563–1572.
28. (a) E. P. Lodge and C. H. Heathcock, J. Am. Chem. Soc., 1987, 109, 3353–3361; (b) L. A. Flippin and C. H. Heathcock, J. Am. Chem. Soc., 1983, 105, 1667–1668.
29. I. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, 1976.
30. (a) J. E. Baldwin, J. Chem. Soc., Chem. Commun., 1976, 738–741; (b) A. J. Stone and R. W. Erskine, J. Am. Chem. Soc., 1980, 102, 7185–7192; (c) C. L. Liotta, E. M. Burgess and W. H. Eberhardt, J. Am. Chem. Soc., 1984, 106, 4849–4852.
31. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
32. (a) H. C. Brown and J. Muzzio, J. Am. Chem. Soc., 1966, 88, 2811–2822; (b) E. L. Eliel and Y. Senda, Tetrahedron, 1970, 26, 2411–2428.
33. I. V. Alabugin, Stereoelectronic Effects: A Bridge Between Structure and Reactivity, John Wiley & Sons, Ltd., Chichester, Online ISBN: 9781118906378,  DOI:10.1002/9781118906378, 2016.
34. L. Raibaut, M. Cargoët, N. Ollivier, Y. M. Chang, H. Drobecq, E. Boll, R. Desmet, J.-C. M. Monbaliu and O. Melnyk, Chem. Sci., 2016, 7, 2657–2665.
35. D. Schwarzer, C. Ludwig, I. V. Thiel and H. D. Mootz, Biochemistry, 2012, 51, 233–242.
36. M. W. Southworth, J. Benner and F. B. Perler, EMBO J., 2000, 19, 5019–5026.
37. (a) A. Hosomi, A. Shirahata, Y. Araki and H. Sakurai, J. Org. Chem., 1981, 46, 4631–4633; (b) R. M. McFadden and B. M. Stoltz, J. Am. Chem. Soc., 2006, 128, 7738–7739.

---

Footnote

† Electronic supplementary information (ESI) available: B3LYP/6-311++G(d,p) energies and Cartesian coordinates of all species; M06-2X/6-311++G(d,p) energies and B3LYP/6-311++G(d,p) free energies of 1, 2, and 3, X = O; calculations of modified Bürgi–Dunitz angles ϕ′_BD; ball-and-stick models of calculated transition states for N-to-X acyl transfer, MOs (HOMO-1) for 2^‡. See DOI: 10.1039/c7sc04046f

---