Evaluating a learning progression on ‘Transformation of Matter’ on the lower secondary level
M.
Emden
 *a,
K.
Weber
b and
E.
Sumfleth
*a,
K.
Weber
b and
E.
Sumfleth
 c
c
aUniversity of Education, Lagerstrasse 2, CH-8090 Zuerich, Switzerland. E-mail: markus.emden@phzh.ch
bUniversity of Duisburg-Essen, Chemistry Education, Schuetzenbahn 70, 45127 Essen, Germany. E-mail: katrin.weber@uni-due.de
cUniversity of Duisburg-Essen, Chemistry Education, Schuetzenbahn 70, 45127 Essen, Germany. E-mail: elke-sumfleth@uni-due.de
First published on 22nd August 2018
Abstract
One of the most central tenets of chemistry education is developing an understanding of the processes that involve the Transformation of Matter. Current German curricula postulate content-related abilities (Kompetenzen) that are expected to be achieved by secondary students when graduating from the lower secondary level at grade 10. These abilities can further be differentiated as relating to either structural aspects of matter or to aspects of chemical reaction. Little is known of how Kompetenzen in these two fields develop over time on the lower secondary level. This study aims at elucidating this development by suggesting a hypothetical learning progression for the lower secondary level. This learning progression is visualised as a Strand Map and is investigated using methods from three statistical approaches: Rasch-analyses, Classical Test Theory, and Bayesian Networks. Concurrent data from all three strands of analyses inform the evaluation of the learning progression and support the notion that an understanding of the Transformation of Matter relies on interrelated Kompetenzen to conceptualize Structure of Matter and Chemical Reaction. Moreover, Bayesian networks underline that there is more than one progression when learning about chemistry on the lower secondary level.
Introduction and background
Learning progressions
Duschl et al. (2007) have stated that “[l]earning progressions are descriptions of the successively more sophisticated ways of thinking about a topic that can follow one another as children learn about and investigate a topic over a broad span of time [… and that…] are crucially dependent on instructional practices if they are to occur” (p. 214). As a result, learning progressions are per se idiosyncratic with respect to students and the instruction they experience (cf.Rogat, 2011) and there is no ultimate one-size-fits-all road map (cf.Smith et al., 2006). Nonetheless, descriptions of learning progressions that aim at identifying ‘bulk’ rather than individual abilities, e.g., the mean abilities within a sample of secondary school students, might inform science education when organizing science content economically along the secondary level.Learning progressions describe the development of a specific topic over a defined time span negotiating between a lower and an upper anchor (cf.Mohan et al., 2009; Stevens et al., 2010). Already formed abilities constitute the lower anchor from which a learning progression reaches towards the upper anchor, which provides a perspective for subsequent learning processes. The development from lower to upper anchor is modelled in one or more progress variables which represent the constructs to be developed and are broken down into detailed performance expectations (cf.Corcoran et al., 2009).
In contrast to traditional curricula that governed teaching organization from a structural stance, i.e. experts decided on which bit of information was necessary in order to acquire the next bit etc., learning progressions focus on students’ actual performance abilities. Thus, learning progressions have an essentially functional view on how to organize learning, rather: how to organize teaching that can facilitate learning (Rogat, 2011). As such, they can never be more than approximations of the ideal. Each and every student's progress can be considered an individual test on a learning progression's feasibility, i.e. validity. For some students its bearings might hold true, for others they might not; these students will take different learning pathways – the ultimate aim is arriving at a suggestion that works for as many students as possible. Easing students’ learning by matching instruction as closely as possible to their needs and potentials arguably results in ‘smoother’ learning and, consequently, better retention of the concepts. This appears to be of special relevance with regard to a subject's most central tenets which need to ‘hold’ throughout an academic career.
We must, therefore, try to hypothesize viable descriptions of which abilities need to unfold in which sequence when mastering, e.g., an idea as central to chemistry as the Transformation of Matter and, subsequently, check this hypothesis in the field. Generating this hypothesis optimally merges findings from empirical research on learning with propositional considerations (e.g., Smith et al., 2006), e.g., from curricula or standard formulations (e.g., Duschl et al., 2011; Rogat, 2011) that focus on student learning outputs (e.g., Kompetenzen).
German science education standards, Kompetenzen and curricula
The German Secondary Science Education system has undergone a substantial change over the past decade. Following dissatisfying results from PISA 2000, German education administrators have reconsidered the then prevalent educational governance through detailing syllabi (Neumann et al., 2010). As of 2005 the basis for all national science curricula is formed by education standards that put performance expectations at their heart rather than lists of science facts. Now, school is expected to equip students with transferable, yet domain-specific abilities (Kompetenzen), that can serve them later in a wide range of situations, be it at home when coming upon a science related problem (e.g., how to get rid of price sticker remnants) or in an actual science context (e.g., investigating solubility), instead of ‘just’ transmitting propositional science knowledge (cf.Kauertz et al., 2012). This reorientation was initiated on the federal level (Klieme et al., 2003) and has subsequently been translated into Germany's federal states’ science curricula.The academic discussion on which features ultimately constituted Kompetenzen took several years (Neumann et al., 2012) and resulted in different structural models (Schecker and Parchmann, 2007), which “[d]espite differences in the details […all…] specify three facets: content structure, activities, levels of achievement […]” (Bernholt and Parchmann, 2011, p. 168, cf.Sevian and Talanquer, 2014). Germany's three science disciplines at the secondary level (biology, chemistry, physics) arrived at a shared consensus model (Kremer et al., 2012). This model distinguishes Kompetenzen in four areas: use of domain-specific content knowledge, acquirement of knowledge (roughly comparable to scientific inquiry), scientific communication (combining receptive and productive aspects), and evaluation and judgement (e.g., KMK, 2005).
Chemistry instruction at the secondary level organizes its standards for domain-specific content knowledge around four Fundamental Chemistry Concepts (Basiskonzepte which are roughly comparable to Disciplinary Core Ideas (NRC, 2011) or Big Ideas (cf.Smith et al., 2006; Hadenfeldt et al., 2016)). These underlie all chemical content and shed specific light on any given phenomenon in chemistry, i.e. from these perspectives: Substance–Particle-Relations, Structure–Property-Relations, Chemical Reaction, Enthalpy Changes (KMK, 2005). Curricula on the state level either adopt these concepts or further differentiate them, e.g., combining Substance–Particle- and Structure–Property-Relations into “Structure of Matter” (MSW, 2008a).
However, in contrast to other nation's science standards documents (cf. Grade Band Endpoints in NRC, 2011), German educational politics has widely refrained from differentiating Kompetenzen with respect to students’ age. This shortcoming has only been remedied in part on the state-level which might differentiate two age levels on the lower secondary stage, i.e. grades 5–10. Therefore, the challenge to describe students’ Kompetenz development over the course of the lower secondary level is largely open to science educators and science education researchers alike (Schecker and Parchmann, 2006). Claesgens and colleagues (2009) claim the same for the development of what they call ‘conceptual understanding’. Accordingly, how an idea of (or Kompetenz relating to) the Transformation of Matter unfolds, in which aspects of the Structure of Matter interact with ones of Chemical Reaction, is unknown. Elucidating this concept's development in students could serve to inform and economize chemistry teaching.
Kompetenzen for chemistry education are operationalized in generalized performance expectations that are largely independent of contexts. They can be further distinguished as being of either procedural or propositional character. While Kompetenzen of the first kind necessarily reflect an exemplary consensus choice from the wide array of procedural abilities from the field of science (e.g., hypothesizing, doing experiments, modelling), Kompetenzen that pertain to content knowledge typically reflect the structure of disciplinary knowledge. The same structure traditionally guides the composition of textbooks and syllabi. Standards for content-related Kompetenzen, therefore, are less arbitrary than the process-oriented ones and implicitly represent the logic of a subject's body of knowledge.
Regarding the idea of Transformation of Matter, content-related Kompetenzen consider increasingly differentiated models of the particulate nature of matter, changes in substance properties, and theories of chemical bonding. While the standards ostentatiously claim not to be hierarchical in nature, there is an inherent sequence to them that has been established through the history of chemistry as well as decades of chemistry teaching. This implicit hierarchy's reasonableness so far has primarily relied on the discipline's logic rather than on students’ actual learning performance; i.e. this hierarchy has been argued for on structural grounds in the traditional syllabi, which is questionable with regard to its functional legitimacy as required by Kompetenzen. As indicated, there might exist some discrepancy between both these perspectives. If instruction in chemistry is to be improved via matching it with students’ needs and potentials, this discrepancy needs to be resolved. Drawing up and validating a learning progression on the Transformation of Matter might prove of value in this enterprise.
Development of content-related Kompetenzen in secondary chemistry education
Some insights on how students develop content-related Kompetenzen on the lower secondary level were provided by Ferber (2014). She investigated students’ understandings of chemistry concepts across three grade levels on the lower secondary level in a pseudo-longitudinal design. She made use of Rasch-modelling combined with repeated measures ANOVA from Classical Test Theory (CTT). She showed that, generally speaking, person abilities to solve chemistry items changed over time. Concerning one concept, Acids and Bases, students’ abilities to solve problems developed in alignment with the curriculum along grades 7–9, i.e. grade 9 students outperformed grade 7 students significantly. Regarding Redox Reactions, however, students’ abilities to solve an item increased throughout an academic year (7, 8 or 9), which might be considered as aligned to the curriculum. Yet, unexpectedly no significant differences between grades were found, which in turn could be read as ‘no progress in learning’. These two seemingly contradictory trends might be indicative of the complicated unfolding of the redox-concept in German chemistry classes: it is encountered first in grade 7 (combustion), becomes more widely defined in grade 8 to account for all reactions involving oxygen, and is redefined a second time in grade 9 when it narrowly focuses the transfer of electrons (cf.MSW, 2008a). Students might, therefore, show decreased abilities when encountering a new/wider definition of the concept in subsequent grades. Lastly, Kompetenzen regarding Mixtures and Separation Processes significantly declined over time. This mirrors common school practice to launch chemistry education with juxtaposing pure substances and mixtures, which eventually channels into an understanding of the chemical reaction as a change of matter. As soon as the latter idea has gained footing in chemistry teaching, mixtures and separation processes do not play any role in the course work and Kompetenzen connected to it appear to atrophy. Enlightening as Ferber's findings are, they were lacking prognostic virtues on which chemistry education could build when designing curricula, which she herself understood as a potential extension of her study (Ferber, 2014).While it appeared to be feasible to combine CTT-methodology with Rasch-modelling to identify differentiated difficulties of Kompetenzen, it could not account for specific learning paths conducive to achieving a Kompetenz. So, the next logical step would be arranging content-related Kompetenzen along a timeline in a learning progression and checking its validity.
Hadenfeldt and colleagues (2013) used a different approach to investigate the unfolding of the matter concept on the lower secondary level: testing students’ understanding with ordered multiple choice items (OMC). In these OMC-items, principally, each choice option can be considered attractive depending on students’ respective levels of understanding. These levels were extracted from a plethora of research on student conceptions. The rationale of OMC is that students tend to opt for that answer closest to their actual understanding. Thus, students will rather relate to a simple particle model early in their chemistry instruction as opposed to relating to differentiated electron shell models later on. The challenge lies in developing options, which are not attractive just because of their degree of differentiation or of linguistic properties (Hadenfeldt et al., 2013). Therefore, the development of test instruments of this kind is very demanding as comparably attractive options need to be composed for shared generalized levels of student understanding.
Irrespective of a notion of Kompetenz, Smith et al. (2006) have suggested a hypothetical learning progression for Matter and the Atomic Model that covers age groups K–8. They grouped propositional knowledge about matter around three Big Ideas (Matter and Material Kinds, Conservation and Transformation of Matter and Material Kinds, Epistemology). The authors derived age-specific operationalisations from literature but did not suggest specific connections between these or between the Big Ideas. Potential and valid learning pathways for mastering the concepts can, thus, not be inferred. Instead, they suggested several ways of surveying learning performances which can inform validation studies. The authors expressed the view that psychometric properties of their suggested items are of secondary interest and conceded that reliable testing for learning performances needs to entail expertise from learning psychologists.
Building on this more coarsely grained learning progression Stevens et al. (2010) introduced a multi-dimensional empirical learning progression (7–14) on the Nature of Matter. They based their learning progression on results from analyses of semi-structured interviews with 37 students, which has the potential to be rich in information but is at the same time very time-consuming. The authors suggested that an idea of nature of matter develops in two separate dimensions which they modelled across four hierarchical levels of performance: Atomic Structure and Electrical Forces. Development in both dimensions can be described to run parallel, while assumed relations between the dimensions are not spelled out. Deriving teaching sequences that consider student needs and potentials in both the dimensions cannot be facilitated.
In general, the development of an understanding of Transformation of Matter has been dealt with in research as one of four specific perspectives on matter: (1) Structure and Composition, (2) Physical Properties and Change, (3) Chemical Properties and Change, (4) Conservation (cf.Liu and Lesniak, 2005, 2006; Hadenfeldt et al., 2014). Most studies have focused on aspects of Structure and Composition and Physical Properties and Change, Chemical Properties and Change – which is the focus of the proposed study – feature least frequently in the studied aspects (Hadenfeldt et al., 2014).
The four aspects were shown to be distinct but interrelated aspects of an overarching concept by Hadenfeldt and colleagues (2016) who fitted their empirical data to several uni-/multidimensional Rasch-models. Chemical Properties and Change proved to be the most difficult aspect in a longitudinal comparison of development (grades 6–13). The remaining aspects developed very much the same, yet proved to be easier for students. If this implies a conditional sequence, arguing for Chemical Change to be introduced after Structure, remains conjectural on basis of their data.
Clues might be found in Philip Johnson's research. In 2013, he culminates a decade of research on the development of an understanding of chemical change in a detailed learning progression for 7–9 students (Johnson, 2013). In it he combines data from a large-scale multiple-choice-test (Johnson and Tymms, 2011) with those from interviews conducted longitudinally in teaching interventions in the UK (e.g., Johnson, 2000a, 2000b, 2002, 2005). Test-data were investigated making use of Rasch (Johnson and Tymms, 2011). The resulting learning progression models Chemical Change along two dimensions: Macroscopic Perspective and Particle Model and Explanations (Johnson, 2013). Johnson and Tymms (2011) found the underlying construct to be sufficiently described in a single construct. Test items were ordered in a learning progression according to their difficulty estimates. Where more than one item captured the same idea, a wider distribution of difficulties resulted; wider spaced boxes to cover the distribution of difficulty were introduced in these cases (e.g., items on ‘Chemical change gives new substances’ cover a range of 67–82 on a 84-point-difficulty scale; Johnson, 2013). The resulting ‘blur’ of the map, combined with a lack of defined pathways through the progression, affects its practical use. With respect to transformative aspects of matter, the learning progression highlights physical change but is much less detailed on particle-based-interpretations of chemical change.
This might in part be due to Johnson's (2000b) observation that there are fundamental misconceptions to overcome with regard to structure and composition of substances before an understanding of their transformation can even occur. Johnson (2002) suggests that an understanding of the particulate nature of matter precedes (and in consequence supports) an understanding of chemical change, so that sophistication in both these aspects develop parallel to some degree.
In a similar vein, Löfgren and Helldén (2009) report on students’ shortcomings to interpret physical changes of matter with regard to the particulate nature of matter. They show that only 20% of students employ a scientifically adequate model of explanation by age 16. The use of models might vary greatly depending on the exemplar phenomenon: changes of state are more readily explained in a particle model than decomposition of fallen leaves. Their analytical categories account for explanations referring to Dalton's atomic model but fall short of Bohr's model.
Rogat's (2011) suggestion of a learning progression is meant to support the National Science Standards and to inform standard-oriented science teaching. He builds a unidimensional learning progression for “Structure, Properties & Transformation of Matter” in which he distinguishes two strands that are meant to develop concurrently in the later stages of instruction: ‘structure and properties of matter’ develop from a macroscopic compositional model of matter towards a sub-atomic model of matter (including aspects of Bohr's and Rutherford's atomic models); the ‘transformation of matter’ in an understanding of chemical change commences at stage 4 with an atomic-molecular model, while stage 3 (particle model) remains largely void of aspects of chemical change. This might be read to be in line with Johnson's claims (2000b, 2002) that an understanding of chemical change presupposes an understanding of the concept of a substance. Rogat (2011) has to concede that when drafting the learning progression (K–12) the research basis for learning performances was found to be lacking with regard to upper middle grades and high school (p. 17). Therefore, he and his collaborators had to draw on professional experience when elaborating the learning progression. He, too, stresses that the term learning progression is misleading in so far that the kind of learning envisioned could not occur without adequate instruction. In consequence, a learning progression can be considered a means to inform effective teaching. Rogat (2011) does not report data from an empirical validation of the proposed learning progression.
Lastly, Claesgens and colleagues (2009) suggested to use IRT-methodology to investigate students’ understanding of three big ideas (matter, change, energy) in a five-level-model. With regard to matter, they claim that arriving at level 3 of understanding – which addresses aspects from Bohr's model for the first time – might be expected after 1 year of college; the most advanced level of understanding would not be attained before graduate school. They find that ‘matter’ and ‘change’ form two separate dimensions that correlate significantly at r = 0.68 accounting for their interrelatedness (as claimed before by, e.g., Liu and Lesniak, 2005). Their approach to using IRT is a model for later studies (e.g., Johnson and Tymms, 2011; Hadenfeldt et al., 2016). They relate their approach to the work on learning progressions in a follow up (Claesgens et al., 2013) in which they investigate aspects of matter (now: atomic view) more closely, expecting its development with students to follow the historical precedent. They find, however that there appear to be more complex influences on student understanding by what they term ‘habits of mind’, i.e. by taking into consideration process skills.
In summary, it appears that although much research has been devoted to structural aspects of matter, comparatively little is known about the development of an understanding of chemical change. This is especially true with regard to the use of differentiated models of matter (e.g., Bohr's atomic model). Therefore, little is known in how far both these aspects form prerequisites for each other in the course of learning. Moreover, it is striking that even the most detailed projections of student development (Johnson and Tymms, 2011; Johnson, 2013) refrain from suggesting viable pathways of instruction. We appear to have rich information on students’ abilities regarding the structural aspects of the matter concept (less so on chemical change) coupled with professional convictions of reasonable teaching sequences (e.g., Rogat, 2011). These two have not yet been merged to inform chemistry education enabling a match of instruction to students’ potentials. It appears that structural and functional perspectives on chemistry instruction are still not reconciled when it comes to developing an understanding of the Transformation of Matter.
Objectives
This study's aim was to develop and to validate a learning progression for chemistry education on the lower secondary level. The learning progression's theme was ‘Transformation of Matter’ accounting for its centrality to chemistry as a discipline.Within the framework of Germany's science education standards the Transformation of Matter builds on several Fundamental Concepts whose interdependencies in the development of Kompetenzen were meant to be investigated. In order to master the Transformation of Matter concept students need to develop Kompetenzen dealing with ideas of Structure of Matter, i.e. encompassing Substance–Particle- and Structure–Property-Relations, as well as ideas about Chemical Reaction; these are essentially the same as two of the aspects of matter identified by Liu and Lesniak (2005): Composition and Structure, Chemical Properties and Change. Being intricately linked and shown to be interrelated (Liu and Lesniak, 2005; Claesgens et al., 2009), it seems reasonable that these two Fundamental Concepts should be developed concurrently in instruction (cf.Rogat, 2011). Yet, in how far progress in one of these presupposes progress in the other is mostly conjecture (cf.Johnson, 2005). In developing the present learning progression mutual dependencies between the Fundamental Concepts were to be anticipated, modelled and investigated.
These questions reflect the investigation's foci: (1) Do Kompetenzen develop in alignment with a standards-based curriculum and, thus, take up student potentials?, (2) Does Transformation of Matter develop as a unified concept or is it derived from two Fundamental Concepts?, (3) Does the concept evolve parallel with the historic precedent process from phenomenology to increasingly differentiated discontinuous models of matter?, (4) Do Kompetenzen presuppose each other?, (5) Do Kompetenzen in the learning progression contribute to learning to differing degrees?
Methods and procedures
Designing the learning progression with a strand map
Designing the hypothetical learning progression started in defining its lower and upper anchors. The lower anchor was derived from the framework for primary science education and the state curriculum (MSW, 2008b; GDSU, 2013). The upper anchor selected students’ Kompetenzen connected to Transformation of Matter taken from the national education standards (KMK, 2005: Fundamental Concepts: Substance–Particle-Relation, Structure–Properties-Relation, Chemical Reaction – examples are provided in Table 1) and the lower secondary chemistry state curriculum (MSW, 2008a: Structure of Matter, Chemical Reaction). Where necessary for matters of operationalisation, standards were split so that each Kompetenz in the learning progression was represented by a single operator. In the learning progression, Kompetenzen were complemented with ones that were not mentioned explicitly in any of the sourced documents but appeared to be tacitly assumed – this holds true for two of 22 Kompetenzen. This modus operandi resembles the creation of a Validation Learning Progression (Duschl et al., 2011) which might be rooted in normative standards documents.| State curriculum (MSW, 2008a, p. 28) | National standards (KMK, 2005, p. 11) | Derived Kompetenz (code in Strand Map) |
|---|---|---|
| a The first author holds the equivalent of a Master's degree in EFL. | ||
| Students have developed a conception of structure of matter so far that they can identify substances on basis of their properties (e.g., colour, smell, solubility, electrical conductivity, points of boiling and melting, state of matter). | Students name and describe important substances relating to their properties. | Students can name substance properties. (SMP.2) |
| Students can identify substances based on their substance properties. (SMP.3) | ||
It is important to note that the underlying content-related standards are in themselves representations of good practice in German Science Education that has been accumulated over the past fifty years. While they necessarily form an exemplary consensus in how detailed they are as well as regarding their wording, they draw heavily on experience on what students of an age group can or cannot accomplish. As a consequence, we understand the standards not to be ignorant of actual student learning and argue for their implicit inclusion of “inherently diverse learners’ perspectives” (Duschl et al., 2011, p. 174). In choosing the standards as a starting point for the learning progression we might appear to violate learning progressions’ need to be substantially founded in concrete research (e.g., Smith et al., 2006). On a different note, we argue that these standards are by no means arbitrary (or non-empirical) and might be considered the result of a long time census amongst primary and secondary students. We understand this suggestion to be considered a hypothetical learning progression (cf.Stevens et al., 2010), which relies more strongly on content-related considerations and is to be developed into an empirical learning progression over time.
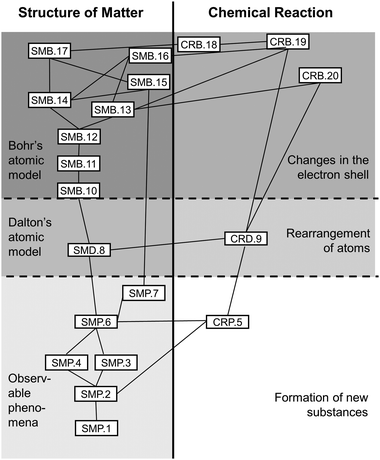
The thus identified Kompetenzen were then arranged in an hierarchical network comparable to the AAAS's (2001) Strand Maps. Harder to acquire Kompetenzen stood near the upper anchor, i.e. at the top of the Strand Map, easier to acquire ones were closer to the lower anchor, i.e. at the Map's bottom. Relations between Kompetenzen were given as lines and served to show which Kompetenzen further up the map needed to rely on others further down (see Fig. 1).
The Strand Map modelled two progress variables that mirror the Fundamental Concepts involved: Structure of Matter and Chemical Reaction (MSW, 2008a). Additionally, both progress variables were differentiated into three stages of progress (cf.Corcoran et al., 2009), which run parallel in both the progress variables (see Table 2). These stages of progress derive from the notion that refining the atomic model should follow the historical precedent process in order to anticipate student misconceptions which often derive from early models (cf.Schmidt and Volke, 2003, Barke et al., 2012). At the same time, the step from Stages 1 to 2 considers multiple findings on specific difficulties for students to tackle discontinuous notions of matter (e.g., Andersson, 1990; Liu and Lesniak, 2005, 2006; Walpuski et al., 2011; Barke et al., 2012; Ferber, 2014; Hadenfeldt et al., 2014) and takes up Johnson's (2013) dimensions of a learning progression on chemical change (which in contrast to our suggestion ends at Dalton's model).
| Stage of progress | Progress variable | |
|---|---|---|
| Structure of matter described in terms of… | Chemical reaction described in terms of… | |
| Stage 3 | … Bohr's atomic model | … changes in the electron shell |
| Differentiated understanding of the composition of matter | ||
| Stage 2 | … Dalton's atomic model | … rearrangement of atoms |
| Basic understanding of the composition of matter | ||
| Stage 1 | … observable phenomena | … formation of new substances |
| Phenomenological approach to matter | ||
The Strand Map's Kompetenzen, their hierarchy, and relations were subjected to an expert rating. The results from this largely confirmed the first draft of the Strand Map (see below and Weber, 2018).
The finalized Strand Map (Fig. 1), that served as a model for test-construction, contains 20 Kompetenzen with 28 interrelations that students need to acquire in two Fundamental Concepts in order to master the Transformation of Matter concept.
Iterative test development and pilot study
Kompetenzen from the Strand Map were translated into test items (multiple-choice-single-select) regarding the transformation of chemical elements into five ionic compounds (NaCl, MgBr2, Mg3N2, Fe2O3, ZnS). The rationale was that having the generalized Kompetenz at their disposal students should be able to apply it autonomously to different specimen (cf.Johnson, 2013). For this reason, items deliberately address compounds more and less typical for school chemistry. Wording for items that applied to the same Kompetenz was largely parallel between example compounds as to prevent potentially undesired effects (see Table 3 for an example). Attractor and distractor formulations took well documented student misconceptions on chemical reactions into consideration. This was meant to enable a validation of the learning progression as closely as possible to students’ actual potentials (Weber, 2018) and, thus, orient it towards “inherently diverse learners’ perspectives” (Duschl et al., 2011).| Item aiming at SMP.4: students can differentiate between pure substance and mixture | |
|---|---|
| ZnS | Mg3N2 |
| Powdered sulphur is put into a porcelain bowl together with powdered zinc. Both the powders are mixed thoroughly until a homogeneous greenish yellow colour can be observed. | When whitish magnesium shavings are burned on a non-flammable surface, magnesium nitride forms. Magnesium nitride is a grey powder. It forms from magnesium and the air's nitrogen. |
| Is there a pure substance in the porcelain bowl or a mixture? Give reasons. | Is magnesium nitride a pure substance or a mixture? Give reasons. |
| ○ There is a pure substance in the porcelain bowl because there are the pure substances sulphur and zinc in it. | ○ Magnesium nitride is a pure substance because it is a single substance with characteristic properties. (attractor) |
| ○ There is a pure substance in the porcelain bowl as no chemical reaction has taken place yet. | ○ Magnesium nitride is a mixture because magnesium and nitrogen have been fused. |
| ○ There is a mixture in the porcelain bowl because two chemical elements have been mixed. (attractor) | ○ Magnesium nitride is a mixture because it is a compound of magnesium and nitrogen. |
| ○ There is a mixture in the porcelain bowl as sulphur and zinc could react with each other. | ○ Magnesium nitride is a pure substance because the naked eye cannot distinguish its components. |
The choice for ionic and against covalent compounds was made with respect to common school practice in Germany which introduces ionic bonds before covalent bonds. Additionally, the differentiation between polarized and non-polarized covalent bonds appeared to be too complex to realize in a first attempt on validating a learning progression.
The item bank, thus, consisted of 100 items. Items were distributed across twelve test booklets of 40 items in a balanced incomplete block design (Frey et al., 2009). Booklet design aimed at surveying student answers to one complete set of Kompetenzen for one compound (20 items) plus selected items from the remaining four compounds (5 items each).
Data from a pilot study served to check the test's general feasibility with regard to the intended student population and provided opportunity to refine formulations of test items and solution options.
Student sample
Students (grades 7–9) for the pilot as well as for the main study were sampled from several academic track secondary schools (Gymnasium) in North Rhine-Westphalia. Students for the pilot and main studies came from different schools. Care was taken that providing schools featured evenly in the sample across grade levels. Nonetheless, sampling did not result in an equal distribution of students across grade levels. Composition of both the student samples can be read from Table 4.| Grade 7 | Grade 8 | Grade 9 | % Female | |
|---|---|---|---|---|
| Pilot study | n = 84 | n = 54 | n = 106 | 42.6 |
| Main study | n = 189 | n = 225 | n = 176 | 53.6 |
Students and their parents were informed about the study's layout and intention in advance. They were guaranteed that student data would be anonymised before analyses. Parents were asked for their written consent as surveyed students were not of legal age. If students chose not to take part in the survey on the days of testing, they were excused from it (without sanction) and worked on other chemistry-related tasks while their fellow students filled in the test.
Analytical approaches
Data analyses made use of methods from three different statistical approaches: Classical Test Theory, Rasch-modelling, and Bayesian statistics. The intention was to gather from this analytical triangulation evidence for the learning progression's validity. Each of the mentioned approaches brings specific strengths to elucidating the learning progression. We will, therefore, briefly outline our reasoning how we have employed the analytical paradigms.As data generated in a balanced incomplete block design necessarily features a large body of missing data, analyses were conducted largely relying on Rasch-modelling with CONQUEST (Wu et al., 2007). The hypothesized learning progression assumed the existence of two progress variables according to the underlying Fundamental Concepts (cf.Hadenfeldt et al., 2016 who found the synonymous Big Ideas to be distinct constructs, similarly: Claesgens et al., 2009). There remained, however, the possibility that this structure was not realized by students and that they would understand Transformation of Matter as a unidimensional concept (cf.Johnson and Tymms, 2011; Rogat, 2011). Therefore, data fit was investigated contrastingly for a one- and a two-dimensional Rasch-model (cf.Hadenfeldt et al., 2016). In addition, item difficulty and person ability estimates were used to gather first indications of the learning progression's validity. A matching of Wright Map outputs with the assumed Strand Map proved to be illustrative of the hypothesized distribution of item difficulty estimates. From this map, one can read easily how hard or easy items of specific Kompetenzen were for students from different grade levels which might be interpreted like a learning progression (Johnson and Tymms, 2011, p. 852). Thus, students from grade 7 were expected to show lower person ability estimates on average than grade 9 students. While this could have been shown with CTT as well, the large amount of missing-data-by-design from the multi-matrix design did not allow for this. As Rasch is a probabilistic approach to data analyses, it is argued that person and item estimates capture latent constructs (Claesgens et al., 2009) and that these can, therefore, be interpreted as expressions of competence instead of mere student performance (Liu and Lesniak, 2005).
Differentiating analyses with respect to item difficulty measures and their location within the learning progression were carried out relying on ANOVA and contrasts from CTT. The goal was to verify the assumed stages of progress within the progression. Significant differences in the mean item difficulty estimates between the stages were expected to be indicative of the stages’ validity. This would need to be done either for a unidimensional concept (Transformation of Matter) or the two-dimensional one depending on the results from Rasch-analyses. Additionally, but not reported in this paper, regression analyses with several control variables (e.g., cognitive abilities, age/grade level, interest) allowed for investigating respective influences on item-difficulty (Weber, 2018).
Lastly, this study made use of Bayesian statistics/networks using the Netica® software (Norsys, 2010). Bayesian statistics is a probabilistic approach to data analysis. It allows one to investigate logical dependencies (conditional probabilities) between points in the data matrix. Analyses carried out under this paradigm allow for more detailed investigations of potential learning paths than can be facilitated by mere juxtaposition of item difficulties (Wright Maps from Rasch-modelling) or means difference analyses (t-test, ANOVA from CTT).
The analysis of Bayesian networks requires an hypothetical hierarchical structure of the data (as provided through the Strand Map). This structure is not generated as part of the analysis. Analyses rather test for the soundness of an hypothetical a priori assumption. Based on a randomized sub-set from the collected data (training cases) Netica® estimates a proposed network's properties; i.e. solution probability estimates for the net's nodes dependent on the solution probability estimates from contributing items. These a posteriori probabilities are then ‘crosschecked’ with the remaining data (test cases; Norsys, 2017). If the conditional probabilities from test cases are consistent with the net's a posteriori probabilities generated from training cases, the net's quality is assumed to be good. A Bayesian network's goodness of fit is expressed through four indices: error ratio (How many faulty prognoses for test cases are there based on estimates from training cases?), Logarithmic Loss (optimally takes a value of 0), Quadratic Loss (optimally: 0), and Spherical Payoff (optimally: 1) (Norsys, 2010, 2012). The two loss measures indicate the misfit of data with a network and, therefore, should approximate zero. The third measure reports the gain from fitting the data with the suggested model. Output probability estimates rely on the maximum set of data; i.e. they are generated from the combined test and training cases.
The basic idea of probabilistic approaches is that item solution rates are a function of their difficulty. Bayesian statistics add to this idea assuming an hierarchy between items. It checks if the probability of a solution to a more difficult problem is dependent on solving a preceding (easier) problem (cf.Norsys, 2010; West et al., 2010; Wei, 2014). If the probability to solve the hierarchically superior item increases with successfully solving hierarchically inferior items, probabilities are understood to be conditionally bound. Solving the easier item is conducive to solving the more difficult one and, consequently, could be interpreted as needing to be addressed explicitly in a teaching process. If the probability to solve a hierarchically superior item decreases with successfully solving the hierarchically inferior problem, addressing this aspect in teaching appears to be detrimental. One might argue to leave it out altogether. Thirdly, solution rates of hierarchically superior items might prove indifferent to successfully solving hierarchically inferior items. Relying on Bayesian networks, thus, allows for investigating the legitimacy of the suggested logic in the learning progression (cf.West et al., 2010). It needs to be stressed, though, that all pathways in Bayesian networks are equally valid; i.e. even small probabilities for apparently ‘unreasonable’ sequences are representative for pathways in reality. Our subsequent interpretations always aim at the aforementioned ‘bulk abilities’ and identify beneficial pathways for instruction that “work for as many students as possible” disregarding, therefore, numerically less probable pathways.
Results
Strand map and expert rating
The first draft of the Strand Map contained 22 Kompetenzen of which six were allocated the progress variable Chemical Reaction – the remaining Kompetenzen lay in Structure of Matter. As this dimension is merged from two Fundamental Chemistry Concepts (Structure–Property- and Substance–Particle-Relations) the overall distribution of items between Fundamental Concepts is roughly balanced. This first Map suggested 30 relations between Kompetenzen. It was presented to 15 experts in chemistry education for rating – among the experts were professors of chemistry education, postdocs and PhD-students. They rated the map for three aspects: (1) are the suggested relations reasonable (i.e. are there redundancies, gaps, or unnecessary relations), (2) do the relations sufficiently capture the interdependencies between student Kompetenzen (to be amended when deemed lacking), (3) does operationalisation of student Kompetenzen state clearly the performance expectations? All the ratings were to be undertaken relating to five nominal categories providing an additional open section for criticism and augmentation.As Cohen's Kappa is known to produce poor values for high concord if there is an imbalance in the marginal totals (Kappa paradoxon: Feinstein and Cicchietti, 1990), an alternate interrater measure was sought. Gwet's AC1 was chosen which is adjusted for problems leading to paradoxical Kappa (Gwet, 2014). Like Kappa, Gwet's AC1 can take values between 0.00 and 1.00 with comparable interpretation of values. With respect to the first aspect – reasonableness of relations – ratings arrived at Gwet's AC1 = 0.65, which is understood to indicate good concord (McCray, 2013; Gwet, 2014). The second and third ratings’ AC1-values even indicated very good concord with 0.95, 0.85 respectively.
Ratings and open comments led to several changes of the Strand Map: mostly in terms of operationalisation but also regarding existence of individual Kompetenzen. Two of these were suggested to be merged, another to be deleted, a third one was relocated from Chemical Reaction to Structure of Matter; relationwise one connection was included from raters’ comments (cf.Weber, 2018 for details). The finalized Strand Map (Fig. 1) consisted of 20 Kompetenzen, five of which fell into Chemical Reaction, and 28 relations (see Appendix A, Table 10 for a full list of Kompetenzen).
With regard to generally high AC1-values in the first expert-rating, the decision was made against a second rating.
Test quality in the pilot study
The Strand Map served as a model to construct test items across five exemplary chemical reactions. Items were administered to students in a multi-matrix-design. A pilot study with 244 students served to improve test items and check for the test's general feasibility.Analyses with CONQUEST were conducted after exclusion of two items for faulty attractors. The resulting test's EAP/PV reliability was estimated at 0.680 with an item separation reliability of 0.845. This suggested that the test needed refinement. Grade 7 students expectedly featured with lower and less homogeneous person ability estimates in the sample and thus affected overall EAP/PV negatively. Yet, even looking at grade 9 students only, EAP/PV arrived at an unsatisfactory.742 (item separation: 0.801), which also called for refinement of the test. Further exclusion of misfitting items (infit MNSQ outside [−0.80; 1.20] and t > |2.0|; insufficient separation indices, respectively; Wilson, 2005; Bond and Fox, 2007) increased overall EAP/PV to 0.697 (item separation: 0.839) on a test of 85 items after the fourth iteration (explained variance raised from 0.612 to 0.855).
Infit MNSQ-values outside the given limits indicate that although item and person estimates lie in close range, the solution rates for the item are unexpectedly low so that an influence other than item difficulty is assumed to interfere. Corresponding t-values give an indication if the observable misfit is statistically significant – the more it deviates from |1.96|, the more probable is this a systematic interference on item solution rates. Lastly, separation indices bear information of how well the solution to a single item allows for prognosis on general person ability estimates. Separation is typically lower for extremely hard/easy items but should – in the interest of test economy – not be too low.
The excluded items (and others whose estimates were not satisfactory) were subjected to detailed distractor analyses investigating reasons for their misfit. Strikingly deviating choice-rates for single distractors, as displayed in their Item Characteristic Curves, were taken as an indicator to take a close reading of the respective items and their distractors. As oftentimes problematic wording in a distractor could be identified, a rewrite commenced in order to reincorporate those items into the final test.
Dimensionality and difficulty maps
The final test form was administered to 590 students from three grade levels. On average, each item was administered to 172–182 students. All items could be fed into Rasch-analyses after the rewrite. The estimated EAP/PV-reliability increased substantially to 0.817 (item separation: 0.934) as opposed to the pilot study, so the rewrite appears to have been successful.With the increased data set, it was possible to analyse whether a one-dimensional Rasch-model accounting for Transformation of Matter in toto represented the data best or whether a two-dimensional model considering Structure of Matter and Chemical Reaction independently better fit the data. Results for the dimensional analyses can be read from Table 5.
| 1-Dimension | 2-Dimensions | ||
|---|---|---|---|
| Transformation of matter | Structure of matter | Chemical reaction | |
| N students | 590 | 590 | |
| N items | 100 | 75 | 25 |
| EAP/PV-reliability | 0.817 | 0.838 | 0.805 |
| Item-separation reliability | 0.934 | 0.933 | |
| Deviance | 30875.879 | 28673.412 | |
| BIC | 31520.270 | 29330.565 | |
| AIC | 31077.879 | 28879.412 | |
| CAIC | 31621.270 | 29433.565 | |
Values for deviance and the information criteria BIC, AIC, CAIC should be as low as possible in order to favour one model over the other. The deviance expresses the degrees of freedom the fit model preserves after matching the data – so, a lower number in deviance is indicative of a high fit between data and the model's expectations. The information criteria carry this idea a step further as they incorporate the number of parameters that are estimated within a model into their calculation and eliminate undesired effects from an inflation of parameters – so, here as well, as lower value speaks of better fit between model and data (cf.Hadenfeldt et al., 2016).
As can be seen, the two-dimensional model fits the data better than the one-dimensional model resulting in an increased EAP/PV reliability for the larger of the dimensions together with a slightly decreased, yet still good EAP/PV for the shorter dimension. Descriptively, all the given information criteria and deviance favour the two-dimensional model over the one-dimensional one. A Likelihood-ratio-test on Δ-Deviance (2202.467, df = 2) shows it to be significant at the p < 0.001-level. Therefore, all the following analyses using methods of Rasch-modelling resort to the two-dimensional model.
Item parameters in the two-dimensional model suggested exclusion of seven items on grounds of fit-indices and another 13 due to insufficient separation (Wilson, 2005; Bond and Fox, 2007), leading to a moderate decrease in item separation reliability of 0.921. EAP/PV-reliabilities increased to 0.843 as a result of this, decreased marginally to 0.804 respectively. The data from the reduced set still speak of a reliable test instrument for the total student sample.
Item difficulties and person ability estimates for the two dimensions are given in the Wright map of Fig. 2. In a Wright Map item difficulty and person ability estimates are noted on the same scale. Their relative position to each other allows for estimating solution probabilities for a given person ability to a given item difficulty: are both the estimates numerically the same, the probability of solving the item correctly is for a given person 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. More difficult items, more able persons respectively, take higher (more positive) estimates, easier items/less able persons take lower (more negative) estimates. The further up a person ability is in relation to a given item difficulty, the higher is the person's probability to solve the respective item correctly. In contrast, the further down the person ability lies with respect to a given item difficulty, the less probable it is that the person will give a correct solution.
50. More difficult items, more able persons respectively, take higher (more positive) estimates, easier items/less able persons take lower (more negative) estimates. The further up a person ability is in relation to a given item difficulty, the higher is the person's probability to solve the respective item correctly. In contrast, the further down the person ability lies with respect to a given item difficulty, the less probable it is that the person will give a correct solution.
So, the positions of the items in the Wright Map are indicative of their empirical difficulty, as were the positions assigned to the corresponding Kompetenzen in drafting the Strand Map. Therefore, relating the item difficulties to their respective position in the assumed Strand Maps gives a first impression of the hypothesized learning progression's validity.
Indeed, it appears that those Kompetenzen that were assumed to be the most difficult to achieve (when drafting the Map) feature relatively high on the Wright Map, thus indicating an increased empirical difficulty. On the other hand, those items that are solved quite frequently (empirically easy) are located closer to the bottom of the Strand Map. While this might be taken as an indicator of face-validity of the learning progression, concessions have to be made for some misfitting items that all load on the same Kompetenz: SMP.4 (“students can differentiate between pure substance and mixture”). As this is a very basic Kompetenz, students should learn this early in their chemistry classes. Related items should, therefore, be solved more frequently than others and appear further down the Wright Map. However, the corresponding items in the test proved to belong to the most difficult ones, which might be attributed to the fact that chemistry instruction disregards mixtures after the introduction to chemistry altogether and exclusively concentrates on pure substances (cf.Ferber, 2014). This might mean that a knowledge about mixtures remains tacit in students and cannot be activated easily from a progressed perspective on chemistry that takes pure substances as a given (i.e. without the specific need for differentiation).
As eliminating these items on purely psychometric grounds would have incriminated subsequent analyses of Bayesian networks, these items were kept for those analyses adhering to propositional considerations. Analyses with Rasch and CTT, however, made use of the limited item set.
Investigation of the stages of progress
First indications of the learning progression's validity can be garnered, thus, from Rasch: data suggest that the understanding of the Transformation of Matter concept develops in two separate traits (i.e. separately evolving understandings of the Structure of Matter and of Chemical Reaction) in much the assumed sequence. Teaching, thus, is well advised to respect both traits individually and refer to them separately in order to support student understanding.In order to investigate the existence of the postulated stages of progress, item difficulties from Rasch-analyses were fed into an SPSS-matrix as individual cases. Items were coded for their respective stages of progress. ANOVAs were conducted with respect to item difficulty separately for both progress variables. Results were expected to confirm the stages through significantly different mean item difficulties between them.
The ANOVA on Structure of Matter shows that there is a significant difference regarding item difficulty (F(2, 56) = 6.124, p = 0.004, η2 = 0.18); non-orthogonal contrasts between the stages yield significant differences between stages 1/2 (ΔM = −0.629, p < 0.05) and 1/3 (ΔM = −0.382, p < 0.01) but not between stages 2/3 (ΔM = 0.247, p > 0.05).
With regard to the second progress variable – Chemical Reaction – these findings can be confirmed. The overall ANOVA indicates very significant differences between stages of progress (F(2, 18) = 22.785, p < 0.001, η2 = 0.71) that can be traced back to stages 1/2 (ΔM = −1.185, p < 0.001) and 1/3 (ΔM = −1.428, p < 0.001), respectively, but not to 2/3 (ΔM = −0.243, p > 0.05).
This might be taken as an indication that mastering the progress from a basic to a differentiated understanding level of the composition of matter (2/3: Dalton → Bohr) is less demanding than anticipated. Overcoming the gap between a phenomenological approach to matter and a particulate conception of matter (1/2), however, poses a large burden on students as reflected in the significantly different item difficulties. This latter interpretation is corroborated by findings from Liu and Lesniak (2005, 2006) or Walpuski et al. (2011). Teaching chemistry needs to pay special attention to introducing discontinuous notions of matter, while differentiating these notions further is easier for students to accomplish.
One caveat needs to be upheld, however, when looking at sheer psychometrics: stages 1 and 2 in Chemical Reaction each contain only one Kompetenz so that the estimates for mean difficulties rely on five items each at most (as does stage 2 in Structure of Matter). This might distort the real differences between the stages in either direction – more finely grained models for stages of progress are in need to further elucidate this aspect.
Bayesian networks
The information gained from Rasch and ANOVA gives rise to the hope that the designed learning progression might actually capture an empirical development of Kompetenz. Both test theories, however, either lack the methods to investigate interrelated strings of items (Rasch) or they are not robust against missing-values by design (e.g., structural equation modelling). Bayesian statistics fills this gap.Bayesian networks take some ratio of the sampled data to ‘learn’ the parameters of the net (training cases), e.g. conditional probabilities that ‘tie’ the net of Kompetenzen (Norsys, 2010; Wei, 2014). The remaining data (test cases) are then fed as evidence into the net. Metaphorically speaking, test cases check if the net can hold them (i.e. the parameters estimated from training cases fit the observed data) or if the net breaks (parameters are not confirmed in test cases).
Large networks necessarily need more data to learn the net's more complex interrelations. The proposed network (Fig. 1) was therefore cut into four non-overlapping but interlinked smaller nets (item clusters) for analytical purposes. Each cluster took five Kompetenzen. Students’ test booklets were composed so that each student worked on items belonging to one complete set of Kompetenzen for one exemplary compound (e.g., booklet #1: items 1–20 for ZnS) and two ‘loose clusters’ across the remaining four compounds (e.g., Cluster 1 (items 1–5) for NaCl and MgBr2 plus Cluster 2 (items 6–10) for Fe2O3 and Mg3N2). The result were twelve interconnected booklets (Table 6). These were handed out randomly in the sample. Each of the loose cluster combinations was investigated separately. Thus, three quality estimates for each of the four smaller networks of five items each were generated.
| Booklet | Loose clusters (items) | Training cases | Test cases | Sample |
|---|---|---|---|---|
| #1, #11 | 1 (1–5) | 30 | 65 | 95 |
| 2 (6–10) | ||||
| #2, #10 | 1 (1–5) | 31 | 70 | 101 |
| 3 (11–15) | ||||
| #6, #9 | 1 (1–5) | 29 | 67 | 96 |
| 4 (16–20) | ||||
| #3, #12 | 2 (6–10) | 37 | 67 | 104 |
| 3 (11–15) | ||||
| #4, #8 | 2 (6–10) | 42 | 63 | 105 |
| 4 (16–20) | ||||
| #5, #7 | 3 (11–15) | 28 | 61 | 89 |
| 4 (16–20) | ||||
| 197 | 393 | 590 |
There is currently little consensus on cut-off-criteria for goodness-of-fit indices for Bayesian networks. Error rates lower than 18.7% (ICES, 2014), logarithmic loss lower than 0.36 (Kallayanamitra et al., 2014), quadratic loss lower than 0.19 (Fuster-Parra et al., 2014), and spherical payoff larger than 0.89 (Fuster-Parra et al., 2014) were considered acceptable. With few exceptions, all items fit well in the suggested Bayesian network (Table 7).
| M | SD | Range | |
|---|---|---|---|
| a Characteristics have been calculated across all estimated cluster combinations, i.e. each item features thrice in the estimates as the network was divided into four clusters (cf.Table 6). | |||
| Error rate | 8.689 | 6.997 | 0–32.86 |
| Logarithmic loss | 0.226 | 0.096 | 0.106–0.666 |
| Quadratic loss | 0.133 | 0.074 | 0.038–0.463 |
| Spherical layoff | 0.928 | 0.044 | 0.739–0.984 |
Further analyses investigate the probabilities with which certain Kompetenzen are reached. The software Netica® calculates the probability with which a Kompetenz is achieved. This probability is generated with reference to the information from five items. For this, Netica® was given a cut-off criterion: two or more of the individual items need to be solved correctly by one student to consider the overall ability achieved. This criterion derives from the booklets’ layout in which students replied to ten Kompetenzen across three different contexts (from 1 complete map + 2 loose clusters in two contexts each) so that they responded to three out of five items addressing the same Kompetenz. Absolute probabilities for achieving a Kompetenz are based on the maximum possible sample (i.e. n ≈ 300 for each Kompetenz depending on booklet distribution – i.e. generalizing across contexts, cf.Table 6). These probability estimates are the basis for the following analyses.
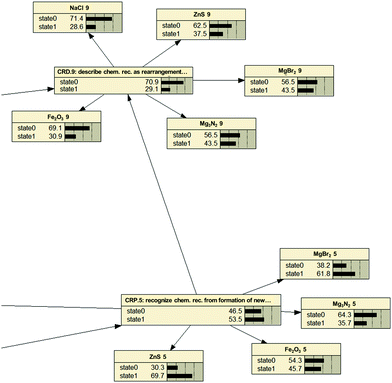
Fig. 3 provides a fragment from the network and illustrates, how item-probabilities relate to Kompetenz-probability. One can see that the probability for each Kompetenz (here formed by the net's nodes: CRD.5, CRP.9) is given as either arriving at state 1 (achieved) or state 0 (failed). At the same time solution rates for individual items are provided (here realized as contributors clustering around the node). From these, Netica® calculates the achievement rate for a Kompetenz based on the cut-off criterion. Note that numerical values of given Kompetenz solution rates are not just averages of the contributing item solution rates.
The higher in the network one progresses (CRD.9 vs. CRP.5), the lower is the probability of achievement (29.1% vs. 53.5%). Indications from Rasch item difficulty estimates had suggested this already (see Wright Map in Fig. 2), where information on a generalized Kompetenz had to be inferred from five individual item difficulty estimates (cf. the ‘blur’ in Johnson, 2013). Still, this first glance at absolute solution probabilities for Kompetenzen confirms the Strand Map's hierarchy as being one governed by difficulty and, thus, one to be mastered through progressive learning.
At the same time, Netica® calculates the conditional probability for achieving a Kompetenz, i.e. the probability of achieving one Kompetenz given the event of one or more preceding Kompetenzen being achieved (or not). On principle, this could be done iteratively along a complete path in the net, so that ultimately a probability is calculated for achieving the uppermost Kompetenz depending on achieving all the ones leading up to it. This would mean to consider all logically possible paths to achieving the uppermost Kompetenz. Each and every Kompetenz along this path would take its individual solution probability and so the number of to be distinguished pathways would grow exponentially with each added Kompetenz. Consequently, the probability for each single path would be numerically small. Therefore, it is reasonable to evaluate conditional probabilities over a limited number of nodes. The following analyses concentrate on directly neighbouring nodes for reasons of limited sample size.
An example for these analyses is provided below in a conditional probability table (CPT: Table 8). One can see that achieving Kompetenz CRD.9 (“Students can describe chemical reactions as the rearrangement of atoms”) is more probable after achieving both preceding Kompetenzen (both state 1; 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60) than achieving either of those (74.3
60) than achieving either of those (74.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.7, 50
25.7, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 respectively) or neither (89.5
50 respectively) or neither (89.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.5). This underscores the assumed relations in the learning progression as the maximum probability for achieving CRD.9 results from treading the suggested pathway correctly. At the same time, it accounts for the existence of alternative progressions. Some of these even suggest the possibility of ‘skipping’ one or more abilities, as the solution probability for achieving CRD.9 never is zero. It has to be stressed, therefore, that the numerically preferable path leading to a 60% achievement turnout on the dependent Kompetenz is only one of four potential and equally realized paths. There is, as a consequence, a substantial number of students who can achieve the goal Kompetenz without achieving all the others beforehand. Again: our interpretation aims at identifying a pathway for instruction that is beneficial to as many students as possible and therefore restricts itself to the numerically superior one.
10.5). This underscores the assumed relations in the learning progression as the maximum probability for achieving CRD.9 results from treading the suggested pathway correctly. At the same time, it accounts for the existence of alternative progressions. Some of these even suggest the possibility of ‘skipping’ one or more abilities, as the solution probability for achieving CRD.9 never is zero. It has to be stressed, therefore, that the numerically preferable path leading to a 60% achievement turnout on the dependent Kompetenz is only one of four potential and equally realized paths. There is, as a consequence, a substantial number of students who can achieve the goal Kompetenz without achieving all the others beforehand. Again: our interpretation aims at identifying a pathway for instruction that is beneficial to as many students as possible and therefore restricts itself to the numerically superior one.
| Absolute probability | Event at parent node | Conditional probability | |||
|---|---|---|---|---|---|
| CRD.9 | SMD.8 | CRP.5 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 89.474 | 10.526 |
| 70.9 | 29.1 | 0 | 1 | 74.286 | 25.714 |
| 1 | 0 | 50 | 50 | ||
| 1 | 1 | 40 | 60 | ||
In more complex parts of the network, the CPTs consequently become more complex (Table 9). In instances like these, one can see that the proposed relations may not stand the test: achieving SMP.6 (“Students can describe chemical elements and compounds as pure substances and can differentiate them from each other”) apparently can do without priorly achieving SMP.3 (“Students can identify substances based on substance properties”). Mastering SMP.6 without having achieved SMP.3 yields the highest conditional probability (22.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77.8) as opposed to an all-state-1-path resulting in a mere two-thirds-odds for acquiring SMP.6. Teaching, one might argue, could skip this aspect as it appears to be (at least) not conducive to learning about a distinction between elements and compounds.
77.8) as opposed to an all-state-1-path resulting in a mere two-thirds-odds for acquiring SMP.6. Teaching, one might argue, could skip this aspect as it appears to be (at least) not conducive to learning about a distinction between elements and compounds.
| Absolute probability | Event at parent node | Conditional probability | ||||
|---|---|---|---|---|---|---|
| SMP.6 | SMP.4 | SMP.3 | CRP.5 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 73.913 | 26.087 |
| 63.4 | 36.6 | 0 | 0 | 1 | 66.667 | 33.333 |
| 0 | 1 | 0 | 75 | 25 | ||
| 0 | 1 | 1 | 60.87 | 39.13 | ||
| 1 | 0 | 0 | 70 | 30 | ||
| 1 | 0 | 1 | 22.222 | 77.778 | ||
| 1 | 1 | 0 | 85.714 | 14.286 | ||
| 1 | 1 | 1 | 33.333 | 66.667 | ||
Additionally, one is led to assume that achieving CRP.5 (“Students recognize chemical reactions from the formation of new substances with new properties”) is most decisive in mastering SMP.6. This can be inferred from the path that realizes SMP.3 and SMP.4 (“Students can differentiate between pure substance and mixture”) but fails with CRP.5, which gives a conditional probability of 85.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14.3 against achieving SMP.6. For chemistry classes, this finding would entail to stress this fundamental characteristic of chemical reactions. As it appears that only few students (14.3%) progress in learning about the Transformation of Matter without it, more time should be spent on this aspect when numerous students keep showing insecurities with the idea of change in substance properties.
14.3 against achieving SMP.6. For chemistry classes, this finding would entail to stress this fundamental characteristic of chemical reactions. As it appears that only few students (14.3%) progress in learning about the Transformation of Matter without it, more time should be spent on this aspect when numerous students keep showing insecurities with the idea of change in substance properties.
Walking piecemeal from top to bottom through the suggested learning progression provides ideas of which Kompetenzen are beneficial for achieving the upper anchor, which ones are potentially detrimental, and which Kompetenzen appear to be somewhat indifferent to the learning progress. Following only those paths in the learning progression that maximize conditional probability on the dependent Kompetenz revises the learning progression as suggested in Fig. 4. Yet again, we want to remind of the underlying rationale: we identify only the numerically most superior pathways in the interest of pinning down those trajectories for instruction that are beneficial to as many students as possible. We concede, at the same time, that conditional probabilities on different trajectories indicate achievement, too – and might in sum even exceed the number of successful students from our preferred pathway. As conclusions from this reading would be tantamount to advocating for anarchy in instruction (“Anything goes”), we prefer keeping to our stated rationale.
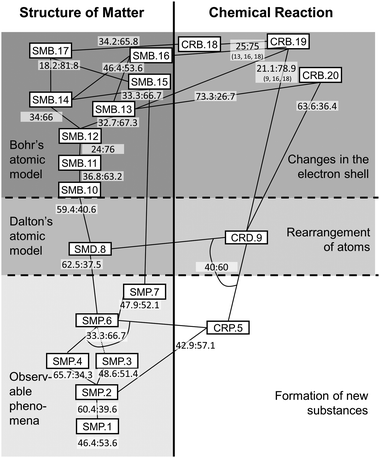 | ||
| Fig. 4 Revised learning progression for Transformation of Matter (given are the probabilities for the goal Kompetenzen as ‘failed:achieved’; continuous lines signify relations conducive to achieving a Kompetenz, dotted lines signify detrimental relations; arches and numbers clarify – where necessary – which Kompetenzen contribute to a given probability measure).† | ||
It is interesting to see that with the sole exception of SMP.3 all the other suggested Kompetenzen prove beneficial for arriving at the upper anchor. It needs to be noted, though, that achievement here does not necessarily mean ‘most of the students achieve a Kompetenz’. As can be seen for CRB.20, SMD.8, SMB.10, SMP.4, and SMP.2 achieving the preceding Kompetenzen merely reduces the proportion of students who do not achieve the aim. The majority of students does not successfully realize the goal Kompetenzen at any rate. For the former three of these, it might be argued that involving a step across a stage of progress might have explanatory power for this observation of difficulty. This peculiar development of conditional probabilities might be considered an indicator of the stages of progress's validity. Difficulties are most prominent between stages, even between stages 2 and 3 for which ANOVA could not find significant differences.
Nonetheless, it needs to be stressed again that pathways different from the one delineated in Fig. 4 are potentially leading up to the desired goal as well (cf.Smith et al., 2006). Speaking from an economic point of view, however, the revised learning progression may serve as the starting point for future investigations and teaching experiments for curricula that are better matched with ‘bulk’ students’ needs and potentials.
Conclusions
The present study undertook to design and evaluate a learning progression on the Transformation of Matter that spans the lower secondary level. It suggested chemistry learning to develop grades 7–9 student Kompetenzen relating to propositional content standards. These were arranged in a Strand Map and subjected to a rating by chemistry education experts who confirmed the Map's layout to a large extent. To our knowledge, there is to date no comparable hypothesis on how abilities on this central tenet of chemistry evolve over the span of three academic years. Johnson's (2013) detailed learning progression on chemical change refers little to explanations of chemical change on the particle level in general, nor to Bohr's atomic model (similarly in Johnson and Tymms, 2011). Moreover, he leaves the identification of valid navigation through the map to the reader which does not inform teaching as it could.Test development on basis of this hypothesis led to an economic Multiple-Choice-test that was refined after a pilot study. The test allowed for surveying large student samples as it was subjected to Rasch-analysis. The test proves to be reliable and valid (as gained from the expert rating) in its current form.
Analyses of test data made use of methods from three statistical approaches: Rasch analyses drawing on probabilistic test theory in order to analyse data sets with large proportions of data missing-by-design (Multi-Matrix-Design); ANOVA from Classical Test Theory to investigate item difficulty estimates from Rasch more closely with respect to their significant mean differences; Bayesian Statistics in order to investigate conditional links between Kompetenzen in the learning progression.
Each of these approaches illuminates another aspect addressed in the validation of the learning progression: (1) Are difficulty estimates for items on specific Kompetenzen well aligned with a standards-based curriculum (Rasch)?, (2) Does Transformation of Matter develop as a unified concept or is it derived from two Fundamental Concepts (Rasch)?, (3) Does the concept evolve parallel to the historic precedent process from phenomenology to increasingly differentiated discontinuous models of matter (CTT and Bayes)?, (4) Does achieving one Kompetenz prove beneficial to achieving successive ones (Bayes)?, (5) Are Kompetenzen in the learning progression conducive to learning to differing degrees (Bayes)?
Results from analyses addressing these questions are discussed in brief and limitations are shown:
(1) Noting item difficulty estimates and person ability estimates in a Wright Map shows that grade 7 students arrive at lower person estimates than grade 8 and grade 9 students. Item difficulty estimates largely correspond to their Kompetenzen's positions in the Strand Map. Few items are located unexpected in the Wright Map: assumedly easy items (SMP.4) prove to be very hard. There might be a curricular influence showing; for the moment, this finding is not supportive of the learning progression. Additionally, difficulty estimates for five individual items corresponding to the same Kompetenz ‘blur’ across the Wright Map so that a direct matching of item and Kompetenz – illustrative as it may be – cannot be the final test of validity. SMP.4's anomaly is mirrored in part in Johnson (2013) who reports a wide difficulty distribution for items on “Recognise mixtures as mixtures” (33–44 on a difficulty scale of 0–84). He claims that students still confuse compounds with mixtures (Johnson, 2013, p. 368) and, therefore, insecurity with both the concepts prevails. As a consequence, there is no solid understanding of substances in place when instruction progresses and the distinction might be lost over time.
(2) The learning progression describes the development of the Transformation of Matter concept along the lines of two progress variables: Structure of Matter and Chemical Reaction. This could be confirmed in dimensional analyses with Rasch and corroborates findings by Hadenfeldt and colleagues (2016) who can show that the assumed aspects of matter are indeed distinct constructs. They report a latent correlation between Structure and Composition and Chemical Reactions of 0.74, while we find one of 0.94 for the two dimensions. Our larger value might be attributed to a more homogeneous student sample in our investigation (7–9) as opposed to Hadenfeldt and colleagues 6–13 sampling (2016). Liu (2001) also postulates two dimensions for a conception of matter: existence forms of matter (roughly comparable to Structure of Matter) and properties of matter, which contains aspects of chemical change. This suggests that students actually perceive these constructs to be distinct from each other but that they are interrelated at the same time (Liu and Lesniak, 2005). This is supported by the notion of Big Ideas (e.g., Smith et al., 2006) that was introduced expressly to lend scaffolding to the eventual building of disciplinary knowledge (Duschl et al., 2011). Differentiating Fundamental Chemistry Concepts (KMK, 2005) is, therefore, not only helpful in organizing text books or curricula but appears to be conducive to learning. This scaffold should, consequently, be made explicit in teaching. Necessary integrations of the concepts in building an idea of Transformation of Matter need therefore to be carefully introduced in classes. This appears to be especially true with respect to introducing and elaborating the structure of matter – or the even more fundamental idea of ‘substance’: “Recognising chemical change is contingent on understanding what is meant by ‘a substance’” (Johnson, 2013, p. 370). Introducing a concept is not synonymous to students’ understanding or actually working with it: “The demands that even the small range of events used [in his interviews] make upon the idea of a substance must not be underestimated. To the learner, there is much to keep in mind and much to ignore (in terms of noise) to see the ‘simplicity’ of the underlying picture” (Johnson, 2000a, p. 84). He, moreover states that “it seems that students make very modest year on year progress and by the end of Year 9 the average student has barely begun to develop the concept of a substance” (Johnson, 2013, p. 370). Löfgren and Helldén's (2009) discouraging finding that only 20% of 16-year-olds could employ an adequate particle model to explain change phenomena underscores this crucial interrelation between the dimensions.
(3) A differentiation of learning progress in three stages, ranging from the phenomenological via a simple Daltonian atomic model to the refined electron shell model of Bohr, could only find limited evidence. Although there appears to be a wide gap between the phenomenological and discontinuous approaches to the Transformation of Matter, evolving from a Daltonian into a Bohrian view requires less of an effort. The broader distinction finds support in research by Walpuski et al. (2011) or Ferber (2014) who could also show that discontinuous approaches to matter made test items more difficult. This rather coarse distinction between the macroscopic and a particulate view of matter is widely consensual (e.g., Smith et al., 2006; Löfgren and Helldén, 2009; Johnson and Tymms, 2011), while markedly fewer studies consider a differentiation between Dalton's and Bohr's atomic model (e.g., Claesgens et al., 2009, who consider Bohr to belong on the college level; Rogat, 2011; Hadenfeldt et al., 2016). The finer distinction between Dalton's and Bohr's models – as argued for by, e.g., Barke et al. (2012) and shown to exist by Hadenfeldt et al. (2016) for structure and composition at least (they do not model the most advanced level for chemical reactions) – could not be found to cause additional difficulty. This might, however, be attributed to sampling only students from German academic track schools whose powers of abstraction might privilege them over students from other school types and, thus, ease their ways between discontinuous models. Moreover, the lower of the assumed two stages (Dalton's model) was modelled on very few test items pertaining to a single Kompetenz on each dimension, which might distort the actual level of difficulty. A more finely grained learning progression appears to be necessary in this respect to further elucidate this finding. This is especially called for considering findings from Bayesian analyses that could be interpreted as supporting the proposed thresholds between stages 2 and 3.
An alternative interpretation of this finding can be found in Liu and Lesniak's (2006) claim that there is considerable overlap of the conceptions of matter between students from different grades; combined with a tendency to “focus on what [students] have seen and disregard what they have not seen” (p. 337), resorting to phenomenology instead of a general particle level might have explanatory power. Students would, in this understanding, readily fall back on phenomenological aspects while they would show increased difficulties relating to discontinuous conceptions of matter. The threshold for referring to a discontinuous character of matter would be so high that further differentiation within this character would not produce substantially more difficulty.
Speaking from the perspective of Liu and Lesniak's (2005) wave model of the matter concept, one might argue that the onset of the wave that entails an explanation with differentiated particle models happens too late for our study to capture (this would be in line with Claesgens et al., 2009). The authors attribute this final wave toward “explaining and predicting matter and changes using bonding theories” to high school specialists which corresponds to grades 11–13 in German secondary school. This argument, however, only holds true if considered from a developmental psychologist's point of view since – normatively speaking – German science education standards require students to perform on Bohr's level by the end of grade 10. Instruction, therefore, should be so aligned as to meet this curricular threshold. Having said that, we have to concede that sampling for our study did (and could) not‡ include grade 10-students which might have resulted in uncovering a developmental step from Dalton's to Bohr's model.
(4) Bayesian statistics has proven to be a most informative addition to the inventory of validity test approaches. First of all, it allows one to generate a generalized probability measure from several individual events – in this case, calculating one Kompetenz-estimate from performance on five different items. Tendencies of blurred item difficulties (Johnson and Tymms, 2011, Johnson, 2013), that were suggestive of an inherent difficulty order between Kompetenzen and could be inferred from Rasch's Wright Map, could thus be corroborated or contradicted. Providing Conditional Probability Tables allows one to directly compare solution rates for achieving a Kompetenz depending on prior performance. Where there are large differences in the odds to achieve a Kompetenz, one might argue for (or against) beneficial influences of preceding learning performance. Where the differences are only small, this influence does not appear to hold true. Additionally, the Bayes approach disclosed peculiar developments of Kompetenz-difficulties between stages 2 and 3 to which Classical Test Theory had a blind eye. Here, again, concessions need to be made with regard to the limited empirical data that were surveyed on stages 2 in both the dimensions.
(5) Furthermore, the work with Bayesian networks has allowed us to inquire into interdependent achievements in a more complex manner than possible with ‘simple’ correlational analyses (be it Pearson's r or the more sophisticated methodology of SEM). Using Bayesian networks, the interplay of multiple Kompetenzen can be modelled and estimated. Thus, Bayesian statistics allows one to investigate conditional probabilities and judge the significance of individual Kompetenzen in their context of performance. We found evidence for a supposedly fundamental Kompetenz (identifying substances with reference to their properties) to be of little importance in the long run. This appears to be contradictive of the value that, e.g., Sevian and Talanquer (2014) assign to this feature with respect to chemistry as an academic discipline, as well as to Johnson's repeated claim (e.g., 2005) that a thorough understanding of substances is prerequisite for learning about chemical change. At the same time, it might inform teachers not to spend too much of their valuable lesson time on this aspect (which might have been functionally overstressed in an essentially structural academic discourse). Especially as other Kompetenzen, e.g., realizing that a chemical reaction has taken place on basis of a change in substance properties, appear to be more decisive. Realising a relation between properties and substance is functionally relevant to recognise chemical change, but it is only structurally significant to categorize substances according to their properties. Students’ who have not adopted the former idea are less likely to progress successfully in the Transformation of Matter Concept. It appears, thus, that – judging from conditional probabilities – some Kompetenzen are more relevant to learning than others. To our knowledge, this so far has necessarily been attributed to some professional gut-feeling but has been lacking empirical evidence. We claim to provide some of the necessary evidence in this study and to introduce a valuable statistical approach to further investigate this. At the same time, we acknowledge that there are many idiosyncratic ways of acquiring a certain Kompetenz. Learning as suggested in a learning progression needs instruction to aid its unfolding (Rogat, 2011). So, there is a need to informedly decide on suited paths of teaching which might be served by identifying those pathways of performance that produce a maximum of successful students.
Naturally, the research presented here does have its flaws and limitations. One always wishes for larger sample sizes, more diverse populations, clearer results for goodness of fit indices, no misfitting items etc. Yet, as a starting point for future research it may claim that taking up Bayesian statistics into the plethora of analytical approaches in science education research might be a valuable enterprise.
Conflicts of interest
There are no conflicts to declare.Appendix A
| Kompetenz code in Strand Map | Underlying performance expectation |
|---|---|
| a Our translations; SM in the codes denotes the progress variable ‘Structure of Matter’, CR denotes the progress variable ‘Chemical Reaction’; blank rows indicate stages of progress as do the codes' third digits P (Stage 1: phenomenological stage), D (Stage 2: Dalton's atomic model), and B (Stage 3: Bohr's atomic model). | |
| SMP.1 | Students can differentiate between substance and object |
| SMP.2 | Students can name substance properties |
| SMP.3 | Students can identify substances based on substance properties |
| SMP.4 | Students can differentiate between pure substance and mixture |
| CRP.5 | Students recognize chemical reactions from the formation of new substances with new properties |
| SMP.6 | Students can describe chemical elements and compounds as pure substances and can differentiate them from each other |
| SMP.7 | Students can describe the building principle of the Periodic Table of the Elements (group, period, atomic number) |
| SMD.8 | Students can describe atoms and the particulate structure of atomic groups by means of Dalton's atomic model |
| CRD.9 | Students can describe chemical reactions as the rearrangement of atoms |
| SMB.10 | Students can describe atoms by means of a simplified Rutherford nucleus-shell-model |
| SMB.11 | Students can identify protons and neutrons as nucleons |
| SMB.12 | Students can derive the number of electrons in an uncharged atom from its number of protons |
| SMB.13 | Students can derive the ionic charge of monoatomic ions from the number of its protons and its electrons |
| SMB.14 | Students can describe atoms using Bohr's atomic orbit-model |
| SMB.15 | Students can explain the relationship between electron configuration and the Periodic Table of the Elements |
| SMB.16 | Students can describe ionic composition on basis of Bohr‘s nucleus-orbit-model |
| SMB.17 | Students can argue for the noble gases‘ inertia on basis of their electron configuration |
| CRB.18 | Students can recall the noble gas rule |
| CRB.19 | Students can describe the formation of ions from atoms (chemical reaction as a change in the electron shell) |
| CRB.20 | Students can describe the formation of ionic bonds between oppositely charged ions as a result of their electrostatic attractions that act uniformly into all spatial directions |
Appendix B
Exemplary item set (item #1–#20) for sodium chloride
(Our translations; German original options are comparable in length for at least two options in each set)Sodium is a silvery metal. Sodium chloride is the same as table salt.
Are sodium and sodium chloride substances or objects? NaClSMP01
□ Sodium is a substance because objects can be manufactured from it. Sodium chloride is an object because it consists of specific substances.
□ Sodium is an object because it is ductile. Sodium chloride is a substance because it is not ductile.
□ Sodium and sodium chloride are objects because you cannot manufacture something new from them as opposed to from a substance.
□ Sodium and sodium chloride are substances because they do not have a characteristic shape as opposed to objects. (attractor = A)
Sodium has characteristic substance properties. With reference to these properties you can identify sodium.
Which of the following substance properties helps identifying sodium? NaClSMP02
□ Sodium can be identified from its characteristic shape under a microscope.
□ Sodium can be identified from its characteristic point of melting. (A)
□ Sodium can be identified from its characteristic temperature.
□ Sodium can be identified from its characteristic volume.
Substance samples formed during several experiments were not labelled. You have to find out which substance is sodium chloride. Four substance samples are tested for their properties (Table 11).
| Sample | Electrical conductivity (solid state) | Solubility in water | Electrical conductivity (aqueous solution) |
|---|---|---|---|
| 1 | No | Yes | Yes |
| 2 | No | Yes | No |
| 3 | No | No | — |
Sodium chloride is table salt. Which one or more of the following substance samples could be sodium chloride? NaClSMP03
□ Substance samples 1, 2, and 3 could be sodium chloride, because none of the samples conducts electrical current in the solid state. Differences in solubility are unimportant under these circumstances.
□ Substance samples 1 or 2 could be sodium chloride because both are water soluble. Conductivity in aqueous solution is not informative.
□ Substance sample 3 could be sodium chloride because the substance does not dissolve in water and does not conduct electrical current.
□ Substance sample 1 could be sodium chloride because it is the only water soluble one, its aqueous solution conducts electrical current, while it does not in solid state. (A)
Heating a piece of sodium to melting and then blowing gaseous chlorine across, a bright yellow flame appears. Sodium and chlorine are transformed completely. Sodium chloride forms and disperses finely in air.
Is there a pure substance or a substance mixture in the reaction vessel? NaClSMP04
□ There is a mixture in the reaction vessel because sodium chloride has formed from sodium and chlorine.
□ There is a pure substance in the reaction vessel because sodium chloride is a white solid substance.
□ There is a pure substance in the reaction vessel because you cannot distinguish sodium chloride from air with the naked eye.
□ There is a mixture in the reaction vessel because it contains the air‘s gases and sodium chloride. (A)
Heating a piece of sodium to melting and then blowing gaseous chlorine across, a bright yellow flame appears. Moreover, a white powder is formed: sodium chloride.
Sodium chloride forms because… NaClCRP05
□ … chlorine discolours sodium.
□ … sodium and chlorine react into a different substance with different properties. (A)
□ … sodium melts and dissolves chlorine.
□ … chlorine turns solid from transferring energy onto sodium.
Heating a piece of sodium to melting and then blowing gaseous chlorine across, forms white sodium chloride.
Is sodium chloride considered a compound or an element? NaClSMP06
□ The pure substance sodium chloride is a chemical compound because it forms from sodium and chlorine. (A)
□ The pure substance sodium chloride is a chemical element because it has a uniform colour.
□ The pure substance sodium chloride is a chemical compound because it encloses chlorine and sodium.
□ The pure substance sodium chloride is a chemical element because it is a single chemical substance.
Chlorine and sodium are two chemical elements.
Are chlorine's and sodium's chemical properties similar? Give reasons referring to the periodic table of the elements. NaClSMP07
□ Chlorine is in the 7th main group, sodium is in the 1st main group. Therefore, they differ in their chemical properties. (A)
□ There are two more elements above sodium in the 1st main group. There is only one element above chlorine in the 7th main group, however. Therefore, they differ in their properties.
□ Chlorine and sodium both are in the 3rd period. They, therefore, have similar properties.
□ Chlorine's atomic number is 17, sodium‘s atomic number is 11. Because this difference is only small, they have similar properties.
Sodium is a silvery metal and chlorine is a greenish-yellow gas. Both the elements differ strongly with respect to their substance properties.
Give reasons why the elements sodium and chlorine differ in their properties. NaClSMD08
□ Sodium and chlorine differ in their colour and their atoms’ density. Chlorine atoms have a lesser density and are placed further apart than sodium atoms.
□ Sodium and chlorine are made of different kinds of atoms. Atoms differ in size and mass and are ordered differently. (A)
□ Sodium and chlorine differ in their atoms’ divisibilities. Chlorine atoms are divisible, sodium atoms are not divisible.
□ Sodium and chlorine are made of atoms that differ in their shape. Sodium atoms are ball shaped, chlorine atoms are flattened.
The reaction of sodium with chlorine forms sodium chloride.
What happens to sodium- and chlorine-atoms in the formation of sodium chloride from sodium and chlorine? NaClCRD09
□ Chlorine-atoms displace sodium-atoms from sodium. So, sodium chloride consists of sodium incorporating chlorine-atoms.
□ Physical properties of sodium- and chlorine-atoms are changed so that sodium and chlorine turn into sodium chloride.
□ Sodium-atoms and chlorine-atoms are transformed into sodium chloride-atoms, so that sodium chloride consists of sodium chloride-atoms.
□ Sodium-atoms and chlorine-atoms break from their particle groups and form another particle group. (A)
Chlorine atoms have a defined mass and contain positive and negative carriers of charge. They appear electrically neutral from the outside.
Which of the following statements describes a chlorine-atom's layout according to RUTHERFORD? NaClSMB10
□ Mass is charged positively and distributes evenly across the atom. Negatively charged electrons are enclosed in the mass.
□ Positive charge and almost the entire mass are in the atom‘s nucleus. Negatively charged and nearly massless electrons are in the atomic shell. (A)
□ Positive charge and negatively charged electrons distribute evenly across the atom. Mass, likewise, distributes across the entire atom.
□ Mass is distributed evenly across the atom. Positive charge is in the atom's nucleus. Negatively charged electrons are in the atom's nucleus and the atomic shell.
Sodium-atoms have eleven electrons, eleven protons and twelve neutrons.
How many electrons, protons and neutrons are there in a sodium atom's nucleus? NaClSMB11
□ Eleven protons, twelve neutrons and no electrons. (A)
□ Six protons, sic neutrons and no electrons.
□ Twelve neutrons, six protons and six electrons.
□ Eleven protons, eleven electrons and twelve neutrons.
A chlorine-atom has 17 protons.
How many electrons are there in a chlorine-atom? NaClSMB12
□ A chlorine-atom has 35 electrons because there additionally are 18 neutrons in the nucleus. Protons and neutrons must not repel each other.
□ A chlorine-atom has 34 electrons because electrons are smaller than protons and therefore twice as many electrons than protons fit in the atom.
□ A chlorine-atom has 18 electrons because the nucleus's attraction forces cannot hold more electrons in an atom of this size.
□ A chlorine-atom has 17 electrons because positive charges of the protons and the electrons’ negative charges must compensate each other. (A)
A chloride-ion has 17 protons and 18 electrons.
What is the chloride-ion's charge? NaClSMB13
□ It is charged positively ninefold because the chloride-ion has eight outer electrons whose charge must be compensated by the protons.
□ It is charged positively 17-fold because the chloride-ion has 17 protons, each of which has a single positive charge.
□ It is charged uninegatively because the chloride-ion has one electron more than protons and so the negative charge dominates. (A)
□ It is charged negatively 18-fold because the chloride-ion has 18 electrons, each of which has a single negative charge.
Sodium atoms have eleven electrons.
What is the composition of sodium's atomic shell? NaClSMB14
□ On the first shell, there are two electrons. On the second shell, there is one electron. On the third shell, there are eight electrons because the outer shell always has eight electrons.
□ On the first shell, there are eight electrons. On the second shell, there are three electrons. Each shell must be filled with eight electrons bevor filling the next one.
□ Because of its small size, the first shell has only two electrons. The larger, second shell has eight electrons. The third shell has one electron. (A)
□ Because of its small size, the first shell has only one electron. The second and third shells each have five electrons because electrons must be distributed evenly.
Chlorine is in the 3rd period of the periodic table.
Which conclusions can you draw from this concerning the chlorine-atomic shell's composition? NaClSMB15
□ There are three electrons on the outer shell.
□ There are three electrons in the atomic shell.
□ There are three electron shells in a chlorine-atom. (A)
□ In each electron shell of a chlorine-atom there are three electrons.
Sodium-atoms have eleven electrons. Sodium-ions can form from sodium-atoms.
Which is the composition of a unipositively charged sodium-ion? NaClSMB16
□ There are eleven protons in the atom‘s nucleus. There are eight electrons on the second shell. The inner shell has two electrons. (A)
□ There are eleven protons in the atom's nucleus. The outer shell has one, the second shell eight electrons. The inner shell has one electron.
□ There are twelve protons in the atom‘s nucleus. The outer electron shell has one electron, the second shell has eight electrons. The inner shell has one electron.
□ There are eleven protons in the atom‘s nucleus. The outer electron shell has two electrons, the second shell has eight electrons. The inner electron shell has two electrons.
Air contains the noble gas neon. A neon-atom has a completely filled outer shell.
Can sodium and the noble gas neon react? NaClSMB17
□ No. Because neon-atoms already have eight outer electrons; they neither lose nor gain electrons. (A)
□ No. Although neon-atoms can lose an electron, the discharged energy is not enough for a reaction to take place.
□ Yes. Neon-atoms gain one electron each from sodium-atoms. Energy discharges and a new substance is formed.
□ Yes. Neon-atoms can lose all eight electrons and sodium-atoms can gain these so that a new substance is formed.
Chlorine-atoms each have seven outer electrons. When reacting with sodium, anions are formed from each chlorine-atom. This anion follows the noble gas rule.
How do numbers of outer electrons differ between anion and atom? NaClCRB18
□ The formed anion has seven fewer outer electrons than a chlorine-atom.
□ The formed anion has one fewer outer electrons than the chlorine-atom.
□ The formed anion has the same number of outer electrons as the chlorine-atom.
□ The formed anion has one outer electron more than the chlorine-atom. (A)
There is a visible bright yellow flame in the reaction of sodium with chlorine. Sodium chloride forms. Sodium chloride is made of sodium- and chloride-ions.
How do sodium- and chloride-ions form from sodium- and chlorine-atoms? NaClCRB19
□ Because of the reaction's great heat sodium-ions form from sodium-atoms by transferring electrons on other sodium-atoms. Chloride-ions form from chlorine-atoms by transferring electrons on other chlorine-atoms.
□ Sodium-ions form from sodium-atoms by the destruction of an electron in the flame. Chloride-ions form from chlorine-atoms by gaining one electron from their surroundings because of the heat.
□ One electron from a sodium-atom and an electron from a chlorine-atom form a bonding electron pair. Sodium-atoms and chlorine-atoms thus become sodium- and chloride-ions. They are held together by the bonding electron pair.
□ Sodium-ions form from sodium-atoms by losing one electron from the outer shell. Chloride-ions form from chlorine-atoms by gaining an electron. Formed ions show noble gas configuration. (A)
Sodium- and chloride-ions form in the reaction of sodium-atoms with chlorine-atoms.
Describe why a sodium-chloride-crystal forms in the process. NaClCRB20
□ Sodium-cations and chloride-anions cluster together. Electrons are spent into the crystal. These electrons hold the ions’ cores together.
□ One sodium-cation and one chloride-anion each share their electrons. Sodium chloride molecules form which cluster together in a sodium chloride-crystal.
□ Sodium-cations and chloride-anions are oppositely charged and attract each other. Because these attraction forces act in all directions, ions cluster together in a crystal lattice. (A)
□ Chloride-anions give two electrons into a bonding electron pair so a chloride-anion can bind to a sodium-cation.
Acknowledgements
The research presented in this article has been conducted as part of project GanzIn which was funded by Stiftung Mercator and the Ministry for Schools and Education in North Rhine-Westphalia. We would like to express our gratitude for this. We would, moreover, like to thank CERP's editor and referees for their insightful comments and criticism which have contributed greatly to the improvement of our article.Notes and references
- AAAS, (2001), Atlas of science literacy, Washington, DC, vol. 1.
- Andersson B., (1990), Pupils’ Conceptions of Matter and its Transformations (age 12–16), Stud. Sci. Educ., 18(1), 53–85.
- Barke H.-D., Harsch G. and Schmid S., (2012), Essentials of Chemical Education, Berlin: Springer.
- Bernholt S. and Parchmann I., (2011), Assessing the complexity of students' knowledge in chemistry, Chem. Educ. Res. Pract., 12(2), 167–173.
- Bond T. G. and Fox C. M., (2007), Applying the Rasch model: Fundamental measurement in the human sciences, Mahwah, NJ: Lawrence Erlbaum.
- Claesgens J., Scalise K. and Stacy A., (2013), Mapping Student Understanding in Chemistry: The Perspectives of Chemists, Educación Química, 24(4), 407–415.
- Claesgens J., Scalise K., Wilson M. and Stacy A., (2009), Mapping student understanding in chemistry: The Perspectives of Chemists, Sci. Educ., 93(1), 56–85.
- Corcoran T., Mosher F. A. and Rogat A. (ed.), (2009), Learning progressions in science – an evidence based approach to reform, Philadelphia, PA: CPRE.
- Duschl R., Maeng S. and Sezen A., (2011), Learning progressions and teaching sequences: a review and analysis, Stud. Sci. Educ., 47(2), 123–182.
- Duschl R. A., Schweingruber H. A. and Shouse A. W. (ed.), (2007), Taking Science to School: Learning and Teaching Science in Grades K-8, Washington, DC: The National Academies Press.
- Feinstein A. R. and Cicchetti D. V., (1990), High Agreement but Low Kappa: The Problems of Two Paradoxes, J. Clin. Epidemiol., 43(6), 543–549.
- Ferber N., (2014), Entwicklung und Validierung eines Testinstruments zur Erfassung von Kompetenzentwicklung im Chemieunterricht der Sekundarstufe I, Berlin: Logos. [Development and validation of a test instrument for capturing competence development in chemistry instruction on the lower secondary level.].
- Frey A., Hartig J. and Rupp A. A., (2009), An NCME Instructional Module on Booklet Designs in Large-Scale Assessments of Student Achievement: Theory and Practice, Educ. Meas.: Issues Pract., 28(3), 39–53.
- Fuster-Parra P., García-Mas A., Ponseti F. J., Palou P. and Cruz J., (2014), A Bayesian network to discover relationships between negative features in sport: a case study of teen players, Qual. Quant., 48, 1473–1491.
- GDSU, (2013), Perspektivrahmen Sachunterricht, Bad Heilbrunn: Verlag Julius Klinkhardt. [Framework Social and Science Education on the Primary Level.].
- Gwet K. L., (2014), Handbook of Inter-Rater Reliability. The Definitive Guide to Measuring the Extent of Agreement among Raters, Gaithersburg: Advanced Analytics.
- Hadenfeldt J. C., Bernholt S., Liu X., Neumann K. and Parchmann I., (2013), Using Ordered Multiple Choice Items to Assess Students’ Understanding of the Structure and Composition of Matter, J. Chem. Educ., 90(12), 1602–1608.
- Hadenfeldt J. C., Liu X. and Neumann K., (2014), Framing students’ progression in understanding matter: a review of previous research, Stud. Sci. Educ., 50(2), 181–208.
- Hadenfeldt J. C., Neumann K., Bernholt S., Liu X. and Parchmann I., (2016), Students’ progression in understanding the matter concept, J. Res. Sci. Teach., 53(5), 683–708.
- International Council for the Exploration of the Sea (ICES), (2014), Report of the Study Group on Spatial Analysis for the Baltic Sea (SGSPATIAL), Gothenburg, Sweden, http://www.ices.dk/sites/pub/Publication%20Reports/Expert%20Group%20Report/SSGRSP/2014/SGSPATIAL14.pdf 〈01/13/2018〉.
- Johnson P., (2000a), Developing Students’ Understanding of Chemical Change: What Should We Be Teaching? Chem. Educ. Res. Pract., 1(1), 77–90.
- Johnson P., (2000b), Children's Understanding of Substances, Part 1: Recognizing Chemical Change, Int. J. Sci. Educ., 22(7), 719–737.
- Johnson P., (2002), Children's Understanding of Substances, Part 2: Explaining Chemical Change, Int. J. Sci. Educ., 24(10), 1037–1054.
- Johnson P., (2005), The Development of Children's Concept of a Substance: A Longitudinal Study of Interaction between Curriculum and Learning, Res. Sci. Educ., 35(1), 41–61.
- Johnson P., (2013), A Learning Progression towards Understanding Chemical Change, Educación Química, 24(4), 365–372.
- Johnson P. and Tymms P., (2011), The Emergence of a Learning Progression in Middle School Chemistry, J. Res. Sci. Teach., 48(8), 849–877.
- Kallayanamitra C., Leeahtam P., Potapohn M., Wilcox B. A. and Sriboonchitta S., (2014), An Integration of Eco-Health One-Health Transdisciplinary Approach and Bayesian Belief Network, in Huynh V.-N., Kreinovich V. and Sriboonchitta S. (ed.), Modeling Dependence in Econometrics, Cham: Springer, pp. 463–478.
- Kauertz A., Neumann K. and Haertig H., (2012), Competence in Science Education, in Fraser B., Tobin K. and McRobbie C. (ed.), Second International Handbook of Science Education, Dordrecht: Springer, pp. 711–721.
- Klieme E., Avenarius H., Blum W., Döbrich P., Gruber H., Prenzel M. et al., (2003), Zur Entwicklung nationaler Bildungsstandards. Eine Expertise, Bonn, Berlin: BMBF. [Concerning the Development of National Education Standards – An Expertise.].
- KMK, (2005), Bildungsstandards im Fach Chemie für den Mittleren Schulabschluss, München: Luchterhand. [Education Standards for Chemistry on the Lower Secondary Level.].
- Kremer K., Fischer H. E., Kauertz A., Mayer J., Sumfleth E. and Walpuski M., (2012), Assessment of standards-based learning outcomes in science education: Perspectives from the German project ESNaS, in Bernholt S., Neumann K. and Nentwig P. (ed.), Making it Tangible – Learning Outcomes in Science Education, Münster: Waxmann, pp. 159–177.
- Liu X., (2001), Synthesizing research on student conceptions in science, Int. J. Sci. Educ., 23(1), 55–81.
- Liu X. and Lesniak K. M., (2005), Students’ progression of understanding the matter concept from elementary to high school, Sci. Educ., 89(3), 433–450.
- Liu X. and Lesniak K., (2006), Progression in children's understanding of the matter concept from elementary to high school, J. Res. Sci. Teach., 43(3), 320–347.
- Löfgren L. and Helldén G., (2009), A Longitudinal Study Showing how Students use a Molecule Concept when Explaining Everyday Situations, Int. J. Sci. Educ., 31(12), 1631–1655.
- McCray G., (2013), Assessing inter-rater agreement for nominal judgement variables, Language Testing Forum, Nottingham, http://www.norbertschmitt.co.uk/uploads/27_528d02015a6da191320524.pdf 〈12/06/2016〉.
- Mohan L., Chen J. and Anderson C. W., (2009), Developing a Multi-Year Learning Progression for Carbon Cycling in Socio-Ecological Systems, J. Res. Sci. Teach., 46(6), 675–698.
- MSW, (2008a), Kernlehrplan für das Gymnasium - Sekundarstufe I in Nordrhein-Westfalen. Chemie, Frechen: Ritterbach. [Core curriculum for academic track schools in North Rhine-Westphalia, Lower Secondary Level. Chemistry].
- MSW, (2008b), Richtlinien und Lehrpläne für die Grundschule in Nordrhein-Westfalen, Frechen: Ritterbach. [Frameworks and Curricula for Primary Schools in North Rhine-Westphalia.].
- NRC, (2011), A Framework for K–12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, D.C.: National Academy Press.
- Neumann K., Fischer H. E. and Kauertz A., (2010), From PISA to Educational Standards: The Impact of Large-Scale-Assessments on Science Education in Germany, Int. J. Sci. Math. Educ., 8(3), 545–563.
- Neumann K., Bernholt S. and Nentwig P., (2012), Learning Outcomes in Science Education: A Synthesis of the International Views on Defining, Assessing and Fostering Science Learning, in Bernholt S., Neumann K. and Nentwig P. (ed.), Making it Tangible – Learning Outcomes in Science Education, Münster: Waxmann, pp. 501–519.
- Norsys, (2010), Netica-J Reference Manual. Version 4.18 and Higher, Vancouver, BC. http://www.norsys.com/downloads/NeticaJ_Man_418.pdf 〈03/02/2017〉.
- Norsys, (2012), Class NetTester, https://www.norsys.com/netica-j/docs/javadocs/norsys/netica/NetTester.html 〈03/03/2017〉.
- Norsys, (2017), Scoring Rule Results & Logarithmic Loss Values, https://www.norsys.com/WebHelp/NETICA/X_Scoring_Rule_Results.htm 〈03/03/2017〉.
- Rogat A., (2011), Developing Learning Progressions in Support of the New Science Standards: A RAPID Workshop Series, New York, NY, https://repository.upenn.edu/cgi/viewcontent.cgi?article=1014&context=cpre_researchreports 〈07/02/2018〉.
- Schecker H. and Parchmann I., (2006), Modellierung naturwissenschaftlicher Kompetenz, Zeitschrift für Didaktik der Naturwissenschaften, 12, 45–66. [Modelling scientific competence.].
- Schecker H. and Parchmann I., (2007), Standards and competence models: The German situation, in Waddington D., Nentwig P. and Schanze S. (ed.), Making it comparable. Standards in science education, Münster: Waxmann, pp. 147–163.
- Schmidt H.-J. and Volke D., (2003), Shift of meaning and students’ alternative concepts, Int. J. Sci. Educ., 25(11), 1409–1424.
- Sevian H. and Talanquer V., (2014), Rethinking Chemistry: A Learning Progression on Chemical Thinking, Chem. Educ. Res. Pract., 15(1), 10–23.
- Smith C. L., Wiser M., Anderson C. W. and Krajcik J., (2006), Implications of Research on Children's Learning for Standards and Assessment, Measurement, 4(1–2), 1–98.
- Stevens S. Y., Delgado C. and Krajcik J. S., (2010), Developing a Hypothetical Learning Progression for the Nature of Matter, J. Res. Sci. Teach., 47(6), 687–715.
- Walpuski M., Ropohl M. and Sumfleth E., (2011), Students’ Knowledge about Chemical Reactions: Development and Analysis of Standard-Based Test Items, Chem. Educ. Res. Pract., 12(2), 174–183.
- Weber K., (2018), Entwicklung und Validierung einer Learning Progression für das Konzept der chemischen Reaktion in der Sekundarstufe I, PhD thesis, Duisburg-Essen University, [Development and Validation of a Learning Progression for the Chemical Reaction Concept on the Lower Secondary Level.].
- Wei H., (2014), Bayesian Networks for Skill Diagnosis and Model Validation. Annual Meeting of the National Council on Measurement in Education, Philadelphia, PA, http://researchnetwork.pearson.com/wp-content/uploads/NCME_HW.pdf 〈02/25/2016〉.
- West P., Rutstein D. W., Mislevy R. J., Liu J., Choi Y., Levy R. et al., (2010), A Bayesian network approach to modeling learning progressions and task performance (CRESST Report 776), Los Angeles, CA: University of California, National Center for Research on Evaluation, Standards, and Student Testing, http://files.eric.ed.gov/fulltext/ED512650.pdf 〈02/28/2016〉.
- Wilson M., (2005), Constructing Measures: An Item Response Modeling Approach, Mahwah, NJ: Lawrence Erlbaum.
- Wu M., Adams R. J. and Wilson M., (2007), Acer Conquest version 2.0: Generalised item response modelling software, Camberwell, Vic: ACER Press.
Footnotes |
| † Probabilities have been estimated for the combination of two clusters. As a rule, those conditional probabilities have been noted here where they were obtainable for directly linked clusters – only few exceptions apply. These cluster combinations have typically proven to be of superior quality to cluster combination analyses with unrelated clusters. Where the same relations were estimated in more than one analyses, results from the better quality estimates were integrated in this map. |
| ‡ German education standards apply to students graduating from lower secondary school. For most school types the final year of lower secondary school is grade 10. For German Gymnasium an oddity occurs: as the students of Gymnasium are regularly expected to follow their education through upper secondary school to the Abitur (graduation exams), no formal exit from lower secondary school is installed. After having reformed formal schooling in the Gymnasium to last 8 years of secondary education as opposed to 9 years in 2004, the last year of lower secondary school (grade 10) was ‘relocated’ as a compensatory academic year to upper secondary school. This is meant to ease students’ travelling between school tracks. At the same time, this implies that lower secondary school is one year ‘short’ of science education at Gymnasium. Sampling in upper secondary school is considerably hard to accomplish. |
| This journal is © The Royal Society of Chemistry 2018 |