Epistemic games in substance characterization
Hannah
Sevian
 * and
Steven
Couture
* and
Steven
Couture

Department of Chemistry, University of Massachusetts Boston, Boston, MA 02125, USA. E-mail: hannah.sevian@umb.edu
First published on 28th May 2018
Abstract
Problem solving is lauded as beneficial, but students do not all learn well by solving problems. Using the resources framework, Tuminaro J., and Redish E. F., (2007), Elements of a cognitive model of physics problem solving: Epistemic games, Physical Review Special Topics-Physics Education Research, 3(2), 020101 suggested that, for physics students, this puzzle may be partially understood by paying attention to underlying epistemological assumptions that constrain the approaches students take to solving problems while working on them. They developed an approach to characterizing epistemic games, which are context-sensitive knowledge elements concerning the nature of knowledge, knowing and learning. As there is evidence that context-activated knowledge influences problem solving by students in chemistry, we explored identifying epistemic games in students’ problem solving in chemistry. We interviewed 52 students spanning six courses from grade 8 through fourth-year university, each solving 4 problems. Using 16 contexts with substance characterization problems, we identified 5 epistemic games with ontological and structural stability that exist in two larger epistemological frames. All of these epistemic games are present at all educational levels, but some appear to grow in across educational levels as others recede. Some games also take lesser and greater precedence depending on the problem and the chemistry course in which students are enrolled and the context of the problem. We analyze these results through a frame of learning progressions, paying attention to students’ ideas and how these ideas are contextualized. Based on this analysis, we propose teaching acts that instructors may use to leverage the natural progressions of how students appear to grow in their capacity to solve problems.
Introduction
Problem-based learning is generally lauded as beneficial and is increasingly part of active learning approaches to science, engineering, and medicine (Prince, 2004). While it is generally agreed that students should learn to solve problems, what a problem is has several definitions in the literature. Jonassen (2000) characterized problems as having two features: (1) there is a difference between a goal state and the current state, and (2) there is some social, cultural, or intellectual value in the work of solving it. Jonassen (2007) later defined a typology of problems that hinges on the problem's structure and aspects of the problem solver. We use this to differentiate questions from problems. A question is well-structured, has one correct answer, and is objective in what knowledge is required to answer it. On the other hand, a problem is ill-structured, does not have one correct answer, and contains insufficient information. As such, a problem's solution depends on what assumptions the problem solvers make to contain the problem, and what outside information the problem solvers deem relevant to solving it. Studies of problem-based learning focus on teachers’ and students’ work and learning while solving “problems” rather than “questions”.Hmelo-Silver (2004) summarized results on the extent to which students engaged in problem-based learning develop flexible knowledge and become better problem solvers, whether students become more self-directed learners and collaborators, and students’ intrinsic motivation. She concluded that there is robust evidence that students successfully construct new knowledge and that students develop problem-solving skills under particular circumstances, but evidence of self-direction, collaboration, and intrinsic motivation is less substantial. Schmidt et al. (2011) provided a review of the process of problem-based learning, primarily in medical education, focusing on what works and why. Considering evidence through a theoretical lens of cognitive constructivism, they concluded that activation of prior knowledge occurs during initial discussion of a problem in small groups, and elaboration occurs while students solve the problem. Considering evidence through a lens of situational interest, they concluded that problems drive learning by generating situational interest.
Despite the benefits of problem-based learning, however, a difficulty remains that some students learn more while solving problems, while others learn less, or even seem not to learn. The evidence presented by the reviews cited above indicates that more cognitive-related knowledge and skills increases are well documented, while the more process, affect and interpersonal-related outcomes of self-direction, collaboration, and intrinsic motivation are less well documented. Scott (2014) examined differences in learning outcomes through the lens of achievement goal theory, which differentiates between a learning goal orientation vs. performance goal orientation that can be adopted by students when faced with a challenge. Students with the former orientation focus on mastery by engaging in challenging activities with an attitude that capabilities can be developed, while the latter is characterized by avoiding mistakes, preferring non-challenging problems, and an apparent need to demonstrate performance in comparison to others. In a multi-level analysis that considered a wide variety of factors that have been identified as influential in the research literature on problem-based learning, Scott found a strong positive relationship between students with a learning goal orientation and self-directed learning. This suggests that a key to understanding why problem-based learning works better for some students than others may lie in examining differences in how individuals operate while solving problems.
There has been increasing study of relationships among students’ internal control of learning and learning outcomes (e.g., Tsai, 2001; Zeineddin and Abd-El-Khalick, 2010). One aspect of these interactions is epistemological commitments, which are the views a student holds on the nature of knowledge, knowing, and learning. An example of an epistemological commitment that students can hold with various levels of strength is commitment to the consistency between theory and evidence (Zeineddin and Abd-El-Khalick, 2010). Tuminaro and Redish (2007) suggested that, for physics students, differences in learning outcomes can be partially understood by paying attention to underlying epistemological assumptions that constrain the approaches students take to solving problems while working on them. They proposed the notion of epistemic games as a “useful way of analyzing students’ problem solving behavior in terms of locally coherent goal-oriented activities” (Tuminaro and Redish, 2007, p. 1). Redish defined an epistemic game as “a coherent activity that uses particular kinds of knowledge and processes associated with that knowledge to create knowledge or solve a problem” (Redish, 2004, p. 30). In the resources framework within which this approach to studying learning falls (Hammer et al., 2005), epistemic games are considered epistemological resources that people use when constructing knowledge. Working in the same resources framework, Hutchinson and Hammer (2010) also studied the general epistemological framing of students studying physics in a preservice elementary education course and found that there were two main frames assumed by the students. An unproductive framing, which they called the “classroom game”, reflects ways of working in which students behave and speak as if “sanctioned by the teacher or textbook”. A more productive framing, which they termed “making sense of phenomena”, reflects behaviors in which students try to understand their observations. These two different ways of framing by students during high school genetics classroom discussions were previously described by Jiménez-Aleixandre et al. (2000) as “doing the lesson” and “doing science”. As this work precedes that of Hutchinson and Hammer, we hereafter adopt Jiménez-Aleixandre's titles for these two frames.
Students bring individual resources to group problem solving. Even when a single epistemic game may take root in a group's process, as studied by Tuminaro and Redish (2007), the collective approach starts with the various resources that individuals bring. In particular, we explored the epistemic games that took hold as students solved substance characterization problems in chemistry. As problem-based learning gains traction in chemistry, we are interested in examining how students solve chemistry problems in a variety of contexts in which students may rely on different resources. In this work, we have two major goals: (1) to provide chemistry teachers with structures to help them recognize common ways in which their students approach solving problems that involve identifying and differentiating chemical substances, and (2) to offer teachers information to guide their design of problems that can best foster learning in groups in which students’ approaches to problem solving are diverse.
Our central hypothesis is that some epistemic games will be conserved across all educational levels due to their considered productivity, while others will emerge only at later educational levels. Therefore, we frame this work by learning progressions research, as substance characterization is a core practice in chemistry and is central in a wide variety of chemistry problems. Because our goals are positioned in providing resources for teachers, we adopt the approach to learning progressions of Acher and Arcà (2014) to organize our analysis, in particular to enable us to draw inferences from the results about teaching acts that may be productive for advancing students’ problem solving in chemistry. In motivating and framing this study, we rely on a number of different resources that introduce terminology. To help readers orient to this terminology, Table 1 summarizes the main terms that are used throughout this paper.
| Term | Brief definition |
|---|---|
| Epistemological frame | A person's view of what is expected or going on in a certain situation with respect to knowing or learning |
| Epistemic game | A pattern of activities activated in a coherent manner by people as they solve problems |
| Structure of a game | A game's pattern of entry and ending conditions, and the specific sequence of moves in between |
| Ontology of a game | A game's coherent manner of combining knowledge base, epistemic form, and epistemological commitments |
| Knowledge base | Sources of knowledge on which a person relies while solving a problem |
| Epistemic form | A mental image that assists in guiding a problem-solving process |
| Epistemological commitments | A person's beliefs about the character of knowledge, knowing, and learning |
Epistemological framing
Redish (2004) proposed epistemological frames as an idea commensurate with framing in linguistics and anthropology. Epistemological framing in learning describes a person's view of what is expected or going on in a certain situation with respect to knowing or learning (Scherr and Hammer, 2009). When an individual frames a situation, she or he brings a structure of expectations about what should or could happen, what information to attend to, and what actions are appropriate in the situation. Researchers working in this perspective (Scherr and Hammer, 2009; Elby and Hammer, 2010) have characterized epistemological resources as small knowledge elements concerning the nature of knowledge, knowing and learning. These resources are context-sensitive and constrain how a person frames his or her work in an activity. For example, when studying for an exam, a student might memorize problems in the textbook, reflecting an epistemological resource of knowledge is something absorbed from an authoritative source (Elby and Hammer, 2010, p. 412).Scherr and Hammer (2009) demonstrated that there are connections between how individual students frame their learning of physics and the nature of the students’ interactions when working in groups as they are learning physics. For example, when students who were working in groups of four were reading from a common worksheet, they exhibited quiet and neutral behaviors with expectations of minimal interaction except for check-ins, but did not attend to details of each others’ words, some of which were muttered. In this behavioral mode, members of the group appeared to adopt a framing consistent with viewing knowledge as provided by experts. In contrast, when the students were engaged in discussion, they exhibited considerable gesturing with animated tones and eye contact, while they sat straighter and spoke more clearly. Their expectations appeared consistent in desiring understanding, focusing attention on each other, interest in each other's ideas, and both intellectual and emotional engagement. In this behavioral mode, some students seemed to adopt a framing consistent with having a role in the construction of knowledge. Recently, working in the same framework of resources, Watkins et al. (2017) added to this an insight that a position of not-understanding, while often discounted in classrooms, could be valuable for learning, as scientists recognize the value of confusion, ambiguity, and uncertainty.
Students’ epistemologies have been studied to some extent in chemistry. Pulmones (2010) studied chemistry students’ epistemological beliefs about science and chemistry and linkages to the students’ metacognitive behavior in learning chemistry. Metacognition is thinking about one's thinking, and thus should have a relationship with epistemological beliefs, which are largely implicit, i.e., unrecognized by the person. Pulmones differentiated between naïve and sophisticated epistemologies as measured by the Epistemological Beliefs Assessment for Physical Science instrument (Elby et al., 2001). He found that students who he measured to have more sophisticated epistemological beliefs also demonstrated high levels of metacognitive behavior as well as performed at consistently high cognitive levels as measured by Bloom's taxonomy. Mazzarone and Grove (2013) used the Chemistry Expectations (CHEMX) survey (Grove and Bretz, 2007) and interviews to explore the epistemological development of 15 chemistry students during the first two years of university education. This instrument measures students’ views toward seven cluster areas as unfavorable or favorable: concepts, effort, laboratory, mathematics links, outcomes, reality links, and visualization. For example, regarding effort, an unfavorable view is not attempting to use available information effectively, while a favorable view is trying to make sense of available information. They found that various course factors had influences on students’ epistemological development as measured by these scales. Grading policies and course structure had the largest influence, followed by how students experienced the chemistry laboratory component and the sense of community that students derived from peer interactions.
There are differences between the approaches described here that have been taken in chemistry and physics, and from here we follow the physics approach of the resources model. Researchers who were involved in developing the resources model cautioned against tying sophistication to one stance over another (Elby and Hammer, 2001). These authors levied two lines of criticism against the consensus view that epistemological sophistication is absolute and measurable outside of the context in which it is relevant. First, they argued that “the student epistemology literature fails to distinguish between the correctness and productivity of an epistemological belief” (Elby and Hammer, 2001, p. 555). Their counterargument was that “a belief is productive if it generates behavior, attitudes, and habits that lead to ‘progress’ as defined by the given person or community”. Second, they argued that “according to the consensus view as reflected in commonly used surveys, epistemological sophistication consists of believing certain blanket generalizations about the nature of knowledge and learning, generalizations that do not attend to context”. Rather, they proposed that blanket assertions like this are “neither correct nor productive”. These lines of criticism contributed to a resources view of epistemological framing, in which such framing is locally coherent, as a dynamic system in which “coherences emerge from the activations and interactions of many cognitive elements” (Scherr and Hammer, 2009, p. 151). An apt example of this is the study by Watkins et al. (2017), showing that a position of not-understanding can be productive. This view is also consistent with the theoretical commitments in our chemical thinking learning progression work (Sevian and Talanquer, 2014).
Our central hypothesis, stated earlier, is consistent with the assertions of Elby and Hammer (2001). We speculate that some epistemic games are more foundational while others begin to take shape later in the educational process. Thus, the epistemic games on which a person relies may depend upon the resources that she or he has built up over years of education. Analysis of our findings from the perspective of the chemical thinking learning progression (briefly described below) enables us to consider ways that teachers can leverage the productivity in how students rely on different epistemic games in different contexts.
To our knowledge, our study is the first attempt to investigate epistemological framing in chemistry problem solving from a resources perspective. Some evidence in the literature, however, suggests that this may be fruitful. In particular, context-activated knowledge elements have been shown to explain problem solving by students in chemistry. For example, Broman and Parchmann (2014) varied tasks with personal, societal, and professional contexts in various chemistry topics. They analyzed how students’ application of chemistry content varied across the tasks during interviews, and found that particular content (e.g., hydrogen bonding) was triggered only by specific contexts (e.g., drug uptake but not soaps) and in relation to some topics but not others (e.g., solubility but not fatty acids). Podschuweit and Bernholt (2017) studied which compositions of contexts are most effective for students’ later transfer to other contexts. They found that more heterogeneous sets of contexts ease transfer of understanding of energy concepts to new contexts. Thus, we expect that epistemological resources are also activated by the contexts in chemistry problems.
Epistemic games
Tuminaro and Redish (2007) sought to learn about the epistemic games that undergraduate physics students rely on as they solve problems in groups during an algebra-based introductory physics course. They considered epistemic games as patterns of activities that are activated in a coherent manner by students as they solve problems. In analyzing 11 hours of videotapes of groups of students solving physics problems, they identified six distinct epistemic games. Each game has entry and ending conditions, and a specific sequence of moves that occur, and is further characterized by the ability to identify the knowledge base and epistemic forms used. An epistemic form is a mental image that assists in guiding a student's problem-solving process, while the knowledge base is the source of knowledge on which the student relies while solving a problem. For example, the game Mapping Mathematics to Meaning, students “develop a conceptual story corresponding to a particular physics equation” (Tuminaro and Redish, 2007, p. 6). In this game, the knowledge base relied upon is mathematics, and the epistemic form is physics equations. Which mathematical knowledge and physics equations vary by problems, however the approach has a consistent sequence of moves. The entry move occurs as students identify target concepts. From here, they find an equation relating the target to other concepts, then tell a story using the mathematical relationships among concepts. The exit move is to evaluate the story. All of the epistemic games characterized by Tuminaro and Redish displayed both structural and ontological stability, as summarized in Table 2.| Structure | Ontology | |
|---|---|---|
| General case | Entry condition, sequence of moves in between, and exit condition | Type of epistemic form, and knowledge base relied upon |
| Mapping meaning to mathematics | Entry: develop story about physical situation | Epistemic form: mathematical expressions |
| Sequence between: translate quantities in story to mathematical entities, relate mathematical entities in accordance with physical story, manipulate symbols | Knowledge base: conceptual understanding | |
| Exit: evaluate and interpret the story | ||
| Mapping mathematics to meaning | Entry: identify target concepts | Epistemic form: physics equations |
| Sequence between: find an equation relating the target to other concepts; tell a story using the mathematical relationships among concepts | Knowledge base: mathematical knowledge | |
| Exit: evaluate the story | ||
| Physical mechanism game | Entry: develop story about physical situation | Epistemic form: description of a mechanism |
| Exit: evaluate the story | Knowledge base: reasoning | |
| Pictorial analysis | Entry: identify target concept | Epistemic form: schematic or diagram generated |
| Sequence between: choose external representation; tell a conceptual story based on spatial relations among the objects | Knowledge base: representational translation | |
| Exit: fill in the “slots” in the representation | ||
| Recursive plug-and-chug | Entry: identify target quantity | Epistemic form: physics equations |
| Sequence between: find equation relating target quantity to other quantities; determine which of the other quantities are known; if additional quantity is unknown, identify new target quantity and cycle back to find equation, otherwise when only the target quantity is unknown… | Knowledge base: syntactic understanding of physics symbols | |
| Exit: calculate target quantity | ||
| Transliteration to mathematics | Entry: identify target quantity | Epistemic form: solution pattern of worked examples |
| Sequence between: find a solution pattern that relates to the problem situation; map quantities in the problem situation into the solution pattern | Knowledge base: example problems | |
| Exit: evaluate mapping | ||
Learning progressions in chemistry
In this study, we analyze our findings from a perspective afforded by learning progressions research. Learning progressions are empirically validatable descriptions of how students develop understanding and utility of big ideas across many years of education (Smith et al., 2006). Substance characterization, or the identification of chemicals, is a central practice in the domain of chemistry, and it is used in all branches of chemistry and disciplines that border chemistry (Hoffmann, 1993). We have previously hypothesized a learning progression on chemical thinking (Sevian and Talanquer, 2014), which proposed organizing the discipline of chemistry into six main questions that chemistry allows us to answer. One of these is the question of chemical identity: What is this substance?The chemical thinking learning progression holds the promise of guiding the coordination of teaching, instructional resources, and assessment through illuminating the many ways in which students develop productive approaches to practicing chemistry. We recognize that progress in learning follows a complex and dynamic landscape that depends on many variables, including the experiences a student has had and the context in which a student is engaging in the practice of chemistry. We consider that a major role of the teacher is to interpret ways that students are using chemical thinking, and respond to what is productive in these ways, in order to help guide students to gain access to and proficiency in more scientific ways of thinking (Thompson et al., 2013; Robertson et al., 2016; Clinchot et al., 2017). Taking this into consideration, we follow an approach developed by Acher and Arcà (2014), to organize our analysis around three elements that can aid in the design of teaching, instructional resources, and assessment: (1) students’ ideas, (2) how these ideas are contextualized, and (3) teaching acts that can promote and sustain students’ gradual accumulation of ways of thinking. This study presents students’ ways of approaching substance characterization problems in 16 contexts. From these, we draw conjectures about teaching acts that can promote learning.
In this study, we build upon our prior work (Ngai et al., 2014; Sevian and Talanquer, 2014) in which we clarified the first design element of Acher and Arcà (2014), articulation of students’ intuitive ideas, through a review of the history and philosophy of chemistry, and a synthesis of students’ ideas across a wide variety of research on students’ thinking about chemical substances. These are reviewed below as the knowledge bases of substance characterization. Our characterization of knowledge bases fits with our perspective on learning that underlies the hypothesis of this study, that the knowledge bases brought to learning and reasoning are accumulated and become more qualified as a person's reliance upon them grows more sophisticated. We also pay attention to more general knowledge bases, i.e., science classroom activities and life experiences outside school. We make use of an instrument, called the chemical substance inventory survey (Ngai and Sevian, 2017), that provides material contexts, the second design element of Acher and Arcà, in which students’ ideas are articulated. Our purpose is the same as theirs: we strive to “inform our LP by examining the extent to which different materials and their manipulations provide a fruitful phenomenological anchorage to support – or to limit – children in generating, using, and revising the different forms of articulated ideas” (Acher and Arcà, 2014, p. 492).
Within the third design element, teacher acts to promote learners’ articulations of ideas through reflection on doing chemistry and thinking with these ideas, we base our work on an assumption that is central to our collaboration with teachers in developing the chemical thinking learning progression (Szteinberg et al., 2014; Banks et al., 2015; Clinchot et al., 2017). Our assumption is that students are more able to make sense of phenomena when teachers advance students toward the scientific view in ways that places responsibility on students for doing the sense-making. This motivates the implications of this study, which are focused on deriving from our findings some hopefully productive teaching acts that would advance students’ chemical thinking. Learning progressions are studied in cycles of validation (Mohan et al., 2009; Sevian et al., 2014), and these implications then create hypotheses for a future study cycle in the research.
Knowledge bases in substance characterization
While substance characterization is highly complex, depending on many variables of the substance under study and a wide variety of experimental methods, reporting on the characterization of chemical substances has been highly conserved throughout the history of chemistry (Schummer, 2003). The characterization of a chemical relies on the idea that every substance exhibits at least one property that makes it unique and differentiable from other substances (Enke, 2001). Over the past centuries, substance characterization reported in the chemical literature has consistently included the method of preparation, visual characteristics, solubility in various solvents, melting or boiling point, elemental analysis, and exemplary reactivities. Chemical structure was added to this only recently, as spectroscopic methods in chemical analysis offered the ability to differentiate structure from composition. Most research reports of substance characterization still include all of these items. The activity of substance characterization relies mainly on ways of identifying and differentiating chemical substances, which we have called chemical identity thinking (Ngai et al., 2014). In practicing chemical identity thinking, both chemists and students of chemistry use properties of a sample to identify potential classes to which the substance may belong, and/or to differentiate it from other substances in order to rule out possible identities.To better understand the chemical identity thinking of learners, we conducted an extensive review of research on how students think about substances (Ngai et al., 2014). The review resulted in a hypothesized learning progression of chemical identity, which organized the ways that students’ ideas about substances appear to accumulate with training in the discipline of chemistry. The hypothetical progression clarified four main ways of thinking, or knowledge bases, on which people may rely as they make decisions about chemical identity:
• Objectivization is the use of object-relevant properties to differentiate materials.
• Principlism relies on the explanation of properties of matter by referring to the presence or absence of ‘principles’ that carry those properties.
• Compositionism is the consideration of substances as mixtures of atoms-elements that each bear characteristic properties.
• Interactionism is a view of properties of matter as emergent from dynamic interactions among components of the matter.
It is important to recognize that each of these knowledge bases is relied upon in different circumstances by experts, who are able to qualify their reliance on the various assumptions they make while reasoning. For example, an expert chemist may identify a brown upholstery material on a sofa as a synthetic polymer, rather than leather cowhide, based upon its shininess, smell and tactile feel, which are object-relevant properties belonging to the objectivization knowledge base. The chemist knows that, in contrast to a synthetic polymer, leather contains an enormous variety of different substances (compositionism) and has been through a treatment process that alters the surface by chemical means (interactionism), leaving residues that contribute a characteristic odor that is carried by each residue (principlism). Thus, the chemist could consider other ways to identify the upholstery material (e.g., characteristic reactivities or elemental analysis of a sample), but it is simpler and probably sufficiently accurate to rely upon object-relevant properties. A novice chemist may perform the same objectivization-based identification of sofa upholstery material as the chemist does without recognizing why this way of thinking is justifiable or having access to other views.
Chemical substances inventory (CSI) survey
The activity of substance characterization relies on ways of identifying and differentiating chemical substances. The CSI survey was based on our hypothesized learning progression of chemical identity, and designed to capture how students identify and differentiate chemical substances (Ngai and Sevian, 2017) in substance characterization problems. The instrument was developed through a design-based process involving multiple stakeholders and was based on our hypothesized learning progression of chemical identity (Ngai et al., 2014). A rigorous qualitative approach involved students, teachers, educational researchers, and disciplinary experts as stakeholders to develop a suite of four classroom formative assessments that ask students to identify and differentiate chemical substances in different contexts. These were shown to be valid and reliable in use with students from grade 8 (age 13) through fourth year of university education.The CSI survey includes four sets of problems (sets A, B, C and D). Each set presents four problems that involve substance characterization: two in which a substance must be identified (odd-numbered problems), and two in which substances must be differentiated (even-numbered problems). All 16 problems are summarized in Table 3. These are problems, rather than questions, by our earlier definition. The CSI survey problems are ill-structured. There are many possible correct answers, which depend on the assumptions and outside knowledge that the problem solver considers relevant. For example, in problem B-Q2, there are many answers to what may be in the bubbles that form when water boils. Certainly there are water molecules in a vapor state. There is also a relatively large amount of empty space between molecules in the bubbles. If the problem solver assumes that it is tap water, it is also valid to say that there could be molecules of oxygen, nitrogen, and carbon dioxide that are likely present in tap water.
| Type of problem | CSI survey set A | CSI survey set B | CSI survey set C | CSI survey set D |
|---|---|---|---|---|
| Q1. Substance identification | AQ1 (silver): How could you determine if a light gray metal earring is silver? | BQ1 (water): How could you determine if an unidentified transparent liquid in a glass is water? | CQ1 (caffeine): What would you tell a person who would like to recognize caffeine? | DQ1 (white crystals): How could you determine if some white crystalline granules on the table in front of you are sucrose (table sugar)? |
| Q2. Substance differentiation | AQ2 (silver earring): A silver earring that was found months after being lost is now dark gray/black. Is it still silver? | BQ2 (water boiling): What is in the bubbles that form when you heat a pot of water and it begins to boil? | CQ2 (caffeine sources): Caffeine is present in many plant seedlings and acts as a pesticide to discourage insects from eating the unprotected plants. Is caffeine found in seedlings the same as or different than caffeine found in energy drinks, such as Red Bull? | DQ2 (heated sucrose): You take some sucrose and heat it over a flame. It turns from solid to liquid and has a brown caramel color. Is it still sucrose? |
| Q3. Substance identification | AQ3 (chlorophyll): Explain to a classmate what chlorophyll is. | BQ3 (gas cylinder): If you have an unlabeled cylinder filled with a gas, how could you determine if it is oxygen gas? | CQ3 (metal block): What could this object be made of? (shown a photo of an irregular shaped shiny gray metal block with texture) | DQ3 (ethanol): How could you determine if an unidentified transparent liquid in a glass is ethanol? |
| Q4. Substance differentiation | AQ4 (chlorophyll sources): Is the chlorophyll isolated from a forest tree the same or different from chlorophyll from pond algae? | BQ4 (oxygen vs. carbon dioxide): How could you tell the difference between carbon dioxide and oxygen gases? | CQ4 (soda can): Could this object be made of the same substance or a different one? (shown a photo of a metal soda can with no label, and referring to photo in CQ3) | DQ4 (ethanol boiling): What is in the bubbles that form when you heat a pot of ethanol and it begins to boil? |
Research questions
This study examines the following research questions and sub-questions:1. What, if any, epistemic games appear to be relied upon by individuals as they solve a variety of substance characterization problems?
1a. What is the structure of each epistemic game?
1b. What is the ontology of each epistemic game? Specifically, what knowledge bases, epistemic forms, and epistemological commitments are relied upon in each game?
2. What patterns emerge in the epistemic games relied upon by students?
2a. In what ways does the use of epistemic games change across educational levels?
2b. In what ways do different epistemic games appear to depend on the material contexts of the problems?
Answering these research questions allows us to advance a cycle in the learning progression research by taking into consideration the three design elements of Acher and Arcà (2014). In this cycle, we refine our understanding of students’ ideas, clarify ways in which material contexts shape and constrain the articulation of those ideas, and derive new hypotheses about teaching acts that may support students to strengthen their chemical thinking.
Method
Sample
The sample included middle and high school students from multiple schools in an urban public school district, and undergraduate students enrolled in first-year chemistry, organic chemistry, and physical chemistry courses at a public university in the same city in the Northeastern United States. The student populations served by these educational institutions is diverse. In the school district, 32% identify as African American/Black, 9% as Asian, 14% as Caucasian/White (non-Hispanic), 42% as Hispanic/Latinx, and 3% as other races or ethnicities. (Note: Latinx is gaining usage in research literature. It is a gender-neutral form, where the -x is written in place of the -o/-a masculine or feminine forms of adjectives in Spanish and Portuguese.) At the university, 15% identify as African American/Black, 12% as Asian, 38% as Caucasian/White (non-Hispanic), 12% as Hispanic/Latinx, and 23% as other races or ethnicities. Since a sampling of CSI survey participants was interviewed, and almost all students in the classes visited in the primary study participated in the study, it is expected that the participant demographics reflected the demographics of the schools and university.As described previously (Ngai and Sevian, 2017), the CSI survey was administered via computer-based platform (GoogleForms). Students were asked to select their birth month, then an algorithm matched each of the four survey sets to three birth months. While evenly distributed, this is not random because there was not an equal likelihood of a student receiving any of the four surveys. Limitations could arise if students born in particular months had educational advantages over students born in other months, or if the reader gives credence to astrology. Participants at the middle and high school levels participated in interviews immediately after completing the CSI survey. While students were not randomly sampled, an effort was made to create an unbiased sample. Students were invited to interview as the interviewer became available and as students completed the survey on which the interview was based. In each class of 15 to 30 consented students, between 2 and 4 students were interviewed. There was no element of selection other than when the interviewer was available, and in this way a sampling was produced across the range of times that the students took to complete the survey. University students in general and organic chemistry courses completed the survey at the conclusion of their laboratory period and were similarly interviewed with this approach immediately afterward. Physical chemistry students were also invited across survey completion times to interview and signed up for pre-determined times since the course did not have a lab component. Most interviews of these students were completed the same or next day and all were completed within three days of completing the survey. The study was carried out as a secondary analysis (further described below), using interview and survey response data from a primary study (Ngai and Sevian, 2017). All students aged 18 and older consented to participate, and students under 18 assented with parent consent (UMass Boston IRB protocols 2012-102 and 2012-133). The participants’ voluntary informed consent covers the present analysis.
Middle and high school participants were from the classes of many teachers in a variety of schools. They were interviewed during their science classes. For this reason, some students may have privileged science ways of talking. However, since students came from multiple classes and schools, they did not have common science lessons. The university students were enrolled in the same courses, i.e., first-year university chemistry, organic chemistry, and physical chemistry. During the data collection weeks, the first-year chemistry students were engaged in laboratory activities about density and stoichiometry, and the organic chemistry students were isolating products and learning to measure melting points of crystalline samples. These students may have privileged laboratory procedures they recently did when solving substance characterization problems.
The secondary data were assigned codes that corresponded to the course in which the data were originally collected (M = grade 8 science, H = grade 10 or 11 chemistry, AP = Advanced Placement Chemistry in high school, F = first-year university general chemistry, R = university organic chemistry, and P = university physical chemistry) and a four-digit number reflecting a random ordering of transcripts at each educational level (code numbers were originally generated as four-digit random numbers when students submitted surveys). Table 4 summarizes the numbers of participants included in the secondary analysis, organized by educational level and CSI survey set. Each participant shown in the table was interviewed about all four problems in the survey set, so the total number of problem-solving instances analyzed was four times the numbers shown in Table 4.
| Course and educational level | CSI survey set | Total | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Grade 8/middle school science (M) | 0 | 1 | 4 | 2 | 7 |
| Grade 10 or 11 chemistry (H) | 2 | 3 | 1 | 3 | 9 |
| Advanced placement chemistry (AP) | 2 | 2 | 1 | 2 | 7 |
| First-year university general chemistry (F) | 4 | 4 | 1 | 2 | 11 |
| University organic chemistry (R) | 3 | 2 | 2 | 3 | 10 |
| University physical chemistry (P) | 2 | 2 | 3 | 1 | 8 |
| Total | 13 | 14 | 12 | 13 | 52 |
Secondary analysis
This study was carried out as a secondary analysis of interviews and survey responses that were collected for investigating the validity of the CSI survey (Ngai and Sevian, 2017). Secondary data analysis typically introduces two issues. The first of these is the validity of the use of data beyond the primary study (Heaton, 2008). De-identified interview transcripts and typed CSI survey responses from 52 participants in six courses across a nine-year educational span (grade 8 through fourth year of tertiary education in chemistry) were obtained through informal data sharing (Heaton, 2008). The de-identified transcripts were produced from audio-recorded interviews of the sample of students who participated in the CSI survey when it was administered during science classes in 2016. The interviews followed a semi-structured protocol, initially asking participants to explain their written answers on the CSI survey. This allowed the interviewer to probe any new thinking that arose during the interview that was not in a participant's initial survey responses. Though probing for problem solving was not the primary purpose of the interviews, the transcripts were rich in explanations that involved reasoning to support participants’ initial responses to the CSI survey, as well as new ideas that participants introduced during the interviews. Since the primary study was carefully planned, including semi-structured interviews with a sample of students, with students’ reasoning explained during the interviews, we anticipated that the data would be sufficiently rich to support a secondary study of problem solving processes.A second issue typically introduced in secondary data analysis is the ethics with respect to maintaining anonymity of the participants (Heaton, 2008). The interviews were conducted by the first author of the primary study (Ngai and Sevian, 2017). One author of the secondary study was involved in the primary data analysis at the point where the analysis reached a meta-level. She did not interact directly with the interview or survey response data during the primary study, nor was she involved in the interview data collection. The researchers in the secondary study did not have access to any documents that would link individuals with their respective interviews, thereby maintaining anonymity of the participants for secondary analysis.
A potential limitation with this secondary analysis is that the researchers who analyzed the data were not present for the data collection. Often in qualitative research, there is knowledge that only the interviewer learns while conducting the interviews. Some of this may remain implicit and unacknowledged by the interviewer, but could influence the analysis in a positive manner. In the case of this study, this possibility is diminished, though not altogether extinguished, since the interviewer followed a protocol designed to pursue students’ explanations of their answers to the CSI survey and did not explicitly question the students about their epistemological beliefs.
A related point that may be considered with the secondary analysis is that epistemology was not directly probed during the interviews. Researchers studying metacognition, which is linked to epistemology, have consistently reported that metacognition is not directly observable (Sperling et al., 2002) and self-reporting is unreliable (Schraw and Moshman, 1995). Specifically, researchers acknowledge that when students are asked to self-report their metacognitive strategies as they are performing, they can be triggered to rely upon the strategies they identify. However, they may espouse these strategies for reasons other than actually relying upon them in that moment, e.g., perceiving that a particular strategy is generally beneficial or demonstrates a certain level of quality. In other words, self-reporting that is not retrospective runs the risk of inducing socially desirable behaviors (Veenman, 2012). Thus, the fact that the interviews did not probe epistemology is a strength of our study design.
Data analysis approach
Directed content analysis was employed in analyzing the data because the existing model of epistemic games was used to interpret the phenomena (Hsieh and Shannon, 2005). Additionally, directed content analysis can offer supporting or non-supporting data for a theory, as well as statistical analysis of the codes (Curtis et al., 2001), which we anticipated might be useful in testing the hypothesis associated with the second research question. The prior research by Tuminaro and Redish (2007) allowed us to begin by identifying key concepts or variables as initial coding categories (Potter and Levine-Donnerstein, 1999).The original interview transcripts were divided into the four problems included in each interview, and these were considered as episodes of problem solving. The student's typed survey responses to that problem were added to the beginning of each problem-solving episode, since the interviewer frequently repeated specific words written by the participant on the CSI survey to begin each interview segment, and then the participant additionally referred to what was written but sometimes without providing enough information to identify the reference. In some cases, the participant brought up new ideas that were not in the participant's original CSI survey response. When these were tied to the student's problem solving, this information was retained in the problem-solving episode. Toward the end of the interview about each problem, the interviewer often asked, “Is there any other information you would like to know in order to decide whether or not it's the same substance?” In four of these instances, the student started talking about an entirely new idea that was not related to the problem. In these four cases, this latter part of the interview was not included in the problem-solving episode analyzed. In addition, in one of the four problems about which one student was interviewed, the student said, “I don’t know, I just made it up,” and then concluded the interview. This student engaged in the interview on the three previous problems. The first three problem-solving episodes of this student were analyzed, but the fourth was not. In total, we analyzed 207 problem-solving episodes from 52 students (see Tables 3 and 4).
Both authors independently analyzed all data. We compared results and discussed disagreements until reaching consensus. We did this in stages that included increasingly larger numbers of problem-solving episodes. We randomly selected sets of problem-solving episodes (initially 5 per set, and then later larger sets) by sorting in numerical order the code numbers of the participants. With each, we identified the cue(s) the participant took from the problem, the knowledge base on which the student appeared to rely, and the sequence of moves associated with the problem solving approach, and we characterized the epistemic form that the student seemed to generate while solving the problem. We frequently found that students seemed to solve a problem that was different from the one originally posed. This often occurs when people rely on heuristics to answer questions and solve problems (Talanquer, 2014), so we also began clarifying the alternative problem solved in these cases. We gave tentative names to sequences of moves that recurred in students’ problem-solving approaches. As we proceeded, we regularly convened meetings of a group of five other chemistry education researchers who were asked to analyze two problem-solving episodes according to our process. In doing so, we developed a form of construct validity (Dalgety et al., 2003) in which we aimed for coherent and consistent operationalization of the theoretical constructs of epistemic games in our analysis of the problem-solving episodes. These perspectives sometimes generated new ways of considering the students’ problem solving. In particular, through these perspectives, we began to realize that there was a general epistemological framing that seemed to govern students’ overall approaches, thus we also began to identify and justify overall epistemological framing as either “doing the lesson” or “doing science” (Jiménez-Aleixandre et al., 2000). After the first 10 inter-rater sessions between the authors, a consistent set of candidate epistemic games emerged. From this point, we selected larger sets (10, 20, 40) for independent analysis and inter-rater discussions. We continued to bring problem-solving episodes to group meetings with others to strengthen the construct validity.
After all data had been analyzed and the epistemic games were stable and sufficiently characterized, one of the authors re-analyzed all of the data without looking at the original consensus agreements. During this phase, consistent metadata were generated for each problem-solving episode in order to facilitate comparison for later consistency checking. The metadata had the following components: participant and problem code (e.g., R10B-Q4), narrative of student's approach, cue, alternative problem (if any) that the student appeared to translate (Talanquer, 2014), general knowledge base (e.g., personal experience, chemistry laboratory), chemical identity knowledge base (Ngai et al., 2014), description of the epistemic form that aided the student's solution of the problem, epistemic game that best fits, organization of the narrative into the moves of the game, and justification (if any) for why this game was the best fit and why other potential fits were rejected, and epistemological commitments with justification. To illustrate this, the metadata from an example, R10 solving B-Q4, are provided in the Appendix.
After reaching consensus on all of the data, we considered the different epistemic games, interrogating their uniqueness. Tuminaro and Redish (2007) found that each of their epistemic games exhibited structural and ontological stability. This phase of our analysis process resulted in merging a few of our candidate games into epistemic games that shared these stabilities when characterized in a more general way. This resulted in 6 unique games. However, one of them (which we called the Consult Authority game), in which students immediately stated that they would ask the teacher, professor, or Google the answer, and then upon prompting said that they had no other ideas, only occurred in 2 instances. Due to its infrequent occurrence in our data, we could not be sure it is a game consistently relied upon by students, so we do not report it in our findings. The remaining 11 instances were a combination of extremely short interviews in which the student gave very little information and we were uncertain how the student approached the problem, and longer interviews in which students seemed to provide data dumps of everything that came into their minds related to the problem, always using vocabulary that did not make sense to us (e.g., “Heating the substance would only change its physical state unless I'm boiling it in a water. Heating it means that I'm going to grill some sucrose on it. So it just, I tried to add because I don't, I'm not really sure when I learned that. It's just that I'm combusting a sucrose. I know that sucrose is a disaccharide, so I'm not sure if adding oxygen into it, it will reduce the sucrose into something else.” R06D-Q2). The only obvious commonalities among the approaches in these 11 instances was that students made associations to information they could say, they seemed to be performing for the interviewer, and we were unable to discern a consistent structure.
Limitations of our approach to understanding problem solving
Our aim in this research is to understand students’ problem solving as students learn chemistry. We are making a first attempt at this by studying individuals’ problem solving during interviews about chemistry problems. There are limitations in our approach, which relate to two differences. The first difference is that interviews are not classroom learning situations. The second is that we studied individuals’ problem solving, although we are interested in understanding how students solve problems in groups during classroom learning situations. Despite these differences, there is some evidence that our findings may shed light on our ultimate aim.Regarding the first difference, in an interview study, Russ et al. (2012) showed that students’ epistemological frames were influenced by their interactions with the interviewer and by their assumptions about what those interactions meant. Students make implicit assumptions about what knowledge the interviewer has and whether the interviewer is judging their understanding. Their findings correspond to the same general framings that have been found in classroom settings (Jiménez-Aleixandre et al., 2000; Hutchinson and Hammer, 2010).
Regarding the second difference, in this study, we have followed a path taken in mathematics education, in which the researchers first investigated individuals’ epistemological resources in approaching the solutions of diverse problems (Hershkowitz et al., 2001), and later tested their findings about epistemic games in ways that students solved problems in groups in the laboratory and then in classroom settings (Hershkowitz et al., 2007). In the latter study, the researchers found that “many times each partner constructed a piece of knowledge in her own way. Yet all three students in the group may have benefited from this multifaceted shared knowledge in their common further work, and may have continued to construct or consolidate constructs in follow-up and assessment situations, where the construct continued to have an individual flavour” (pp. 63–64).
Results
Epistemic games of substance characterization
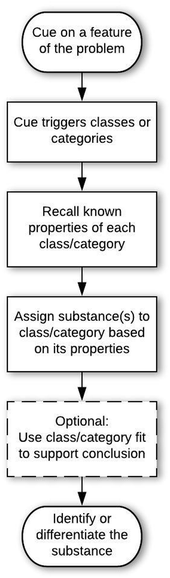
In answer to the first research question, analysis of the 207 problem-solving episodes resulted in 5 epistemic games that occurred with sufficient frequency to characterize stability in structure and ontology. These games occurred in the context of two general epistemological frames. An epistemological frame is an answer to, “What is expected of me in this situation?” The epistemic games are the patterns of activities (i.e., problem-solving approaches) that were activated in a coherent manner by students when solving the problems. In other words, epistemic games can be considered as more specific epistemological frames that answer the question, “How should I solve this kind of problem?” Although the 5 epistemic games occurred with consistent structures and ontologies, there were variations that depended on the general epistemological framing by the student. Thus, we begin by describing the two general epistemological frames we observed. After this, we describe the stabilized structures of the games (Research Question 1a), and then the stabilized ontologies (Research Question 1b).General epistemological framing
Two general epistemological frames were observed in the interviews. These corresponded to the same epistemological frames found by Hutchinson and Hammer (2010), as the “classroom game” and “making sense of phenomena”, and by Jiménez-Aleixandre et al. (2000), as “doing the lesson” and “doing science”, respectively. We have adopted the latter terminology. Our participants were interviewed during or after the students’ science (grade 8) or chemistry (all other educational levels) class or laboratory. The students first responded in writing to questions posed about four substance characterization problems, and then were interviewed about their responses. Many students appeared to respond to the situation (the lab or classroom, and an interviewer who could have appeared a few years older than them) by making implicit assumptions about science questions requiring science ways of answering, as well as about what the interviewer's judgments of their answers may be.There were often clear markers of students’ general framing. Students who framed the situation as doing the lesson tended to check in frequently with the interviewer about whether the answer was correct, and they expressed doubts about whether they were correct. Examples of this include:
• “I don’t want to say the wrong thing.” (H07D-Q2)
• “It is interesting, but since I got no idea what test I should run into, so I would say I’m not sure.” (R06D-Q4)
• “Oh uh well it says chlorophyll, which are in the chloroplasts.” (Interviewer responds: “Ok”.) “Are they?” (F04A-Q3)
Students operating in a doing the lesson frame also referred to authorities (what the teacher said, how the textbook shows a solution of the problem, or trying to recall the exact lab procedure they used in an experiment) and expressed scientific vocabulary that they did not appear to understand, often using many scientific words together in ways that made no sense, either grammatically or contextually. For example:
• “I just feel like you need to know what ethanol really is, so you need to do some background information on that, or you can have prior knowledge and just ask your professors and everything.” (F08D-Q3)
• “And there are no green things, hopefully the teacher has told you that it's no color. But what you look at a plant cell, there are bright green things and that you don’t need to inject it with like, you don’t need to have like, JFP?” (R04A-Q3)
• “Well, ethanol is mainly consists of carbon, hydrogen, and oxygen in this molecular formula. By heating it I might disturb the system there, it's either breaking the hydrogen bond or the intramolecular bond inside. So it is most possible that when you break down that molecule you only get half, either C–H or C–O bond so I think it's usually a bubble it is carbon dioxide in gas form. Because I did some enzymatic pass with something else, hydrogen peroxides, it is a CO2 and O2 gas.” (R06D-Q4)
In addition, students who framed their work as doing the lesson quite often positioned themselves outside of the problem, using “you” and “they” instead of “I” (Watkins et al., 2017).
In contrast, students who framed the situation as doing science tended to look for evidence in the problems that were posed and try to relate it to other experiences they had. Often, this co-occurred with explicit thinking aloud and reasoning through apparent contradictions. Examples of this include:
• “I guess maybe if you were isolating oxygen from two different things it would still be the same oxygen, um, but then the more I think about it I don't know how you could determine um what the chlorophyll came from just having the isolated material.” (F09A-Q4)
• “Silver, how we find it, before we do anything to it, in its natural state. I have never seen silver that way, so I don’t know what it's going to be like. But I do know that we talk about in class that elements can have different forms based on…is it ions or isotopes? I think it's isotopes, but it can have different… and I’m not sure how that rule applies to silver. But I know since they have different forms there, there is a possibility that it can appear naturally different in nature before we manipulate it.” (F19A-Q2)
Structures of the epistemic games
The 5 epistemic games are coherent problem-solving approaches that related to the problem at hand, answering the question, “How should I solve this kind of problem?” Each game had entry and exit conditions, with “doing the lesson” and “doing science” paths of moves that corresponded to the same structural components. Overall, 194 of 207 interview episodes were found to be described by the 5 games. One other game began to emerge, which we called the Consult Authority game. However, there were only two instances of this game, thus we could not consider it as having stable structure and ontology. The remaining 11 interview episodes were inconclusive, due to either having very few words by the student or utterances which we were unable to parse.H08 solved problem D-Q3 using the Compare game in a doing science frame. In this problem, the student had to say how to determine if a transparent liquid in a glass is ethanol.
Interviewer: You said, I could assume it's some sort of alcohol and like if it evaporates more rapidly compared to a glass of water filled with the same volume of liquid. Also, I could probably tell by the smell. However, I am not sure how I would tell if the liquid is specifically ethanol or not. Can you tell me what you were thinking here?
H08: I remember, alcohol, if you rub it on your skin, rubbing alcohol, it evaporates very quickly. So if, I didn’t know if the question was specifically asking if it's ethanol or alcohol. The only thing I could see if it was alcohol or not was seeing if it evaporates faster compared to water. Or usually, alcohol has that smell… [makes a whoosh sound]
Interviewer: A bad smell from the looks of it.
H08: Yeah, that strong like rubbing alcohol is really strong, nail polish has a unique smell, you could probably tell, but I didn’t know how to tell if it was exactly ethanol or any other kind of alcohol.
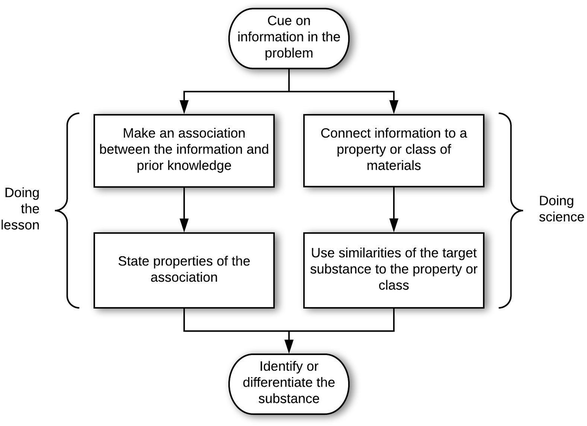
This high school student first cued on the “-ol” suffix on ethanol (entry condition) and noticed that this is in common with the class of alcohols (connection move). H08 then began recalling other properties belonging to the class of alcohols: they evaporate more rapidly than water, they have a characteristic (bad) odor. In the properties move, the student then considered other substances that belong to this class (rubbing alcohol, nail polish), and through this reasoned how to tell if the unknown substance is an alcohol (exit condition). Notably, the student also did more sense making in qualifying this by saying that it could be a different kind of alcohol.
In contrast to the productive epistemological framing of H08, the Compare game approach of R05 on problem A-Q4 manifested as doing the lesson. The A-Q4 problem asks the student whether chlorophyll isolated from a forest tree is the same as or different from chlorophyll isolated from pond algae.
Interviewer: You said the chlorophyll from the tree is the same as the chlorophyll from the algae and they should be the same as they both have the same function to produce energy through photosynthesis. So can you tell me how, like why that means they would be the same?
R05: I based it on animals, for example, my mitochondria should be the same as the mitochondria of a horse. Because I think we are equal. We have eukaryotic cells, so the structures will be the same.
Interviewer: Eukaryotic cells.
R05: Yeah.
Interviewer: Ok.
R05: So thinking about the structure of the cell between two plants, I think the structure is square. So, it's the same. The organization between the organelles should be placed in the same way. So I think everything should have the same shape and the same size.
Interviewer: Okay, and so if something has the same shape and the same size, that means it's the same?
R05: Yeah, I think so because it have the same name it should be the same thing.
Interviewer: Okay, so they wouldn’t be different from each other because they’re both called chlorophyll?
R05: No, they won’t be different they should be the same, must be the same.
R05 initially cued on the tree and algae (entry condition), and considered their chlorophylls to be the same because they have the same function. This commonality comes about through the association of chlorophyll to photosynthesis (connection move). The student then named this association: they both produce energy through photosynthesis. The student then turns to providing properties of the association as the properties move: in animals the mitochondria are the same, animal cells are eukaryotic so they have the same structure, the structure of plant cells is square, the organization of organelles is the same, shape and size are the same. The student concludes that the chlorophylls are the same (exit condition). R05 did not attend to any coherence between these properties.
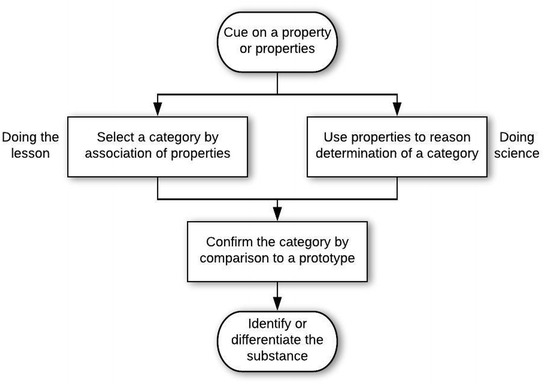
For R08, the experience of working as an electrician was salient to solving problem C-Q3, which provided a color photo of an irregularly shaped gray block and asked what substance it could be.
Interviewer: You said aluminum, I would speculate due to the color and shape. Aluminum is a very soft metal and it appears to have been broken several times in shape, which lead me to believe it is a soft metal. Can you tell me where this thinking is coming from?
R08: Yeah, you know I was an electrician and we use aluminum sometimes as a conductor instead of copper because it is cheaper and aluminum, we would, the applications that we would use to install it like if we were trying to terminate it you know in a lug nut and tie it down we would need to use different specifications because it is soft with the temperature it can expand or decrease. So that was my thinking, and I know also from cashing it in when you have scrap aluminum it's always thrown in the soft metal pile at the scrap yard. So that was the association I made and just looking at the surface of this image it looks like that it was cut one way to make it circular cut another way inside and then maybe scraped along the edges, which made me think that it was easy to shape and soft.
This student identified the color and shape of the block, and noticed that it appeared to have been broken several times (entry condition). From this, the student placed the block into a category of soft metals (category determination move), and then worked on confirming this through how aluminum is (category confirmation move): aluminum gets thrown in the soft metal pile at scrap yard, it cuts like a soft metal. Based on these, the student also generalized through these properties, e.g., speculating on how the object was cut based on evidence in the picture. Throughout this process, the student demonstrated back-and-forth sense making, sometimes expressing awareness of his or her thinking: “so that was the association I made” and “which made me think that it was easy to shape and soft”.
Some students also used the Prototype Mapping game with framing consistent with doing the lesson. For example, R10 followed a stream-of-consciousness approach to working on the problem, with an overall structure of mapping to a prototype.
Interviewer: You said, we could light a match and open the container and thrown the match in. If the fire increases, then it's oxygen. This is a very unsafe way to do it. Can you tell me more about what you were thinking here?
R10: You know oxygen is flammable, so you, for instance, if I was to light a match, and I put it over a container that is filled with oxygen and open the lid of the container, the match, the flame would definitely be increased so I guess that's all I put.
Interviewer: Okay, and how did you know that the flame would be increased?
R10: We did this, actually, in Chem I. We did this lab, so all this stuff that I’m sort of remembering back from general chemistry.
Interviewer: Okay, so you remember doing this somewhere else?
R10: The combustion also, so yeah… Like, um, you know in a car engine, so for example you have, when you’re driving it, it's taking the air and the engine combusts basically oxygen helps combusts, which I think would produce carbon dioxide.
The student cued on oxygen, then identified the property that oxygen is flammable (entry condition). This led the student to a category of fire (category determination move), as indicated by multiple associated words: light, match, flame. The student confirmed this (category confirmation move) through a lab performed in the Chem I course (in which testing for oxygen involves detecting whether a glowing splint glows more brightly when placed in a test tube where oxygen might be a product of a reaction), which the student generalized to lighting a match and putting it over a container filled with oxygen and then opening the lid of the container. This led the student to talking about combustion in a car engine, which the student seemed to consider as related to determining whether a gas in a cylinder is oxygen. Students who relied on this game in a doing the lesson frame often tended toward hyperbole in the last move, e.g., “because normally like the teachers, they're mad tired in the mornings and they always have a cup of coffee” (reasoning provided by H03 when solving problem C-Q1 about how to help someone recognize caffeine).
An example of multiple cycles is seen in the approach that F10 took to solving problem C-Q2, which presented the situation of two sources of caffeine, plant seedlings and energy drinks. Information was provided that caffeine present in many plant seedlings acts as a pesticide to discourage insects from eating the unprotected plants. In deciding whether the two caffeines are the same, F10 explained the following:
Interviewer: you said that the two caffeines would be the same, caffeine is the same in both because it is found naturally. The reason it acts as a pesticide is because just like sugar and dogs, some animals can't process it and can be harmful if consumed. Can you tell me a little bit more about what you were thinking here?
F10: Uh well I wasn't really sure if the caffeine was artificial or not that we had in our coffee, but I kind of figured that animals can't eat the same things we can, so in a diet where we would have caffeine it wouldn't kill us, cause it still increases our heart rate, it could do that same to an insect or a small animal and they just can't handle the capacity, and it would kill them.
Interviewer: I see, ok. Can you tell me what you meant when you said in plants, or it's found naturally and you weren't sure if it was artificial or not, the one that we drink, can you tell me what you mean by artificial and natural?
F10: Uh natural is like how it's found in nature, while artificial would be like whether we tampered with it, so that it would have a stronger effect or less effective, or if we actually made it in the lab.
Interviewer: Ok. Would that make the caffeine different?
F10: Uh, I think it would, mostly for the fact if you make it in the lab you can change certain aspects of the caffeine.
Interviewer: Ok, but it's still caffeine?
F10: Yeah.
Interviewer: Ok, so what sort of aspects do you think could change about the caffeine?
F10: Uh well they could make the caffeine stronger if they wanted to, so you wouldn't have to take such a big dose of it.
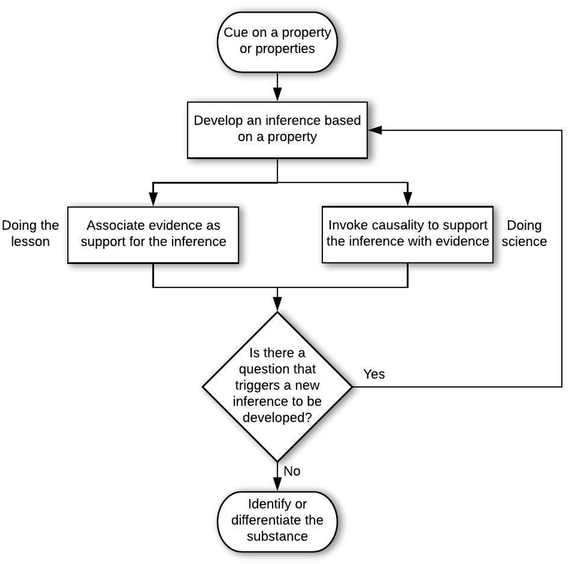
This interview continued with F10 additionally discussing whether “caffeine could be artificially replicated, such as artificial sugar, and this could make it so that the caffeine is changed for human consumption”. The excerpt above can be organized in to the cycles of inference shown in Fig. 4.
F10 supplies causal arguments for most assertions: animals cannot handle the capacity of increased heart rate, if caffeine is made stronger in the lab by changing certain aspects of it then you would not have to take such a big dose of it.
The Inference game was also employed by students using associative arguments. An example of this can be seen in the interview of M11 in solving B-Q4, which posed the problem of telling the difference between carbon dioxide and oxygen gas:
Interviewer: So you said I'm pretty sure that I couldn't be able to tell the difference between carbon dioxide and oxygen. I can tell the difference between regular air and gasoline, but I don't think that I could tell the difference between carbon dioxide and oxygen unless carbon dioxide also has a smell of pollution. So can you tell me what you were thinking here?
M11: I was thinking that I can't really tell the difference between carbon dioxide and oxygen, and I wasn't even sure if carbon dioxide had a smell to it. So I was wondering if I'm not sure, how can I know?
Interviewer: Yeah, ok. So that would make it difficult without a smell. Is there anything else that you think you might use to tell the difference?
M11: Hmm…I'd like to know more information on some differences between carbon dioxide and oxygen, other than what I already know. Something I could tell from afar.
Interviewer: Ok, why from afar?
M11: Because I'm not going to have my notes with me if I have to do some kind of test where I have to tell the difference.
Interviewer: Yeah, ok. And what sort of test might, do you think might be able to do, or you might like want to do?
M11: I don't know if I have to do some weird science test in the future, where I have to tell the difference and I can't really tell the difference.
M11 considered that there must be a difference between the gases in order to tell them apart, which is a sound basis for arguing about good differentiating characteristics of substances. The student also considered gases dangerous, therefore tests should be done from afar. The approach taken by M11 can be organized into the cycles of inference shown in Fig. 5.
The structure of M11's inference cycles is the same as F10's, but the arguments employed by M11 are associative. The difference in smell between oxygen and carbon dioxide is associated to the difference in smell between regular air and gasoline, and the next difference is associated to doing a test from afar. Both students substantiated claims with evidence, and each new cycle began with developing an inference from a property of the substances that arose in relation to a question that grew out of the just-completed cycle.
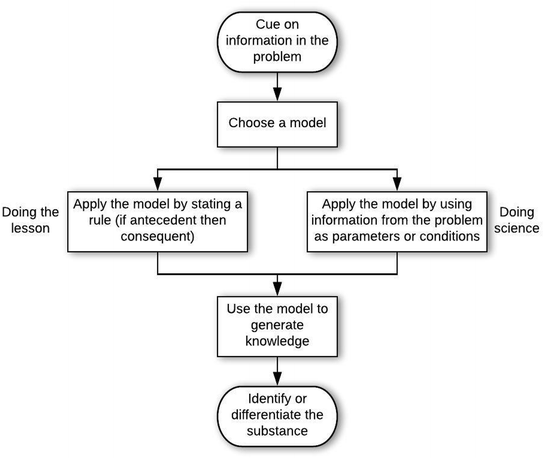
Students who used the Model-based Reasoning game in their approaches to problem solving more often demonstrated sense making (21 of 33 instances were doing science framing). The difference between manifestations of this game in doing the lesson vs. doing science was the way in which the model was applied. In the framing of doing the lesson, models were applied as rules (generally “if antecedent then consequent”), while in a doing science frame, students paid attention to parameters of the model and conditions under which the model was valid. The pattern of this game can be observed in the following doing science example, in which AP03 solves problem A-Q1, which asks how one may determine if a light gray metal earring is silver.
Interviewer: You said you would do a flame test on the earring, put it over a flame and record the color the flame becomes when it comes in contact with the earring. You could also make an electrochemical cell, one side has solution with ions that have a higher reduction potential than silver, and the metal of that ion. The other side has silver ions and silver metal. There must be a salt bridge connecting the two solutions, measure the voltage and find the cell potential of the earring. If it matches the cell potential of pure silver then the earring must be pure silver. So can you tell me what you were thinking about here?
AP03: Well I was just trying to see if it was silver, or maybe if it was silver like mixed with another substance.
Interviewer: And what made you think about doing the flame test and the electrochemical cell?
AP03: Well because I knew you could tell different metals cause of the color that the flame would get, and I forgot what color, I forgot if silver would give off a specific color and like what color it would be, but I figured I would just put it there anyway. And then for the electrochemical cell, because I don't know I just remember studying that and each element has different reduction potentials so we could measure the voltage and subtract the cell potential of the known one.
Interviewer: And how would the cell potential help you determine whether or not this is silver?
AP03: Um well I figured the total voltage of the cell, and then you would just subtract the reduction potential of the other metal like the one that's not silver, and if the answer you got matched the listed cell potential of silver then it would be silver, and if it didn't then it would be another thing.
The student's problem-solving process was aided by an epistemic form of a model cued by the word “metal” in the problem (entry condition). That the student cued on “metal” is evidenced by an initial thought of doing a flame test (which the student likely connected to an experiment in chemistry lab), which was quickly discarded in favor of the electrochemical cell model (choose model move). The student then described this model, in which s/he also indicated that it contains the oxidation and reduction half-reactions, along with the reduction potentials associated with each half-reaction. Next, the student reasoned that the silver earring can replace one of the electrodes in order to determine “the cell potential of the earring” in order to identify it (apply model move). The student's response to the interviewer's last question, about how the cell potential would help to determine if the earring is silver, confirms that AP03 is reasoning using the model (generate knowledge move) to solve the problem (exit condition).
Interviewer: You said this object is probably made of smooth material such as metal or granite, I think this is because the object does not seem to be from sediments due to its smooth look. I have prior knowledge that materials such as metal can be formed as a smooth solid. Can you tell me what you were thinking here?
M09: So it looks like a type of rock, and I know that there are different types of rocks, and one type are sedimentary rocks which are made of sand and stuff. And those are usually more bumpy and usually aren't smooth because of the sediments, and I also know that some people have granite countertops and like some things are made of metals and they can be like really smooth, and the top of the rock reminds me of that.
Interviewer: Ok, anything else that you were noticing as you were looking at this that was helping you to determine what it might be?
M09: Um it seems like the rock was cut, so maybe the material has, can't be that hard to cut through.
Interviewer: All right and is there anything you would want to know in order to figure out what this object is made of?
M09: Um where it came from, because the area of like a rock determines where it's made, and also the time it came from.
Interviewer: Ok, the time? How would the time help you?
M09: Because like fossils and stuff, you can determine the things inside and try to determine how the area was at that time.
As M09 is arguing about evidence for how the rock is composed, the view of substances is a compositionism view due to considering the substances as mixtures of particles that bear particular properties. The student's approach to solving this problem fits the Contrast game as follows: cueing on the object (entry condition), the student considers the object to be a rock, which triggers using the classes of sedimentary and not-sedimentary (cue trigger move). The student then composes sets of properties of each class (recall properties move). Sedimentary rocks are not smooth, made of sand and stuff, and bumpy, while not-sedimentary rocks have these properties: smooth, examples are metal or granite, and one can make countertops from it. M09 next assigns the object to not-sedimentary, based on it being smooth and not bumpy (assign substances move). Finally, the student uses the idea of geologic time to further support the conclusion that it is sedimentary rock (optional support conclusion move).
Ontologies of the epistemic games
In answer to Research Question 1b, stable ontologies were observed in some aspects for each epistemic game. The characteristic knowledge bases, epistemic forms, and epistemological commitments of the games are summarized in Table 5.| Epistemic game | Knowledge bases | Epistemic forms | Epistemological commitments |
|---|---|---|---|
| Compare game | General: daily life | Representation from a science lab experience or memory of a science lab | Science can explain the real world |
| Chemical identity: usually objectivization | |||
| Prototype Mapping game | General: lab or work | Experience, either from the lab or from other work (e.g., job, being a student) | Empirical results are trustworthy |
| Chemical identity: objectivization or compositionism | |||
| Inference game | General: wide range | Not easily discerned, could be different with each cycle | Science is about substantiating claims with sufficient evidence that irrefutability is reached |
| Chemical identity: all views observed | |||
| Model-based Reasoning game | General: chemistry | Abstractions representing systems, events, or processes | Models can explain and predict empirical data |
| Chemical identity: all views observed | |||
| Contrast game | General: chemistry | Visualizations of particle level, or unique properties (surface features if doing the lesson, characteristic properties if doing science) | Science is built on consistency |
| Chemical identity: all views observed, but objectivization and compositionism most prevalent | |||
Students who relied on the Compare game nearly always combined an epistemic form associated with a chemistry course and a general knowledge base associated with daily life. Examples of epistemic forms included representations from science courses, such as biological mechanism process diagrams, molecular structures, and an infrared spectroscopy diagram with typical ranges of particular bond types labeled. Epistemic forms also included specific memories from daily life, such as holding a bottle of water and a health safety sign on the wall, or memories from science labs, such as a piece of steel wool used in an experiment and bubbles fizzing in a test tube. The chemical identity knowledge base was nearly always objectivization (27 of 31 instances). For example, when H08 solved D-Q3 (transcript above in Compare game description) s/he relied upon objectivization, although appearing to know a fair amount of chemistry. H08 paid attention to explicit features (the chemical name spelling, faster evaporation) and invoked similar aspects of the epistemic form (odor, sense of coldness). Similarly, R05 (described above in Compare game structure) relied on an objectivization view of substances, focusing on shape and size (square, organization) as well as functional usage (producing energy).
The Compare game rests upon an epistemological view that science is capable of explaining the real world. It was typical for students operating in a doing science frame to seamlessly blend chemistry language with daily life language, indicating a level of comfort with connecting knowledge from these two worlds. For example, H08's epistemic form was an experience in chemistry lab with rubbing alcohol on the skin and feeling the rapid evaporation (although the student did not say this, we know that this specific activity is in the curriculum used in this school district, so it is likely the student had experienced this), but the student also connected this science experience with daily life (e.g., the odor of nail polish). Students in a doing the lesson frame also put together knowledge from daily life and science to explain the real world. For example, R05 drew a parallel between how human and horse cells both have mitochondria, thus are eukaryotes, and how plants have square shapes, thus they are plants. The student applied this parallel to explain how chlorophylls from different sources must be the same.
Common to all of the observed instances of the Prototype Mapping game was students’ reliance on an experience as the epistemic form. Students referred to experiences in their jobs or their parents’ jobs, such as working at a car dealership, and in the laboratory, such as measuring density of polystyrene spheres in the general chemistry lab. There was consistency in an epistemological commitment that empirical results are trustworthy (see Appendix for an example). Students who approached problems as Prototype Mapping mainly relied on an objectivization (38 of 50) or compositionism (10 of 50) view of substances as they identified and differentiated substances.
The Inference game relied on an epistemological commitment of substantiating claims with evidence. An underlying goal of reaching irrefutability seemed to drive students to continue substantiating claims with evidence as they pursued new inference–evidence–questions cycles (see Fig. 4 and 5 for examples). Students used a wide variety of knowledge bases, often different with each cycle of inference. Likewise, the epistemic forms that aided students are not easily discerned. For example, F10 (whose logic is shown in Fig. 4) may have been thinking of a stimulant-effect diagram learnt in biology for one cycle, and M11 (whose logic is shown in Fig. 5) may have been imagining being the actor in a weird science show for one cycle. In general, the epistemic forms of students who employed the Inference game were difficult to discern. This may be because the path depends on whatever is in the evidence brought to each cycle's argument, so all the cycles may not connect to a single epistemic form.
The epistemological commitment common to instances of the Model-based Reasoning game was that models can explain and predict empirical data. In our data, students relied on all four chemical identity knowledge bases: objectivization (9 of 33), principlism (4 of 33), compositionism (13 of 33), and interactionism (7 of 33). Models exist in all of these knowledge bases, so this makes some sense. The models themselves served as the epistemic forms that aided students’ problem solving. For example, AP03's epistemic form was an electrochemical cell diagram typically used in teaching this topic, with two half-cells as beakers full of labeled 1.0 M solutions, a labeled metal electrode in each beaker made of the same metal whose metal ion is in the solution, a salt bridge, and electrodes connected by a wire with a voltmeter.
Students’ Model-based Reasoning games were all aided by epistemic forms which were abstractions representing systems, events, or processes. These models took various forms, such as chemical equations, free energy diagrams, molecular structures of various sorts (e.g., structural, ball-and-stick, blobs with features), labeled diagrams, imagined molecular dynamics simulations, protein-binding specificity, and mathematical equations. AP03's epistemic form of an electrochemical cell was more mathematically based, but other students’ epistemic forms were based on structure. For example, R08's problem solving appeared to be supported by an epistemic form something like the model shown in Fig. 8. In problem C-Q2, this student said that the two caffeines (in plant seedlings and energy drinks) would be the same because “the physical characteristics that make caffeine a stimulant also make it a deterrent for insects”. The interviewer asked the student to tell her more about this, to which the student answered: “Yeah, I started to think about it on a molecular scale. And I know that the shapes of molecules really affect their function and their purpose. So, when I think about caffeine and its effects on a person as a stimulant, or just as a stimulant, I assumed it had something to do with the shape. And for the same reasons that it's a deterrent, I assumed that it had something to do with the shape. And now the more that I think it through, maybe it's different qualities of that shape or structure that give it those two different functions, but that's where my mind was at.”
 | ||
| Fig. 8 Inferred epistemic form in R08's solution of C-Q2: the molecule has various features, each maps to a different function. | ||
All four chemical identity knowledge bases were used in the Model-based Reasoning game, which may stand to reason as different models can be tied to different assumptions about substances. For example, R08, in the problem described just above, relied on compositionism in relating how different components of the molecule would render different functions. Another student, R09, when solving the same problem relied on interactionism to reason about protein binding: “I was thinking because it is a neurological agent, it has to bind to some sort of protein usually, and by the nature of proteins they require extremely specific functions in order for them to work otherwise the substrate just won’t fit or it just will fit differently and then it doesn’t work… a bond line representation of it would be useful since it would allow the identification of any chiral centers thereby illustrating any possible alternate structures. Optical data from caffeine extracted from both natural and synthetic sources would also aid in pointing out any structural differences. It's about the specificity.”
When students approached problems with the Contrast game, they did so with an epistemological commitment that science is built on consistency. As in the Model-based Reasoning game, students who used the Contrast game also relied on the full range of knowledge bases about chemical identity, but with more objectivization than any other: objectivization (23 of 33), principlism (2 of 33), compositionism (7 of 33), and interactionism (1 of 33). The epistemic form of about half the students was lists of properties belonging to each class. Students who framed their work as doing the lesson almost always listed surface features of classes (e.g., color, odor, how it makes one feel), whereas lists in doing science often included implicit features (e.g., oxidation states, functional groups implied by chemical name).
Many students who approached the problems with the Contrast game were aided by epistemic forms that were visualizations or models at the particle level. For example, in solving a problem of how to differentiate between oxygen and carbon dioxide, P08 relied on an interactionism view of chemical identity, and was aided by an epistemic form of energy states of different particles (“nature tends toward lower energy states” so “this particle would rather be carbon dioxide”). As another example, AP08 relied on a compositionism view of chemical identity in reasoning about why caramelized sucrose is the same substance as crystals of sucrose: “it's still the same substance, it's just that for example like an H2O molecule would break from an H2O molecule. I think when I was thinking of this question I was thinking the Hs would separate from the Os, like as an example, but it's still the same substance”. M09 (whose interview is given in the Contrast game structure above) also had an epistemic form that was a visualization of different types and arrangements of “particles” in sedimentary and metamorphic rock. Considerable evidence in the literature suggests that many students at this age consider particles to be granular (cf.Talanquer, 2009).
Students also solved problems with reference to unique properties of members of classes being contrasted. Some epistemic forms took shape as logic flowcharts. For example, as P07 solved problem D-Q1 (how to tell if some white crystals are sucrose), this student also used the word “definitive” and proposed a series of tests to narrow toward a more definitive conclusion about the identity, recognizing that “it couldn’t be definitive but it could be very very probable”. The tests described by the student seemed to be envisioned as a flowchart (Fig. 9), with classes as sucrose and not-sucrose, which were increasingly specified by more additions to the sets of properties that these tests would reveal.
 | ||
| Fig. 9 Inferred epistemic form in P07's solution of D-Q1: a series of tests to narrow toward a more definitive identification of sucrose. | ||
Patterns in epistemic games observed
Table 6 presents a summary of which games were observed at different educational levels. As noted earlier, 13 of the 207 episodes did not fall within the 5 games reported. To provide further detail, for the games that occurred in both the doing the lesson and doing science general framings, Table 7 breaks these out by educational level for which frame was assumed.| Epistemic game | M | H | AP | F | R | P | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lsn | Sci | Lsn | Sci | Lsn | Sci | Lsn | Sci | Lsn | Sci | Lsn | Sci | |
| Compare | 2 | 4 | 2 | 2 | 1 | 2 | 2 | 1 | 4 | 4 | 3 | 4 |
| Prototype Mapping | 4 | 3 | 5 | 0 | 4 | 2 | 12 | 5 | 8 | 4 | 4 | 4 |
| Inference | 2 | 4 | 1 | 7 | 4 | 2 | 7 | 3 | 1 | 3 | 2 | 6 |
| Model-based Reasoning | 0 | 1 | 2 | 3 | 3 | 2 | 2 | 6 | 2 | 7 | 3 | 2 |
| Contrast | 2 | 4 | 4 | 5 | 2 | 4 | 1 | 3 | 1 | 4 | 2 | 1 |
| Total | 10 | 16 | 14 | 17 | 14 | 12 | 24 | 18 | 16 | 22 | 14 | 17 |
Several findings about the patterns of epistemic games relied upon by students at different educational levels (Research Question 2a) can be inferred from the results in Tables 6 and 7. First, as seen in Table 7, all games are used by students at every educational level. Across all the data, 51% of students had an overall epistemology of doing the lesson, while 49% were doing science, and as can be seen in Table 7, this split was present in all games at all educational levels. On average, participants relied on a mean of 2.83 (SD 0.68) games across 4 problems. Two participants used only one game, 11 used two games, 33 used three games, and 6 used four games. Beyond descriptive statistics, the numbers of participants and conditions are too small to support further statistical analyses.
When examining the reliance on different games across educational levels, some trends appear. A clear trend is that the Model-based Reasoning game grows in across educational levels. Students are introduced to more models as their training in science progresses, and if students have access to more models on which to rely, they may find more relevance for models in solving problems. The Inference game meanwhile remains mostly steady across all educational levels, and the Contrast game diminishes. The Inference game is closest to claims–evidence–reasoning argumentation patterns that are explicitly taught in many science courses, which may explain students’ steady use of this game.
The Contrast game is a basic approach to solving problems that is taught from very early years of education, and it is surprising to see it diminish in prevalence. It appeared that a more sophisticated approach to using the Contrast game, as sets of properties connected to tests as in a flowchart (see Fig. 9 for an example of P07's epistemic form in solving D-Q1) emerges only later as a variation on the Contrast game. In our data, we only saw the flowchart as an epistemic form in the Contrast game at the highest educational levels, when students composed classes as sets of properties connected to various tests that could be performed. At lower educational levels, the properties of classes in the Contrast game tended to include extensive or functional properties. For example, M11 relied on an objectivization view of chemical identity to solve problem B-Q1 (determining whether the liquid in a glass is water) by creating two classes, water and not-water, and relying on explicit properties: “water doesn't really smell, it doesn't have a definitive thing about it, so if it was something definitive then I would decide that it might not be water and probably not taste it… tasting would help me because if it had a strong taste then it would probably not be water, and if it had somewhat of a bland taste then it would probably be water”.
Other trends are more difficult to rationalize. These include that the Compare game is in high use in middle school and in later years of university education, but dips in use through high school and first-year university. Prototype Mapping may have some unique relationships with the courses in which students were enrolled. In particular, this was the game most relied upon by far of students taking organic chemistry, which could be due to substance characterization being a consistent activity in many of the laboratory experiments typically conducted in organic chemistry, and students likely can recall easily their recent experiences.
Table 8 shows the epistemic games organized by problem, as a heat map to assist interpretation. In relation to Research Question 2b, different material contexts appeared to evoke different games. This can support implications for which contexts may be most useful for teachers to use when trying to guide students to develop versatility in the epistemic games on which they rely. For example, Model-based Reasoning was the most popular game for problem B-Q2, which asked what is in the bubbles when water boils. This probably reflects that the boiling of water is the example most often used when learning about how the kinetic molecular theory and intermolecular forces are relevant in phase changes. Problem D-Q4, which asked the same question about ethanol boiling, saw more reliance on Prototype Mapping, Inference, and Model-based Reasoning. Problem A-Q1, which asked how to determine if a gray metal earring is silver, almost exclusively evoked Prototype Mapping. Nearly all of the epistemic games that aided students’ solutions of A-Q1 were chemistry labs they had experienced, e.g., electrochemical cells, density experiments, flame tests, electroplating a penny, precipitation reactions, melting point procedures, etc.
Of all the epistemic games, the Compare game is likely the one that is least taught explicitly in school (Ngai and Sevian, 2017). Students may figure out from repeated practice that chemists tend to form classes that can support some generalizations, e.g., molecular vs. ionic, oxidizing agent vs. reducing agent, weak and strong acids and bases. These are nearly always loose categories with large gray areas of overlap, and it is difficult to learn the boundaries. It may be useful to know that the Compare game is evoked in the contexts of problems A-Q4 (are the chlorophylls from algae vs. trees the same), C-Q1 (what is caffeine), C-Q3 (what could a block that looks like metal be) and C-Q4 (how to tell whether a soda can and a metal block are the same substance). A further examination of the ways in which middle school vs. organic/physical chemistry students used the Compare game reveals that the middle school students who employed the Compare game were all aided by an epistemic form of a specific object they remember seeing or holding (a piece of steel, a soda can, water with something gray in it). While some organic/physical chemistry students also had similar epistemic forms to this, most were aided by epistemic forms that were abstract representations (biological mechanism diagrams, molecular structures, a generic IR spectrum showing wavenumber regions of particular functional groups).
Discussion
In this study, students at six educational levels spanning from grade 8 (age 13) to upper-level university (physical chemistry course) were asked to solve problems of substance characterization. Each student solved four problems. We observed 5 epistemic games that were distinct in their structural and ontological stability. Some common approaches to teaching students how to solve problems were reflected in the games. The construction of scientific arguments emerged in the Inference game, and modeling appeared in Model-based Reasoning. The Contrast game follows a pattern used throughout many subjects in school. Prototype Mapping relates new information to remembered examples, as analogical reasoning does. Although we could focus the Discussion on the ways in which the epistemic games we observed relate to a wide variety of studies in cognition research, we are instead interested in illuminating the value of this study for teaching and learning chemistry through the frame of learning progressions research. Thus, we limit the scope of the discussion.The epistemic games we observed were present at all educational levels, however not equally. In this sense, there appears to be some validity to our hypothesis that some epistemic games are conserved across all educational levels due to their considered productivity, while others emerge only at later educational levels. The Model-based Reasoning game grew in, the Inference game remained steady, and the Contrast game receded. Prototype Mapping may depend on the course in which students were enrolled. The Compare game exhibits some unique characteristics. These findings about students’ ideas and the contexts in which different ideas had greater and lesser prevalence have implications for teaching acts that could leverage students’ repertoires of epistemic games, as well as ways to discern when particular approaches to problem solving are likely to be more productive.
We framed this study using the approach of Acher and Arcà (2014) to learning progressions research. Our analysis was organized around three elements: (1) the articulation of students’ ideas, (2) the material contexts in which these idea articulations occur, and (3) teaching acts that can promote and sustain students’ gradual accumulation of ways to solve problems involving substance characterization. Based on the findings, we offer assertions about teaching acts that could leverage the advancement of students’ substance characterization practices. These teaching acts could also comprise hypotheses to test in a next cycle of learning progression validation, which would pay attention to how students solve problems involving substance characterization in classrooms in which teachers try these teaching acts.
The epistemic games were problem-solving approaches and occurred with both of the main epistemological framings, doing the lesson and doing science. We consider it a central goal of teaching science for students to do their own meaning making, thus we examine differences between the doing the lesson and doing science versions of these five games. The idea articulations that occurred differently depending on material contexts can offer suggestions for teaching acts that could be leverage points toward strengthening students’ meaning making. In earlier work within the chemical thinking learning progression (Banks et al., 2015; Cullipher et al., 2015), we called these ‘stepping stones’, to invoke an image of possible pathways in the progress of learning. Armed now with an understanding of students’ ideas in various contexts (Acher and Arcà, 2014), we hypothesize teaching acts (Table 9) that could bridge students to greater meaning making, and useful contexts that could be productive toward these ends.
| Problem solving approach | Doing the lesson frame | Teaching acts: teachers can create opportunities for students to… | Doing science frame |
|---|---|---|---|
| Overall epistemology | Say and write what is perceived to be correct, using scientific vocabulary where possible | • Acknowledge not understanding, then point out its usefulness, and clarify possible/alternative solutions | Blend daily life and chemistry knowledge, juxtaposing possible solutions and making sense of their appropriateness |
| Compare | Identify object-relevant properties (surface similarity, functional usage, history) that are similar in objects that are considered familiar examples of substances | • Sort substances from daily life into classes that can support predictions, then develop more abstract generalizations of the classes | Identify implicit features of substances (e.g., structural components, reactive capacities) that enable identifying them as members of classes that share characteristic sets of properties (e.g., low boiling points, characteristic odor) |
| • Identify and differentiate unfamiliar substances | |||
| • Useful contexts: differentiation of large molecules such as chlorophyll and caffeine, differentiation of metals | |||
| Prototype Mapping | Choose prototype of a substance or experience by most immediate association to obvious explicit characteristics of a substance | • Organize purposes for measuring different properties used to characterize substances | Observe multiple characteristics of substances and choose prototype substance or laboratory test based on similarity to several differentiating characteristics |
| • Recognize types of substances the procedures are typically used to identify | |||
| • Useful contexts: identification of metals, identification and differentiation of alcohols, differentiating reactants and products in dissociation reactions | |||
| Inference | Use associations based on object-relevant properties (surface similarity, functional usage, history) to connect claims to evidence | • Notice relationships between explicit (e.g., which elements) and implicit (e.g., acidic or basic character) features of molecules | Recognize causal links between claims and evidence based on compositional and structural differences between substances |
| • Useful contexts: changes in which only part of the sample changes (e.g., boiling of ethanol, metal earring changing color) | |||
| Model-based Reasoning | Apply models as rules (if antecedent then consequent) | • Draw representations of models and explain causal links between aspects of the model and properties of specific substances | Use information from the problem as parameters or conditions that constrain the applicability of a model |
| • Useful contexts: differentiation of liquids that look like water | |||
| Contrast | Recognize surface features of substances (color, organoleptic properties, which elements are in it) that form the basis for contrasts | • Express procedures for identifying and differentiating substances as flowcharts | Perform/propose tests based on characteristic properties to effect a sequential narrowing toward a more definitive identification or differentiation |
| • Useful contexts: identification and differentiation of white crystals, identification of liquids that look like water | |||
Positioning
Considering the main difference between epistemological frames of doing the lesson and doing science, this could be bridged by recognizing the value in learning of not-understanding. Watkins and coauthors (2017) found that, in order to observe how productive was the nature of students’ positioning, it was important to consider how students marked their relationships to the substance of their utterances, and how they positioned each other with respect to knowledge. Some students in the study of Watkins and coauthors took an impersonal stance with respect to what they said, for example marked by a flat tone and not displaying any uncertainty. Other students took a more personal stance toward what they communicated, for example telling a first-person story and announcing ongoing uncertainty. We also observed these positionings in our data, and relied upon them to help determine whether the student was doing the lesson vs. doing science, but these signals were not always consistent with how we coded students’ overall epistemology as other signs also contributed. However, we conjecture that if a student is clearly in a doing the lesson frame, but there are signs of a personal positioning, it could signal a student being poised to move from doing the lesson to doing science. Thus, these may be signs that a teacher could watch for in a classroom to gauge which students may be ready to be challenged.Comparing vs. contrasting
Students articulated chemistry problem solving in the form of five epistemic games. Two of these – the Compare and Contrast games – had very different expressions in the data. Comparing focuses on commonalities while contrasting focuses on differences. From very early in education, students are taught to contrast. Examples of contrasting are ubiquitous. Contrasting is used in language arts to analyze differences between stories, and in teaching languages to specify verb conjugations. It is used in mathematics when making “T-charts” that list x and y values for making a graph of how y varies with x. It is used in life sciences to tell apart similar organisms, such as alligators and crocodiles, and contrasting also provides an explanation for how molecular recognition works in cellular processes. When two objects are placed side by side, the similarities fall away and the differences stand out (Apthorp et al., 2012). By the time students reach the middle grades, they have had an enormous amount of practice with contrasting. It is not surprising, then, that the Contrast game is a problem-solving approach that can be used productively by students at all educational levels.Identification by comparison to a class, however, is a powerful but often neglected approach to identifying substances. Students of chemistry have considerable difficulty identifying whether a compound is molecular or ionic, for example, yet many problems to be solved in chemistry require proficiency in this. There are different rules for naming molecular compounds and ionic compounds. Predicting which intermolecular forces are prevalent depends on whether a compound is ionic or molecular, as does writing net ionic equations or acid-ionization reactions. Classes of substances have fuzzy boundaries in chemistry, e.g., semimetals have some metallic and some non-metallic characteristics, and polar molecules have differing degrees of ionic character. However, membership in a class bestows predictability of properties that are common to most members of the class, e.g., alcohols are miscible with water, confer an anti-knocking effect to combustion reactions, and can be converted to alkoxides.
The fact that the Compare game was used productively mainly by students at the highest educational levels in this study supports our interpretation. The question is how to facilitate students to develop the capacity to use the Compare game. An answer may rest in using specific material contexts to help students gain practice with this epistemic game. Based on the findings of this study, differentiation of large molecules, such as chlorophyll and caffeine, and differentiation of metals, which look similar and are often unfamiliar, appear to be useful material contexts that could promote students’ development of more abstract generalizations that can support defining classes of substances.
Explicit vs. implicit features
The objectivization view of substances generally focuses on explicit features of substances (surface similarity, functional usage, and history) in order to make determinations of chemical identity (Ngai et al., 2014). Paying attention to explicit features is useful and quite common in daily life, so it may be the case that promoting students’ reliance on more sophisticated ways of using the Compare game, which blends objectivization (chemical identity knowledge base), daily life (as general knowledge), and epistemic forms based on chemistry learning, is an approach that could be leveraged to help students connect their knowledge inside and outside of chemistry learning as they make sense of phenomena. This might be facilitated by asking students to speculate on ways of grouping different substances from their daily lives, in order to derive classes of substances that can support predictions.The major difference between students who used Prototype Mapping, Inference, and Contrast games in a doing the lesson vs. doing science frame was also based on focusing on explicit vs. implicit features of substances. Each of these games, however, has telltale features that teachers can recognize. Prototype Mapping refers to a specific example or experience. The Inference game tends to occur in cycles of inference–evidence–questioning. The Contrast game specifies groupings that function as either/or bins, and often coincides with epistemic games that are lists of properties. Different material contexts seemed to evoke doing science manifestations of these games, and these are suggested in Table 9 along with teaching acts that may facilitate student meaning making if a student is employing a particular game. Finally, doing the lesson vs. doing science framing of the Model-based Reasoning game seemed to be differentiated by the ways in which students used models. Based on our data, student meaning making is predicted to be advanced by the choice of substance differentiation problems in which explicit features are the same (e.g., samples that look like water), combined with asking students to draw representations of their models and then use those models to provide causal explanations or predictions of properties.
Language games
There were many different ways that students solved substance characterization problems. Students who framed their activity as doing science were dynamically making sense of phenomena as they solved the problems, which gives us reason to trust that their approaches are valid ways that students can both learn and do chemistry. Another way of considering sense making as it is being spoken is Wittgenstein's notion of language games (1958). Wittgenstein defined language games in terms of the meanings of words being used, which may be different for different individuals as they speak them. He pointed out that individual language games are distinguished by unique rules (passage 23, Wittgenstein, 1958). For example, a student's words “the silver earring is not silver” can be understood differently depending on whether the student is forming a hypothesis about the earring, describing the appearance of the earring, or presenting an analysis of the evidence. Wittgenstein explained that (Wittgenstein, 1958, p. 50):130. Our clear and simple language-games are not preparatory studies for a future regularization of language – as it were first approximations, ignoring friction and air-resistance. The language-games are rather set up as ‘objects of comparison’ which are meant to throw light on the facts of our language by way not only of similarities, but also of dissimilarities.
Studying students’ ways of speaking and the meanings students intend words to have as they use them can shine more light on how students think and learn than studying the extent/sophistication to which students’ approaches to problem solving follow argumentative structures (e.g., Toulmin analysis) or speak content in scientifically canonical ways. Which epistemic game may be constraining a student's problem solving approach is an entry point to unpacking the meanings students intend. Identifying the epistemic game opens up the ways of speaking by elucidating the structures of the games, in the same sense that identifying the structure of a protein allows us to begin understanding the molecular details of how a protein functions.
Conclusions
Substance characterization is fundamental to chemistry. When students solve problems in chemistry, they may be expected to bring epistemological resources to their work in solving these problems. The epistemic games uncovered in this study can assist chemistry teachers in recognizing the common ways that students approach solving chemistry problems that involve identifying and differentiating substances. Teachers can look for the underlying epistemological commitments in how students approach a problem, the epistemic forms aiding students in a solution process, and the patterns of moves taken when solving the problem. Discerning whether a student is framing the situation as doing the lesson or doing science can help a teacher determine whether particular teaching acts may be beneficial to guide the student toward deeper sense making. Particular teaching acts and specific problem contexts may be more productive than others in leveraging students’ efforts toward greater sense making.Conflicts of interest
There are no conflicts to declare.Appendix: metadata example
To illustrate how the data were analysed, we provide an example of participant R10 (enrolled in a university organic chemistry course) solving problem B-Q4. The problem prompt (from Ngai and Sevian, 2017) is shown, with the participant's survey responses in italics. Next, the interview transcript is provided followed by the metadata from the analysis.B-Q4 prompt
Carbon dioxide also occurs naturally as a gas. How would you tell the difference between carbon dioxide and oxygen? Please explain your response.The difference between carbon dioxide and oxygen is that the molecule contains more carbons. In order to determine the gas one should look at the smell, the way the gas flows, etc.
Is there other information you would like to know in order to tell the difference between carbon dioxide and oxygen? If so, what information? How would this information help you tell the difference between carbon dioxide and oxygen?
I would want to know the density and molecular weight.
Interview transcript
Interviewer: Okay cool, so then for question four. How do you tell the difference between carbon dioxide and oxygen? You said the smell.R10: Yeah, I just took a guess on that.
Interviewer: Why was smell the first thing you thought of?
R10: Well, I thought that carbon dioxide would have an odor to it versus oxygen but you think there's no odor, so, I was definitely wrong with that.
Interviewer: Okay, but what made you think of the smell because I’m curious. Why was smell the first thing you thought of?
R10: Well, because, you know how they say that you were to, I used to work in a car dealership and um, anytime when someone would turn on the car engine inside the showroom. You can smell, it's probably gasoline that I’m thinking of but it could definitely make you sick.
Interviewer: So you think the smell of the carbon dioxide?
R10: Yes, I know because I feel nauseated a couple of times when that happened.
Interviewer: Okay, so how it made you feel?
R10: Like, yeah, I wanted to throw up.
Interviewer: Okay, that's not good. So then for further information, you would want to know the density and molecular weight. So how would this help you tell the difference?
R10: Well, like, oxygen err carbon dioxide so basically there's carbon and two oxygens. Obviously it's going to be heavier than oxygen itself. So, that's how you would definitely tell the difference between the two.
Interviewer: Okay, alright, and is there anything else you would want to know in order to tell the difference?
R10: I think about distillation, but that wouldn’t work. At this point, I don’t know.
Metadata
Narrative: Carbon dioxide has an odor to it. I have smelled it and it makes me want to throw up, but maybe that was because of gasoline not carbon dioxide. Another difference is the molecular weight and density (equated). Carbon and two oxygens is heavier than oxygen itself. Another possible test to tell the difference is distillation, but that wouldn’t work here.Alternative problem: What does carbon dioxide do (that oxygen doesn’t do)?
Cue: Carbon dioxide (comes from car emissions).
General knowledge base: Worked in a car dealership. Organic chemistry laboratory activities.
Chemical identity knowledge base: Principlism (considers carbon dioxide to be a carrier of nausea-making, smell is part of the mechanism) and compositionism (carbon dioxide contains a carbon and two oxygens, thus is heavier than oxygen which has two oxygens only).
Epistemic form: Substance as container of properties.
Epistemic game: Prototype Mapping.
Match of moves:
Entry move: identify properties: has an odor or not;
Select category move: bad gases are carbon dioxide which have odors or cause health problems;
Confirm category through prototype move: Carbon dioxide is in car exhaust, experience with car exhaust in car dealership work, when someone started a car engine inside there was carbon dioxide which makes you feel like throwing up;
Exit move: Reason the conclusion through prototype; If it's carbon dioxide, it is also different from oxygen by having carbon and two oxygens which makes it heavier than only having oxygens.
Justification/ruling out other games: The only other game that could potentially fit is contrast game, but can't find “assignment” move: Entry cue: carbon dioxide comes from car emissions; Classes/Categories: bad vs. good; Properties move: bad = (smells bad, makes you want to throw up); good = (doesn’t smell bad); Assignment move:???; Exit move: change to carbon dioxide vs. oxygen somehow.
Epistemological framing: Evidence for ‘doing the lesson’. Student indicates perception of interviewer as judging responses as incorrect, even though interviewer was well trained and did not display judgment during interview (e.g., “but you think there's no odor so I was definitely wrong with that”), expresses doubt/apology (“I just took a guess on that”), positions self outside the problem (uses “you” when talking about chemistry), however does trust personal experience (uses “I”).
Epistemological commitment: Empirical results are trustworthy. Although positions self outside of science, trusts personal experiences. Also values empirical evidence (feeling of nausea).
Acknowledgements
The authors are grateful to our research team members who helped to strengthen construct validity in the analysis: Klaudja Caushi, Vesal Dini, Jessica Karch, Clarissa Keen, Courtney Ngai, and Raúl Orduña Picón, as well as Orlando Aguiar, who was a visiting scientist in our group. The authors also thank Professor Vicente Talanquer for insightful comments and suggestions that helped enrich the manuscript. The authors acknowledge the funding sources that supported our work, US National Science Foundation awards 1222624 and 1621228.References
- Acher A. and Arcà M., (2014), Designing a learning progression for teaching and learning about matter in early school years, in Bruguière C., Tiberghien A. and Clément P. (ed.), Topics and trends in current science education, Dordrecht: Springer, pp. 489–503.
- Apthorp H. S., Igel C., and Dean C., (2012), Using similarities and differences: A meta-analysis of its effects and emergent patterns, School Science and Mathematics, 112(4), 204–216.
- Banks G., Clinchot M., Cullipher S., Huie R., Lambertz J., Lewis R., Ngai C., Sevian H., Szteinberg G., Talanquer V., and Weinrich M., (2015), Uncovering chemical thinking in students’ decision making: A fuel-choice scenario, J. Chem. Educ., 92(10), 1610–1618.
- Berland L. K., and McNeill K. L., (2010), A learning progression for scientific argumentation: Understanding student work and designing supportive instructional contexts, Sci. Educ., 94(5), 765–793.
- Broman K., and Parchmann I., (2014), Students’ application of chemical concepts when solving chemistry problems in different contexts, Chem. Educ. Res. Pract., 15(4), 516–529.
- Clinchot M., Ngai C., Huie R., Talanquer V., Lambertz J., Banks G., Weinrich M., Lewis R., Pelletier P., and Sevian H., (2017), Better formative assessment, Sci. Teach., 84(3), 69–75.
- Coll R. K., and Treagust D. F., (2003), Investigation of secondary school, undergraduate, and graduate learners' mental models of ionic bonding, J. Res. Sci. Teach., 40(5), 464–486.
- Cullipher S., Sevian H., and Talanquer V., (2015), Reasoning about benefits, costs, and risks of chemical substances: mapping different levels of sophistication, Chem. Educ. Res. Pract., 16(2), 377–392.
- Curtis J. R., Wenrich M. D., Carline J. D., Shannon S. E., Ambrozy D. M., and Ramsey P. G., (2001), Understanding physicians’ skills at providing end-of-life care: Perspectives of patients, families, and health care workers, J. Gen. Intern. Med., 16, 41–49.
- Dalgety J., Coll R. K., and Jones A., (2003), Development of chemistry attitudes and experiences questionnaire (CAEQ), J. Res. Sci. Teach., 40(7), 649–668.
- Elby A., and Hammer D., (2001), On the substance of a sophisticated epistemology, Sci. Educ., 85(5), 554–567.
- Elby A. and Hammer D., (2010), Epistemological resources and framing: A cognitive framework for helping teachers interpret and respond to their students’ epistemologies, in Bendixen L. D. and Feucht F. C. (ed.), Personal epistemology in the classroom: Theory, research, and implications for practice, Cambridge, UK: Cambridge University Press, pp. 409–434.
- Elby A., Frederiksen J., Schwarz C. and White B., (2001), Epistemological Beliefs Assessment for Physical Science (EBAPS), Retrieved December 30, 2017, from http://www2.physics.umd.edu/~elby/EBAPS/home.htm.
- Enke C., (2001), The art and science of chemical analysis, New York: Wiley.
- Gilbert J. K., (2004), Models and modelling: Routes to more authentic science education, Int. J. Sci. Math. Educ., 2(2), 115–130.
- Grove N., and Bretz S. L., (2007), CHEMX: An instrument to assess students' cognitive expectations for learning chemistry, J. Chem. Educ., 84(9), 1524–1529.
- Hammer D. M., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer, in Mestre J. (ed.), Transfer of learning from a modern multidisciplinary perspective, Greenwich, CT: Information Age Publishing, pp. 89–120.
- Harrison A. G. and Treagust D. F., (1996), Secondary students’ mental models of atoms and molecules: Implications for learning chemistry, Sci. Educ., 80(5), 509–534.
- Heaton J., (2008), Secondary analysis of qualitative data: an overview, Hist. Soc. Res., 33(3), 33–45.
- Hershkowitz R., Schwarz B. B., and Dreyfus T., (2001), Abstraction in context: Epistemic actions, J. Res. Math. Educ., 195–222.
- Hershkowitz R., Hadas N., Dreyfus T., and Schwarz B., (2007), Abstracting processes, from individuals’ constructing of knowledge to a group's “shared knowledge”, Math. Educ. Res. J., 19(2), 41–68.
- Hmelo-Silver C. E., (2004), Problem-based learning: What and how do students learn? Educ. Psychol. Rev., 16(3), 235–266.
- Hoffmann R., (1993), How should chemists think? Sci. Am., 268(2), 66–73.
- Hsieh H. F., and Shannon S. E., (2005), Three approaches to qualitative content analysis, Qual. Health Res., 15(9), 1277–1288.
- Hutchinson P., and Hammer D., (2010), Attending to student epistemological framing in a science classroom, Sci. Educ., 94(3), 506–524.
- Ingham A. M. and Gilbert J. K., (1991), The use of analogue models by students of chemistry at higher education level, Int. J. Sci. Educ., 22(9), 1011–1026.
- Jiménez-Aleixandre M. P., Bugallo Rodríguez A., and Duschl R. A., (2000), ‘Doing the lesson’ or ‘doing science’: Argument in high school genetics, Sci. Educ., 84(6), 757–792.
- Jonassen D. H., (2000), Toward a design theory of problem solving, Educ. Technol. Res. Dev., 48(4), 63–85.
- Jonassen D. H., (2007), What makes scientific problems difficult? in Jonassen D. H. (ed.), Learning to solve complex, scientific problems, Mahwah, NJ: Lawrence Erlbaum Associates, pp. 3–23.
- Mazzarone K. M., and Grove N. P., (2013), Understanding epistemological development in first-and second-year chemistry students, J. Chem. Educ., 90(8), 968–975.
- Mohan L., Chen J., and Anderson C. W., (2009), Developing a multi-year learning progression for carbon cycling in socio-ecological systems, J. Res. Sci. Teach., 46(6), 675–698.
- Ngai C., and Sevian H., (2017), Capturing chemical identity thinking, J. Chem. Educ., 94(2), 137–148.
- Ngai C., Sevian H., and Talanquer V., (2014), What is this substance? What makes it different? Mapping progression in students’ assumptions about chemical identity, Int. J. Sci. Educ., 36(14), 2438–2461.
- Podschuweit S. and Bernholt S., (2017), Composition-effects of context-based learning opportunities on students’ understanding of energy, Res. Sci. Educ., DOI:10.1007/s11165-016-9585-z.
- Potter W. J., and Levine-Donnerstein D., (1999), Rethinking validity and reliability in content analysis, J. Appl. Commun. Res., 27, 258–284.
- Prince M., (2004), Does active learning work? A review of the research, J. Eng. Educ., 93(3), 223–231.
- Pulmones R., (2010), Linking students’ epistemological beliefs with their metacognition in a chemistry classroom, Asia-Pacific Educ. Res., 19(1), 143–159.
- Redish E. F., (2004), A theoretical framework for physics education research: Modeling student thinking, arXiv preprint physics/0411149, https://arxiv.org/pdf/physics/0411149.pdf.
- Robertson A. D., Scherr R. and Hammer D. (ed.), (2016), Responsive teaching in science and mathematics, Abingdon, UK: Routledge.
- Russ R. S., Lee V. R., and Sherin B. L., (2012), Framing in cognitive clinical interviews about intuitive science knowledge: Dynamic student understandings of the discourse interaction, Sci. Educ., 96(4), 573–599.
- Sampson V., and Clark D., (2009), The impact of collaboration on the outcomes of scientific argumentation, Sci. Educ., 93(3), 448–484.
- Scherr R. E., and Hammer D., (2009), Student behavior and epistemological framing: Examples from collaborative active-learning activities in physics, Cogn. Instr., 27(2), 147–174.
- Schmidt H. G., Rotgans J. I., and Yew E. H., (2011), The process of problem-based learning: what works and why, Med. Educ., 45(8), 792–806.
- Schraw G. and Moshman D., (1995), Metacognitive theories, Educ. Psychol. Rev., 7(4), 351–371.
- Schummer J., (2003), The notion of nature in chemistry, Stud. Hist. Philos. Sci., Part A, 34(4), 705–736.
- Scott K. S., (2014), A multilevel analysis of problem-based learning design characteristics, Interdisciplinary Journal of Problem-Based Learning, 8(2), 5, DOI:10.7771/1541-5015.1420.
- Sevian H., and Talanquer V., (2014), Rethinking chemistry: a learning progression on chemical thinking, Chem. Educ. Res. Pract., 15(1), 10–23.
- Sevian H., Talanquer V., Bulte A. M., Stacy A. and Claesgens J., (2014), Development of understanding in chemistry, in Bruguière C. et al. (ed.), Topics and trends in current science education, Springer, Dordrecht, pp. 291–306.
- Smith C. L., Wiser M., Anderson C. W. and Krajcik J., (2006), Implications of research on children's learning for standards and assessment: A proposed learning progression for matter and the atomic molecular theory, Measurement: Interdisciplinary Research and Perspectives, 4(1-2), 1–98.
- Sperling R. A., Howard B. C., Miller L. A., and Murphy C., (2002), Measures of children's knowledge and regulation of cognition, Contemp. Educ. Psychol., 27, 51–79.
- Szteinberg G., Balicki S., Banks G., Clinchot M., Cullipher S., Huie R., Lambertz J., Lewis R., Ngai C., Weinrich M., Talanquer V., and Sevian H., (2014), Collaborative professional development in chemistry education research: bridging the gap between research and practice, J. Chem. Educ., 91(9), 1401–1408.
- Taber K. S., (2003), Mediating mental models of metals: Acknowledging the priority of the learner's prior learning, Sci. Educ., 87(5), 732–758.
- Talanquer V., (2009), On cognitive constraints and learning progressions: The case of structure of matter, Int. J. Sci. Educ., 31(15), 2123–2136.
- Talanquer V., (2014), Chemistry education: Ten heuristics to tame, J. Chem. Educ., 91(8), 1091–1097.
- Thompson J., Windschitl M., and Braaten M., (2013), Developing a theory of ambitious early-career teacher practice, Am. Educ. Res. J., 50(3), 574–615.
- Tsai C. C., (2001), A review and discussion of epistemological commitments, metacognition, and critical thinking with suggestions on their enhancement in Internet-assisted chemistry classrooms, J. Chem. Educ., 78(7), 970.
- Tuminaro J., and Redish E. F., (2007), Elements of a cognitive model of physics problem solving: Epistemic games, Physical Review Special Topics-Physics Education Research, 3(2), 020101.
- Veenman M. V., (2012), Metacognition in science education: Definitions, constituents, and their intricate relation with cognition, in Zohar A. and Dori Y. J. (ed.), Metacognition in science education, pp. 21–36, Dordrecht: Springer.
- Vosniadou, S. and Ortony, A. (ed.), (1989), Similarity and analogical reasoning, Cambridge University Press.
- Watkins J., Hammer D., Radoff J., Jaber L. Z., and Phillips A. M., (2017), Positioning as not-understanding: The value of showing uncertainty for engaging in science, J. Res. Sci. Teach., 2018, 55(4), 573–599.
- Wittgenstein L., (1958), Philosophical investigations (G. E. M. Anscombe, Trans. 2nd. edn.), Oxford, England: Basil Blackwell, (Original work published 1953).
- Zeineddin A., and Abd-El-Khalick F., (2010), Scientific reasoning and epistemological commitments: Coordination of theory and evidence among college science students, J. Res. Sci. Teach., 47(9), 1064–1093.
| This journal is © The Royal Society of Chemistry 2018 |