DOI:
10.1039/C8RA08028C
(Paper)
RSC Adv., 2018,
8, 41756-41761
Design of localized spatiotemporal pH patterns by means of antagonistic chemical gradients†
Received
27th September 2018
, Accepted 6th December 2018
First published on 13th December 2018
Abstract
Spatially localized moving and stationary pH patterns are generated in two-side-fed reaction-diffusion systems. The patterns are sandwiched between two quiescent zones and positioned by the antagonistic gradients of the reactants of the self-activatory process. Spatial bistability, spatiotemporal oscillations, and formation of stationary Turing patterns have been predicted by numerical simulations and observed in experiments performed by using different hydrogen ion autocatalytic chemical systems. The formation of stationary patterns due to long-range inhibition is promoted by a large molecular weight hydrogen ion binding polymer.
1 Introduction
The two most influential ideas about the origin of biological patterns are Turing's reaction-diffusion (RD) model1 and Wolpert's processing of positional information.2 The Turing model describes the autonomous pattern generation in a two variable activator–inhibitor model, where the effective diffusivity of the activator component is smaller than that of the inhibitor. Among the different RD patterns predicted by Turing, the stationary ones, which are formed by a spontaneous symmetry breaking process and characterized by their intrinsic wavelength, are the most striking. The biological relevance of this mechanism has been demonstrated by Kondo and coworkers on horizontal stripes of zebrafish3 and on the formation of regularly spaced transverse ridges of the palate.4 The Wolpert model implies the existence of a morphogen concentration gradient which is interpreted in a threshold-dependent way. This mechanism which results in distinct regions with sharp borders is widely accepted as a paradigm in developmental biology,5 and it can be observed in a synthetic biochemical system.6 Chemical RD systems are ready to form a large variety of biologically relevant spatiotemporal phenomena,7,8 and autonomous living-like soft structures as well.9 The coupling of reactions which are capable of producing pH patterns with responsive materials is a quite promising approach for developments along this latter line.10
Here, we present a method to generate localized pH patterns in the presence of antagonistic gradients maintained by the counter-diffusion of different chemicals. A Wolpert type mechanism, the interplay of gradients and the self-activatory process, is used to create a spatially organized state of the system where a localized high extent of reaction zone is separated by sharp thresholds from the outer nonreactive regions. Besides this one, a flat, unstructured spatial state also can be generated. The coexistence of two stable spatial steady states, characterized by different spatial concentration distributions, at the same boundary conditions is not trivial and called spatial bistability. We have demonstrated the existence of this nonlinear phenomenon in our system, as the spatially organized state coexists with the flat spatial state over a finite range of parameters. In the high extent of reaction zone of the spatially organized state, kinetic and diffusion driven instabilities may lead to the formation of different RD patterns. The proposed approach has been tested by numerical simulations and in experiments made in two-side-fed reactors (TSFR).11 In the TSFR used here the two tanks, fed continuously with different chemicals, are connected through an agarose gel (Fig. 1a). The chemicals are distributed in a way to avoid any significant reactions in the tanks. In the gel, diffusion establishes concentration gradients of the chemical species and the RD patterns develop perpendicular to that. TSFRs have been already used to study Turing patterns in the chlorite-iodide-malonic acid (CIMA) reaction,12 and waves in the Belousov–Zhabotinsky (BZ) reaction.13 In both cases the input feed chemicals are the precursors of the main dynamical species, thus the patterns form in a more or less thick layer of the medium in which the simultaneous development of different spatial instabilities is possible at different positions.14,15 This aspect makes difficult the interpretation and the control of the developing patterns. In the systems we use here, the input feed chemicals are directly involved in the positive and the negative feedback processes. This allows to create a localized zone with a single dynamic state and provides an unambiguous control of the dynamics through the variation of the boundary conditions.
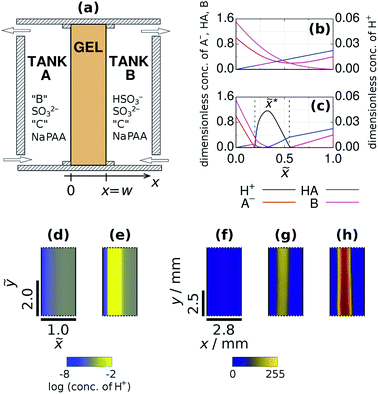 |
| | Fig. 1 Sketch of the open two-side-fed gel reactor (TSFR) with a thin gel strip (a). Typical concentration profiles at the F state (b) and at the M state (c) of the gel content obtained by numerical simulations. Numerical (d and e) and experimental (f, g and h) snapshots of the stationary spatial states. The parameters used in the simulations are: aA0 = 1, ahA0 = 0, bA0 = 1.5, aB0 = 0.4, ahB0 = 0.6, bB0 = 0, cX0 = 0 and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 1.0. The input feed concentrations in the experiments were: [bromocresol green]X0 = 0.21 mM, [Na2SO3]X0 = 80 mM, [BrO3−]A0 = 200 mM, [Fe(CN)64−]X0 = 0 mM, [H2SO4]B0 = 6 mM (f and g) and [Na2SO3]X0 = 89 mM, [IO3−]A0 = 150 mM, [(NH2)2CS]X0 = 5 mM, [H2SO4]B0 = 7 mM (h). The pseudocolor images were derived from grayscale ones by mapping each intensity value to a color according to the presented lookup table. High intensity (yellow) color indicates a pH below 4.8. = 1.0. The input feed concentrations in the experiments were: [bromocresol green]X0 = 0.21 mM, [Na2SO3]X0 = 80 mM, [BrO3−]A0 = 200 mM, [Fe(CN)64−]X0 = 0 mM, [H2SO4]B0 = 6 mM (f and g) and [Na2SO3]X0 = 89 mM, [IO3−]A0 = 150 mM, [(NH2)2CS]X0 = 5 mM, [H2SO4]B0 = 7 mM (h). The pseudocolor images were derived from grayscale ones by mapping each intensity value to a color according to the presented lookup table. High intensity (yellow) color indicates a pH below 4.8. | |
We use Landolt-type pH oscillators, as these proved to be beneficial in previously tested RD pattern design concepts.16–20 These systems can be described by the following reactions:21
| |
 | (R2) |
In this model B stands for the oxidant (
e.g. BrO
3−, IO
3− or H
2O
2), A
− is the main reductant (
e.g. SO
32−), C denotes a second reductant (
e.g. [Fe(CN)
6]
4− or (NH
2)
2CS), and P and Q are products. Reactions
(R1) and
(R2) implement the H
+-autocatalytic oxidation of the substrate, that is the positive feedback, while the delayed consumption of H
+ ions
(R3) and the protonation of the substrate
(R1) are responsible together for the negative feedback in the chemical kinetics. Reaction
(R4) represents the protonation equilibrium of polyacrylate, which is used to create long range inhibition by slowing down the effective diffusivity of hydrogen ions. Despite its simplicity this model successfully describes the general characteristics of the different spatial states and the dynamics of the systems investigated here. The aim of our work is to produce spatial bistability, spatiotemporal oscillations and Turing patterns in the presence of antagonistic gradients of certain reactants. Experimental evidence is provided by using various types of pH oscillators,
22 namely the bromate-sulfite-ferrocyanide (BSF), the iodate-sulfite-ferrocyanide (FIS), the iodate-sulfite-thiourea (TuIS) and the hydrogen peroxide-sulfite-ferrocyanide (HPSF) reactions. As these reactions show sustained homogeneous oscillations only in CSTRs (continuously fed and stirred tank reactors) in the presence of nonstop inflow of the initial reactants, the appearance of RD patterns, especially Turing-type patterns, is not trivial.
2 Methods
2.1 Experimental
The experiments were performed in a TSFR, where a thin strip of a 2% agarose (Sigma-Aldrich, A2929) gel is in contact with two stirred tanks. The width (w), the length and the height of the gel strip was 2.8 mm, 23 mm and 1 mm, respectively, and the residence time in the tanks was fixed to 120 s. The experiments in the BSF, FIS and TuIS reactions were made at T = 35 °C and at T = 25 °C in the HPSF reaction. The feed solutions of the major chemicals were stored in three separated reservoirs but entered premixed into the tanks. Reactants were distributed as follows: Reservoir 1: oxidant (NaBrO3 (Sigma-Aldrich, ≥99%) or H2O2 (VWR, 30% aqueous solution) or KIO3 (Sigma-Aldrich, ≥98%)); Reservoir 2: Na2SO3 (Sigma-Aldrich), Na4Fe(CN)6·10H2O (Sigma-Aldrich) or (NH2)2CS (Sigma-Aldrich) and the indicator; Reservoir 3: H2SO4 (diluted from 1.0 mol L−1 standard solution (VWR)). Sodium-polyacrylate (Sigma-Aldrich) was added to Reservoir 2. All solutions were prepared with ion-exchanged water and chemicals were used without further purification. The input feed concentrations ([X]0) of the reagents are indicated in the text. Here [X]0 denotes the concentration that species X would have in the total inlet flow prior to any reaction. Tank A is fed from Reservoir 1 and 2, while Tank B is fed from Reservoir 2 and 3. At the applied pH and residence time, the content of both tanks should be considered as nonreactive, in spite of the fact that the oxidant and reductant are both fed from Tank A. In Tank B, the role of H2SO4 is to protonate a part of SO32− to HSO3−. To visualize the pH patterns bromocresol green (BCG) (Sigma-Aldrich, 90%, pKa = 4.8) or bromocresol purple (BCP) (Sigma-Aldrich, indicator grade, pKa = 6.3) was selected. The pictures were taken by an AVT Stingray F-033B (14 bit) camera, and recorded by the Streampix (Norpix) software. The camera was fixed above the experimental setup, which was enlightened by a LED source through a 530 nm long-pass filter to provide better contrast and to protect the ferrocyanide from light. We used the ImageJ program for image processing.23
2.2 Computational details
The simulations were made by the dimensionless equations derived from the model represented by reactions (R1)–(R4). The details of the derivation are presented in the ESI.† Here, dot, ∂t and Δ denote the dimensionless time derivatives and Laplacian. The state of the content of Tank A and B are calculated by the following dimensionless equations:| | |
ȧX = −κ1aXhX + κ−1ahX + aX0 − aX
| (1) |
| |
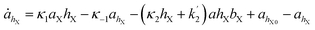 | (2) |
| |
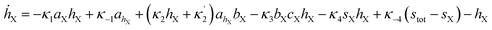 | (3) |
| |
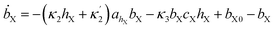 | (4) |
| | |
ċX = −κ3bXcXhX + cX0 − cX
| (5) |
| | |
ṡX =−κ4sXhX + κ−4(stot − sX) − sX
| (6) |
Here X refers either to Tank A or B. The variables aX, ahX, hX, bX, cX and sX denote the dimensionless concentrations of species A−, HA, H+, B, C and S−, respectively (for the definitions see ESI†). The typical dimensionless input feed concentrations in Tank A are aA0 = 1, ahA0 = 0 and bA0 > 1, while in Tank B these are aB0 = 1 − ahB0, 0 < ahB0 < 1 and bB0 = 0. The input feed of C and S− is the same for both tanks as cA0 = cB0 ≥ 0 and sA0 = sB0 ≥ 0. The values of κ2, 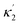 , κ3, κ4 and κ−4 are set to 5 × 105, 5 × 101, 5 × 103, 5 × 1010, 5 × 107 respectively. The composition of the gel content is calculated by the following equations:
, κ3, κ4 and κ−4 are set to 5 × 105, 5 × 101, 5 × 103, 5 × 1010, 5 × 107 respectively. The composition of the gel content is calculated by the following equations:| | |
∂ta = −κ1ah + κ−1ah + Δa
| (7) |
| |
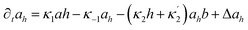 | (8) |
| |
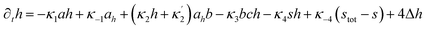 | (9) |
| |
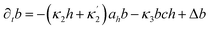 | (10) |
| | |
∂ts = −κ4sh + κ−4(stot − s) + 0.01Δs
| (12) |
The dimensionless variables a, ah, h, b, c and s correspond to the concentrations of A−, HA, H+, B, C and S− in the gel, respectively. These variables are time and space dependent. We assume that the diffusion coefficient of the H+ in the gel is four times larger,24 while the diffusion coefficient of low mobility polyacrylate is 100 times smaller than that of the other species. The concentrations at x = 0 and at x = w are the same as that of Tank A and B, respectively.
The partial differential equations were discretized with standard second order finite difference scheme on a 100×400 mesh. The resulting systems were solved by the SUNDIALS CVODE25 solver using backward differentiation formula method. The absolute and the relative error tolerances were 10−12 and 10−7, respectively.
3 Results and discussion
To achieve suitable conditions for the development of localized patterns we apply a uniaxial bipolar design with the antagonistic gradients of the reactants of reaction (R2), the main step of the positive feedback process. This means that B and HA are only present in Tank A and B, respectively. This distribution establishes the localization of the autocatalytic zone in the direction of the concentration gradients, because reaction (R2) proceeds only in the middle zone of the gel. The separation of these two chemicals is necessary and sufficient for our purpose, namely to generate a three-zoned structured spatial state, so the other input chemicals (A−, C, polycarboxylate, and the pH indicator) are fed from both sides. In the experiments the concentration of HSO3− in Tank B is controlled by the input feed concentration of H2SO4. This configuration results in the appearance of two different stationary states. At the one we call F (“Flow”) state, there is no significant chemical reaction inside the gel, therefore all gradients are smooth (Fig. 1b and d). In the experiments, the indicator shows its high pH color all along the gel at this state (Fig. 1f). The other spatial state is characterized by three distinct zones (Fig. 1c and e) and we designate it as the M (“Mixed”) state of the gel. The composition of the three zones is essentially different. At the left zone the concentration of A− and B is high, but the concentration of HA is low. In the middle zone A− is totally consumed and accordingly H+ appears in a relatively high concentration. The right zone is characterized by the presence of HA and A− and the lack of B. The position of the maximum of the H+ concentration distribution (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) *) is mainly determined by the concentration gradient of B and can be calculated as:
*) is mainly determined by the concentration gradient of B and can be calculated as:| |
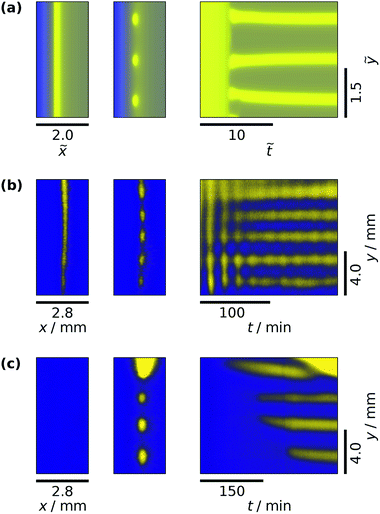
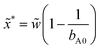 | (13) |
Here, bA0 is the dimensionless concentration of B in Tank A. This formula, which is based on the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry of reaction (R2) and on a linear approximation of the gradients, is in good agreement with the numerical simulations. The width of the high H+ concentration band is directly proportional to w (Fig. S1 in ESI†). This type of size invariance of the three-zoned-pattern is the consequence of the bipolarity of the system.2 In the experiments, at the M state of the system a sharp zone forms inside the gel, where the indicator switches to its low pH color (Fig. 1g). When iodate was used as the oxidant, iodine precipitate formation was observed within the acidic zone due to the Dushman reaction (Fig. 1h).26 According to the simulations and also the experiments made in four different systems (BSF, FIS, TuIS, and HPSF), the F and the M states may coexist, that is spatial bistability. In chemical RD systems this behavior have been demonstrated only in the presence of unidirectional concentration gradients (e.g. in one-side-fed reactors), previously.27–29
1 stoichiometry of reaction (R2) and on a linear approximation of the gradients, is in good agreement with the numerical simulations. The width of the high H+ concentration band is directly proportional to w (Fig. S1 in ESI†). This type of size invariance of the three-zoned-pattern is the consequence of the bipolarity of the system.2 In the experiments, at the M state of the system a sharp zone forms inside the gel, where the indicator switches to its low pH color (Fig. 1g). When iodate was used as the oxidant, iodine precipitate formation was observed within the acidic zone due to the Dushman reaction (Fig. 1h).26 According to the simulations and also the experiments made in four different systems (BSF, FIS, TuIS, and HPSF), the F and the M states may coexist, that is spatial bistability. In chemical RD systems this behavior have been demonstrated only in the presence of unidirectional concentration gradients (e.g. in one-side-fed reactors), previously.27–29
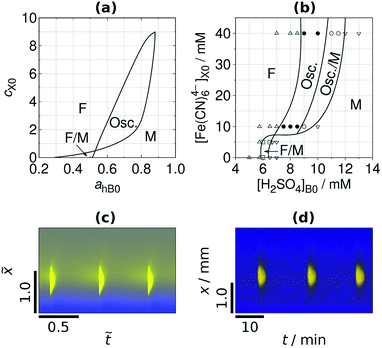
The width of the low pH zone of the M state and the parameter domain of spatial bistability decreases when the negative feedback is enhanced by the increase of the input feed concentration of C (Fig. 2a). Spatial bistability vanishes at a critical value and spatiotemporal oscillations appear with nonzero amplitude and frequency, which is signature of a subcritical Hopf bifurcation. The simulated and the experimental phase diagrams (Fig. 2a and b) show a cross-shaped topology, that is typical for open activatory–inhibitory systems.30 In the oscillatory domain there are still three distinct zones in the gel, but now the central one is periodic as it can be seen in the time-space plots in Fig. 2c and d (simulation and experiment). In the presented cases the acidic signal appears and disappears abruptly. The formation of localized spatiotemporal oscillations have been observed in experiments made by bromate (BSF) and iodate (FIS and TuIS) oxidants, but not by hydrogen peroxide (see the movies in ESI†). The period of the spatiotemporal oscillations in the investigated systems is about 12–20 min at the applied conditions (Fig. 2d). The correspondence between the simulated and experimentally recorded dynamics (Fig. 2) reveals the relevance of the simple mechanism presented by reactions (R1)–(R4). Representative time-space plots of the oscillations and the local time evolution at the center of the middle zone in the FIS and the TuIS systems are shown in Fig. 3. We assume that the failure of finding oscillations in the HPSF case is connected to the rather complex kinetics of the reaction between hydrogen peroxide and ferrocyanide,31 which provides the negative feedback. The rate of the oxidation steps, reaction (R2) and (R3) are quite different in case of bromate, iodate and hydrogen peroxide. We have tested this effect by numerical simulations and we have found a square root scaling (Fig. S2 in ESI†) between the relevant kinetic parameters (the rate constants of reaction (R2) and (R3)) and the parameter which determines the diffusive gradients, that is the thickness of the gel. Besides, the large amplitude oscillations presented in Fig. 2 the simulations predict also small amplitude ones (Fig. S3 in ESI†), where the pH variation of the middle zone is so tiny, that the experimental observation is unlikely by using standard pH indicators.
 |
| | Fig. 2 Simulated (a) and experimental (b) nonequilibrium phase diagram and time-space plots of simulated (c) and experimental (d) oscillations. The dimensionless parameters used in the simulations are: aA0 = 1, bA0 = 1.5 and ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 2.0. The numerical time-space plot is made at cX0 = 1.5, aB0 = 0.4 and ahB0 = 0.6. The experiments were made with BSF reaction, and the input feed concentrations are: [Na2SO3]X0 = 80 mM, [BrO3−]A0 = 200 mM, [bromocresol green]X0 = 0.21 mM. The time-space plot was recorded at [Fe(CN)64−]X0 = 10 mM, [H2SO4]B0 = 8 mM. = 2.0. The numerical time-space plot is made at cX0 = 1.5, aB0 = 0.4 and ahB0 = 0.6. The experiments were made with BSF reaction, and the input feed concentrations are: [Na2SO3]X0 = 80 mM, [BrO3−]A0 = 200 mM, [bromocresol green]X0 = 0.21 mM. The time-space plot was recorded at [Fe(CN)64−]X0 = 10 mM, [H2SO4]B0 = 8 mM. | |
 |
| | Fig. 3 Sustained localized oscillations in the FIS (a and b) and in the TuIS reaction (c and d). Time-space plots along the axis x (a and c) and the local oscillations at x = x* on arbitrary grayscale (b and d). Input feed concentrations: [Na2SO3]X0 = 89 mM, [IO3−]A0 = 150 mM, [BCG]X0 = 0.21 mM. In the FIS reaction [Fe(CN)64−]X0 = 20 mM and [H2SO4]B0 = 5.5 mM. In the TuIS reaction: [(NH2)2CS]X0 = 5 mM and [H2SO4]B0 = 7.0 mM. | |
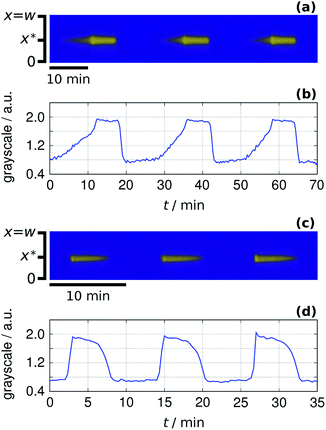
At this point, we could adapt the design method which was originally developed to produce stationary patterns in one-side-fed reactors.16 The key points of this method are finding spatial bistability and spatiotemporal oscillations in a controlled way and ensuring long-range inhibition by using an appropriate large molecular weight complexing agent. In hydrogen ion self-activated RD systems sodium polyacrylate (NaPAA) have been efficiently used for the second purpose.32 In the model the NaPAA only reacts with hydrogen ions in reaction (R4) and its diffusion coefficient is set to be a hundred times smaller than that of the other components. According to the simulations, above a critical input feed concentration of the polycarboxylate compound, symmetry breaking patterns, a row of spots develop (Fig. 4a). The asymmetric shape of these spots is the consequence of the antagonistic gradients. In the experiments, different pattern formation scenarios could be detected above a critical concentration of NaPAA. A single row of low pH spots may appear through an oscillatory destabilization of the M state (Fig. 4b) or by step-by-step formation from the F state (Fig. 4c). In the first scenario, starting from a stable M state (Fig. 4b) the decrease of the concentration of HSO3− in Tank B leads to transient spatiotemporal oscillations. The oscillations stop as low pH spots form and are stabilized in the gel. In the second case (Fig. 4c), the spots appear in the originally F state of the gel, when the concentration of HSO3− in Tank B is increased. The wavelength of the experimentally observed pattern is about 2–3 mm.
 |
| | Fig. 4 Simulated (a) and experimental (b and c) formation of Turing patterns. In each case the two snapshots show the starting and the final state, while the time-space plot represents the transitions. The dimensionless parameters used in the simulations are: aA0 = 1, bA0 = 1.5, cX0 = 2.0, aB0 = 0.4, ahB0 = 0.6, sX0 = 0.5 and w = 2.0. The experiments were made with the input feed concentrations: [Na2SO3]X0 = 80 mM, [BrO3−]A0 = 200 mM, [bromocresol green]X0 = 0.21 mM, [–COO−]X0 = 16 mM, [Fe(CN)64−]X0 = 10 mM, [H2SO4]B0 = 7.4 mM (b) and [Fe(CN)64−]X0 = 5 mM, [H2SO4]B0 = 7.0 mM. | |
4 Conclusions
In this report, we presented a method to produce different types of positional chemical patterns by the interplay of appropriately designed antagonistic gradients of chemicals and the activatory–inhibitory kinetics. This arrangement could be relevant to biological systems where uniform spatial distribution is rare. Here we used it to generate pH patterns by different reactions which do not show oscillations in batch reactor only in the presence of continuous feed. We anticipate that this method can be applied to any chemical or biochemical RD system, where the diffusive gradients of the reagents of the positive feedback process can be maintained. This is the case in most of the reactions which are known as CSTR oscillators.7 The use of TSFRs broadens the scope of the investigation of patterns in spatially distributed systems compared to the popular one-side-fed reactors, as the separation of the reactants avoids the development of oscillations or other instabilities in the feed tanks.33 In a pure Wolpert mechanism, the process which generates the gradients is separated from the one which interprets the positional information. In our design method, the chemicals which provide the gradients are also involved in the signaling mechanism, which makes a direct coupling between these two ingredients and results in the formation of spatial bistability. This arrangement also allows the coupling of an additional physico-chemical process to this core mechanism to induce an additional localized chemical signal. The formation of the stripe of iodine in the FIS experiments (Fig. 1f) is an example of it. We have shown that by introducing a proper chemical negative feedback process localized time-periodic pattern can be induced. The experimental confirmations were made by using four different variants of Landolt type pH oscillators. To initiate Turing instability we have added a large molecular weight hydrogen ion binding agent, in this wise we have created a system, where the Wolpert mechanism is used to localize Turing patterns. The spatially periodic positional pH pattern is an example of the rational combination of the two developmental concepts.34
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank the support of the National Research, Development and Innovation Fund (119360).
Notes and references
- A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37–72 CrossRef.
- L. Wolpert, J. Theor. Biol., 1969, 25, 1–47 CrossRef CAS.
- S. Kondo and T. Miura, Science, 2010, 329, 1616–1620 CrossRef CAS.
- A. D. Economou, A. Ohazama, T. Porntaveetus, P. T. Sharpe, S. Kondo, M. A. Basson, A. Gritli-Linde, M. T. Cobourne and J. B. Green, Nat. Genet., 2012, 44, 348 CrossRef CAS PubMed.
- G. Forgacs and S. A. Newman, Biological physics of the developing embryo, Cambridge University Press, 2005 Search PubMed.
- A. S. Zadorin, Y. Rondelez, G. Gines, V. Dilhas, G. Urtel, A. Zambrano, J.-C. Galas and A. Estevez-Torres, Nat. Chem., 2017, 9, 990 CrossRef CAS PubMed.
- I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press New York, 1998 Search PubMed.
- A. S. Mikhailov and G. Ertl, Chemical Complexity: Self-Organization Processes in Molecular Systems, Springer, 2017 Search PubMed.
- M. Onoda, T. Ueki, R. Tamate, M. Shibayama and R. Yoshida, Nat. Commun., 2017, 8, 15862 CrossRef PubMed.
- J. Horváth, Chem. Commun., 2017, 53, 4973–4976 RSC.
- P. De Kepper, J. Boissonade and I. Szalai, in From sustained oscillations to stationary reaction-diffusion patterns, Springer, 2009, pp. 1–37 Search PubMed.
- V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Phys. Rev. Lett., 1990, 64, 2953 CrossRef CAS.
- Z. Noszticzius, W. Horsthemke, W. McCormick, H. L. Swinney and W. Tam, Nature, 1987, 329, 619–620 CrossRef CAS.
- I. Lengyel, S. Kádár and I. R. Epstein, Phys. Rev. Lett., 1992, 69, 2729 CrossRef CAS.
- B. Rudovics, E. Dulos and P. De Kepper, Phys. Scr., 1996, 1996, 43 CrossRef.
- J. Horváth, I. Szalai and P. De Kepper, Science, 2009, 324, 772–775 CrossRef PubMed.
- J. Horváth, I. Szalai and P. De Kepper, Phys. D, 2010, 239, 776–784 CrossRef.
- I. Szalai, J. Horváth, N. Takács and P. De Kepper, Phys. Chem. Chem. Phys., 2011, 13, 20228–20234 RSC.
- H. Liu, J. A. Pojman, Y. Zhao, C. Pan, J. Zheng, L. Yuan, A. K. Horváth and Q. Gao, Phys. Chem. Chem. Phys., 2012, 14, 131–137 RSC.
- I. Molnár and I. Szalai, J. Phys. Chem. A, 2015, 119, 9954–9961 CrossRef PubMed.
- G. Rabai, ACH - Models Chem., 1998, 135, 381–392 CAS.
- M. Orbán, K. Kurin-Csörgei and I. R. Epstein, Acc. Chem. Res., 2015, 48, 593–601 CrossRef PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS.
- G. Schuszter, T. Gehér-Herczegh, Á. Szűcs, Á. Tóth and D. Horváth, Phys. Chem. Chem. Phys., 2017, 19, 12136–12143 RSC.
- A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, ACM Trans. Math. Softw., 2005, 31, 363–396 CrossRef.
- S. Dushman, J. Phys. Chem., 1904, 8, 453–482 CrossRef.
- P. Blanchedeau and J. Boissonade, Phys. Rev. Lett., 1998, 81, 5007–5010 CrossRef CAS.
- P. Borckmans, K. Benyaich and G. Dewel, Int. J. Quantum Chem., 2004, 98, 239–247 CrossRef CAS.
- J. Boissonade, P. De Kepper, F. Gauffre and I. Szalai, Chaos, 2006, 16, 037110 CrossRef CAS.
- J. Boissonade and P. De Kepper, J. Phys. Chem., 1980, 84, 501–506 CrossRef CAS.
- G. Rabai and I. R. Epstein, Inorg. Chem., 1989, 28, 732–736 CrossRef CAS.
- I. Szalai and P. De Kepper, J. Phys. Chem. A, 2008, 112, 783–786 CrossRef CAS PubMed.
- I. Szalai, J. Horváth and P. De Kepper, Chaos, 2015, 25, 064311 CrossRef PubMed.
- J. B. Green and J. Sharpe, Development, 2015, 142, 1203–1211 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Derivation of the numerical model, additional figures & movies of spatiotemporal oscillations. See DOI: 10.1039/c8ra08028c |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
István Szalai
and
István Szalai *
*

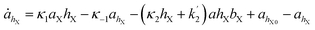
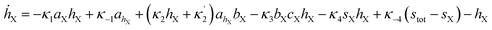
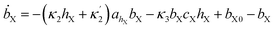
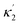 , κ3, κ4 and κ−4 are set to 5 × 105, 5 × 101, 5 × 103, 5 × 1010, 5 × 107 respectively. The composition of the gel content is calculated by the following equations:
, κ3, κ4 and κ−4 are set to 5 × 105, 5 × 101, 5 × 103, 5 × 1010, 5 × 107 respectively. The composition of the gel content is calculated by the following equations: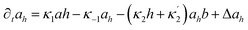
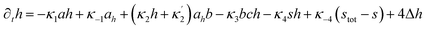
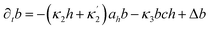
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) *) is mainly determined by the concentration gradient of B and can be calculated as:
*) is mainly determined by the concentration gradient of B and can be calculated as: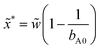
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry of reaction (R2) and on a linear approximation of the gradients, is in good agreement with the numerical simulations. The width of the high H+ concentration band is directly proportional to w (Fig. S1 in ESI†). This type of size invariance of the three-zoned-pattern is the consequence of the bipolarity of the system.2 In the experiments, at the M state of the system a sharp zone forms inside the gel, where the indicator switches to its low pH color (Fig. 1g). When iodate was used as the oxidant, iodine precipitate formation was observed within the acidic zone due to the Dushman reaction (Fig. 1h).26 According to the simulations and also the experiments made in four different systems (BSF, FIS, TuIS, and HPSF), the F and the M states may coexist, that is spatial bistability. In chemical RD systems this behavior have been demonstrated only in the presence of unidirectional concentration gradients (e.g. in one-side-fed reactors), previously.27–29
1 stoichiometry of reaction (R2) and on a linear approximation of the gradients, is in good agreement with the numerical simulations. The width of the high H+ concentration band is directly proportional to w (Fig. S1 in ESI†). This type of size invariance of the three-zoned-pattern is the consequence of the bipolarity of the system.2 In the experiments, at the M state of the system a sharp zone forms inside the gel, where the indicator switches to its low pH color (Fig. 1g). When iodate was used as the oxidant, iodine precipitate formation was observed within the acidic zone due to the Dushman reaction (Fig. 1h).26 According to the simulations and also the experiments made in four different systems (BSF, FIS, TuIS, and HPSF), the F and the M states may coexist, that is spatial bistability. In chemical RD systems this behavior have been demonstrated only in the presence of unidirectional concentration gradients (e.g. in one-side-fed reactors), previously.27–29


![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif)


