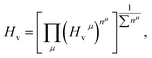Open Access Article
Open Access ArticleCrystal structures of transition metal pernitrides predicted from first principles†
Rongmei Yu ab,
Ermiao Suna,
Liguang Jiaoa,
Yongmao Caid,
Hongbo Wang
ab,
Ermiao Suna,
Liguang Jiaoa,
Yongmao Caid,
Hongbo Wang *a and
Yansun Yaoc
*a and
Yansun Yaoc
aState Key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun, 130012, P. R. China. E-mail: whb2477@jlu.edu.cn
bCollege of Physics and Electronic Engineering, Nanyang Normal University, Nanyang, 473061, P. R. China
cDepartment of Physics and Engineering Physics, University of Saskatchewan, Saskatoon, Saskatchewan S7N 5E2, Canada
dSchool of Science, Northeast Electric Power University, Jilin, 132012, P. R. China
First published on 26th October 2018
Abstract
We have extensively explored the stable crystal structures of early-transition metal pernitrides (TMN2, TM = Ti, V, Cr, Mn, Zr, Nb, Mo, Hf, and Ta) at ambient and high pressures using effective CALYPSO global structure search algorithm in combination with first-principles calculations. We identified for the first time the ground-state structures of MnN2, TaN2, NbN2, VN2, ZrN2, and HfN2 pernitrides, and proposed their synthesis pressures. All predicted crystal structures contain encapsulated N2 dumbbells in which the two N atoms are singly bonded to a [N2]4− pernitride unit utilizing the electrons transferred from the transition metals. The strong nature of the single dinitrogen bond and transition metal–nitrogen charge transfer induce extraordinary mechanic properties in the predicted transition metal pernitrides including large bulk modulus and high Vickers hardness. Among the predictions the hardness of MnN2 is 36.6 GPa, suggesting that it is potentially a hard material. The results obtained in the present study are important to the understanding of structure–property relationships in transition metal pernitrides and will hopefully encourage future synthesis of these technologically important materials.
Introduction
Transition metal (TM) nitrides have attracted considerable attention due to their fundamental importance in crystal chemistry and applications in industry. Most TM nitrides exist on the metal-rich side of the stoichiometric diagram (TM:N > 1), and therefore often exhibit metallic properties. Nitrogen-rich TM nitrides (N:TM > 1) can be synthesized by reacting elemental TM or TM simple nitrides with excess of N2 gas under high pressure and high temperature conditions. The most common stoichiometry for nitrogen-rich TM nitrides is TMN2, often referred to as the ‘pernitrides’. Since the initial success on the synthesis of platinum nitride,1 experimental exploration for novel TM nitrides has expanded substantially, and uncovered new members including PtN2,2 IrN2,2,3 OsN2,3 PdN2,4 RuN2,5 RhN2,6 TiN2,7 and FeN2.8 The list is still growing rapidly. Most of these new compounds have very high bulk modulus, a property that potentially leads to applications such as cutting tools and wear-resistant coatings. In particular, the bulk modulus of platinum nitride is comparable to that of cubic BN, a known superhard material, which is about 100 GPa higher than that of pure platinum.1 The extraordinary mechanical properties of TM pernitrides are associated with a particular structural motif. Although their crystal structures may be different, most TM pernitrides contain ultra-incompressible N2 dumbbells which are held together by strong covalent N–N interaction. Albeit similar to the N2 molecule in geometry, these N2 dumbbells are single-bonded in nature, utilizing the electrons transferred from the TM atoms. The strength of the N–N interactions in the N2 dumbbells are comparable to that in the single-bonded polymeric phase of nitrogen.9 As such, the nitrogen atoms in most TM pernitrides are octahedrally coordinated with TM atoms by strong, directional TM–N bonds and form TMN6 octahedrons which are then interconnected through N–N bonds in three dimensions. Clearly, knowing the crystal structures of TM pernitrides are very important for understanding their extraordinary mechanic properties, however, this is not always an easy task in experiment. A known difficulty is that X-ray diffraction is unable to determine the positions of the nitrogen atoms in TM nitrides due to the large TM/N atomic mass ratio.Meanwhile, many theoretical studies have been carried out to help resolving the crystal structures of TM pernitrides, and to predict new targets for future synthesis. The structure of OsN2 was determined to be isostructural to that of marcasite with orthorhombic Pnnm space group.10 PtN2 and PdN2 were found to form in the cubic pyrite structure with the Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group.11 RuN2 and RhN2 were predicted to have marcasite structure as well10 which was then experimentally confirmed.5,6 The IrN2 was predicted to be isostructural to CoSb2 or arsenopyrite10,12 however the subsequently synthesized IrN2 has a baddeleyite-type structure.4 For ReN2, three structures were predicted as possible candidates, namely, rutile structure (P42/mnm),13 Pbcn structure,14 and distorted rhenium diboride structure (P4/mmm),15 but the synthesized ReN2 has the MoS2 structure.16 On early TM side, MoN2 was synthesized with a rhombohedral MoS2 structure.17 However, a theoretical study suggests that the thermodynamic ground state of MoN2 should have a hexagonal structure.18 TiN2 has been predicted to have the tetragonal CuAl2-type structure (I4/mcm)19 which was successfully synthesized soon after.7 It is noteworthy that the synthesized TiN2 has a very high bulk modulus of 385 GPa.7 In addition to the realized pernitrides, many others were predicted to exist as well, await for future synthesis. The long list includes ZrN2,20 CrN2,21 NbN2,22 HfN2,23 WN2,24 and others.25–27 Several new prototypic structures were proposed for TM pernitrides, including the pyrite-type, P63/mmc and P
space group.11 RuN2 and RhN2 were predicted to have marcasite structure as well10 which was then experimentally confirmed.5,6 The IrN2 was predicted to be isostructural to CoSb2 or arsenopyrite10,12 however the subsequently synthesized IrN2 has a baddeleyite-type structure.4 For ReN2, three structures were predicted as possible candidates, namely, rutile structure (P42/mnm),13 Pbcn structure,14 and distorted rhenium diboride structure (P4/mmm),15 but the synthesized ReN2 has the MoS2 structure.16 On early TM side, MoN2 was synthesized with a rhombohedral MoS2 structure.17 However, a theoretical study suggests that the thermodynamic ground state of MoN2 should have a hexagonal structure.18 TiN2 has been predicted to have the tetragonal CuAl2-type structure (I4/mcm)19 which was successfully synthesized soon after.7 It is noteworthy that the synthesized TiN2 has a very high bulk modulus of 385 GPa.7 In addition to the realized pernitrides, many others were predicted to exist as well, await for future synthesis. The long list includes ZrN2,20 CrN2,21 NbN2,22 HfN2,23 WN2,24 and others.25–27 Several new prototypic structures were proposed for TM pernitrides, including the pyrite-type, P63/mmc and P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 structures, some of which were suggested based on the structure analogy with chemically similar materials. Mechanic properties in particular the elasticity and hardness of TM pernitrides was one of the focal points of these investigations.
m2 structures, some of which were suggested based on the structure analogy with chemically similar materials. Mechanic properties in particular the elasticity and hardness of TM pernitrides was one of the focal points of these investigations.
In the present study, we systematically explored the stable phases of TM pernitides adding several new ones (TM = Ti, V, Cr, Mo, Mn, Zr, Nb, Hf, and Ta). Some of these compounds have been studied before but the methods used based on known structure analogy may not guarantee finding the global minima of these phases, as shown in several cases above. To this end we employed a global structure search in combine with first principle calculations aiming to find the true thermodynamic ground states of these compounds. Since the laboratory synthesis of TM pernitrides often requires high pressure, the search is expanded from ambient to high pressures range up to 100 GPa. The CrN2 and MoN2 were found to have the same hexagonal structure (P63/mmc), while MnN2 has a P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structure. TaN2 is predicted to have an orthorhombic Cmca structure. For NbN2, the present study uncovers a new monoclinic structure (Cc) which is thermodynamically more stable than the previously proposed Cmca structure. TiN2 was found to have the CuAl2-type structure (I4/mcm), which is in agreement with previous experimental and theoretical reports. In addition, VN2, ZrN2 and HfN2 were predicted to have the same CuAl2-type (I4/mcm) structure. All predicted TM pernitrides are thermodynamically stable with respect to decomposition to elemental TM and N2 at ambient pressure. CrN2, MoN2, and MnN2 are also found stable against decomposition to simple nitride TMN and N2 at ambient pressure. The established thermal stability suggests that the predicted TM pernitrides are likely synthesizable at high pressure and can be quench recovered at ambient conditions.
structure. TaN2 is predicted to have an orthorhombic Cmca structure. For NbN2, the present study uncovers a new monoclinic structure (Cc) which is thermodynamically more stable than the previously proposed Cmca structure. TiN2 was found to have the CuAl2-type structure (I4/mcm), which is in agreement with previous experimental and theoretical reports. In addition, VN2, ZrN2 and HfN2 were predicted to have the same CuAl2-type (I4/mcm) structure. All predicted TM pernitrides are thermodynamically stable with respect to decomposition to elemental TM and N2 at ambient pressure. CrN2, MoN2, and MnN2 are also found stable against decomposition to simple nitride TMN and N2 at ambient pressure. The established thermal stability suggests that the predicted TM pernitrides are likely synthesizable at high pressure and can be quench recovered at ambient conditions.
Computational approaches
The investigation of TM pernitrides consists of the determination of ground state crystalline structures and calculation of the properties of interest. The density functional theory (DFT)28 based calculations reported in the present work were carried out using the Vienna ab initio simulation package (VASP)29,30 with the projector augmented wave scheme (PAW).31 The exchange correlation functional with the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)32 was used to solve the Kohn–Sham equations. Global crystal structure searches for TM pernitrides were performed using the particle-swarm optimization (PSO) algorithm for structural prediction as implemented in the CALYPSO code, which has been proved to be effective and accurate in predicting the crystal structures of a large variety of materials.33,34 The structure searches were performed using the CALYPSO code in combination with DFT total energy calculations and system sizes ranging from 1 to 4 formula units (f.u.) per simulation cell at several pressure points in the pressure range of 0–100 GPa. The obtained low-enthalpy structures were then further optimized using more strict more convergence criteria with a kinetic energy cutoff of 750 eV and k-point meshes of spacing 2π × 0.03 Å−1 for Brillouin zone integration. The energy convergence with respect to these parameters was set to be better than 1 meV per atom. Phonon dispersion relations were calculated on the basis of the supercell approach by using the PHONOPY package.35 A 2 × 2 × 2 supercell was constructed for VN2, ZrN2, HfN2, and MnN2, 3 × 3 × 3 for NbN2 and 2 × 1 × 2 for TaN2 to calculate forces. Bulk modulus, shear modulus, Young's modulus, and Poisson's ratio were estimated by using Voigt–Reuss–Hill approximation.36 Chemical bonding analyses for the crystal structures of interest were carried out by means of the crystal orbital Hamilton population (COHP) method implemented in the LOBSTER program package.37,38Results and discussion
The most energetically favored crystal structure for each TM pernitride of interest was successfully obtained from the global structure search. The enthalpies for these structures (H) were calculated in the pressure range 0–100 GPa, and compared to the enthalpies of the decomposition products along two possible decomposition routes:| ΔHf(I) = HTMN2 − HTM − HN2 | (1) |
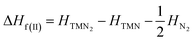 | (2) |
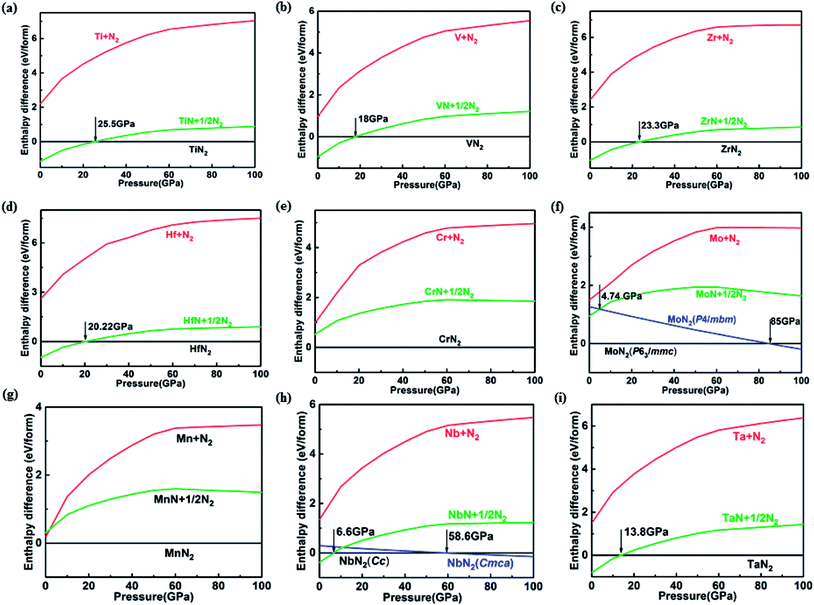
The route (1) describes the decomposition to elemental TM and solid N2, while route (2) is for the decomposition to simple TM nitride (TMN) and solid N2. The relative enthalpy of formation ΔHf has been calculated using the lowest-enthalpy structures of TMN2, TMN, and N2 previously known or obtained from the structure searches as reference structures (see ESI† for details). The results shown in Fig. 1 reveal that all predicted structures of TM pernitrides are thermodynamically stable against the decomposition route (1) at ambient pressure (shown by negative ΔHf). For decomposition route (2), the CrN2, MoN2, and MnN2 are stable at ambient pressure. The rest TM pernitrides are thermodynamically unstable at ambient pressure but quickly become stable at moderate pressures (4.74–25.5 GPa). The calculated ΔHf(I) and ΔHf(II) are listed in Table 1. The proposed pressures of formation for these nitrides (arrows in Fig. 1) are well within the reach of current high-pressure synthesis, which provides a good chance that they can be synthesized under high pressure and then quench recovered to ambient conditions. Among these nitrides the TiN2 has already been realized in laboratory at pressures at a pressure of 73 GPa.7 Although the starting materials (TiN and N2) and product (I4/mcm TiN2) are the same, the calculated pressure for its formation is 25.5 GPa, which is lower than the experimental pressure by about 50 GPa. The large discrepancy is mainly attributed to the known large energy barrier associated with the formation of TM pernitrides. To overcome the barrier, high temperature is usually required for the synthesis. Thus, we expect moderated higher formation pressures than what calculated here for all predicted TM pernitrides.
| Crystal | Phases | a0 | b0 | c0 | V0 | dTM–N | dN–N | Hf(I) | Hf(II) | Hv (GPa) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TiN2 | Our | I4/mcm | 4.347 | 4.347 | 5.314 | 25.1 | 2.201 | 1.378 | −2.194 | 1.153 | 32.6 |
| Ref. 19 | I4/mcm | 4.334 | 4.334 | 5.294 | 1.383 | 26 | |||||
| VN2 | Our | I4/mcm | 4.308 | 4.308 | 4.955 | 23.0 | 2.133 | 1.382 | −0.960 | 0.955 | 35.6 |
| ZrN2 | Our | I4/mcm | 4.600 | 4.600 | 5.766 | 30.5 | 2.357 | 1.424 | −2.412 | 1.060 | 26.4 |
| HfN2 | Our | I4/mcm | 4.549 | 4.549 | 5.673 | 29.4 | 2.318 | 1.458 | −2.600 | 0.972 | 27.6 |
| CrN2 | Our | P63/mmc | 2.733 | 2.733 | 7.382 | 23.87 | 1.968 | 1.336 | −0.973 | −0.526 | 34.0 |
| Ref. 21 | P63/mmc | 2.733 | 2.733 | 7.382 | 23.87 | 1.968 | 1.336 | 45.9 | |||
| MoN2 | Our | P63/mmc | 2.934 | 2.934 | 7.766 | 28.94 | 2.106 | 1.380 | −1.500 | −0.950 | 27.7 |
| Ref. 17 | P63/mmc | 2.927 | 2.927 | 7.762 | |||||||
| MnN2 | Our | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
4.851 | 4.791 | 4.791 | 23.71 | 1.981 | 1.309 | −0.178 | −0.307 | 36.6 |
| NbN2 | Our | Cc | 12.584 | 3.105 | 6.092 | 28.89 | 2.150 | 1.344 | −1.347 | 0.385 | 3.27 |
| Ref. 22 | Cmca | 12.496 | 4.224 | 4.222 | 27.85 | 2.199 | 1.324 | 12.06 | |||
| TaN2 | Our | Cmca | 4.206 | 12.332 | 4.203 | 27.26 | 2.188 | 1.371 | −1.494 | 0.810 | 13.6 |
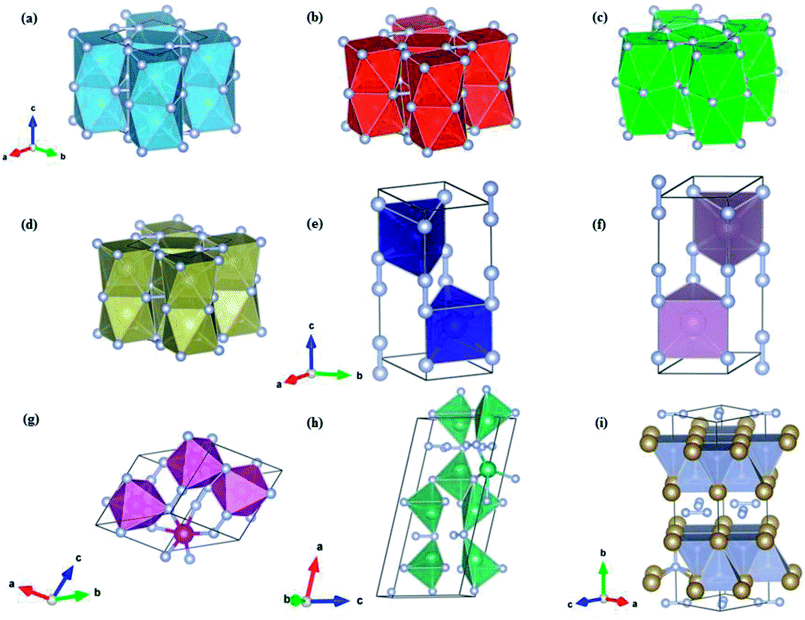
The crystal structure and optimized lattice parameters of the predicted TM pernitrids are shown in Fig. 2 and Table 1. For previously synthesized TiN2, our structure search correctly produces its structure at ambient and high pressures, the CuAl2-type structure (I4/mcm) (Fig. 2a). The calculated lattice parameters are a = 4.35 Å, c = 5.31 Å, very close to the experimental values, a = 4.33 Å and c = 5.29 Å.7 For CrN2, which has yet to be synthesized, we predict its ground state is a hexagonal structure with the P63/mmc structure (Fig. 2e). This prediction agrees with a previous theoretical report.21 The P63/mmc structure is the lowest enthalpy phase of CrN2 from ambient pressure to at least 100 GPa, the highest pressure used in the present study. The P63/mmc structure is consisting of MoS2-type CrN2 slabs stacked by covalent N–N bonds with an ABA sequence (Fig. 2e). If the N2 units are considered as a single entity, this structure would reduce to a NiAs-type hexagonal structure. The N–N distance within the N2 units is 1.336 Å, which is much longer than the bondlength in triply bonded N2 molecule (1.10 Å). The bondlength in the N2 units is close to that of a single bond in hydrazine (1.45 Å), and longer than that of a double bond in dinitrogen difluoride (1.21 Å). Thus, we may consider the N2 unit singly bonded, formally a [N2]4− anion. The CrN2 is nominally a charge transfer Cr4+N24−, which should form a semiconducting state. The P63/mmc structure is also the ground state structure for MoN2 at ambient pressure. A phase transition is predicted for MoN2 at 85 GPa, at where it transforms to a P4/mbm structure. This prediction agrees with previous theoretical study as well.18 The experimentally discovered MoS2 structure of CrN2 (ref. 17) was calculated to be a metastable phase. The P4/mbm structure contains MoN8 cuboids that are interconnected by edge-sharing and staked along the perpendicular direction through Mo–N bonds. The N2 dumbells are still retained in the P4/mbm structure and singly bonded. Unlike CrN2 and MoN2, the other stable pernitride MnN2 has a low symmetry monoclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structure. In this structure, the Mn atom is octahedrally coordinated with six N atoms to MN6 octahedra that are interconnected through N–N bonds. The bondlength of the N–N bonds is 1.31 Å, similar to those in CrN2 and MoN2.
structure. In this structure, the Mn atom is octahedrally coordinated with six N atoms to MN6 octahedra that are interconnected through N–N bonds. The bondlength of the N–N bonds is 1.31 Å, similar to those in CrN2 and MoN2.
The NbN2 and TaN2 compounds have been previously investigated theoretically,24,27 and several candidate structures were proposed based on educated guesses from known structures of chemically similar compounds. The considered structures include P63/mmc, P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2, Pa
m2, Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , pyrite and fluorite structures. In the present study, however, we found none of this structure corresponding to the ground state of NbN2 and TaN2. The predicted ground state of TaN2 has the Cmca space group instead. In this structure, the Ta and N are sandwiched to form distorted TaN5 quadrangular pyramid which are extended to two dimensional slabs with shared edges. The slabs are intercalated with the N2 dimers along the c-axis (Fig. 2i). According to the N–N bondlength, i.e., 1.37 Å, the N2 dimers are singly bonded. The Cmca structure is predicted to form at pressures above 13.8 GPa and stays stable to at least 100 GPa. For NbN2, our structure search establishes a monoclinic structure with the Cc space group as its ground state at ambient pressure. The previously proposed Cmca structure22 is found to have slightly higher enthalpy, e.g., ∼29.2 meV f.u.−1 at ambient pressure. On the other hand, the Cmca structure is more stable at high pressures which surpasses the Cc structure at 58.6 GPa to become the thermodynamic ground state (Fig. 1h).
, pyrite and fluorite structures. In the present study, however, we found none of this structure corresponding to the ground state of NbN2 and TaN2. The predicted ground state of TaN2 has the Cmca space group instead. In this structure, the Ta and N are sandwiched to form distorted TaN5 quadrangular pyramid which are extended to two dimensional slabs with shared edges. The slabs are intercalated with the N2 dimers along the c-axis (Fig. 2i). According to the N–N bondlength, i.e., 1.37 Å, the N2 dimers are singly bonded. The Cmca structure is predicted to form at pressures above 13.8 GPa and stays stable to at least 100 GPa. For NbN2, our structure search establishes a monoclinic structure with the Cc space group as its ground state at ambient pressure. The previously proposed Cmca structure22 is found to have slightly higher enthalpy, e.g., ∼29.2 meV f.u.−1 at ambient pressure. On the other hand, the Cmca structure is more stable at high pressures which surpasses the Cc structure at 58.6 GPa to become the thermodynamic ground state (Fig. 1h).
To date, VN2, ZrN2 and HfN2 have not been synthesized. In a previous theoretical study,23 ZrN2 and HfN2 are assumed to have the same ground state structure as TiN2 since the three TMs are in the same group in the periodic table. Our structure search confirmed this conjecture. Both ZrN2 and HfN2 adopt the CuAl2-type structure (I4/mcm) and no phase transitions are found over the entire pressure range investigated (0–100 GPa). A unique feature of the I4/mcm structure is that the TM and N atoms form TMN8 face-sharing tetragonal antiprisms, rather than TMN6 octahedrons commonly seen in TM pernitrides (Fig. 2). The neighboring antiprism are connected through N2 dumbbells along a- and b-axis. The N–N bondlengths are 1.42 and 1.46 Å, respectively, for ZrN2 and HfN2. These values are very close to the ideal length of single nitrogen bond (1.45 Å) and those observed in some transition metal pernitrides such as PtN2 (1.41 Å) and OsN2 (1.43 Å).2,3 This indicates that the N2 dumbbells are singly bonded with a nominal [N2]4− state, which is isoelectronic to difluorine F2 (1.43 Å). The previously unknown VN2 is predicted to have the same I4/mcm structure with slightly shorter N–N bondlength (1.38 Å).
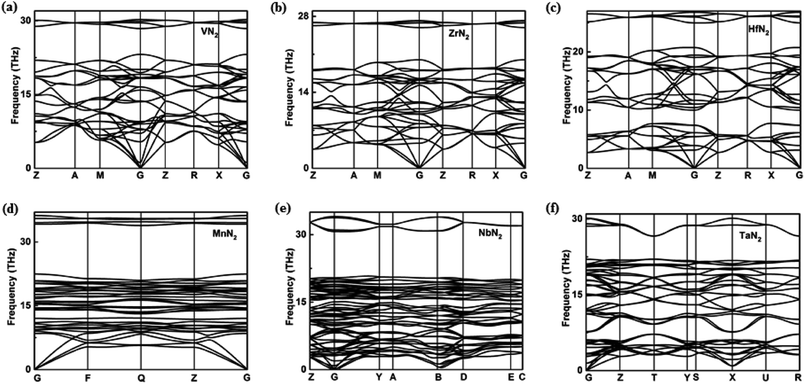
In view of the pernitride structures described above, TiN2 and VN2 have almost same N–N bond lengths (1.37 Å and 1.38 Å), but ZrN2 and HfN2 have longer bond lengths (1.42 Å, 1.46 Å), suggesting the presence of more ‘soften’ N2 in the latter. Clearly, the bondlength here is an indicator of bonding interaction, where the ‘shorter bond equals stronger bond’ conjecture prevails. For N2 quasimolecules, specifically, this also reveals the degree of electron sharing between two N atoms, from triply bonded N2, to doubly bounded [N2]2−, and to singly bonded [N2]4−. The amount of electrons transferred from the transition metal therefore determines the bonding type, and ultimately determine the crystal structure. This is manifested by the fact that the Vickers hardness of the 3d TM pernitrides (32.6 GPa (TiN2), 35.6 GPa (VN2)) are in general higher than those of 4d and 5d TM pernitrides (26.4 GPa (ZrN2), 27.6 GPa (HfN2)). The dynamical stability of the predicted TM pernitrides are verified by the analysis of phonon-dispersion relations in the pressure range of 0–100 GPa (Fig. 3).
Among which, the dynamical stability of TiN2, CrN2, and MoN2 have already been established in previous theoretical studies.18,19,21 The new pernitrides predicted in the present study, namely, VN2, ZrN2, HfN2, MnN2, NbN2, and TaN2, are confirmed dynamically stable from ambient pressure to their thesis pressure, by the absence of imaginary phonon frequency in the entire BZ (Fig. 3). The dynamic stabilities of predicted pernitrides provide a very strong case that they can be recovered at ambient conditions once synthesized under high pressure and high temperature.
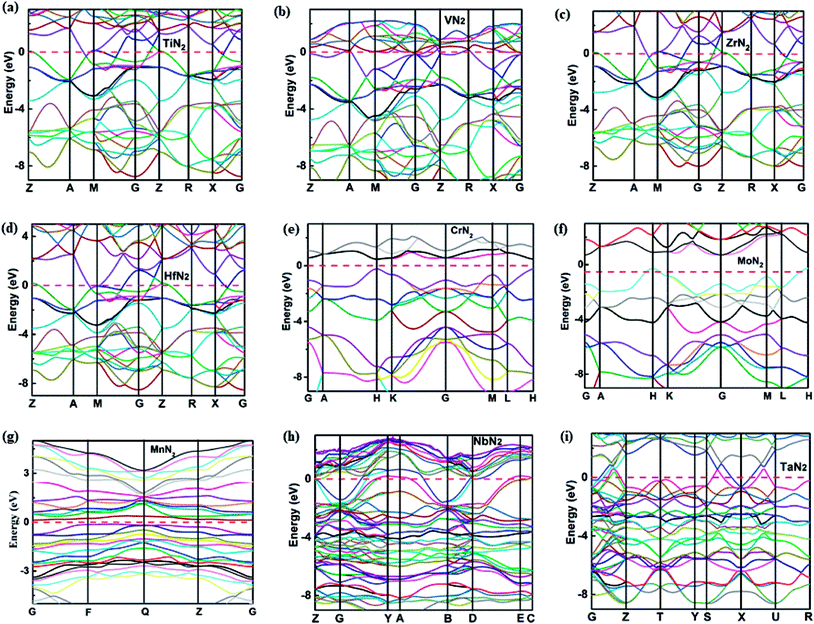
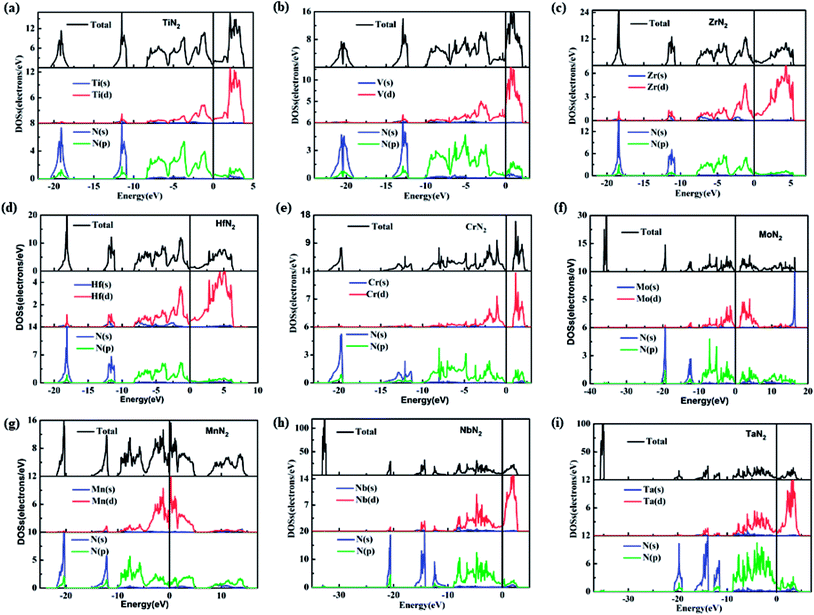
To understand the electronic properties and bonding features of these pernitrides, we have calculated their electronic band structure and density of states (DOS) at ambient pressure. The results are presented in Fig. 4 and 5. From the band structures and DOS, all compounds having the I4/mcm structure (TiN2, VN2, ZrN2, and HfN2), the Cc structure (NbN2) and the Cmca structure (TaN2) are metallic owing to the finite DOS at the Fermi level due to multiple bands crossing. Projected DOS reveals that the electronic states at the Fermi level are dominated by the d electrons of TM and p electrons of N (Fig. 5). In particular, there are strong orbital hybridization between the d orbital of TM and p orbital of N in the energy range from −10 to 0 eV, indicating the interactions between TM and N are covalent in nature. Moreover, in most of the pernitrides the total DOS has a minimum value at the Fermi level (pseudo gap), which limits the possibility of achieving credible electrical conductivity, but the tendency of opening a band gap at the Fermi level is seen as a stabilization to the structures due to strong interactions between TM and N. The VN2 is an exception in which the Fermi level shifts toward higher energy range and lies outside the pseudogap with relative higher electronic density of states. On the other hand, the compounds with the P63/mcm structure (CrN2 and MoN2) and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structure (MnN2) are semiconductors. In particular the CrN2 is predicted as a direct band gap semiconductor with the band gap of 0.51 eV. The other two pernitrides have indirect band gaps, i.e., 0.38 eV for MoN2 and 1.0 eV for MnN2, respectively.
structure (MnN2) are semiconductors. In particular the CrN2 is predicted as a direct band gap semiconductor with the band gap of 0.51 eV. The other two pernitrides have indirect band gaps, i.e., 0.38 eV for MoN2 and 1.0 eV for MnN2, respectively.
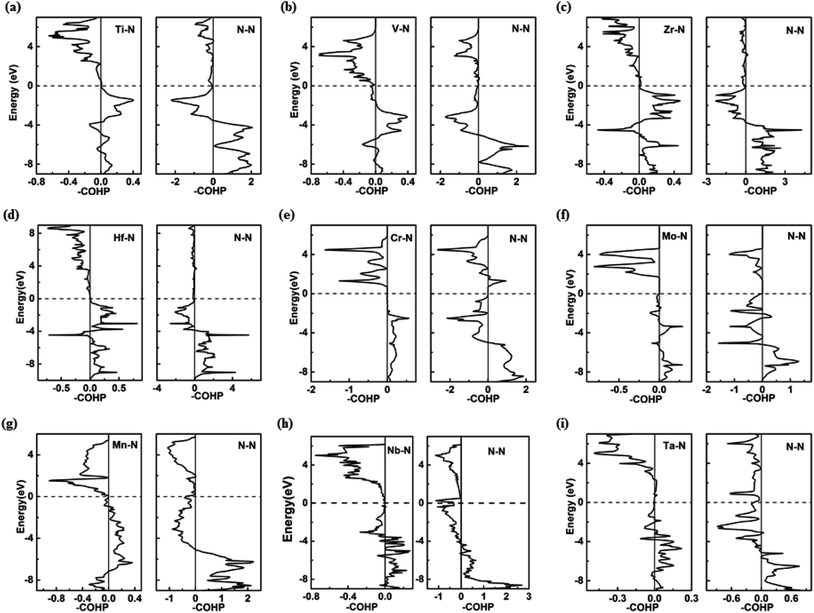
Further analysis of chemical bonding in these pernitride has been carried out through crystal orbital Hamilton population (COHP) analysis (Fig. 6). COHP partitions the band-structure energy into different orbital–pair interactions, which can be used to index bonding, nonbonding, and antibonding contributions to the band-structure. Similar to the crystal-orbital overlap population (COOP), the COHP analysis provides a quantitative measure of the bond strengths in crystal structures by the –COHP values, where the positive and negative signs represent bonding and antibonding states, respectively. Here we draw positive –COHP values to the right and negative ones to the left, so the spikes on the left/right hand side correspond to antibonding/bonding states. In general, for TM–N interactions in predicted pernitrides the antibonding states show up in the unoccupied crystal orbitals well above the Fermi level (dotted horizontal zero line), whereas for N–N interactions, the antibonding 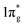 states are primarily between −4 eV and the Fermi level. This is a significant finding, that the
states are primarily between −4 eV and the Fermi level. This is a significant finding, that the 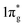 states are mostly occupied in TMN2 pernitrides. For neutral N2 molecule, the
states are mostly occupied in TMN2 pernitrides. For neutral N2 molecule, the 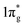 states are completely empty, resulting in exceedingly strong triple bonds. Adding two electrons to the
states are completely empty, resulting in exceedingly strong triple bonds. Adding two electrons to the 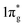 states would result in double-bonded [N2]2−, which is isoelectronic to O2. Adding two more electrons would fully occupy the
states would result in double-bonded [N2]2−, which is isoelectronic to O2. Adding two more electrons would fully occupy the 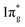 states and produce single-bonded [N2]4−, which is isoelectronic to F2. As demonstrated in previous work,39 for the case of PtN2, electrons transferred from Pt to N results in the full filling of antibonding
states and produce single-bonded [N2]4−, which is isoelectronic to F2. As demonstrated in previous work,39 for the case of PtN2, electrons transferred from Pt to N results in the full filling of antibonding 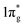 states for which a plausible electronic formulation should be Pt4+[N2]4−. This single-bond scenario is also applicable to predicted pernitrides TMN2, as seen from the results of the COHP analysis and very similar N–N bondlengths in TMN2 matching to that of F–F distance (1.42 Å), although the exact occupation of the
states for which a plausible electronic formulation should be Pt4+[N2]4−. This single-bond scenario is also applicable to predicted pernitrides TMN2, as seen from the results of the COHP analysis and very similar N–N bondlengths in TMN2 matching to that of F–F distance (1.42 Å), although the exact occupation of the 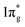 states may vary in different TMN2 pernitrides.7,19 This is fundamentally different from alkaline-earth pernitrides such as BaN2,40 and SrN2 (ref. 41) which only contain double-bonded [N2]2− units.
states may vary in different TMN2 pernitrides.7,19 This is fundamentally different from alkaline-earth pernitrides such as BaN2,40 and SrN2 (ref. 41) which only contain double-bonded [N2]2− units.
Previously, it is suggested that the extraordinary mechanical properties and hardness of TM pernitrides are induced by the single nature of dinitrogen bond and charge transfer from TM to N. In opposite, BaN and SrN have only two electrons in the 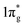 states and therefore exhibit much smaller hardness.39 The charge transfer controls the length of the single bond by providing Coulomb repulsion between two N atoms, and influences the bulk modulus.26 As the predicted TM pernitrides fall into this category, it is interesting to examine their mechanic properties and hardness. The total Vickers hardness (Hv) of a compound is expressed as the geometric average of the hardnesses of individual bonds,
states and therefore exhibit much smaller hardness.39 The charge transfer controls the length of the single bond by providing Coulomb repulsion between two N atoms, and influences the bulk modulus.26 As the predicted TM pernitrides fall into this category, it is interesting to examine their mechanic properties and hardness. The total Vickers hardness (Hv) of a compound is expressed as the geometric average of the hardnesses of individual bonds,
| Hμv (GPa) = 423.8NvXabe−2.7fi − 3.4 |
The calculated Vickers hardness of predicted TMN2 pernitrides are shown in Table 1. It is worth noting that MnN2 has the highest hardness (36.6 GPa) among them, while VN2 has a near second value (35.6 GPa). The NbN2 and TaN2 on the other hand have very low hardness as what one would expect for metals. The high hardness in MnN2 is facilitated by the formation of three-dimensional (3D) covalent networks driven by hybridizations of N-p and TM-d electrons. For VN2, the hardness is associated to the short V–N bonds: the V–N bonds is 2.133 Å at ambient pressure, even shorter than the Ti–N bond (2.201 Å) in the isostructural TiN2, a known hard material. In the case of isostructural pernitrides, clearly there is a correlation between the hardness and the strength of the covalent bonds. The calculated bulk (B), shear (G), Young's (E) moduli and Poisson's ratio for predicted TMN2 pernitrides are presented in Table 2 and compared with the previous theoretical or experimental results available. The results agree well with the reported theoretical values, demonstrating the reliability of the present calculations. Pugh's ratio (G/B) and Poisson's ratio (Pr) are the factors which describe the ductile/brittle nature of a material. In 1954, Pugh43 has proposed that a high value (>0.57) is associated with brittleness and a low value (<0.57) indicates the ductile nature of materials. Frantsevich et al.44 has also separated the ductility and brittleness of a material in terms of Poisson's ratio (Pr) and suggested that if the Poisson's ratio is less than 0.26 then the material will be brittle otherwise the material will be ductile. The calculated Pugh's ratios and Poisson's ratio show that all predicted TMN2 pernitrides are intrinsically brittle except the two metallic ones (NbN2 and TaN2). The obtained bulk modulus for TiN2 is 288 GPa, which is consistent to the theoretical value (284 GPa) predicted by Yu et al.,19 but substantially lower than the measured values (360–385 GPa).7 In view of the discrepancy, the experimental uncertainties in fitting the EOS and density functional calculation errors in estimating the crystal volumes should be both taken into consideration. In general, the predicted TMN2 pernitrides have high bulk moduli close to that of IrN2 (B = 327 GPa), PtN2 (B = 272 GPa) and OsN2 (B = 359 GPa),3,23 indicating that these materials are highly incompressible. From Table 2 one can also see that for isostructural pernitrides, TiN2, VN2, ZrN2 and HfN2, the highest bulk modulus goes to VN2 which has the shortest TM–N distances. The correlation between the bulk modulus and bondlength may be understood from the charge transfer from TM to N. The charge transfer influences the dinitrogen bond strength by increasing Coulomb repulsion between two N atoms and populating the antibonding 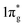 states, which jointly lead to the elongation of N–N bond and destabilization of the N2 units. Interestingly, MnN2 exhibits the highest Vickers hardness (36.6 GPa) among all pernitrides but only have a moderate bulk modulus (306 GPa), suggesting that the estimate of hardness goes far beyond the bulk modulus.
states, which jointly lead to the elongation of N–N bond and destabilization of the N2 units. Interestingly, MnN2 exhibits the highest Vickers hardness (36.6 GPa) among all pernitrides but only have a moderate bulk modulus (306 GPa), suggesting that the estimate of hardness goes far beyond the bulk modulus.
| Crystal | Phases | B | G | G/B | E | Pr |
|---|---|---|---|---|---|---|
| TiN2 | I4/mcm | 288 | 220 | 0.763 | 525 | 0.196 |
| Other theory19 | I4/mcm | 284 | 197 | 0.693 | 481 | 0.218 |
| Expt.7 | I4/mcm | 385 | ||||
| VN2 | I4/mcm | 324 | 225 | 0.698 | 550 | 0.217 |
| ZrN2 | I4/mcm | 270 | 175 | 0.647 | 432 | 0.234 |
| HfN2 | I4/mcm | 294 | 204 | 0.693 | 497 | 0.219 |
| CrN2 | P63/mmc | 344 | 245 | 0.710 | 593 | 0.213 |
| Other theory21 | P63/mmc | 326 | 231 | 0.709 | 561 | |
| MoN2 | P63/mmc | 339 | 211 | 0.622 | 525 | 0.242 |
| Other theory18 | P63/mmc | 338 | 206 | |||
| MnN2 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
306 | 206 | 0.674 | 505 | 0.225 |
| NbN2 | Cc | 263 | 102 | 0.388 | 271 | 0.328 |
| TaN2 | Cmca | 340 | 193 | 0.569 | 488 | 0.261 |
Conclusions
In summary, we have carried out a thorough investigation of transition metal (TM) pernitrides using the CALYPSO global structure search method and predicted/determined the ground-state crystal structures of TiN2, VN2, CrN2, MnN2, HfN2, NbN2, MoN2, ZrN2, and TaN2 in the pressure range of 0–100 GPa. The structures obtained for TiN2, CrN2 and MoN2 known previously compare well with the available experimental and theoretical results reported in literature. For VN2, ZrN2, HfN2, MnN2, NbN2 and TaN2, which have yet to be synthesized, the predicted structures and properties can be used as a guide for future synthesis and theoretical studies. Phonon dispersion relation and formation enthalpy calculations suggest that the predicted TMN2 pernitrides are all thermodynamic and dynamically stable at ambient conditions, which provides a good possibility that they can be quench recovered once synthesized under high pressure conditions. Similar to PtN2, the predicted TM pernitrides have extraordinary mechanic properties including high bulk modulus and Vickers hardness which are originated from the single nature of N–N bond in [N2]4− pernitride unit and the TM–N charge transfer. New results obtained in the present study push forward the understanding of the crystal structures and electronic properties of transition metal pernitrides at high pressures.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by NSAF (No. U1530124), the National Natural Science Foundation of China (No. 11474128), Science Challenge Project (No. TZ2016001), Program for JLU Science and Technology Innovative Research Team and Natural Sciences and Engineering Research Council of Canada (NSERC).References
- E. Gregoryanz, C. Sanloup, M. Somayazulu, J. Badro, G. Fiquet, H. K. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 294 CrossRef CAS PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275 CrossRef CAS PubMed.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. K. Mao, Phys. Rev. Lett., 2006, 96, 155501 CrossRef PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, J. M. Zaug, D. Aberg, Y. Meng and V. B. Prakapenka, J. Mater. Res., 2008, 23, 1 CrossRef CAS.
- K. Niwa, K. Suzuki, S. Muto, K. Tatsumi, K. Soda, T. Kikegawa and M. Hasegawa, Chem.–Eur. J., 2014, 20, 13885 CrossRef CAS PubMed.
- K. Niwa, D. Dzivenko, K. Suzuki, R. Riedel, I. Troyan, M. Eremets and M. Hasegawa, Inorg. Chem., 2014, 53, 697 CrossRef CAS PubMed.
- V. S. Bhadram, D. Y. Kim and T. A. Strobel, Chem. Mater., 2016, 28, 1616 CrossRef CAS.
- D. Laniel, A. Dewaele and G. Garbarino, Inorg. Chem., 2018, 57, 6245 CrossRef CAS PubMed.
- A. F. Young, J. A. Montoya, C. Sanloup, M. Lazzeri, E. Gregoryanz and S. Scandolo, Phys. Rev. B, 2006, 73, 153102 CrossRef.
- R. Yu, Q. Zhan and L. C. Angew, Angew. Chem., Int. Ed., 2007, 46, 1136–1140 CrossRef CAS PubMed.
- D. Åberg, B. Sadigh, J. Crowhurst and A. F. Goncharov, Phys. Rev. Lett., 2008, 100, 095501 CrossRef PubMed.
- Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B, 2007, 76, 054115 CrossRef.
- E. Zhao and Z. Wu, Comput. Mater. Sci., 2008, 44, 531 CrossRef CAS.
- Y. Li and Z. Zeng, Chem. Phys. Lett., 2009, 474, 93 CrossRef CAS.
- X. P. Du, Y. X. Wang and V. C. Lo, Phys. Lett. A, 2010, 374, 2569 CrossRef CAS.
- F. Kawamura, H. Yusa and T. Taniguchi, Appl. Phys. Lett., 2012, 100, 251910 CrossRef.
- S. M. Wang, H. Ge, S. L. Sun, J. Z. Zhang, F. M. Liu, X. D. Wen, X. H. Yu, L. P. Wang, Y. Zhang and H. W. Xu, J. Am. Chem. Soc., 2015, 137, 4815–4822 CrossRef CAS PubMed.
- S. Y. Yu, B. Huang, X. J. Jia, Q. F. Zeng, A. R. Oganov, L. T. Zhang and G. Frapper, J. Phys. Chem. C, 2016, 120, 11060 CrossRef CAS.
- S. Yu, Q. Zeng, A. R. Oganov, G. Frapper and L. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 11763 RSC.
- S. Y. Yu, Q. F. Zeng, A. R. Oganov, G. Frapper, B. Huang, H. Y. Niu and L. T. Zhang, RSC Adv., 2017, 7, 4697 RSC.
- Z. L. Zhao, K. Bao, F. B. Tian, D. F. Duan, B. B. Liu and T. Cui, Phys. Rev. B, 2016, 93, 214104 CrossRef.
- Z. L. Zhao, K. Bao, F. B. Tian, D. F. Duan, B. B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2015, 17, 22837 RSC.
- M. G. Zhang, K. Cheng, H. Y. Yan, Q. Wei and B. B. Zheng, Sci. Rep., 2016, 6, 36911 CrossRef CAS PubMed.
- G. Soto, Comput. Mater. Sci., 2012, 61, 1–5 CrossRef CAS.
- H. Y. Yan, M. G. Zhang, Q. Wei and P. Guo, J. Alloys Compd., 2013, 581, 508–514 CrossRef CAS.
- Z. T. Y. Liu, D. Gall and S. V. Khare, Phys. Rev. B, 2014, 90, 134102 CrossRef.
- J. Zhou, Z. M. Sun and R. Ahuja, J. Alloys Compd., 2009, 472, 425–428 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B, 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter, 2008, 78, 134106 CrossRef.
- R. Hill, Proc. Phys. Soc., London, 1952, A65, 349 CrossRef.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- M. Stefan, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef PubMed.
- M. Wessel and R. Dronskowski, J. Am. Chem. Soc., 2010, 132, 2421 CrossRef CAS PubMed.
- G. V. Vajenine, G. Auffermann, Y. Prots, W. Schnelle, R. K. Kremer, A. Simon and R. Kniep, Inorg. Chem., 2001, 40, 4866 CrossRef CAS PubMed.
- G. Auffermann, Y. Prots and R. Kniep, Angew. Chem., Int. Ed., 2001, 40, 547 CrossRef CAS PubMed.
- K. Y. Li, X. T. Wang, F. F. Zhang and D. F. Xue, Phys. Rev. Lett., 2008, 100, 235504 CrossRef PubMed.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1983, pp. 60–180 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07814a |
| This journal is © The Royal Society of Chemistry 2018 |