Open Access Article
Open Access ArticleDissipative particle dynamics simulation of multicompartment micelle nanoreactor with channel for reactants
Seung Min Leea,
Nicholas Bonda,
Connor Callawaya,
Benjamin Clarka,
Emily Farmera,
MacKensie Mallarda and
Seung Soon Jang *abcd
*abcd
aComputational NanoBio Technology Laboratory, School of Materials Science and Engineering, Georgia Institute of Technology, 771 Ferst Drive NW, Atlanta, GA 30332-0245, USA. E-mail: seungsoon.jang@mse.gatech.edu
bInstitute for Electronics and Nanotechnology, Georgia Institute of Technology, Atlanta, GA, USA
cParker H. Petit Institute for Bioengineering and Bioscience, Georgia Institute of Technology, Atlanta, GA, USA
dStrategic Energy Institute, Georgia Institute of Technology, Atlanta, GA 30332, USA
First published on 12th November 2018
Abstract
The structural variation of multicompartment micelles is investigated using a dissipative particle dynamics simulation method for nano-reactor application. It turns out that well-defined multicompartment micelles with channel structures can be generated through the self-assembly of triblock copolymers consisting of a hydrophilic (A), a lipophilic (B), and a fluorophobic (C) block arranged in a B–A–C sequence: The corona and core are formed by the hydrophilic A block and the fluorophilic C block, respectively while the channel between the aqueous phase and core is formed by the lipophilic B block and the core. By performing a set of simulations, it is confirmed that channel size can be controlled as a function of the block length ratios between blocks A and B. Furthermore, it is also confirmed that the reactants pass through such channels to reach the micelle core by analyzing the pair correlation functions. By monitoring the change of the number of reactants in the multicompartment micelle, it is revealed that the diffusion of reactants into the core is slowed down as the concentration gradient is decreased. This work provides mesoscopic insight for the formation of multicompartment micelles and transport of reactants for use in the design of micelles as nanoreactors.
1. Introduction
Multicompartment micelles (MCMs) have attracted intensive attention recently in the colloidal science community since the MCMs contain multiple well-defined spaces in a nanoscale structure, which has shown great potential for nanoreactor technology.1–10 Thanks to the successful progress in fine synthesis in polymer chemistry, well-defined architecture in a multi-block copolymer chain can lead to highly controlled configurations in their aggregates.7In general, a simple micelle is comprised of a hydrophilic shell and a hydrophobic core. MCMs are comprised of hydrophilic shells and segregated hydrophobic cores.11 MCMs have been studied for their unique structures with distinct spaces which can potentially see use in applications of drug-delivery by selectively encapsulating drugs11 and by releasing the drugs under changes in external conditions like temperature and pH.12 These ideas can be applied for nanoreactors by equipping catalysts in the cores of MCMs.5 The outer corona of MCMs can be used to stabilize the hydrophobic core and immobilize a catalytic site, preventing the active center from precipitating in water.13,14
An additional advantage of MCMs is that the internal structure of a multicompartment micelle is precisely tunable by altering polymer block lengths and functional groups.15,16 Previous studies by Weck et al. suggested that the shell cross-linked MCM could be used as nanoreactors for the hydrolysis kinetic resolution of epoxides.5 The outer shell of the MCM can provide increased selectivity for catalysis by modifying the polymers that make up the corona.
Although many experimental studies have been conducted to study the behavior of micelles, it is not easy to experimentally obtain detailed information regarding the internal structures of the MCM with high resolution.17 In this context, the computer simulation methods have become powerful tools for studying the structures and behaviors of micelles consisting of amphiphilic multiblock copolymers. Dissipative particle dynamics (DPD) has been effectively used in simulating amphiphilic copolymers at the mesoscale18 by employing the Flory–Huggins parameter theory.19 In our previous study, indeed, such DPD simulation has been used to study the feasibility of producing complex-structures of MCMs formed from multiblock copolymers.20–22
After these previous works, our interest has been focused on how to regulate the transport of reactant molecules into the MCM.19 Therefore, using DPD simulation method, first, we investigate how the channel structures can be designed on the corona of MCM built from B–A–C triblock copolymers, and secondly, we characterize the effects of such channel size on the transport of reactants.
2. Models and simulation method
2.1 DPD simulation method
In a dissipative particle dynamics simulation, we use bead-spring model, meaning that one bead represents a group of multiple atoms. This approach is very beneficial to simulate mesoscale systems which is very hard to be described by full-atomistic methods.18The motions of beads are described by integrating Newton's equations of motion
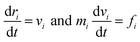 | (1) |
 | (2) |
 | (3) |
| aij = aij + 3.5χij | (4) |
The dissipative force FDij and the random force FRij depend on only on the position and velocity of the i-th particle. The position and velocity are given by rij = ri − rj and νij = νi − νj, respectively. The forms of these forces are expressed as:
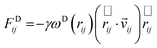 | (5) |
 | (6) |
2.2 Coarse-grained model and simulation details
In this study, the triblock copolymer in a block sequence of B–A–C was used to form micelle in DPD simulations, in which the blocks B, A, and C are covalently bound. All DPD simulations were performed in a simulation box of size 30 × 30 × 30 rc3 with periodic boundary conditions with a reduced bead density ρ(rc3/Vm) of 3, meaning that the number of DPD beads are the same 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for all DPD simulation. The concentration of triblock copolymer is 5% of the total number of beads, and the remainder of the system (95%) is beads representing water.
000 for all DPD simulation. The concentration of triblock copolymer is 5% of the total number of beads, and the remainder of the system (95%) is beads representing water.
All the simulations were started from a random configuration. The repulsive parameters used for our DPD simulations are summarized in Table 1. Although, this study was primarily based on DPD simulations, the relevance of reactant transport to the physical scale can be made through assuming a bead has the volume of 5 water molecules, about 150 Å3, as demonstrated by Wang and coworker.17 Thus, the physical length scale from the reduced length is  , the average mass is about 90 g mol−1. The reduced time step was 0.05 and, accordingly, the physical time scale from the reduced time scale is
, the average mass is about 90 g mol−1. The reduced time step was 0.05 and, accordingly, the physical time scale from the reduced time scale is  . Since the friction coefficient (γ) and noise amplitude (σ) are calculated by the fluctuation–dissipation theorem,23
. Since the friction coefficient (γ) and noise amplitude (σ) are calculated by the fluctuation–dissipation theorem,23  and σ = 25kBT/rc. The harmonic spring constant for the bond between beads was set to be 4. The equilibration of the system was confirmed by monitoring the pressure and temperature of the system. The simulations were run for 3.5 × 105 reduced time steps until the equilibrium states of micelle structures are obtained; the details of the block lengths of triblock copolymers used in this study are summarized in Table 2. The blocks A is hydrophilic while the blocks B and C are hydrophobic and more hydrophobic, respectively. The simulations were perform using DPD module in Materials Studio.24
and σ = 25kBT/rc. The harmonic spring constant for the bond between beads was set to be 4. The equilibration of the system was confirmed by monitoring the pressure and temperature of the system. The simulations were run for 3.5 × 105 reduced time steps until the equilibrium states of micelle structures are obtained; the details of the block lengths of triblock copolymers used in this study are summarized in Table 2. The blocks A is hydrophilic while the blocks B and C are hydrophobic and more hydrophobic, respectively. The simulations were perform using DPD module in Materials Studio.24
| Block A | Block B | Block C | Water | Reactant | |
|---|---|---|---|---|---|
| Block A | 25 | 35 | 75 | 35 | 60 |
| Block B | 35 | 25 | 35 | 40 | 28 |
| Block C | 75 | 35 | 25 | 75 | 28 |
| Water | 35 | 40 | 75 | 25 | 60 |
| Reactant | 60 | 28 | 28 | 60 | 25 |
| Micelle systems | Block length | ||
|---|---|---|---|
| A | B | C | |
| A | 13 | 5 | 9 |
| B | 11 | 7 | 9 |
| C | 9 | 9 | 9 |
| D | 7 | 11 | 9 |
| E | 5 | 13 | 9 |
2.3 Association of reactants into micelle
After the micelle structures were prepared in equilibrium state, 1% of the water beads were randomly replaced with reactant beads in order to simulate the association of reactants into the micelle. Although the simulations were run for 5 × 104 time steps, most reactants were associated into micelle within 1.0 × 104 time steps.After the association of reactants into micelle, the gyration tensors were calculated for the core of the micelle and the principal moments were calculated. To determine whether or not the core of the micelle is spherical, the asphericity was calculated for each of the micelles. It is noted that the micelle is a perfect sphere if the asphericity is zero. The asphericity of the core of Micelle C system was 3.31 × 10−4, indicating that the micelle core is nearly spherical. It is found that all other micelle systems have similar values for the asphericity. In our analysis, any reactant beads found in this spherical region was counted as the associated reactants penetrating the outer layer of the micelle. The number of reactant beads were monitored during the simulation in order to characterize the effect of the channel size.
3. Results and discussion
3.1 Self-assembly of triblock copolymers
The self-assemblies of the B–A–C triblock copolymer are shown in Fig. 1. The total block length of the triblock copolymer is 27 while the block length of blocks A and B are varied with a fixed block length of 9 for the block C. In this study, we focus on five ratios between Blocks A and B, such as 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 11
5, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 9
7, 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, 7
9, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11, and 5
11, and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13, with as shown in Table 2 to investigate how the shell structure of the micelle changes.
13, with as shown in Table 2 to investigate how the shell structure of the micelle changes.
 | ||
Fig. 1 Self-assembly process of the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 B–A–C triblock copolymers (Micelle C in Table 2) in water. The blocks A, B, and C are colored by blue, red, and green, respectively. The water are hidden for clear view. 9 B–A–C triblock copolymers (Micelle C in Table 2) in water. The blocks A, B, and C are colored by blue, red, and green, respectively. The water are hidden for clear view. | ||
Snapshots of the equilibrated micelles are presented in Fig. 2, showing that the block length ratio has a strong effect on the shell structure of the micelle: larger block length ratio of the block B produces larger domain (red color) and vice versa. Furthermore, it should be noteworthy from the cross-sectional views that both domains from blocks A and B contact the core consisting of block C directly, which strongly support that the domains made of block B could be used as channels for hydrophobic reactants to reach the micelle core. If the core is equipped with catalysts, it is anticipated to have reaction in the core. In order to evaluate the outer surface area of the micelles, Connolly surface analysis was performed using the probe diameter of 1.4 Å, approximately that of a water molecule. Fig. 3 shows the outer surface area ratio of region consisting of block B with respect to the total surface area from each micelle system. These results confirm that the surface area from the block B region is increased by increasing the B block length as visually displayed in Fig. 2.
 | ||
| Fig. 2 Snapshots of the equilibrated micelles consisting B–A–C triblock copolymers: (a) Micelle A; (b) Micelle B; (c) Micelle C; (d) Micelle D; (e) Micelle E. | ||
 | ||
| Fig. 3 Surface area ratio of the region consisting of block B with respect to the total outer surface area of micelle. | ||
Another point suggested from the cross-sectional views in Fig. 2 is that the core of the MCM has nearly spherical shape. The asphericity calculations further support this assumption, as the asphericity were around 0.003 for all micelles. Since the length of the block C was constant regardless of the block length ratios in this study, it is observed that the cores of these MCMs have the almost same dimension as expected. Thus, the differences among the micelles in Table 2 is mainly found in the shell structures.
3.2 Selective diffusion into micelle
Once we prepared the equilibrated micelle systems, we replaced 1% of water beads with reactant beads. Fig. 4 shows the time evolution of the Micelle A (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9) system in the presence of reactants. First, from the time-resolved cross-sectional images of the Micelle A system in Fig. 4, it is clearly observed that the reactants primarily diffuse through the domain consisting of block B (red color) to reach the core of the micelle consisting of block C (green color), which is commonly observed in all other micelle systems although we do not include those figures explicitly.
9) system in the presence of reactants. First, from the time-resolved cross-sectional images of the Micelle A system in Fig. 4, it is clearly observed that the reactants primarily diffuse through the domain consisting of block B (red color) to reach the core of the micelle consisting of block C (green color), which is commonly observed in all other micelle systems although we do not include those figures explicitly.
 | ||
Fig. 4 Cross-sectional view of Micelle A (A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 13 C = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9). The reactant beads are colored yellow. Other micelle systems have a similar feature with Micelle A system. 9). The reactant beads are colored yellow. Other micelle systems have a similar feature with Micelle A system. | ||
Such reactant diffusion into micelle systems is attributed to the favorable interactions of reactants with blocks B and C, as presented in Table 1. Considering higher repulsion interaction parameters of reactant against water and block A, the reactants can find more stable states in (1) the domain in the shell formed by block B and (2) the core form by block C. Therefore, we think that the reactant diffusion takes place mainly due to the thermodynamic driving force as well as the concentration gradient. From this aspect, we also expect that such domain in the shell formed by block B can be used as a channel for reactants reaching the core in which catalysts will be equipped for reactions.
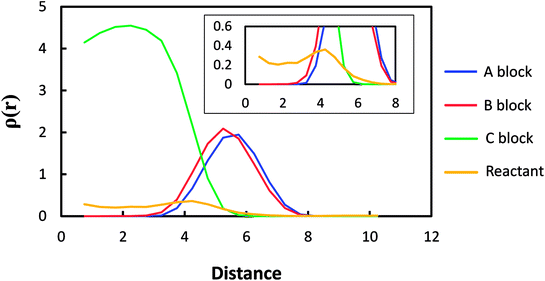
The radial density profile of the micelle was calculated using the equilibrium state after adding the reactants. Fig. 5 shows its representative feature for Micelle C. Other micelle systems have a similar feature. The distribution of the blocks and reactants are well defined: the block C is concentrated in the core whereas the blocks A and B are positioned in the outer shell. It is noted that the block A is slightly extended more in comparison to the block B, which is due to the less repulsive interaction of the block A with the solvent phase. Although the reactant is expected to be more or less uniformly distributed through the micelle core, it seems to have a peak at ∼4 reduced distance unit as shown in the inset of Fig. 5. Since the reactant has the same affinity with the blocks B and C (Table 1), this result is because the reactants in the regions of blocks C and B are counted together at ∼4 reduced distance unit. Next, to characterize this selective diffusion quantitatively, the correlations of reactant with blocks A, B, and C in the micelle systems were analyzed using pair correlation function (ρg(r)) defined as
 | (7) |
Fig. 6 shows the evolution of pair correlation function for each pair in Micelle A system as a function of time. First of all, it is common feature the intensity of the pair correlation is increased as the simulation proceeds, which indicates that the reactants diffuse into micelle and thereby each reactant bead get surrounded by more number of block beads. However, it is observed that the correlation distance for the reactant-block A pair has very broader distribution while those for the reactant-block B and reactant-block C pairs have very well defined correlation distance at ∼0.9 DPD reduced unit. This difference is due to the selective diffusion of reactants. In other words, since the block A domains in the shell are not used for the channel, most of the signals in Fig. 6a are due to the correlation made at the surface of the block A domain. In contrast, since the reactants diffuse through block B domain and enter the core, the correlations found in Fig. 6b and c are originated from the bead–bead pairs in the middle of block B domain and block C core. In particular, it is inferred from the strong intensity found in Fig. 6c that the reactants are well associated in the core of micelle.
 | ||
| Fig. 6 Time evolution of pair correlation analysis for the pairs of reactant with blocks A, B, and C. This is for Micelle A system, and other micelle systems have a similar feature. | ||
3.3 Effect of domain size on reactant diffusion
For a quantitative analysis, the reactants associated within the micelles are counted as shown in Fig. 7. It is commonly observed that the number of reactants is increased as a function of simulation time, indicating that the reactants diffuse into the micelle. As the reactant diffusion proceeds more, the concentration gradient is decreased, so that the diffusion rate of reactant is decreased accordingly. Another point stressed in Fig. 7 is the structure dependency of the reactant diffusion. From Fig. 2, it was found that the larger block length can form larger domain in the shell of the micelle. Since that the hydrophobic block B has more favorable interaction with reactant, it is expected that the larger domain in the shell consisting longer block B will facilitate a favorable influx of reactant into micelle. Indeed, compared to Micelle A consisting of the shortest block B, other micelles with longer block B show higher initial reactant diffusion during the first 4000 simulation time steps. However, Micelles B, C, D, and E demonstrate similar levels of initial diffusion to one another, meaning that the domain size formed by block B whose block length is longer than 7, is already large enough.4. Summary
In this work, DPD simulations were applied to investigate the self-assembly of triblock copolymer consisting of hydrophilic (A), a lipophilic (B), and a fluorophobic (C) block in a block sequences of B–A–C to form multicompartment micelles and the diffusion of reactant into the micelle from aqueous phase.From the snapshots of the self-assembled micelles, it was found that the higher the block length ratios of the block B to block A produce micelles with larger block B domains in the shell. Furthermore, it was also found that these domains acted as channels for the diffusion of reactants towards the core of micelle, which is due to the preferred thermodynamic interaction of the reactant with the block B. Therefore, it is inferred that the channel structures are very effective in selective diffusion of reactants into micellar nano-reactors. This was further confirmed through the pair correlation analysis for the reactant-block pairs.
The variation of the block length ratios of the block B to block A had no obvious effects on the block C cores and the cores remained spherical in shape and roughly the same size for all micelles simulated in this study. The channel size effect on the reactant transport rate was found: the longer block B length result in the higher reactant diffusion. However, such effect seems to be saturated when the block B length is longer than 7.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Catalysis Science Program under Award DE-FG02-03ER15459.REFERENCES
- A. Lu and R. K. O'Reilly, Curr. Opin. Biotechnol., 2013, 24, 639–645 CrossRef CAS PubMed.
- R. Chandrawati, M. P. van Koeverden, H. Lomas and F. Caruso, J. Phys. Chem. Lett., 2011, 2, 2639–2649 CrossRef CAS.
- V. Balasubramanian, O. Onaca, M. Ezhevskaya, S. Van Doorslaer, B. Sivasankaran and C. G. Palivan, Soft Matter, 2011, 7, 5595–5603 RSC.
- P. Cotanda, A. Lu, J. P. Patterson, N. Petzetakis and R. K. O'Reilly, Macromolecules, 2012, 45, 2377–2384 CrossRef CAS.
- Y. Liu, Y. Wang, Y. Wang, J. Lu, V. Piñón and M. Weck, J. Am. Chem. Soc., 2011, 133, 14260–14263 CrossRef CAS PubMed.
- A. Lu, P. Cotanda, J. P. Patterson, D. A. Longbottom and R. K. O'Reilly, ChemComm, 2012, 48, 9699–9701 RSC.
- M. J. Monteiro, Macromolecules, 2010, 43, 1159–1168 CrossRef CAS.
- O. Onaca, D. W. Hughes, V. Balasubramanian, M. Grzelakowski, W. Meier and C. G. Palivan, Macromol. Biosci., 2010, 10, 531–538 CAS.
- K. Renggli, P. Baumann, K. Langowska, O. Onaca, N. Bruns and W. Meier, Adv. Funct. Mater., 2011, 21, 1241–1259 CrossRef CAS.
- R. K. O'Reilly, C. J. Hawker and K. L. Wooley, Chem. Soc. Rev., 2006, 35, 1068–1083 RSC.
- S. Kubowicz, J. F. Baussard, J. F. Lutz, A. F. Thunemann, H. von Berlepsch and A. Laschewsky, Angew. Chem., Int. Ed., 2005, 44, 5262–5265 CrossRef CAS PubMed.
- C. F. Yang, Z. L. Xue, Y. L. Liu, J. Y. Xiao, J. R. Chen, L. J. Zhang, J. W. Guo and W. J. Lin, Mater. Sci. Eng., C, 2018, 84, 254–262 CrossRef CAS PubMed.
- N. Semagina, E. Joannet, S. Parra, E. Sulman, A. Renken and L. Kiwi-Minsker, Appl. Catal., A, 2005, 280, 141–147 CrossRef CAS.
- P. D. Stevens, J. D. Fan, H. M. R. Gardimalla, M. Yen and Y. Gao, Org. Lett., 2005, 7, 2085–2088 CrossRef CAS PubMed.
- A. H. Gröschel, F. H. Schacher, H. Schmalz, O. V. Borisov, E. B. Zhulina, A. Walther and A. H. E. Müller, Nat. Commun., 2012, 3, 710 CrossRef PubMed.
- Y. Zhang, C. Z. Zhao, L. Liu and H. Y. Zhao, ACS Macro Lett., 2013, 2, 891–895 CrossRef CAS.
- X. M. Wang, J. B. Gao, Z. K. Wang, J. C. Xu, C. L. Li, S. Q. Sun and S. Q. Hu, Chem. Phys. Lett., 2017, 685, 328–337 CrossRef CAS.
- P. J. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- B. J. Chun, J. Lu, M. Weck and S. S. Jang, Phys. Chem. Chem. Phys., 2015, 17, 29161–29170 RSC.
- B. J. Chun, C. C. Fisher and S. S. Jang, Phys. Chem. Chem. Phys., 2016, 18, 6284–6290 RSC.
- C. P. Callaway, K. Hendrickson, N. Bond, S. M. Lee, P. Sood and S. S. Jang, ChemPhysChem, 2018, 19, 1655–1664 CrossRef CAS PubMed.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- Materials Studio, v. 5.5, Accelrys, 2010, San Diego Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |