Open Access Article
Open Access ArticleStabilization of divalent Eu2+ in fluorosilicate glass-ceramics via lattice site substitution†
Chenhao Wangab,
Xiaotong Chena,
Xue Luoa,
Junjie Zhaoa,
Xvsheng Qiao *a,
Yong Liua,
Xianping Fan
*a,
Yong Liua,
Xianping Fan a,
Guodong Qian
a,
Guodong Qian a,
Xianghua Zhangc and
Gaorong Hana
a,
Xianghua Zhangc and
Gaorong Hana
aState Key Laboratory of Silicon Materials & School of Materials Science and Engineering, Zhejiang University, Hangzhou 310027, China. E-mail: Qiaoxus@zju.edu.cn
bSchool of Materials Science and Engineering, Tianjin University, Tianjin, 300350, China
cLaboratory of Glasses and Ceramics, Institute of Chemical Science UMR CNRS 6226, University of Rennes 1, 35042 Rennes, France
First published on 8th October 2018
Abstract
Fluorosilicate glasses and glass-ceramics with MF2 (M = Ca, Sr, Ba), ZnF2 or LaF3 components were investigated to host divalent Eu2+ for photoluminescence (PL) application. X-ray diffraction phase identification and a series of spectroscopic analyses were performed to reveal the relationship between microstructure and the reduction of Eu3+ → Eu2+. The precursor glasses were believed being constituted by silicate-rich phases and fluoride-rich phases, due to the immiscibility of fluoride-and-silicate mixed glass system. After heat treatment, the fluoride-rich glass phases could transform into fluoride crystalline phase in the glass-ceramics. Europium tended to enrich in the fluoride-rich phases in the glasses or in the precipitated fluoride crystalline phases in the glass-ceramics. Small amounts of Eu3+ were reduced to Eu2+ in the glasses where the electronegativity had a crucial impact. In contrast, large amounts of Eu3+ were reduced to Eu2+ in the glass-ceramics containing MF2 nanocrystals, where the reduction was determined by lattice site substitution. Using ZnAl2O4 containing glass-ceramics as reference, it was evidenced that the similar and a little larger radii between sites and substitution ions are the prerequisite for Eu3+/M2+ substitution. And using LaF3 containing glass-ceramics as reference, it was certified that unbalanced charge at substitution sites induce the Eu3+ → Eu2+ reduction.
Introduction
As Eu2+ possesses ideal properties for light emission such as large absorption cross section, broad band spectrum, and highly efficient photoluminescence (PL), it has been wildly adopted as active center in phosphor materials.1,2 Owing to the exposure of 5d-shell of Eu2+ to ligands, it is also facile to tune its emission from violet to red by adjusting host lattice.3 Thus, Eu2+-doped inorganic phosphors have been widely used in commercial lighting and display devices, such as epoxy resin-or-silica mixed phosphor converted light emitting diodes (PC-LED) by mixing with resin or silica as spectrum transfer material.4 However, such PC-LED structure usually suffers from thermal deterioration because of different thermal expansions and conductivities between phosphors and epoxy resin. In order to solve this problem, researchers recently developed glass-ceramics5–9 with Eu-doped fluoride crystalline phases. It showed great advantages in thermal resistance, durability, and microstructure manipulation. Eu could enrich in fluoride phase, such as MF2 (M = Ca, Sr, Ba), of glass-ceramics to adapt itself with well-behaved PL performance.However, Eu2+ and Eu3+ always coexist in the host, because Eu cation has variable valences. It thus becomes crucial to keep divalent Eu2+ as the majority. Generally, there are several ways to transform Eu3+ into Eu2+: (i) adding reducing agents,10–12 (ii) inputting reducing atmosphere during preparation processes,13,14 (iii) adjusting optical basicity or electronegativity of host,15,16 (iv) substituting M2+ sites in crystalline lattices.17,18 As strategies (i) and (ii) accompany drawbacks such as introducing impurities into the system or leading to infeasibility for elaborated optimization of concentration and distribution of Eu2+, strategies (iii) and (iv) are usually considered to be more executable. Using strategy (iv), silicate,19,20 aluminosilicate,10,15,21 borophosphate22,23 and fluoride crystalline phases24–26 have been reported as good stabilizers for divalent Eu2+. Among them, fluoride crystalline phases show most advantages owing to their ultrasmall sizes down to several nanometers, similar refractive indices with silicate glasses, ideal host to selectively enrich Eu2+. Hence, fluorosilicate glass-ceramics containing Eu2+-enriched fluoride nanocrystals could achieve high transparency, large Eu3+/Eu2+ reduction ratio, enhanced PL performance and ideal physicochemical properties.
Our previous studies5–7 have evidenced that alkaline earth fluoride (MF2, where M = Ca; Sr; Ba) nanocrystals could be good hosts to precipitate and enrich Eu2+ by Eu2+/M2+ lattice substitution. But there is still a lack of systematical dissertation summarizing such lattice substitution strategy for stabilizing Eu2+ in the fluorosilicate glass-ceramics. In this study, we prepared glass and glass-ceramic samples with the composition of 50SiO2–20Al2O3–20MF2–7NaF–3EuF3 (M = Ca, Sr, Ba, Zn) and 50SiO2–20Al2O3–20LaF3–7NaF–3EuF3. By comparative study of the valence state evolution and spectroscopic behaviors of Eu cations, we demonstrate the feasibility of the proposed site substitution strategy to stabilize the divalent Eu2+ in the fluorosilicate glass-ceramics containing MF2 nanocrystals.
Experimental methods
Oxyfluoride glasses (and a glass-ceramic sample) with the compositions of 50SiO2–20Al2O3–20MFx–7NaF–3EuF3 in mol%, named as G1–4, GC5 (M = Ca, Sr, Ba, La, or Zn; x is the valence of ion M) was prepared by a melt-quenching method. Total weight of 50 g raw materials was weighed and mixed well in a RETSCH RM 200 mortar grinder. The batches of the raw materials were melted at 1500 °C for 45 min in air. Plain glass was obtained by quenching the melt between two brass plates. The subsequent crystallization temperature of 660 °C was selected between the first crystallization temperature (Tc1) and the second crystallization temperature (Tc2) for G1–4 (Fig. 1 (a)). The glass-ceramics GC1–4 were obtained by annealing the glasses at the above temperatures for 45 min in air. The compositions and crystallization temperatures of the groups are demonstrated below in Table 1. Note that the ZnF2-based sample (GC5) loses its transparency due to an uncontrollable crystallization during the melt-quenching process.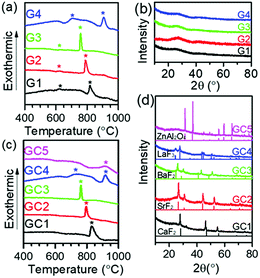 | ||
| Fig. 1 DTA curves and XRD patterns of the G1–G4 glasses (a and b) and the GC1–GC5 glass-ceramics (c and d) with reference to the standard JCPDS cards. | ||
| Sample | Composition (mol%) | Tc1 | Tc2 |
|---|---|---|---|
| G1 | 50SiO2–20Al2O3–20CaF2–7NaF–3EuF3 | 602 °C | 800 °C |
| G2 | 50SiO2–20Al2O3–20SrF2–7NaF–3EuF3 | 598 °C | 750 °C |
| G3 | 50SiO2–20Al2O3–20BaF2–7NaF–3EuF3 | 597 °C | 752 °C |
| G4 | 50SiO2–20Al2O3–20LaF3–7NaF–3EuF3 | 650 °C | 882 °C |
| GC5 | 50SiO2–20Al2O3–20ZnF2–7NaF–3EuF3 | 815 °C |
Differential thermal analysis (DTA) measurement was carried out on a CDR-1 differential thermal analyzer with fixed specimen weight of 60 mg. XRD analysis was carried out on a PANalytical B.V. Empyrean 200895 X-ray diffractometer with Cu Kα radiation (λ = 1.54 Å), and the scan speed was 2.00 deg min−1. The excitation and emission spectra combining quantum yields were measured by an Edinburgh Instruments fluorospectrometer FLS 920 equipped with a red-sensitive photomultiplier (Hamamatsu R928P) in a Peltier-cooled housing in the single photon counting mode and with the aid of an integration sphere. A 450 W ozone-free xenon lamp was used as the excitation source for steady-state measurements. The calibrations for quantum yields were made by the Edinburgh Instrument and the measurements were repeated three times at room temperature for each excitation scheme and then averaged overall.
Results and discussion
Transition from glasses to glass-ceramics
Evidenced by differential thermal analysis (DTA, Fig. 1(a and c)) and X-ray diffraction (XRD, Fig. 1(b and d)), sample G1–4 referred to typical inorganic glasses without any crystalline phase, while sample GC5 was glass-ceramic constituted by the precipitated ZnAl2O4 crystalline phases and residual glass phase. Glass samples G1–G4 have two exothermic DTA peaks, where the first peaks (which appeared at lower temperature) correspond to the precipitation of fluoride nanocrystals (CaF2, SrF2, BaF2, LaF3). Such kinds of crystalline phases were revealed by XRD patterns (Fig. 1(d)) of the glass-ceramics, GC1–GC4. These samples were obtained by annealing G1–G4 at 660 °C, which were located between two crystallization peaks for 45 minutes. In contrast, the as-melt sample, GC5, was already glass-ceramic with opaque appearance due to the uncontrollable crystallization of ZnAl2O4 during the quenching process of the melt. According to the Scherrer formula, the crystal sizes could be estimated from peak width of XRD patterns. As a result, the sizes of CaF2, SrF2, BaF2, LaF3 and ZnAl2O4 crystals in the glass-ceramics were evaluated as 19.3 ± 0.2 nm, 14.6 ± 0.2 nm, 16.0 ± 0.3 nm, 17.9 ± 2.7 nm and >100 nm, respectively. GC1–4 have high transparency, but GC5 lost its transparency. This is due to much smaller size of precipitated MFx nanocrystals than the visible-near infrared wavelength, as well as similar refractive indices between MFx nanocrystals and silicate hosts. So the fluorosilicate glass-ceramics show more optical merits than the reported oxide glass-ceramics.17–21 The volume fractions of the precipitated nanocrystals (crystallinity) could also be evaluated by the integral intensity ratio of crystalline diffraction to all the diffraction. And the crystallinities were estimated to around 20% for all the glass-ceramic samples. Therefore, the glasses were converted into the glass-ceramics containing CaF2, SrF2, BaF2, LaF3 nanocrystals except the ZnF2-based GC5.Spectroscopic behaviors of Eu3+ and Eu2+
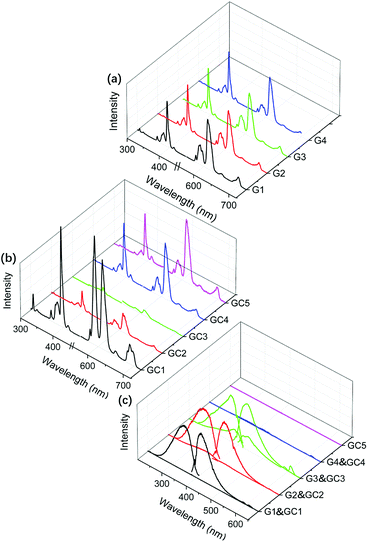
The sharp PL peaks in Fig. 2(a and b) were assigned to the 4f–4f transitions of Eu3+, while the broad PL bands in Fig. 2(c) could be assigned to 4f7–4f65d1 transitions of Eu2+. For Eu3+, the PL excitation peaks of 363, 381, 393 and 414 nm were attributed to the transitions of 7F0 → 5D4, 5G4, 5L6, 5D3, respectively. And the PL emission peaks were ascribed to 5D0 → 7FJ where J = 1, 2, 3 and 4 correspond to 590, 612, 650 and 689 nm, respectively. As the 4f electron shell was shielded by the outer shells (5d and 6s), the 4f–4f transition was less influenced by coordination surroundings, which led the parabolas of 4fn excited states to be located in parallel and directly above the ground state in the configuration coordinate. Therefore, the band widths of Eu3+ PL peaks appeared as narrow linear shapes. On the contrary, the PL bands of Eu2+ have large band width covering more than 100 nm with the maxima at 350 and 420 nm. As d shell is exposed to ligands, there was offset between the equilibrium position of both the 4f65d1 and 4f7 states of Eu2+. Therefore, the f–d transition presented large Stokes shift, and electron–phonon coupling further broadened the PL bands.27 Such a Stokes shift and spectral broadening are depicted in Fig. S1.† It shows that Eu2+ has similar PL bands in the glasses and glass-ceramics. But there are large Stokes shifts on the PL excitation and emission spectra. Between the glass and glass-ceramic samples, more or less Stokes difference exists, where GC3 exhibits the largest Stokes shift (4712 cm−1) among all the samples. These are attributed to the different coordination environments around Eu2+ in the glass and glass-ceramics. In the glass samples, Eu2+ is mainly surrounded by both O2− and F−, while Eu2+ ions are predominantly enriched in fluoride phase in glass-ceramics. With the enrichment of Eu2+ in different nanocrystals, the Stokes shifts of Eu2+ also appear to have some differences due to the lattice difference of MF2 (M = Ca, Sr, Ba) nanocrystals. With configuration coordinates, Fig. S2† illustrates Stokes shift order of Δstokes(G3) < Δstokes(GC3) and Δstokes(G3) < Δstokes(GC1) < Δstokes(GC2).All the glasses and glass-ceramics showed PL feature of both Eu2+ and Eu3+, except that the LaF3-based samples only exhibited the PL feature of Eu3+. For comparison, the PL intensities of each group were normalized according to glasses for Eu3+ and glass-ceramics for Eu2+. Compared to the glasses, most of the glass-ceramics possessed stronger PL for Eu2+, owing to the reduction of Eu3+ into Eu2+ during the treatment. The Eu2+ bands also existed in glass samples and increased by the sequence of G1 to G3 according to Fig. 2(c). The appearance of PL bands implied that reduction of Eu3+ started in the glass forming stage. However, the PL of Eu3+ displayed intricate changes before and after heat treatment. The Eu3+ PL peaks of CaF2 and LaF3 based glass-ceramics (GC1 and GC4) strengthened after heat treatment, while the PL peaks of SrF2 and BaF2 based glass-ceramics (GC2 and GC3) were weaker than those of the glasses. In addition, sample G4, GC4 and GC5 almost had no intense PL bands of Eu2+ according to Fig. 2(c), which indicates the absence of Eu2+ in those samples. The evolution of PL intensity could be also evidenced by the integral sphere collected spectra (Fig. 3(a and b)). We believe that the PL behavior of the material was mainly influenced by: (i) the ratio diversification of Eu3+/Eu2+ due to the Eu3+ → Eu2+ reduction; (ii) the coordination of Eu2+/Eu3+ into the precipitated crystalline phases. These two factors will be discussed in subsequent passages.
Electronegativity related reduction of Eu3+ → Eu2+ in the glasses
The reduction of Eu3+ → Eu2+ in glass is usually believed to relate with the optical basicity. This parameter was primarily used to describe the “electron donor ability” of oxygen as well as the concentration of non-bridging oxygen.28,29 From Fig. 2(c), the PL of Eu2+ increased by the consequence of G1 < G2 < G3. However, this trend contradicted the well-developed theory of optical basicity that the lower optical basicity (Λ(Ca2+) < Λ(Sr2+) < Λ(Ba2+)) determined the higher reduction ratio of Eu2+ (G1 > G2 > G3).15 (Herein, due to relatively small concentration of Eu2+, it could be assumed to still be lower than the PL quenching concentration and thus be correlated with PL intensity.) We believed that the contradiction was primarily because the investigated glasses were fluoride and oxide mixed glass system. Oxide (silicate) glass is covalent bond majored “random tetrahedral network” and linked by sharing corners, while fluoride glass is ionic bond majored “random polyhedral packing” and linked by sharing corners, edges and planes. In the high fluoride content (30 mol%) mixed system, we have revealed that the glass was indeed constructed by separated fluoride-rich glass phases and silicate-rich glass phases.30 Thus, the Eu3+ → Eu2+ reduction could not be well interpreted by optical basicity, but we tried to relate it with “electronegativity”, which was the primary origin of “optical basicity”.Electronegativity, χ, is a chemical property that describes the tendency of an atom or ion to attract electron clouds towards itself.31 Due to the electronegativity differences between Eu3+ and other cations, Eu3+ tended to attract more electron density around its neighboring cations with lower electronegativity, and eventually captured an electron from fluorine. Thus, the Eu3+ → Eu2+ reduction was more likely to happen where electronegativity of neighboring cations of Eu3+ were lower. In the glass samples, there were indeed two kinds of separated glass phases: fluoride-rich glass phases and silicate-rich glass phases.30 It has been well evidenced that lanthanides, such as europium, could selectively enrich in fluoride rich phases.32 According to the “random polyhedral packing” model, [AlF6] coordination octahedra could form the skeleton of fluoride rich glass phases, and other metal ions such as Ca2+, Sr2+, Ba2+ and Eu2+/3+ filled the pores of [AlF6] framework.33 In G1–G3, the electronegativity decreases as per the sequence χ(Ca2+) > χ(Sr2+) > χ(Ba2+), Eu2+ ions were more likely to form in the latter groups. In G4, χ(Eu3+) is close to χ(La3+), and in GC5 χ(Zn2+) is much larger than χ(Eu3+), so only slight amounts of Eu2+ were found in G4 and no Eu2+ was detected in GC5, as shown in Fig. 2(c).
Stabilization of Eu2+ in the glass-ceramics via lattice site substitution
Lattice site substitution has been considered as a facile Eu2+ doping strategy to avoid other impurities, uncontrollable redox reaction and large aggregation. The conversion ratio of reduction through this method was mainly influenced by two crucial factors: the charge and radius of the site. In order to form stable divalent Eu2+, the lattice sites should meet the following criteria: (i) the sites should be originally divalently charged, (ii) the radii of the sites should be close to the radii of Eu2+.34,35The site charge requisition of Eu2+ substitution could be examined by comparison between the MF2 (M = Ca, Sr, Ba)-based (G1, G2, G3) and the LaF3-based (G4) samples. The crystalline phases of G4 were LaF3. The trivalent La3+ sites rather than divalent ones led to no transition of Eu3+ to Eu2+ and absence of the Eu2+ PL (Fig. 2(c)), although the radii of La3+ was close to Eu2+ (RLa3+(1.160 Å) < REu2+(1.25 Å)). Thus, the divalent sites were required for reduction. As previously reported, the mechanism of the Eu3+ → Eu2+ reduction was expressed by a series of defect equations. When Eu3+ enters the lattice containing M2+ with similar radii, a cation vacancy with two negative charges is formed
 | (1) |
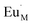 for the doping Eu3+ ion which occupied the lattice of metal ion with one extra positive charge, and
for the doping Eu3+ ion which occupied the lattice of metal ion with one extra positive charge, and  for the vacancy of metal ion with two negative charges.
for the vacancy of metal ion with two negative charges.
As the vacancy act as electron donor, Eu3+ was reduced to Eu2+.
 | (2) |
 | (3) |
 stands for the vacancy of metal ion with no extra charge,
stands for the vacancy of metal ion with no extra charge,  for the doping Eu3+ with no extra charge.
for the doping Eu3+ with no extra charge.
These substitution effects were illustrated in Fig. 4. Accordingly, the Eu3+ → Eu2+ reduction took place and alkaline earth cation vacancies formed in GC1–3 (Fig. 4(a–c)), and broad PL bands of Eu2+ were found. The lattice constants were calculated by Bragg's Law, as listed in Table 2. The site substitution can be further verified according to lattice constant change. The expansion of CaF2 lattice in GC1 corresponded with smaller radius of Ca2+(1.12 Å) compared to that of Eu2+(1.25 Å), and the shrinkage of SrF2/BaF2 lattice in GC2 and GC3 for larger radii of Sr2+(1.26 Å) and Ba2+(1.42 Å). Also, the Eu3+/La3+ substitution took place in LaF3 lattice of GC4 without the Eu3+ → Eu2+ reduction. The very small deviation from standard lattice constant of LaF3 in GC4 was due to the very similar radii of La3+ (1.160 Å) and Eu3+(1.066 Å).
| Crystalline phase | Lattice constant (Å) | Standard value (Å) |
|---|---|---|
| CaF2 in GC1 | 5.545 | 5.463 (PDF#35-0816) |
| SrF2 in GC2 | 5.760 | 5.800 (PDF#06-0262) |
| BaF2 in GC3 | 5.929 | 6.200 (PDF#04-0452) |
| LaF3 in GC4 | 7.184 × 7.184 × 7.351 | 7.187 × 7.187 × 7.35 (PDF#32-0483) |
| ZnAl2O4 in GC5 | 8.072 | 8.089 (PDF#05-0669) |
When the site was divalently charged, the radius difference between substitution cation pairs would play a prime role for the Eu3+ → Eu2+ reduction. By reference to ZnF2-based sample (GC5), the influence of the radius difference on the lattice site substitution could be clearly observed. The ionic radii36 with 8 coordination number were demonstrated as below: RZn2+(0.60 Å) < REu3+(1.066 Å) < RCa2+(1.12 Å) < REu2+(1.25 Å) < RSr2+(1.26 Å) < RBa2+(1.42 Å). Due to the huge difference between doping cations (REu3+(1.066); REu2+(1.25 Å)) and lattice cations (RZn2+(0.60 Å)), a barrier was created in the Eu3+/Zn2+ substitution. Moreover, less deviation of ZnAl2O4 lattice constant in GC5 also confirmed the above theory. Furthermore, the radius differences between Eu3+ and M2+ sites would determine how much Eu3+ would be reduced into Eu2+. The PL intensity of Eu2+ increased by the order of GC1 < GC2 < GC3, while that of Eu3+ decreased by GC1 > GC2 > GC3 (Fig. 2(b)). Thus, the ratio of Eu2+/Eu3+ should be GC1 < GC2 < GC3 assuming that the concentrations of Eu2+ and Eu3+ were lower than the PL quenching concentrations. The Eu3+ → Eu2+ reduction was indeed driven by the radius difference between different Eu3+/M2+ pairs. On the one hand, for Eu3+/Ca2+ substitution with small radius difference (Ca2+(1.12 Å) vs. Eu3+(1.066 Å)) and Ca2+ sites with smaller radii than Eu2+ (1.25 Å), it only drived Eu3+ to be partially reduced to Eu2+, so Eu3+/Eu2+ coexisted in GC1. The inversion of PL peak intensities at 590 nm and 612 nm for G1 (Fig. 2(a)) and GC1 (Fig. 2(b)) well verified the CaF2 crystalline coordination environment of Eu3+ in GC1. The PL enhancement of Eu3+ (Fig. 2(b)) was due to lower phonon energy and lower multi-phonon transition ratio of Eu3+ in CaF2 lattice of GC1. As both the Eu3+ and Eu2+ were enriched in the CaF2 nano-crystals, the strengthened cross relaxation transition between Eu2+/Eu3+ coincidentally eliminated the weakening of multi-phonon transition, so the PL lifetime of GC1 had no significant change compared to G1 (Fig. 5 and Table 3). On the other hand, Eu3+/Ba2+ or Eu3+/Sr2+ substitution with large radius difference (Sr2+(1.26 Å)/Ba2+(1.42 Å) vs. Eu3+(1.066 Å)) and Sr2/Ba2+ sites with larger radii than Eu2+(1.25 Å) drived more Eu3+ to be reduced to Eu2+. Accordingly, large amounts of Eu3+ remained trivalent in GC1, while small amounts remained in GC2 and GC3. No inversion of PL peak intensities at 590 nm and 612 nm for G2 and G3 (Fig. 2(a)) and GC2 and GC3 (Fig. 2(b)) implied that all Eu3+ in GC2 and GC3 corresponded to those remaining in the glassy phase, which exhibited much shorter PL lifetimes (Fig. 5; Table 3).
 | ||
| Fig. 5 PL Decay curves of samples. (a and b) the glass and glass-ceramics samples excited at 393 nm and monitored at 612 nm for Eu3+ (c and d) Excited at 350 nm and monitored at 420 nm for Eu2+. | ||
| Sample | Eu3+ (μs) | Eu2+ (ns) | Sample | Eu3+ (μs) | Eu2+ (ns) |
|---|---|---|---|---|---|
| G1 | 3.06 | 174 | GC1 | 3.03 | 321 |
| G2 | 3.29 | 206 | GC2 | 2.32 | 476 |
| G3 | 3.08 | 342 | GC3 | 1.77 | 612 |
| G4 | 2.48 | 112 | GC4 | 2.58 | 168 |
| GC5 | 1.96 | 85 |
Quantum yield (QY) improvement and PL enhancement of Eu2+
After heat treatment, large quantities of Eu2+ formed by Eu3+/M2+ substitution in GC1–GC3, QY of the Eu2+ PL (Fig. 3) was improved to about 4–7 times of QY of precursor glasses. QY is dominated by two competitive processes: radiative transition (RT) and non-radiative transition (NRT). Theoretically, the probability of RT and NRT, WRT and WNRT have the following relationships:
 | (4) |
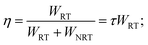 | (5) |
Besides a high QY value, strong PL still requires high concentration of the active center (Eu2+) without serious concentration quenching. The BaF2-based glass-ceramics possessed high solubility of Eu2+ rather than SrF2 or CaF2-based glass-ceramics. Larger radii as well as large radius difference were found to play almost equal roles when reducing Eu3+ into Eu2+. Therefore, the BaF2-based rather than the SrF2-based glass-ceramics got the highest QY and the strongest PL, simultaneously. It also demonstrates that the proposed MF2 lattice site substitution strategy is very suitable for alkaline earth fluorosilicate glass-ceramics showing great advantages in large amount (3–5 mol%) of Eu introduction, high reduction ratio of Eu3+/Eu2+ than in other hosts and efficiently enhanced PL of Eu2+ compared to that of oxide glass-ceramics.19–23
We also evaluate the reproducibility and applicability of the present lattice substitution method for fabrication of Eu2+-doped fluorosilicate glass-ceramics. From Fig. S3,† it is evidenced that the glass-ceramics could be well reproduced with a highly similar PL bands and the PL performance could also be well maintained even after 3 years. Moreover, the lattice substitution strategy primarily relies on the annealing processes, which has been widely applied in the glass and ceramic industry. Therefore, the proposed preparation method has good applicability in large scale applications.
Conclusions
The separated fluoride glass phases formed in the precursor fluorosilicate glasses transformed into fluoride nanocrystals in the glass-ceramics after heat treatment. The inclined precipitation of alkaline earth fluoride nanocrystals and the Eu3+/M2+ lattice site substitution enabled the facile Eu3+ → Eu2+ reduction and stabilization of Eu2+ in the fluorosilicate glass-ceramics. The Eu tended to enrich in fluoride-rich phases of the glasses and in the fluoride nanocrystalline phases of the glass-ceramics. In glasses, the Eu3+ → Eu2+ reduction depended on the electronegativity of fluoride glass phases, while in glass-ceramics, the Eu3+ → Eu2+ reduction depended on the lattice site substitution in fluoride crystalline phases. The lattice site substitution depended on two key factors: the radii and the valency difference between sites and substitution ions. The similar radii between sites and ions were the prerequisites of the doping. Too small radii of doping ions (like Zn2+) were not preferred for Eu3+/M2+ substitution, while comparably larger radii (like Ba2+) were more facile for both Eu3+/M2+ substitution and Eu3+ → Eu2+reduction. And to some extent, larger the radii, easier it was for the Eu3+/M2+ substitution to take place. The unbalanced charge at the substitution sites drived the reduction of Eu3+ → Eu2+. The Eu3+/M2+ substitution was attributed to the Eu3+ → Eu2+ reduction, while Eu3+/La3+ substitution led to almost no reduction of Eu3+. High Eu2+ doping concentration and enhanced luminescent QY of Eu2+ were simultaneously achieved in BaF2-based glass-ceramic.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Key Research and Development Program of China (No. 2016YFB0303700), the National Nature Science Foundation of China (No. 51672243), Zhejiang Provincial Natural Science Foundation of China (No. LY16E020003), the Fundamental Research Funds for the Central Universities (No. 2016QNA4005; No. 2016FZA4007).Notes and references
- P.-P. Dai, C. Li, X.-T. Zhang, J. Xu, X. Chen, X.-L. Wang, Y. Jia, X. Wang and Y.-C. Liu, Light: Sci. Appl., 2016, 5, E16024 CrossRef CAS PubMed.
- Y. H. Kim, P. Arunkumar, B. Y. Kim, S. Unithrattil, E. Kim, S.-H. Moon, J. Y. Hyun, K. H. Kim, D. Lee, J.-S. Lee and W. B. Im, Nat. Mater., 2017, 16, 543–550 CrossRef CAS PubMed.
- X. Zhang, J. Wang, L. Huang, F. Pan, Y. Chen, B. Lei, M. Peng and M. Wu, ACS Appl. Mater. Interfaces, 2015, 7, 10044–10054 CrossRef CAS PubMed.
- S. Ye, F. Xiao, Y. X. Pan, Y. Y. Ma and Q. Y. Zhang, Mater. Sci. Eng., R, 2010, 71, 1–34 CrossRef.
- Q. Luo, X. Qiao, X. Fan, S. Liu, H. Yang and X. Zhang, J. Non-Cryst. Solids, 2008, 354, 4691–4694 CrossRef CAS.
- Q. Luo, X. Qiao, X. Fan and X. Zhang, J. Am. Ceram. Soc., 2010, 93, 2684–2688 CrossRef CAS.
- Q. Luo, X. Fan, X. Qiao, H. Yang, M. Wang and X. Zhang, J. Am. Ceram. Soc., 2009, 92, 942–944 CrossRef CAS.
- J. Fu, J. M. Parker, P. S. Flower and R. M. Brown, Mater. Res. Bull., 2002, 37, 1843–1849 CrossRef CAS.
- L. Zur, J. Janek, M. Soltys, T. Goryczka, J. Pisarska and W. A. Pisarski, J. Non-Cryst. Solids, 2016, 431, 145–149 CrossRef CAS.
- Y. Gao, J. Qiu and D. Zhou, J. Am. Ceram. Soc., 2017, 100, 2901–2913 CrossRef CAS.
- T. Grzyb, A. Szczeszak, Z. Sniadecki, B. Idzikowski and S. Lis, J. Alloys Compd., 2016, 686, 489–495 CrossRef CAS.
- G. Chen, L.-J. Yin, J.-T. Dong, Y.-Y. Feng, Y. Gao, W. He, Y. Jia, X. Xu and H. T. Hintzen, J. Am. Ceram. Soc., 2016, 99, 183–190 CrossRef CAS.
- H. Bian, Y. Liu, D. Yan, H. Zhu, C. Liu, C. Xu, X. Wang and H. Zhang, J. Am. Ceram. Soc., 2017, 100, 3467–3477 CrossRef CAS.
- M. Nogami, A. Koiwai and T. Nonaka, J. Am. Ceram. Soc., 2016, 99, 1248–1254 CrossRef CAS.
- S. Liu, G. Zhao, W. Ruan, Z. Yao, T. Xie, J. Jin, H. Ying, J. Wang and G. Han, J. Am. Ceram. Soc., 2008, 91, 2740–2742 CrossRef CAS.
- H. Wang, S. Ye, S. Li, T. Liu, J. Lin and D. Wang, J. Alloys Compd., 2015, 648, 13–17 CrossRef CAS.
- W. Chen, X. Chen, F. Sun and X. Wang, J. Alloys Compd., 2017, 698, 565–570 CrossRef CAS.
- C. Zhu, D. Wu, Y. Zhang, M. Zhang and Y. Yue, J. Alloys Compd., 2015, 632, 291–295 CrossRef CAS.
- G. Gao, N. Da, S. Reibstein and L. Wondraczek, Opt. Express, 2010, 18(suppl. 4), A575–A583 CrossRef CAS PubMed.
- G. Gao, S. Reibstein, M. Peng and L. Wondraczek, J. Mater. Chem., 2011, 21, 3156 RSC.
- H. Bouchouicha, G. Panczer, D. de Ligny, Y. Guyot, M. L. Baesso, L. H. C. Andrade, S. M. Lima and R. Ternane, J. Lumin., 2016, 169, 528–533 CrossRef CAS.
- K. Qiu, S.-c. Xu, H. Tian, X. Zheng, T.-s. Lv, Q.-f. Lu and D.-j. Wang, Optoelectronics Letters, 2011, 7, 350–353 CrossRef.
- C. Zhu, Y. Yang, X. Liang, S. Yuan and G. Chen, J. Am. Ceram. Soc., 2007, 90, 2984–2986 CrossRef CAS.
- Y. Jiang, P. Zhang, T. Wei, J. Fan, B. Jiang, X. Mao and L. Zhang, RSC Adv., 2016, 6, 55366–55373 RSC.
- K. Biswas, A. D. Sontakke and K. Annapurna, Int. J. Appl. Glass Sci., 2012, 3, 154–162 CrossRef CAS.
- B. Henke, C. Passlick, P. Keil, J. A. Johnson and S. Schweizer, J. Appl. Phys., 2009, 106, 113501 CrossRef CAS PubMed.
- G. Blasse and B. C. Grabmaier, Luminescent Materials, Springer-Verlag, Berlin Heidelberg, 1997 Search PubMed.
- J. A. Duffy and M. D. Ingram, J. Inorg. Nucl. Chem., 1976, 38, 1831–1833 CrossRef CAS.
- J. A. Duffy, J. Non-Cryst. Solids, 1989, 109, 35–39 CrossRef CAS.
- J. Zhao, R. Ma, X. Chen, B. Kang, X. Qiao, J. Du, X. Fan, U. Ross, C. Roiland, A. Lotnyk, L. Kienle and X. Zhang, J. Phys. Chem. C, 2016, 120, 17726–17732 CrossRef CAS.
- W. L. Jolly, in Modern Inorganic Chemistry, McGraw-Hill, New York, 2nd edn, 1991, pp. 71–76 Search PubMed.
- D. Chen, Z. Wan, Y. Zhou, P. Huang, X. Zhou, Y. Yu, J. Zhong, M. Ding and Z. Ji, J. Eur. Ceram. Soc., 2016, 36, 679–688 CrossRef CAS.
- M. E. Lines, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 5793–5801 CrossRef CAS.
- C. Zhu, Y. Yang, X. Liang, S. Yuan and G. Chen, J. Am. Ceram. Soc., 2007, 90, 2984–2986 CrossRef CAS.
- Z. Lian, J. Wang, Y. Lv, S. Wang and Q. Su, J. Alloys Compd., 2007, 430, 257–261 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06843g |
| This journal is © The Royal Society of Chemistry 2018 |