Open Access Article
Open Access ArticleStructural and electronic properties of KY(BH4)4: DFT+U study†
Chuan Liu *a,
Ting Zhanga,
Xiangju Yea,
Xuemei Zhanga and
Shengli Zhang
*a,
Ting Zhanga,
Xiangju Yea,
Xuemei Zhanga and
Shengli Zhang b
b
aCollege of Chemistry and Materials Engineering, Anhui Science and Technology University, Fengyang, Anhui Province 233100, China. E-mail: liuxc@ahstu.edu.cn
bInstitute of Optoelectronics & Nanomaterials Herbert Gleiter Institute of Nanoscience, College of Materials Science and Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China
First published on 8th October 2018
Abstract
The structure, composition, and electronic property of mixed-cation borohydrides are of significant importance for understanding and improving their thermodynamic and kinetic activities. Conventional density functional theory (DFT) fails to correctly describe the electronic structure of the system due to insufficient cancellation of the self-interaction energy and underestimation of the band gap. In the present work, we present a systematic investigation of the structural and electronic properties of KY(BH4)4 for the first time at the DFT+U level of theory. It is found that the LDA+U method underestimates the lattice volume by ∼17.36%, while the PBE+U and PW91+U methods show good agreement with the experimental value at U = 3 and U = 4, respectively. The total energy of KY(BH4)4 calculated by PW91+U method at U = 4 is 0.97 eV lower than that calculated by PBE+U method at U = 3. We suppose that the PW91+U method is more suitable for the structural and electronic properties study of KY(BH4)4 due to the lower total energy. K+ connects with BH4− complex through electrostatic attraction, while weak covalent interaction exists between Y3+ and BH4− complex.
Introduction
Metal borohydrides are a class of solid-state materials actively investigated for hydrogen storage applications. In view of the large gravimetric hydrogen density (20.8 wt% for Be(BH4)2, 18.4 wt% for LiBH4), borohydrides of alkaline and alkaline earth metals are of interest for hydrogen storage in mobile applications.1–4 Even though their high gravimetric hydrogen densities satisfy the technical targets of the US Department of Energy (DOE) for vehicular applications,5 practical use of these metal borohydrides is hindered by their stability. The decomposition temperatures are often too high due to the high enthalpies of hydrogen release, the reaction kinetics for H2 releasing are slow, the rehydrogenation is irreversible or only partly reversible, and the evolved H2 is contaminated with BxHy.6,7 A number of methods have been attempted in order to tackle the problems, such as mechanical alloying, nanoconfinement, using catalytic additives, and meaningful advances have been achieved.8–12The stability of single-cation borohydrides (M(BH4)n) are recently empirically related to the Pauling electronegativity of the cation.13,14 Based on the report of Nakamori et al.,13,14 the electrostatic interaction between metal cation (Mn+) and the [BH4]− complex anion plays an important role in determining the stability of the metal borohydride. Thus, adjusting the Pauling electronegativity, χp, by employing more than one metal cation, such as MM′(BH4)m, appears to be a promising new route for tuning the thermodynamic properties of metal borohydrides. While the import of heavier transition metal ions will decrease the gravimetric capacities, it may also improve hydrogen storage reactivities and kinetics of borohydrides.4 Consequently, many mixed-cation borohydrides have been synthesized, including NaSc(BH4)4,15 KY(BH4)4,16,17 KSc(BH4)4,18 LiLa(BH4)3Cl,19 LiSc(BH4)4,20 NaLa(BH4)4,21 and K3La(BH4)6.21 Based on the experimental results of Jaroń et al.,16 the rietveld refinement yields 24.4 mol% of KY(BH4)4 in the post-milled samples, testifying to a high degree of conversion of 98%. In addition, the diffraction peaks of the monoclinic KY(BH4)4 appear at 350 K, which implies that monoclinic KY(BH4)4 is either a partially dehydrogenated K–Y–B–H compound or a high-temperature polymorph of KY(BH4)4. According to the experimental results, it infers that orthorhombic KY(BH4)4 is more thermodynamically stable than monoclinic KY(BH4)4. Therefore, orthorhombic KY(BH4)4 is used here for the first-principles calculations.
Despite many experimental investigations, information about the synthesis and structure of mixed-cation borohydrides, there are few theoretical data about their structural and electronic properties. Thus, it becomes very important to theoretically give the structural and electronic data of mixed-cation borohydrides for further studying their thermodynamic and kinetic properties. For crystalline solids, researchers tend to apply DFT for band structure calculations.22,23 In mixed-cation borohydrides, MM′(BH4)m, we know that heavier transition-metal ions are introduced for adjusting the Pauling electronegativity. Standard DFT predicts narrow eigenvalue gaps due largely to the self-interaction error incurred by using approximate exchange–correlation functionals. The shortcoming of DFT is corrected in practice by either of two semiempirical approaches: hybrid functional24,25 method, or DFT+U26,27 method.
In the present study, we perform DFT+U calculations on the structural and electronic properties of KY(BH4)4. Our main aims are to test the functionals and basis sets used here.
Computational details
All the spin-polarized DFT+U calculations are performed using the Vienna Ab-Initio Simulation Package (VASP).28 Pseudopotentials are generated with projector augmented wave (PAW) method.29 For exchange–correlation functional, the local density approximation (LDA)30 of Perdew and Zunger, and the generalized gradient approximation (GGA) of Perdew and Wang (PW91)31 and Perdew–Burke–Ernzerhof (PEB)32 versions are tested. In the DFT+U calculations, the approach of Dudarev et al.33 is employed. The effective U (Ueff) value is determined by the difference of parameters of U and J. We first set U as 1 eV, and change the value of J from 0.1 to 1.0 eV. The value of 0.2 eV is found to perform well in estimating the lattice parameter of KY(BH4)4. Then, J is set as 0.2 eV, and change the value of U from 1 to 10 eV. Due to KY(BH4)4 is isostructural to NaSc(BH4)4, NaSc(BH4)4 is used as the initial geometry to perform structure optimization. The plane-waves basis with cut-off energy of 450 eV and the conjugate gradient algorithm are applied to determine the electronic ground state. A 5 × 5 × 5 Monkhorst–Pack34 k-point mesh is used for sampling the Brillouin zone. Structures are relaxed until the forces on each ion are below 0.01 eV Å−1 and the total energy is converged within 1 × 10−5 eV.Results and discussion
In KY(BH4)4, the B atom is coordinated by four H atoms to form BH4− complex, and four BH4− complex coordinate with one central Y3+ through its H atoms to form a slightly distorted tetrahedral complex anion, [Y(BH4)4]−. While K+ is coordinated by six BH4− complex to form an octahedral configuration, as shown in Fig. 1. KY(BH4)4 is synthesized at ambient conditions in ball-milled mixtures of Y(BH4)3 and KBH4 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio for 60 min in an Ar atmosphere. KY(BH4)4 is isostructural to NaSc(BH4)4 with the unit cell axes ratio of a
1 molar ratio for 60 min in an Ar atmosphere. KY(BH4)4 is isostructural to NaSc(BH4)4 with the unit cell axes ratio of a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = 1
c = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.47
1.47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.13, resembling the one for NaSc(BH4)4, a
1.13, resembling the one for NaSc(BH4)4, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = 1
c = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.45
1.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
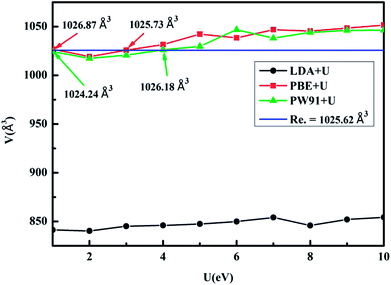
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.13. KY(BH4)4 crystallises in the Cmcm space group with the lattice volume of 1025.62 Å3.16 Fig. 2 shows the relation of the lattice volume of optimized KY(BH4)4 with different values of U. In terms of the experimental value of the lattice volume of optimized KY(BH4)4, LDA+U method underestimates the lattice volume by ∼17.36%. The lattice volume predicted by PBE+U method at U = 3 is 1025.73 Å3, closest to the experimental value. For PW91+U method, it occurs at U = 4, where the calculated lattice volume is closest to the experimental value. To determine which method is more suitable for calculating the structural and electronic properties of KY(BH4)4, we therefore compare the calculated bond lengths and bond angles in optimized KY(BH4)4 with experimental value. Table 1 summarizes the bond lengths and bond angles in optimized KY(BH4)4. It can be seen that the calculated results by PBE+U method at U = 3 and by PW91+U method at U = 4 are all in good agreement with the experimental results. For ascertaining the suitable hybrid functional, we therefore calculate the total energy of KY(BH4)4 using these two different hybrid functionals. The results show that the total energy of KY(BH4)4 calculated by PW91+U method at U = 4 is 0.97 eV lower than that calculated by PBE+U method at U = 3. This demonstrates that PW91+U method is more suitable for the structural and electronic properties study of KY(BH4)4 due to the lower total energy. In this, the hybrid functional of PW91+U is used for the electronic properties analysis of KY(BH4)4.
1.13. KY(BH4)4 crystallises in the Cmcm space group with the lattice volume of 1025.62 Å3.16 Fig. 2 shows the relation of the lattice volume of optimized KY(BH4)4 with different values of U. In terms of the experimental value of the lattice volume of optimized KY(BH4)4, LDA+U method underestimates the lattice volume by ∼17.36%. The lattice volume predicted by PBE+U method at U = 3 is 1025.73 Å3, closest to the experimental value. For PW91+U method, it occurs at U = 4, where the calculated lattice volume is closest to the experimental value. To determine which method is more suitable for calculating the structural and electronic properties of KY(BH4)4, we therefore compare the calculated bond lengths and bond angles in optimized KY(BH4)4 with experimental value. Table 1 summarizes the bond lengths and bond angles in optimized KY(BH4)4. It can be seen that the calculated results by PBE+U method at U = 3 and by PW91+U method at U = 4 are all in good agreement with the experimental results. For ascertaining the suitable hybrid functional, we therefore calculate the total energy of KY(BH4)4 using these two different hybrid functionals. The results show that the total energy of KY(BH4)4 calculated by PW91+U method at U = 4 is 0.97 eV lower than that calculated by PBE+U method at U = 3. This demonstrates that PW91+U method is more suitable for the structural and electronic properties study of KY(BH4)4 due to the lower total energy. In this, the hybrid functional of PW91+U is used for the electronic properties analysis of KY(BH4)4.
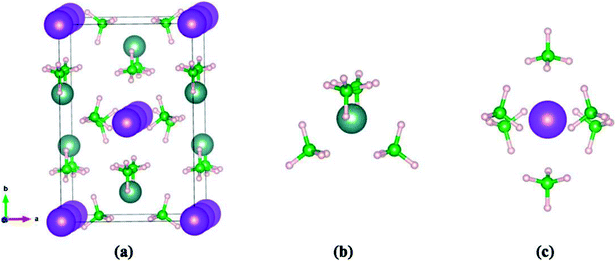 | ||
| Fig. 1 The geometries of (a) unit cell of KY(BH4)4, (b) coordination sphere of yttrium by four BH4− complex, (c) coordination sphere of potassium by six BH4− complex. | ||
| Item | U = 3 | U = 4 | |
|---|---|---|---|
| Y–H (Å) | Re. | 2.20 × 4, 2.29 × 4, 2.35 × 2, 2.41 × 2 | |
| PW91+U | — | 2.34 × 2, 2.37 × 4, 2.39 × 2, 2.39 × 4 | |
| PBE+U | 2.33 × 2, 2.36 × 2, 2.38 × 2, 2.38 × 2 | — | |
| K–B (Å) | Re. | 3.259 × 2, 3.354 × 4 | |
| PW91+U | — | 3.161 × 2, 3.273 × 4 | |
| PBE+U | 3.163 × 2, 3.280 × 2 | — | |
| B–K–B (°) | Re. | 87.21–92.79 | |
| PW91+U | — | 86.46–93.54 | |
| PBE+U | 86.82–93.17 | — | |
| K–H (Å) | Re. | 2.60–2.84, 3.299–3.37 | |
| PW91+U | — | 2.63–2.73, 3.23–3.38 | |
| PBE+U | 2.63–2.73, 3.24–3.39 | — | |
For addressing the relationship between the electronic structure and the nature of bonding in KY(BH4)4, we calculate the total and partial densities of states (DOS) of KY(BH4)4, K, Y, B, and H atoms with the Fermi energy set to zero. Fig. 3 shows the DOS of KY(BH4)4 calculated by the PW91+U method at U = 4 only. The DOS of KY(BH4)4 calculated by the PBE+U method at U = 3 is shown in the ESI† due to it shows similar plots with the former. It is found from the total DOS that the spin up and down states are symmetrical, which indicates that KY(BH4)4 is nonmagnetic. The total DOS of KY(BH4)4 below the Fermi energy are split into sever regions, and the antibonding conduction bond are mainly composed of K 3d and Y 4d orbitals. The two bonding peaks in the energy ranges from −3.12 to −0.39 eV and from −7.78 to −5.84 eV are mainly derived from H 1s, B 2p orbitals and H 1s, B 2s orbitals, respectively. The orbital hybridizations between H 1s and B 2s, 2p orbitals clearly demonstrate the covalent interaction between H and B atoms. Interestingly, it is found from the PDOSs of H and B atoms that the shapes of the peaks of H 1s orbitals are not the same with those of B 2s and 2p orbitals. There are two peaks in the PDOS of H 1s orbital in the energy range from −7.78 to −5.84 eV with the maximum state at −7.00 and −6.42 eV, respectively. Actually, the difference is generated from the import of Y atom. It can be seen from Fig. 3b that using same scale of vertical axis, the PDOS of Y atom also has peaks in the energy ranges from −3.12 to −0.39 eV and from −7.78 to −5.84 eV. In the energy range from −7.78 to −5.84 eV, the maximum state of Y 5s orbital is located at −7.00 eV, while the maximum states of Y 5p and 4d orbitals are all located at −6.42 eV. Clearly, the maximum states of Y 5s, 5p, and 4d orbitals are in accord with those in the PDOS of H 1s orbital. In the energy range from −7.78 to −5.84 eV, the states of Y 5p and 4d orbitals are obvious, while the state of Y 5s orbital is not. The orbital hybridizations between H 1s and Y 5s, 5p, and 4d orbitals demonstrate that Y atom interacts with H atom in covalent bond. However, the PDOS of Y atom also has two obvious peaks at lower energy level, which respectively correspond to Y 5p orbital and Y 5s orbital. These two peaks show no significant correlation with the PDOS of H 1s orbital. It is thus concluded that the interaction between the central Y3+ and its four BH4− ligands is mainly electrostatic attraction, while weak covalent interaction also exists between central Y3+ and the coordinating atom of H. The peaks in the energy ranges from −28.38 to −27.41 eV and from −12.06 to −10.89 eV are derived from K 4s and 4p orbitals, respectively. No hybridization between K and H atoms clearly shows the characteristics of ionic bond between K+ and BH4− unit.
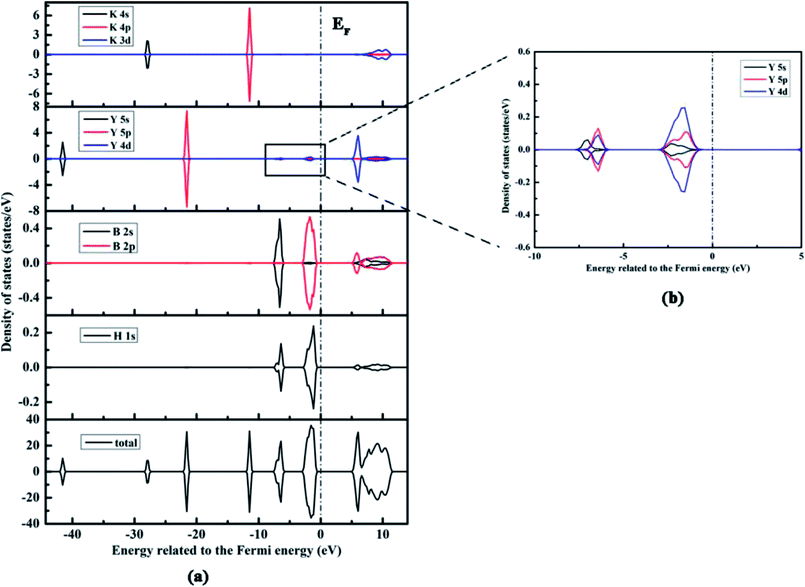 | ||
| Fig. 3 The calculated total and partial density of states of KY(BH4)4 by the PW91+U method at U = 4 eV, and the Fermi energy is set to zero, labeled as EF. | ||
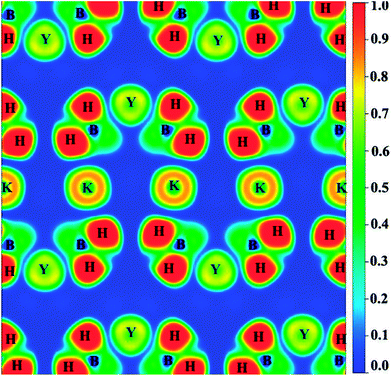
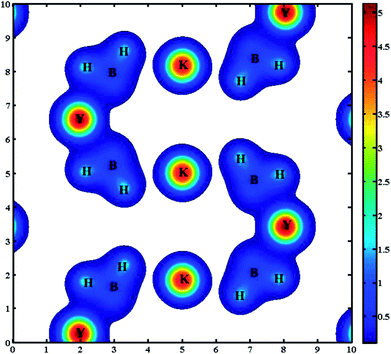
In order to better explain the bonding characteristics and the distribution of electronic information in KY(BH4)4, we therefore calculate the electron localization function (ELF) and the total charge density of KY(BH4)4, as shown in Fig. 4 and 5. ELF is one of the most widely used and robust quantum-mechanical tools to analyze electron localization and chemical bonds.35 The value of ELF is defined as a function of ratio in order to vary the electron localization measure in the interval [0, 1].36 As shown in Fig. 4, electrons are strongly localized around H atom to form electron pairs, keeping hydrogen in the form of H−. On the contrast, the very low values of ELF are observed at the B sites, indicating that electrons are delocalized in these regions. The covalent bonding between the central B and its neighboring four H atoms is well-supported by the continuous ELF between B and its around four H atoms. The ELF of K+ and Y3+ should be small, but it is found that the ELF of K+ is about 0.8 and that of Y3+ is about 0.7. Actually, it is generally considered to be caused by the inner 3p orbital of K+ and 4p orbital of Y3+.37 Negligibly low ELF between K+ and BH4− complex indicates that the nature of interaction between them is ionic interaction. In addition, the total charge density of KY(BH4)4 shows no charge overlap exists between K+ and BH4− complex, which further verifies that the interaction between K+ and BH4− complex belongs to ionic interaction. However, due to Y3+ is more closer to BH4− complex than K+, weak covalent interaction is found between Y3+ and its four neighboring BH4− complex. This can be concluded from the continuous ELF (about 0.2) between Y3+ and BH4− complex. What is more, it can be seen from Fig. 5 that the charge of Y3+ and BH4− complex are connected together, shaped like a butterfly. This further suggests that there exists covalent interaction between Y3+ and BH4− complex excepting ionic interaction.
Conclusions
In summary, the structural and electronic properties of KY(BH4)4 has been studied by DFT+U method. The LDA+U method fails to estimate the crystal structure of KY(BH4)4 and underestimates the lattice volume by ∼17.36%. The lattice volume predicted by PBE+U method at U = 3 is 1025.73 Å3 and that predicted by PW91+U method at U = 4 is 1026.18 Å3. Although the lattice volume predicted by PBE+U at U = 3 is much closer to the experimental result, the bond lengths and bond angles in optimized KY(BH4)4 by PW91+U method at U = 4 also show good agreement with experiments. Both PBE+U and PW91+U methods give a similar description of DOS, ELF, and total charge density of KY(BH4)4, while the band gap depends on the method employed. The band gap is 3.499 eV estimated by the PW91+U method at U = 4. Experimental measurements are needed to determine the precise band gap of KY(BH4)4. The total energy of KY(BH4)4 calculated by PW91+U method at U = 4 is 0.97 eV lower than that calculated by PBE+U method at U = 3. This demonstrates that PW91+U method is more suitable for the structural and electronic properties study of KY(BH4)4. Based on the results of DOS, ELF, and total charge density of KY(BH4)4, K+ connects with BH4− complex through electrostatic attraction, while weak covalent interaction exists between Y3+ and BH4− complex. These findings will serve as a basis to advance the understanding of thermodynamic and kinetic behaviors of KY(BH4)4.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Scientific Research Foundation of Anhui Science and Technology University (Grant no. HCYJ201602), the NSFC (21603002), the NSF of Education Department of Anhui (KJ2018A0525, KJ2017A507), and the Materials Science and Engineering Key Discipline Foundation (No. AKZDXK2015A01).References
- H. W. Li, Y. Yan, S. Orimo, A. Züttel and C. M. Jensen, Energies, 2011, 4, 185–214 CrossRef CAS.
- L. H. Rude, T. K. Nielsen, D. B. Ravnsbæk, U. Bösenberg, M. B. Ley, B. Richter, L. M. Arnbjerg, M. Dornheim, Y. Filinchuk, F. Besenbacher and T. R. Jensen, Phys. Status Solidi A, 2011, 208, 1754–1773 CrossRef CAS.
- S. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- M. Paskevicius, L. H. Jepsen, P. Schouwink, R. Černý, D. B. Ravnsbæk, Y. Filinchuk, M. Dornheim, F. Besenbacher and T. R. Jensen, Chem. Soc. Rev., 2017, 46, 1565–1634 RSC.
- S. Satyapal, J. Petrovic, C. Read, G. Thomas and G. Ordaz, Catal. Today, 2007, 120, 246–256 CrossRef CAS.
- D. B. Ravnsbæk, Y. Filinchuk, R. Černý and T. R. Jensen, Z. Kristallogr., 2010, 225, 557–569 CrossRef.
- W. Grochala and P. P. Edwards, Chem. Rev., 2004, 104, 1283–1315 CrossRef CAS PubMed.
- X. Wan, T. Markmaitree, W. Osborn and L. L. Shaw, J. Phys. Chem. C, 2008, 112, 18232 CrossRef CAS.
- J. Huot, D. B. Ravnsbæk, J. Zhang, F. Cuevas, M. Latroche and T. R. Jensen, Prog. Mater. Sci., 2013, 58, 30–75 CrossRef CAS.
- T. K. Nielsen, T. R. Jensen and F. Besenbacher, Nanoscale, 2011, 3, 2086–2098 RSC.
- X. B. Yu, Z. Wu, Q. R. Chen, Z. L. Li, B. C. Weng and T. S. Huang, Appl. Phys. Lett., 2007, 90, 034106 CrossRef.
- A. F. Gross, J. J. Vajo, S. L. Van Atta and G. L. Olson, J. Phys. Chem. C, 2008, 112, 5651 CrossRef CAS.
- N. Yuko, M. Kazutoshi, N. Akihito, L. Haiwen, O. Nobuko, T. Shin-Ichi, Z. Andreas and O. Shin-Ichi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045126 CrossRef.
- Y. Nakamori, H. W. Li, K. Kikuchi, M. Aoki, K. Miwa, S. Towata and S. Orimo, J. Alloys Compd., 2007, 446–447, 296–300 CrossRef CAS.
- R. Černý, G. Severa, D. B. Ravnsbæk, Y. Filinchuk, V. D'Anna, H. Hagemann, D. Haase, C. M. Jensen and T. R. Jensen, J. Phys. Chem. C, 2010, 114, 1357–1364 CrossRef.
- T. Jaroń and W. Grochala, Dalton Trans., 2011, 40, 12808–12817 RSC.
- Y. Sadikin, K. Stare, P. Schouwink, M. B. Ley, T. R. Jensen, A. Meden and R. Černý, J. Solid State Chem., 2015, 225, 231–239 CrossRef CAS.
- R. Černý, D. B. Ravnsbæk, G. Severa, Y. Filinchuk, V. D'Anna, H. Hagemann, D. Haase, J. Skibsted, C. M. Jensen and T. R. Jensen, J. Phys. Chem. C, 2010, 114, 19540–19549 CrossRef.
- A. V. Skripov, A. V. Soloninin, M. B. Ley, T. R. Jensen and Y. Filinchuk, J. Phys. Chem. C, 2013, 117, 14965–14972 CrossRef CAS.
- C. Kim, S. J. Hwang, R. C. Bowman Jr, J. W. Reiter, J. A. Zan, J. G. Kulleck, H. Kabbour, E. H. Majzoub and V. Ozolins, J. Phys. Chem. C, 2009, 113, 9956–9968 CrossRef CAS.
- S. P. GharibDoust, M. Heere, M. H. Sørby, M. B. Ley, D. B. Ravnsbæk, B. C. Hauback, R. Černý and T. R. Jensen, Dalton Trans., 2016, 45, 19002–19011 RSC.
- S. Md. Pratik, A. Nijamudheen and A. Datta, Chem.–Eur. J., 2015, 21, 18454–18460 CrossRef CAS PubMed.
- W. Kohn and L. J. Shan, Phys. Rev., 1965, 140, A1133 CrossRef.
- M. Ernzerhof, J. P. Perdew and K. Burke, Int. J. Quantum Chem., 1997, 64, 285–295 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- L. De Santis and R. Resta, Surf. Sci., 2000, 450, 126–132 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06742b |
| This journal is © The Royal Society of Chemistry 2018 |