Strain-engineering the electronic properties and anisotropy of GeSe₂ monolayers

Abstract

As a new two-dimensional (2D) material, GeSe₂ has attracted significant attention recently due to its distinctive in-plane anisotropic properties originated from the in-plane anisotropic crystal structure, high air stability and excellent performance in polarization-sensitive photodetection. However, no systematic study of the strain effect on the electronic properties and anisotropy of GeSe₂ has been reported, restricting the relevant applications such as mechanical-electronic devices. Here we investigate the change of the electronic properties and anisotropy of GeSe₂ monolayer under strains along x and y directions through first-principle calculations. The electronic band structure and effective mass of charge carriers are highly sensitive to the strain. Notably, through appropriate x or y directional strain, the anisotropy of the hole effective mass can even be rotated by 90°. These plentiful strain-engineering properties of GeSe₂ give it many opportunities in novel mechanical-electronic applications.

---

1. Introduction

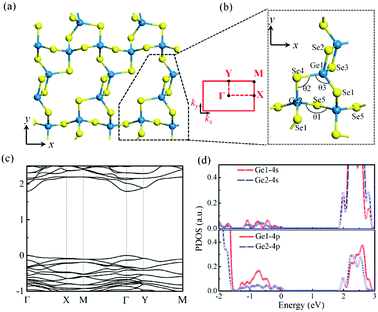
Strain has served as an effective and convenient tool for modulating electronic, transport, and optical properties of semiconductors.^1–5 Such strain effects can be interpreted as an elastic field applied to materials, which modifies the geometrical structure of the crystal due to the interaction between the elastic field and crystalline field, then influences the electronic band structure,⁶ and finally tunes the physical^7,8 (such as the optical absorption anisotropy) and chemical properties⁹ (catalytic properties) of materials. This tool is particularly suitable for the engineering of two-dimensional (2D) crystals because this low-dimensional structure can sustain much larger strain compared with bulk crystals.^10–13 For example, monolayer black phosphorus (BP), the most recently studied 2D material, has been reported to be strained up to a remarkable strain of 30% without any dislocation or plastic deformation in its crystal structure,¹⁴ providing a wide range for tuning its mechanical and electronic properties.^15,16 Furthermore, as the prototypical 2D material with in-plane anisotropy, the anisotropic electrical and thermal properties of ultrathin BP can also be modified by strain.¹⁷ It is predicted that the preferred conducting direction of BP can be rotated by 90° in plane through the appropriate biaxial or uniaxial strain (4–6%), providing great opportunities for novel mechanical-electronic device applications.^9,10,18,19 Those studies forcefully demonstrated the important function of strain as a powerful tool to modulate the physical properties of materials.²⁰

Germanium diselenide (GeSe₂), another new important member of in-plane anisotropic 2D materials, has attracted significant attention recently due to its high performance in polarization-sensitive photodetection as well as its great stability in ambient environment.^21–27 It adopts a monoclinic crystal structure with the P2₁/c space group.²⁸ As shown in Fig. 1a and b, the basic building blocks of GeSe₄ tetrahedra are mutually connected via corner-sharing forming (GeSe₄)_n chains along x-axis and via edge-sharing Ge₂Se₈ double tetrahedral along y-axis. Therefore, the different connection modes lead to in-plane structural anisotropy, which induces strong in-plane anisotropic behaviors of electronic and optical properties. In particular, as a powerful complement to the conventional members of this family with narrow bandgaps such as BP (0.3 eV (ref. 14)), ReS₂ (1.5 eV (ref. 28)) and GeSe (1.14 eV (ref. 29 and 30)), GeSe₂ has a wide direct bandgap of 2.74 eV,²¹ making it ideal for the short-wavelength polarized photodetection. In this regard, it will be exciting if we can further modulate the physical properties and anisotropy of GeSe₂, thus enabling versatile functionality in this material. Until now, however, there has been no report engineering the physical and corresponding anisotropic properties of GeSe₂, and the most recent work only focused on the investigation of the basic in-plane anisotropic properties such as structural, electrical, optical and vibrational anisotropies.

Fig. 1 Snapshots of 2D GeSe₂ monolayer (a) and the building blocks (b). (c) DFT-calculated band structure of GeSe₂ monolayer. The Fermi level is set to zero on the energy axis. (d) Calculated PDOSs of Ge1 and Ge2 atoms labeled in (b).

In this study, through first-principles calculations, we investigate the change of the electronic properties and anisotropy of GeSe₂ monolayer under strains along x and y directions. The mechanism for the gap transition is discussed in detail. Furthermore, the strain effects on the effective masses of electrons and holes are systematically investigated. The results of this study indicate that GeSe₂, as a new member of anisotropic 2D materials, has promising practical applications in novel mechanical-electronic devices.

2. Computational methods

Based on density functional theory, the geometric and electronic structures of GeSe₂ are performed using the Vienna ab initio simulation package (VASP).^31,32 Generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) simulates the exchange–correlation energy.^33,34 The interactions between valence electrons and ions are described by projector-augmented wave (PAW) potentials.³⁵ Reciprocal space of 6 × 6 × 1 grid is adopted for geometry relaxations and the plane wave basis cutoff energy is set as 600 eV. A sufficiently large vacuum region of 20 Å is applied to avoid the interaction between layers. The convergence criterion is set to be 10⁻⁵ eV and the residual force acting on each atom is 10⁻² eV Å⁻¹. Since the DFT method is known to underestimate the band gap of semiconductors, it is important to test the robustness of strain effects on the properties of GeSe₂. For comparison, we have calculated the band structures of GeSe₂ monolayer by DFT and advanced hybrid functional HSE06 methods under different values of axial strains.³³ Therefore, the DFT method is employed in this paper to predict the general trends of strain engineering on the band structure of GeSe₂ monolayer.

For the relaxed GeSe₂ monolayer, the applied strain is defined as 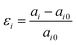, where a_i and a_i0 are the lattice constants along i (=x and y) direction. The positive values refer to tension while negative values refer to compression. With each applied axial strain, the lattice constant in the transverse direction is fully relaxed for the minimum force. Meanwhile, effective masses of charge carriers are calculated according to the formula 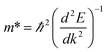through the calculated band structures, where ℏ is the reduced Planck's constant, E is the energy, and k is the momentum.

3. Results and discussions

We start from the calculation of electronic band structure of GeSe₂ monolayer as presented in Fig. 1a. As shown in Fig. 1c, a direct band gap appears at Γ point. It is noteworthy to mention that GeSe₂ has highly anisotropic band dispersion along Γ–X and Γ–Y directions of conduct band minimum (CBM) and valence band maximum (VBM), resulting in significantly anisotropic electronic properties. As shown in Fig. 1d and S1,† we further calculate the partial densities of state (PDOS) of unequal Ge atoms and their near-neighbor Se atoms. The results reveal that shallow valence band (SVB, ranging from −1.5 to 0 eV) mainly originate from 4p states of Ge atoms, while Ge1-4p state provides larger contribution than Ge2-4p state. Yet, for the conduction band, Ge-4s states provide larger contribution than Ge-4p states. As shown in Fig. S1a and b,† the VBM is formed mainly by the 4p states of Se atoms in GeSe₄ tetrahedra (from Se1 to Se4), while Se5-4p state contributes to SVB. Combining with the large overlap of Ge1-4p and Se-4s states (see in Fig. S1c and d†), the higher contributions to SVB indicates the stronger covalent bond energies of Ge1–Se compared to that of Ge2–Se, resulting in the in-plane anisotropic natural structure of GeSe₂ monolayer as shown in Fig. 1a. Therefore, different Ge–Se bonds along x and y directions lead to low in-plane lattice symmetry of GeSe₂.

We now focus on the band gap modulating of GeSe₂ monolayer at different values of axial strains. The components of strain along x and y directions are labeled as ε_x and ε_y, respectively. As shown in Fig. 2, it is clear that the HSE06 has a better prediction on the band value of 2.62 eV for GeSe₂ monolayer, which is good agreement with our former experimental value of 2.74 eV,²⁰ and has a 0.828 eV energy difference to DFT value. Meanwhile, comparing the calculated band gap values based on HSE06 and DFT methods, one can conclude that the band structures strongly depend on the strains while the both methods give the same band gap variation results as a function of strain. Therefore, the DFT can be employed to predict the general trends of strain engineering on the band structure of GeSe₂ monolayer. For the strain ε_y in Fig. 2a, the maximal band gap of 2.83 eV for HSE06 is obtained at strain ε_y = −4% and then dropped linearly to 2.01 eV at strain ε_y = −12%. On the side of tensile strain, the gap shows linear reduction with strain increasing and reaches to 1.51 eV of ε_y = 12%. To see if the gap could reduce to zero with further increased tensile strain, we explore even larger strain up to +32%. The gap is not found to close while it reaches a minimal value 0.98 eV at +28% strain and then opens up again for larger strain value. Notably, the tensile strain ε_y presents a strategy for the direct band gap modification with a wide range exceed 1.85 eV. With regard to the strain ε_x shown in Fig. 2b, the band gap drops to 1.63 eV at compressive strain ε_x = −12% without sudden change. For the tensile cases, it initially increases from 2.62 eV for the relaxed structure (RS) to a maximal value of 2.83 eV at ε_x = +8%, and then drops rapidly with further increased expansion. Through the above analysis of strains applied in the two directions, it is obvious that three strain zones are identified for strain ε_y and two for ε_x, and the direct band gap is particularly maintained under the in-plane tensile strain along two directions. Briefly, it confirms that the strains can effectively tune the band gap of GeSe₂ monolayer in a wide range.

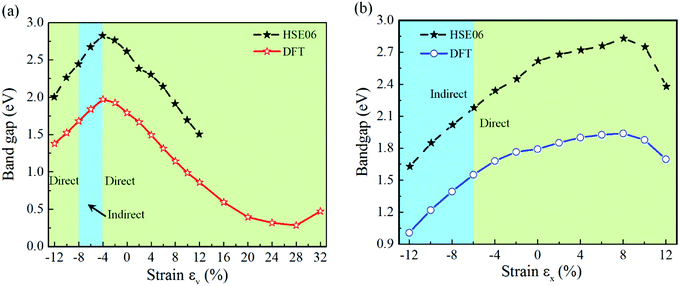Fig. 2 Band gap of GeSe₂ monolayer as a function of strain ε_y (a) and ε_x (b) based on the methods of HSE06 and PBE, respectively. Direct/indirect band zones are listed with green/blue color.

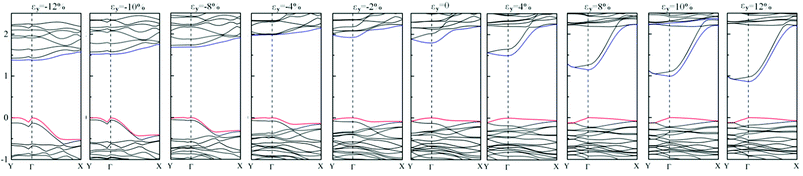
To further investigate the specific effect of strain on the band gap turning, the band structures of GeSe₂ monolayer under strain in two directions are calculated based on the fully relaxed in-plane anisotropic natural structures. For simplification, we only plot the band structure along remarkable Γ–X (0.5, 0, 0) and Γ–Y (0, 0.5, 0) directions as shown in Fig. 3 and 4, respectively. The red and blue lines are used to highlight the change of the near-gap states of GeSe₂ monolayer. As shown in Fig. 3, with the increase of compressive strain ε_y, the VBM along Γ–Y direction almost unchanged while a steep slope appears along Γ–X direction with the SVB state shifts to lower energy at X point. For CBM, a parallel downward removal introduced with a flat slope along Γ–X(Y) direction accompanied by the compressive strain increasing. On the other side of the increasing tensile strain, the CBM at Γ point has an obviously downward and at Y point moves synchronously, while that at X point almost immovable. Meanwhile, the VBM is always locates at Γ point in the Fermi level with almost invariable slopes along Γ–X and Γ–Y directions. The changes predict that the effect of compressive/tensile strain ε_y mainly results in a steep slope of the VBM/CBM along Γ–X direction while invariable change along Γ–Y direction. It thus directly reflects the enhanced electrical/hole transport along Γ–X direction under tensile/compressive strain ε_y because of the larger CBM/VBM slope value, further implies the enhanced anisotropic electrical/hole conductance in-plane of GeSe₂ monolayer. And above all, these results reveal that the larger tensile strain ε_y introduces larger anisotropic electrical properties of GeSe₂ than compressive strain ε_y.

Fig. 3 Strain ε_y manipulated band gap transition in GeSe₂ monolayer. The Fermi level is set to 0 eV on the energy axis. The red and blue lines are used to highlight the changing of the energy levels of the VBM and CBM.

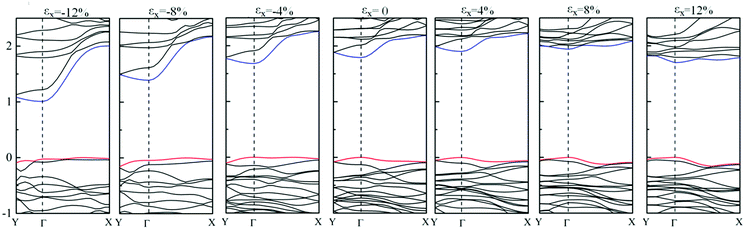Fig. 4 Strain ε_x manipulated band gap transition in GeSe₂ monolayer. The Fermi level is set to 0 eV on the energy axis. All energies are referenced to vacuum level.

Furthermore, it is well known that the direct or indirect nature of the band structure is the result of energy competitions of near-band-edge states under different strains. Fig. 3 exhibits an indirect band in the strain range of −4% to −8%, and then transitions back to direct with larger strain. For example, at ε_y = −8%, it shows an indirect band gap with the CBM shifts from Γ point to Y with a small energy difference, while the VBM remains at Γ point. Furthermore, the calculated PDOSs for ε_y = −12% (in Fig. S2†) show that the VBM in the Fermi level mainly originated from Se5/Se1-4p states, SVB is contributed mainly by Se4/Se3-4p states, while Ge-4p states provide large contribution to the VBM. Likewise, at ε_y = 12% (in Fig. S3†), Se5-4p and Ge2-4s/4p orbitals result mainly in the CBM.

Meanwhile, Fig. 4 shows the effect of strain ε_x on the band structure of GeSe₂ monolayer. In contrast to the effect of strain ε_y on tuning of CBM/VBM, the change of CBM/VBM on the compressive/tensile strain ε_x exhibits a reverse tendency that tensile strain affects the VBM while compressive strain CBM. In summary, for the case of the two applied strains, the CBM tuning along Γ–X can be easier obtained by lattice expansion along y direction and introduced anisotropic electrical properties, especially the anisotropy electrical/hole conductance.

To further investigate the changes of the electronic structures under different strains, the crystal parameters (denoted in Fig. 1b) of GeSe₂ monolayer are listed in Table 1 for the major strain of ε_x = 12% and −12%, while the crystal structures are shown in Fig. S4.† As shown in Table 1, the change of parameter b (along y direction) is smaller than that of parameter a under strains, which shows large crystal distort in-plane of GeSe₂. For example, with the change of parameter a as 12% (ε_x = 12%), the change of b is ∼−2.14%, respectively. Under strains, it reveals that the bond lengths substantially retained while angels show marked change. The in-plane unsynchronized lattice change induces corrugated structure along x direction (see Fig. S4†), then enhance the structural anisotropy of GeSe₂ monolayer, further introduce the anisotropy of electronic structure (see Fig. 3 and 4). Form the decomposed charge density of the CBM under different strains, it can be seen that the strain ε_x = −12% introduces a significant enhanced charge distribution along x direction in real space while almost average in two directions under strain ε_x = 12%, which coincides with the band structure analysis in Fig. 4.

Table 1 The calculated lattice parameters, bond lengths and angels with major change in lattice of GeSe₂ monolayer under strains of ε_x = 12% and ε_x = −12%. That of intrinsic GeSe₂ monolayer are also listed for comparison

Strain εx	Lattice parameters (Å)		Bond length (Å)					Angle (°)
	a	b	Ge2–Se4	Ge2–Se1	Ge1–Se4	Ge1–Se1	Ge1–Se2	θ1	θ2	θ3
12%	7.957	16.73	2.370	2.350	2.373	2.373	2.373	109.38	101.54	113.85
0	7.104	17.095	2.360	2.353	2.372	2.392	2.375	100.18	98.45	100.49
−12%	6.252	17.416	2.346	2.368	2.355	2.409	2.370	88.96	93.99	106.65

---

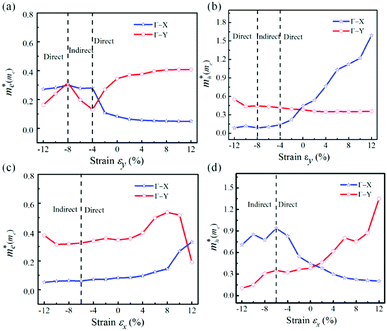
Because the electrical/hole transport behavior is usually decided by the lowest/highest-energy edge, the obvious edges variety indicate the effective mass change, then approximately implied the alterable mobility along two directions. Fig. 5 demonstrates the evolution of the electron and hole effective masses as a function of both strain ε_x and ε_y. It is obvious that a significant enhanced anisotropic electron (hole) appears for the strain larger than ε_y = −4%. In the strain range from −8% to −4% in Fig. 5a, a sudden jump of electronic effective mass along Γ–Y is due to the completion of CBM at Y and Γ points for the direct–indirect band gap transition. For the larger strain at ε_y = 12%, the effective mass of electron along Γ–Y direction is an order of magnitude bigger than that along Γ–X direction, indicating that the electron prefers transport in-plane x direction of crystal structure. On the other hand, the small hole effective mass shows the preferred transport direction along y of the direct band structure (Fig. 5b). With the case of strain applied in x direction, a noticeable anisotropy is introduced to the hole effective mass (Fig. 5d), while the electron effective mass shows a small anisotropic variation (Fig. 5c). As shown in Fig. 5d, the opposite change presents the fact that the hole prefers transport along x direction under strain. Therefore, the above discussion reveals that the strain can dramatically increase or decrease the effective masses of carriers in the GeSe₂ monolayer with a noticeable anisotropy introduced, and even reverse the anisotropy of hole effective mass.

Fig. 5 Effective masses of the electron (left) and hole (right) as a function of strain ε_y (top) and ε_x (bottom). Three (two) strain zones for ε_y (ε_x) are also labelled. m_e depicts the free electron mass.

4. Conclusions

In summary, we have studied the strain effect on the electronic band structure and anisotropy of GeSe₂ monolayer through first-principle calculations. The band gap of GeSe₂ monolayer can be effectively tuned by strain in a wide range. The effective mass of electrons and holes are also highly sensitive to the strain. Particularly, the anisotropy of hole effective mass can even be rotated by 90° through applying appropriate x or y direction strain. These intriguing properties demonstrate the great potential of GeSe₂ monolayer for novel mechanical-electronic device applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (21573249, 21403078), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB12020100), the Youth Innovation Promotion Association CAS (2017050), Natural Science Foundation of Guizhou Province (20161150, 201567), and Provincial Key Disciplines of Chemical Engineering and Technology in Guizhou Province (No. ZDXK20178).

References

1. R. S. Jacobsen, K. N. Andersen, P. I. Borel, J. Fage-Pedersen, L. H. Frandsen, O. Hansen, M. Kristensen, A. V. Lavrinenko, G. Moulin, H. Ou, C. Peucheret, B. Zsigri and A. Bjarklev, Nature, 2006, 441, 199–201.
2. V. Tran, R. Soklaski, Y. Liang and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235319.
3. W. Y. Yu, C. Y. Niu, Z. L. Zhu, X. F. Wang and W. B. Zhang, J. Mater. Chem. C, 2016, 4, 6581–6587.
4. J. K. Jiang, Q. H. Liang, S. L. Zhang, R. S. Meng, C. J. Tan, Q. Yang, X. Sun, H. Y. Ye and X. P. Chen, J. Mater. Chem. C, 2016, 4, 8962–8972.
5. M. J. Zhang, Y. P. An, Y. Q. Sun, D. Peng, X. N. Chen, T. X. Wang, G. L. Xu and K. Wang, Phys. Chem. Chem. Phys., 2017, 19, 17210.
6. D. Çakır, H. Sahin and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205421.
7. J. Feng, X. Qian, C. W. Huang and J. Li, Nat. Photonics, 2012, 6, 866–872.
8. Z. Zhang, L. Li, J. Hong, N. Z. Wang, F. Yang and Y. Yu, Nano Lett., 2017, 17, 6097–6103.
9. H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. H. Zhao, H. S. Han, H. C. Manoharan, A. P. frank, J. K. Norskov and X. L. Zheng, Nat. Mater., 2016, 15, 48–53.
10. A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2014, 112, 176801.
11. X. H. Peng, Q. Wei and A. Copple, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085402.
12. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
13. C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
14. Q. Wei and X. Peng, Appl. Phys. Lett., 2014, 104, 251915.
15. H. F. Lin, L. M. Liu and J. J. Zhao, J. Mater. Chem. C, 2017, 5, 2291–2300.
16. V. Tran, R. Soklaski, Y. Liang and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 817.
17. R. Fei and L. Yang, Nano Lett., 2014, 14, 2884–2889.
18. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041.
19. J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475.
20. Y. L. Mao, C. S. Xu, J. M. Yuan and H. Q. Zhao, Phys. Chem. Chem. Phys., 2018, 20, 6929–6935.
21. Y. S. Yang, S. C. Liu, W. Yang, Z. B. Li, Y. Wang, X. Wang, S. S. Zhang, Y. Zhang, M. S. Long, G. M. Zhang, D. J. Xue, J. S. Hu and L. J. Wan, J. Am. Chem. Soc., 2018, 140, 4150–4156.
22. X. Zhou, X. Hu, S. Zhou, Q. Zhang, H. Li and T. Zhai, Adv. Funct. Mater., 2017, 27, 1770279.
23. Y. Q. Wei, L. Huang, J. He, Y. P. Guo, R. H. Qin, H. Q. Li and T. Y. Zhai, Adv. Energy Mater., 2018, 8, 1703635.
24. B. Mukherjee, Z. B. Hu, M. R. Zheng, Y. Q. Cai, Y. P. Feng, E. S. Tok and C. H. Spw, J. Mater. Chem., 2012, 22, 24882–24888.
25. X. F. Fang, B. Liu, Q. F. Wang, W. F. Song, X. J. Hou, D. Chen, Y. B. Cheng and G. Z. Shen, Adv. Mater., 2013, 25, 1479–1486.
26. M. Xu, S. Jakobs, R. Mazzarello, J. Y. Cho, Z. Yang, H. Hollermann, D. H. Shang, X. S. Miao, Z. H. Yu, L. Wang and M. Wutting, J. Phys. Chem. C, 2017, 121, 25447–25454.
27. Q. Lin, Y. Li, M. Xu, Q. Cheng, H. Qian, J. L. Feng, H. Tong and X. S. Miao, IEEE Electron Device Lett., 2018, 39, 496–499.
28. F. C. Liu, S. J. Zheng, X. X. He, A. Chaturvedi, J. F. , He, W. L. Chow, T. R. Mion, X. L. Wang, J. D. Zhou, Q. D. Fu and H. J. Fan, Adv. Funct. Mater., 2016, 26, 1169–1177.
29. X. Wang, Y. Li, L. Huang, X. W. Jiang, L. Jiang, H. Dong, Z. Wei, J. Li and W. Hu, J. Am. Chem. Soc., 2017, 139, 14976–14982.
30. S. C. Liu, Y. Mi, D. J. Xue, Y. X. Chen, C. He, X. F. Liu, J. S. Hu and L. J. Wan, Adv. Electron. Mater., 2017, 3, 1700141.
31. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
33. J. White and D. Bird, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 4954.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06606j

---