Ingenious modification of molecular structure effectively regulates excited-state intramolecular proton and charge transfer: a theoretical study based on 3-hydroxyflavone

Abstract

Harnessing ingenious modification of molecular structure to regulate excited-state intramolecular proton transfer (ESIPT) and intramolecular charge transfer (ICT) characteristics holds great promise in fluorescence sensing and imaging. Based on the 3-hydroxyflavone (3HF) molecule, 2-(2-benzo[b]furanyl)-3-hydroxychromone (3HB) and 2-(6-diethylamino-benzo[b]furan-2-yl)-3-hydroxychromone (3HBN) were designed by the extension of the furan heterocycle and the introduction of a diethylamino group. The analysis of important hydrogen bond length, frontier molecular orbitals, infrared spectra, and potential curves have cross-validated our results. The results indicate that proper site furan heterocycle extension and diethylamino donor group substitution not only shift the absorption and emission spectra to the red but also effectively modulate the excited-state dynamic behaviors. Strengthened ICT characteristics from 3HF to 3HB and to 3HBN make the occurrence of ESIPT increasingly difficult due to the higher energy barriers, which indicates that the ESIPT and ICT processes are competitive mechanisms. We envision that our work would open new windows for improving molecular properties and developing more fluorescent probes and organic radiation scintillators.

---

1. Introduction

Flavones and related compounds of the flavonoid group are widespread in plants¹ and their importance is not limited to the survival of plants in the natural environment. They can effectively protect photo-sensitive biological targets such as DNA, proteins, polymers and phospholipids.^2–5 More importantly, flavone compounds have a broad range of therapeutic applications such as reducing agents, hydrogen-donating antioxidants, active against cancers, tumors and cardiac problems and having low systemic toxicity.^6–10 These extensive applications are closely related to their intrinsic physical characteristics. A large number of studies regarding excited-state intramolecular proton transfer (ESIPT) and intramolecular charge transfer (ICT) processes have been reported in different systems.^11–14 As a representative member of the flavones family, 3-hydroxyflavone (3HF) is well known for its characteristics of ESIPT and ICT processes.^15–19 However, the absorption maximum in the near UV region and narrow fluorescence emission wavelength scope for 3HF greatly restrict its applications as probes in molecular and cellular biology and in nanoscale sensor technologies. Therefore, it is urgent to look for effective methods to improve these properties. Fortunately, Chou and his colleagues in previous studies have demonstrated that the addition of 4′-dialkylamino group on the β-phenyl ring of 3HF can greatly change the electron density distribution and affects ICT dynamic process.^20,21 Klymchenko et al. have synthesized experimentally the structures of 2-(2-benzo[b]furanyl)-3-hydroxychromone (3HB) and 2-(6-diethylamino-benzo[b]furan-2-yl)-3-hydroxychromone (3HBN) based on the simple 3HF structure.^22–25 And they have elaborated that the introduction of furan heterocycle on 3HF derivatives showed stronger fluorescence emission and longer emission position. However, the underlying causes for the effect of changing functional groups on ICT dynamic process, and the internal connection between ESIPT and ICT processes of 3HF remain unclear.

In our work, we substituted 2-(2-benzo[b]furanyl) for 2-phenyl and introduced diethylamino group to form 3HB and 3HBN structures separately based on original 3HF structure. The attention is focused on analyzing the regulation of absorption and emission spectra by structural changes and exploring the relationship between ESIPT and ICT dynamic processes of 3HF, 3HB and 3HBN molecules. Achieving absorption and fluorescence spectra shift toward the desired direction and understanding the dynamic relationship between ESIPT and ICT processes are valuable for the future molecular design and the modulation of dynamic progress.

2. Computational methods

All the calculations presented were accomplished depending on the Gaussian 09 program suite.²⁶ The hybrid functional PBE0 was performed in current system and it was composed of 25% Hartree–Fock exchange and 75% PBE.^27–30 In fact, a number of functionals, including B3LYP, PBE0, CAM-B3LYP, M062X were tested before designating functional, among which the PBE0 functional provides the most satisfactory agreement with experimental results. The triple-ζ valence quality with one set of polarization functions (TZVP) was used as basis sets.³¹ The geometric configurations of the 3HF, 3HB, and 3HBN were optimized using the density functional theory (DFT) method in the ground-state and the time-dependent DFT (TDDFT) method in the excited-state, respectively.^32–37 The TDDFT method has become a very useful tool to analyze the hydrogen bonding in the excited-states of the hydrogen-bond system theoretically.^38–41 In the optimized structures, vibrational frequencies were analyzed to obtain thermodynamic corrections and to confirm the structures were minima (no imaginary frequency). Considering that the experiments were implemented in toluene solvent, the solvent corrections were also taken into account in all computations. The integral equation formalism variant of polarizable continuum model (IEFPCM) with radii and cavity-dispersion-solvent-structure terms in Truhlar and coworkers' SMD solvation model for toluene was carried out.^42–44 The reduced density gradient (RDG) function was introduced to investigate non-covalent interactions using the Multiwfn program.^45–47 Chemcraft software was exploited to visualize the RDG in a real place.⁴⁸ Potential energy curves have been performed beginning from normal to tautomer form, constraining the bond strength O–H and optimizing all other coordinates at every scan point. The transition state (TS) search was performed and verified by just only one imaginary frequency of energy second derivatives (Hessian) matrices.⁴⁹

3. Results and discussion

3.1 Electronic excitation energies and optimized geometric structures

Based on Salaeh et al. 's theoretical research on the ESIPT process of 3HF molecule under different polar solvents at the B3LYP/TZVP level, solvation effect and more functionals (PBE0, M062X, B3LYP and CAM-B3LYP) were selected to ensure the validity of the calculation for our studied system.¹⁹ The electronic excitation energies of different functional were calculated and corresponding results are shown in Table 1. The results indicate that the PBE0 functional keeps the most satisfactory agreement with experimental results.²⁴ Therefore, the PBE0 functional was adopted in our whole calculation process. The oscillator strengths in first two excited-state and corresponding orbital transitions of 3HF, 3HB and 3HBN at PBE0/TZVP level are presented in Table 2. The S₀ → S₁ transitions correspond to the maximum oscillator strength of 3HF, 3HB, and 3HBN structures. On the contrary, the S₀ → S₂ transitions for these three structures have small oscillator strengths. Therefore, only the S₀ → S₁ transitions of 3HF, 3HB and 3HBN and their molecular orbitals are considered in current system.

Table 1 Calculated absorption peak values (nm) with different functional methods and experimental (Exp.) data in toluene solvent for 3HF, 3HB, and 3HBN structures

	M062X	CAM-B3LYP	B3LYP	PBE0	Exp.^a
a See ref. 24.
3HF	313	318	354	343	343
3HB	335	344	392	378	364
3HBN	392	381	478	455	446

---

Table 2 Calculated the oscillator strengths (f) in first two excited-state and corresponding frontier molecular orbital transitions (MOs) of 3HF, 3HB, and 3HBN structures are listed

	Transition	f	MOs
3HF	S0 → S1	0.54	H-L
	S0 → S2	0.00	H-4-L
3HB	S0 → S1	0.83	H-L
	S0 → S2	0.03	H-1-L
3HBN	S0 → S1	0.89	H-L
	S0 → S2	0.08	H-1-L

---

The optimized lowest energy geometric configurations of 3HF, 3HB and 3HBN in the ground-state (S₀) and the first excited-state (S₁) are shown in Fig. 1. Some crucial bond length parameters for these three stable structures are listed in Table 3. For 3HF, the bond lengths of O₂–H₁ and C₁=O₁ are increased from 0.979 Å and 1.234 Å in the S₀ state to 1.011 Å and 1.257 Å in the S₁ state. The intramolecular hydrogen bond (IMHB) O₂–H₁⋯O₁ length is decreased from 1.946 Å in the S₀ state to 1.734 Å in the S₁ state. Moreover, for 3HB structure, the bond lengths of O₂–H₁, C₁=O₁ and O₂–H₁⋯O₁ change from 0.978 Å, 1.232 Å and 1.984 Å to 0.999 Å, 1.256 Å and 1.817 Å, respectively. For 3HBN, the bond lengths of O₂–H₁, C₁=O₁ and O₂–H₁⋯O₁ from 0.977 Å, 1.235 Å and 1.985 Å change to 0.992 Å, 1.259 Å and 1.841 Å. Based on the above analysis of bond length, the IMHB was significantly strengthened in the S₁ state compared with that in the S₀ state for these three stable structures. Furthermore, it should be noted that the intramolecular hydrogen bond lengths for these three structures in the S₁ state were increased from 1.734 Å for 3HF, 1.817 Å for 3HB and to 1.841 Å for 3HBN. This phenomenon indicates that the modifications of molecular structure decrease the strength of excited-state IMHBs.

Fig. 1 Optimized geometric structures of 3HF, 3HB and 3HBN in the ground-state and excited-state.

Table 3 Calculated important bond lengths (Å) for the optimized structure of 3HF, 3HB and 3HBN in the ground-state (S₀) and in the excited-state (S₁ and )

	3HF			3HB			3HBN
	S0	S1		S0	S1		S0	S1
H1–O2	0.979	1.011	—	0.978	0.999	—	0.977	0.992	—
C1=O1	1.234	1.257	—	1.232	1.256	—	1.235	1.259	—
H1⋯O1	1.946	1.734	—	1.984	1.817	—	1.985	1.841	—
C2=O2	—	—	1.271	—	—	1.262	—	—	1.261
H1–O1	—	—	0.979	—	—	0.980	—	—	0.987
H1⋯O2	—	—	1.996	—	—	1.992	—	—	1.902

---

3.2 Non-covalent interactions analysis

An approach developed by Yang et al. to visualize non-covalent interactions in real space could be adopted to investigate hydrogen bond properties.^45,46 Different interaction types and corresponding intensities can be clearly displayed by electron density (ρ(r)) and their reduced density gradient (RDG) isosurfaces analysis. Herein, the eqn (1) of RDG function can be expressed as

Furthermore, based on Bader's Atoms in Molecules theory,⁵⁰ the second largest eigenvalue λ₂ of Hessian matrix of electron density and ρ(r) can be contacted in the eqn (2)

Ω(r) = sign(λ₂(r))ρ(r) (2)

Herein the eigenvalue λ₂ > 0 and λ₂ < 0 stand for bonding and anti-bonding interactions, respectively. The sign(λ₂(r))ρ(r) is large and negative value stands for attractive interaction like hydrogen bond interaction. In contrast, sign(λ₂(r))ρ(r) is large and positive value means the anti-bonding interaction like steric repulsion interaction. The sign(λ₂(r))ρ(r), nearly zero value, means van der Waals interaction. Herein, scatter diagrams in 3HF, 3HB, and 3HBN of the Ω(r) value (function value 1) versus the RDG(r) value (function value 2) are plotted in Fig. 2. The contour value is set as 0.5. For 3HF, the spike peaks almost located at −0.03 in S₀ state and −0.05 in S₁ state are observed and they have been confirmed to be the hydrogen bond interactions. Furthermore, the spike peak occurs left shift in the S₁ state compared with the S₀ state proved intramolecular hydrogen bond interactions are strengthened. For 3HB and 3HBN structures, the hydrogen bond interaction type and S₁ state strengthen trend were further proved. By comparison, the strength of hydrogen bond interactions in the S₀ state is similar since the spike peaks are close to −0.03 for these three structures. Compared with the spike peak of 3HF (−0.05) in the S₁ state, the spike peaks of 3HB and 3HBN located in −0.04 and −0.037, respectively. The spike peaks occur right-shift indicates the hydrogen bond interaction of 3HF was stronger than 3HB and 3HBN structures. The results of non-covalent interactions greatly corroborate to the above-mentioned hydrogen-bonding length analysis results.

Fig. 2 Plots of function value 1 versus function value 2 for 3HF, 3HB and 3HBN conformations in the ground-state and excited-state, as well as the assignments of each spike by gradient isosurfaces.

3.3 Absorption and emission spectra analysis

Klymchenko et al. have measured the absorption and the emission spectra of 3HF, 3HB and 3HBN using Cary 3 Bio Spectrophotometer and Quanta Master spectrofluorometer, respectively.²⁴ The calculated absorption peaks of three target molecules at PBE0/TZVP level occur remarkable red-shift from 3HF (343 nm) to 3HB (378 nm) and to 3HBN (455 nm), achieving a leap from ultraviolet (UV) to visible (VIS) band (see Table 1). Such a significant red-shift can be explained by the orbital transition energy gaps. The calculated results show that the energy level of highest occupied molecular orbital (HOMO) is elevated from 2.19 eV (3HF) to 2.34 eV (3HB) due to the extension of furan heterocycle. The lowest unoccupied molecular orbital (LUMO) energy level is pulled down from 6.41 eV (3HF) to 5.36 eV (3HBN) for the introduction of electron-withdrawing group (dialkylamino). Therefore, a conclusion can be drawn that the rise of HOMO orbital energy level and the decrease of LUMO orbital energy level effectively reduce the energy level gap between them and induce the red shift of the spectra.

For exploring the effects of chromophore length and electron-donor ability on the positions of emission spectra, simulated normalized emission spectra of 3HF, 3HB and 3HBN structures in toluene solvent are shown in Fig. 3. Upon photoexcitation to the S₁, only the 528 nm Keto* fluorescence emission peak is observed for 3HF in toluene solvent, which can reasonably be explained through a fast proton transfer channel between normal and tautomer forms.²⁰ For excited-state 3HB and 3HBN structures, two fluorescence emission peaks are observed simultaneously. The Enol* form fluorescence peak is 428 nm for 3HB and 500 nm for 3HBN, which is in accordance with experimental results (414 nm for 3HB and 508 nm for 3HBN). Besides, the Keto* form fluorescence is 567 nm (3HB), and 623 nm (3HBN), which is also in agreement with the experiment peak values 547 nm and 613 nm, respectively. Therefore, as the molecular structure changes from 3HF to 3HB and to 3HBN, the emission spectra were greatly shifted to the red region.

Fig. 3 Plotted normalized emission spectra of 3HF, 3HB and 3HBN in toluene solvent. Black wavelength values stand for theoretical simulation results and numbers in brackets represent experimental values (see ref. 24).

3.4 Frontier molecular orbitals analysis

It is known to all that charge transfer deriving from photoexcitation could reasonably describe the nature of electronically excited-state dynamic behavior.^51–53 In order to have a clear-cut description of charge distribution and charge transfer, the HOMO and LUMO of frontier molecular orbitals (FMOs) of 3HF, 3HB, and 3HBN structures are displayed in Fig. 4. The π character of HOMO and the π* character of LUMO can be seen clearly, which indicates S₀ → S₁ transition is belong to predominantly ππ* type transition. For 3HF, 3HB, and 3HBN structures, the charge transfer of significant sites involved in intramolecular hydrogen bond is analyzed. As seen in Fig. 4, conspicuous charge transfer phenomenon both in the HOMO and in the LUMO is observed from 3HF changes to 3HB and 3HBN whereas the charge transfer direction of two orbitals is opposite. Specifically, when the molecular structure changes from 3HF to 3HBN along with the charge in the HOMO is transferred from phenyl ring on the left to diethylamino site located on the right. It is interesting that the exact opposite transition happens in the LUMO. After molecular orbitals from HOMO transition to LUMO, the electron densities of hydroxyl moiety decrease and that of the acceptor O atom increase for these three structures. As a consequence, obvious intramolecular charge transfer leads to the H atom of hydroxyl moiety more acidic and the O atom of carboxyl group more basic. Therefore, the qualitative variation of the basicity/acidity is a strong proof for the occurrence of ICT process of target molecules.

Fig. 4 Frontier molecular orbitals (HOMO and LUMO) of 3HF, 3HB and 3HBN structures.

3.5 Electrostatic potential analysis

A close inspection of the charge distribution over the atoms involved in intramolecular hydrogen-bond directly provides a window towards examining the ESIPT process. The electrostatic potential (ESP) pictures in the ground-state and excited-state of 3HF, 3HB, and 3HBN are drawn in Fig. 5. The color changes from red, green to blue delegate the increasing of ESP, which is closely connected with the changes of electron density. The red and blue regions stand for negative ESP and positive ESP, respectively. For 3HF, the negative charge distribution on O atom of O–H moiety decreases from 0.251 in the S₀ state to 0.238 in the S₁ state, whereas the O atom of C=O moiety increases from 0.381 to 0.392. Furthermore, similar charge change trend also was found both in 3HB and 3HBN structures. To be more specific, for 3HB and 3HBN structures, the charge density of donor O in the O–H moiety was decreased from 0.217, 0.223 in the S₀ state to 0.209, 0.220 in the S₁ state, respectively. Meanwhile, the charge density of acceptor O in C=O moiety was increased from 0.370, 0.379 in the S₀ state to 0.386, 0.394 in the S₁ state, respectively. Therefore, the conclusion can be drawn based on above ESP analysis that the capabilities of electron-withdrawing group (C=O) and electron-donating group (O–H) were strengthened in the S₁ state compared with those in the S₀ state for these three structures. Such strengthen effectively shortens excited-state intramolecular hydrogen bond distance and leads to the proton transfer processes are easier to proceed in the S₁ state than S₀ state.

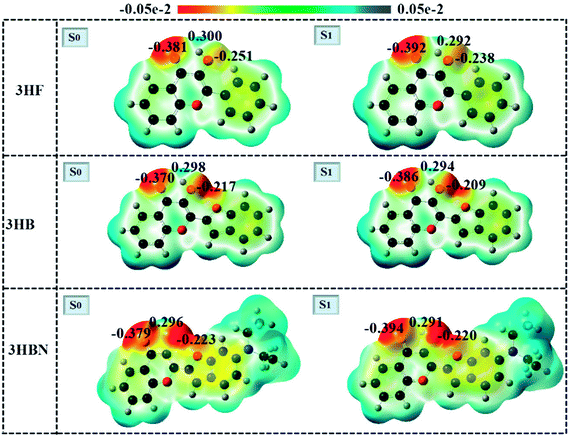Fig. 5 The molecular electrostatic potentials of 3HF, 3HB, and 3HBN in the ground-state and excited-state.

3.6 Infrared spectra analysis

Infrared (IR) spectrum is an effective tool to analysis intra- and inter-molecular hydrogen bond strengthening or weakening through an electronic spectral red-shift or blue-shift.^54,55 As shown in Fig. 6, the IR spectra of different electronic states of 3HF, 3HB, and 3HBN structures are depicted. Obviously, two stretching vibrational peaks connected to intramolecular hydrogen bond were interested for 3HF, 3HB, 3HBN structures. For 3HF, C₁=O₁ and H₁–O₂ stretching vibrational peaks change from S₀ state 1709 cm⁻¹ to S₁ state 1663 cm⁻¹ and from S₀ state 3567 cm⁻¹ to S₁ state 3057 cm⁻¹ respectively. Meanwhile, the similar red-shift trend also was found in 3HB and 3HBN structures. Compared with the S₀ state, the 51 cm⁻¹ red-shift for C₁=O₁ and 351 cm⁻¹ dramatic red-shift for H₁–O₂ were found in the S₁ state for 3HB. Similarly, the 44 cm⁻¹ red-shift for C₁=O₁ and 254 cm⁻¹ red-shift for H₁–O₂ were found for 3HBN. So conspicuous red-shift as a result of photoexcitation indicates that the intramolecular hydrogen bond in the excited-state was strengthened for these three structures, which further demonstrated above discussion regarding bond length and non-covalent interactions. After excited-state intramolecular proton transfer process, the tautomer species were formed, the new intramolecular hydrogen bonds replace original intramolecular hydrogen bonds. The new stretching vibrational peaks C₂=O₂, O₁–H₁ for 3HF, 3HB and 3HBN are explored. Therefore, it is reasonable to say that the analysis of IR spectra indirectly depicts the occurrence of ESIPT process of 3HF, 3HB and 3HBN structures. The detailed ESIPT process is analyzed in the following Potential energy curve section.

Fig. 6 Calculated IR spectra of the 3HF, 3HB, and 3HBN in different electronic states. Black line, red line and blue line stands for Enol, Enol* and Keto* form of IR spectra, respectively.

3.7 Potential energy curves and mechanism analysis

To gain more insight into the intramolecular proton transfer mechanism, the potential energy curves for 3HF, 3HB, and 3HBN structures in the S₀ and S₁ states are constructed and shown in Fig. 7. In the S₀ state, the potential barrier is 12.38 kcal mol⁻¹ for 3HF, 13.62 kcal mol⁻¹ for 3HB, and 13.49 kcal mol⁻¹ for 3HBN respectively. Obviously, it is difficult to proceed intramolecular proton transfer spontaneously in the ground-state due to the higher energy barriers. After vertical excitation to S₁ state, the potential barrier is 1.34 kcal mol⁻¹ for 3HF, 2.75 kcal mol⁻¹ for 3HB, and 4.98 kcal mol⁻¹ for 3HBN respectively. Lower excited-state barriers demonstrate that trigger ESIPT process for 3HF, 3HB and 3HBN is relatively easy. Furthermore, for the reverse ESIPT process, the potential barriers decrease from 10.56 kcal mol⁻¹ to 8.76 kcal mol⁻¹ and to 4.72 kcal mol⁻¹ with the structure changes from 3HF, 3HB and to 3HBN, which indicates that 3HBN structure easier to occur reverse ESIPT process compared with 3HF and 3HB structures. Meanwhile, a phenomenon should be noticed that the potential energy barriers of forward ESIPT get higher along with the strengthened ICT from 3HF to 3HB and to 3HBN. Therefore, ESIPT and ICT processes are competitive mechanism in current research system.

Fig. 7 The potential energy curves of the ground-state and excited-state for 3HF, 3HB, and 3HBN structures.

4. Conclusion

In summary, we theoretically investigated the characteristics of intramolecular hydrogen bonds and dynamic behaviors of excited-state intramolecular proton transfer and intramolecular charge transfer for 3HF, 3HB, and 3HBN structures. The calculation results demonstrated that proper site furan heterocycle extension and diethylamino donor group substitution based on 3HF structure effectively modulated the absorption peak values from UV to visible band. Moreover, the fluorescence emission wavelength of 3HB and 3HNB structures exhibited strong red shift compared with the original 3HF structure. More importantly, as the structure changes from 3HF to 3HB and to 3HBN, intramolecular charge transfer characteristics got increased accompanied with higher energy barriers of excited-state intramolecular proton transfer. This observation leads to a conclusion that excited-state intramolecular proton transfer and intramolecular charge transfer processes are competitive mechanism. Therefore, reasonable structure design achieved the control of excited-state dynamic behaviors in the current system. We envision that our work would provide paradigmatic guidance for designing and developing new fluorescent sensors and organic radiation scintillators.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 11574115); the Natural Science Foundation of Jilin Province of China (Grant No. 20150101063JC).

References

1. S. A. Ahmed, B. Maity, S. S. Duley and D. Seth, J. Photochem. Photobiol., B, 2017, 168, 132–141.
2. A. Sytnik and I. Litvinyuk, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 12959–12963.
3. J. R. Dharia, K. F. Johnson and J. B. Schlenoff, Macromolecules, 1994, 27, 5167–5172.
4. S. M. Dennison, J. Guharay and P. K. Sengupta, Spectrochim. Acta, Part A, 1999, 55, 1127–1132.
5. O. P. Bondar, V. G. Pivovarenko and E. S. Rowe, Biochim. Biophys. Acta, 1998, 1368, 119–130.
6. E. Karakus, M. Ucuncu and M. Emrullahoglu, Anal. Chem., 2016, 88, 1039–1043.
7. G. J. Zhao and K. L. Han, J. Comput. Chem., 2008, 29, 2010–2017.
8. L. G. Korkina and I. B. Afanas'ev, Adv. Pharmacol., 1997, 38, 151–163.
9. A. Bocco, M.-E. Cuvelier, H. Richard and C. Berset, J. Agric. Food Chem., 1998, 46, 2123–2129.
10. R. Bouhamidi, V. Prevost and A. Nouvelot, Life Sci., 1998, 321, 31–38.
11. J. S. Chen, P. W. Zhou, L. Zhao and T. S. Chu, RSC Adv., 2014, 4, 254–259.
12. J. S. Chen, P. W. Zhou, S. Q. Yang, A. P. Fu and T. S. Chu, Phys. Chem. Chem. Phys., 2013, 15, 16183–16189.
13. Y. Li, J. S. Chen and T. S. Chu, J. Lumin., 2016, 179, 203–210.
14. J. S. Chen, L. Zhao and T. S. Chu, Journal of Atomic and Molecular Sciences, 2015, 6, 1–10.
15. A. S. Klymchenko, T. Ozturk and A. P. Demchenko, Tetrahedron Lett., 2002, 43, 7079–7082.
16. A. S. Klymchenko and A. P. Demchenko, Phys. Chem. Chem. Phys., 2003, 5, 461–468.
17. T. C. Swinney and D. F. Kelley, J. Chem. Phys., 1993, 99, 211–221.
18. A. J. G. Strandjord and P. F. Barbara, J. Phys. Chem., 1985, 89, 2355–2361.
19. R. Salaeh, C. Prommin, W. Chansen, K. kerdpol, R. Daengngern and N. Kungwan, J. Mol. Liq., 2018, 252, 428–438.
20. P.-T. Chou, M. L. Martinez and J. H. Clements, J. Phys. Chem., 1993, 97, 2618–2622.
21. A. P. Demchenko, K. C. Tang and P. T. Chou, Chem. Soc. Rev., 2013, 42, 1379–1408.
22. A. S. Klymchenko, V. G. Pivovarenko, T. Ozturk and A. P. Demchenko, New J. Chem., 2003, 27, 1336–1343.
23. A. P. Demchenko, S. Ercelen, A. D. Roshal and A. S. Klymchenko, Pol. J. Chem., 2002, 76, 1287–1299.
24. A. S. Klymchenko, T. Ozturk, V. G. Pivovarenkob and A. P. Demchenko, Tetrahedron Lett., 2001, 42, 7967–7970.
25. A. S. Klymchenko, T. Ozturk, V. G. Pivovarenko and A. P. Demchenko, Can. J. Chem., 2001, 79, 358–363.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision B 01, Gaussian, Inc., Wallingford, CT, 2010.
27. C. Adamo and V. Barone, Theor. Chem. Acc., 2000, 105, 169–172.
28. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
31. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
32. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447.
33. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
34. C. Z. Li, Y. G. Yang, C. Ma and Y. F. Liu, RSC Adv., 2016, 6, 5134–5140.
35. D. P. Yang, J. F. Zhao, M. Jia and X. Y. Song, RSC Adv., 2017, 7, 34034–34040.
36. D. P. Yang, G. Yang, J. F. Zhao, R. Zheng and Y. S. Wang, RSC Adv., 2017, 7, 1299–1304.
37. H. P. Ma and J.-D. Huang, RSC Adv., 2016, 6, 96147–96153.
38. J. F. Zhao, J. S. Chen, Y. L. Cui, J. Wang, L. X. Xia, Y. M. Dai, P. Song and F. C. Ma, Phys. Chem. Chem. Phys., 2015, 17, 1142–1150.
39. D. P. Yang, Y. G. Yang and Y. F. Liu, J. Cluster Sci., 2014, 25, 467–481.
40. G.-Y. Li and T. S. Chu, Phys. Chem. Chem. Phys., 2011, 13, 20766–20771.
41. P. W. Zhou and K. L. Han, Acc. Chem. Res., 2018, 51, 1681–1690.
42. C. Z. Li, C. Ma, D. L. Li and Y. F. Liu, J. Lumin., 2016, 172, 29–33.
43. G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107.
44. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
45. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
46. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Carcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
47. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
48. Website of ChemCraft software, https://www.chemcraftprog.com.
49. A. E. Shchavlev, A. N. Pankratov and A. V. Shalabay, J. Phys. Chem. A, 2005, 109, 4137–4148.
50. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
51. J. S. Chen, R. Z. Liu, Y. Yang and T. S. Chu, Theor. Chem. Acc., 2014, 133, 1411.
52. J. F. Zhao and P. Li, RSC Adv., 2015, 5, 73619–73625.
53. P. Song, Y. Z. Li, F. C. Ma, T. Pullerits and M. T. Sun, J. Phys. Chem. C, 2013, 117, 15879–15889.
54. J. S. Chen, M. H. Yuan, J. P. Wang, Y. Yang and T. S. Chu, J. Phys. Chem. A, 2014, 118, 8986–8995.
55. J. S. Chen, P. W. Zhou, G. Y. Li, T. S. Chu and G. Z. He, J. Phys. Chem. B, 2013, 117, 5212–5221.

---