Does the compound hexaaqua-zinc(II)bis(hydrogensulfate)dihydrate, [Zn(H₂O)₆](HSO₄·H₂O)₂, really exist?

Abstract

A careful examination of the crystal structure of the hydrogensulfate compound [Zn(H₂O)₆](HSO₄·H₂O)₂ reported in this journal shows that the sample used for X-ray diffraction was almost certainly the Tutton salt [Zn(H₂O)₆](SO₄·NH₄)₂, isoelectronic with the former elusive compound (F₀₀₀ = 416, P2₁/c space group). Indeed, any chemistry involving ammonium and sulfate moieties in an aqueous medium containing a transition metal cation should afford the corresponding Tutton salt as a by-product. We redetermined the structure of [Zn(H₂O)₆](SO₄·NH₄)₂, on the basis of high-resolution X-ray data (d = 0.47 Å), with the purpose of illustrating that at such resolution, difference Fourier maps may be used to unambiguously differentiate between a sulfate and a hydrogensulfate ion. On the other hand, regardless of the data resolution, geometrical considerations may be enough to avoid misassignment of such small ions in crystal structures, providing that some knowledge about the average shape of these ions is available from curated crystallographic databases.

---

Introduction

Within the tools available for the structural characterization of new chemical compounds, X-ray crystallography is certainly one of the most preferred in the chemical community. Although the bottleneck created by the prerequisite of having good enough crystals may be a serious drawback, once single crystals are available, the crystallographic workup, including data collection, structure solution and structure refinement, is almost always routine.

The success of this technique lies in both hard and software considerations. The availability of very sensitive area detectors based on CMOS (Complementary Metal-Oxide Semiconductor) or HPAD (Hybrid Pixel Array Detector) technology makes data collection straightforward over short times (minutes to hours).¹ On the other hand, intuitive graphical user interfaces (GUIs) embedding all crystallographic software required to deal with structure solution and refinement have been developed. As an example, OLEX2, under development at Durham University,² is now a very popular platform, which is used not only to solve and refine crystal structures, but also to interpret and report structural studies, since the system includes advanced visualization tools and allows integration with other software. Moreover, OLEX2, as much as other crystallographic software, is distributed with permissive free software licenses and is thus disseminated to the relevant end-users without any restrictions.

The evolution of the technique over the past decade was certainly a move in the right direction, as reflected in the ever increasing rate of deposited new structures.³ One would also expect a significant enhancement in the reliability of published X-ray structure analysis. However, as evidenced by many reports, this is not the case.^4,5 We interpret this non-desirable evolution as a consequence of a failure to critically interpret the outcome of a crystallographic study. In other words, there is a strong temptation to blindly believe in the results achieved by the easy-to-do X-ray study, even when they are unbelievable.⁶ This departure from good practices is, in turn, a consequence of a natural evolution, visualized by Angelo Gavezzotti and Howard Flack more than ten years ago; in the concluding remarks of their IUCr pamphlet about crystal packing,⁷ they mention: “There is very little that can be added to the average intramolecular geometrical data collected by use of the Cambridge Structural Database; anything at variance with these well-established averages is most probably wrong. […] So, if you are an X-ray diffractionist, instead of looking at your molecule, try looking at your crystal. There is plenty to be discovered, at a low cost and with perfectly high confidence, by looking at what molecules do when they interact with each other […]”.

We would like to illustrate this mantra with an example related to a paper issued recently in this journal.⁸ Dey et al. reported on the synthesis and characterization of an unexpected hydrated Zn(II) hydrogensulfate compound, with formula [Zn(H₂O)₆](HSO₄·H₂O)₂. The work is supported by its X-ray structure analysis, along with spectroscopic data and DFT calculations. However, a careful examination of the reported structure shows, with a high degree of confidence, that the crystal diffracted by Dey et al. was rather a sample of diammonium hexaaquazinc(II)bis(sulfate), a compound with formula [NH₄]₂[Zn(H₂O)₆](SO₄)₂ belonging to an extensive series of isotypic double salts of ammonium sulfate with transition metal sulfate. These compounds are best known as Tutton's salts, who published the very first article on their crystallographic aspects, long before the birthday era of X-ray diffraction.⁹ The crystal structure of [NH₄]₂[Zn(H₂O)₆](SO₄)₂ has been reported afterwards several times, first by Hofmann,¹⁰ then by Montgomery & Lingafelter,¹¹ Maslen et al.,¹² Cotton et al.¹³ and Simmons et al.¹⁴ We now report a high resolution study for this compound, which confirms that the hydrogensulfate compound claimed by Dey et al. is still to be discovered.

Experimental

Synthesis of the Zn Tutton salt, 1

A mixture of ZnO (3.25 g, 40 mmol) and NH₄Cl (2.14 g, 40 mmol) was magnetically stirred in 60 mL of distilled water. A second solution of concentrated sulfuric acid (2.13 mL, ρ = 1.84 g mL⁻¹, 40 mmol in 20 mL of distilled water) was added slowly at room temperature. The mixture became clearer, but a small amount of white precipitate appeared. The mixture was heated in a water bath for 10 min and then filtrated by gravity. The homogeneous solution was left to evaporate at ambient conditions, and after several days, very large (centimetre scale, Fig. 1), prismatic, colourless crystals were separated by decantation. Anal. calc. for H₂₀N₂O₁₄S₂Zn [%]: N, 6.97, H, 5.02, S, 15.97; found: N, 7.16(2), H, 5.14(2), S, 15.89(5).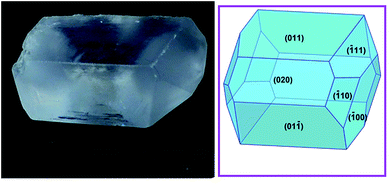

Fig. 1 A crystal of the Tutton salt 1 with the largest edge measuring 13 mm; the predicted crystal morphology using the Donnay and Harker model is shown on the right panel,^15,16 including indexation for the visible faces.

X-ray diffraction study

Diffraction data were collected on a Stoe Stadivari diffractometer equipped with an Axo microfocus source (Ag-Kα, λ = 0.56083 Å) and a Dectris Pilatus-100K detector, at room temperature (Table 1).¹⁷ Given the strong scattering power of the crystal, data were collected at high resolution [(sin θ)/λ = 1.07 Å⁻¹, corresponding to a resolution in the direct space d = 0.47 Å], with the hope of determining accurate parameters for all H atoms. The structure was refined with SHELXL,¹⁸ using free coordinates and isotropic displacement parameters for all H atoms. Data mining for sulfate- and hydrogensulfate-containing crystals was carried out using the current release of the Cambridge Structural Database (CSD v. 5.39, updated May 2018).³

Table 1 Crystal data for compound 1

Empirical formula	H20N2O14S2Zn
Formula weight	401.67
Temperature (K)	295(1)
Wavelength (Å)	0.56083
Space group	P21/c
a, b, c (Å), β (°)	6.2425(2), 12.5020(4), 9.2298(3), 106.810(3)
V (Å^3)	689.55(4)
ρ (g cm^−3)	1.935
θ range (°)	2.6–37.0
Data completeness at θmax (%)	99.4
Refl. collected/independent	66 179/7096 (Rint = 0.0287)
Refined parameters	129
Final R indices [I > 2σ(I)]	R1 = 0.0242, wR2 = 0.0695
Final R indices (all data)	R1 = 0.0352, wR2 = 0.0736
Goodness of fit on |F|^2	1.016
Extinction parameter	0.062(4)
Largest peak and hole (e^− Å^−3)	0.57, −0.71

---

Results and discussion

The structure reported by Dey et al.⁸ was originally refined on the basis of X-ray intensities collected at room temperature with the Mo-Kα radiation. Although the CIF file deposited in the CSD includes a refinement in space group P2₁ (refcode TUKHEO), it is quite obvious that actual symmetry is P2₁/c: the expected extinction for a c glide plane is observed in the diffraction pattern, and an inversion centre is present in the deposited structural model. Indeed, the authors described the structure in space group P2₁/c, with the metal lying on an inversion centre. We thus used the structure factors deposited by the authors, and refined their model in P2₁/c.

The model proposed by Dey et al. for [Zn(H₂O)₆](HSO₄·H₂O)₂ shows unrealistic features, the most prominent being physically unreasonable H⋯H contacts involving the HSO₄⁻ anion and water molecules. The most offending separation, H7⋯H1SA = 1.37 Å, is observed in the asymmetric unit, between the O–H group of the anion, and the lattice water molecule (see Fig. 2). A difference Fourier map (Fig. 2a) is however poorly informative regarding the actual location for these H atoms, as a consequence of the limited data resolution, d = 0.84 Å.

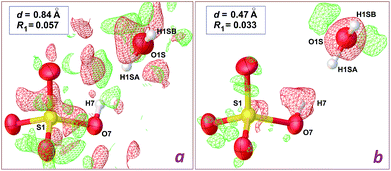Fig. 2 Difference density maps in the vicinity of the hydrogensulfate ion in the crystal structure of [Zn(H₂O)₆](HSO₄·H₂O)₂, computed with OLEX2.² Red and green electron difference densities are negative and positive, respectively. (a) Refinement using the 0.84 Å data deposited by Dey et al.⁸ (plot at 0.72 e⁻ Å⁻³ level); (b) refinement using our 0.47 Å data (plot at 0.46 e⁻ Å⁻³ level). The wR₂ residuals are given in the main text.

We then crystallized a genuine sample for the Tutton salt [Zn(H₂O)₆](SO₄·NH₄)₂, 1 (Table 1), which presented identical cell parameters, at the 3σ level, when compared to those reported for [Zn(H₂O)₆](HSO₄·H₂O)₂.⁸ Using our high resolution data and the model refined for [Zn(H₂O)₆](HSO₄·H₂O)₂, a clear image of the actual structure can be obtained. A difference density map in the vicinity of the HSO₄⁻ anion (Fig. 2b) shows an isosurface corresponding to a negative difference on the hydrogensulfate H atom. On the other hand, the O atom for the water molecule is also wrapped by an isotropic negative difference surface, while two positive residuals are observed, which are well localized at ca. 0.90 Å from the O atom. As a consequence, the HSO₄⁻ anion should be a sulfate, SO₄²⁻, while the lattice water molecule should be an ammonium cation NH₄⁺, giving the neutral charge balance for the crystal.

In the case of the data set collected at 0.84 Å resolution, a difference map computed after refinement of the [NH₄]₂[Zn(H₂O)₆](SO₄)₂ model affords a map without interpretable residues (Fig. 3a). However, the wR₂ residual calculated using all data is decreased from 0.2489 to 0.2296, and, most importantly, short H⋯H contacts are no longer present. Instead, all potential donor groups for hydrogen bonding, N–H and O–H functionalities, are then engaged in strong contacts with water O atoms as acceptors. The enhancement is similar for the refinement based on high resolution data, but the final difference map is almost featureless (Fig. 3b), and the drop for wR₂ is more pronounced, from 0.1140 to 0.0736 (Table 1). It is thus clear that it is not possible to rely on diffraction data at 0.84 Å in order to discriminate between the elusive hydrogensulfate compound and the isoelectronic Tutton salt 1, while ambiguity disappears if intensities are collected at higher Bragg angles, to reach a resolution around 0.50 Å. Once the correct chemical composition is used, data resolution is no longer a key factor: for the herein reported refinements, the crystallographic wR₂ residual is always significantly better for the Tutton model, at any resolution between 0.47 and 0.93 Å.

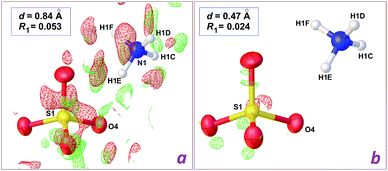Fig. 3 Difference density maps in the vicinity of the sulfate ion in the crystal structure of the Tutton salt [Zn(H₂O)₆](SO₄·NH₄)₂, 1, computed using low resolution data (a) and high resolution data (b). Details for computations are as in Fig. 2.

On the other hand, even in the event of restrictions concerning the diffraction at high resolution, the knowledge accumulated on the chemical crystallography for a given class of compounds can be used, following the advice of Gavezzotti and Flack quoted in Introduction. In the present case, the hydrogensulfate anion HSO₄⁻ and its conjugate base, the sulfate dianion SO₄²⁻, are both built on a tetravalent S centre, and are thus treated as AX₄E₀ bodies in the Gillespie-Nyholm theory.¹⁹ Assuming a free sulfate in a crystal structure (i.e. not coordinated nor engaged in strongly anisotropic hydrogen bonds), this anion can be considered as belonging to the tetrahedral point group T_d. In contrast, a free hydrogensulfate should be distorted toward lower symmetry, for example C_3v or C_s, unless the ionisable H atom is equally disordered over the four O atoms.

Many metrics may be used for the description of the overall shape of such anions. As an example, Fig. 4 correlates the variation of O–S–O valence angles (xy plane) with the variation observed for S–O bond lengths (z axis). The figure includes all non-disordered structures found in the CSD with at least one uncoordinated sulfate and/or one uncoordinated hydrogensulfate. It is clear that, regardless of the quality of the reported refinements, and regardless of data resolution, each anion displays averaged geometric parameters clustered in a given region of the used space, with little overlap between them: sulfate ions are in the blue zone, while HSO₄⁻ ions are found in the green zone. The shape of the hydrogensulfate included in the structure of [Zn(H₂O)₆](HSO₄·H₂O)₂ (refinement corresponding to Fig. 2a) affords metrics which do not match for this anion.

Fig. 4 Statistical analysis of the dimensions for free hydrogensulfate and sulfate ions. Data were retrieved from the CSD,³ omitting disordered structures, and the analysis was carried-out with Mercury¹⁶ and Origin.²⁰ Sulfate ions (1080 data) are represented with cubes and hydrogensulfate ions (424 data) with balls. The (xy) plane plots the smallest and largest O–S–O valence angles for each ion, while the z axis is devoted to bond lengths, plotting the difference between the largest and the smallest S–O bond lengths in each ion. For the sake of clarity, very few outliers have been omitted in the figure, and full data are deposited as ESI (Origin file†). The colour of data maps the Yang τ₄ parameter calculated for each ion,²¹ using a rainbow scheme (blue: τ₄ = 1 for an ideal T_d symmetry; red: τ₄ = 0.90; grey ions have τ₄ < 0.90). The red star at coordinates (108.3°, 110.0°, 0.035 Å) corresponds to the shape of the HSO₄⁻ ion in the structure reported by Dey et al.⁸ An idealized tetrahedral SO₄²⁻ ion is at coordinates (109.5°, 109.5°, 0 Å), with τ₄ = 1.

Indeed, easy-to-compute dimensionless indexes have been devised with the purpose of quickly check for the departure from an idealized symmetry. For the T_d point group, the most used is the Yang τ₄ parameter,²¹ based on valence angles (see colour scheme in Fig. 4). Again, the hydrogensulfate in [Zn(H₂O)₆](HSO₄·H₂O)₂, with τ₄ = 0.99, is most likely a sulfate ion. Alternative structural τ₄ parameters have been proposed for tetravalent centres,²² which afford very close results for SO₄²⁻ and HSO₄⁻, since departures from the tetrahedral shape are anyway small for both ions.

Conclusions

The synthetic procedure used by Dey et al.⁸ is in agreement with the re-interpreted structure described in the previous section: they reacted ZnSO₄·7H₂O with 4,4′-bipyridine and NH₄SCN in a mixture of methanol and water. The most reasonable outcome is that only two products were obtained, namely (bipyridinium)⁺SCN⁻ and [NH₄]₂[Zn(H₂O)₆](SO₄)₂, 1. The authors sought to explain the protonation of the sulfate via a not experimentally supported mechanistic pathway, which is chemically inconsistent: given that ammonium cations are the unique source of protons in the medium, their hypothetical reaction course involves a proton transfer from a weak acid to a weak base (pK_a = 9.3 for NH₄⁺ vs. pK_b = 12.1 for SO₄²⁻). In our synthesis, using very cheap starting materials, a standard acid–base reaction between H₂SO₄ and ZnO produces ZnSO₄·7H₂O in situ, affording 1 and ZnCl₂, in presence of NH₄Cl (Scheme 1).

Scheme 1 Synthesis of the Zn Tutton double salt 1 used in this work.

Our re-interpretation of the published structure for an unexpected hydrogensulfate salt does not mean that we pretend we can answer the question raised in the title. Nevertheless, whenever possible, a hitherto unseen compound should not be characterized relying only on the crystal structure of a unique crystal: the crystal picked-up from a sample may be poorly representative of the actual content of the whole sample, especially if very stable ionic compounds, like the Tutton salts, may appear. On the other hand, the general strategy of collecting diffraction data at high as possible Bragg angles should not be considered as a waste of time and resources.²³ The optimistic threshold at (sin θ)/λ = 0.6 Å⁻¹ (d = 0.84 Å in the direct space), recommended by the IUCr, makes sense only if the formula of the crystal is based on firm and unquestionable grounds gathered from other analytical techniques. The case of a new compound is always more challenging, and should be scrutinized with a healthy dose of scepticism. Finally, from the statistical point of view, even a powerful knowledge-based library like Mogul may result insufficient,²⁴ because only one-dimensional metrics are handled (namely distances, angles, torsion angles and ring conformations).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by CONACyT-México (grant 268178) and VIEP-BUAP (projects 100500599-VIEP2018 and 100142933-VIEP2018). We thank Karla Mayte Germán Tepetla (UPMP, Puebla) and Rosa Elena Arroyo Carmona (Ciencias Químicas, BUAP) for their involvement in the general project.

Notes and references

1. P. Allé, E. Wenger, S. Dahaoui, D. Schaniel and C. Lecomte, Phys. Scr., 2016, 91, 063001.
2. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
3. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
4. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
5. M. Weil, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 990–994.
6. J. M. Jefferis and G. S. Girolami, Organometallics, 1998, 17, 3630–3632.
7. A. Gavezzotti and H. Flack, IUCr pamphlet N° 21, 2005, https://www.iucr.org/education/pamphlets/21/full-text, accessed June, 2018.
8. D. Dey, S. Pal, H. R. Yadav, P. S. Sengupta, A. R. Choudhury, N. Kole and B. Biswas, RSC Adv., 2015, 5, 42681–42688.
9. A. E. Tutton, Proc. R. Soc. London, 1901, 67, 58–84.
10. W. Hofmann, Z. Kristallogr., 1931, 78, 279–333.
11. H. Montgomery and E. C. Lingafelter, Acta Crystallogr., 1964, 17, 1295–1299.
12. E. N. Maslen, K. J. Watson, S. C. Ridout and F. H. Moore, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 1510–1514.
13. F. A. Cotton, L. M. Daniels, C. A. Murillo and J. F. Quesada, Inorg. Chem., 1993, 32, 4861–4867.
14. C. J. Simmons, M. A. Hitchman and H. Stratemeier, Inorg. Chem., 2000, 39, 6124–6126.
15. J. D. H. Donnay and D. Harker, Am. Mineral., 1937, 22, 446–467.
16. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
17. X-Area 1.80 and X-Red32 1.62, Stoe & Cie (2015), Darmstadt, Germany.
18. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
19. R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327.
20. OriginPro 9.1, OriginLab Corp., Northampton, MA, USA.
21. L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964.
22. A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Polyhedron, 2015, 90, 47–57.
23. W. F. Sanjuan-Szklarz, A. A. Hoser, M. Gutmann, A. O. Madsen and K. Wozniak, IUCrJ, 2016, 3, 61–70.
24. I. J. Bruno, J. C. Cole, M. Kessler, J. Luo, W. D. S. Motherwell, L. H. Purkis, B. R. Smith, R. Taylor, R. I. Cooper, S. E. Harris and A. G. Orpen, J. Chem. Inf. Comput. Sci., 2004, 44, 2133–2144.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1848083. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8ra05162c.

---