Open Access Article
Open Access ArticlePeriodic DFT study of structural transformations of cocrystal NTO/TZTN under high pressure†
Guo-zheng Zhao * and
Dong-fang Yang
* and
Dong-fang Yang
Key Laboratory of Magnetic Molecules & Magnetic Information Materials Ministry of Education, The School of Chemical and Material Science, Shanxi Normal University, Linfen 041004, China. E-mail: zhaoguozheng99@126.com
First published on 18th September 2018
Abstract
Density functional theory (DFT) periodic calculations were performed to study the geometrical and electronic structures of energetic cocrystal NTO/TZTN under pressures ranging from 0 to 80 GPa. The optimized crystal structure by the GGA/PW91 (Perdew–Wang-91) and dispersion corrections corresponds well with the experimental values under ambient pressure. With the pressure increasing, the lattice constants, unit cell volumes, interatomic distances, H-bond energies, atomic charges, and bond populations of cocrystal NTO/TZTN change gradually. At pressures of 4, 8, and 23 GPa, three structural transformations occurred, shown by the results. The cyclization plays an important role in stabilizing the systems. The increasing pressure contributes to the increase of interaction force gradually. At 4 GPa, a new hydrogen bond O3⋯H5 is formed. At 8 GPa, the formation of eight membered rings is because of the existence of a covalent bond O1–H3 between two NTO molecules. In addition, a covalent interaction is formed between N2 and H4 atoms with the biggest H-bond energy compared to the others. As the pressure reaches 23 GPa, another new hydrogen bond forms between N8 and H5 atoms, which contributes to the formation of a five membered ring between NTO and TZTN. The electrons can move freely according to the results of the density of states between the valence and conduction bands when the pressure is high. This work will provide useful information in understanding the high-pressure effect on the structural transformation.
1. Introduction
High energetic nitrogen-rich compounds have received a substantial amount of interest due to their merits, such as low vapor pressures, favorable insensitivity, excellent explosive performance, and environmental acceptability.1–4 On account of pursuing high energy and safe explosives, many scientists have paid considerable attention to compounds' design and synthesis over several decades.5–7 As is known, due to the inherent power-safety contradiction, it is still a challenging task to achieve a fine balance between high detonation properties and low sensitivity.8–10 Recently, an ideal method in terms of obtaining explosives with excellent comprehensive performance by cocrystallizing energetic compounds was reported.11–14 The thermal properties of HMX (1,3,5,7-tetranitro-1,3,5,7-tetrazacyclooctane) were changed by Landenberger et al. by cocrystallizing with seven nonenergetic compounds.15 Pei et al. prepared the cocrystal HMX/TATB which featured good thermal stability and insensitivity to impact, in comparison to HMX.16 Huang et al. modified the structure and properties of cocrystal explosive of HNIW and BTF (benzotrifuroxan).17 Matzger et al. reduced the impact sensitivity of HNIW (2,4,6,8,10,12-hexanitrohexaazaisowurtzitane) via the incorporation of TNT with the same molar ratio.18 The physico-chemical properties of HNIW was adapted by Millar et al. through the formation of cocrystals with several solvents.19 Bolton et al. explored a cocrystal HNIW/HMX with high explosive power and good mechanical sensitivity in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio.20 Due to completely different packing model of energetic compounds, cocrystallization offers an alteration of properties including density, impact sensitivity, and explosive performance, which help to obtain explosives with better comprehensive performance. This provides an opportunity to modify the physico-chemical properties of existing explosive and prepare superior cocrystal with better integrated properties at the molecular level.
1 molar ratio.20 Due to completely different packing model of energetic compounds, cocrystallization offers an alteration of properties including density, impact sensitivity, and explosive performance, which help to obtain explosives with better comprehensive performance. This provides an opportunity to modify the physico-chemical properties of existing explosive and prepare superior cocrystal with better integrated properties at the molecular level.
In 1905, a nitrogen-rich explosive, named 3-nitro-1,2,4-triazol-5-one (NTO), was synthesized for the first time, with sensitivity comparable to that of 1,3,5-triamino-2,4,6-trinitro benzene (TATB), while the performance are as same as that of RDX. However, it is a dibasic acid explosive, which limits its further applications.21–23 For the sake of decreasing the acidity of NTO, Zhang et al. cocrystallized NTO with 5,6,7,8-tetrahydrotetrazolo[1,5-b][1,2,4]-triazine (TZTN), which demonstrated that the cocrystal contributed to the enhancement of thermal stability and became less sensitive to impact, compared with the TZTN.24 Chen et al. conducted a research about the cocrystal NTO/TZTN with the application of GGA/PBE method and analyzed its structural, mechanical, and thermodynamic properties and impact sensitivity.25 As a complex chemical behavior, it is challengeable to investigate the microscopic properties of energetic crystals. At the same time, the research of high pressure behavior of energetic crystals plays a significant role in experimental measurements. Theoretical calculation is an effective way to model the properties of energetic crystals in physical and chemical fields in comparison to the experimental work.26–29 Deep research on the behavior of cocrystal NTO/TZTN under high pressures is of vital importance for the understanding of its chemical reactivity, detonation process, structural stabilities, and sensitivity. However, the cocrystal experiments mainly focus on the preparation, characterization, and performance test as well as the evaluation of impact sensitivities.30–33 Fewer research focused on the relationship between structure and properties under high pressures. According to the application of density functional theory method with pseudopotentials and a planewave of basis set, the investigation of the structures and properties of energetic crystals has been successfully performed under hydrostatic compression.34 Sorescu et al. predicted the crystallographic lattice parameters of representative molecular explosive crystals by DFT-D as implemented in a pseudopotential plane-wave code under the ambient and high pressure conditions,35 which shown that the cell parameters were obtained with an accuracy less 2% in comparison to the experimental values at ambient pressures, and also can be predicted accurately at high pressures. Hu et al. calculated the elastic stability of β-Ti at various pressures by the first-principles plane-wave pseudopotential method.36 It is found that, the pseudopotential results are the same as and ideally close to all-electron full-potential augmented plane-wave calculations under low and high pressure, respectively. Currently, the first principle periodic calculations were performed to study the crystal, molecular, and electronic structures of cocrystal NTO/TZTN. The high pressure behavior of cocrystal NTO/TZTN were investigated in the range of 0–80 GPa.
2. Computational methods
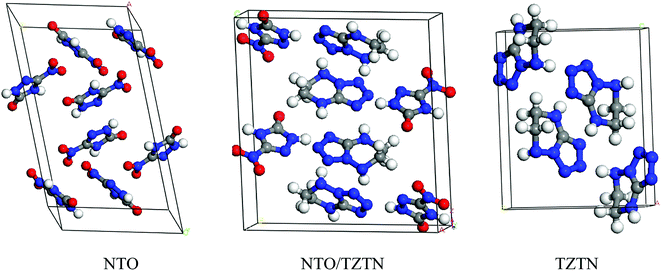
The first-principle calculations were performed by the application of DFT method with the combination of Vanderbilt-type ultrasoft pseudopotential35,36 and a plane-wave expansion of the wave functions37 implemented in the CASTEP38 module of Materials Studio 6.0.39 The initial crystal was taken from Zhang et al. (CCDC 1042895)24 and designed to the following computations. The cocrystal NTO/TZTN crystallizes in monoclinic space group P21/c with a = 27.104 Å, b = 10.093 Å, and c = 14.741 Å. Fig. 1 illustrates the crystal structures of NTO, TZTN and cocrystal NTO/TZTN. Under the hydrostatic pressures of 0–80 GPa, the research has been conducted to investigate the pressure effect on the geometrical and electronic structures of cocrystal NTO/TZTN.Single point energies calculations were conducted at the B97-D/6-311++G** level of DFT with Gaussian 09 (ref. 40) suite. The Quantum theory of atoms in molecules (QTAIM) analyses were performed by employing Multiwfn41 with the input files (.wfn) generated from Gaussian. The electron density (ρCP) and its Laplacian (∇2ρ) at the critical point, the electron potential energy density (VBCP), the total electron energy density (HBCP), and the Lagrangian kinetic energy (GBCP) were obtained based on the characteristics of the bond critical point (BCP). The relations between the topology parameters are shown in eqn (1):
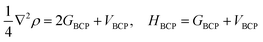 | (1) |
Espinosa et al. introduced eqn (2) which was used for obtaining of the relationship between H-bond energy (EH) and VBCP:42
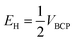 | (2) |
3. Results and discussion
Seven different functionals, local density approximation (LDA) and generalized gradient approximation (GGA), as a test, were applied to the computation of cocrystal NTO/TZTN. To benchmark the performance of theoretical approach, LDA/CA-PZ, GGA/PBE (Perdew–Burke–Ernzerhof),43 GGA/PW91(Perdew–Wang-91)44 and dispersion corrections were selected to fully relax the cocrystal NTO/TZTN without any constraint at ambient pressure. The experimental and relaxed cell parameters of cocrystal NTO/TZTN are listed by Table 1. The relative errors of the calculated values to the experimental ones indicate that the calculated values of GGA/PW91-OBS is much closer to the experimental ones than the others. The GGA/PW91-OBS method is more suitable for studying cocrystal NTO/TZTN, which is different from the previous studies in term of energetic crystals45,46 show that more reliable lattice parameters could be produced by the LDA functional than the GGA. Therefore, GGA/PW91-OBS method has been employed in the present study.| Method | a (Å) | b (Å) | c (Å) | β (deg) | Vol. (Å3) |
|---|---|---|---|---|---|
| a The values in parentheses correspond to the percentage differences relative to the experimental data. | |||||
| LDA/CA-PZ | 13.107 (−3.14) | 5.015 (−2.32) | 14.741 (0.10) | 95.81 (3.87) | 963.9 (−5.72) |
| LDA/CA-PZ-OBS | 13.146 (−2.85) | 4.635 (−9.72) | 13.509 (−8.27) | 88.63 (−3.91) | 822.8 (−19.52) |
| GGA/PBE | 13.308 (−1.66) | 5.982 (16.52) | 17.665 (19.97) | 95.25 (3.26) | 1400.4 (36.97) |
| GGA/PBE-TS | 13.611 (0.58) | 5.158 (0.47) | 15.118 (2.65) | 91.83 (−0.44) | 1060.9 (3.77) |
| GGA/PBE-G06 | 13.405 (−0.94) | 5.096 (−0.74) | 15.289 (3.82) | 93.03 (0.86) | 1043.0 (2.01) |
| GGA/PW91 | 13.539 (0.05) | 5.783 (12.64) | 17.219 (16.92) | 93.86 (1.76) | 1345.1 (31.56) |
| GGA/PW91-OBS | 13.552 (0.15) | 5.046 (−1.71) | 14.741 (0.10) | 90.99 (−1.36) | 1008.0 (−1.41) |
| Exp. | 13.532 | 5.134 | 14.727 | 92.24 | 1022.4 |
3.1 Crystal structure
In general, intermolecular interactions, with the feature of weakness, are easy to compress in comparison with chemical bonds. The reduction of structural spaces in the crystal is the first structural response under an applied pressure. Because the flexible conformation of molecule, the changes of molecular conformation or the transformation of structure lead to the transitions of phase and the formation of denser packed materials under higher pressure. The crystals NTO and NTO/TZTN exist in space groups of P21/c, and space group of P21/n for TZTN crystal. The molecules per unit cell are irreducible by the number of 4, 4, and 8 (4 for NTO and 4 for TZTN) in NTO, TZTN, and cocrystal NTO/TZTN, respectively. Fig. 2 described the relaxed lattice constants, compression rates, and unit cell volumes of cocrystal NTO/TZTN in the pressure range of 0–80 GPa. At 0 GPa, the experimental values are agreed with the calculated lattice constants. With the pressure increasing, the lattice constants (a, b, c) and unit cell volume (V) decrease gradually. c is easier to compress than a and b from 0 to 80 GPa, due to the enough external pressure, which is able to overcome the intermolecular repulsion along the crystallographic directions and leads the crystal structure shrinkable, which is in line with the experimental result that the cocrystal NTO/TZTN becomes more and more compact.24 Resultantly, the unit cell volume shrinks slowly and accordingly the rise of cocrystal density and total energy is evident with the increase of pressure.47–49 Intermolecular interaction becomes more and more strong as the molecules get closer with each other. Comparing to the crystallographic density (1.665 g cm−3), cocrystal density increased by around 99.76% and reached the biggest value under 80 GPa.24 Knowingly, with the increasing of crystal density, the detonation velocity increases as well resulted from K–J empirical equations,47 which are also shown that detonation pressure varies with the square of crystal density. The detonation velocity and pressure are improved remarkably when the cocrystal density increases to 2.022 g cm−3 at 4 GPa.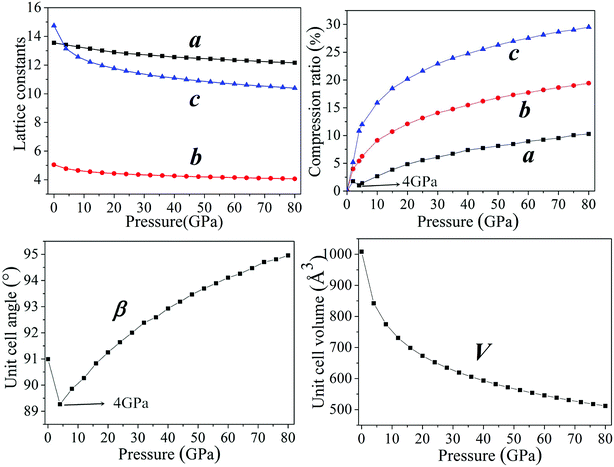 | ||
| Fig. 2 The description of lattice constants and unit cell volume of cocrystal NTO/TZTN under various pressures. | ||
According to Fig. 2, the ratio of total compression reaches 49.22% under the pressure range 0–80 GPa. The largest compression of unit cell takes place in the pressure region below 20 GPa. The compression ratio a at 4 GPa is anomalously smaller than that at 3 GPa, and increases abnormally again at 5 GPa. In the pressure range of 0–80 GPa, the compression ratios along three directions are not tantamount. The one in c-direction is significantly greater than those in a- and b-directions in a sequence of c > b > a. At 30 GPa, the total compression ratios along three directions of a, b, and c are 6.09%, 14.07%, and 22.90%, respectively, which shows that cocrystal compressibility is anisotropic and the structure is much stiffer in a direction in comparison with those in b and c directions. Moreover, it is noticeable that the unit cell angle β decrease gradually under the pressure range 0–4 GPa. Comparing with that at 4 GPa, β is remarkably larger at 5 GPa, which matches well with the change of compression ratio, meanwhile introducing the suggestion that the large changes have taken place in crystalline form under the pressure of 4 GPa. The perspective view of the cocrystal NTO/TZTN with pressures is also demonstrated in Fig. 3. With the structural transformations of cocrystal NTO/TZTN have firstly taken place under the pressure of 4 GPa, the large changes in the structures of cocrystal followed.
3.2 Molecular structure
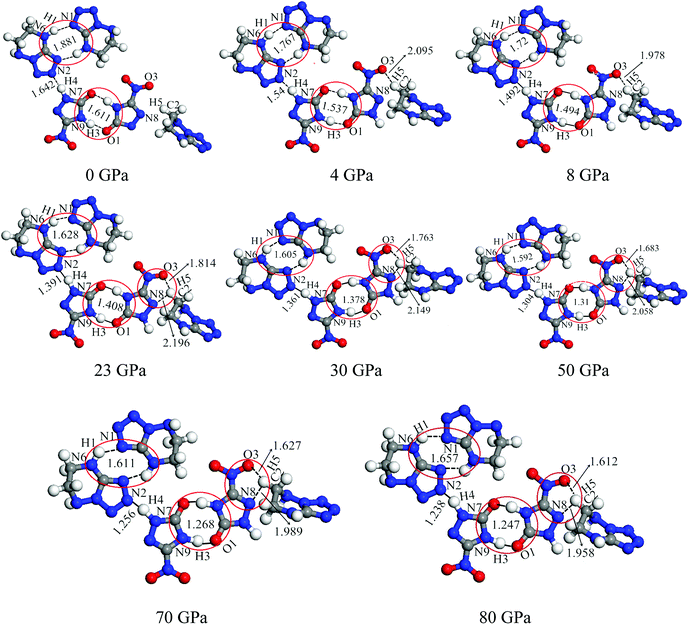
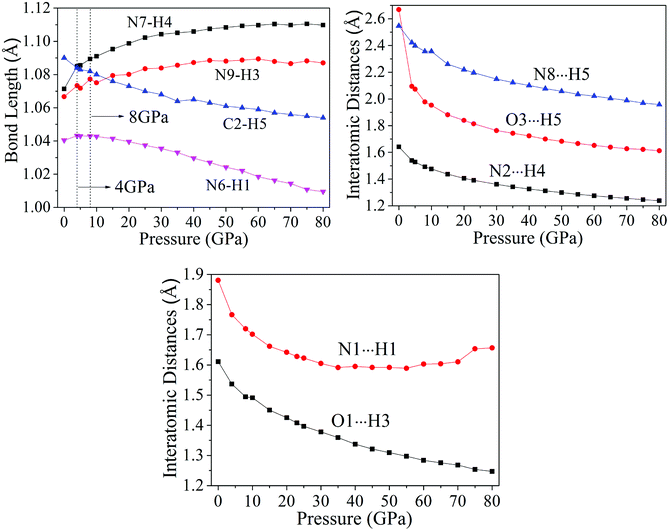
From Fig. 4, after 8 GPa, bond N6–H1 shorten gradually and the covalent interaction increases, which forms the eight membered ring with the H-bond N1⋯H1 (1.590–1.881 Å). The length of intermolecular H-bond O1⋯H3 decreases obviously with increasing pressure. At 8 GPa, the H-bond O1⋯H3 transforms into covalent bond (1.494 Å), which forms the eight membered ring between two NTO molecules. In addition, as the pressure augments further to 8 GPa, the intermolecular N2⋯H4 contact (1.492 Å) has become more closer which leads to the transferring of hydrogen atom and formation of new covalent bond N2–H4. At 4 GPa, the hydrogen bond forms between O3 and H5 atoms (2.095 Å), and a large change in molecular structure has taken place. The interaction force of H-bond O3⋯H5 increase gradually with the pressure increasing to 80 GPa. When 23 GPa is applied, the other new hydrogen bond forms between N8 and H5 atoms (2.196 Å), and the five membered ring is built between NTO and TZTN, which leads to a larger conjugation system and makes cocrystal NTO/TZTN more stable as a whole. As the pressure increases, the formation of five and eight membered rings significantly improve the stability of cocrystal NTO/TZTN, which agree well with the resulted concluded from the structure determination.24
The calculations of crystal NTO51 and TZTN52 were carried out by DFT method at the same level in the pressure range of 0–80 GPa. For crystal NTO and TZTN, from 0 to 80 GPa, the applied compression basically reduces the intermolecular voids. There is no large change in the bond length (all less than 1.5 Å), and transformation or fracture of chemical bond, which is different from the fact that three structural transformations occurred for cocrystal NTO/TZTN with the pressure of 4, 8, and 23 GPa.
| Pressure (GPa) | Interaction | H⋯Y [Å] | ρCP | ∇2ρ | VBCP | GBCP | HBCP | EH |
|---|---|---|---|---|---|---|---|---|
| 0 | N9–H3⋯O1 | 1.613 | 0.035 | 0.283 | −0.064 | 0.067 | 0.003 | −84.02 |
| N6–H1⋯N1 | 1.881 | 0.025 | 0.151 | −0.033 | 0.036 | 0.003 | −43.32 | |
| N7–H4⋯N2 | 1.642 | 0.036 | 0.270 | −0.067 | 0.067 | 0.000 | −87.95 | |
| C2–H5⋯N8 | 2.562 | 0.009 | 0.032 | −0.006 | 0.007 | 0.001 | −7.88 | |
| C2–H5⋯O3 | 2.670 | 0.005 | 0.021 | −0.004 | 0.005 | 0.001 | −5.25 | |
| 4 | N9–H3⋯O1 | 1.540 | 0.041 | 0.344 | −0.081 | 0.084 | 0.003 | −106.33 |
| N6–H1⋯N1 | 1.768 | 0.031 | 0.203 | −0.048 | 0.050 | 0.002 | −63.01 | |
| N7–H4⋯N2 | 1.540 | 0.044 | 0.352 | −0.092 | 0.090 | −0.002 | −120.77 | |
| C2–H5⋯N8 | 2.080 | 0.013 | 0.049 | −0.009 | 0.011 | 0.002 | −11.81 | |
| C2–H5⋯O3 | 2.097 | 0.017 | 0.080 | −0.015 | 0.018 | 0.003 | −19.69 | |
| 8 | N9–H3⋯O1 | 1.497 | 0.044 | 0.387 | −0.093 | 0.095 | 0.002 | −122.09 |
| N6–H1⋯N1 | 1.723 | 0.034 | 0.229 | −0.056 | 0.057 | 0.001 | −73.51 | |
| N7–H4⋯N2 | 1.493 | 0.048 | 0.398 | −0.107 | 0.103 | −0.004 | −140.46 | |
| C2–H5⋯N8 | 2.422 | 0.016 | 0.059 | −0.011 | 0.013 | 0.002 | −14.44 | |
| C2–H5⋯O3 | 1.980 | 0.022 | 0.112 | −0.021 | 0.024 | 0.003 | −27.57 | |
| 23 | N9–H3⋯O1 | 1.411 | 0.052 | 0.492 | −0.123 | 0.123 | −0.000 | −161.47 |
| N6–H1⋯N1 | 1.634 | 0.042 | 0.290 | −0.075 | 0.074 | −0.001 | −98.46 | |
| N7–H4⋯N2 | 1.391 | 0.058 | 0.517 | −0.148 | 0.139 | −0.009 | −194.29 | |
| C2–H5⋯N8 | 2.242 | 0.022 | 0.092 | −0.019 | 0.021 | 0.002 | −24.94 | |
| C2–H5⋯O3 | 1.816 | 0.030 | 0.180 | −0.038 | 0.042 | 0.004 | −49.88 |
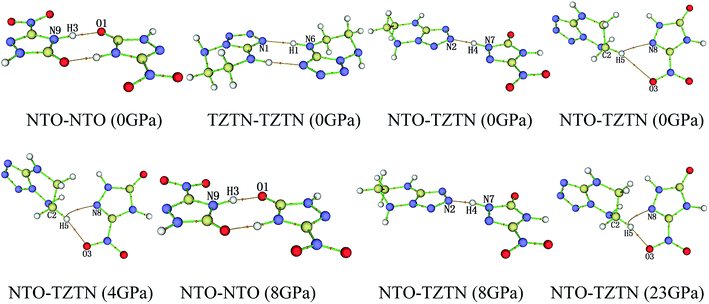 | ||
| Fig. 5 The display of molecular structures and their corresponding H-bond interactions at 0, 4, 8, and 23 GPa. | ||
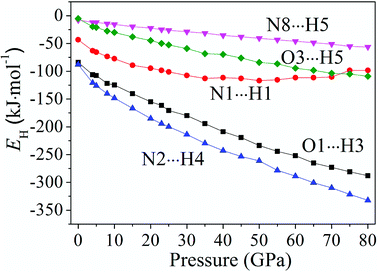
Fig. 6 displays the tendency about H-bond energies of cocrystal NTO/TZTN under different pressures. Obviously, O1⋯H3, N2⋯H4, N8⋯H5, O3⋯H5, and N1⋯H1 have the largest and smallest H-bond energies at 80 GPa and 0 GPa, respectively, which indicates that the structural voids is reduced by the applied compression in cocrystal NTO/TZTN and causes the increase of the H-bond intermolecular interaction. To a certain degree, the applied compression contributes the improvement of cocrystal NTO/TZTN stability, which matches perfectly with the result from the analysis of bond length and interatomic distance. At the same pressure, N2⋯H4 has the biggest H-bond energies and N8⋯H5 has the smallest. The stability increases in the order of N8⋯H5 < O3⋯H5 < O1⋯H3 < N2⋯H4, which signify that the formation of covalent interaction (O1 and H3, N4 and H2) at 8 GPa increase thermal stability significantly.
3.3 Electronic structure
The variation trends of several bonds' atomic charges and bond populations55–58 with pressure to cocrystal NTO/TZTN are depicted by Fig. 7. From 0 to 80 GPa, the positive charges on H1, H3, H4, and H5 decrease gradually, as same as the negative charges on N8, but increase on the negative charges of N6, N7, and N9. From 45 to 55 GPa, the atom charges, without significant change, tend to be more delocalized. With the formation of five membered rings at 23 GPa, the charge on H5 becomes less positive from 0.31 to 0.30e, and the charge on C2 becomes less negative from −0.34 to −0.30e. The atom N8 obtains amount of charges considerably from −0.26 to −0.28e. This means the transferring of the electron from C2 to N8. Due to the electron transfer, the bond C2–H5 becomes stronger because the bond order increases from 0.86 to 0.92, and the bond N8⋯H5 turns to be weaker for the bond order decreases. As a result, the five membered rings in cocrystal NTO/TZTN are formed. Comparing with the formation of eight membered rings at 8 GPa, the atoms N9 and O1 lose a considerable amount of charges and become less negative from −0.51 to −0.49e and from −0.62 to −0.60e, respectively. The charge of H3 is unchanged. This means that the electron is transferred from the atoms N9 and O1 to the triazole rings. Under the same pressure, it has the biggest and smallest H-bond order for N2⋯H4 and N8⋯H5, respectively. The increase of stability, by the order, is N8⋯H5 < O3⋯H5 < O1⋯H3 < N2⋯H4, which agrees better with the result concluded from H-bond energies.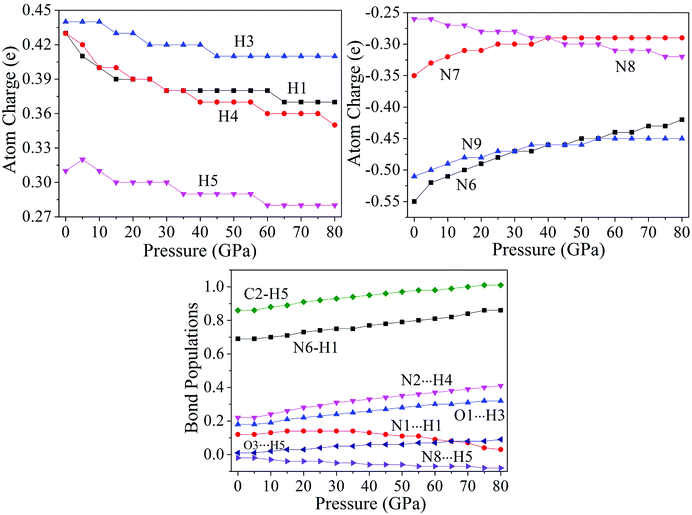 | ||
| Fig. 7 Corresponding curves on atomic charges and bond populations of cocrystal NTO/TZTN under different pressures. | ||
According to the equilibrium crystal structures under different pressures, the calculation on the self-consistent band structures along different symmetry directions of the Brillouin zone59–61 has been pictured by Fig. 8. For the sake of a visualized view, there is merely a presentation of range from −1.0 to 4.0 eV. From 0 to 80 GPa, the energy bands between 1.0 and 2.0 eV shift to the areas of lower energy. Below 4 GPa, the energy bands are flat and fluctuate little because cocrystal NTO/TZTN is a molecular crystal and the molecular interactions are weak. The energy bands become less flat across the Brillouin zone, and the bandwidth increases remarkably with the pressure increases from 4 to 80 GPa. This indicate that molecular interactions increase caused by the applied pressure. Important changes in the electronic properties can be obtained on the basis of the transformation in cocrystal NTO/TZTN at 8 and 23 GPa. As is shown, the energy bands get to a higher energy region, which means much wider on the conduction bands and much narrower on the valence bands than that in lower pressures.
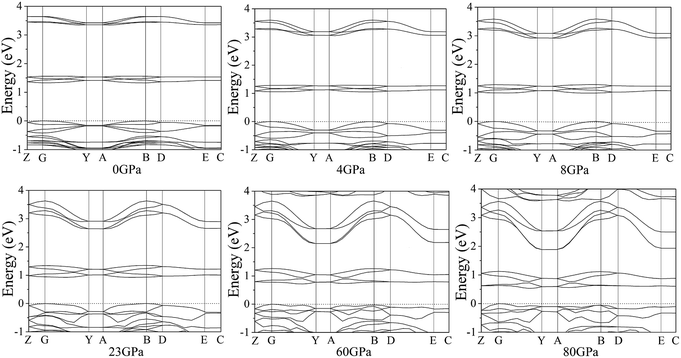 | ||
| Fig. 8 Self-consistent band structures of cocrystal NTO/TZTN under different pressures. The Fermi energy is marked by a dashed horizontal line. | ||
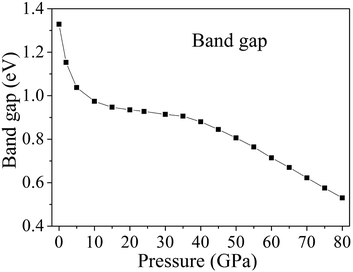
Fig. 9 displays the band gaps of cocrystal NTO/TZTN under different pressures. With the pressure ranging from 0 to 80 GPa, illustrated by Fig. 9, the band gap shows continuous reduction. From 0 to 7 GPa, the decrease in band gaps causes the reduction of maximum energy in comparison with the high pressure region, which shows that a slight variation takes place in the electronic structure even though no evident change in molecular geometry. With the gradual increase of pressure from 0 to 7 GPa, the band gaps decrease suddenly and rapidly from 1.329 to 0.992 eV. Cocrystal NTO/TZTN transfers from the semiconductor to the metallic system under compression, which indicates that the electrons are more easily to transfer from occupied valence bands to empty conduction bands. From 8 to 35 GPa, the reduction of the band gap is in a slow way, because no obvious change occurred during the electron transitions from the occupied valence bands to the empty conduction bands. After 35 GPa, the band gap reduces significantly, which means that the electron is still more likely to transfer from occupied valence bands to empty conduction bands. The reduction tendency of band gap is related to the decrease in intermolecular space, which causes an increase of electron overlap between molecules in cocrystal NTO/TZTN under compression. To a certain extent, based on the principle of the easiest transition of electrons,62,63 with the pressure increasing, the decreasing gap reduces to the increasing sensitivity.64,65
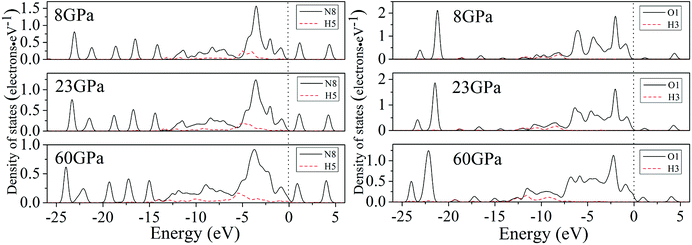
For a better understanding on the bond nature and electronic structure of cocrystal NTO/TZTN under different pressures, we conduct the investigation about the total density of states (DOS) and partial density of states (PDOS).66 The calculation of DOS for cocrystal NTO/TZTN under different pressures is illustrated by Fig. 10. According to Fig. 10, the curves of DOS have sharp peaks under low pressure, while the peaks become wider under higher pressure. The electrons demonstrate better mobility and moving freedom between the valence and conduction bands, hence, the cocrystal NTO/TZTN turns into metal under high pressure. That the conduction bands shift to the lower energy, not only reduces the band gap but also conclude a result that the probability of electronic excitations are augmented by crystal compression. Besides, electronic delocalization in cocrystal NTO/TZTN steadily increases. Because of some broadening effect in DOS curves, they are confined at the Fermi energy level. From −10 eV to the Fermi level, the p states are the dominating feature in the sharp peaks of valence and conduction band within the area of low or high pressure, which indicates p states play an irreplaceable role in terms of effect on the chemical reaction of cocrystal NTO/TZTN. At 4 and 8 GPa, it is noticeable that the DOS turns the double peaks into single peaks between −3.40 and −2.00 eV with the formation of H-bond O3⋯H5 and covalent bond O1–H3, N2–H4, respectively. The formation of H-bond N8⋯H5 caused that the DOS at 23 GPa are quite different from that at 0 GPa, which matches well with the results concluded from molecular structure section. Fig. 11 describes the calculation of PDOS of the N8, H5, O1, and H3 atoms at 8, 23, and 60 GPa. Under different pressures, the existence of good interactions is obvious between N8 and H5 atoms, particularly in the energy range from −13.29 to −0.92 eV, where the peaks tendency are in common with each other. At 8 GPa, a strong peak of the N8 atom appears at −4.35 eV, while H5 atom shows the feature of weakness here. However, at 23 GPa, a strong peak appears at −4.64 eV for both N8 and H5 atoms. The main reason is that the N8 and H5 atoms are independent at 8 GPa but form a H-bond N8⋯H5 at 23 GPa, which is in agreement with the analysis of molecular structure. Furthermore, at 8 GPa, the shape of the peaks are even very alike between O1 and H3 atoms from −12.27 to −7.13 eV, which is attribute to the formation of covalent bond and the eight membered ring between two NTO molecules. Eventually, at 8 and 23 GPa, the upper valence bands and the lower conduction bands are predominated by the N, C states in skeleton rings, O states linked to the triazole rings and N states in nitro groups, respectively, which indicate that C and N atoms in skeleton rings, O atoms linked to the triazole rings, and N atoms in nitro groups act as the active center.
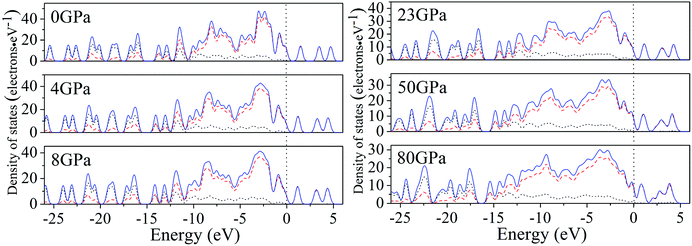 | ||
| Fig. 10 Calculated total DOS for cocrystal NTO/TZTN under various pressures: s, p, and total states are marked by dotted, dashed, and solid curves, respectively. | ||
4. Conclusions
In this work, the effect of high pressure on the geometrical and electronic structures of cocrystal NTO/TZTN has been explored by the periodic first-principle calculations under hydrostatic pressure of 0–80 GPa. The GGA/PW91-OBS method has been employed in the present study. The optimized crystal structure by the GGA/PW91-OBS method at ambient pressure, matches better with the experimental constants in comparison with the other functionals. At 4, 8, and 23 GPa, molecular structure transforms due to the induced pressure. The stability of cocrystal system has been remarkably improved by the formation of five and eight membered rings during external compression. At 4 GPa, the hydrogen bond forms between O3 and H5 atoms, and the interaction force increases gradually with the pressure increasing to 80 GPa. At 8 GPa, the transformation from H-bond O1⋯H3 to covalent bond contributes to the formation of the eight membered ring. Furthermore, a new covalent bond forms between N2 and H4 atoms. After 8 GPa, the covalent interaction of bond N6–H1 increases, which forms the eight membered ring with the H-bond N1⋯H1 between two NTO molecules. When 23 GPa is applied, the formation of H-bond N8⋯H5 leads to the build of the five membered ring between NTO and TZTN. From the study of H-bond energies, after 8 GPa, the covalent interaction between O1 and H3 atoms, N4 and H2 atoms, intensifies the thermal stability of cocrystal system significantly. With the growing increase of pressure, the energy bands show fluctuation across the Brillouin zone, while the bandwidth augments obviously. From 0 to 80 GPa, the reduction of band gap is connected with the decrease in intermolecular space, which makes the electron overlap increasing between molecules in cocrystal NTO/TZTN. The probability of electronic excitations are increased by the crystal compression, which has been proved by the analysis of density of states. The p state is the main character in the sharp peaks of valence and conduction band from −10 eV to the Fermi level. Basic information is provided by these results for the high pressure behavior of cocrystal NTO/TZTN.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (No. 2016157), and Natural Science Foundation of Shanxi Normal University Modern College of Humanities and Sciences (No. 2018JCYJ03). We are indebted to Associate Prof. Lei Zhang and Prof. Jun Chen for providing the crystal structure of the TZTN explosive.References
- Y. G. Xu, Q. Wang, C. Shen, Q. H. Lin, P. C. Wang and M. Lu, Nature, 2017, 549, 78 CrossRef PubMed.
- W. Q. Zhang, J. H. Zhang, M. C. Deng, X. J. Qi, F. D. Nie and Q. H. Zhang, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- K. B. Landenberger, O. Bolton and A. J. Matzger, J. Am. Chem. Soc., 2015, 137, 5074 CrossRef PubMed.
- D. Fischer, J. L. Gottfried, T. M. Klapötke, K. Karaghiosoff, J. Stierstorfer and G. Witkowski, Angew. Chem., Int. Ed., 2016, 55, 16132 CrossRef PubMed.
- H. Niu, S. S. Chen, Q. H. Shu, L. J. Li and S. H. Jin, J. Hazard. Mater., 2017, 338, 208 CrossRef PubMed.
- S. Elbasuney, M. G. Zaky, M. Radwan and S. F. Mostafa, Appl. Surf. Sci., 2017, 419, 328 CrossRef.
- T. M. Klapötke, B. Krumm and T. Reith, Eur. J. Org. Chem., 2017, 25, 3666 CrossRef.
- D. Kumar, G. H. Imler, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2017, 23, 7876 CrossRef PubMed.
- C. Deng, X. G. Xue, Y. Chi, H. Z. Li, X. P. Long and C. Y. Zhang, J. Phys. Chem. C, 2017, 121, 12101 CrossRef.
- Z. B. Zhang, C. X. Xu, X. Yin and J. G. Zhang, Dalton Trans., 2017, 45, 19045 RSC.
- J. C. Bennion, Z. R. Siddiqi and A. J. Matzger, Chem. Commun., 2017, 53, 6065 RSC.
- S. R. Anderson, P. Dube, M. Krawiec, J. S. Salan, D. J. A. Ende and P. Samuels, Propellants, Explos., Pyrotech., 2016, 41, 783 CrossRef.
- H. F. Gao, S. H. Zhang, F. D. Ren, F. Liu, R. J. Gou and X. Ding, Comput. Mater. Sci., 2015, 107, 33 CrossRef.
- D. Z. Guo, Q. An, S. V. Zybin, W. A. Goddard, F. L. Huang and B. Tang, J. Mater. Chem. A, 2015, 3, 5409 RSC.
- K. B. Landenberger and A. J. Matzger, Cryst. Growth Des., 2012, 12, 3603 CrossRef.
- J. P. Shen, X. H. Duan, Q. P. Luo, Y. Zhou, Q. L. Bao, Y. J. Ma and C. H. Pei, Cryst. Growth Des., 2011, 11, 1759 CrossRef.
- Z. W. Yang, H. Z. Li, X. Q. Zhou, C. Y. Zhang, H. Huang, J. S. Li and F. D. Nie, Cryst. Growth Des., 2012, 12, 5155 CrossRef.
- O. Bolton and A. J. Matzger, Angew. Chem., Int. Ed., 2011, 50, 8960 CrossRef PubMed.
- D. I. A. Millar, H. E. Maynard-Casely, D. R. Allan, A. S. Cumming, A. R. Lennie, A. J. Mackay, I. D. H. Oswald, C. C. Tang and C. R. Pulham, CrystEngComm, 2012, 14, 3742 RSC.
- O. Bolton, L. R. Simke, P. F. Pagoria and A. J. Matzger, Cryst. Growth Des., 2012, 12, 4311 CrossRef.
- V. W. Manchot and R. Noll, Justus Liebigs Ann. Chem., 1905, 343, 1 CrossRef.
- M. Zhang, C. Li, H. Q. Gao, W. Fu, Y. Y. Li, L. W. Tang and Z. M. Zhou, J. Mater. Sci., 2016, 51, 10849 CrossRef.
- A. Golius, L. Gorb, A. M. Scott, F. C. Hill and J. Leszczynski, Struct. Chem., 2015, 226, 1281 CrossRef.
- J. T. Wu, J. G. Zhang, T. Li, Z. M. Li and T. L. Zhang, RSC Adv., 2015, 5, 28354 RSC.
- L. Zhang, J. Z. Wu, S. L. Jiang, Y. Yua and J. Chen, Phys. Chem. Chem. Phys., 2016, 18, 26960 RSC.
- P. Y. Chen, L. Zhang, S. G. Zhu and G. B. Cheng, Def. Technol., 2015, 11, 132 CrossRef.
- G. Z. Zhao and X. L. Yan, Quim. Nova, 2017, 40, 1141 Search PubMed.
- G. Z. Zhao, J. F. Jia and H. S. Wu, J. Chem. Sci., 2016, 128, 1223 CrossRef.
- Z. A. Dreger, A. I. Stash, Z. G. Yu, Y. S. Chen, Y. C. Tao and Y. M. Gupta, J. Phys. Chem. C, 2016, 120, 1218 CrossRef.
- H. Gao, P. Du, X. Ke, J. Liu, G. Z. Hao, T. Chen and W. Jiang, Propellants, Explos., Pyrotech., 2017, 42, 889 CrossRef.
- H. Lin, J. F. Chen, S. G. Zhu, H. Z. Li and Y. Huang, J. Energ. Mater., 2017, 35, 95 CrossRef.
- K. Liu, G. Zhang, J. Y. Luan, Z. Q. Chen, P. F. Su and Y. J. Shu, J. Mol. Struct., 2016, 1110, 91 CrossRef.
- Z. B. Zhang, T. Li, L. Yin, X. Yin and J. G. Zhang, RSC Adv., 2016, 6, 76075 RSC.
- Q. Wu, H. Chen, G. L. Xiong, W. H. Zhu and H. M. Xiao, J. Phys. Chem. C, 2015, 119, 16500 CrossRef.
- D. C. Sorescu and B. M. Rice, J. Phys. Chem. C, 2010, 114, 6735 CrossRef.
- Q. M. Hu, S. Lu and R. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 052102 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr.–Cryst. Mater., 2005, 220, 567 Search PubMed.
- Materials Studio 6.0, Accelrys, 2012 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- Z. C. Liu, Q. Wu, W. H. Zhu and H. M. Xiao, RSC Adv., 2015, 5, 34216 RSC.
- Q. Wu, W. H. Zhu and H. M. Xiao, J. Phys. Chem. C, 2013, 117, 16830 CrossRef.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23 CrossRef.
- M. H. Keshavarz, K. Esmailpour, M. Zamani and A. G. Roknabadi, Propellants, Explos., Pyrotech., 2015, 40, 886 CrossRef.
- Q. Yu, Z. X. Wang, B. Wu, H. W. Yang, X. H. Ju, C. X. Lv and G. B. Cheng, J. Mater. Chem. A, 2015, 3, 8156 RSC.
- G. A. Jeffrey, An introduction to hydrogen bonding, Oxford University Press: New York, 1997 Search PubMed.
- N. B. Bolotina, K. Kirschbaum and A. A. Pinkerton, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 577 CrossRef PubMed.
- L. Zhang and J. Chen, personal communication.
- D. E. Hibbs, J. Overgaard and R. O. Piltz, Org. Biomol. Chem., 2003, 1, 1191 RSC.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154 CrossRef.
- E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319 CrossRef.
- M. D. Segall, C. J. Pickard, R. Shah and M. C. Payne, Mol. Phys., 1996, 89, 571 CrossRef.
- M. D. Segall, R. Shah, C. J. Pickard and M. C. Payne, Phys. Rev. B, 1996, 54, 16317 CrossRef.
- B. Winkler, C. J. Pickard, M. D. Segall and V. Milman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 214103 CrossRef.
- P. Bag, M. E. Itkis, D. Stekovic, S. K. Pal, F. S. Tham and R. C. Haddon, J. Am. Chem. Soc., 2015, 137, 10000 CrossRef PubMed.
- M. Konyk, L. Romaka, P. Demchenko, V. V. Romaka, Y. Stadnyk and A. Horyn, J. Alloys Compd., 2014, 589, 200 CrossRef.
- P. V. Hatcher, J. H. Reibenspies, R. C. Haddon, D. W. Li, N. Lopez and X. L. Chi, CrystEngComm, 2015, 17, 4172 RSC.
- J. J. Gilman, Philos. Mag. Lett., 1998, 77, 79 CrossRef.
- S. V. Bondarchuk, Int. J. Quantum Chem., 2017, 117, e25430 CrossRef.
- H. Zhang, F. Cheung, F. Zhao and X. L. Cheng, Int. J. Quantum Chem., 2009, 109, 1547 CrossRef.
- W. H. Zhu and H. M. Xiao, Struct. Chem., 2010, 21, 657 CrossRef.
- F. S. Saoud, J. C. Plenet and M. Henini, J. Alloys Compd., 2015, 619, 812 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra05029e |
| This journal is © The Royal Society of Chemistry 2018 |