Open Access Article
Open Access ArticleInsight into the electronic and thermodynamic properties of NbSi2 from first-principles calculations†
Shuanglun Wang ,
Yong Pan
,
Yong Pan *,
Yuanpeng Wu and
Yuanhua Lin
*,
Yuanpeng Wu and
Yuanhua Lin
School of Materials Science and Engineering, Southwest Petroleum University, Chengdu 610500, China. E-mail: panyong10@mails.jlu.edu.cn; Fax: +86-028-83037406; Tel: +86-028-83037401
First published on 13th August 2018
Abstract
The electronic and thermodynamic properties of NbSi2 with four structures (C40, C11b, C54 and C49) were studied in terms of first-principle calculations. The band structure and density of states of four NbSi2 are calculated. Those disilicides show electronic properties because the band gap between the conduction band and the valence band is near the Fermi level. Their metallic character is mainly due to the strong metallic interaction between the Nb-4d state and Si-3p state. The formed Si–Si covalent bond is mainly concentrated in the valence band. The valence electron configuration of Nb–Si and Si–Si bonds is also explored. Besides, we study the thermodynamic properties of NbSi2 as a function of temperature. The results indicate that the C54 structure has the best thermal stability in the obtained phases. In particular, the Debye temperature and heat capacity of the C54 structure are 547.8 K and 142.7 J mol−1 K−1, respectively. The calculated phonon DOS provides the explanation that the nature of the thermodynamic properties is mainly derived from the vibration of Si atoms.
1. Introduction
Transition metal disilicides (TMSi2) have spurred significant interest because of their high electrical conductivity, thermal stability, excellent high-temperature oxidation resistance, strength, etc.1–5 These properties can be exploited in a variety of applications in the microelectronics industry, such as ohmic contacts, interface diffusion barriers and interconnections.6–8 In addition to these applications, TMSi2 also exhibits great advantages in the field of lithium-ion batteries. For example, a number of transition metal disilicides, such as MoSi2, CrSi2, TiSi2, NiSi2, TaSi2 and VSi2, are used as anode materials or anode coating materials for lithium-ion batteries.9–12Previous studies have reported that there are four typical crystal structures in transition metal disilicides, i.e., hexagonal C11b (space group I4/mmm, no. 139), tetragonal C40 (space group P6222, no. 180), orthorhombic C54 (space group Fddd, no. 70) and orthorhombic C49 (space group Cmcm, no. 63) structures.13–16 MoSi2 and WSi2 have C11b and C40 structures under different temperature, and the differences between C11b structure and C40 structure in performance are great.17,18 CrSi2, TaSi2, NbSi2 and VSi2 are the hexagonal C40 structure while ZrSi2 and HfSi2 have C54 structure.19–22 TiSi2 has the C49 structure and high pressure can result in phase transition from C49 structure to C54 structure.23
Among these transition metal disilicides, NbSi2 is known as the hexagonal C40 structure.24,25 In recent years, the physical properties of hexagonal NbSi2 have been widely investigated.26–29 For example, Xu et al. have studied the electronic, elastic and thermodynamic properties of NbSi2 under high temperature and pressure using first-principle calculations.30 Gottlieb et al. have investigated some transport properties of NbSi2 single crystal.31 Specifically, our recent studies indicated that vacancy can influence the structural and elastic properties of NbSi2.32 In addition, Lasjaunias et al. have shown that the obtained Debye temperature of hexagonal NbSi2 was 579 ± 10 K from low-temperature specific heat measurement.33 As mentioned by Antonov et al., the optical properties of NbSi2 are studied theoretically and experimentally.34 However, the other phases of NbSi2 are rarely studied until now. Hence, we attempt to design three new phases (C11b, C54 and C49) for NbSi2. Importantly, our recent work has indicated these three phases for NbSi2 are stables at the ground state. Unfortunately, the electronic and thermodynamic properties of NbSi2 with these new structures are unknown.
Herein we investigate the electronic and thermodynamic properties of NbSi2 with four crystal structures (C40, C11b, C54 and C49) using the first-principle calculation. Firstly, we compare the energy band structure and density of state of these new phases with that of C40–NbSi2. To better understand the origin of internal bonding, we study the valence electron configuration of Nb–Si bond and Si–Si bond. Then, their thermodynamic properties (including Debye temperature, heat capacity, enthalpy and entropy) are calculated and discussed in detail. Finally, in order to explore the nature of thermodynamic properties of these phases, we also calculate and analyze their phonon DOSs.
2. Models and theoretical methods
Our calculations were carried out within the density function theory (DFT), as implemented in the CASTEP packages.35 The exchange–correlation functions were treated by using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional.36 The valence electronic configurations of Nb and Si atoms were selected as 4p64d45s1 and 3s23p2, respectively. The cutoff energy with plane-wave basis was 450 eV for all structures. The Monkhorst–Pack k-point grids of 17 × 17 × 10, 20 × 20 × 8, 8 × 14 × 8 and 18 × 4 × 18 were chosen for C40, C11b, C54 and C49 structures, respectively. In the process of structural optimization, the energies, maximum ionic displacement and maximum stress were converged within 1 × 10−5 eV per atom, 1 × 10−3 Å and 0.05 GPa, respectively.3. Results and discussion
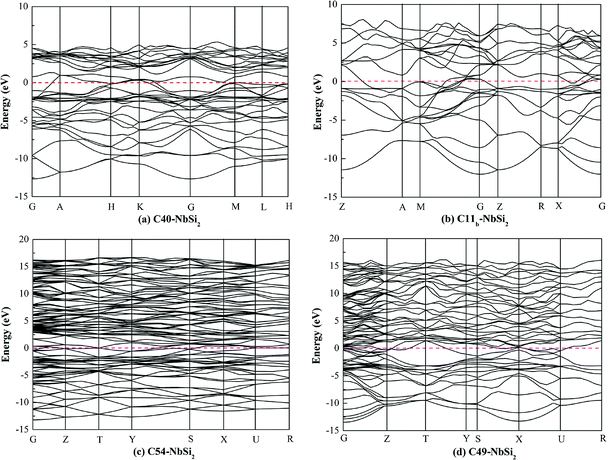
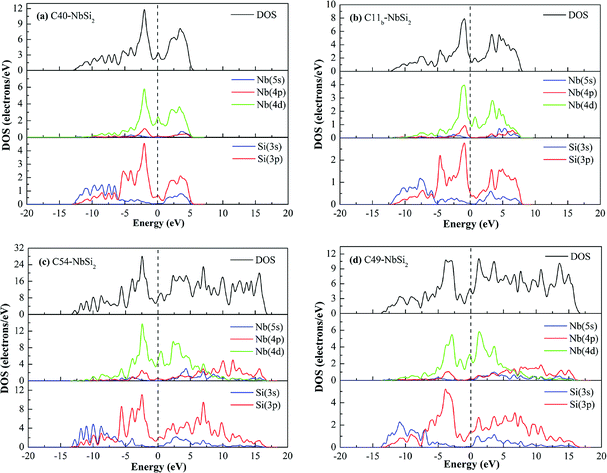
To investigate the electronic properties of NbSi2 with four structures, the calculated band structure along the high symmetric direction within the Brillouin zone have been plotted in Fig. 1. The pink dashed line at zero represents the Fermi level (EF). It is found that the high symmetric direction of C40–NbSi2 is G → A → H→ K → G → M → L → H direction while that of C11b–NbSi2 is Z → A → M → G → Z → R → X → G direction. For orthorhombic C54– and C49–NbSi2, their high symmetric direction is G → Z → T → Y → S → X → U → R. Furthermore, as with C40–NbSi2 (see Fig. 1(a)), although there is no band overlap between the valence band (VB) and the conduction band (CB). In particular, the energy of electrons at the top of the valence band is higher than that of the bottom of the conduction band. Thus, the electron in valence band can enter the conduction band through the Fermi level so as to make C40–NbSi2 exhibit metallic behavior. For the other three structures, there is the band overlap between the valence band and the conduction band, indicating that they have metallic behavior. Compared with C40–NbSi2, we can see that the predicted three phases exhibit the better electronic properties.To gain more insight into the origin of electronic properties of various NbSi2 phases, the total and partial density of states (DOSs) are calculated and displayed in Fig. 2. It is clearly observed that the total DOS of four structures at the Fermi level are positive, indicating that they exhibit metallic behavior in their crystal phases. Furthermore, we find that the DOS of these phases are characterized by a small peak close to the Fermi level. The hybridized orbital of this peak are composed of Nb-4d and Si-3p orbital. This is to say, there is the formation of Nb–Si bond at the Fermi level. Hence, we can conclude that their metallic behavior may be attributed to the strong metallic interaction between Nb atom and Si atom. Moreover, the existence of a pseudogap, i.e., a deep valley through the Fermi level, differentiates the bonding state from the anti-bonding/non-bonding state.37
In the valence band zone, we can see that the DOS of C40–, C11b– and C54–NbSi2 located from about −5–0 eV mainly come from Nb-4d and Si-3p orbital. Moreover, the hybridized orbital in the range from about −13 eV to −5 eV is mainly composed of Si-3s and Si-3p orbital, which will drive the formation of Si–Si covalent bond. However, for C49–NbSi2, its DOS in the valence band zone is almost made up of Nb-4d and Si-3p orbitals. Furthermore, the significant hybridization peak below the Fermi level in the DOS of these phases manifests that the strong chemical bond is formed between Nb atoms and Si atoms. The Mulliken population can reflect the bond strength to some extent.38 Hence, in this article, the calculated bond lengths of Nb–Si bond with the largest Mulliken population are 2.743 Å, 2.706 Å, 2.689 Å and 2.577 Å for C40–, C11b–, C54– and C49–NbSi2, respectively. The calculated bond length of Nb–Si bond in C40–NbSi2 is in good agreement with experimental data (2.770 Å).33 This result also reflects that the electronic properties of these predicted phases better than C40–NbSi2. As mentioned above, we conclude that the electronic properties of various NbSi2 phases are mainly derived from Nb–Si metallic bond, and Si–Si covalent bond makes a little contribution to their electronic properties.
Previous studies have shown that there are Nb–Si and Si–Si bonds in C40–NbSi2 phases.24,29,38 To further reveal the nature of these bonds in various NbSi2, Fig. 3 depicts the valence electron configuration for Si–Si and Nb–Si bonds, and the bond with an asterisk exhibits anti-bonding behavior. From Fig. 3(a), it is clearly found that a electron of Si-3s orbital jump to Si-3p orbital, producing four hybridized orbitals, which forms the normal tetrahedron sp3 hybridization. This sp3 hybridization can be called σsp bond. The interaction between Si-3p orbitals can form π3p bond. However, the interaction between Nb and Si atoms, i.e., the overlap between sp and d orbital, is very complicated. Here, we simplify their bonding model and just predict that the possible bonding styles. We can see from Fig. 3(b) that the bonding and antibonding orbitals are formed between the hybridized orbitals of Si atom and the atomic orbital of Nb atom. Besides, there is non-bonding orbital in the atomic orbital on Nb atom. Therefore, we suggest that the structural stability of various NbSi2 phases is mainly attributed to the Nb–Si bond and Si–Si covalent bond.
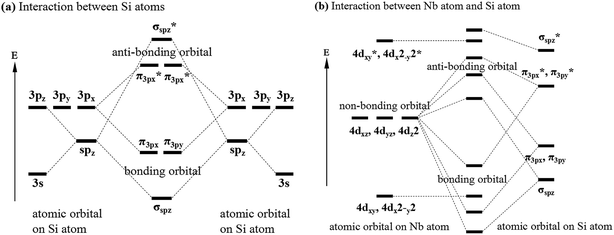 | ||
| Fig. 3 Valence electron configuration for (a) interaction between Si atoms and (b) interaction between Nb atom and Si atom. | ||
Furthermore, both sp and d orbital can carry the electronic current in NbSi2 with the overlap between them. To our knowledge, the conductivity of each orbital is a proportional to the velocity of electron on the corresponding orbital at the Fermi level. Hence, the sp orbitals composed of s and p orbital are expected to carry larger current than d orbitals characterized by a lower electron velocity. Besides, the effective mass of sp orbital is higher than d orbital in NbSi2 phase. As mentioned above, it is essential to take the valence electron configuration into account for analyzing the calculated electronic properties of NbSi2 phases in the present study.
3.1 Thermodynamic properties
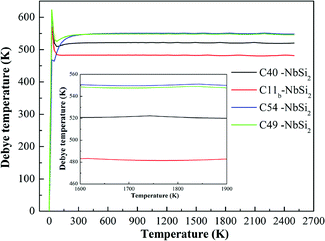
To examine the thermodynamic properties of various NbSi2 phases, the quasiharmonic Debye model at finite temperature is used.39 In this quasiharmonic Debye model, the Gibbs function (G) is obtained by G(V, P, T) = E(V)+ PV + FVib(θ(V), T), where E(V) represents the total energy of NbSi2 per unit cell and can be calculated by density function theory (DFT). θ(V) is the Debye temperature and FVib indicates the vibrational Helmholtz free energy.Fig. 4 displays the calculated the Debye temperature (θD) as a function of temperature (0–2500 K). As is well-known, the higher Debye temperature of a material, the stronger interactions between atoms. From Fig. 4, it is observed that the calculated Debye temperature of various NbSi2 increases sharply at low-temperature. We suggest this phenomenon may be due to the fact that the vibration of atoms in crystals is very sensitive to temperature under low-temperature. Furthermore, the Debye temperature of various NbSi2 tends to be a constant to some degree under high-temperature. The calculated Debye temperature of C40–NbSi2 is 522 K, which is slightly lower than previous experimental result.33 The order of obtained Debye temperature for these structures is: C54 > C49 > C40 > C11b. The calculated Debye temperature of C54 structure is about 548 K. It is worth mentioned that the Debye temperature of C54 and C49 structures is very similar. We can conclude that C54–NbSi2 exhibits the best thermal stability among considered structures.
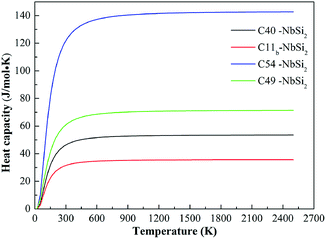
In addition to the Debye temperature, the calculated isochoric heat capacity (Cv) curves of various NbSi2 are illustrated in Fig. 5. It is observed clearly that the Cv of NbSi2 with four structures is a proportional to T3 at temperature close to 0 K and then retains a constant when the temperature increases above 500 K. This trend satisfies the Dulong–Petit limit40 (Cv = 3nR, where n represents the number of atoms per unit cell). The obtained Cv constants of C40, C11b, C54 and C49 structures are 53.54 J mol−1 K−1, 35.70 J mol−1 K−1, 142.73 J mol−1 K−1 and 71.37 J mol−1 K−1, respectively. In particular, the calculated Cv value of C40–NbSi2 is in good consistent with previous theoretical value (52.21 J mol−1 K−1 at 300 K).30 We suggest the discrepancies are attributed to the fact that the different structural characteristics affect the vibration of internal atoms under high-temperature. Importantly, C54–NbSi2 possesses the largest Cv value in comparison to other phases, implying it exhibits best thermal stability in our considered structures. However, the Cv value of C11b structure is smallest among all phases. As mentioned above, C54 structure is expected to a new phase for NbSi2 used as electronic material in future high-temperature application.
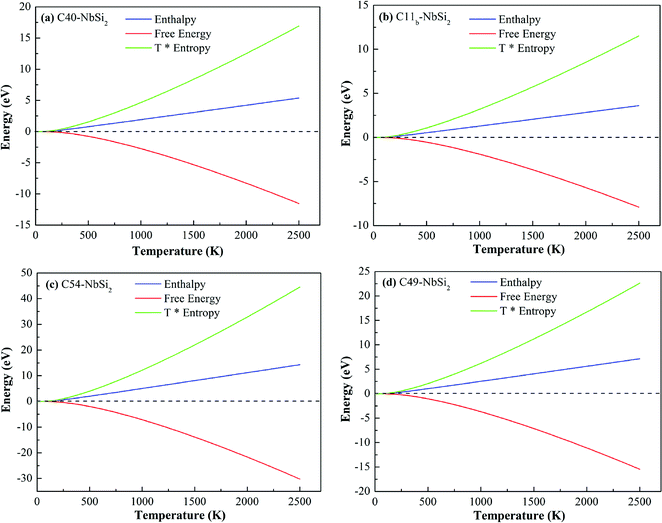
Fig. 6 depicts the other thermodynamic functions of various NbSi2 phases, i.e., enthalpy (H), entropy (S) and free energy. Enthalpy of a material can be calculated by H = F + TS. From Fig. 6, we can find that the thermal electronic contributions (TEC) can significantly influence enthalpy and entropy. For four NbSi2 phases, H exhibits an approximately linear relationship with the temperature (>300 K), and their average slopes of C40, C11b, C54 and C49 structures are 0.22 kJ mol−1 K−1, 0.14 kJ mol−1 K−1, 0.60 kJ mol−1 K−1 and 0.30 kJ mol−1 K−1. The result also confirms the analysis of heat capacity.
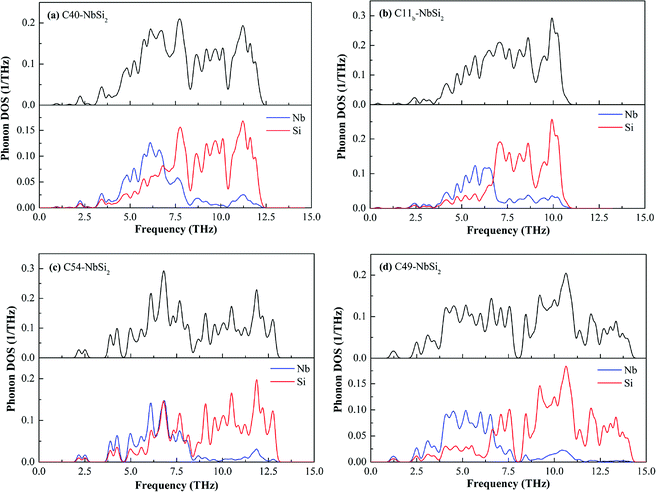
To deeper understand the mechanism of dynamic stability, we carefully calculated the full and partial phonon density of state (DOS) of various NbSi2 phases, the results are shown in Fig. 7. It is observed that various NbSi2 are mechanically stable due to there is no negative frequency. With the increase of temperature, the vibration of atoms intensifies. Therefore, it can be seen clearly from Fig. 7 that the low frequency zone (below about 7.0 THz−1) mainly composed of the vibration of Nb atom, indicating that the structural stability of various NbSi2 under low-temperature are determined by the Nb atoms. However, the high frequency zone (about 7.0–15.0 THz−1) is almost all made up of the vibration of Si atoms. Hence, the structural stability of various NbSi2 under high-temperature is dominated by the Nb–Si bond and Si–Si covalent bond. It is worth pointing out that the vibration of Nb atoms is almost identical to that of Si atoms with the range from 6.30–8.50 THz−1 in Phonon DOS of C54–NbSi2 (see Fig. 7(c)), which indicates the structural stability in this range are caused of Nb–Si bond.
4. Conclusion
In summary, on the basis of density function theory (DFT), the electronic and thermodynamic properties of various NbSi2 are systematically investigated. Firstly, the analyses of band structure and density of states show that NbSi2 with four structures exhibits metallic behavior, which is mainly derived from the Nb–Si metallic bond and some Si–Si covalent bonding in these phases. The three new phases exhibit better electronic properties in comparison to C40–NbSi2. Based on the molecular hybridization theory, we also explore the mechanism of Si–Si and Nb–Si bonds using the valence electron configuration. Furthermore, it is found that the sp orbital composed of s and p orbitals are expected to carry more current than the d orbital. Finally, we calculate the thermodynamic properties of these phases, including Debye temperature, heat capacity, enthalpy and entropy. The calculated Debye temperature and heat capacity of C54–NbSi2 are 547.8 K and 142.7 J mol−1 K−1 under high-temperature, respectively, which indicate C54–NbSi2 exhibits better thermal stability than the other three phases. The thermal stability of C11b–NbSi2 is the worst in the considered phases.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the State Key Laboratory of Advanced Technology for Comprehensive Utilization of Platinum Metals (Grant No. SKL-SPM-201816) and Innovative Research Team of Southwest Petroleum University (Grant No. 2017CXTD01) and Sichuan Provincial Colleges' State Key Laboratory of Oil and Gas Reservoir Project (X151517KCL36).References
- F. Nava, E. Mazzega and M. Michelini, J. Appl. Phys., 1989, 65, 1584–1590 CrossRef.
- Y. Pan, Y. Lin, Q. Xue, C. Ren and H. Wang, Mater. Des., 2016, 89, 676–683 CrossRef.
- R. Hao, X. Y. Zhang, J. Q. Qin, S. H. Zhang, J. L. Ning, N. Sun, M. Z. Ma and R. P. Liu, RSC Adv., 2015, 5, 36779–36786 RSC.
- Y. Pan, Y. Lin, H. Wang and C. Zhang, Mater. Des., 2015, 86, 259–265 CrossRef.
- Y. Pan, W. M. Guan and Y. Q. Li, Phys. Chem. Chem. Phys., 2018, 20, 15863–15870 RSC.
- A. Anani and R. A. Huggins, J. Power Sources, 1992, 38, 351–362 CrossRef.
- O. P. Balkashin, A. G. M. Jansen, U. Gottlieb, O. Laborde and R. Madar, Solid State Commun., 1996, 100, 293–296 CrossRef.
- Y. Nakamura, S. Amari, N. Naruse, Y. Mera, K. Maeda and M. Lchikawa, Cryst. Growth Des., 2008, 8, 3019–3023 CrossRef.
- F. Nava, K. N. Tu, O. Thomas, J. P. Senateur, R. Madar, A. Borghesi, G. Guizzetti, U. Gottlieb, O. Laborde and O. Bisi, Mater. Sci. Rep., 1993, 4–5, 141–200 CrossRef.
- F. M. Courtel, D. Duguay, Y. Abu-Lebdeh and I. J. Davidson, J. Power Sources, 2012, 202, 269–275 CrossRef.
- Y. Pan, Int. J. Hydrogen Energy, 2018, 43, 3087–3091 CrossRef.
- M. S. Shin, T. W. Lee, J. B. Park, S. H. Lim and S. M. Lee, J. Power Sources, 2017, 344, 152–159 CrossRef.
- Y. Pan and W. M. Guan, Phys. Chem. Chem. Phys., 2017, 19, 19427–19433 RSC.
- K. Hagihara, H. Araki, T. Ikenish and T. Nakano, Acta Mater., 2016, 107, 196–212 CrossRef.
- K. Tanaka, K. Nawata, H. Inui, M. Yanmaguchi and M. Koiwa, Intermetallics, 2001, 9, 603–607 CrossRef.
- Y. Pan, S. Wang, X. Zhang and L. Jia, Ceram. Int., 2018, 44, 1744–1750 CrossRef.
- X. Zhang, Z. Wang and Y. Qiao, Acta Mater., 2011, 59, 5584–5592 CrossRef.
- L. G. Briquet and P. Philipp, J. Alloys Compd., 2013, 553, 93–98 CrossRef.
- L. F. Mattheiss, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 3252 CrossRef.
- X. Chen, J. C. Guan, G. Y. Sha, Z. M. Gao, C. T. Williams and C. H. Liang, RSC Adv., 2014, 4, 653–659 RSC.
- B. Wan, F. Xiao, Y. Zhang, Y. Zhao, L. Wu, J. Zhang and H. Gou, J. Alloys Compd., 2016, 681, 412–420 CrossRef.
- Y. Imai, M. Mukaida and T. Tsunoda, Intermetallics, 2000, 8, 381–390 CrossRef.
- J. A. Kittl, D. A. Prinslow, P. P. Apte and M. F. Pas, Appl. Phys. Lett., 1995, 67, 2308–2310 CrossRef.
- Y. Pan, P. Mao, H. Jiang, Y. Wan and W. Guan, Ceram. Int., 2017, 43, 5274–5282 CrossRef.
- Y. Umakoshi, T. Nakano, E. Yanagisawa, T. Takezoe and A. Negishi, Mater. Sci. Eng., A, 1997, 239, 102–108 CrossRef.
- T. Nakano and K. Hagihara, Scr. Mater., 2013, 68, 313–316 CrossRef.
- Y. J. Choi, J. K. Yoon, G. H. Kim, W. Y. Yoon and J. M. Doh, Corros. Sci., 2017, 129, 102–114 CrossRef.
- Y. Pan, Adv. Eng. Mater., 2017, 19, 1700099 CrossRef.
- I. Papadimitriou, C. Utton, A. Scott and P. Tsakiropoulos, Intermetallics, 2014, 54, 125–132 CrossRef.
- N. Xu, Y. Xu and J. Ma, Mater. Sci. Semicond. Process., 2015, 30, 636–644 CrossRef.
- U. Gottlieb, O. Laborde, O. Thomas, A. Rouault, J. P. Senateur and R. Madar, Appl. Surf. Sci., 1991, 53, 247–253 CrossRef.
- Y. Pan, J. Zhang, C. Jin and X. Chen, Mater. Des., 2016, 108, 13–18 CrossRef.
- J. C. Lasjaunias, O. Laborde, U. Gottlieb, R. Madar and O. Thomas, J. Low Temp. Phys., 1993, 92, 335–351 CrossRef.
- V. N. Antonov, B. Yu. Yavorsky and A. P. Shpak, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 15631–15637 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- Y. Pan and B. Zhou, Ceram. Int., 2017, 43, 8763–8768 CrossRef.
- Y. Pan, Mater. Res. Bull., 2017, 93, 56–62 CrossRef.
- Y. Pan, P. Wang and C. Zhang, Ceram. Int., 2018, 44, 12357–12362 CrossRef.
- M. A. Blanco, E. Francisco and V. Luana, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04959a |
| This journal is © The Royal Society of Chemistry 2018 |