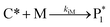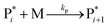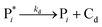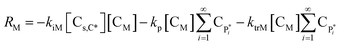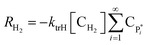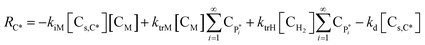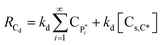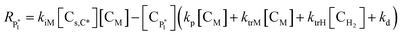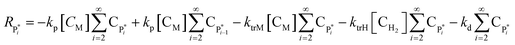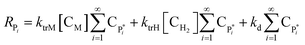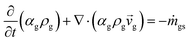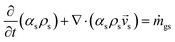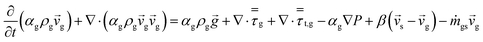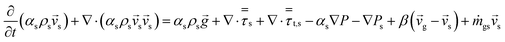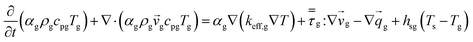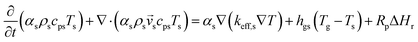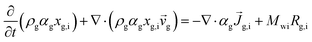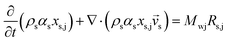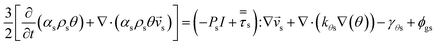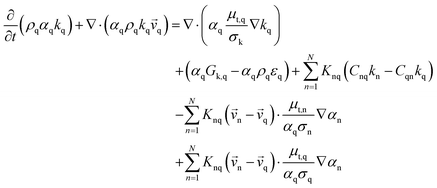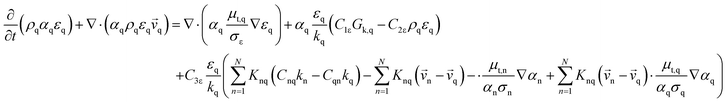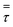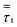Open Access Article
Open Access ArticleHeat transfer effect in scaling-up a fluidized bed reactor for propylene polymerization
Panut Bumphenkiattikulabc,
Sunun Limtrakul *abc,
Terdthai Vatanathamabc,
Parinya Khongpromd and
Palghat A. Ramachandrane
*abc,
Terdthai Vatanathamabc,
Parinya Khongpromd and
Palghat A. Ramachandrane
aDepartment of Chemical Engineering, Faculty of Engineering, Kasetsart University, Bangkok 10900, Thailand. E-mail: fengsul@ku.ac.th
bCenter of Excellence on Petrochemical and Materials Technology, Department of Chemical Engineering, Faculty of Engineering, Kasetsart University, Bangkok 10900, Thailand
cCenter for Advanced Studies in Industrial Technology, Faculty of Engineering, Kasetsart University, Bangkok 10900, Thailand
dDepartment of Industrial Chemistry, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok 10800, Thailand
eDepartment of Energy, Environmental & Chemical Engineering, Washington University, St. Louis, USA
First published on 7th August 2018
Abstract
The effects of operating conditions and scaling-up on reactor temperature control and performance in propylene polymerization fluidized bed reactors were studied by phenomenological and CFD models. A phenomenological model with CFD hydrodynamics parameters predicts average information, while a CFD-based reactor model provides local information. Results suggest improved productivity and reactor temperature control by cautiously increasing catalyst feed rate, operating temperature, reactor size and superficial velocity, with consideration of hot spots and catalyst deactivation. High catalyst loading increases productivity but involves risk with regards to the control of oscillating temperature and hot spots. The model identifies an operating window to improve productivity and temperature control and to study operation details. Mixing effect is important to heat transfer but not to propylene conversion. Scaling-up cannot provide similarity of heat transfer. Keeping the same temperature when scaling up from 0.2 to 4 m in diameter requires heat transfer area multiplying factors of 2.43 to 5.26 or lowering the wall temperature by 7 to 18 K. Hot spots are detected with a temperature variation of 10 to 14 K. The results are useful for analyses of laboratory and industrial scale reactors and provide information on scale up.
1. Introduction
Polypropylene (PP) polymerization is usually operated in either three-phase slurry or gas fluidized reactors.1 A slurry mode of operation provides good temperature control due to the liquid solvent being able to provide good heat transfer. However, by the nature of high viscosity of the slurry, the solid content has to be limited. Moreover, an additional evaporation unit is needed. In contrast, a gas-phase polypropylene polymerization fluidized bed is more attractive due to the fact that it can be operated with a high solid loading, requires neither drying nor separation of polymers from solvents and has relatively low environmental impact.2,3 Nevertheless, heat transfer in a gas-phase fluidized bed is limited, especially in a high-solid-loading mode of operation, due to highly exothermic polymerization and poor heat transfer in the gas phase of the system. Thus, the bed temperature is difficult to control. The temperature of the polymer particles tends to rise, leading to particle overheating, sintering, catalyst deactivation, and loss of control over polymer product properties, including particle morphology. Polymer particles can melt and stick together to form bigger particles or fuse into a sheet or large chunk because the temperature in the reactor is greater than the melting point of the polymer. The fluidized bed operation can then approach a de-fluidized regime. A PP industrial fluidized bed reactor needs to shut down for clearing plastic chunks accumulated in the reactor over time. Thus temperature control is of primary concern to the overall reactor performance. The major challenges in this present work are to achieve faster reactions and higher production of PP with appropriate catalyst feed rate while retaining product quality and overcoming the heat transfer limitations. In addition, the problem of heat transfer limitation in reactor scaling up has to be focused on.Models for fluidized bed reactors with reasonable simplifications are useful for this challenge. Two modeling approaches—phenomenological model and computational fluid dynamic based model—can be used for modeling the polymerization reactor. A phenomenological model is capable of predicting overall performance, i.e., monomer concentration, polymer production rate, bed temperature, molecular weight in a polymerization reactor as an averaged solution with reasonably computational time. However, the spatial variation of reactor performance cannot be obtained. Fortunately, the conversion of this reaction is in a low range, e.g., less than 10%.3–5 This model, based on average bed phenomena, can thus sufficiently estimate the operating variables. However, the high degree of heat released from the exothermic polymerization reaction can cause a non-uniform temperature distribution, leading to hotspot generation. CFD-based reactor analysis is able to provide necessary information on the spatial distributions of phase movements and local temperature distribution.
Species balance of multiple components, heat transfer for both phases, and method of moments, can be used for predicting reactor performance by considering the hydrodynamic and transport parameters, which may be treated as constant values for simplicity. Several researchers5–10 have applied a well-mixed model for polypropylene production. In the literature, the hydrodynamic parameters such as bed expansion and solid holdup were mainly obtained from the correlations based on Geldart A. Polymerization is usually carried out in a wide range of particle sizes, ranged from Geldart A to Geldart B. In addition, the reactor is operated at high temperature and pressure. The available correlations are usually based on cold models and in the regime of Geldart A. Thus the hydrodynamic parameters should be modified such that they better approximate real operating conditions. Hydrodynamics based on hot models obtained by CFD are required so as to obtain key parameters for accurate prediction of heat and mass transfer in a fluidized bed reactor.
Phenomenological models cannot provide local variation of temperature in the reactor, which is useful for monitoring hotspots and the possibility of polymer melting. CFD-based reactor analysis can capture local behavior of gas–solid in a fluidized bed reactor. The temperature distribution can be clearly explored by this model. An Eulerian–Eulerian approach to CFD has been successful to describe the hydrodynamics of gas–solid systems.11–13 Xu et al. (2012)14 and Yao et al. (2014)15 applied CFD to polypropylene in a fluidized bed reactor. Li et al. (2016)16 used a computational fluid dynamics-discrete element model for studying temperature variation in fluidized beds. In their work, a constant heat source was added into the energy balance equation for the solid phase so as to mimic the propylene polymerization reaction heat. Temperature distribution and hotspots occurrence were found. The extension of Li et al.'s work considered here includes species balance for polymerization for non-uniformity of heat effect.
Combining the momentum, energy and species balances in the CFD models with the complex kinetic polymerization model as well as the method of moments can provide the distributions of solid holdup, temperature, polymerization conversion and polymer molecular weight. Although a CFD approach is useful to improve our understanding of this polymerization, it has a limitation in term of simulation time. Therefore, in this work, the limitation will be avoided by seperating the simulation into two levels of study. At the first level, a phenomenological model will be used to predict the overall performance in terms of monomer concentration, polymer production rate, bed temperature, and molecular weight in the polymerization reactor as an averaged solution. Subsequently, the solution obtained from the phenomenological model is used to provide the starting conditions for a CFD model. So as to get more detailed understanding, CFD will be used to provide additional information on local distributions of studied variables as well as hotspots in the fluidized bed reactor.
A heat transfer limitation problem can occur during reactor scaling up from a laboratory scale to industrial scale. To keep hydrodynamic similarity, Glicksman17,18 proposed a set of non-dimensional parameters by non-dimensionalizing the governing equations of motion for the fluids and the solids in a fluidized bed. In addition, similarity in weight space time should be a criterion in order to have reactor performance similarity. These two criteria of similarities were used in the scaling-up work.
The aim of this work is to develop models at two levels and point out the utility of such an approach for carrying out simulations of a fluidized bed reactor for propylene polymerization. To improve productivity and change product properties, the operating variables studied are catalyst feed rate, operating temperature, hydrogen feed, reactor size and superficial velocity, and the sensitivity to operation window will be examined. In addition, local distributions of phase movements and local temperature distribution will be also studied in order to avoid polymer overheating, hot spots and possibility of polymer melting. The combination model presented in this work is unique and will be useful for improving the understanding of propylene polymerization in fluidized bed reactors and analysis both of a laboratory reactor and industrial reactor.
2. Mathematical model
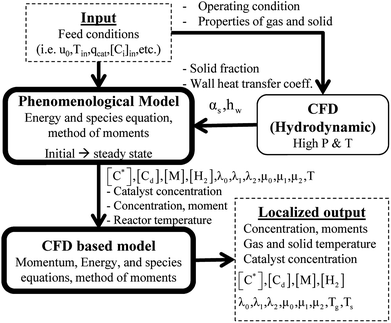
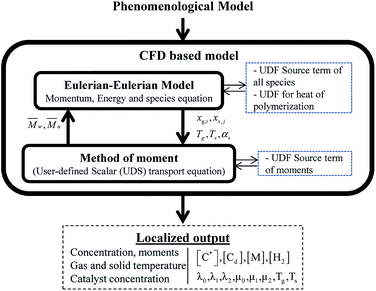
Two models—a phenomenological model and a CFD-based model—are developed in this work. The phenomenological model is capable of predicting average monomer concentration, polymer production rate, bed temperature, and molecular weight in a polymerization reactor as an averaged solution. Meanwhile the CFD-based model is able to provide the local distributions of phase movements and the local temperature distribution. CFD simulation has a limitation in term of simulation time. Therefore, in this work, the phenomenological model is used to provide starting conditions for the CFD based model, as shown in Fig. 1. The phenomenological model is based on a well-mixed model which consists of energy balance, species balance for gas and solid phases and moment equations. The solid holdup and heat transfer parameters in this model were obtained from CFD hydrodynamic simulation based on high temperature and pressure conditions (see Fig. 1). The solutions for concentration of each species, concentration of catalyst, moments, and reactor temperature obtained from the phenomenological model were used to initialize the CFD-based model for local parameters studies.2.1 Phenomenological model
The fluidized bed reactor in this work is operated with a continuous feed of gas and solid catalyst. In the simulation, the product removal rate is accounted for, and the reactor performance is monitored as a function of time. The gas and solid flows are assumed to be those of a well-mixed continuous reactor. Heat and mass transfer between bubble and emulsion phase are fast and also relatively unimportant since almost pure propylene is used as a feed. Hence the difference of monomer concentrations in the bubble and emulsion are expected to be quite small. The volume fraction of solid, temperature and concentrations of gas and solid are treated as uniform in the reactor, with each value represented as its average. However, they vary with operation time.The solid holdup in the reactor is a significant factor in the definition of reactor performance and is usually obtained from available correlations.19,20 Available correlations are not suitable for a fluidized bed reactor operated in severe conditions. The solid holdup obtained for high temperature and pressure in this work is obtained from the CFD hydrodynamic model to supersede the usual cold model correlations.
A transient mass balance for gas and solid phases based on a well-mixed model for each species then can be shown as follows.
The gas phase species balance is written as the terms of convection, accumulation, and reaction:
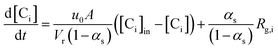 | (1) |
The unsteady-state species conservation equation for the solid phase:
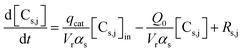 | (2) |
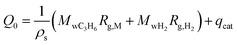 | (3) |
An energy balance based on a pseudo-homogeneous phase is used to predict the temperature of the reactor. In the system, heat is mainly generated from propagation. The unsteady-state energy equation is as follows:
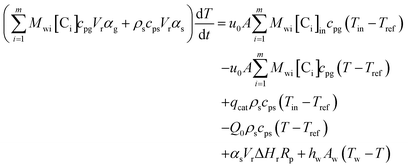 | (4) |
The local bed-to-wall heat transfer coefficient was calculated from the following equation:
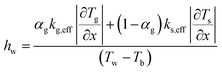 | (5) |
The temperature gradient and phase holdups in eqn (5) were calculated in each computational node in the computational domain using CFD model.
The effective thermal conductivity, keff, consists of molecular and turbulent thermal conductivities.24 The latter is derived using the analogy between heat and momentum transfer. Therefore, the effective thermal conductivity can be written as:
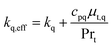 | (6) |
The turbulent viscosity of phase q, μt,q, is obtained from solving the conservation of turbulent kinetic energy and turbulent dissipation in CFD hydrodynamic and KTGF models as mentioned in Section 2.4.
2.2 Kinetic rate
The mechanism of propylene polymerization in gas and solid phases is shown in Table 1. It consists of the steps of initiation, propagation, chain transfers, site transformation and deactivation.25 Active catalyst in the solid phase reacts with propylene monomer to form an active monomer. Then, the active monomer reacts repeatedly with propylene to form active dimers and continues to form longer polymer chains. Propagation of active polypropylene with monomer to form longer active polymer chain then proceeds. Finally, the active polymer terminates and becomes a dead polymer chain in either of two mechanisms: chain transfer or termination. The kinetic rate constants for each reaction rate is defined as a function of temperature as Arrhenius' law, with frequency factors and activation energy in terms of a one-site kinetic model, as presented in Table 1.26–28The propagation and deactivation steps are essential steps to define activity of catalysts and productivity. Previously, Zacca and coworkers27 have used a one-site model in good agreement with the experimental data of Drusco and Rinaldi.29 Only small differences between a one-site and a two-site model in terms of overall yield and productivities in polypropylene reactor were found. One site of catalyst was good enough for evaluating the overall yield, productivities and averaged molecular weight, which is our main objective here. Likewise a single lumped model of the reaction rate is adequate for the purpose of this work, giving a reasonable calculation time. The rate constants for this polymerization at 69 °C are obtained from literatures,27,28 and the activation energy is obtained from Boor.26 The frequency factor and activation energy for this polymerization are shown in Table 1. The reaction rate expressions can be written as shown in eqn (7)–(13) in Table 2.where [CM] is the concentration of monomer (kmol m−3), [Cs,C*] the molar concentration of active catalyst (kmol m−3), 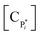 the molar concentration of active polymer of length i (kmol m−3), [CH2]the concentration of hydrogen (kmol m−3), i the degree of polymerization,
the molar concentration of active polymer of length i (kmol m−3), [CH2]the concentration of hydrogen (kmol m−3), i the degree of polymerization, 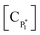 the molar concentration of active polymer of length 1 or active monomer (kmol m−3), and [CPi] the molar concentration of dead polymer of length i (kmol m−3).
the molar concentration of active polymer of length 1 or active monomer (kmol m−3), and [CPi] the molar concentration of dead polymer of length i (kmol m−3).
2.3 Method of moments
A method of moments permits one to solve for moments of chain length distribution with relatively small computational effort. Average chain length can then be easily calculated from the moments and is used for predicting average molecular weight.5,9,30 Eqn (7)–(13) give the reaction rates based on chain length, which can then be modified into the form of moments by applying the method of moments.31–33 The zeroth moments of active polymer and dead polymer can be defined as the summation of active and dead polymer, as shown in eqn (14):
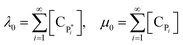 | (14) |
| RM = −kiM[Cs,C*][CM] − (kp + ktrM)[CM]λ0 | (15) |
| RH2 = −ktrH[CH2]λ0 | (16) |
| RC* = −kiM[Cs,C*][CM] + ktrM[CM]λ0 + ktrH[CH2]λ0 − kd[CC*] | (17) |
| RCs,d = kdλ0 + kd[Cs,C*] | (18) |
| Rλ0 = kiM[Cs,C*][CM] − λ0(ktrM[CM] + ktrH[CH2] + kd) | (19) |
| Rμ0 = λ0(ktrM[CM] + ktrH[CH2] + kd) | (20) |
Solving the equations of mass balances, eqn (15)–(20), combined with the kinetic rates in Table 1, the solutions of concentrations of monomer (CM) and hydrogen (CH2) in gas phase, concentrations of active (Cs,C*) and dead (Cs,Cd) catalyst can be obtained. In addition, the moments—i.e. zero, first and second moments—of active polymer (λ0,λ1,λ2) and the same of dead polymer (μ0,μ1,μ2) can be calculated using a moment balance:
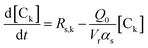 | (21) |
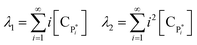 | (22) |
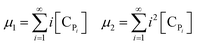 | (23) |
The rate of reaction for higher moments can be written as in eqn (24)–(27):
| Rλ1 = kiM[Cs,C*][CM] − λ1 (ktrM[CM] + ktrH[CH2] + kd) + kp[CM]λ0 | (24) |
| Rλ2 = kiM[Cs,C*][CM] − λ2(ktrM[CM] + ktrH[CH2] + kd) + kp[CM](2λ1 + λ0) | (25) |
| Rμ1 = λ1(ktrM[CM] + ktrH[CH2] + kd | (26) |
| Rμ2 = λ2(ktrM[CM] + ktrH[CH2] + kd | (27) |
Ultimately, using the following equation, the number and weight average molecular weight (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n,
n,![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w) are determined:30
w) are determined:30
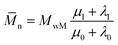 | (28) |
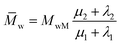 | (29) |
2.4 Mathematical model based on CFD
Gas–solid propylene polymerization in a fluidized bed reactor was investigated using a CFD approach for local information prediction. The mathematical models in the overall CFD approach based on conservation for mass, momentum, energy, and species are summarized in Table 3. The interphase momentum transfer coefficient is obtained from Gidaspow's correlations.34 The corresponding shear stress for solid phase is estimated from the kinetic theory of granular flow (KTGF). Granular temperature is proportional to the kinetic energy of the random motion of the particles. The granular temperature transport equations for solid phase is provided by Ding and Gidaspow13 as shown in Table 3. Assuming that the granular energy is in steady state and dissipated locally, the convection and diffusion were neglected. Chen35 and coworker has indicated that the results show no significant differences in using this simplification. The granular temperature transport equation can be simplified to an algebraic equation. The closure transport coefficients for solving granular temperature transport equation are listed in Table 4. The Reynold stress related to turbulent viscosity is estimated from the standard k–ε turbulent model. The turbulent kinetic energy, k, and the turbulent dissipation rate, ε, for phase q are obtained by solving eqn (40) and (41) in Table 3. The solutions of turbulent kinetic energy and turbulent dissipation rate of phase q were used to calculate turbulent viscosity as
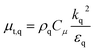 | (30) |
| Constitutive equations |
|---|
| Solid pressure38 |
| Ps = αsρsθ + 2g0αs2ρsθ(1 + e) |
| Radial distribution function39 |
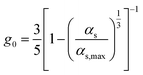 |
| Solid bulk viscosity39 |
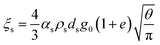 |
| Solid shear viscosity34 |
| μs = μs,collision + μs,kinetic + μs,friction |
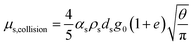 |
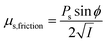 |
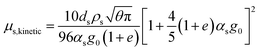 |
| Diffusion coefficient for granular temperature34 |
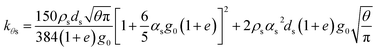 |
| Collisional dissipation of solid fluctuating kinetic energy39 |
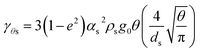 |
| Energy exchange between gas and solid34 |
| ϕgs = −3βθ |
| Interphase momentum transfer coefficient34 |
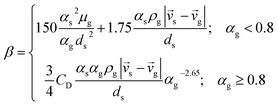 |
| Interphase heat transfer coefficient37 |
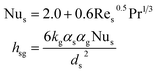 |
| Stress tensor |
| Gas phase |
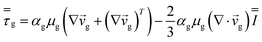 |
| Solid phase |
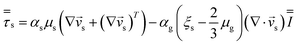 |
| Reynolds stress |
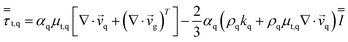 |
2.5 Simulation conditions
In this work, a fluidized bed reactor used for polymerization of propylene is continuously fed with propylene, nitrogen and hydrogen at the bottom of the fluidized bed. Hydrogen is a terminator. Solid catalyst particles with a size of 500 microns are also fed continuously at the bottom of the reactor. Polymer product is removed from the bottom of reactor to maintain the level of the bed.Here a fluidized bed reactor of height 8 m and 2 m in diameter is used in a 2D CFD approach in order to reduce simulation time. The feed and reactor conditions are shown in Table 5. The effects of key process parameters including those of feed catalyst rate, temperature, gas velocity, hydrogen concentration are studied as shown in Table 6.
| Value | |
|---|---|
| Gas phase | |
| Concentration of each species in feed gas mixture | |
| - Propylene (kmol m−3) | 1.267 |
| - Hydrogen (kmol m−3) | 0.01–0.03 |
| - Nitrogen (kmol m−3) | 0.056 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Solid phase | |
| Density, ρs (kg m−3) | 910 |
| Diameter, ds (μm) | 500 |
| Mass fraction of each specie in solid catalyst | |
| - Active catalyst | 0.008 |
| - Non-active catalyst | 0.992 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Operating conditions | |
| Pressure, (bar) | 25 |
| Simulation case | u0/umf | Solid loading (kg) | Reactor temperature (K) | Catalyst feed (mg s−1) | Hydrogen feed concentration (kmol m−3) |
|---|---|---|---|---|---|
| Effect of superficial gas velocity | 1.5 | 2333 | 330 | 18.3 | 0.02 |
| 2.25 | 3500 | 27.5 | |||
| 3 | 4666 | 36.7 | |||
| Effect of feed and wall temperature | 2.25 | 3500 | 325 | 27.5 | 0.02 |
| 330 | |||||
| 335 | |||||
| Effect of catalyst feed | 2.25 | 3500 | 330 | 19.2 | 0.02 |
| 27.5 | |||||
| 35.8 | |||||
| Effect of hydrogen feed concentration | 2.25 | 3500 | 330 | 27.5 | 0.01 |
| 0.02 | |||||
| 0.03 |
2.6 Scaling up
Scale-up of fluidized bed reactors is an attractive challenge. It can be carried out with appropriate criteria so as to obtain similarities in hydrodynamic and reactor performance. The traditional approach focuses on finding scaling laws for various sets of dimensionless numbers.17,18 Glicksman et al.17 proposed a set of constant dimensionless parameters obtained by non-dimensionalizing the governing equations of motion for the fluids and the solids in a fluidized bed with expectation to obtain hydrodynamic similarity upon scaling up. Glickman's set of dimensionless numbers are ρs/ρg, u02/gD, u0/umf, Gs/ρsu0 and H/D. Nevertheless, scaling up by hydrodynamic similarity is not able to directly predict behavior in a fluidized bed with polymerization. Polymerization does not scale proportionally with increasing reactor size. To maintain polymerization similarity, the weight space time, which is the ratio of the weight of solid particles to the flow rate of monomer, should be fixed in order to have a similar reactor performance. This work studies the effect of scale-up using two different criteria—Set I based on weight space time (τ) similarity and Set II based on H/D similarity—with two different catalyst feed rates.The scaling relationships and operating conditions of the base case and scaled fluidized beds used for all cases studied are shown in Table 7.
| Reactor diameter (m) | ρs/ρg (—) | u02/gD × 104 (—) | u0/umf (—) | Gs/ρsu0 × 105 (—) | H/D (—) | W/FA0 (s) | |
|---|---|---|---|---|---|---|---|
| Set I, 0.044 mg s−1 | 0.2 | 24.4 | 7.25 | 2.25 | 4.10 | 6.13 | 251 |
| 2 | 24.4 | 7.25 | 2.25 | 4.10 | 1.22 | 251 | |
| 4 | 24.4 | 7.25 | 2.25 | 4.10 | 0.87 | 251 | |
| Set I, 0.087 mg s−1 | 0.2 | 24.4 | 7.25 | 2.25 | 8.06 | 6.13 | 251 |
| 2 | 24.4 | 7.25 | 2.25 | 8.06 | 1.22 | 251 | |
| 4 | 24.4 | 7.25 | 2.25 | 8.06 | 0.87 | 251 | |
| Set II, 0.044 mg s−1 | 0.2 | 24.4 | 7.25 | 2.25 | 4.10 | 6.13 | 251 |
| 2 | 24.4 | 7.25 | 2.25 | 4.10 | 6.13 | 793 | |
| 4 | 24.4 | 7.25 | 2.25 | 4.10 | 6.13 | 1121 | |
| Set II, 0.087 mg s−1 | 0.2 | 24.4 | 7.25 | 2.25 | 8.06 | 6.13 | 251 |
| 2 | 24.4 | 7.25 | 2.25 | 8.06 | 6.13 | 793 | |
| 4 | 24.4 | 7.25 | 2.25 | 8.06 | 6.13 | 1121 |
2.7 Simulation methodology
The results from the phenomenological model, with hydrodynamic CFD results of solid fraction and wall heat transfer coefficient, are used as input conditions to solve the Eulerian–Eulerian two-fluid model equations of momentum, continuity, species and energy. To set up the species equations, source terms of gaseous and solid species in terms of complex polymerization rates as a function of moments are included via adding User-Defined Functions (UDF) of source terms. In addition, user-defined equations for transport scalar of each moment (λ0,λ1,λ2,μ0,μ1,μ2), coupled with moments reaction rates, are included. A source term of heat released from polymerization in a UDF form is included in the energy equation. Simulations were carried out in a transient mode. All of the above equations are solved simultaneously via CFD method to provide local mass fraction of each species, phase holdup, phase velocity, phase temperature and active and dead polymer concentrations as seen in Fig. 2. Active and dead polymer concentrations are used for molecular weight calculation. In the present work, all the simulations were carried out in the commercial software ANSYS Fluent 15.0.Inlet velocity, temperature and compositions were specified at the inlet boundary. Pressure with zero gradient conditions of temperature and concentration was defined at the outlet boundary. No slip conditions were specified at the wall for both gas and solid phases. A constant temperature was specified at the wall. The simulation with the time step of 10−3 s and a convergence criterion of 10−5 for each scale residual component with 50 iterations per time step was used.
Grid independency has been checked to ensure that accurate results were obtained. In grid independence studies, the hydrodynamics of systems with three sizes of grid—14,400, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 and 32
600 and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cells—are simulated. The system with a grid of 25
400 cells—are simulated. The system with a grid of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cells offers both good precision and appropriate computational effort and is used to calculate all results.
600 cells offers both good precision and appropriate computational effort and is used to calculate all results.
3. Results and discussion
The results of this work are divided into two main parts: the results based on the phenomenological model and the model based on CFD.3.1 Results based on phenomenological model
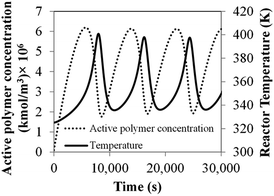
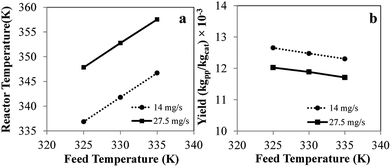
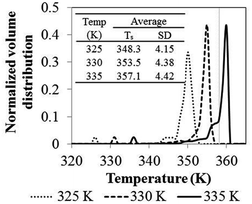
Comprehensive simulated results were obtained to evaluate the effect of the key process parameters—i.e., superficial velocity, feed temperature, catalyst feed rate, hydrogen concentration and reactor size—on production yield, conversion and bed temperature. The results from phenomenological model are as given in the following subsections:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, the temperature increases with time and becomes constant. Nevertheless, product yield is not changed significantly with catalyst feed rate. Over the range of higher catalyst feed rate, i.e. 35.8 to 41.2 mg s−1, the reactor temperature fluctuates strongly and can surge up to 400 K. Fig. 3a shows that using the feed temperature of 325 K and the catalyst feed rate of 35.8 mg s−1, the reactor temperature oscillates considerably, over a range of approximately 36 K. With higher catalyst feed rates, 38.5 mg s−1, the reactor temperature overshoot is much higher, and the reactor cannot be operated due to overheating and melting down of the polymer. Then the bed temperature sharply drops from its peak value mainly due to fast active polymer termination arising from high temperature as shown in Fig. 4. The reactor temperature peak lags the active polymer concentration by approximately 2000 seconds. Using the highest catalyst feed rate, 41.2 mg s−1, the bed temperature surges, leading to a runaway condition caused by high active polymer production and its associated high exothermic heat. Fig. 3a–c gives result for different feed temperatures; though exact values differ, for a given catalyst feed rate, reactor temperature follows a similar trend, regardless of feed temperature. However, the amplitude of reactor temperature oscillation is persistently very high for a low feed temperature of 325 K, due to occurring of less catalyst deactivation and active polymer termination, leading to a higher reaction rate and a higher reactor temperature (see Fig. 3a). Such a low-feed temperature condition should be avoided. On the other hand, for higher feed temperatures, less fluctuation of reactor temperature was found due to higher deactivation and termination leading to a lower reaction rate with less heat released (see Fig. 3c); in such a case, the overshooting is minor. Practically, propylene polymerization manufacture is not operated with high range of reactor temperature oscillation because wide range of polymer properties and hotspots has to be avoided. Nevertheless, temperature oscillation behavior upon increasing catalyst flow rate has also found by Ghasem,40 Hatzantonis7 and Hyanek.41 Several other papers have also indicated this behavior in polyethylene production. In conclusion, the catalyst feed rate mostly affects the bed temperature. Operating with too high a catalyst feed rate contributes to temperature fluctuation, which leads to overheating and unprofitable catalyst consumption. Using the higher catalyst feed rates (38.5, 41.2 mg s−1), the feed temperature must be increased cautiously so as to moderate both the active catalyst and active polymer concentrations, avoiding overheating, despite these temperature giving higher polymer production rates. The bed temperature is more important to control and focus on than yield in order to improve operability of the polymerization system.
000 s, the temperature increases with time and becomes constant. Nevertheless, product yield is not changed significantly with catalyst feed rate. Over the range of higher catalyst feed rate, i.e. 35.8 to 41.2 mg s−1, the reactor temperature fluctuates strongly and can surge up to 400 K. Fig. 3a shows that using the feed temperature of 325 K and the catalyst feed rate of 35.8 mg s−1, the reactor temperature oscillates considerably, over a range of approximately 36 K. With higher catalyst feed rates, 38.5 mg s−1, the reactor temperature overshoot is much higher, and the reactor cannot be operated due to overheating and melting down of the polymer. Then the bed temperature sharply drops from its peak value mainly due to fast active polymer termination arising from high temperature as shown in Fig. 4. The reactor temperature peak lags the active polymer concentration by approximately 2000 seconds. Using the highest catalyst feed rate, 41.2 mg s−1, the bed temperature surges, leading to a runaway condition caused by high active polymer production and its associated high exothermic heat. Fig. 3a–c gives result for different feed temperatures; though exact values differ, for a given catalyst feed rate, reactor temperature follows a similar trend, regardless of feed temperature. However, the amplitude of reactor temperature oscillation is persistently very high for a low feed temperature of 325 K, due to occurring of less catalyst deactivation and active polymer termination, leading to a higher reaction rate and a higher reactor temperature (see Fig. 3a). Such a low-feed temperature condition should be avoided. On the other hand, for higher feed temperatures, less fluctuation of reactor temperature was found due to higher deactivation and termination leading to a lower reaction rate with less heat released (see Fig. 3c); in such a case, the overshooting is minor. Practically, propylene polymerization manufacture is not operated with high range of reactor temperature oscillation because wide range of polymer properties and hotspots has to be avoided. Nevertheless, temperature oscillation behavior upon increasing catalyst flow rate has also found by Ghasem,40 Hatzantonis7 and Hyanek.41 Several other papers have also indicated this behavior in polyethylene production. In conclusion, the catalyst feed rate mostly affects the bed temperature. Operating with too high a catalyst feed rate contributes to temperature fluctuation, which leads to overheating and unprofitable catalyst consumption. Using the higher catalyst feed rates (38.5, 41.2 mg s−1), the feed temperature must be increased cautiously so as to moderate both the active catalyst and active polymer concentrations, avoiding overheating, despite these temperature giving higher polymer production rates. The bed temperature is more important to control and focus on than yield in order to improve operability of the polymerization system.
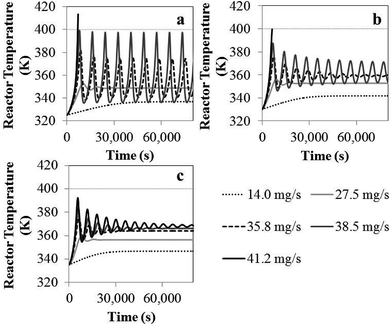 | ||
| Fig. 3 Reactor temperature as a function of time for different catalyst flow rate and feed temperatures: (a) 325 K, (b) 330 K, (c) 335 K. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000,
000,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167
167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 141
000 and 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. A higher hydrogen concentration leads to a lower molecular weight because of more chain transfer and thus a shorter chain length. The trend of hydrogen concentration effect on polypropylene molecular weight was also found in Kissin43 and Zhang.44
000, respectively. A higher hydrogen concentration leads to a lower molecular weight because of more chain transfer and thus a shorter chain length. The trend of hydrogen concentration effect on polypropylene molecular weight was also found in Kissin43 and Zhang.44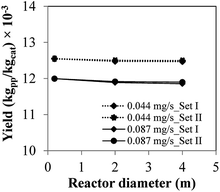 | ||
| Fig. 7 Product yield applying polymerization similarity (Set I) and hydrodynamic similarity (Set II) with catalyst feed rates of 0.044 mg s−1 and 0.087 mg s−1 for the base case (laboratory scale). | ||
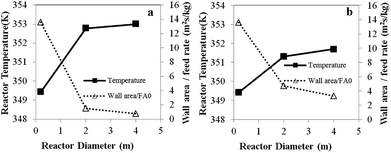 | ||
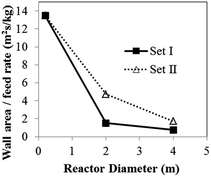
| Fig. 8 Effects of reactor scale on reactor temperature and wall area per monomer feed rate for (a) Set I and (b) Set II. | ||
The foregoing differences between heat transfer effects in a small and those in a large reactor depend on the wall area per gas feed rate. As the reactor size increases, the wall surface area per monomer feed rate decreases, resulting in an increase in bed temperature especially in scaling up from 0.2 to 2 m.
In this work, the wall surface area can be obtained using the bed expansion calculated in CFD hydrodynamic simulations. Although the phenomenological model alone cannot provide the bed expansions by itself, in combination with hydrodynamic information from CFD on bed expansion it can provide the wall surface area. Table 8 shows the heat transfer coefficient and wall surface area for different reactor scales following Set I criteria. As the reactor size increases from the laboratory to semi-industrial scale, the heat transfer area per monomer feed rate drops significantly, resulting in an increase in bed temperature. In order to keep the same temperature in scaling up, the heat transfer surface area thus has to be extended. The ways to increase the surface area, such as adding cooling coils, may need to be considered.
| Reactor diameter (m) | |||
|---|---|---|---|
| 0.2 | 2 | 4 | |
| Volume fraction | 0.406 | 0.369 | 0.363 |
| Conversion | 9.09 | 9.96 | 10.01 |
| Reactor temperature, T (K) | 349.4 | 352.8 | 353.0 |
| Heat transfer coefficient, h (W m−2 K−1) | 71.30 | 123.84 | 164.99 |
| Solid loading (kg) | 11 | 3500 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 799 |
| Bed height at steady state (m) | 0.95 | 3.32 | 4.77 |
| Reactor heat transfer area, A (m2) | 0.60 | 20.85 | 59.99 |
| Heat transfer area/monomer feed rate, A/FA0 (m2 s kg−1) | 13.57 | 1.49 | 0.76 |
| Heat transfer area multiplying factor, f, to keep the same T (349.4 K) | 1 | 4.36 | 5.26 |
| Adjusted wall temperature to keep same T (349.4 K) | 330.15 | 314.62 | 312.52 |
Increasing the reactor diameter from 2 to 4 m has less effect on surface area per monomer feed rate than scaling up from 0.2 to 2 m. Table 8 shows that increasing the reactor size to a semi-industrial scale (2 m), the reactor surface area per monomer feed rate is reduced to 1.49 m2 s kg−1 in while the bed temperature increases to 352.8 K. In order to maintain the bed temperature of 349.4 K, the desired surface area can be obtained by providing the additional wall surface area. The surface area of the semi-industrial reactor should be increased 4.36 times. That is the surface area of 20.85 m2 should be extended to be 90.9 m2. To increase the heat transfer area, internal cooling coils or extended surface can be provided. The heat transfer area required to obtain the bed temperature in a semi-industrial scale to match the temperature in a laboratory scale was obtained by trial and error in the full simulation of scaled-up reactors. The required heat transfer area is much larger than available wall surface area with the factor, f, i.e. 4.36. The multiplying factors (f), which can provide the same bed temperatures for all three scales, were obtained and reported in Table 8.
Alternative to extend the wall surface area, the wall temperature can be reduced in order to increase the wall heat removal driving force. The wall temperature for maintaining the same bed temperature was obtained by trial and error of wall temperature in our simulation. In a simulation of scaling up from 0.2 m to 4 m, the wall temperature must be decreased from 330 to 312.5 K to keep a bed temperature of 349.4 K, as shown in Table 8 (the results of other cases are also shown).
Table 9 shows heat transfer parameters in a fluidized bed obtained from Set I scaling-up compared with those from a tubular reactor referred in Nauman,45 with the same reaction time throughout. Although the scaling-up from Nauman is for a tubular reactor, it is considered here for comparative discussion. Removal heat from both fluidized bed and tubular reactor is mainly through the wall. In the scaling-up of a tubular reactor with weight space time similarity, the product of heat transfer coefficient and area (hA) can be scaled up by a factor of m1.7 (see Item 2), as suggested in Nauman.45 It was found that increasing from 0.2 m to 4 m, the hA product increased from 43 to 7013 W K−1 for a tubular reactor (Item 2). This can be compared to the simulations in Set I, for which the hA product increases from 43 to 9898 W K−1 (Item 1); note that here the hA product is somewhat higher than that of a tubular reactor.
| Item | Reactor diameter (m) | |||
|---|---|---|---|---|
| 2 | 4 | 0.2 | ||
| Scaling-up ratio, m | 1 | 10 | 20 | |
| 1 | hA for fluidized bed with weight space time similarity (W K−1) | 43 | 2564 | 9898 |
| 2 | hA provided for tubular reactor with weight space time similarity = m1.7 (W K−1) | 43 | 2159 | 7013 |
| 3 | hA suggested for tubular reactor based on heat transfer similarity = m2.5 (W K−1) | 43 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 620 |
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 045 |
| 4 | Adjusted hA (fhA) for fluidized bed with weight space time similarity to maintain the same temperature (W K−1) | 43 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 256 256 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 061 |
Using weight space time similarity, the reactor temperature cannot be assured constant during scaling up, as indicated in Table 9. Thus, the scaling-up rule based on similarity in heat transfer should be applied. It is suggested that heat transfer similarity in a tubular reactor can be obtained when the hA product has to be scaled up by the factor of m2.5 (Item 3).45 Table 9 shows that as the reactor diameter is increased from 0.2 m to 4 m, the hA product has to be high enough to yield the same bed temperature. It has to be increased from 43 to 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 W K−1 in order for a tubular reactor to maintain the reactor temperature of 349.4 K (see Item 3). Referring to this tubular reactor scale-up rule, the hA product in the fluidized bed reactor should be increased in order to maintain the same temperature (see Item 1). In our simulation of a fluidized bed, the heat transfer area multiplying factor, f, has been proposed as shown in Table 8. These multiplying factors are obtained by extensive trial and error in our simulations to keep the same targeted temperature of reactor during the scaling-up process. Table 9 shows that for scaling up from 0.2 to 4 m, the required product of hA for the fluidized bed increases from 43 to 52
045 W K−1 in order for a tubular reactor to maintain the reactor temperature of 349.4 K (see Item 3). Referring to this tubular reactor scale-up rule, the hA product in the fluidized bed reactor should be increased in order to maintain the same temperature (see Item 1). In our simulation of a fluidized bed, the heat transfer area multiplying factor, f, has been proposed as shown in Table 8. These multiplying factors are obtained by extensive trial and error in our simulations to keep the same targeted temperature of reactor during the scaling-up process. Table 9 shows that for scaling up from 0.2 to 4 m, the required product of hA for the fluidized bed increases from 43 to 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 W K−1 (see Item 4 in Table 9). At 4 m, the hA product of 52
061 W K−1 (see Item 4 in Table 9). At 4 m, the hA product of 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 W K−1 is required while the hA product of only 9898 W K−1 is available with weight space time similarity (see Item 1). The required hA product is higher (f = 5.26).
061 W K−1 is required while the hA product of only 9898 W K−1 is available with weight space time similarity (see Item 1). The required hA product is higher (f = 5.26).
The heat transfer parameters in our fluidized bed are of a similar order of magnitude as those in a tubular reactor using the criteria of heat transfer similarity to maintain reactor temperature. They have to be much larger than those obtained from the criteria of weight space time similarity.
Considering reactor scaled up by 20 times based on Set II of hydrodynamic similarity, the criteria yield a slightly lower temperature rise in the order of 1.4 K as shown in Fig. 8. Even though, both criteria give the similar wall heat transfer coefficient, wall surface area from Set II is approximately four times as high as one from Set I. Therefore, heat transfer area multiplying factor for Set II does not require as much as Set I to maintain the same reactor temperature. Moreover, alternative wall temperature reduction for Set II criteria does not need to decrease as low as one from Set I criteria.
In conclusion, to scale up the PP reactor, the overheating of the bed has to be of greater concern than the product yield. Neither criterion (Set I or Set II) can provide heat transfer similarity in scaling up. However, the bed temperature similarity can be achieved by increasing of the wall surface area or decreasing of wall temperature.
3.2 Results based on CFD approach
CFD simulation work was carried out to study the local behavior of reactive flow system. The initializing parameters of the simulation—gas and solid temperatures, gas feed velocity, species concentration, and catalyst concentration—are obtained from the steady-state period of the phenomenological model in order to reduce time required for the full CFD simulation. The simulation results obtained from the model based on CFD can show the local bed temperature variation and other phenomena in the reactor which cannot be provided by the phenomenological model. These simulations can provide information of non-uniformity, overheating and hot spot zones.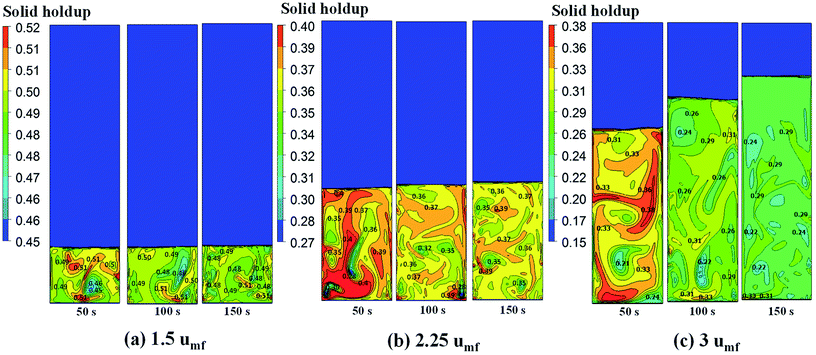 | ||
| Fig. 10 Contour of solid fraction distribution as well as the isolines indicating quantitative solid fraction at various times of operation for different feed velocities. | ||
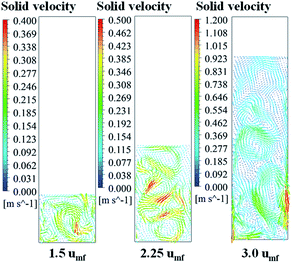
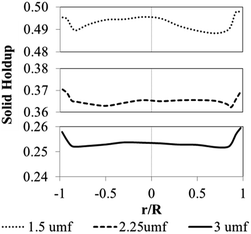
Fig. 11 shows the radial profile of solids holdup averaged between 100 to 200 s for various superficial gas velocities. No significant variation of solid holdup is found with radial position, except near the wall where solid holdup is higher due to the friction between the solid phase and the wall. Similar results have been found in experiments by Wang and co-workers.48 At low feed velocity, the radial solid distribution in the bed is relatively non-uniform, while at high feed velocity, more uniformity of solid holdup occurs, as seen in Fig. 11. This characteristic of the radial profile of solid holdup was also found by published literature.11,49 At low velocity, less bed expansion with high solid holdup was found, leading to less uniformity. On the other hand, at high velocity, high solid movement and bed expansion lead to low solid holdup and more uniformity. The solid holdup can be ranked in order of the cases of 1.5umf > 2.25umf > 3.0umf.
Fig. 12 shows the contour and radial profiles of monomer concentrations as well as axial profile of monomer conversion for various superficial gas velocities. The monomer decreases slightly with bed height due to monomer being consumed by reaction. However, the conversion of this polymerization is relatively low. Although the flow in the reactor does not behave in a completely well-mixed way (see the vector plot in Fig. 9), the flow has no significant effect on the mass balance.
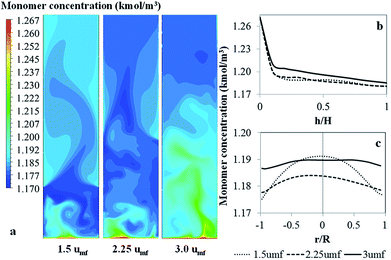 | ||
| Fig. 12 Contour and radial profiles of monomer concentrations as well as axial profile of monomer conversion for various superficial gas velocities. | ||
The assumption of well-mixed flow in the phenomenological model can be applied globally without significant error. However, due to the reaction being highly exothermic, the effect of the flow on the energy balance cannot be ignored. Thus the effects of operating conditions on flow patterns and the local bed temperature are still of significant concern.
Fig. 13 shows the bed temperature contour plot, and the axial and radial profiles of averaged bed temperature for various superficial gas velocities. The bed temperature is non-uniform due to the reaction being non-isothermal and non-uniformity of flow. The bed is cooler near the cold gas feed zone and rises up along the bed height, but it gradually increases with distance upwards, as shown in Fig. 13b. The temperature difference along the bed height is on the order of 11.1–14.6 K. This axial profile of bed temperature corresponds to the monomer conversion one.
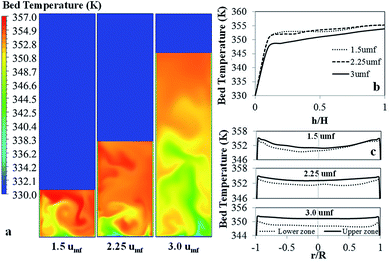 | ||
| Fig. 13 Contour of bed temperature with axial and radial profiles of bed temperature for various superficial gas velocities. | ||
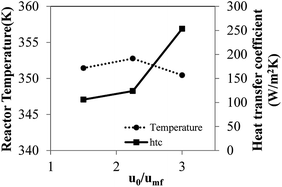
At lower velocity, the radial temperature profile is less uniform. The difference between the maximum and minimum temperatures is 4 K (not including the wall temperature). Compared to the highest velocity (3umf), the temperature is lower, and the radial temperature profile is flatter, with a difference between minimum and maximum temperature of 0.87 K. The effect of superficial velocity can be seen in both the radial profile of temperature and the radial profile of monomer concentration, though the effect on one is the opposite of the effect on the other.
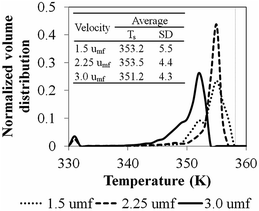
Fig. 14 shows the bed temperature distribution curve in terms of normalized volume distribution. At high feed gas velocity (3umf), low mean temperature with less standard deviation (more uniformity of temperature distribution) was found due to high heat transfer and bed expansion. Lower superficial gas velocity creates high solid holdup, leading to higher bed temperature and less uniformity and higher standard deviation than those obtained from high velocity operation. The conversions and product yield change slightly with changes to the superficial gas velocity, as seen in Table 10.
| Simulation case | u0/umf | Bed temperature (K) | Catalyst feed rate (mg s−1) | H2 feed concentration (kmol m−3) | Conversion (%) | Product yield (kg gcat−1) |
|---|---|---|---|---|---|---|
| Effect of superficial velocity | 1.5 | 330 | 27.5 | 0.02 | 7.18 | 12.6 |
| 2.25 | 7.21 | 12.7 | ||||
| 3 | 6.85 | 12.4 | ||||
| Effect of feed temperature | 2.25 | 325 | 27.5 | 0.02 | 6.85 | 13.0 |
| 330 | 7.21 | 12.7 | ||||
| 335 | 7.32 | 12.6 | ||||
| Effect of catalyst feed rate | 2.25 | 330 | 19.3 | 0.02 | 5.32 | 12.9 |
| 27.5 | 7.21 | 12.7 | ||||
| 35.8 | 9.15 | 12.4 | ||||
| Effect of hydrogen feed concentration | 2.25 | 330 | 27.5 | 0.01 | 7.22 | 12.7 |
| 0.02 | 7.21 | 12.7 | ||||
| 0.03 | 7.20 | 12.6 |
In conclusion, the superficial gas velocity has an effect mainly on the bed temperature and its degree of uniformity with minimal effect on product yield/unit weight of catalyst for the same reaction time, as the system is in a low conversion range. Higher superficial velocity gives more uniformity of bed temperature.
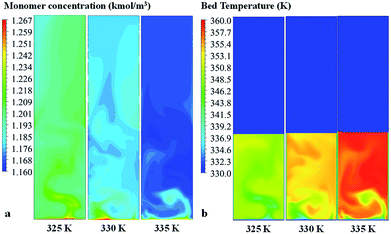 | ||
| Fig. 15 Contour of (a) propylene concentration and (b) bed temperature in the fluidized bed for various feed temperatures. | ||
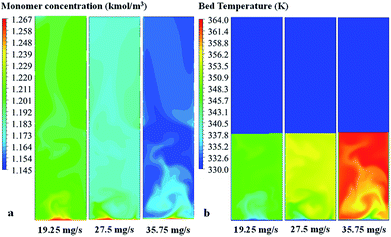 | ||
| Fig. 17 Contours of (a) propylene concentration and (b) bed temperature in the fluidized bed for various catalyst feed rates. | ||
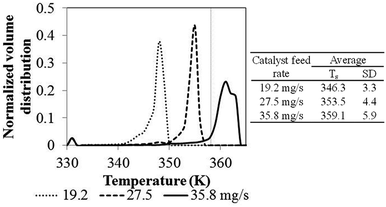
Comparing to phenomenological model, at this high catalyst feed rate (35.8 mg s−1), both results show that the system cannot be operated at the limit temperature wise (358 K), whereas the CFD based model shows a significant problem of hotspots. At the low feed catalyst rates of 19.2 and 27.5 mg s−1, the problem in overheating was not found. In conclusion, the non-uniformity of bed temperature and overheating in the bed has to be of concern when increasing the catalyst flow rate for improving production.
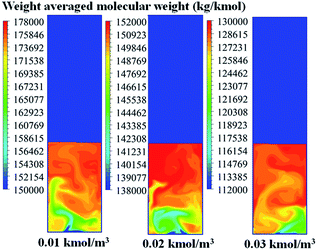
To study its effect on the local distribution of the weight average molecular weight, CFD calculation was carried out from the beginning to 100 seconds of operation. Fig. 19 shows that the weight average molecular weight increases with decreasing hydrogen concentration, due to lower chain transfer to hydrogen. The molecular weight is clearly non-uniform and increases significantly with position along the bed height for all cases studied. Short chain polymer was found near the bed bottom because more fresh catalyst and hydrogen are found near the feed area. On the other hand, longer polymer chain was found near the top of the bed due to a longer residence time with less transfer and termination. The finding is beneficial for positioning product withdrawal outlet.
Fig. 20a and b show the solid holdup contours for different sizes of fluidized bed reactors using weight time (Set I) and H/D (Set II) constants, respectively. Fig. 20a shows that the ratio of fluidized bed height to bed diameter (Hexpand/D) decreases as the reactor is scaled up for Set I (resulting from decreasing of the ratio of initial bed height to diameter (Hini/D) as the reactor size increases). In spite of there being a lower bed height at the industrial scale, the solid holdup is also lower, as shown in Fig. 20a. Fig. 20b shows the effect of scaling up on the solid holdup based on Set II criteria. H/D constant was carried out by keeping the same ratio of initial solid bed height to reactor diameter (Hini/D), in expectation that the same ratio of fluidized bed height to diameter (Hexpand/D) would also ensure. The results show that the hydrodynamics are not similar for these three scales. As the reactor diameter is increased from 0.2 to 4 m, Hexpand/D increases from 4.7 to 5.4 and the solid holdup decreases from 0.41 to 0.36 at the same ratio of u0/umf. Neither criterion provides similar hydrodynamic results. Thus similarity in heat and mass transfer in scaling up is not obtained. One can adjust the superficial gas velocity or particle size to obtain the same solid holdup. Even though, the same solid holdup is obtained, the same heat transfer in the bed cannot be ensured.
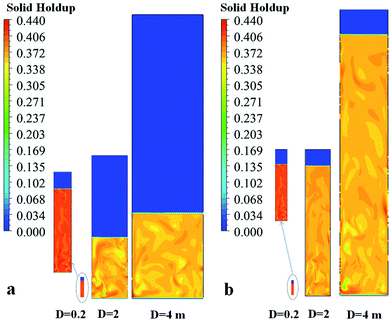 | ||
| Fig. 20 Contours of solid holdup for different reactor scales for (a) Set I with weight space time similarity, and (b) Set II with hydrodynamic similarity. | ||
Fig. 21 and 22 show the contour and radial profiles of bed temperature for different reactor sizes and scaling criteria. For the semi-industrial and industrial scale reactors (D = 2, 4 m, respectively), the magnitudes of bed temperature in Fig. 22 are not much different.
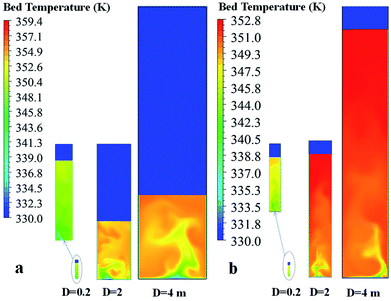 | ||
| Fig. 21 Contour of bed temperature for different reactor scales obtained using (a) Set I with weight space time similarity, and (b) Set II with hydrodynamic similarity. | ||
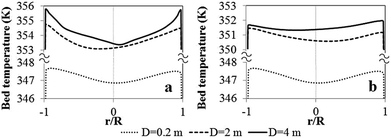 | ||
| Fig. 22 Radial profiles of bed temperature for different reactor scales for (a) Set I and (b) Set II criteria. | ||
In the laboratory reactor scale, the bed temperature is lower and its radial profile is flatter than those of the semi-industrial and industrial reactors due to better heat removal at the smaller scale. It should be noted that, although the solid holdup obtained in the largest scale is lower, the temperature is higher. Scaling up the reactor from the laboratory scale to industrial scale, the temperature increases due to lower wall heat transfer area per unit of feed rate, as seen in Fig. 23. The ratio decreases with rector size.
Fig. 24 shows the temperature distribution for various reactor scales calculated using weight time similarity (Set I) criteria. The standard deviation of temperature in the reactor is in the range of 2.9–4.5 K and increases with reactor scale, as shown in Fig. 24. This trend was also found in the results of phenomenological model shown in Section 3.1.5. It confirms that more non-uniformity of bed temperature occurs in a larger scale reactor. In conclusion, neither scaling-up criterion can provide uniformity and similarity of temperature in reactor. Scaling up using Set II criteria provides more uniformity of temperature due to the advantage of higher ratio of wall surface area to monomer feed rate.
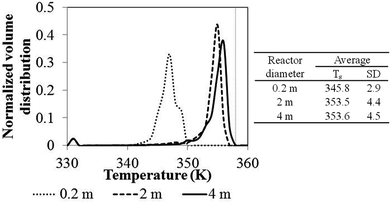 | ||
| Fig. 24 Bed temperature distribution for different reactor scales using weight time similarity (Set I) criteria. | ||
In all, the results based on the CFD approach coupled with phenomenological model gives a new insight of the heat effect and temperature distributions in fluidized bed for propylene polymerization. A better operation, design, and scale up of reactor should be realized.
3.3 Comparison of the results from the phenomenological model and available results in literature
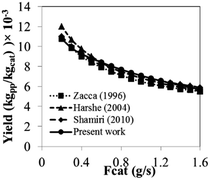
The operating information of polyolefin industrial systems is proprietary and extremely hard to find. Therefore, the results of the phenomenological model used here are compared to previously published simulation work. Fig. 25 shows the comparison in terms of product yield based on the effect of catalyst feed rate for an isothermal operation. A list of simulation parameters used for comparison is shown in Table 11. It can be observed that the product yield predicted from this current model agrees well with the previously published work of Harshe,6 Shamiri9 and Zacca.27 Polymer properties are basically defined by molecular weight. The mass averaged molecular weight at steady state calculated from this current model compares satisfactory to the work of Shamiri, as they give values of 166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 and 163
700 and 163![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200, respectively. The percent difference is 2.12%. Moreover the calculated results from this model were validated with the previous experimental data obtained by Shamiri.51 The experiments were carried out in a fluidized bed of 0.1016 m in diameter, feed temperature of 333 K and catalyst flow rate of 3.02 g h−1. The time plots of propylene concentration and reactor temperature obtained from the phenomenological model and the experiments at the same conditions were compared as shown in Fig. 26. It can be observed that the results of this current model show a satisfactory level of agreement with the experimental results of Shamiri.51 The phenomenological model is applicable and comparable with previous work in terms of product yield and molecular weight. However, from this work, additional information of heat transfer effect is available especially in scaling-up. Detailed information of heat effects in a polymerization fluidized bed reactor obtained from this work is an insight which will be useful for reactor operation, analysis, designs and scaling-up improvement.
200, respectively. The percent difference is 2.12%. Moreover the calculated results from this model were validated with the previous experimental data obtained by Shamiri.51 The experiments were carried out in a fluidized bed of 0.1016 m in diameter, feed temperature of 333 K and catalyst flow rate of 3.02 g h−1. The time plots of propylene concentration and reactor temperature obtained from the phenomenological model and the experiments at the same conditions were compared as shown in Fig. 26. It can be observed that the results of this current model show a satisfactory level of agreement with the experimental results of Shamiri.51 The phenomenological model is applicable and comparable with previous work in terms of product yield and molecular weight. However, from this work, additional information of heat transfer effect is available especially in scaling-up. Detailed information of heat effects in a polymerization fluidized bed reactor obtained from this work is an insight which will be useful for reactor operation, analysis, designs and scaling-up improvement.
| Operating conditions and physical parameters |
|---|
| Tr (K) = 343.15 Vr (m3) = 50 |
| P (bar) = 25 u0 (m s−1) = 0.35 |
| Propylene concentration (kmol m−3) = 1.267 |
| Hydrogen concentration (kmol m−3) = 0.02 |
| Weight fraction of titanium in catalyst = 0.4 |
| Fraction of active titanium = 2% |
| ρs (kg m−3) = 910 dp (micron) = 500 |
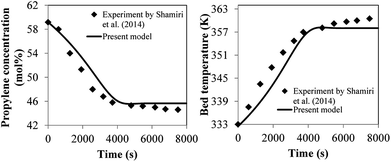 | ||
| Fig. 26 Comparison between experimental data and calculated results of propylene concentration and reactor temperature. | ||
3.4 Practical significance and limitation of the models
The combined model consisting of phenomenological model and CFD-based reactor model can predict various level scales of reactor performance. The former model can provide overall information while the latter can provide local information. The average results suggest improved productivity and reactor temperature control done by cautiously adjusting the operating conditions e.g. increasing catalyst feed rate, operating temperature, reactor size and superficial velocity, with consideration of catalyst deactivation. Improper conditions for increasing productivity can involve a risk with regards to control of oscillating temperature. The model identifies an operating window to improve productivity and temperature control and to study operation details. The local information obtained from the CFD-based reactor model is useful to find the region of hotspots by evaluating the temperature distribution in the reactor. Both models provides information for the selection of the proper operating conditions and safe range of operation. They are useful for analysis of a laboratory reactor and an industrial scale reactor and provide information on scale up. Hydrodynamic and heat transfer similarities in different reactor scales, which can be predicted by this model, are useful for scaling up.Upon scaling up, the finding shows that heat transfer area is critical for design and need a careful consideration by either increasing the area to satisfy the requirement or increasing temperature driving force by reduction of wall temperature, especially in large scale reactor. CFD spends a large of computational time. If only global information is needed, the phenomenological model is sufficiently applied. The combined model cannot provide details of molecular weight distribution unless more detailed kinetic rates are used. However, with the limitation in term of large computational time, the CFD based model is impractical. Only the phenomenological model can be used. The CFD-based model is based on two-fluid model which assumes a continuum phase of solid particles. Therefore, this model can be applied for different modes of fluidized bed with a small particle size, but not for the one with a large particle size. For instance, a fluidized bed with a spouted mode of operation cannot be studied accurately by this model. Other models, e.g. Lagrangian model, should be used instead.
4. Summary
This work has presented a detailed performance model of propylene polymerization in a continuous fluidized bed reactor, using both a phenomenological model and CFD combined with the method of moment. The phenomenological model provides average bed temperature, monomer concentration, polymer production rate and molecular weight in polymerization reactor. Meanwhile, CFD-based reactor analysis provides distributions of phase movements and temperature. The effects of operating conditions and scaling up on the reactor temperature control were focused on. Based on the results of these two approaches, suggestions can be drawn for improving productivity and reactor temperature control include cautiously increasing catalyst feed rate, operating temperature, hydrogen concentration, reactor size and superficial velocity. The details and highlight of key results are as follows.• In general, high catalyst loading is beneficial only up to a certain point, beyond which the phenomenological model showed that a sustained oscillation of productivity and reactor temperature occurs.
• The benefits of increasing productivity by increasing catalyst feed rate should be balanced with consideration of hotspots occurrence and control of oscillating temperature. Additionally, the reactor temperature and production yield need to be balanced with consideration of a risk of the hotspot formation.
• Increasing operating temperature does not always increase production rate because of catalyst deactivation. Reactor performance can be identified by the simple well-mixed model to improve productivity and study operation details.
• Propylene conversions from both CFD and the phenomenological model show that the mixing effect is not very significant excepting in hotspot generation.
• Superficial gas velocity strongly affects the fluidized regime and heat transfer. Scaling up using two different criteria—Set I based on weight space time (τ) similarity and Set II based on H/D similarity—can not provide heat transfer similarity.
• In scaling up the PP fluidized bed, the operating temperature in the reactor should be chosen while taking into account the ratio of internal wall area to monomer feed rate and the temperature difference between bulk and wall, as well as hydrodynamic behavior in the reactor.
• To keep the same reactor temperature in scaling up a reactor from 0.2 to 4 m in diameter requires a heat transfer area multiplying factor of 2.43 to 5.26 or lowering the wall temperature in the range of 7 to 18 K.
• The CFD model is therefore more useful than the phenomenological model to find the region of hotspots, as it works by evaluating the temperature distribution in each section of fluidized bed reactor.
• Temperature variations in the range of 10 to 14 K were observed in the top section of the reactor in the CFD model and fall within an acceptable operating window. However, when the operating conditions are changed, CFD should be applied to check again for the possibility of local hotspots.
Both models provide useful information for the selection of appropriate operating conditions and a safe range of operation windows. They are useful for analysis of both laboratory reactors and industrial-scale reactors and provide information on scaling up.
Conflicts of interest
There are no conflicts to declare.Notation
| A | Cross sectional area of fluidized bed reactor, (m2) |
| Aw | Reactor wall area, (m2) |
| [Ci] | Molar concentration of species i in the gas phase, (kmol m−3) |
| [Cs,j] | Molar concentration of species j in the solid phase, (kmol m−3) |
| [Ck] | Molar concentration of moments k in solid phase, (kmol m−3) |
| CD | Drag function |
| cpq | Heat capacity of phase q, (kJ kg−1 K−1) |
| ds | Particle diameter, (m) |
| e | Restitution coefficient between particle |
| FA0 | Monomer flow rate, (kg s−1) |
| g0 | Radial distribution function |
| Gs | Solids mass flux, (kg m−2 s−1) |
| Gk,q | Production of turbulent kinetic energy of phase q, (kg m s−3) |
| hg | Specific enthalpy of gas phase, (kJ kg−1) |
| ΔHr | Heat of propylene polymerization, (kJ kmol−1) |
| H | Bed height, (m) |
| hgs | Heat transfer coefficient between gas and solid, (W m−2 K−1) |
| hw | Wall heat transfer coefficient, (Wm−2 K−1) |
| I | Unit tensor |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) g,i g,i | The diffusion flux of gas phase for species i, (kg m−2 s−1) |
| kq | Turbulent kinetic energy of phase q, (m2 s−2) |
| kiM | Frequency factors for initiation, (m3 kmol−1 s−1) |
| kp | Frequency factors for propagation, (m3 kmol−1 s−1) |
| ktrM | Frequency factors for chain transfer to monomer, (m3 kmol−1 s−1) |
| ktrH | Frequency factors for chain transfer to hydrogen, (m3 kmol−1 s−1) |
| kd | Frequency factors for chain termination, (1/s) |
| keff,q | Effective thermal conductivity of phase q, (W m−1 K−1) |
| kθs | Diffusion coefficient for granular temperature, (kg m−1 s−1) |
| Knq | Turbulent interphase momentum transfer coefficient between phase n and phase q, (kg m−3 s−1) |
| m | Diameter scale ratio |
| ṁgs | Mass transfer rate between gas and solid phases, (kg m−3 s−1) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n n | Number average molecular weight, (kg kmol−1) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w w | Weight average molecular weight, (kg kmol−1) |
| Mwi | Molecular weight of species i, (kg kmol−1) |
| P | Pressure, (Pa) |
| Ps | Solids pressure, (Pa) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) g g | Heat flux from species diffusion, (W m−2) |
| qcat | Volumetric flow rate of catalyst feeding, (m3 s−1) |
| Q0 | Volumetric flow rate of polymer removal, (m3 s−1) |
| Q | Heat transfer from the bed to wall, (W m−3) |
| Rp | Rate of propagation, (kmol m−3 s−1) |
| Rg,i | Production rate of species i from gas to solid, (kmol m−3 s−1) |
| Rs,j | Production rate of species j in solid phase, (kmol m−3 s−1) |
| Rs,k | Production rate of moments k in solid phase, (kmol m−3 s−1) |
| Ss | Heat production of reaction on solid phase, (kJ m−3 s−1) |
| T | Reactor temperature, (K) |
| Tq | Temperature of phase q, (K) |
| Tw | Wall temperature, (K) |
| u0 | Superficial velocity of gas, (m s−1) |
| umf | Minimum fluidized velocity, (m s−1) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) q q | Velocity of phase q, (m s−1) |
| Vr | Reactor volume, (m3) |
| W | Solid loading, (kg) |
| WTi | Weight fraction of titanium in the catalyst |
| xq,i | Mass fraction of i species in phase q |
| XTi | Fraction of titanium atoms that are catalyst sites |
| x | The distance from the computational node to the heating wall, (m) |
| MwM | Molecular weight of monomer (kg kmol−1) |
Greek letters
Subscriptions
| g | Gas phase |
| s | Solid phase |
| t | Turbulent |
Acknowledgements
This work was financially supported by the Kasetsart University Research and Development Institute (KURDI), the Faculty of Engineering of Kasetsart University, the Centre of Excellence on Petrochemical and Materials Technology (PETROMAT) and the Centre for Advanced Studies in Industrial Technology.References
- R. Fan, PhD thesis, Iowa State University, Iowa, 2006.
- A. Ahmadzadeh, H. Arastoopour, F. Teymour and M. Strumendo, Chem. Eng. Res. Des., 2008, 86, 329–343 CrossRef.
- J. Y. Kim and K. Y. Choi, Chem. Eng. Sci., 2001, 56, 4069–4083 CrossRef.
- K. B. McAuley, J. F. MacGregor and A. E. Hamielec, AIChE J., 1990, 36, 837–850 CrossRef.
- K. B. McAuley, J. P. Talbot and T. J. Harris, Chem. Eng. Sci., 1994, 49, 2035–2045 CrossRef.
- Y. M. Harshe, R. P. Utikar and V. V. Ranade, Chem. Eng. Sci., 2004, 59, 5145–5156 CrossRef.
- H. Hatzantonis, H. Yiannoulakis, A. Yiagopoulos and C. Kiparissides, Chem. Eng. Sci., 2000, 55, 3237–3259 CrossRef.
- A. Shamiri, M. A. Hussain, F. S. Mjalli and N. Mostoufi, Comput. Chem. Eng., 2012, 36, 35–47 CrossRef.
- A. Shamiri, M. A. Hussain, F. S. Mjalli and N. Mostoufi, Chem. Eng. J., 2010, 161, 240–249 CrossRef.
- A. Shamiri, S. W. Wong, M. F. Zanil, M. A. Hussain and N. Mostoufi, Chem. Eng. J., 2015, 264, 706–719 CrossRef.
- S. Benzarti, H. Mhiri and H. Bournot, World Acad. Sci. Eng. Technol., 2012, 6, 111–116 Search PubMed.
- P. Khongprom, A. Aimdilokwong, S. Limtrakul, T. Vatanatham and P. A. Ramachandran, Chem. Eng. Sci., 2012, 73, 8–19 CrossRef.
- J. Ding and D. Gidaspow, AIChE J., 1990, 36, 523–538 CrossRef.
- M. Xu, F. Chen, X. Liu, W. Ge and J. Li, Chem. Eng. J., 2012, 207–208, 746–757 CrossRef.
- Y. Yao, Y. J. He, Z. H. Luo and L. Shi, Adv. Powder Technol., 2014, 25, 1474–1482 CrossRef.
- Z. Li, M. van Sint Annaland, J. A. M. Kuipers and N. G. Deen, Chem. Eng. Sci., 2016, 140, 279–290 CrossRef.
- L. R. Glicksman, M. R. Hyre and P. A. Farrell, Int. J. Multiphase Flow, 1994, 20, 331–386 CrossRef.
- L. R. Glicksman, M. Hyre and K. Woloshun, Powder Technol., 1993, 77, 177–199 CrossRef.
- D. Kunii and O. Levenspiel, Fluidization engineering, Butterworth-Heinmann, Boston, MA, 2nd edn, 1991 Search PubMed.
- H. Cui, N. Mostoufi and J. Chaouki, Chem. Eng. J., 2000, 79, 133–143 CrossRef.
- J. C. Chen, J. R. Grace and M. R. Golriz, Powder Technol., 2005, 150, 123–132 CrossRef.
- P. Basu, Combustion and Gasification in Fluidized Beds, CRC Press, 2006 Search PubMed.
- A. Blaszczuk, W. Nowak and J. Krzywanski, Powder Technol., 2017, 316, 111–122 CrossRef.
- ANSYS, FLUENT Theory Guide, Northbrook, IL, 2009 Search PubMed.
- Y. P. Zhu, Z. H. Luo and J. Xiao, Comput. Chem. Eng., 2014, 71, 39–51 CrossRef.
- J. Boor, Ziegler-Natta Catalysts Polymerizations, Academic Press, New York, 1st edn, 1979 Search PubMed.
- J. J. Zacca, J. A. Debling and W. H. Ray, Chem. Eng. Sci., 1996, 51, 4859–4886 CrossRef.
- Z. H. Luo, P. L. Su, D. P. Shi and Z. W. Zheng, Chem. Eng. J., 2009, 149, 370–382 CrossRef.
- G. Di Drusco and R. Rinaldi, Hydrocarbon Process., 1984, 55, 113–117 Search PubMed.
- J. B. P. Soares, Chem. Eng. Sci., 2001, 56, 4131–4153 CrossRef.
- S. Zhu, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 2692–2704 CrossRef.
- W. Zhou, E. Marshall and L. Oshinowo, Ind. Eng. Chem. Res., 2001, 40, 5533–5542 CrossRef.
- R. Wang, Y. Luo, B. Li, X. Sun and S. Zhu, Macromol. Theory Simul., 2006, 15, 356–368 CrossRef.
- D. Gidaspow, R. Bezburuah and J. Ding, Proc. Seventh Eng. Foundation Conf. Fluid Search PubMed.
- X. Z. Chen, D. P. Shi, X. Gao and Z. H. Luo, Powder Technol., 2011, 205, 276–288 CrossRef.
- B. E. Launder and D. B. Spalding, Comput. Methods Appl. Mech. Eng., 1974, 3, 269–289 CrossRef.
- W. E. Ranz and W. R. Marshall, Chem. Eng. Prog., 1952, 48, 141–146 Search PubMed.
- M. Syamlal, W. Rogers and T. J. O'Brien, MFIX documentation theory guide, 1993 Search PubMed.
- C. K. K. Lun, S. B. Savage, D. J. Jeffrey and N. Chepurniy, J. Fluid Mech., 1984, 140, 223–256 CrossRef.
- N. M. Ghasem, W. L. Ang and M. A. Hussain, Korean J. Chem. Eng., 2009, 26, 603–611 CrossRef.
- I. Hyanek, J. Zacca, F. Teymour and W. H. Ray, Ind. Eng. Chem. Res., 1995, 34, 3872–3877 CrossRef.
- Q. Wang, Y. Lin, Z. Zhang, B. Liu and M. Terano, J. Appl. Polym. Sci., 2006, 100, 1978–1982 CrossRef.
- Y. V. Kissin, L. A. Rishina and E. I. Vizen, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 1899–1911 CrossRef.
- H. X. Zhang, Y. J. Lee, J. R. Park, D. H. Lee and K. B. Yoon, Polym. Bull., 2011, 67, 1519–1527 CrossRef.
- E. B. Nauman, Chemical Reactor Design, Optimization, and Scaleup, John Wiley & Sons, Inc., Hoboken, New Jersey, New York, 2008 Search PubMed.
- G. Wu, Q. Wang, K. Zhang and X. Wu, Powder Technol., 2016, 304, 120–133 CrossRef.
- L. Wang, X. Xie, G. Wei and R. Li, Part. Sci. Technol., 2017, 35, 177–182 CrossRef.
- Z. Wang, D. Bai and Y. Jin, Powder Technol., 1992, 70, 271–275 CrossRef.
- R. Gujjula and N. Mangadoddy, Part. Sci. Technol., 2015, 33, 593–609 CrossRef.
- G. B. Meier, G. Weickert and W. P. M. Van Swaaij, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 500–513 CrossRef.
- A. Shamiri, M. A. Hussain, F. S. Mjalli, M. S. Shafeeyan and N. Mostoufi, Ind. Eng. Chem. Res., 2014, 53, 8694–8705 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |