Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oscillating Seebeck coefficients in π-stacked molecular junctions†
Mohsin K. Al-Khaykanee *ab,
Ali K. Ismael
*ab,
Ali K. Ismael ac,
Iain Gracea and
Colin J. Lambert
ac,
Iain Gracea and
Colin J. Lambert *a
*a
aDepartment of Physics, University of Lancaster, Lancaster LA1 4YB, UK. E-mail: c.lambert@lancaster.ac.uk; mohsin.kad@gmail.com
bDepartment of Physics, College of Science, University of Babylon, Babel, Iraq
cDepartment of Physics, College of Education for Pure Science, Tikrit University, Tikrit, Iraq
First published on 10th July 2018
Abstract
When a linear aromatic molecule within a nanogap is bound only to a source electrode, and an adjacent molecule is bound only to a drain electrode, the two molecules can interact via pi–pi stacking, which allows electrons to flow from the source to the drain, via pi–pi bonds. Here we investigate the thermoelectric properties of such junctions, using mono-thiol oligo-phenylene ethynylene (OPE3)-based molecules as a model system. For molecules which are para-connected to the electrodes, we show that the Seebeck coefficient is an oscillatory function of the length L of the pi–pi overlap region and exhibits large positive and negative values. This bi-thermoelectric behavior is a result of quantum interference within the junction, which behaves like a molecular-scale Mach–Zehnder interferometer. For junctions formed from molecular monolayers sandwiched between planar electrodes, this allows both hole-like and electron-like Seebeck coefficients to be realized, by careful control of electrode separation On the other hand for meta-connected molecules, the Seebeck coefficient is insensitive to L, which may be helpful in designing resilient junctions with more stable and predictable thermoelectric properties.
Introduction
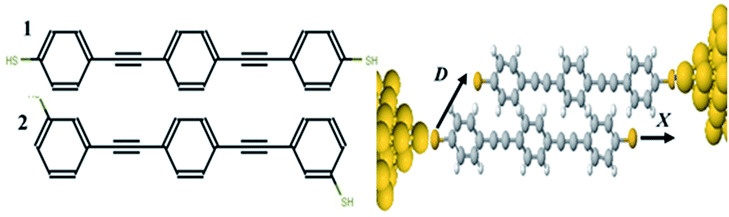
Measurement of the Seebeck coefficient S in single-molecule junctions1–9 has opened up the possibility of utilizing molecular-scale thin-film materials in flexible thermoelectric devices. A wide variety of single molecules have been measured with reported values of S up to 100 μV K−1.9 A key property determining the sign and magnitude of S is the position of the Fermi energy of the electrodes relative to the middle of the HOMO–LUMO gap of the molecule; a positive S implies that the Fermi energy EF is closes to the highest occupied molecular orbital (HOMO) and a negative S means it is closer to the lowest unoccupied molecular orbital (LUMO). Recently it has been demonstrated both experimentally and theoretically that single molecules can display bi-thermoelectric behaviour, in which the sign of S changes in response to both geometric changes10–12 and the application of pressure,11 which shift the positions of the HOMO and LUMO transport resonances relative to EF. An alternative approach to the control of quantum transport through single molecules involves utilizing quantum interference (QI) of de Broglie waves associated with electrons passing through the molecule,13–25 which can increase or decrease the electrical conductance depending on whether QI is constructive or destructive. One type of molecular junction that has shown QI involves two pi-stacked molecules,26–30 as shown in Fig. 1, where each molecule is attached to only one electrode by a thiol anchor and electrons flow from one electrode to the other via the overlap between the pi-orbitals of the two molecules.Measurements of the electrical conductance of monothiol-terminated pi-stacked oligo-phenylene ethynylene molecules were first reported in,26 while in,27 the pi-stacking of these molecules was switched on and off using bulky tertiary butyl groups, which controlled the spacing between the pi systems of adjacent molecules groups. In28 it was shown that for pi-stacked junctions formed from two amine-terminated conjugated molecules, the conductance, force and flicker noise differ dramatically when compared with the corresponding monomer junctions, thereby highlighting key differences between intra- and inter-molecular charge transport.
In29 conductance oscillations of pi stacked OPE3 with either one (S–OPE3) or two (S–OPE3–S) thiol anchoring groups as a function of their overlap length were measured. Pi-stacking has also been used to design molecular junctions30 that either enhance or suppress a phonon transport, while maintaining electrical conductance. In ref. 31 the symmetry breaking effects involved in chemisorbing π-stacked benzene rings to metallic electrodes was shown to have a significant impact on their transport properties. In32 five representative pi-stacked systems were studied to show how conjugation length and substituent groups influence their electrical conductance and Seebeck coefficient. These studies clearly demonstrate that the length of the overlap region between the two molecules controls the electronic structure of the junction and the nature of the quantum interference.
In this work we investigate whether the ability to tune the transport properties of such pi-stacked junctions can be used to control their Seebeck coefficient. We show that by varying the length of the pi-overlap region, not only can the magnitude of S be increased, but also the molecule can display both positive and negative S. This bi-thermoelectric behaviour is attractive, because compatible materials with both positive and negative Seebeck coefficients are needed in the construction of useable thermoelectric modules.33
Theoretical methods
To calculate the electronic transport properties of OPE π-conjugated molecules shown in Fig. 1, we use a combination of the density functional code SIESTA34 and the quantum transport code Gollum.35 The optimum geometry was calculated for molecules 1 and 2 by relaxing them to a force tolerance of 0.01 eV Å−1 using Troullier–Martins pseudopotentials to represent the potentials of the atomic cores,36 a generalized gradient approximation (GGA–PBE) functional to describe the exchange correlation,37 double-ξ polarized basis set, and a real-space grid was defined with an energy cutoff 150 Rydberg.In what follows, we study the effect of varying the pi-overlap length, for molecules with either para or meta connectivities to the electrodes. The optimal stacking geometry for both molecules was calculated initially without the gold electrodes by altering the displacement X, and the inter-molecular spacing D of junction containing either para-connected molecules 1, or meta-connected molecules 2, as shown in Fig. 1 (more details are shown in the ESI†) and then relaxing the dimer to minimize the total energy. We define X to be the distance between the sulfur atoms along the axis of the molecule, i.e. when X = 0 the overlap of the molecule is a maximum. In the case of both OPEs 1 and 2 the optimum values found are X = 0.161 nm and D = 0.33 nm, and this configuration has a binding energy of −0.77 eV (for binding energies a van der Waals38 functional was used see Fig. S3 in the ESI†). Within the DFT simulations, each molecule was then attached to one gold electrode as shown in Fig. 1. The electrodes consist of 6 layers of (111) gold each containing 25 gold atoms, and are terminated by a pyramid of gold atoms. The terminal sulfur atom of the thiol group loses it hydrogen atom when it attaches to a gold electrode, resulting in an optimised gold–sulfur binding distance of 2.4 Å. The hydrogen atom of the unattached thiol group remains bound to the sulfur. The zero-bias transmission coefficient T(E), which is the probability for an electron of energy E of electrons to transfer from left-to-right of electrodes24 was calculated by using the SIESTA code to obtain the DFT mean-field Hamiltonian, and then using Gollum to compute T(E). The slope of the natural logarithm of the transmission coefficient then yields the Seebeck coefficient S via the relation39
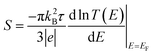 | (1) |
Results and discussions
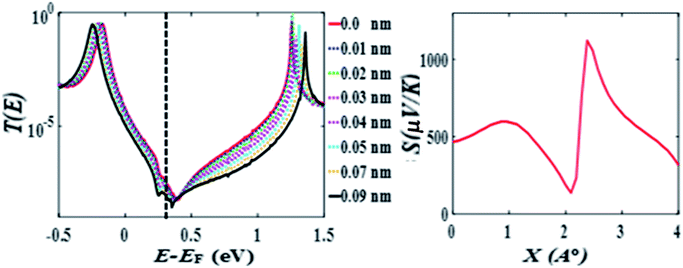
After choosing the optimum molecule separation of D = 0.33 nm, we varied the displacement X of the molecule and calculated the transmission coefficient T(E). Fig. 2 shows the results for X varying between 0 and 0.23 nm for the para connected molecule 1, (transmission data for a larger range of X are presented in the ESI Fig. S6 and S7†). At a value of X = 0.161 nm (which is the optimum stacking geometry) the Fermi energy (E−EF = 0 eV) lies close to the HOMO resonance, and there is a sharp dip in T(E) near E−EF = 0.1 eV in the gap between the HOMO and LUMO transmission resonances. This destructive interference feature is attributed to the multiple transport paths through the stacked molecule, which cause Mach–Zehnder-type interference effects. Fig. 2 shows that as X is increased, the anti-resonance moves towards the LUMO resonance and at value of X = 0.23 nm the interference dip sits at E−EF = 0.6 eV. The transmission curves also show that the HOMO–LUMO gap increases as X increases, due to the splitting between the two LUMO resonances of the individual molecules, which decreases as the coupling between the two molecules becomes weaker.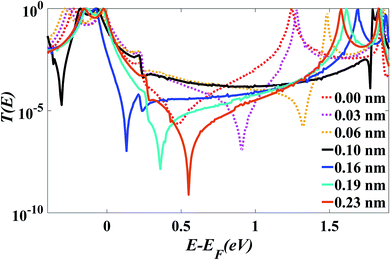 | ||
| Fig. 2 Zero bias transmission coefficient T(E) of molecule 1 against electron energy E for different displacements X and fixed separation D = 0.33 nm. | ||
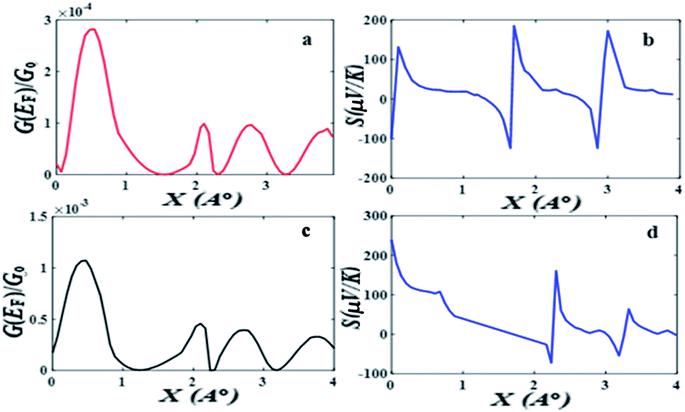
Fig. 2 shows when an anti-resonance passes through the Fermi energy, the gradient of T(E) changes sign, which demonstrates that the Seebeck coefficient S is sensitive to the stacking geometry. Fig. 3 (right panel) shows the calculated value of S at room temperature, for a Fermi energy of E−EF = 0.5 eV (see in Fig. 3(a and b)), E−EF = 0.3 eV (see in Fig. 3(c and d)), and a separation of D = 0.33 nm for values of X between 0 and 0.4 nm. At X = 0 the sign of S is negative and has a magnitude of −100 μV K−1. As the displacement X is increased the sign of S is switched and at a value of S at X = 0.02 nm is 100 μV K−1. The anti-resonance then moves away from the Fermi energy and S remains positive with a value of approximately 25 μV K−1. At greater displacements the sign of S oscillates. Fig. 3 left shows that these oscillations in the sign of S are accompanied by oscillations in the electrical conductance.
The above calculations were repeated for the meta-connected molecule 2 and the results are presented Fig. 4 (the separation is D = 0.33 and the displacement X is varied between 0 and 0.09 nm). Here the transmission T(E), shows an anti-resonance at 0.4 eV, which does not move across the HOMO–LUMO gap as X is increased. The value of the Seebeck coefficient is therefore positive for all values of X between 0 and 0.4 nm (see Fig. 4 right panel). This demonstrates that quantum interference effects in the meta-connected of molecule 2 are less sensitive to the pi–pi overlap displacement.
Conclusions
In a previous study of pi-stacked phenyl and anthracene derivatives32 it was shown that the Seebeck coefficient can change sign by displacing the molecules both parallel and perpendicular to the direction of current flow. Here, we show similar behaviour in linear pi-stacked OPE3 molecules with para connectivity to the electrodes, which have been shown to form pi-stacked junctions experimentally,26 but no such oscillatory behaviour occurs for meta-connected OPEs. When molecules are para-connected to the electrodes, the location of an anti-resonance due to destructive quantum interference is sensitive to the displacement of the molecules and causes the Seebeck coefficient to alternate in sign. This novel bi-thermoelectric behaviour has the potential to inform the design of thin-film thermoelectric materials and devices based on self-assembled molecular layers, where the spacing between planar electrodes could be controlled by introducing electrically insulating molecules of known length into a film of electrically-active pi–pi stacked molecules, thereby tuning the sign of their Seebeck coefficient. This is important technologically, because junctions with Seebeck coefficients of both signs are needed to boost the thermovoltage. On the other hand when molecules are meta-connected to the electrodes, the anti-resonance is less sensitive to the displacement of the molecules and the Seebeck coefficient is consistently positive. This is useful in the design of stable junctions with predictable Seebeck coefficients, since small fluctuations in the electrode separation have little effect.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by the UK EPSRC through grant nos. EP/M014452/1, EP/P027156/1 and EP/N03337X/1. Support from the European Commission is provided by the FET Open project 767187 – QuIET. M. K. A. acknowledges support from the Higher Committee for Education Development, and Babylon University in Iraq. A. K. I. acknowledges financial support from Tikrit University (Iraq).References
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Thermopower measurements in molecular junctions, Chem. Soc. Rev., 2016, 45(15), 4285–4306 RSC.
- L. Cui, R. Miao, C. Jiang, E. Meyhofer and P. Reddy, Perspective: Thermal and thermoelectric transport in molecular junctions, J. Chem. Phys., 2017, 146(9), 092201 CrossRef.
- P. Reddy, S. Y. Jang, R. A. Segalman and A. Majumdar, Thermoelectricity in molecular junctions, Science, 2007, 315(5818), 1568–1571 CrossRef PubMed.
- S. V. Aradhya and L. Venkataraman, Single-molecule junctions beyond electronic transport, Nat. Nanotechnol., 2013, 8(6), 399 CrossRef PubMed.
- A. Tan, J. Balachandran, S. Sadat, V. Gavini, B. D. Dunietz, S. Y. Jang and P. Reddy, Effect of length and contact chemistry on the electronic structure and thermoelectric properties of molecular junctions, J. Am. Chem. Soc., 2011, 133(23), 8838–8841 CrossRef PubMed.
- A. Tan, S. Sadat and P. Reddy, Measurement of thermopower and current–voltage characteristics of molecular junctions to identify orbital alignment, Appl. Phys. Lett., 2010, 96(1), 013110 CrossRef.
- M. Pfeiffer, A. Beyer, T. Fritz and K. Leo, Controlled doping of phthalocyanine layers by cosublimation with acceptor molecules: A systematic Seebeck and conductivity study, Appl. Phys. Lett., 1998, 73(22), 3202–3204 CrossRef.
- M. Tsutsui, T. Morikawa, Y. He, A. Arima and M. Taniguchi, High thermopower of mechanically stretched single-molecule junctions, Sci. Rep., 2015, 5, 11519 CrossRef PubMed.
- J. Duan, X. Wang, X. Lai, G. Li, K. Watanabe, T. Taniguchi and E. Y. Andrei, High thermoelectric power factor in graphene/hBN devices, Proc. Natl. Acad. Sci., 2016, 113(50), 14272–14276 CrossRef PubMed.
- J. Vacek, J. V. Chocholoušová, I. G. Stará, I. Starý and Y. Dubi, Mechanical tuning of conductance and thermopower in helicene molecular junctions, Nanoscale, 2015, 7(19), 8793–8802 RSC.
- C. M. Finch, V. M. Garcia-Suarez and C. J. Lambert, Giant thermopower and figure of merit in single-molecule devices, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(3), 033405 CrossRef.
- L. A. Algharagholy, T. Pope and C. J. Lambert, Strain-induced bi-thermoelectricity in tapered carbon nanotubes, J. Phys.: Condens. Matter, 2018, 30(10), 105304 CrossRef PubMed.
- L. Rincón-García, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis and C. J. Lambert, Molecular design and control of fullerene-based bi-thermoelectric materials, Nat. Mater., 2016, 15(3), 289 CrossRef PubMed.
- A. K. Ismael, I. Grace and C. J. Lambert, Increasing the thermopower of crown-ether-bridged anthraquinones, Nanoscale, 2015, 7(41), 17338–17342 RSC.
- W. Hong, H. Valkenier, G. Mészáros, D. Z. Manrique, A. Mishchenko, A. Putz and T. Wandlowski, An MCBJ case study: the influence of π-conjugation on the single-molecule conductance at a solid/liquid interface, Beilstein J. Nanotechnol., 2011, 2, 699 CrossRef PubMed.
- C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. Van Der Molen, Observation of quantum interference in molecular charge transport, Nat. Nanotechnol., 2012, 7(5), 305 CrossRef PubMed.
- T. Markussen, J. Schiötz and K. S. Thygesen, Electrochemical control of quantum interference in anthraquinone-based molecular switches, J. Chem. Phys., 2010, 132(22), 224104 CrossRef PubMed.
- Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong and S. X. Liu, Magic ratios for connectivity-driven electrical conductance of graphene-like molecules, J. Am. Chem. Soc., 2015, 137(13), 4469–4476 CrossRef PubMed.
- S. Sangtarash, H. Sadeghi and C. J. Lambert, Exploring quantum interference in heteroatom-substituted graphene-like molecules, Nanoscale, 2016, 8(27), 13199–13205 RSC.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi and M. R. Bryce, A quantum circuit rule for interference effects in single-molecule electrical junctions, Nat. Commun., 2015, 6, 6389 CrossRef PubMed.
- G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Exploring local currents in molecular junctions, Nat. Chem., 2010, 2(3), 223 CrossRef PubMed.
- M. Gantenbein, L. Wang, A. A. Al-jobory, A. K. Ismael, C. J. Lambert, W. Hong and M. R. Bryce, Quantum interference and heteroaromaticity of para-and meta-linked bridged biphenyl units in single molecular conductance measurements, Sci. Rep., 2017, 7(1), 1794 CrossRef PubMed.
- D. Nozaki and C. Toher, Is the Antiresonance in Meta-Contacted Benzene Due to the Destructive Superposition of Waves Traveling Two Different Routes around the Benzene Ring?, J. Phys. Chem. C, 2017, 121(21), 11739–11746 CrossRef.
- C. J. Lambert, Basic concepts of quantum interference and electron transport in single-molecule electronics, Chem. Soc. Rev., 2015, 44(4), 875–888 RSC.
- C. J. Lambert and S. X. A. Liu, Magic Ratio Rule for Beginners: A Chemist's Guide to Quantum Interference in Molecules, Chem.–Eur. J., 2018 Mar 20, 24(17), 4193–4201 Search PubMed.
- S. Wu, M. T. González, R. Huber, S. Grunder, M. Mayor, C. Schönenberger and M. Calame, Molecular junctions based on aromatic coupling, Nat. Nanotechnol., 2008, 3(9), 569 CrossRef PubMed.
- S. Martín, I. Grace, M. R. Bryce, C. Wang, R. Jitchati, A. S. Batsanov, S. J. Higgins, C. J. Lambert and R. J. Nichols, Identifying diversity in nanoscale electrical break junctions, J. Am. Chem. Soc., 2010, 132(26), 9157–9164 CrossRef PubMed.
- A. Magyarkuti, O. Adak, A. Halbritter and L. Venkataraman, Electronic and Mechanical Characteristics of Stacked Dimer Molecular Junctions, Nanoscale, 2018, 10(7), 3362–3368 RSC.
- R. Frisenda, V. A. Janssen, F. C. Grozema, H. S. van der Zant and N. Renaud, Mechanically controlled quantum interference in individual π-stacked dimers, Nat. Chem., 2016, 8(12), 1099 CrossRef PubMed.
- G. Kiršanskas, Q. Li, K. Flensberg, G. C. Solomon and M. Leijnse, Designing π-stacked molecular structures to control heat transport through molecular junctions, Appl. Phys. Lett., 2014, 105(23), 233102 CrossRef.
- G. C. Solomon, C. Herrmann, J. Vura-Weis, M. R. Wasielewski and M. A. Ratner, The chameleonic nature of electron transport through π-stacked systems, J. Am. Chem. Soc., 2010 May 20, 132(23), 7887–7889 Search PubMed.
- Q. Li and G. C. Solomon, Exploring coherent transport through π-stacked systems for molecular electronic devices, Faraday Discuss., 2014, 174, 21–35 RSC.
- G. S. Nolas, J. Sharp and J. Goldsmid, Thermoelectrics: basic principles and new materials developments, Springer Science & Business Media, 2013, p.45 Search PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745 CrossRef.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany and H. Sadeghi, GOLLUM: a next-generation simulation tool for electron, thermal and spin transport, New J. Phys., 2014, 16(9), 093029 CrossRef.
- N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(3), 1993 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef PubMed.
- L. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92(24), 22–25 CrossRef PubMed.
- M. Paulsson and S. Datta, Thermoelectric effect in molecular electronics, Phys. Rev. B, 2003, 67(24), 241403 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04698k |
| This journal is © The Royal Society of Chemistry 2018 |