Improved hydrogen storage kinetics of nanocrystalline and amorphous Ce–Mg–Ni-based CeMg₁₂-type alloys synthesized by mechanical milling

Abstract

In this paper, ball milling was used to prepare CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys having nanocrystalline and amorphous structures. The structures of the alloys and their electrochemical and gaseous kinetic performances were systematically investigated. It was shown that the increase in Ni content was beneficial to the formation of nanocrystalline and amorphous structures, and it significantly enhanced the electrochemical and gaseous hydrogen storage performances of as-milled alloys. In addition, the hydrogen storage capacities of the alloys fluctuated greatly with variation in milling duration. The maximum values of hydrogen capacity detected by varying the milling durations were 5.949 wt% and 6.157 wt% for x = 100 and 200 alloys, respectively. Similar results were observed for the hydriding rates and high-rate discharge abilities (HRD) of the as-milled alloys. The dehydriding rate increased with the increase in milling duration. The reduction in hydrogen desorption activation was the reason for enhanced gaseous hydrogen storage kinetics.

---

Introduction

Fossil fuels mainly consist of hydrocarbons and their polymers, and they are non-renewable sources of energy. The use of fossil fuels can generate carbon dioxide and pollution, which are detrimental to ecological environment and human health. Thus, clean energy, especially hydrogen energy, has received considerable attention worldwide. A large share of energy demand comes from the transport sector, accounting for about a quarter of the world's total energy consumption.¹ In addition, automobile exhaust is one of the biggest pollutant sources, especially due to the high rate of car ownership in Beijing, according to the Ministry of Ecology and Environment of China. Therefore, the development of clean energy can help improve the living environment. As a clean and available alternative energy, hydrogen power has become one of the most promising new energies owing to its highly stable, efficient and pollution-free power.^2,3 Storage system is one of the main technical obstacles that limits the exploitation and utilization of hydrogen energy; to solve this major technical obstacle for realizing clean energy vehicles, developing a hydrogen storage system with excellent performance is a necessary prerequisite.⁴ Metal hydrides with good performances are preferred as they meet the requirements of mobile applications.⁵ Researchers have conducted extensive and successful studies in the search for ideal metal hydrides, and numerous results have been reported in many papers. Regrettably, none of these results meet all the property requirements suggested by the U.S. Department of Energy (DOE) for vehicular applications.^6,7 Hydrogen storage material is considered as one of the most potential negative electrodes of Ni-MH cells, and it is also one of the current research hotspots. In some areas, AB₅- and AB₂-type alloys based on RE have been commercialized on a large scale, but both are unsatisfactory as electrode materials for applications in EV or HEV because of their relatively low specific capacities. Mg-based alloys are promising candidates for negative electrodes in Ni-MH cells or hydrogen fuel-cell vehicles considering their hydrogen absorption capacities.⁸ Especially, REMg₁₂-type alloys have received extensive attention owing to their gaseous hydrogenation capacities of 3.7–6.0 wt% and theoretical electrochemical capacities of over 1000 mA h g⁻¹;^9,10 however, their inherent problems of sluggish hydriding/dehydriding kinetics, relatively high temperatures of hydrogen desorption and remarkably low electrochemical discharge capacities at room temperature have seriously hindered their practical applications. Therefore, further efforts are needed to enhance the hydrogenation capacity for applications in new energy vehicles in the future.

Hydrogen storage properties can be effectively enhanced by methods such as alloying and microstructure modification.¹¹ Particularly, partially replacing Mg with RE elements (La, Pr, Y, Nd, and Ce) in hydrogen storage alloys can facilitate hydrogen desorption and decrease the stability of the hydride.^12–14 Also, the corrosion resistances of alloys can be enhanced by elemental substitution, thereby improving their cycle performances.^15,16 Furthermore, it was documented that the microstructures of Mg-based alloys influenced their hydriding and dehydriding kinetics.¹⁷ The hydrogenation/dehydrogenation performances of Mg-based alloys can be significantly enhanced by reducing their grain sizes far below the micrometer scale.¹⁸ Kumar et al.¹⁹ stated that the temperature of hydrogen absorption/desorption of polycrystalline Mg₂Ni decreased from 573 K to 473 K due to nanocrystallization. Wu et al.²⁰ reported that amorphous and/or nanocrystalline structures can help increase the electrochemical absorption and desorption performances of Mg–Ni-based alloys. Few techniques are used to synthesize Mg-based alloys with different compositions such as (a) mechanical milling,²¹ (b) rapid solidification (RS),²² (c) hydriding combustion synthesis and (d) equal channel angular pressing (ECAP).^23,24 The universally accepted methods of obtaining amorphous and/or nanocrystalline alloys are mechanical milling and melt spinning. Spassov et al.²⁵ reported that the maximum hydrogen absorption capacity of Mg₆₃Ni₃₀Y₇ hydrogen storage alloy was about 3.0 wt%, which was prepared by rapid solidification. Huang et al.²⁶ prepared amorphous and nanocrystalline Mg₆₅Ni₂₇La₈ alloys by melt-spinning, obtaining the highest discharge capacity of about 582 mA h g⁻¹ at room temperature. Wang et al.²⁷ found that the initial discharge capacity of ball-milled MmMg₁₂ alloy with Ni powders was enhanced from 770 to 1200 mA h g⁻¹ when the amount of Ni was increased from 150 to 200 wt%. Zhang et al.²⁸ found that the addition of different RE elements can have beneficial effects on the kinetics of hydriding and dehydriding of as-spun Mg₁₀NiRE (RE = La, Nd and Sm) alloys. Yartys et al.²⁹ found that LaMg₁₁Ni alloy prepared by solidifying at the highest cooling rate has the maximum hydrogenation capacity of about 5.02 wt% H and the fastest hydrogenation kinetics.

In the present study, mechanical milling, a method of powder metallurgy, was used to prepare nanocrystalline and amorphous CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys. The gaseous and electrochemical performances were systematically studied at different Ni contents and milling durations.

Experimental

Prior to the preparation of the experimental alloy CeMg₁₁Ni, a vacuum induction furnace was filled with 0.04 MPa pure helium gas as a shielding gas to prevent the sample from being volatilized during preparation. The molten alloy prepared by induction melting was then poured into an iron mold. The columnar ingots obtained were ground to fine powders below 200 mesh by mechanical crushing and then mixed with Ni powders at mass ratios of 1 : 1 and 1 : 2. The mixed alloy powders and Cr–Ni stainless steel balls were put into Ar-filled Cr–Ni stainless steel vials at a mass ratio of 1 : 35, and the whole operation was carried out in an Ar-filled glove box. Finally, a planetary-type mill was selected for mechanical milling, and the milling duration times were set at 5, 10, 20, 40 and 60 h with milling speed of 135 rpm.

Inductively coupled plasma atomic emission spectrometry (ICP-AES) was used to measure the actual compositions of the sample alloys. D/max/2400 X-ray diffraction (XRD) filtered Cu-K_α1 radiation with graphite was used to help determine the phase structures; 40 kV, 160 mA and 10° min⁻¹ were the experimental parameters of diffraction. HRTEM (JEM-2100F, 200 kV) equipped with electron diffraction (ED) was used to observe the samples and their crystalline states.

The experimental alloys were activated by a Sieverts equipment, and kinetics curves were measured at a fixed initial pressure and different temperatures (553, 573, 593 and 613 K). The initial pressures of the hydriding and dehydriding processes were set as 3 MPa and 1 × 10⁻⁴ MPa, respectively. In fact, the values of these pressures changed as the experiment progressed. The sample mass required for each experiment was 300 mg, and the temperature accuracy of the sample room was controlled to ±2 K. Thermal gravity analysis (TGA, Q600) was also used to measure hydrogen desorption properties at different heating rates.

The alloy powder (0.25 g) was thoroughly mixed with 0.75 g of carbonyl nickel powder and then pressed under 35 MPa into a round electrode pellet having a diameter of 15 mm. The measurements of electrochemical kinetics were obtained using a tri-electrode open cell (Hg/HgO as the reference electrode and sintered Ni(OH)₂/NiOOH as the counter electrode) at 303 K. KOH solution (6 mol L⁻¹) was used as the electrolyte for the tri-electrode open cell. The difference between the voltages of the reference electrode and negative one was defined as the discharge voltage. The alloy electrodes were charged and discharged at the same current density, and the interval between charging and discharging was set as 15 min in each cycle. The discharge cut-off voltage was set at −500 mV.

An electrochemical workstation (PARSTAT 2273) was used to measure EIS at different temperatures. At 50% depth of discharge, the measurement was performed from 10 kHz to 5 mHz frequency domain with an amplitude of 5 mV, and the number of points per decade of frequencies was 60. For potentiostatic discharge, the experimental electrodes in fully charged states were tested using the electrochemical workstation, and the parameter of discharging was set to 500 mV potential steps for 5000 s; experimental data were collected and analyzed by the electrochemistry corrosion software (CorrWare).

Results and discussion

Composition, microstructure characteristics

The actual compositions of CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200) alloys were measured by ICP-AES, as shown in Table 1. To explore the changes in phase structures and components before and after hydriding, the sample alloys were analyzed using XRD, as displayed in Fig. 1. The results revealed that the alloy had multiphase structures, which contained a host phase CeMg₁₂ and a minor phase Mg₂Ni. The diffraction peaks of mechanically milled samples were apparently merged and broadened, indicating nanocrystallization or amorphization. Moreover, increasing the Ni content clearly lowered the intensity of the diffraction peaks and visibly increased their widths; in other words, the increase in Ni content was beneficial for the formation of alloy glass. The activation energy of the crystalline-to-amorphous phase transformation of the REMg₁₂ alloy was reduced with an increase in the Ni content, as stated by Abdellaoui et al.³⁰ Three hydrides including CeH₃, MgH₂ and Mg₂NiH₄ were produced during the hydrogenation reaction of the as-cast alloy, and their production pathways are as follows:³¹

CeMg₁₂ + H₂ → MgH₂ + CeH₃;

Mg₂Ni + H₂ → Mg₂NiH₄.

Table 1 The actual compositions of CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200) alloys measured by ICP

CeMg11Ni + x wt% Ni	Ce (wt%)	Mg (wt%)	Ni (wt%)
x = 0	30.05 ± 0.28	57.35 ± 0.54	12.59 ± 0.12
x = 100	15.07 ± 0.13	28.68 ± 0.27	56.31 ± 0.51
x = 200	10.02 ± 0.11	19.13 ± 0.21	70.85 ± 0.71

---

Fig. 1 XRD profiles of as-cast and milled (10 h) CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200) alloys (a) before and (b) after hydriding.

Furthermore, it is noteworthy that the H atoms entered the alloy lattice interstitials causing lattice stress and expansion during hydrogenation, which was the primary cause for significant broadening of the diffraction peaks of the as-cast and milled alloy samples. The nanocrystalline and amorphous structures were still present in the as-milled sample alloys in a saturated hydrogenation state, which meant that the structural stability of the as-milled alloy was excellent.

HRTEM micrographs and ED patterns of the as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys presented in Fig. 2 show that the alloy particles clearly agglomerated, which was due to cold welding of the alloy and Ni particles during ball milling. Using the linear intercept method, it was observed that the average sizes of the alloy particles ranged from 30 to 50 nm, which was consistent with the observations of the nitrogen physisorption analysis. Moreover, a careful observation revealed that there was no significant decrease in the particle sizes of the alloys when the milling duration was increased from 10 to 60 h, indicating that the particle sizes did not always decrease with the extension in milling duration. However, an interesting point to note was that the particle boundaries of the alloy powder milled for 60 h became more indiscernible, indicating that prolonging the milling time greatly modified the particle surface states and interfacial structures. Crystal defects were observed from local amplification of the sample alloys. Moreover, extending the milling duration from 10 to 60 h markedly decreased the alloy grain sizes and increased the degree of disorder, indicating that much internal energy was stored during ball milling; this made the lattice unstable, eventually resulting in fine grain sizes. It was observed that the amorphous phase notably increased with the extension of milling duration, which was confirmed by analyzing the Debye–Scherrer rings.

Fig. 2 HRTEM micrographs and ED patterns of the as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys: (a) and (d) x = 100 alloy milled for 10 h; (b) and (e) x = 200 alloy milled for 10 h; (c) and (f) x = 200 alloy milled for 60 h.

Gaseous hydrogen absorption and desorption kinetics

At 593 K and 3 MPa, the relationships between the hydrogenation capacities of the sample alloys and hydriding reaction times were obtained to assess the hydrogenation kinetics, as illustrated in Fig. 3. The sample alloys exhibited extremely rapid rates of hydrogen absorption in the beginning of the hydrogenation reaction, after which the rate slowed down, and the alloys reached a saturated state for a long period of time. Meanwhile, the milling duration influenced the hydrogenation capacity. For better comparison, we approximated the hydrogen absorption capacity C^a(100) at 100 min as its saturated capacity. With respect to the values of all the alloys tested, we found that the error between the C^a(100) values and the value of saturated hydrogen absorption capacity did not exceed 2%. Therefore, it was reasonable to use the value of C^a(100) to approximate saturation hydrogen absorption.

Fig. 3 Hydrogen absorption kinetic curves of the as-milled CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200) alloys at 593 K: (a) x = 0, (b) x = 100, (c) x = 200.

Thus, numerical correspondences between the C^a(100) values and milling time were easily established, as shown in the insets of Fig. 3. The capacities increased at first and then decreased with the increase in milling duration. The maximum C^a(100) values were 5.698 wt%, 5.949 wt% and 6.157 wt% for the x = 0, 100, 200 alloys, respectively. We did not consider the weight of the added Ni while calculating gaseous hydrogen capacities. By comparing the alloys with different Ni contents, we found that Ni could effectively improve the capacity. However, the hydrogen absorption rate is also a key factor that restricts the application of hydrogen storage materials in the field of mobile transportation. Herein, the hydrogenation kinetics of the alloys were characterized by the hydrogenation saturation ratio (R^a(t)), which can be defined as R^a(t) = C^a(t)/C^a(100) × 100%, where C^a(t) is the hydrogenation capacity at t min, and C^a(100) has been defined previously. Similarly, the dehydrogenation ratio (R^d(t)) is defined as R^d(t) = C^d(t)/C^a(100) × 100%, where C^d(t) is the dehydrogenation capacity at t min, and it represents dehydrogenation kinetics. We set the reference times for hydrogen absorption and hydrogen desorption to 10 and 20 min, respectively, to easily explore the correspondences between the values of R^a(t) and R^d(t) and the milling duration. The relationships between the values of R^a(10) (t = 10) and R^d(20) (t = 20) were established, as displayed in Fig. 4. Apparently, the R^a(10) values increased at first and then decreased with the increase in milling duration. The corresponding maximum values of x = 0, x = 100 and x = 200 alloys were 88.15%, 97.8% and 100% at 593 K and 3 MPa. However, the hydrogen desorption rates displayed monotonic increase as the ball milling duration was prolonged, which was different from the trend of hydrogen absorption kinetics. In particular, extending the milling duration from 5 to 60 h increased the R^d(20) values (x = 0, 100, 200) from 32.1% to 43.6%, 37.55% to 47.21% and 47.29% to 61.70%, respectively.

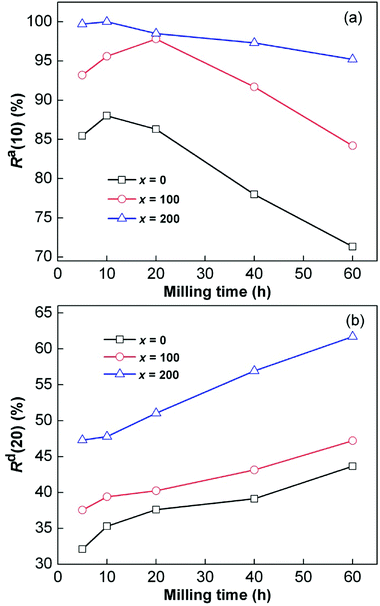Fig. 4 Evolutions of R^a(10) (a) and R^d(20) (b) values at 593 K of the as-milled CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200) alloys with milling time.

Furthermore, it was found by comparison that the x = 200 alloy possessed higher R^a(10) and R^d(20) values than x = 100 alloy at the same milling time, which was due to the relatively catalytic alloy surface for hydrogen reactions in the process of ball milling as a result of increase in Ni content; this was previously stated by Anik et al.⁵

According to the above-mentioned results, we can infer that the increase in milling time can positively and negatively affect the capacity and kinetics. The change in the microstructure of the alloy caused by ball milling can have beneficial effects on the capacity and kinetics. Meanwhile, the capacity can be improved by the crystallites and grain boundaries caused by ball milling, because the H concentration in the grain boundary is much higher than that in the grain interior and in the amorphous region.^24,32 Moreover, the large number of sites with low diffusion activation energy provided by the grain boundaries facilitate the diffusion of H atoms, thereby enhancing the hydrogenation kinetics of the alloys.^19,33 The formation of glass has a negative influence on the hydrogenation capacity and kinetics because the diffusion ability of H atoms in the amorphous phase is hindered, and it is lower than that in the nanocrystalline phase. Meanwhile, the reduction of grain size and the increase in internal strain caused by mechanical milling can positively contribute to the dehydrogenation kinetics.³⁴ It can be clearly determined that the dehydrogenation performances of Mg-based alloys can be greatly enhanced when the grain size is much lower than the micrometer scale.³⁵ The stored internal strain increases with milling duration, as stated by Niu et al.³⁶ The increase in the internal strain consequently results in great decrease in the hydride stability, thus facilitating dehydrogenation. The improved kinetics of hydrogenation and dehydrogenation due to the increase in the Ni content are ascribed to the high catalytic alloy surface created by mechanical milling.³⁷

The hydrogen absorption kinetic curves were analyzed using the Johnson–Mehl–Avrami (JMA) model.

ln[−ln(1 − α)] = η ln k + η ln t (1)

here, α is the reaction fraction, which ranges from 0 to 1; the reaction order η and the effective kinetic parameter k can be obtained from the slope and intercept by plotting ln[−ln(1 − α)] versus ln t. The values of η range from 0.9292 to 1.1212, as illustrated in Table 2, indicating that the hydriding reaction of the alloys follows a diffusion-controlled mechanism.³⁸ The hydrogen absorption reaction of an alloy is actually a chemical reaction between a solid phase and a gaseous phase. The reaction process can be divided into three stages:^4,39 (1) surface activation; (2) nucleation and growth of the initial hydride, accompanied by lattice expansion; and (3) generation of a large number of hydrides until saturation of hydrogen absorption. Mg present on the alloy surface can rapidly absorb hydrogen and form a metal hydride layer in the initial stage of hydrogen absorption. As the reaction progresses, the hydride layer on the alloy surface is gradually thickened. At this point, the hydrogenation kinetic property is no longer constrained by the nucleation and growth factors, but it is constrained by the hydride layer on the alloy surface. Thus, the hydrogenation rate during the later stage gradually slows down.¹⁶

Table 2 The reaction order η values obtained from the JMA plots for CeMg₁₁Ni + x wt% Ni (x = 0, 100, 200)

Milling time	x = 0	x = 100	x = 200
5 h	0.9427	0.9650	1.1048
10 h	0.9291	0.9343	1.0965
20 h	1.0775	0.9578	1.0567
40 h	0.9722	0.9808	1.0956
60 h	0.9704	1.0961	1.1212

---

Hydrogen desorption activation energy

Herein, the Kissinger method is introduced to evaluate the dehydrogenation activation energy, thereby revealing the mechanism of the function of the increase in Ni content and milling duration with respect to dehydrogenation kinetics. Generally, the reaction activation energy, which is the decisive factor concerning kinetics, refers to the total potential barrier that must be overcome during the reaction. The dehydrogenation activation energy (E^de) generally refers to the total energy barrier concerning the gaseous dehydrogenation reaction.⁴⁰ E^de is estimated using the following Kissinger equation:⁴¹

d[ln(β/T_p²)]/d(1/T_p) = −E^de(k)/R (2)

here, β, R, E^de(k) and T_p are the heating rate, ideal gas constant, activation energy and absolute temperature, respectively, which correspond to the maximum desorption rate in the DSC curves. To calculate the value of E^de(k) using the Kissinger equation, DSC was used to measure the dehydrogenation reactions of the alloys in a saturated hydrogenation state (573 K, 3 MPa) at heating rates of 5, 10, 15 and 20 K min⁻¹.

Fig. 5 shows the hydrogen desorption DSC curves. A clear endothermic peak for dehydrogenation can be observed in the DSC curves of all the alloys, which indicates that the same reaction proceeds throughout each system. Simultaneously, the temperature corresponding to the endothermic peak of the x = 200 alloy is lower than that of the x = 100 alloy at each heating rate, which indicates that increasing the Ni content can be helpful for enhancing the reaction rate during the desorption of hydrogen. Using the logarithmic transform of eqn (1), the Kissinger graphs of ln(β/T_p²) vs. 1/T_p can be obtained, as illustrated in Fig. 5, and they are nearly linear. Thus, E^de(k) can be calculated from the slopes of the Kissinger plots. The variations in E^de(k) values of the as-milled sample alloys with milling duration are presented in Fig. 6. It can be observed that the increase in milling duration can lead to clear reduction in the E^de(k) values. Also, the dehydrogenation activation energy shows a significant downward trend with the increase in Ni content. Thereby, we can infer that the increase in Ni content and milling time can lead to lower dehydrogenation activation energy, which enhances the dehydrogenation kinetics.

Fig. 5 DSC curves of the as-milled (10 h) CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys at various heating rates and corresponding Kissinger plots: (a) x = 100, (b) x = 200.

Fig. 6 Variations of E^de(k) values of the as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys with milling time.

Discharge capacity and electrochemical kinetics

At a current density of 60 mA g⁻¹, the discharge potential curves of the as-milled alloy electrodes were obtained, as shown in Fig. 7. The discharge capacity of the alloys as a function of milling duration is also inserted in Fig. 7. An increasing trend was observed with the extension of milling duration for the same alloy. By comparing the x = 100 and x = 200 alloys, we inferred that Ni played a key role in improving the discharge capacity. HRD quantitatively characterizes the electrochemical kinetics of the alloy electrodes, and it is defined as HRD = C_i/C₆₀ × 100%; C_i and C₆₀ in this formula represent the maximum discharge capacity at different current densities, and the subscripts i and 60 are state variables representing the current density at charge–discharge. Fig. 8 displays the relationships between HRDs of the as-milled sample alloys and current densities. The HRD values decrease sharply with the increase in current density. For ease of comparison, we consider the current density of 600 mA g⁻¹ as a standard to investigate HRD as a function of milling duration, as inserted in Fig. 8. The HRD values show an increasing trend at first and then a decreasing trend with the increase in milling duration; the maximum HRD values of the as-milled (x = 100, 200) alloys are 72.20% and 77.55% respectively, which are nearly equivalent to those of RE-based AB₅-type alloy electrodes that have exceptional kinetic performances. Furthermore, the x = 200 alloy possesses superior HRD compared to the x = 100 alloy at each milling duration, which indicates that the alloy electrochemical kinetics can be enhanced by increasing the Ni content. It is generally accepted that there are two basic factors that determine HRD including surface charge-transfer rate and H diffusion capability in the alloy bulk.⁴² The milling time and Ni content are used as independent variables to study their influences on the rate of charge-transfer and H diffusion ability, which further reveal the kinetic mechanisms of the sample alloys. On the basis of the slope of the linear region of Fig. 8, the diffusion coefficient of H atoms can be easily calculated by eqn (2) and eqn (3) and with the help of White's model.⁴³

lg i = lg[±6FD(C₀ − C_s)/(da²)] − π²Dt/(2.303a²) (3)

D = −2.303a²[d(lg i)/d(lg t)]/π² (4)

here, a, d, i, t, C_s, D and C₀ are the radius of the alloy particles (cm), density of the alloy (g cm⁻³), diffusion current density (A g⁻¹), discharge time (s), H concentration (mol cm⁻³), H diffusion coefficient (cm² s⁻¹) and initial H concentration in the alloy bulk (mol cm⁻³), respectively. The relationship between the milling durations and the D values calculated from eqn (4) is inserted in Fig. 9. Clearly, the D values increase at first and then decrease as the milling duration is extended. A careful analysis indicates that H diffusion ability is not the only factor that affects the electrochemical kinetics because the milling durations corresponding to the maximum HRDs are not equal to those at which the alloys obtain the maximum D values. Apparently, this factor is undoubtedly the charge-transfer rate, which can be evaluated by EIS in terms of the Kuriyama's model.⁴² EIS curves of x = 200 alloy are displayed as a typical representative in Fig. 10. Each EIS is divided into three parts: high, middle and low frequency regions, which accurately interpret the electrode electrochemical process; the smaller semicircle located in the high frequency region corresponds to the contact resistance between the conductive material and the alloy powder, and the larger one located in the middle frequency region represents the surface charge-transfer resistance (R_ct). Finally, the straight line located in the low frequency region corresponds to the Warburg impendence. Based on the equivalent circuit inserted in Fig. 10, the R_ct values can be calculated by the Z-View fitting program. As considered by Kuriyama et al.,⁴⁴ the surface reactivity and reaction area of the alloy are the two crucial parameters for determining the R_ct value. The apparent activation enthalpy Δ_rH*, which can accurately evaluate the electrochemical reactivity of the alloy surface, can be calculated by the following formula:

ln[(T/R_ct)/(K Ω⁻¹)] = C₀ − Δ_rH*/(RT) (5)

here, R_ct, R, T and C₀ are the charge-transfer resistance, gas constant, temperature of the sample and a constant that includes surface area. EIS curves of the as-milled alloys are measured at 303 K, 313 K and 323 K considering the calculation condition of eqn (5). The as-milled (10 h) alloys are depicted in Fig. 11. According to the data from Fig. 11, the Kuriyama graph of ln(T/R_ct) vs. 1/T can be plotted using the logarithmic transform of eqn (4), as inserted in Fig. 11. The Δ_rH* values can be calculated using the slopes of the Kuriyama plots. We thus established the relationship between Δ_rH* values and milling duration, as presented in Fig. 12. The Δ_rH* values decrease at first and then increase with variations in milling duration. By comparing Fig. 8 and 12, the milling duration corresponding to the maximum HRDs of the as-milled alloys is almost equivalent to the milling duration corresponding to the minimum Δ_rH* values, which implies that the charge-transfer ability is a principal factor determining the electrochemical kinetics. Hence, it can be concluded that the decrease in activation enthalpy Δ_rH* is the reason for improved HRD.

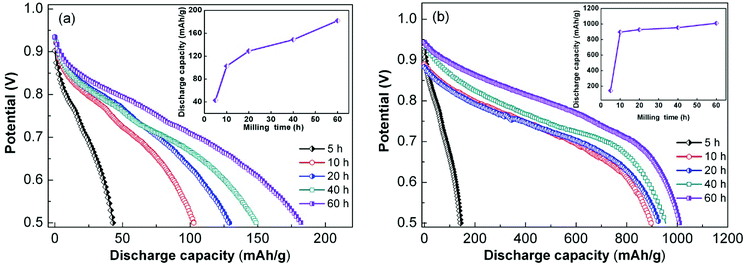Fig. 7 Discharge potential curves of as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys (a) x = 100, (b) x = 200.

Fig. 8 Evolution of HRD of the as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys with current density: (a) x = 100, (b) x = 200.

Fig. 9 Semilogarithmic curves of anodic current vs. time response of the as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys: (a) x = 100, (b) x = 200.

Fig. 10 Electrochemical impedance spectra (EIS) of the as-milled CeMg₁₁Ni + 200 wt% Ni alloy and the equivalent circuit.

Fig. 11 EIS curves of as-milled (10 h) CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys and plots of ln(T/R_ct) vs. 1/T: (a) x = 100, (b) x = 200.

Fig. 12 Evolution of the Δ_rH* values of as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys with milling time.

The electrochemical charging/discharging reactions can be summarized according to the following equation:

M + x/2H₂O + x/2 e⁻ ↔ MH_x + x/2OH⁻ (6)

here, M is the hydrogen storage alloy. Considering the charging process of the sample electrode in KOH solution, the electrolytic hydrogen atoms gradually diffuse from the alloy-electrolyte interface into the bulk alloy and are then stored as hydrides in the metallic lattice, according to eqn (6). During the process of discharging, H diffuses from the bulk alloy to the alloy surface and then reacts with O₂ to generate H₂O. There are two feasible approaches for H atom diffusion to the alloy surface: (a) formation of H molecules by combining together or (b) production of metal hydrides via diffusion. The ratio of the diffusion current to the imposing current is defined as the utilization of charging current. The diffusion rate of H atoms within the alloy surface layer is a main factor affecting the utilization of the charging current. We can infer that the increase in milling duration most likely has multifaceted influences on the electrochemical kinetics, both positive and negative. The positive impact of the increase in milling duration can be due to the following aspects: first, many crystal defects created by mechanical milling are helpful in enhancing the rates of hydrogen diffusion and charge transfer; second, the size of alloy particles can be sharply decreased by mechanical milling, thereby increasing the interface area. Increasing the milling time leads to more amorphous phases, which is one of the reasons for the negative effects on the alloy hydrogen storage performances. The above-mentioned phenomenon can be due to the amorphous phase, which can effectively suppress alloy pulverization during the charge–discharge cycle, due to which the new electrode effective surface is reduced, thus impairing the hydrogen diffusion ability and charge transfer rate.⁴⁵

Conclusions

A systematic study of as-milled CeMg₁₁Ni + x wt% Ni (x = 100, 200) alloys was conducted including both gaseous hydrogen storage and electrochemical properties, and the related key conclusions are summarized as follows:

(1) Increasing the Ni content can reduce the dehydrogenation activation energy and activation enthalpy, which can significantly improve the kinetics of the as-milled alloys, including both gas and electrochemistry.

(2) The maximum values of C^a(100) and R^a(10) of the alloys are observed as the milling duration is varied, but R^d(20) is continuously enhanced as the milling duration is extended, which can be ascribed to the facilitated glass and decreased dehydrogenation activation energy.

(3) The Kissinger method was introduced to assess the dehydrogenation activation energy; it revealed that the dehydrogenation activation energies decreased as the milling duration and Ni content increased, which improved the dehydrogenation kinetics.

(4) HRDs of the alloys have maximum values as the milling duration is varied, and the maximum HRD values correspond to the minimum Δ_rH* values. Hence, it can be inferred that the charge transfer ability within the electrode surface is a key controlling factor of the alloy electrochemical kinetics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundations of China (51761032 and 51471054), and the Natural Science Foundation of Inner Mongolia, China (2015MS0558).

References

1. D. Mori and K. Hirose, Int. J. Hydrogen Energy, 2009, 34, 4569–4574.
2. P. Dibandjo, C. Zlotea, R. Gadiou, C. M. Ghimbeu, F. Cuevas, M. Latroche, E. Leroy and C. Vix-Guterl, Int. J. Hydrogen Energy, 2013, 38, 952–965.
3. T. N. Veziroglu and S. Sahin, Energy Convers. Manage., 2008, 49, 1820–1831.
4. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
5. M. Anik, F. Karanfil and N. Küçükdeveci, Int. J. Hydrogen Energy, 2012, 37, 299–308.
6. Y. Zhang, M. Ji, Z. Yuan, W. Bu, Y. Qi and S. Guo, RSC Adv., 2017, 7, 37689–37698.
7. L. E. Klebanoff and J. O. Keller, Int. J. Hydrogen Energy, 2013, 38, 4533–4576.
8. S. S. Makridis, E. I. Gkanas, G. Panagakos, E. S. Kikkinides, A. K. Stubos, P. Wagener and S. Barcikowski, Int. J. Hydrogen Energy, 2013, 38, 11530–11535.
9. Y. Wang, X. Wang and C. M. Li, Int. J. Hydrogen Energy, 2010, 35, 3550–3554.
10. Y. Wang, S. Z. Qiao and X. Wang, Int. J. Hydrogen Energy, 2008, 33, 5066–5072.
11. Y. F. Liu, H. G. Pan, M. X. Gao and Q. D. Wang, J. Mater. Chem., 2011, 21, 4743–4755.
12. E. A. Lass, Int. J. Hydrogen Energy, 2011, 36, 10787–10796.
13. N. Juahir, N. S. Mustafa, A. M. Sinin and M. Ismail, RSC Adv., 2015, 5, 60983–60989.
14. Z. M. Yuan, W. Zhang, P. L. Zhang, Y. H. Zhang, W. G. Bu, S. H. Guo and D. L. Zhao, RSC Adv., 2017, 7, 37689–37698.
15. M. V. Simičić, M. Zdujić, R. Dimitrijević, L. Nikolić-Bujanović and N. H. Popović, J. Power Sources, 2006, 158, 730–734.
16. S. Kalinichenka, L. Röntzsch, T. Riedl, T. Weißgärber and B. Kiebac, Int. J. Hydrogen Energy, 2011, 36, 10808–10815.
17. A. Teresiak, A. Gebert, M. Savyak, M. Uhlemann, C. Mickel and N. Mattern, J. Alloys Compd., 2005, 398, 156–164.
18. S. Kalinichenka, L. Röntzsch, T. Riedl, T. Gemming, T. Weißgärber and B. Kieback, Int. J. Hydrogen Energy, 2011, 36, 1592–1600.
19. L. H. Kumar, B. Viswanathan and S. S. Murthy, J. Alloys Compd., 2008, 461, 72–76.
20. M. S. Wu, H. R. Wu, Y. Y. Wang and C. C. Wan, J. Alloys Compd., 2000, 302, 248–257.
21. M. Y. Song, Y. J. Kwak, H. S. Shin, S. H. Lee and B. G. Kim, Int. J. Hydrogen Energy, 2013, 38, 1910–1917.
22. T. Spassov, L. Lyubenova, U. Koster and M. D. Baro, Mater. Sci. Eng., A, 2004, 375–377, 794–799.
23. H. Gu, Y. Zhu and L. Li, Int. J. Hydrogen Energy, 2008, 33, 2970–2974.
24. A. M. Jorge Jr, E. Prokofiev, G. F. de Lima, E. Rauch, M. Veron, W. J. Botta, M. Kawasaki and T. G. Langdon, Int. J. Hydrogen Energy, 2013, 38, 8306–8312.
25. T. Spassov and U. Köster, J. Alloys Compd., 1998, 279, 279–286.
26. L. J. Huang, Y. X. Wang, D. C. Wu, J. G. Tan, Y. Wang, J. X. Liu, Z. Huang, J. Q. Jiao and J. Q. Liu, J. Power Sources, 2014, 249, 35–41.
27. Y. Wang, X. Wang and C. M. Li, Int. J. Hydrogen Energy, 2010, 35, 3550–3554.
28. Q. A. Zhang, C. J. Jiang and D. D. Liu, Int. J. Hydrogen Energy, 2012, 37, 10709–10714.
29. A. A. Poletaev, R. V. Denys, J. P. Maehlen, J. K. Solberg, B. P. Tarasov and V. A. Yartys, Int. J. Hydrogen Energy, 2012, 37, 3548–3557.
30. M. Abdellaoui, S. Mokbli, F. Cuevas, M. Latroche, A. Percheron-Guegan and H. Zarrouk, J. Alloys Compd., 2003, 356–357, 557–561.
31. R. V. Denys, A. A. Poletaev, J. K. Solberg, B. P. Tarasov and V. A. Yartys, Acta Mater., 2010, 58, 2510–2519.
32. K. Tanaka, Y. Kanda, M. Furuhashi, K. Saito, K. Kuroda and H. Saka, J. Alloys Compd., 1999, 295, 521–525.
33. T. Spassov, L. Lyubenova, U. Köster and M. D. Baró, Mater. Sci. Eng., A, 2004, 375–377, 794–799.
34. Y. Wu, W. Han, S. X. Zhou, M. V. Lototsky, J. K. Solberg and V. A. Yartys, J. Alloys Compd., 2008, 466, 176–181.
35. B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140.
36. H. Niu and D. O. Northwood, Int. J. Hydrogen Energy, 2002, 27, 69–77.
37. K. J. Laidler, Pure Appl. Chem., 1996, 68, 149–192.
38. J. W. Christian, Mater. Today, 2008, 6, 53.
39. M. U. Niemann, S. S. Srinivasan, A. R. Phani, A. Kumar, D. Yogi-Goswami and E. K. Stefanakos, J. Nanomater., 2008, 2008, 950967.
40. T. Sadhasivam, M. S. L. Hudson, S. K. Pandey, A. Bhatnagar, M. K. Singh, K. Gurunathan and O. N. Srivastava, Int. J. Hydrogen Energy, 2013, 38, 7353–7362.
41. H. E. Kissinger, Anal. Chem., 1957, 29, 1702–1706.
42. X. Y. Zhao, Y. Ding, L. Q. Ma, L. Y. Wang, M. Yang and X. D. Shen, Int. J. Hydrogen Energy, 2008, 33, 6727–6733.
43. G. Zhang, B. N. Popov and R. E. White, J. Electrochem. Soc., 1995, 142, 2695–2698.
44. N. Kuriyama, T. Sakai, H. Miyamura, I. Uehara, H. Ishikawa and T. Iwasaki, J. Alloys Compd., 1993, 202, 183–197.
45. Y. H. Zhang, Z. M. Yuan, T. Yang, Y. Qi and D. L. Zhao, J. Solid State Electrochem., 2015, 19, 1187–1195.

---