 Open Access Article
Open Access ArticleSynergistic effect of temperature and background counterions on ion-exchange equilibria
Masami Shibukawa *a,
Masaru Yanagisawaa,
Ryota Morinagaa,
Tomomi Shimasakia,
Shingo Saito
*a,
Masaru Yanagisawaa,
Ryota Morinagaa,
Tomomi Shimasakia,
Shingo Saito a,
Shao-ting Wangb and
Yu-qi Feng
a,
Shao-ting Wangb and
Yu-qi Feng b
b
aGraduate School of Science and Engineering, Saitama University, 255 Shimo-Okubo, Sakura-ku, Saitama 338-8570, Japan. E-mail: sibukawa@apc.saitama-u.ac.jp
bKey Laboratory of Analytical Chemistry for Biology and Medicine (Ministry of Education), Department of Chemistry, Wuhan University, Wuhan 430072, P. R. China
First published on 27th July 2018
Abstract
The effects of temperature and background counterions on ion-exchange selectivity for alkali metal ions and tetraalkylammonium ions on strongly acidic cation-exchange resins have been investigated using superheated water ion-exchange chromatography (SW-IEC). We have found out that alkali metal ions show reversal in the order of the distribution coefficient (KD), from Li+ < Na+ < K+ < Rb+ in water at ordinary temperature to Rb+ < K+ < Na+ < Li+ in superheated water, when a relatively large cation such as cesium ion is used as the background counterion. The effect of counterion on the ion-exchange selectivity is enhanced with the ion-exchange resins of higher ion-exchange capacity and cross-linking degree. Tetraalkylammonium ions chosen as model ions for poorly hydrated ions also exhibit reversal in the order of KD at around 430 K in superheated water. However, the effect of the nature of alkali metal counterions on the change in KD values of tetraalkylammonium ions is rather small compared with the effect on the KD of alkali metal ions. These results are attributed to the change in local hydration structures of the ions in the ion-exchange resin due to dehydration of alkali metal ions enhanced by interionic contacts of the analyte ion with the coexisting counterion and lower hydration energy of the ions at elevated temperatures. Although it has been considered that temperature is not effective at changing the ion-exchange separation selectivity, significant selectivity changes can be achieved by SW-IEC.
Introduction
Ion-exchange chromatography has a long history of applications, including the separation, identification, and quantification not only of simple inorganic ions but also of various organic ionic compounds such as amino acids, proteins, and nucleic acids, etc.1–3 Ion-exchange separation is based on the fact that different ions have different degrees of interaction with the ion-exchanger. Although it is obvious that the charge on the ionic solutes is a decisive factor determining the selectivity of ion-exchange separations, the natures of ions as well as those of the fixed functional groups and the resin matrices are equally important parameters.Ion-exchange is the process in which ionic solutes in solution bind to charged functional groups on a solid matrix, which in turn releases different counterions of like sign. Therefore the stoichiometric ion-exchange reaction between an analyte ion AzA and the counterion of the fixed charged groups of the exchanger EzE may be written as1
| zEAzA(s) + zAEzE(r) ⇄ zEAzA(r) + zAEzE(s) | (1) |
| αA/B = KD(A)/KD(B) | (2) |
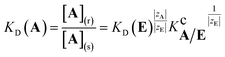 | (3) |
 | (4) |
This equation indicates that the separation factor or the selectivity coefficient of a pair of analyte ions of equal charge should be constant independent of the nature of the background counterion. However, it has been known that the selectivity coefficient is characteristic of the nature and concentration of the counterion even when the other equilibria than ion-exchange such as complexation of the analyte ion with coexisting species in the system and specific adsorption onto the surface of the exchanger matrix are negligible.1,4–8 This reveals that the selectivity coefficient cannot be regarded as a thermodynamic equilibrium constant but depends on the nature of coexisting counterions particularly in the exchanger phase.
Most of the studies that have so far been devoted to the prediction of the selectivity coefficient are based on empirical or semi-empirical estimation of the activity coefficients of the chemical species in the solution and the exchanger. Several physicochemical models have also been set up on the basis of electrical double layer theories to estimate the activity coefficient of the analyte ion in the exchanger phase.4–13 However, no rational explanation has yet been given with regard to the dependence of the selectivity coefficient on the type of the counterion.
It must be noted that the interaction of ions with water molecules or hydration is always involved in ion-exchange processes whatever the main mechanisms contributing to the separation are. In particular, it is essential to clarify the manner in which the hydration of ions is affected by the presence of the coexisting counterion in the exchanger phase in order to understand the change in the separation factor with the nature of background counterion.
We recently developed superheated water ion-exchange chromatography (SW-IEC) that uses liquid water under pressure at temperatures above 100 °C and clarified that the change in hydration structure of ions with temperature causes a drastic change in the ion-exchange separation selectivity.14–16 For example, the selectivity coefficient for a pair of alkali metal ions or that of halide ions approaches unity as temperature increases. Therefore the distribution coefficient of an analyte ion decreases with an increase in temperature when the background eluent counterion in the mobile phase has stronger affinity than that of the analyte ion for the ion-exchanger, whereas it increases when eluted by a weaker counterion.14–18 Presuming that the dependence of ion-exchange selectivity observed for simple inorganic ions on temperature can be attributed to the change in hydration of the ions in the solution phase and/or in the ion-exchange resin with temperature, we investigated the effect of temperature on the first-shell coordination structures of Rb+, Sr2+, Br− and I− in aqueous solution and those for Rb+ and Sr2+ in a sulfonated styrene-divinylbenzene copolymer cation-exchange resin in the temperature range from ambient temperature to 450 K by X-ray absorption fine structure (XAFS) spectroscopy.19 The spectral changes observed for these ions indicate that the number of coordinated first shell water molecules decreases with an increase in temperature. It has thus been concluded that the effect of temperature on separation selectivity in ion-exchange processes can be interpreted by the change in hydration of ions due to disruption of ion-dipole bonding by thermal motion of water molecules, which makes the charge and the size of an ion decisive factors determining the separation selectivity in ion-exchange processes at elevated temperatures.
On the other hand, the experimental results obtained by SW-IEC reveal that not only the ion-exchange selectivity itself but also its temperature dependence varies depending on the nature of the co-existing background counterion.14,15 This suggests that the counterion may affect the hydration structure of the analyte ion in the internal region of the ion-exchange resin. However, the origin of the effect of the co-existing counterion on the ion-exchange selectivity has not been clarified yet. In the present work, the effect of elevated temperature on the distribution coefficients of alkali metal ions and tetraalkylammonium ions on strongly acidic sulfonated ion exchangers has been examined over a wide temperature range using SW-IEC with aqueous solutions of alkali metal and tetraalkylammonium salts. We will show that the effect of the co-existing counterion on the ion-exchange selectivity is attributable to the change in the ion hydration structure caused by the counterion in the resin. A drastic change in separation selectivity of ionic solutes will also be demonstrated using a synergistic effect of temperature and the counterion on the hydration structure of analyte ions.
Experimental
Chemicals
All chemicals used in this study were obtained from commercial sources and were of analytical reagent-grade unless otherwise stated. Deuterated water (D2O) for NMR use was purchased from Wako Pure Chemicals (Tokyo, Japan) and Blue Dextran 2000 was obtained from Pharmacia Fine Chemicals (Uppsala, Sweden). Water was purified subsequently with an ion-exchange cartridge PF-III H10 (Organo, Tokyo, Japan) and an Arium 611 DI (Sartorius, Tokyo, Japan). The cation-exchangers used were sulfonated polystyrene-divinylbenzene copolymer resins, DIAION MCI GEL CK10S (degree of crosslinking = 10%, particle diameter = 11 μm) and CK02A (degree of crosslinking = 2%, particle diameter = 20 μm), purchased from Mitsubishi Chemical (Tokyo, Japan), and a tetrafluoroethylene-perfluoro[2-(fluorosulfonylethoxy)-propylvinylether] copolymer resin, Nafion (35–60 mesh), from Sigma-Aldrich Japan (Tokyo, Japan). The Na+ form of MCI GEL CK10S or CK02A was slurry packed into a stainless steel column with water. The H+ form of Nafion was converted to the Na+ form by decantation with 50 mM Na2SO4 and then packed into a stainless steel column with the same solution.Determination of cation-exchange capacities of the cation-exchange resin columns
The ion-exchange capacity of the MCI GEL CK10S column was determined by titrating hydrogen ion eluted from the H+ form resin column by passing a sufficient amount of Na2SO4 solution with standard NaOH solution. On the other hand, the ion-exchange capacities of the MCI GEL CK02A and the Nafion columns were measured in the following manner because the value of the ion-exchange capacity is rather small. An aqueous solution containing 25 mM Li2SO4 was passed through the column at the flow rate of 0.5 mL min−1 for 2 h. After the column was washed with pure water at the flow rate of 0.5 mL min−1 for 1 h, 10 mM K2SO4 solution was passed into the column at the flow rate of 0.5 mL min−1 for 3 h and the effluent from the column was collected into a 100 mL volumetric flask. The concentration of lithium ion in the solution was determined by means of an inductively coupled plasma atomic emission spectrometer, OPTIMA 5300DV (Perkin Elmer, Yokohama, Japan). The capacity of every column used for the study was determined just after a series of experiments conducted with superheated water.SW-IEC conditions
Chromatographic measurements were performed on an HPLC system consisting of a GL Science (Tokyo, Japan) Model DG660 degasser, a Hitachi (Tokyo, Japan) Model L-6000 pump, a Rheodyne (Cotati, CA, USA) Model 7215 loading injector fitted with a 1 or 20 μL sample loop, and a Showa Denko (Tokyo, Japan) Model Shodex RI-101 refractometric detector. A preheating coil (Hastelloy, 0.5 m × 0.5 mm I.D.) and a backpressure coil (stainless steel, 1.5 m × 0.1 mm I.D.) were placed between the injector and the column inlet and between the column outlet and the detector, respectively. The preheating coil and the column were thermostated using a Sandra Selerity Technologies (Salt Lake City, UT, USA) Model Polaratherm Series 9000 column temperature controller for SWC. The temperature of the oven was monitored with a mercury thermometer inserted into the oven.Aqueous solutions of alkali metal sulfates or tetramethyammonium bromide were used as eluents. All the eluents were filtered through a 0.45 μm membrane filter and degassed with an aspirator in an ultrasonic bath, US CLEANER US-2R (AS ONE, Tokyo, Japan) before use.
The extra column volume was determined by measuring the elution volume of a sample solute through the system from which the column had been removed. The volumetric flow rates F were measured using a volumetric flask and the exact values of the flow rates F′ in the column were calculated according to the following equation:
 | (5) |
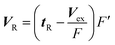 | (6) |
Test solutions were prepared by dissolving analyte compounds in the eluent to be used. The retention volumes for each analyte ion was measured in the temperature range of 273–473 K for the MCI GEL CK10S column, 298–403 K for the MCI GEL CK02A column and 308–423 K for the Nafion column, respectively. The detection signal was fed into a CDS plus data analysis system (LA Soft, Tokyo, Japan).
Measurement of temperature-dependent swelling properties of a cation-exchange resin
The Na+ form of MCI GEL CK10S was slurry packed into a stainless steel column (150 mm × 4.6 mm i.d.) with water. The Li+, Na+, K+, Rb+ and Cs+ forms of the cation-exchange resin column were prepared by passing 120 mL of aqueous solutions containing the respective metal sulfates (25 mM) through the column at 60 °C and then washing the column with water. The total water volume and the interstitial volume or interparticulate volume in the column were determined by measuring the retention volumes of D2O and Blue Dextran 2000, respectively.Results and discussion
Effects of temperature and counterion on the distribution coefficients of alkali metal ions and tetraalkylammonium ions
Assuming that the mobile phase is the space occupied by water in the column and the stationary phase is the other part of the column, i.e., the resin matrix, we calculated the KD value of an analyte ion by the following equation:
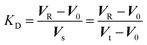 | (7) |
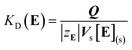 | (8) |
We reported in a previous paper that the KD values of alkali metal ions on the MCI GEL CK10S column appear to converge on the KD(E) value or the KcA/E approaches unity with an increase in temperature when Li+, Na+ or K+ is used as the eluent ion.14 The results shown in Fig. 1, however, indicate that the selectivity coefficient does not approach unity with an increase in temperature but is reversed at a temperature specific to the background counterion. The reversal of the order of KD for Li+ and Na+ occurs at around 290 K in the Cs2SO4 eluent system, while it does at 360 K in the Rb2SO4 system.
We clarified by XAFS measurements that hydration of alkali metal ions and halide ions in the ion-exchange resin as well as aqueous solutions becomes weaker as the temperature rises due to disruption of ion-dipole bonding by thermal motion of water molecules.19 We thus concluded that the ion-exchange selectivity for simple inorganic ions decreases with an increase in temperature by the reduction of the difference in hydration structure between different ions. However, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD vs. 1/T plots shown in Fig. 1 suggest that the coexisting counterion may also affect the hydration structures of analyte ions resulting in the drastic change in ion-exchange selectivity due to the synergistic effect of temperature and the background counterion.
KD vs. 1/T plots shown in Fig. 1 suggest that the coexisting counterion may also affect the hydration structures of analyte ions resulting in the drastic change in ion-exchange selectivity due to the synergistic effect of temperature and the background counterion.
We have shown that smaller tetraalkylammonium ion with a shorter alkyl chain exhibits lower KD value at lower temperatures, while at higher temperatures the larger ion is eluted faster than the smaller one, indicating that the electrostatic interaction is a predominant mechanism and then ionic size is a determinant in retention in SW-IEC.14 Taking into account the fact that the order of hydrated ionic radii for alkali metal ions at ordinary temperature is Rb+ < K+ < Na+ < Li+, whereas that of crystal ionic radii is Li+ < Na+ < K+ < Rb+,20,21 it is presumed that a similar phenomenon to that of tetraalkylammonium ion may also be observed even for relatively strongly hydrated alkali metal ions by the synergistic effect of temperature and counterion when cesium is used as the background eluent ion.
Fig. 2 shows the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD vs. 1/T plots for tetraalkylammonium ions when eluted with 25 mM Cs2SO4 solution. Although the temperature at which the reversal of retention order occurs appears to be a little lower in Cs2SO4 eluent system than in Na2SO4 system,14 the effect of the nature of alkali metal counterions on the change in retention of tetraalkylammonium ions is not very large. This is probably because tetraalkylammonium ions are poorly hydrated even at lower temperatures. The SW-IEC chromatograms obtained by elution with 25 mM Cs2SO4 aqueous solution are shown in Fig. 3 and 4 for mixtures of alkali metal ions and tetraalkylammonium ions, respectively. It will be noted that lithium is selectively separated from the other alkali metal ions and the retention order of tetraalkylammonium ions is completely reversed in superheated water.
KD vs. 1/T plots for tetraalkylammonium ions when eluted with 25 mM Cs2SO4 solution. Although the temperature at which the reversal of retention order occurs appears to be a little lower in Cs2SO4 eluent system than in Na2SO4 system,14 the effect of the nature of alkali metal counterions on the change in retention of tetraalkylammonium ions is not very large. This is probably because tetraalkylammonium ions are poorly hydrated even at lower temperatures. The SW-IEC chromatograms obtained by elution with 25 mM Cs2SO4 aqueous solution are shown in Fig. 3 and 4 for mixtures of alkali metal ions and tetraalkylammonium ions, respectively. It will be noted that lithium is selectively separated from the other alkali metal ions and the retention order of tetraalkylammonium ions is completely reversed in superheated water.
Fig. 5(a) and (b) show the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD vs. 1/T plots for alkali metal ions obtained by elution with 25 mM Cs2SO4 aqueous solution on the columns packed with MCI GEL CK02A and Nafion, respectively. These ion-exchange resins are not so stable that they decompose and lose the fixed ions over 403 K and 423 K, respectively, probably due to relatively low cross-linking degree. Actually the other commercially available ion-exchange resins that we tried to use have even lower heat stability than MCI GEL CK02A and Nafion. We have thus carried out a series of experiments for MCI GEL CK02A and Nafion in the range of 313–390 K. The upper temperature limits of the cation-exchange resins used in this study determined by measurements of the change in ion-exchange capacity are listed in Table 1 together with other characteristics of the resins. As shown in Fig. 5(b), the retention order of alkali metal ions on the Nafion column does not change in the temperature range examined. On the other hand, the reversal of the retention order for Li+ and Na+ was observed at 340 K for the MCI GEL CK02A column. However, the change in retention selectivity with temperature is much smaller than that observed on the MCI GEL CK10S column. These results indicate that the change in the hydration structure of an analyte ion caused by the counterion (Cs+) does not take place in the solution but in the ion-exchange resin.
KD vs. 1/T plots for alkali metal ions obtained by elution with 25 mM Cs2SO4 aqueous solution on the columns packed with MCI GEL CK02A and Nafion, respectively. These ion-exchange resins are not so stable that they decompose and lose the fixed ions over 403 K and 423 K, respectively, probably due to relatively low cross-linking degree. Actually the other commercially available ion-exchange resins that we tried to use have even lower heat stability than MCI GEL CK02A and Nafion. We have thus carried out a series of experiments for MCI GEL CK02A and Nafion in the range of 313–390 K. The upper temperature limits of the cation-exchange resins used in this study determined by measurements of the change in ion-exchange capacity are listed in Table 1 together with other characteristics of the resins. As shown in Fig. 5(b), the retention order of alkali metal ions on the Nafion column does not change in the temperature range examined. On the other hand, the reversal of the retention order for Li+ and Na+ was observed at 340 K for the MCI GEL CK02A column. However, the change in retention selectivity with temperature is much smaller than that observed on the MCI GEL CK10S column. These results indicate that the change in the hydration structure of an analyte ion caused by the counterion (Cs+) does not take place in the solution but in the ion-exchange resin.
| Resin | Functional group | Cation-exchange capacity (meq. mL−1) | Upper temperature limita (K) | Cross-linking degreeb (%) | Particle diameterb |
|---|---|---|---|---|---|
| a The highest temperature at which the decrease in cation-exchange capacity of the resin by elution with 25 mM Na2SO4 for 30 h is less than 5%.b Manufactures' data. | |||||
| MCI GEL CK10S | –SO3− | 2.2 | 473 | 10 | 11 μm |
| MCI GEL CK02A | –SO3− | 0.66 | 403 | 2 | 20 μm |
| Nafion | –SO3− | 0.35 | 423 | — | 35–60 mesh |
It has been reported that the number of water molecules hydrated to some ions such as Na+ and H2PO4− decreases with an increase in the ion-exchange capacity and the cross-linking degree and this experimental result can be ascribed to dehydration of the ion by a decrease in the void space for the ions in the ion-exchange resins.22–26 The difference in the distribution coefficients of alkali metal ions between Nafion, MCI GEL CK02A and MCI GEL CK10S may also be attributed to differences in the ion-exchange capacity and crosslinking degree of these resins (Table 1). Since Cs+ has relatively large ionic size and its concentration is larger in MCI GEL CK 10S than in CK02A and Nafion, the remaining void space should be smaller than in the other two resins. The counterion effect on the hydration structure of the analyte ion is thus expected to be enhanced in MCI GEL CK10S resin at elevated temperatures.
From the results shown above, it is expected that counter cations larger than Cs+ may cause more drastic change in retention of alkali metal ions. Fig. 6(a) and (b) demonstrate the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD vs. 1/T plots for alkali metal ions obtained on MCI GEL CK02A and Nafion columns by elution with 50 mM tetramethylammonium bromide (TMABr) aqueous solution. The counterion (Na+) of MCI GEL CK10S could not completely be replaced by TMA+ probably because TMA+ is partly excluded from the pores of the resin owing to the relatively large size of TMA+ and high cross-linking degree or small pore size of the resin. As can be seen from the comparison of Fig. 6(a) with Fig. 5(a), the KD value of Li+ on MCI GEL CK02A is larger not only than the value for Na+ but also than that for K+ even at ambient temperature and becomes larger than the value for Rb+ at 320 K or above in the TMABr elution system. On the Nafion column, Li+ also has the larger KD value than Na+ by elution with the TMABr aqueous solution although the difference in KD value between Li+ and Na+ is rather small probably because of the low ion-exchange capacity (Fig. 6(b)). These results indicate that the relative size of the background counterion with respect to the inner pore size of the ion-exchange resin as well as the hydration energy governs the ion-exchange selectivity.
KD vs. 1/T plots for alkali metal ions obtained on MCI GEL CK02A and Nafion columns by elution with 50 mM tetramethylammonium bromide (TMABr) aqueous solution. The counterion (Na+) of MCI GEL CK10S could not completely be replaced by TMA+ probably because TMA+ is partly excluded from the pores of the resin owing to the relatively large size of TMA+ and high cross-linking degree or small pore size of the resin. As can be seen from the comparison of Fig. 6(a) with Fig. 5(a), the KD value of Li+ on MCI GEL CK02A is larger not only than the value for Na+ but also than that for K+ even at ambient temperature and becomes larger than the value for Rb+ at 320 K or above in the TMABr elution system. On the Nafion column, Li+ also has the larger KD value than Na+ by elution with the TMABr aqueous solution although the difference in KD value between Li+ and Na+ is rather small probably because of the low ion-exchange capacity (Fig. 6(b)). These results indicate that the relative size of the background counterion with respect to the inner pore size of the ion-exchange resin as well as the hydration energy governs the ion-exchange selectivity.
Effects of temperature and counterion on the swelling of the cation-exchange resin
The swelling or water absorbing properties of the cation-exchange resin in different counterion forms were evaluated by measuring the volumes of water-swollen ion-exchange resin and water absorbed in the resin at different temperatures in order to further investigate the origin of the effect of counterion on the temperature dependence of the ion-exchange equilibria. The volume of the water-swollen ion-exchange resin VIER was determined by a chromatographic method using a stainless steel column packed with the resin according to the following equation:| VIER = Vt − Vint | (9) |
The change in VIER with temperature in the range of 308 K to 433 K for alkali metal forms of MCI GEL CK10S is shown in Fig. 7. It is noteworthy that the VIER values for the K+, Rb+ and Cs+ forms of the resin gradually increase with an increase in temperature, while those for the resins in Li+ and Na+ forms decrease. Especially the resin in Li+ form shows remarkable decrease of VIER with an increase in temperature. On the contrary, the Vs value for each alkali metal form of the resin was approximately constant independent of temperature as shown in Fig. 8. The VIER can be given by the sum of the volumes of hydrated metal counterion VHM and fixed sulfonate ion VHF, the resin polymer matrix VP and the free water in the resin VW as follows:
| VIER = VHM + VHF + VP + VW | (10) |
| Vs = VM + VF + VP | (11) |
 | ||
Fig. 7 Dependence of the VIER values on temperature for MCI GEL CK10S resin in alkali metal ion forms. Symbols: ( ) Li+, ( ) Li+, ( ) Na+, ( ) Na+, ( ) K+, ( ) K+, ( ) Rb+, ( ) Rb+, ( ) Cs+. ) Cs+. | ||
 | ||
| Fig. 8 Dependence of the Vs values on temperature for MCI GEL CK10S resin in alkali metal ion forms. For other details see Fig. 7. | ||
We have shown that the hydration number of Rb+ as well as Sr2+ present as the counterions of fixed sulfonate groups in MCI GEL CK10S slightly decreases with an increase in temperature similarly to the changes observed for their aqueous solutions.19 The thermal motion of the resin polymer chains would be intensified at higher temperatures, leading to expansion of the resin network or increase in VW. Therefore, the decrease in VIER of the cation-exchange resin in Li+ and Na+ forms with an increase in temperature indicates that the hydration numbers of these metal ions in the resin remarkably decrease as the temperature rises compared to the other alkali metal ions.
The VIER of the resin in Li+ form is the largest up to 403 K, while that for the Cs+ form resin becomes larger over 418 K, which reveals that the swelling energy of the resin in Cs+ form is larger than those for the other alkali metal forms of the cation-exchange resin at 418 K or above. The swelling pressure Π may be one of the important determinants of the ion-exchange selectivity as indicated by the Gregor equation:27–29
 | (12) |
However, this simple model cannot completely account for the observed selectivity reversals with change in temperature because the temperature at which the reversal of the retention order of alkali metal ions occurs depends on the background counterion in the resin. The chemical components of the Gregor's model are the hydrated ions as well as the resin matrix with its solvated fixed ions and the solvent. The hydration of the ions in the resin phase is assumed to be the same as that in the solution phase in this model. The results shown in Fig. 1 and 5–7, however, reveal that the hydration structure of an analyte ion in the resin is different from that in the aqueous solution and it also depends on the nature of the background counterion of the ion-exchange resin. At elevated temperatures, the hydration energy of ions becomes smaller so that the cations with smaller ionic radii are easily dehydrated and selectively distribute into the cation-exchange resin. Large counterions present in high density in the resin may enhance the dehydration of the analyte ions at elevated temperatures, leading to quite different ion-exchange selectivity from that observed at ambient temperature.
Conclusions
We have made a new finding by SW-IEC that even relatively strongly hydrated small metal ions show a drastic change in ion-exchange selectivity on a usual cation-exchange resin by synergistic effect of temperature and the nature of the background counterion in the aqueous solution. With the ion-exchange resin of higher ion-exchange capacity and cross-linking degree, large sized counterions such as Cs+ and tetramethylammonium ion cause a drastic change in retention order from Li+ < Na+ < K+ < Rb+ in water at ordinary temperature to Rb+ < K+ < Na+ < Li+ in superheated water. These observations can be ascribed to the change in local hydration structures of the ions in the resin phase due to dehydration enhanced by interionic contacts with a large coexisting counterion and lower ionic hydration energy at elevated temperatures.These results suggest that even at ambient temperature the separation of analyte ions in ion-exchange processes is affected by the nature of the coexisting counterions. It has been well known that larger separation factor is usually obtained with weaker counterions.7 For example, the difference in the distribution coefficient between analyte cations is better with Li+ counterion than with Cs+ at ambient temperature. The mechanism presented in this study may explain this phenomenon, which has not been successfully interpreted yet. In other words, the change in the hydration of the exchanging ions upon their transition from the solution phase to the resin phase or vice versa may play a predominant role in determining the ion-exchange selectivity. SW-IEC with the aqueous mobile phase containing large eluting ions may also bring about drastic change in separation selectivity and can improve the separation of ionic solutes through temperature programming.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by a Grant-in-Aid for Scientific Research No. 20350034 from Ministry of Education, Culture, Sports, Science and Technology, Japan.References
- R. W. Grimshaw and C. E. Harland, Ion-Exchange: Introduction to Theory and Practice, The Chemical Society, London, 1975 Search PubMed.
- P. G. Rigas, Instrum. Sci. Technol., 2012, 40, 161–193 CrossRef.
- F. Helfferich, Ion Exchange, McGraw-Hill, New York, 1962 Search PubMed.
- J. S. Fritz, J. Chromatogr. A, 2005, 1085, 8–17 CrossRef PubMed.
- G. Stahlberg, Anal. Chem., 1994, 66, 440–449 CrossRef.
- T. Okada, Anal. Sci., 1998, 14, 469–477 CrossRef.
- T. Okada, Anal. Chem., 1998, 70, 1692–1700 CrossRef PubMed.
- T. Okada, J. Chromatogr. A, 1999, 850, 3–8 CrossRef PubMed.
- S. Afrashtehfar and F. F. Cantwell, Anal. Chem., 1982, 54, 2422–2427 CrossRef.
- R. A. Hux and F. F. Cantwell, Anal. Chem., 1984, 56, 1258–1263 CrossRef.
- H. Liu and F. F. Cantwell, Anal. Chem., 1991, 63, 993–1000 CrossRef.
- H. Liu and F. F. Cantwell, Anal. Chem., 1991, 63, 2032–2037 CrossRef.
- A. I. Liapis and B. A. Grimes, J. Sep. Sci., 2005, 28, 1909–1926 CrossRef.
- M. Shibukawa, T. Shimasaki, S. Saito and T. Yarita, Anal. Chem., 2009, 81, 8025–8032 CrossRef PubMed.
- M. Shibukawa, A. Taguchi, Y. Suzuki, K. Saitoh, T. Hiaki and T. Yarita, Analyst, 2012, 137, 3154–3159 RSC.
- M. Shibukawa, R. Morinaga and S. Saito, Bunseki Kagaku, 2016, 65, 615–623 CrossRef.
- N. E. Fortier and J. S. Fritz, Talanta, 1987, 34, 415–418 CrossRef PubMed.
- P. Hatsis and C. A. Lucy, Analyst, 2001, 126, 2113–2118 RSC.
- M. Shibukawa, M. Harada, T. Okada, Y. Ogiyama, T. Shimasaki, Y. Kondo, A. Inoue and S. Saito, RSC Adv., 2012, 2, 8985–8991 RSC.
- E. R. Nightingale, J. Phys. Chem., 1959, 63, 1381–1387 CrossRef.
- R. L. David, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, 84th edn, 2004 Search PubMed.
- A. Yuchi, S. Kuroda, M. Takagi, Y. Watanabe and S. Nakao, Anal. Chem., 2010, 82, 8611–8617 CrossRef PubMed.
- Y. Watanabe, K. Ohnaka, S. Fujita, M. Kishi and A. Yuchi, Anal. Chem., 2011, 83, 7480–7485 CrossRef PubMed.
- D. Nandan, B. Venkataramani and A. R. Gupta, Langmuir, 1993, 9, 1786–1793 CrossRef.
- R. W. Creekmore and C. N. Reilley, Anal. Chem., 1970, 42, 570–575 CrossRef.
- H. D. Sharma and N. Subramanian, Can. J. Chem., 1971, 49, 3948–3955 CrossRef.
- H. P. Gregor, J. Am. Chem. Soc., 1948, 70, 1293 CrossRef.
- H. P. Gregor, J. Am. Chem. Soc., 1951, 73, 642–650 CrossRef.
- H. P. Gregor and J. I. Bregman, J. Colloid Sci., 1951, 6, 323–347 CrossRef.
- http://www.spiraxsarco.com/esc/SW_Properties.aspx.
| This journal is © The Royal Society of Chemistry 2018 |
























