Behaviour of the XH-*-π and YX-*-π interactions (X, Y = F, Cl, Br and I) in the coronene π-system, as elucidated by QTAIM dual functional analysis with QC calculations

Abstract

The dynamic and static nature of XH-*-π and YX-*-π in the coronene π-system (π(C₂₄H₁₂)) is elucidated by QTAIM dual functional analysis, where * emphasizes the presence of bond critical points (BCPs) in the interactions. The nature of the interactions is elucidated by analysing the plots of the total electron energy densities H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 [=(ħ²/8m)∇²ρ_b(r_c)] for the interactions at BCPs, where V_b(r_c) are the potential energy densities at the BCPs. The data for the perturbed structures around the fully optimized structures are employed for the plots in addition to those of the fully optimized structures. The plots are analysed using the polar coordinate of (R, θ) for the data of the fully optimized structures, while those containing the perturbed structures are analysed using (θ_p, κ_p), where θ_p corresponds to the tangent line of each plot and κ_p is the curvature. Whereas (R, θ) show the static nature, (θ_p, κ_p) represent the dynamic nature of the interactions. All interactions in X–H-*-π(C₂₄H₁₂) (X = F, Cl, Br and I) and Y–X-*-π(C₂₄H₁₂) (Y–X = F–F, Cl–Cl, Br–Br, I–I, F–Cl, F–Br and F–I) are classified by pure CS (closed shell) interactions and are characterized as having the vdW nature, except for X–H = F–H and Y–X = F–Cl, F–Br and F–I, which show the typical-HB nature without covalency. The structural features of the complexes are also discussed.

---

Introduction

Hydrogen bonds (HBs) and halogen bonds (XBs) are of current and continuous interest. HBs and XBs are fundamentally important for their ability to give rise to molecular association caused by the energy stabilization of the system.^1–11 The direction-control through the formation of HBs plays a crucial role in all fields of chemical and biological sciences. The opening and closing of the duplex DNA structure in active proliferation at around room temperature is a typical example of the effect of HBs.¹² HBs also play an important role in the very specific conformation of hormones with the HBs of the dimers controlling the characteristic biological properties.¹³ Conventional HBs of the shared proton interaction type⁴ are formed with atoms of the main group elements, which are usually not very strong in the neutral form (≤ approximately 40 kJ mol⁻¹),^1,5 albeit usually stronger than the van der Waals (vdW) interactions. Contributions from the charge transfer (CT) interaction become more important as the strength of HBs increases in addition to the vdW interactions, where attractive electrostatic interactions and the dispersion force mainly contribute to form the vdW adducts. Conversely, the attractive interactions, between the electrophilic σ*-orbitals of halogen or inter-halogen molecules with the non-bonding orbitals (n-orbitals), must be the driving force for the formation of typical XBs. The nature of XBs has been discussed based on the theoretical background of the molecular orbital description for the bonding and the σ-hole developed on the halogen atoms together with the stability based on the structural aspects.¹⁴ XBs are applicable to a wide variety of fields in chemical and biological sciences, such as crystal engineering, supramolecular soft matter and nanoparticles.

π-orbitals also give rise to similar HBs and XBs with hydrogen halides and halogen or inter-halogen molecules, respectively. Similar to the case of n-orbitals, π-orbitals act as electron donors to form such adducts. The π-electron systems usually construct planar molecules. Benzene and coronene¹⁵ are the typical examples of the planar π-systems, together with graphene. Graphene shows unique physical properties. Graphene-based carbon allotropes, such as graphene, graphite, fullerenes¹⁶ and carbon nanotubes, have attracted considerable attention owing their many potential applications in nanotechnology, including nanoelectronics, energy storage and biosensing.^17–19 Coronene, a typical planar molecule, is often employed as a model of graphene in the study of adsorption phenomena, even though it is suggested that coronene may, in certain cases, not be a good model of graphene due to the larger HOMO–LUMO gap in coronene.

We recently investigated the dynamic and static behaviour of the XH-*-π and/or YX-*-π interactions (π-HBs and/or π-XBs, respectively) (X, Y = F, Cl, Br and I) in the π-systems of benzene, π(C₆H₆),^20,21 naphthalene, π(C₁₀H₈)²² and anthracene, π(C₁₄H₁₀).²³ What is the behaviour of the π-HBs and π-XBs interactions in the coronene π-system, π(C₂₄H₁₂)? What are the differences and similarities in the interactions between π(C₂₄H₁₂) and π(C₆H₆), π(C₁₀H₈) and π(C₁₄H₁₀)? The nature of the interactions should be elucidated to obtain a better understanding of the chemistry arising from the interactions. The π-HB and π-XB interactions with the planer π(C₂₄H₁₂) system will supply an important starting point for the interactions with the bent π-systems, such as fullerenes and carbon nanotubes, and the circulene molecules, together with the non-covalent functionalization based on the interactions.²⁴

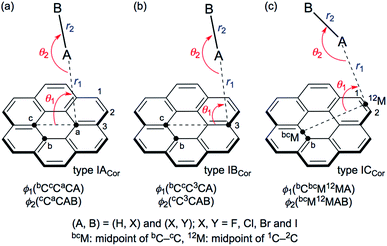
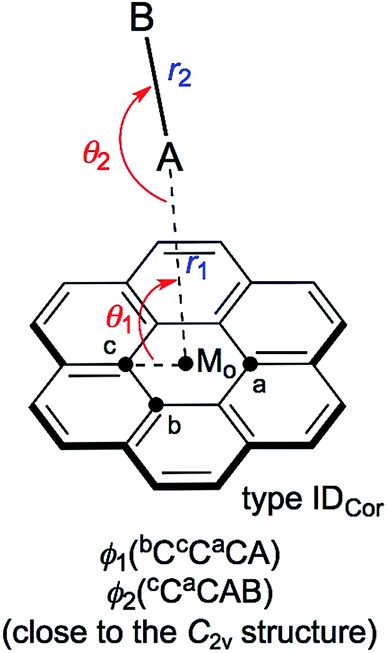
Scheme 1 illustrates the structures of X–H⋯π(C₂₄H₁₂) (X = F, Cl, Br and I) and Y–X⋯π(C₂₄H₁₂) (Y–X = F–F, Cl–Cl, Br–Br, I–I, F–Cl, F–Br and F–I) to be elucidated in this work.²⁵ The scope of the properties in the Y–X⋯π interactions have been demonstrated to be covered by those with Y–X = F–F, F–Cl, F–Br and F–I.¹⁰ The structural parameters are defined in Scheme 1 together with the types. The structures of the adducts will be called type I_Cor, if X–H or Y–X appears to interact with the coronene π-system through only a single site of X–H or Y–X. Namely, X–H or Y–X should be placed almost parallel to the normal line of the coronene molecular plane. Type I_Cor will be called type IA_Cor, if X–H or Y–X interacts with a carbon atom in the central ring of coronene. On the other hand, the structure will be type IB_Cor, when X–H or Y–X is expected to interact with a carbon atom bearing no hydrogen atom in the outside ring of coronene, whereas it will be type IC_Cor when X–H or Y–X appears to interact with the midpoint between the adjacent carbon atoms bearing the hydrogen atoms of the outside ring of coronene. Type ID_Cor in Scheme 2 is discussed later.

Scheme 1 Structures of X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂) to be clarified with the definition of structural parameters and types, where A–B = X–H = F–H, Cl–H, Br–H and I–H and A–B = Y–X = F–F, Cl–Cl, Br–Br, I–I, F–Cl, F–Br and F–I.

The QTAIM (quantum theory of atoms-in-molecules) approach, introduced by Bader,^26,27 enables us to analyse the nature of chemical bonds and interactions.^26–30 Interactions are defined by the corresponding bond paths (BPs), but we must be careful to use the correct terminology with this concept.³¹ The bond critical point (BCP) is an important concept in QTAIM and is a point along the BP at the interatomic surface where the charge density, ρ(r), reaches a minimum.³² This point is denoted by ρ_b(r_c), as are the other QTAIM functions at BCPs, such as the Laplacians of ρ_b(r_c) (∇²ρ_b(r_c)), total electron energy densities H_b(r_c), potential energy densities V_b(r_c), kinetic energy densities G_b(r_c) and k_b(r_c) (= V_b(r_c)/G_b(r_c)).³³

In QTAIM, chemical bonds and interactions are classified by the signs of ∇²ρ_b(r_c) and H_b(r_c). Indeed, H_b(r_c) − V_b(r_c)/2 = 0 (∇²ρ_b(r_c) = 0) corresponds to the borderline between the classical covalent bonds of shard shell (SS) interactions and the noncovalent closed shell (CS) interactions, but H_b(r_c) = 0 appears to be buried in the noncovalent interactions of CS. (See eqn (S2) of the ESI† for the relation, (ħ²/8m)∇²ρ_b(r_c) = H_b(r_c) − V_b(r_c)/2.) Therefore, it seems difficult to characterize the CS interactions, such as van der Waals (vdW) interactions,^34,35 typical hydrogen bonds (t-HBs),^2,3,36,37 interactions in molecular complexes formed through charge transfer (CT-MCs),³⁸ trihalide ions (X₃⁻)³⁸ and interactions in trigonal bipyramidal adducts formed through CT (CT-TBPs).³⁸ Then, we proposed employing the signs of the first derivatives of H_b(r_c) − V_b(r_c)/2 and H_b(r_c) (d(H_b(r_c) − V_b(r_c)/2)/dr and dH_b(r_c)/dr, respectively) to characterize these interactions. The borderline between CT-MC and CT-TBP (containing X₃⁻) is defined by d(H_b(r_c) − V_b(r_c)/2)/dr = 0, while that between vdW and t-HB is by dH_b(r_c)/dr = 0, as shown by the experimental results, with the presumption that the CS interactions are reasonably characterized as expected. The proposed definitions for the classification of interactions are summarized in Table S1 of the ESI,† together with those tentatively proposed,³⁹ for convenience of discussion.

Recently, we proposed QTAIM dual functional analysis (QTAIM-DFA),^40–43 according to QTAIM.^{26–29,44,45} QTAIM-DFA provides an excellent approach for evaluating, classifying and understanding weak to strong interactions in a unified form.^40–43 In QTAIM-DFA, H_b(r_c) are plotted versus H_b(r_c) − V_b(r_c)/2 [= (ħ²/8m) ∇²ρ_b(r_c)]. In our treatment, data for perturbed structures around fully optimized structures are employed for the plots, in addition to those from the fully optimized structures.^40–43 QTAIM-DFA can incorporate the classification of interactions by the signs of ∇²ρ_b(r_c), H_b(r_c), d(H_b(r_c) − V_b(r_c)/2)/dr and dH_b(r_c)/dr with the definitions, tentatively proposed.⁴⁶ We have proposed the concept of “the dynamic nature of interactions” which originates from the data containing the perturbed structures.^40a,41–43 Data from the fully optimized structures correspond to the static nature of interactions. QTAIM-DFA is applied to typical chemical bonds and interactions and rough criteria are established. The rough criteria can distinguish the chemical bonds and interactions in question from other types of interactions. QTAIM-DFA and these criteria are explained in the ESI using Schemes S1 and S2, Fig. S1 and eqn (S1)–(S6).† The basic concept of the QTAIM approach is also surveyed.

We consider QTAIM-DFA to be well-suited to elucidate the dynamic and static nature of the π-HBs and π-XBs interactions in π(C₂₄H₁₂), even though static behaviour of π-HBs in π(C₂₄H₁₂) has been discussed.^47,48 In this study, we present the results of the investigations on the nature of the interactions. The interactions are classified and characterized based on the above criteria.

Methodological details in calculations

The structures were optimized using the Gaussian 09 programme package.⁴⁹ The basis set system (BSS) from the Sapporo Basis Set Factory⁵⁰ (BSS-S) was employed for the calculations. In the calculations with BSS-SA, the (7433211/743111/7411/2 + 1s1p) type was employed for I, the (743211/74111/721/2 + 1s1p) type for Br, the (63211/6111/31/2 + 1s1p) type for Cl and the (6211/311/21/2 + 1s1p) type for F with the (6211/311/21/2 + 1s1p) type for C and the (411/21/2 + 1s1p) type for H. BSS-SA was applied for the calculations at the M06-2X (M06-2X/BSS-SA) level of density functional theory (DFT). Optimized structures were confirmed by the frequency analysis. QTAIM functions were similarly calculated using the Gaussian 09 programme package⁴⁹ with the same method of the optimizations and the data were analysed with the AIM2000 ⁵¹ and AIMAll⁵² programmes. The results obtained at the M06-2X/BSS-SA level of theory will be mainly discussed in the text.

For BSS-SB, the (743321/74321/742 + 1s1p) type was employed for I, the (74321/7421/72 + 1s1p) type for Br, the (6321/621/3 + 1s1p) type for Cl and the (621/31/2 + 1s1p) type for F with the (621/31/2 + 1s1p) type for C and the (31/3 + 1s1p) type for H. The calculations were also performed at the M06-2X/BSS-SB level of theory to search for the potential energy surface minima as the pre-optimizations, when necessary. M06-2X/BSS-SB is also employed to confirm the minima and BPs with BCPs around the interactions in question, if they are not obtained satisfactorily with M06-2X/BSS-SA.

The results obtained using M06-2X/BSS-SB are discussed in Tables S1 and S2 of the ESI† and/or the text, if necessary. M06-2X/BSS-SA was also applied to the benzene π-system for convenience of comparison. The calculations were similarly performed using MP2/6-311G(d,p)^53,54 for the convenience of comparison. The results are collected in the ESI.†

Normal coordinates of internal vibrations (NIV) obtained by the frequency analysis were employed to generate the perturbed structures.^41,42 This method is explained by eqn (1). A k-th perturbed structure (S_kw) was generated by the addition of the normal coordinates of the k-th internal vibration (N_k) to the standard orientation of the fully optimized structure (S_o) in the matrix representation.⁵⁵ The coefficient f_kw in eqn (1) controls the difference in the structures between S_kw and S_o: f_kw are determined to satisfy eqn (1) for the interaction in question, where r and r_o show the distances under investigation in the perturbed and fully optimized structures, respectively, and a_o is the Bohr radius (0.52918 Å).⁵⁶ Namely, the perturbed structures with NIV correspond to those with r being elongated or shortened by 0.05a_o or 0.1a_o, relative to r_o. N_k of five digits are used to predict S_kw. We refer to this method to generate the perturbed structures as NIV.

S_kw = S_o + f_kw × N_k (1)

r = r_o + wa_o (w = (0), ±0.05 and ±0.1; a_o = 0.52918 Å) (2)

y = a_o + a₁x + a₂x² + a₃x³ (3)

In the QTAIM-DFA treatment, H_b(r_c) are plotted versus H_b(r_c) − V_b(r_c)/2 for five data points of w = 0, ±0.05 and ±0.1 in eqn (2). Each plot is analysed using a regression curve of the cubic function as shown in eqn (3), where (x, y) are (H_b(r_c) − V_b(r_c)/2, H_b(r_c)) (R_c² (square of correlation coefficient) > 0.99999 in usual).⁴³

Results and discussion

Optimizations of X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂)

The structures were optimized for X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂). The optimizations were initially performed with M06-2X/BSS-SB, assuming the C₁ symmetry. The X–H and Y–X components were placed in close proximity to types IA_Cor, IB_Cor and IC_Cor together with type ID_Cor (see Schemes 1 and 2) in the optimization processes, but the systematic search was not performed. Each adduct finally converged to a structure with the C₁ symmetry. The structures were optimized again with M06-2X/BSS-SA. The optimized structures are confirmed by all positive frequencies after the frequency analysis. Then, the C₁ structures with all positive frequencies were further optimized, assuming the C_s symmetry in the cases where the C₁ structures appeared to be very close to the C_s symmetry. The frequency analysis was also performed on the C_s structures. The IB_Cor and IC_Cor types were predicted for X–H⋯π(C₂₄H₁₂), while the IA_Cor and IC_Cor types were used for Y–X⋯π(C₂₄H₁₂), when optimized with M06-2X/BSS-SA.

Scheme 2 Structures of X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂) (A–B = X–H or Y–X: X, Y = F, Cl, Br and I). The structural parameters are defined, together with the types, where M_o is the centre point of C₂₄H₁₂.

All positive frequencies were confirmed for all adducts, except for F–H⋯π(³C) (C₁: IB_Cor), Cl–H⋯π(¹²M) (C₁: IC_Cor), Cl–Cl⋯π(^aC) (C₁: IA_Cor), Cl–Cl⋯π(¹²M) (C₁: IC_Cor) and F–Cl⋯π(¹²M) (C₁: IC_Cor). The motion of each imaginary frequency mainly corresponds to the angular displacements between π(C₂₄H₁₂) and X–H or Y–X. In the case of Cl–H⋯π(²C) (C₁: IB_Cor), the calculation converged to Cl–H⋯π(¹²M) (C₁: IC_Cor), which did not give positive frequencies only after the frequency analysis. Table 1 summarizes the structural parameters (r₁, r₂, θ₁, θ₂, ϕ₁ and ϕ₂) of X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂), defined in Scheme 1. The optimized structures are not shown in figures, but a number of them can be observed in Fig. 1 and 2. The magnitudes of the θ₁, θ₂, ϕ₁ and ϕ₂ values are close to 90°, 180°, 90° and 180° (or 0°), respectively, for the most cases.

Table 1 Structural parameters for X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂), optimized with M06-2X/BSS-SA^a,b

Y–X-*-π(C24H12), (symmetry: type)	r1, (Å)	r2, (Å)	θ1, (°)	θ2, (°)	ϕ1, (°)	ϕ2, (°)	ΔEES^c^,^d, (kJ mol^−1)	ΔEEnt^c^,^e, (kJ mol^−1)
a See text for BSS-SA.b See Scheme 1 for the definition of the structural parameters.c ΔE = E(X–H⋯π(C24H12)/Y–X⋯π(C24H12)) − (E(X–H/Y–X) + E(C24H12)).d ΔEES represents ΔE on the energy surface.e ΔEEnt represents ΔE with the correction of the heat of enthalpy.f One imaginary frequency being predicted for each, of which motion mainly corresponds to the angular displacements between π(C24H12) and X–H or Y–X.g Br–H being placed above the midpoint between ^2C and ^3C, which is defined by type . In this case, the r1 value is measured from ^2C.h Close to the Cs symmetry, where Cl in F–Cl pointing to ^12M, the midpoint between ^1C and ^2C.
F–H⋯π(^3C) (C1: IBCor)^f	2.2609	0.9243	80.09	169.69	−89.91	180.00	−17.5	−15.5
Br–H⋯π(^2C) (C1: )^g	2.6197	1.4243	78.28	166.98	−114.35	52.29	−16.8	−10.0
I–H⋯π(^3C) (C1: IBCor)	2.6427	1.6219	77.03	162.89	−108.52	−12.06	−16.9	−11.2
F–H⋯π(^12M) (Cs: ICCor)	2.1815	0.9261	83.01	177.80	−90.00	180.00	−19.4	−15.1
Cl–H⋯π(^12M) (C1: ICCor)^f	2.4502	1.2840	68.93	179.73	−90.00	179.97	−16.1	−14.9
Br–H⋯π(^12M) (Cs: ICCor)	2.5236	1.4244	68.68	167.96	−90.00	0.00	−17.2	−10.3
I–H⋯π(^12M) (Cs: ICCor)	2.5847	1.6222	68.98	164.38	−90.00	0.00	−17.3	−12.2
F–F⋯π(^aC) (Cs: IACor)	2.7873	1.3685	90.62	177.95	−89.96	0.00	−7.5	−3.1
Cl–Cl⋯π(^aC) (C1: IACor)^f	3.0381	1.9950	90.95	178.16	−89.95	0.03	−16.0	−13.5
Br–Br⋯π(^aC) (Cs: IACor)	3.1293	2.2912	90.95	177.03	−89.95	0.00	−20.1	−14.1
I–I⋯π(^aC) (Cs: IACor)	3.3116	2.6768	89.61	178.88	−89.92	180.00	−23.5	−20.2
F–Cl⋯π(^aC) (Cs: IACor)	2.9409	1.6257	90.82	177.56	−90.07	0.00	−20.4	−16.5
F–Br⋯π(^aC) (Cs: IACor)	3.0096	1.7632	92.21	174.94	−90.11	0.00	−27.4	−22.8
F–I⋯π(^aC) (Cs: IACor)	3.1554	1.9216	93.14	178.55	−90.00	0.00	−35.6	−32.0
F–F⋯π(^12M) (Cs: ICCor)	2.9010	1.3677	72.64	162.12	−90.00	0.00	−7.0	−3.5
Cl–Cl⋯π(^12M) (C1: ICCor)^f	3.0107	1.9990	87.28	178.12	−90.00	0.00	−14.3	−13.2
Br–Br⋯π(^12M) (C1: ICCor)	3.0801	2.2975	90.46	176.98	−88.52	65.27	−17.8	−13.3
I–I⋯π(^12M) (Cs: ICCor)	3.3370	2.6788	86.08	179.26	−90.00	180.00	−20.6	−16.5
F–Cl⋯π(^12M) (C1: ICCor)^f^,^h	2.8523	1.6323	91.82	178.00	−90.02	−0.09	−21.7	−19.3
F–Br⋯π(^12M) (Cs: ICCor)	2.8616	1.7699	98.68	178.24	−90.00	180.00	−30.0	−25.3
F–I⋯π(^12M) (Cs: ICCor)	3.0277	1.9269	94.21	179.61	−90.00	0.00	−36.5	−32.8

---

Fig. 1 Molecular graphs for F–H-*-π(C₂₄H₁₂) (C₁: IB_Cor) (a), Br–H-*-π(C₂₄H₁₂) (C₁: ) (b), I–H-*-π(C₂₄H₁₂) (C₁: IB_Cor) (c), F–H-*-π(C₂₄H₁₂) (C_s: IC_Cor) (d), Cl–H-*-π(C₂₄H₁₂) (C₁: IC_Cor) (e), Br–H-*-π(C₂₄H₁₂) (C_s: IC_Cor) (f) and I–H-*-π(C₂₄H₁₂) (C_s: IC_Cor) (g), calculated with M06-2X/BSS-SA. BCPs are denoted by red dots, RCPs by yellow dots, CCPs by green dots and BPs by pink lines. Carbon atoms are in black and hydrogen atoms are in grey, with fluorine, chlorine, bromine and iodine atoms in dark yellow, green, dark purple and purple, respectively. The contour plot of ρ(r) is also drawn for each on the plane containing the H-*-³C(C₂₄H₁₂) moiety for type IB_Cor with the H-*-²C(C₂₄H₁₂) moiety for type or on the plane of the H-*-¹²M(C₂₄H₁₂) moiety for type IC_Cor, where the contour plot is drawn on each plane.

Fig. 2 Molecular graphs for F–F-*-π(C₂₄H₁₂) (C_s: IA_Cor) (a), F–Cl-*-π(C₂₄H₁₂) (C_s: IA_Cor) (b), F–Br-*-π(C₂₄H₁₂) (C_s: IA_Cor) (c), F–I-*-π(C₂₄H₁₂) (C_s: IA_Cor) (d), F–F-*-π(C₂₄H₁₂) (C_s: IC_Cor) (e), F–Cl-*-π(C₂₄H₁₂) (C₁: IC_Cor) (f), F–Br-*-π(C₂₄H₁₂) (C_s: IC_Cor) (g) and F–I-*-π(C₂₄H₁₂) (C_s: IC_Cor) (h), calculated with M06-2X/BSS-SA. BCPs are denoted by red dots, RCPs by yellow dots and BPs by pink lines. Carbon atoms are in black and hydrogen atoms are in grey, with fluorine, chlorine, bromine and iodine atoms in dark yellow, green, dark purple and purple, respectively. The contour plot of ρ(r) is also drawn for each on the plane containing the X-*-³C(C₂₄H₁₂) moiety for type IB_Cor or on the plane of X-*-¹²M(C₂₄H₁₂) moiety for type IC_Cor, where the contour plot is drawn on each plane.

However, significant deviations are observed in some cases. The (ϕ₁, ϕ₂) values of (−114.4°, 52.3°) for Br–H⋯π(²C) (C₁: ) are the typical example, taken from the intermediate structure between Br–H⋯π(²C) (C₁: IB_Cor) and typical Br–H⋯π(¹²M) (C_s: IC_Cor). The lack of convergence of Cl–H⋯π(C₂₄H₁₂) to the IB_Cor type with all positive frequencies is related to the formation of Br–H⋯π(²C) (C₁: ).

This is a very gentle potential energy surface around the inter-conversion between Cl–H⋯π(C₂₄H₁₂) (IC_Cor) and the related structure. Similarly, for the cases discussed above, all positive frequencies only were not predicted for F–H⋯π(³C) (C₁: IB_Cor) and Cl–H⋯π(¹²M) (C₁: IC_Cor) in X–H⋯π(C₂₄H₁₂). This is also owing to the very gentle potential energy surface around the motions of the imaginary frequencies for Cl–Cl⋯π(^aC) (C₁: IA_Cor), Cl–Cl⋯π(¹²M) (C₁: IC_Cor) and F–Cl⋯π(¹²M) (C₁: IC_Cor) in Y–X⋯π(C₂₄H₁₂). Nevertheless, with the exception of Cl–H⋯π(¹²M) (C₁: IC_Cor), positive frequencies only are predicted for these cases when the calculations are performed with M06-2X/BSS-SB. The results are collected in Table S1 of the ESI.†

The energy differences between X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂) and the components, ΔE (= E(X–H⋯π(C₂₄H₁₂)/Y–X⋯π(C₂₄H₁₂)) − (E(X–H/Y–X) + E(C₂₄H₁₂))) (ΔE_ES and ΔE_Ent), are also given in Table 1. ΔE_ES and ΔE_Ent represent ΔE on the energy surface and ΔE with the collections by the enthalpy for the formation of the adducts at 25 °C, respectively. The plot of ΔE_Ent versus ΔE_ES gave a (very) good correlation (y = 0.992x + 3.85: R_c² = 0.955 (n (number of data points) = 21)) even though the data for Cl–H⋯π(¹²M) (C₁: IC_Cor), Br–H⋯π(¹²M) (C_s: IC_Cor), Br–H⋯π(²C) (C₁: ), Br–Br⋯π(^aC) (C_s: IA_Cor) and Cl–Cl⋯π(¹²M) (C₁: IC_Cor) appear to deviate somewhat from the correlation (Fig. S2 of the ESI†). A much better correlation was obtained if the data for the five species are omitted from the correlation (y = 1.000x + 3.90: R_c² = 0.986 (n = 16)). Therefore, ΔE_ES can be used for the discussion of ΔE.

After the elucidation of the structural feature of X–H⋯π(C₂₄H₁₂) and Y–X⋯π(C₂₄H₁₂), molecular graphs, contour plots, negative Laplacians and trajectory plots are examined next.

Molecular graphs, contour plots, negative Laplacians and trajectory plots for X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂)

Fig. 1 illustrates the molecular graphs for F–H-*-π(C₂₄H₁₂) (C₁: IB_Cor), Br–H-*-π(C₂₄H₁₂) (C₁: ), I–H-*-π(C₂₄H₁₂) (C₁: IB_Cor), F–H-*-π(C₂₄H₁₂) (C_s: IC_Cor), Cl–H-*-π(C₂₄H₁₂) (C₁: IC_Cor), Br–H-*-π(C₂₄H₁₂) (C_s: IC_Cor) and I–H-*-π(C₂₄H₁₂) (C_s: IC_Cor), calculated with M06-2X/BSS-SA. Each molecular graph contains the contour plot of ρ(r) drawn on the plane containing the H-*-³C moiety for F–H-*-π(C₂₄H₁₂) (IB_Cor) and I–H-*-π(C₂₄H₁₂) (IB_Cor) with the H-*-²C moiety for Br–H-*-π(C₂₄H₁₂) () or on the plane of H-*-¹²M moiety for X–H-*-π(C₂₄H₁₂) (IC_Cor), albeit partially. Fig. 2 shows the molecular graphs for the IA_Cor and IC_Cor types of F–X-*-π(C₂₄H₁₂) (X = F, Cl, Br and I), calculated with M06-2X/BSS-SA. The contour plot of ρ(r) is drawn for each adduct partially, similar to Fig. 1.

In Fig. 1, all expected BCPs are clearly observed, including those for the XH-*-π and YX-*-π interactions in question, together with ring critical points (RCPs) and cage critical points (CCPs), if such exist. The structural feature is visualized well by the molecular graphs. The BPs for H-*-π and X-*-π in question seem linear for most of X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂), although some seem somewhat bending. BCPs are well located at the (three-dimensional) saddle points of ρ(r). Negative Laplacians and trajectory plots are drawn for X–H-*-π(C₂₄H₁₂), similar to Fig. 1 and are shown in Fig. S3 and S4 of the ESI,† respectively. Negative Laplacians and trajectory plots are also drawn for Y–X-*-π(C₂₄H₁₂), similar to Fig. 2, and are shown in Fig. S5 and S6 of the ESI,† respectively. The behaviour of the BCPs is well-visualized through ∇²ρ(r) as shown in Fig. S3 and S5 of the ESI.† All BCPs in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) are placed in the blue areas of the negative Laplacians; therefore, the interactions corresponding to the BCPs should be classified by the CS interactions. The space around the species around the interactions in question is well divided into atoms, as demonstrated in Fig. S4 and S6 of the ESI.†

Survey of X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions, evaluated with M06-2X/BSS-SA

How can the X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions be described? The interactions can be defined by the corresponding BPs, although we must be careful to use the correct terminology with this concept.³¹ As shown in Fig. 1 and 2, BPs for the adducts appear to be straight, with the exception of X–H-*-π(C₂₄H₁₂) (C₁: IB_Cor) (X = Br and I) and Y–X-*-π(¹²M) (C₁: IC_Cor) (Y–X = F–Cl and Br–Br). The lengths of BPs (r_BP) and the straight-line distances (R_SL) evaluated with M06-2X/BSS-SA, are collected in Table S3 of the ESI† together with the Δr_BP (= r_BP − R_SL) values. The Δr_BP value are 0.68 Å for F–Cl-*-π(¹²M) (C₁: IC_Cor), 0.41 Å for Br–Br-*-π(¹²M) (C₁: IC_Cor), 0.35 Å for Br–H-*-π(²C) (C₁: IB_Cor) and 0.17 Å for I–H-*-π(³C) (C₁: IB_Cor). However, the Δr_BP values are smaller than 0.064 Å for X–H-*-π(C₂₄H₁₂) and smaller than 0.015 Å for Y–X-*-π(C₂₄H₁₂) (C_s: IA_Cor) (X, Y = F, Cl, Br and I), as shown in Table S3.† Therefore, the H-*-π and X-*-π interactions in the coronene π-system can be approximated as straight lines, except for the four species, although Δr_BP = 0.064 Å for F–H-*-π(³C) (C₁: IB_Cor). The plot of r_BP versus R_SL for the adducts gave an excellent correlation (y = 0.966x + 0.1079; R_c² = 0.999 (n = 16)), if the data of the four species are neglected from the correlation (not shown in the figure).

QTAIM functions are evaluated for the H-*-π and X-*- π interactions at BCPs in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) (X, Y = F, Cl, Br and I) using the M06-2X functional. The obtained values are presented in Table 2. Fig. 3 shows the plot of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for the data in Table 2 and those from the perturbed structures around the fully optimized structures. All data in Fig. 3 appear in the region of H_b(r_c) − V_b(r_c)/2 > 0 and H_b(r_c) > 0, and therefore, all interactions in question are classified by the pure CS interactions.

Table 2 QTAIM functions and QTAIM-DFA parameters for X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) (X, Y = F, Cl, Br and I), evaluated with M06-2X/BSS-SA and M06-2X/BSS-SB^a,b

Y–X-*-π(C24H12), (symmetry: type)	ρb(rc), (eao^−3)	c∇^2ρb(rc)^c, (au)	Hb(rc), (au)	kb(rc)^d	R, (au)	θ, (°)	Freq, (cm^−1)	kf, (mDyne Å^−1)	θp, (°)	κp, (au^−1)
a See text for BSS-SA and BSS-SB.b Data are given at BCP, which is shown by X-*-π.c c∇^2ρb(rc) = Hb(rc) − Vb(rc)/2, where c = ħ^2/8m.d kb(rc) = Vb(rc)/Gb(rc).e One imaginary frequency being predicted for each.f BCP (and BP) being not detected.g Perturbed structures for Cl–H-*-π(^2C) (C1: IACor) are generated employing w = −0.1, −0.05, (0), 0.01 and 0.015 in eqn (2); therefore, some intervals in the plot are shorter than others.
M06-2X/BSS-SA
F–H-*-π(^3C) (C1: IBCo)^e	0.0146	0.0053	0.0005	−0.948	0.0053	84.4	84.4	0.024	113.0	172.1
Br–H-*-π(^2C) (C1: )	0.0090	0.0037	0.0012	−0.801	0.0039	71.6	60.4	0.025	82.4	162.5
I–H-*-π(^3C) (C1: IBCor)	0.0089	0.0035	0.0012	−0.785	0.0037	70.5	49.1	0.017	83.7	156.9
F–H-*-π(^12M) (Cs: ICCor)	0.0172	0.0057	0.0001	−0.992	0.0057	89.1	134.4	0.059	129.1	242.5
Cl–H-*-π(^12M) (C1: ICCor)^e^,^f	Non	Non	Non	Non	Non	Non	Non	Non	Non	Non
Br–H-*-π(^12M) (Cs: ICCor)	0.0099	0.0038	0.0012	−0.814	0.0039	72.6	60.4	0.027	86.4	181.1
I–H-*-π(^12M) (Cs: ICCor)	0.0093	0.0035	0.0012	−0.798	0.0037	71.4	53.5	0.020	83.7	171.6
F–F-*-π(^aC) (Cs: IACor)	0.0097	0.0056	0.0023	−0.735	0.0061	67.3	72.5	0.035	71.7	32.9
Cl–Cl-*-π(^aC) (C1: IACor)^e	0.0113	0.0050	0.0015	−0.828	0.0052	73.6	74.5	0.036	87.2	96.5
Br–Br-*-π(^aC) (Cs: IACor)	0.0115	0.0047	0.0012	−0.847	0.0048	75.1	59.2	0.024	87.9	121.0
I–I-*-π(^aC) (Cs: IACor)	0.0109	0.0040	0.0011	−0.846	0.0042	75.1	44.9	0.013	89.4	144.6
F–Cl-*-π(^aC) (Cs: IACor)	0.0131	0.0058	0.0014	−0.858	0.0060	76.0	79.5	0.037	92.0	108.4
F–Br-*-π(^aC) (Cs: IACor)	0.0137	0.0056	0.0012	−0.880	0.0057	77.9	67.4	0.033	94.5	135.3
F–I-*-π(^aC) (Cs: IACor)	0.0134	0.0049	0.0009	−0.904	0.0050	80.1	66.6	0.027	104.1	227.6
F–F-*-π(^12M) (Cs: ICCor)	0.0081	0.0046	0.0020	−0.716	0.0050	66.2	61.2	0.026	68.1	24.5
Cl–Cl-*-π(^12M) (C1: ICCor)^e	0.0124	0.0053	0.0017	−0.814	0.0055	72.6	170.6	0.070	86.4	98.1
Br–Br-*-π(^12M) (C1: ICCor)	0.0132	0.0051	0.0014	−0.843	0.0053	74.8	54.1	0.032	89.3	178.7
I–I-*-π(^12M) (Cs: ICCor)	0.0108	0.0039	0.0012	−0.821	0.0040	73.1	48.1	0.012	87.1	107.5
F–Cl-*-π(^12M) (C1: ICCor)^e	0.0163	0.0067	0.0016	−0.867	0.0069	76.8	73.8	0.023	95.8	92.0
F–Br-*-π(^12M) (Cs: ICCor)	0.0189	0.0070	0.0011	−0.918	0.0071	81.4	108.7	0.042	109.6	220.8
F–I-*-π(^12M) (Cs: ICCor)	0.0177	0.0059	0.0005	−0.951	0.0059	84.7	106.8	0.039	124.8	375.2
M06-2X/BSS-SB
F–H-*-π(^3C) (Cs: IBCor)	0.0142	0.0053	0.0014	−0.852	0.0055	75.6	115.5	0.051	78.7	68.4
Cl–H-*-π(^2C) (C1: IACo)^g	0.0118	0.0041	0.0009	−0.870	0.0042	77.0	310.7	0.231	75.7	535
Br–H-*-π(^2C) (C1: IBCor)	0.0092	0.0033	0.0008	−0.871	0.0034	77.1	59.2	0.025	82.0	12.2
I–H-*-π(^3C) (C1: IBCor)	0.0093	0.0033	0.0009	−0.847	0.0034	75.2	49.5	0.019	84.7	81.0
Cl–H-*-π(^12M) (C1: ICCor)	0.0108	0.0036	0.0007	−0.895	0.0037	79.2	24.6	0.003	81.9	149.9

---

Fig. 3 QTAIM-DFA plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) (X, Y = F, Cl, Br and I). Marks and colours are shown in the figure, where circle and square marks correspond to the data evaluated with M06-2X/BSS-SA.

Nature of X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions, evaluated with M06-2X/BSS-SA

The plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 in Fig. 3 are analysed according to eqn (S3)–(S6) of the ESI,† which provide the QTAIM-DFA parameters of (R, θ) and (θ_p, κ_p). Table 2 collects the frequencies, correlated to NIV employed to generate the perturbed structures and the force constants, k_f. The nature of the interactions in question is classified and characterized based on the QTAIM-DFA parameters, employing the standard values (criteria) as the reference. Table 3 summarizes the predicted nature of H-*-π in X–H-*-π(C₂₄H₁₂) and X-*-π in Y–X-*-π(C₂₄H₁₂), employing the θ and θ_p values evaluated with M06-2X/BSS-SA.

Table 3 Nature of the H-*-π and X-*-π interactions in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂), respectively, evaluated with M06-2X/BSS-SA^a

Y–X-*-π(C24H12), (symmetry: type)	θ, (°)	θp, (°)	Predicted nature	Y–X-*-π(C24H12), (symmetry: type)	θ, (°)	θp, (°)	Predicted nature
a See text for BSS-SA.b One imaginary frequency being predicted for each.c Classified by the pure closed shell (CS) interactions and characterized as the typical hydrogen bonds (t-HB) with no covalency.d Very close to the regular CS (r-CS) interactions and characterized as t-HB with covalency (t-HBwc).e Predicted to be the vdW interactions appeared in the p-CS region.
X–H-*-π(C24H12)
F–H-*-π(^3C) (C1: IBCor)^b	84.4	113.0	p-CS/t-HBnc^c	F–H-*-π(^12M) (Cs: ICCor)	89.1	129.1	p-CS/t-HBnc^c^,^d
Br–H-*-π(^2C) (C1: IBCor)	71.6	82.4	p-CS/vdW^e	Br–H-*-π(^12M) (Cs: ICCor)	72.6	86.4	p-CS/vdW^e
I–H-*-π(^3C) (C1: IBCor)	70.5	83.7	p-CS/vdW^e	I–H-*-π(^12M) (Cs: ICCor)	71.4	83.7	p-CS/vdW^e
Y–X-*-π(C24H12)
F–F-*-π(^aC) (Cs: IACor)	67.3	71.7	p-CS/vdW^e	F–F-*-π(^12M) (Cs: ICCor)	66.2	68.1	p-CS/vdW^e
Cl–Cl-*-π(^aC) (C1: IACor)^b	73.6	87.2	p-CS/vdW^e	Cl–Cl-*-π(^12M) (C1: ICCor)^b	72.6	86.4	p-CS/vdW^e
Br–Br-*-π(^aC) (Cs: IACor)	75.1	87.9	p-CS/vdW^e	Br–Br-*-π(^12M) (C1: ICCor)	74.8	89.3	p-CS/vdW^e
I–I-*-π(^aC) (Cs: IACor)	75.1	89.4	p-CS/vdW^e	I–I-*-π(^12M) (Cs: ICCor)	73.1	87.1	p-CS/vdW^e
F–Cl-*-π(^aC) (Cs: IACor)	76.0	92.0	p-CS/t-HBnc^c	F–Cl-*-π(^12M) (C1: ICCor)^b	76.8	95.8	p-CS/t-HBnc^c
F–Br-*-π(^aC) (Cs: IACor)	77.9	94.5	p-CS/t-HBnc^c	F–Br-*-π(^12M) (Cs: ICCor)	81.4	109.6	p-CS/t-HBnc^c
F–I-*-π(^aC) (Cs: IACor)	80.1	104.1	p-CS/t-HBnc^c	F–I-*-π(^12M) (Cs: ICCor)	84.7	124.8	p-CS/t-HBnc^c

---

As summarized in Table 3, the θ and θ_p values in X–H-*-π(C₂₄H₁₂) decrease in the order of X–H- = F–H- > Br–H- > I–H-, even though θ_p for X–H- = I–H- appears to be somewhat larger than that for the case of X–H- = Br–H-. The results show that θ and θ_p in X–H-*-π(C₂₄H₁₂) are controlled by the electronegativity of X. Namely, the values will be larger if the polarity of the X^δ−–H^δ+ type becomes larger. Conversely, θ and θ_p in Y–X-*-π(C₂₄H₁₂) become larger in the order of Y–X- = F–F- < Cl–Cl- < Br–Br- < I–I- < F–Cl- < F–Br- < F–I-. These results would be the reflection of two factors. The first is the softness of X. The θ and θ_p values become larger with increasing softness of X. The second factor is the polarity of Y^δ−–X^δ+. The θ and θ_p values increase with increasing polarity, resulting in the larger extension of σ*(X–Y) at the X side. This is very interesting because the θ and θ_p values are larger for Y–X- = F–Cl-, relative to the case of Y–X- = I–I-. The predicted nature is discussed next.

It would be instructive to review the criteria before the detailed discussion of the nature for H-*-π and X-*-π. The criteria specify that θ < 180° (H_b(r_c) − V_b(r_c)/2 > 0) for the CS interactions and θ > 180° (H_b(r_c) − V_b(r_c)/2 < 0) for the SS interactions. The CS interactions for θ < 180° are sub-divided into the pure CS interactions for 45° < θ < 90° (H_b(r_c) > 0) and the regular CS interactions for 90° < θ < 180° (H_b(r_c) < 0). The θ_p value plays an important role in characterizing the interactions. In the pure CS region of 45° < θ < 90°, the character of interactions will be the vdW type for 45° < θ_p < 90° and the typical-HB type (t-HB) with no covalency (t-HB_nc) for 90° < θ_p < 125°, where θ_p = 125° is tentatively given, corresponding to θ = 90°. The regular CS (90° < θ < 180°) and SS (180° < θ) interactions are not discussed here, since the interactions in this region are not detected in this work.

The θ values are less than 90° for all X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions examined in this work. Therefore, the H-*-π and X-*-π interactions are all classified by the pure CS interactions. On the other hand, the θ_p values are less than 90° for all interactions with the exception of F–H-*-π(C₂₄H₁₂) of the IB_Cor and IC_Cor types and F–X-*-π(C₂₄H₁₂) (X = Cl, Br and I) of the IA_Cor and IC_Cor types. The interactions in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) are all characterized as the vdW nature for those with θ_p < 90°. The interactions with θ_p > 90° are characterized to have the nature of typical hydrogen bonds with no covalency (t-HB_nc). However, the nature of the H-*-π interactions in F–H-*-π(¹²M) (C_s: IC_Cor) should be examined carefully. The θ_p value is 129.1°, which is larger than 125°. The results suggest that the H-*-π interaction should be characterized as t-HB with covalency (t-HB_wc). However, the θ value of 89.1° is less than 90°, therefore, the interaction must have no covalency. In this case, the θ value should have the priority to the θ_p value in the prediction of the nature of the interaction, since θ_p is only given tentatively corresponding to θ = 90°. Therefore, the H-*-π interaction in F–H-*-π(¹²M) (C_s: IC_Cor) would be better characterized as t-HB_nc. However, the interaction appears to be close to the borderline area between t-HB_nc and t-HB_wc, since θ = 89.1° is close to 90°, while θ_p = 129.1° > 125°.

The X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions (X, Y = F, Cl, Br and I) were also analysed for the ID_Cor type with M06-2X/BSS-SA (see Scheme 2). The results of this analysis are discussed next.

Nature of X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions of the ID_Cor type, evaluated with M06-2X/BSS-SA

Indeed, the ID_Cor type is not optimized for X–H-*-π(C₂₄H₁₂) with M06-2X/BSS-SA, even though they are optimized when calculated at the MP2 level. The nature of the Y–X-*-π(C₂₄H₁₂) interactions around the main axis of π(C₂₄H₁₂) is also very interesting. Therefore, X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) are optimized assuming the C_2v symmetry. The structural parameters are presented in Table S4 of the ESI,† and are defined in Scheme 2. Table S5 of the ESI† presents the QTAIM-DFA parameters of (R, θ) and (θ_p, κ_p) evaluated with M06-2X/BSS-SA, together with the frequencies correlated to NIV employed to generate the perturbed structures and the force constants k_f.

The nature of the interactions in question is classified and characterized based on the QTAIM-DFA parameters, employing the standard values as the reference. Table 4 summarizes the predicted nature of the H-*-π and X-*-π interactions in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) of the C_2v symmetry, respectively, employing the θ and θ_p values evaluated with M06-2X/BSS-SA. As summarized in Table 4, the θ and θ_p values in X–H-*-π(C₂₄H₁₂) (C_2v: ID_Cor) decrease in the order of X–H- = F–H- > Cl–H- > I–H- > Br–H-. On the other hand, the θ_p values in Y–X-*-π(C₂₄H₁₂) increase in the order of F–F- < Cl–Cl- < I–I- and F–Cl- < Br–Br- < F–Br- < F–I-. The θ and θ_p are smaller than 90° for all interactions in X–H-*-π(C₂₄H₁₂) (C_2v: ID_Cor) and Y–X-*-π(C₂₄H₁₂) (C_2v: ID_Cor) (see Table 4). Therefore, the H-*-π and X-*-π interactions are all classified by the pure CS interactions and are characterized to be of the vdW nature (p-CS/vdW).

Table 4 Nature of the H-*-π and X-*-π interactions in X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) of the C_2v symmetry, respectively, evaluated with M06-2X/BSS-SA^a

Y–X-*-π(C24H12), (symmetry: type)	θ, (°)	θp, (°)	Predicted nature	Y–X-*-π(C24H12), (symmetry: type)	θ, (°)	θp, (°)	Predicted nature
a See text for BSS-SA.b Classified by the p-CS interactions and characterized as the vdW interactions.
F–H-*-π(Mo) (C2v: IDCor)	70.4	79.5	p-CS/vdW^b	Cl–H-*-π(Mo) (C2v: IDCor)	69.7	75.5	p-CS/vdW^b
Br–H-*-π(Mo) (C2v: IDCor)	69.5	76.1	p-CS/vdW^b	I–H-*-π(Mo) (C2v: IDCor)	69.6	76.5	p-CS/vdW^b
F–F-*-π(Mo) (C2v: IDCor)	65.9	66.6	p-CS/vdW^b
Cl–Cl-*-π(Mo) (C2v: IDCor)	66.7	74.4	p-CS/vdW^b	F–Cl-*-π(Mo) (C2v: IDCor)	67.4	75.1	p-CS/vdW^b
Br–Br-*-π(Mo) (C2v: IDCor)	69.0	76.0	p-CS/vdW^b	F–Br-*-π(Mo) (C2v: IDCor)	69.9	76.1	p-CS/vdW^b
I–I-*-π(Mo) (C2v: IDCor)	69.1	75.1	p-CS/vdW^b	F–I-*-π(Mo) (C2v: IDCor)	70.6	77.3	p-CS/vdW^b

---

Nature of X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) versus that of X–H-*-π(C₆H₆) and Y–X-*-π(C₆H₆)

The Y–X-*-π(C₆H₆) and X–H-*-π(C₆H₆) interactions (X, Y = F, Cl, Br and I) are similarly evaluated with M06-2X/BSS-SA. The results are presented in Table S6 and S7 of the ESI.† Fig. 4 shows the plots of θ and θ_p for Y–X-*-π(C₂₄H₁₂) versus those of Y–X-*-π(C₆H₆) for convenience of comparison. As shown in Fig. 4, the θ and θ_p values for Y–X-*-π(^aC: C₂₄H₁₂) (IA_Cor) appear to be somewhat smaller than those for Y–X-*-π(C₆H₆) (C_s: IB_Bzn), respectively, if those of the same Y–X are compared, whereas the values for Y–X-*-π(¹²M: C₂₄H₁₂) (IC_Cor) are predicted to be larger than those for Y–X-*-π(C₆H₆) (C_s: IB_Bzn), respectively. Conversely, the θ and θ_p values for Y–X-*-π(M_o: C₂₄H₁₂) (C_2v: ID_Cor) are very close to those for Y–X-*-π(C₆H₆) (C_2v: ID_Bzn), respectively, if those of the same Y–X are compared.

Fig. 4 Plots of θ and θ_p for Y–X-*-π(C₂₄H₁₂) (X, Y = F, Cl, Br and I) versus those for Y–X-*-π(C₆H₆), respectively, evaluated with M06-2X/BSS-SA.

What is the reason for the predicted results shown in Fig. 4? The charge developed on the C and H atoms of benzene and coronene is examined as the possible origin of these results. Scheme 3 shows the charge evaluated based on the natural population analysis (Q_n) with MP2/6-311G(d,p).⁵⁷ The outside ^CC–H bonds in coronene are predicted to be substantially positively charged relative to the case of benzene, and the inside ^AC₆ atoms are almost neutral, resulting in the negative charge accumulated on the ^BC atoms (see, Scheme 3). The results show that the θ and θ_p values for Y–X-*-π(C₂₄H₁₂) would be larger than those for Y–X-*-π(C₆H₆), respectively, if Q_n for the former or around the interaction is smaller than for the latter. For the small range of the interactions in the adducts, the electron–electron repulsion may play a more important role in the strength of the X-*-π interaction rather than the attractive interaction such as the CT interaction.

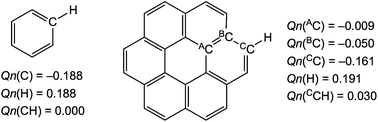Scheme 3 Natural charges (Q_n) on the C and H atoms in benzene and coronene evaluated with MP2/6-311G(d,p).

The θ and θ_p values for X–H-*-π(C₂₄H₁₂) are similarly plotted versus those for X–H-*-π(C₆H₆), as shown in Fig. S9 of the ESI.† In this case, the θ and θ_p values increase in the order of π(M_o: C₂₄H₁₂) (ID_Cor) < π(C₆H₆) ≤ π(³C: C₂₄H₁₂) (IB_Cor) < π(¹²M: C₂₄H₁₂) (IC_Cor), if those of the same X–H are compared. These results appear to be in close agreement to those for Y–X-*-π(C₂₄H₁₂) with Y–X-*-π(C₆H₆) (see, Fig. S9 of the ESI†), even though small differences between the two cases are observed.

The H-*-π and X-*-π interactions in the bent π-systems are also of highly interest. An investigation of such interactions is currently in progress.

Conclusions

QTAIM-DFA was applied to the X–H-*-π(C₂₄H₁₂) (X = F, Cl, Br and I) and Y–X-*-π(C₂₄H₁₂) (Y–X = F–F, Cl–Cl, Br–Br, I–I, F–Cl, F–Br and F–I) interactions, which must be of fundamental importance. The structures were optimized mainly at the M06-2X/BSS-SA level of theory. Four types of structures were optimized for X–H⋯π(C₂₄H₁₂) and Y–X⋯π (C₂₄H₁₂) (types IA_Cor, IB_Cor, IC_Cor and ID_Cor) (see, Schemes 1 and 2). The IB_Cor and IC_Cor types were predicted for X–H⋯π(C₂₄H₁₂), while the IA_Cor and IC_Cor types were for Y–X⋯π(C₂₄H₁₂), if optimized with M06-2X/BSS-SA. All BCPs expected are clearly observed in the molecular graphs drawn on the optimized structures.

QTAIM-DFA parameters of (R, θ) and (θ_p, κ_p) are calculated for H-*-π in X–H-*-π(C₂₄H₁₂) and X-*-π in Y–X-*-π(C₂₄H₁₂) by analysing the plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 at BCPs. The θ values are smaller than 90° for all X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions, and are therefore classified as the pure CS interactions. The θ_p values are larger than 90° for F–H-*-π(C₂₄H₁₂) of the IB_Cor and IC_Cor types and F–X-*-π(C₂₄H₁₂) (X = Cl, Br and I) of the IA_Cor and IC_Cor types; therefore, they have the t-HB_nc nature. The H-*-π interaction in F–H-*-π(C₂₄H₁₂) (C_s: type IC_Cor) appear to be present close to the borderline area between t-HB_nc and t-HB_wc, since θ = 89.1°, which is close to 90°, while θ_p = 129.1° > 125°. The H-*-π and X-*-π interactions other than above have the vdW nature due to θ_p < 90°. The θ and θ_p values are smaller than 90° for all interactions in question in X–H-*-π(C₂₄H₁₂) (C_2v: ID_Cor) and Y–X-*-π(C₂₄H₁₂) (C_2v: ID_Cor). Therefore, the H-*-π and X-*-π interactions around the main axis of π(C₂₄H₁₂) in the adducts are all predicted to have the nature of p-CS/vdW. The θ and θ_p values for Y–X-*-π(M_o: C₂₄H₁₂) (C_2v: ID_Cor) are very close to the corresponding values for Y–X-*-π(C₆H₆) (C_2v: ID_Bzn), respectively. Conversely, the θ and θ_p values for Y–X-*-π(^aC: C₂₄H₁₂) (IA_Cor) appear to be somewhat smaller than the corresponding values for Y–X-*-π(C₆H₆) (C_s: IB_Bzn), respectively, whereas the values for Y–X-*-π(¹²M: C₂₄H₁₂) (IC_Cor) are predicted to be larger than those for Y–X-*-π(C₆H₆) (C_s: IB_Bzn), respectively.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was partially supported by a Grant-in-Aid for Scientific Research (No. 17K05785) from the Ministry of Education, Culture, Sports, Science and Technology, Japan.

Notes and references

1. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960.
2. S. Scheiner, Hydrogen Bonding, A Theoretical Perspective, Oxford University Press, Oxford, U.K., 1997.
3. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology (IUCr Monographs on Crystallography), Oxford University Press, Oxford, 1999.
4. G. Gilli and P. Gilli, The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory (IUCr Monographs on Crystallography), Oxford University Press, Oxford, 2009.
5. S. Hayashi, K. Matsuiwa, M. Kitamoto and W. Nakanishi, J. Phys. Chem. A, 2013, 117, 1804–1816.
6. M. Meot-Ner (Mautner), Chem. Rev., 2005, 105, 213–284.
7. G. Buemi, Intramolecular Hydrogen Bonds. Methodologies and Strategies for Their Strength Evaluation. in Hydrogen Bonding – New Insights, Vol. 3, Challenges and Advances in Computational Chemistry and Physics, ed. S. J. Grabowski, Springer, New York, 2006, ch. 2.
8. Halogen Bonding: Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Series: Structure and Bonding, vol. 126, Springer, New York, 2008.
9. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
10. (a) A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2013, 113, 2100–2138; (b) M. Alberti, A. Aguilar, J. M. Lucas and F. Pirani, J. Phys. Chem. A, 2010, 114, 11964–11970.
11. See references cited ref. 5.
12. C. Otto, G. A. Thomas, K. Rippe, T. M. Jovin and W. L. Peticolas, Biochemistry, 1991, 30, 3062–3069.
13. The temperature effect on the low frequency Raman spectra of hormones was investigated, which should be closely related to the specific conformation, together with the intra- and inter-molecular interactions employing QTAIM. See, V. A. Minaeva, B. F. Minaev, G. V. Baryshnikov, N. V. Surovtsev, O. P. Cherkasova, L. I. Tkachenko, N. N. Karaush and E. V. Stromylo, Opt. Spectrosc., 2015, 118, 214–223.
14. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
15. (a) S. Yoshimoto, E. Tsutsumi, O. Fujii, R. Narita and K. Itaya, Chem. Commun., 2005, 1188–1190; (b) T. Kato and T. Yamaba, Chem. Phys. Lett., 2005, 403, 113–118; (c) M. D. Watson, F. Jäckel, N. Severin, J. P. Rabe and K. Müllen, J. Am. Chem. Soc., 2004, 126, 1402–1407; (d) X. Chi, C. Besnard, V. K. Thorsmølle, V. Y. Butko, A. J. Taylor, T. Siegrist and A. P. Ramirez, Chem. Mater., 2004, 16, 5751–5755.
16. M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1183.
17. Carbon Nanomaterials: Synthesis, Structure, Properties and Applications, ed. R. B. Mathur, B. P. Singh and S. Pande, CRC Press, Taylor & Francis, Boca Raton, FL, USA, 2017.
18. C. Cheng, S. Li, A. Thomas, N. A. Kotov and R. Haag, Chem. Rev., 2017, 117, 1826–1914.
19. (a) J. Wu, W. Pisula and K. Müllen, Chem. Rev., 2007, 107, 718–747; (b) M. D. Watson, A. Fechtenkotter and K. Müllen, Chem. Rev., 2001, 101, 1267–1300; (c) H. Seyler, B. Purushothaman, D. J. Jones, A. B. Holmes and W. W. H. Wong, Pure Appl. Chem., 2012, 84, 1047–1067; (d) X. Feng, W. Pisula and K. Müllen, Pure Appl. Chem., 2009, 81, 2203–2224; (e) J.-L. Wang, J. Yan, Z.-M. Tang, Q. Xiao, Y. Ma and J. Pei, J. Am. Chem. Soc., 2008, 130, 9952–9962; (f) W. Pisula, X. Feng and K. Müllen, Adv. Mater., 2010, 22, 3634–3649; (g) K. Kawasumi, Q. Zhang, Y. Segawa, L. T. Scott and K. Itami, Nat. Chem., 2013, 5, 739–744; (h) L. Chen, Y. Hernandez, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2012, 51, 7640–7654; (i) J. Wei, B. Han, Q. Guo, X. Shi, W. Wang and N. Wei, Angew. Chem., Int. Ed., 2010, 49, 8209–8213; (j) J. Li, M. Kastler, W. Pisula, J. W. F. Robertson, D. Wasserfallen, A. C. Grimsdale, J. Wu and K. Müllen, Adv. Funct. Mater., 2007, 17, 2528–2533; (k) W. Jin, T. Fukushima, A. Kosaka, M. Niki, N. Ishii and T. Aida, J. Am. Chem. Soc., 2005, 127, 8284–8285; (l) W. Jin, Y. Yamamoto, T. Fukushima, N. Ishii, J. Kim, K. Kato, M. Takata and T. Aida, J. Am. Chem. Soc., 2008, 130, 9434–9440; (m) K. Müllen and J. P. Rabe, Acc. Chem. Res., 2008, 41, 511–520.
20. Y. Sugibayashi, S. Hayashi and W. Nakanishi, Phys. Chem. Chem. Phys., 2015, 17, 28879–28891 . The Y–X-*-π(C₆H₆) interactions are evaluated somewhat stronger than the X–H-*-π(C₆H₆) interactions (X, Y = F, Cl, Br and I).
21. Y. Sugibayashi, S. Hayashi and W. Nakanishi, ChemPhysChem, 2016, 17, 2579–2589.
22. S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2016, 6, 49651–49660.
23. S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2017, 7, 31858–31865.
24. (a) D. Umadevi, S. Panigrahi and G. N. Sastry, Acc. Chem. Res., 2014, 47, 2574–2581; (b) N. N. Karaush, G. V. Baryshnikov, V. A. Minaeva and B. F. Minaev, New J. Chem., 2015, 39, 7815–7821; (c) N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, RSC Adv., 2015, 5, 24299–24305 . See also the references cited therein.
25. The stacked structures for the interaction between halogen molecules and coronene were reported, in addition to the T-shaped (edge-to-face) structures. The X–H-*-π(C₂₄H₁₂) and Y–X-*-π(C₂₄H₁₂) interactions of the 3c–4e type are discussed in this paper, while the nature of the interactions in the stacked structures will be discussed elsewhere. For the stacked structures, see D. Y. Kim, J. M. L. Madridejos, M. Ha, J.-H. Kim, D. C. M. Yang, C. Baig and K. S. Kim, Chem. Commun., 2017, 53, 6140–6143.
26. (a) Atoms in Molecules. A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, Oxford, UK, 1990; (b) C. F. Matta and R. J. Boyd, An Introduction to the Quantum Theory of Atoms in Molecules In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007, ch. 1.
27. (a) R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928; (c) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323; (d) F. Biegler-König, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317–328; (e) R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15; (f) T. H. Tang, R. F. W. Bader and P. MacDougall, Inorg. Chem., 1985, 24, 2047–2053; (g) F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559; (h) F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489–1494.
28. J. Molina and J. A. Dobado, Theor. Chem. Acc., 2001, 105, 328–337.
29. J. A. Dobado, H. Martinez-Garcia, J. Molina and M. R. Sundberg, J. Am. Chem. Soc., 2000, 122, 1144–1149.
30. Some specific interactions are tried to analyze employing QTAIM. See, I. S. Bushmarinov, M. Y. Antipin, V. R. Akhmetova, G. R. Nadyrgulova and K. A. Lyssenko, J. Phys. Chem. A, 2008, 112, 5017–5023 , for an example.
31. Interactions would be easily imaged by means of QTAIM if they can be defined as the corresponding bond paths (BPs), especially for experimental chemists. However, it is demonstrated that the detection of the BPs between two atoms in a molecule emerging from natural alignment of the gradient vector held of the one-electron density of a molecule is neither necessary nor a sufficient condition for the presence of a chemical bond between those atoms.⁵⁸ In this connection, it is pointed out that the terms line paths (LPs) and line critical points (LCPs) should be used in place of BPs and BCPs, respectively.^58b Consequently, the dynamic and static nature in this work should be regarded as the investigation performed at LCPs on LPs corresponding to the XH…π and YX…π interactions in the corannulene π-system. Nevertheless, the interactions expected between π(C₂₄H₁₄) and XH or YX are clearly detected by BPs with BCPs which is another reason to use BPs and BCPs in this work.
32. Critical points (CPs) are characterized by the rank (ω) and the signature (σ). The CPs of the species in the three-dimensional space are classified by ω = 3, which generally corresponds to all species. On the other hand, σ is defined by the simple algebraic sum of the signs of ∂²ρ_b(r_c)/∂r_i² (r_i = x, y and z for i = 1, 2 and 3, respectively), where the + and – signs of ∂²ρ_b(r_c)/∂r_i² are counted as +1 and –1, respectively. Therefore, σ = –3, –1, 1 and 3 correspond to attractors (nuclei), bond critical points (BCPs), ring critical points (RCPs) and cage critical points (CCPs), respectively. Namely, BCP is characterized by (ω, σ) = (3, –1).²⁶.
33. The borderline between the pure-CS and regular-CS interactions is described by k_b(r_c) (= V_b(r_c)/G_b(r_c)) = –1 and that between the regular-CS and SS interactions by k_b(r_c) = –2. For the characterization of interactions by means of k_b(r_c), see (a) R. Bianchi, G. Gervasio and D. Marabello, Inorg. Chem., 2000, 39, 2360–2366; (b) E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 12, 5529–5542.
34. Molecular Interactions. From van der Waals to Strongly Bound Complexes, ed S. Scheiner, Wiley, New York, 1997. For example, (a) A. van der Avoird, P. E. S. Wormer and R. Moszynski, Theory and Computation of Vibration, Rotation and Tunneling Motions of Van der Waals Complexes and their Spectra, ch. 4; (b) J. E. Del Bene and L. Shavitt, The Quest for Reliability in Calculated Properties of Hydrogen-bonded Complexes, ch. 5; (c) T. A. Ford, Ab Initio Predictions of the Vibrational Spectra of Some Molecular Complexes: Comparison with Experiment, ch. 6. See also other chapters.
35. For vdW interactions, see (a) C. E. H. Dessent and K. Müller-Dethlefs, Chem. Rev., 2000, 100, 3999–4021; (b) P. E. S. Wormer and A. van der Avoird, Chem. Rev., 2000, 100, 4109–4144.
36. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
37. (a) M. Nishio, CrystEngComm, 2004, 6, 130–158; (b) E. Espinosa, M. Souhassou, H. Lachekar and C. Lecomte, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 563–572; (c) E. Espinosa, C. Lecomte and E. Molins, Chem. Phys. Lett., 1999, 300, 745–748; (d) E. Espinosa, I. Alkorta, I. Rozas, J. Elguero and E. Molins, Chem. Phys. Lett., 2001, 336, 457–461; (e) C. Gatti and L. Bertini, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 438–449.
38. (a) Chemistry of Hypervalent Compounds, ed K.-y. Akiba, Wiley-VCH, New York, 1999; (b) W. Nakanishi, Hypervalent Chalcogen Compounds in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova, Royal Society of Chemistry, Cambridge, 2006, ch. 10.3, pp. 644–668.
39. The border between t-HB and CT-MC is tentatively defined as θ_p = 90° − tan⁻¹ ([dH_b(r_c)/dr]/[d(H_b(r_c) − V_b(r_c)/2)/dr] = 90° − tan⁻¹ (dH_b(r_c)/d(H_b(r_c) − V = (r_c)/2) = 150°, where θ = 115° corresponds to θ_p = 150°. The border between Cov-w and Cov-s is similarly tentatively defined as R = [(H_b(r_c) − V_b(r_c)/2)² + (H_b(r_c))2]^1/2 = 0.15 au.
40. (a) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057; (b) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2008, 112, 13593–13599.
41. W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197.
42. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423–7430.
43. W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293–1305.
44. See also, D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628.
45. QTAIM-DFA is successfully applied to analyse weak to strong interactions in the gas phase. It could also be applied to the interactions in crystals and that in larger systems containing bioactive materials. The methodological improvement is inevitable to generate perturbed structures suitable for the systems.
46. The concept of a dynamic molecular graph was recently proposed by Cortés-Guzmán and co-workers through the investigation of the Born–Oppenheimer molecular dynamics (BOMD), which was exemplified by [Fe{C-(CH₂)₃}(CO)₃]. The investigation illustrates the change in the behavior of the molecular graph.⁵⁹ The concept of the dynamic molecular graph would be closely related to that of the dynamic nature of interactions predicted by employing the perturbed structures generated with the normal coordinate of internal vibrations (NIV). In this treatment, the selected vibration for NIV must contain the motion of the interaction in question most effectively among all the zero-point internal vibrations. A structural catastrophe is confirmed not to occur for the perturbed and fully optimized structures for the elucidation of the dynamic nature of the interaction in question with NIV.⁵⁴.
47. (a) J. Granatier, P. Lazar, M. Otyepka and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3743–3755; (b) P. Lazar, F. Karlický, P. Jurečka, M. Kocman, E. Otyepková, K. Šafářova and M. Otyepka, J. Am. Chem. Soc., 2013, 135, 6372–6377; (c) M. A. Hussain, D. Vijay and G. N. Sastry, J. Comput. Chem., 2016, 37, 366–377.
48. (a) J. Kysilka, M. Rubes, L. Grajciar, P. Nachtigall and O. Bludsky, J. Phys. Chem. A, 2011, 115, 11387–11393; (b) Y. Wang, H. Qian, K. Morokuma and S. Irle, J. Phys. Chem. A, 2012, 116, 7154–7160.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
50. T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124.
51. The AIM2000 program (Version 2.0) is employed to analyze and visualize atoms-in-molecules: F. Biegler-König, J. Comput. Chem., 2000, 21, 1040–1048.
52. T. A. Keith, AIMAll (Version 17.11.14), TK Gristmill Software, Overland Park KS, USA, 2017, aim.tkgristmill.com.
53. (a) C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622; (b) J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643; (c) J. Gauss, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1001–1008.
54. The basis set of the (5211111111/411111111/31111) type was employed for I in the calculations of I–H⋯π(C₂₄H₁₂) and Y–I⋯π(C₂₄H₁₂) (Y = F and I), which was obtained from EMSL Basis Set Exchange Library. The basis set is called 6–311G(d) for I. (See also ref. 60 and 61).
55. For the m × n matrix representation, m corresponds to the number of atoms and n (=3) to the x, y and z components of the space.
56. The values of w = (0), ±0.1 and ±0.2 in r = r_o + wa_o were employed for the perturbed structures in POM (partial optimization method) in ref. 40b and 41 because the bond orders become 2/3 and 3/2 times larger at w = +0.2 and –0.2, respectively, relative to the original values at w = 0. However, it seems better to employ the perturbed structures closer to the fully optimized one, which will reduce errors in the QTAIM functions at the perturbed structures generated by using NIV and/or POM (see ref. 40–43). Therefore, w = (0), ±0.05 and ±0.1 for r = r_o + wa_o were used for the analysis herein.
57. The reliable Q_n values could not be obtained if evaluated with M062X/BSS-SA.
58. (a) R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396; (b) C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem.–Eur. J., 2012, 18, 4982–4993; (c) M. Garcıa-Revilla, E. Francisco, P. L. A. Popelier and A. M. Pendás, ChemPhysChem, 2013, 14, 1211–1218; (d) Z. A. Keyvani, S. Shahbazian and M. Zahedi, Chem.–Eur. J., 2016, 22, 5003–5009.
59. F. Cortés-Guzmán, T. Rocha-Rinza, J. M. Guevara-Vela, G. Cuevas and R. M. Gómez, Chem.–Eur. J., 2014, 20, 5665–5672.
60. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
61. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.

---

Footnote

† Electronic supplementary information (ESI) available: QTAIM-DFA approach, computational data, and the fully optimized structures given by Cartesian coordinates, together with total energies of the coronene π-system. See DOI: 10.1039/c8ra01862f

---