Surface-tension-confined assembly of a metal–organic framework in femtoliter droplet arrays

Abstract

Metal–organic frameworks (MOFs), produced by metal ions coordinated to organic linkers, have attracted increasing attention in recent years. For the utilization in MOFs in numerous applications, achieving positioned MOF growth on surfaces is essential to fabricate multiple-functional devices. We develop a novel miniaturized method to realize surface-tension-confined assembly of HKUST-1 in femtoliter droplet arrays. HKUST-1 crystal arrays grown by evaporation-induced crystallization are observed, and five typical crystal morphologies (i.e., hexagonal, irregular hexagonal, triangular, arc-like and ribbon-like crystals) are found in the large area on the patterned substrate during crystallization. Our research provides a better understanding of the formation mechanism of MOF crystals in confined sessile droplets. The key factors determining HKUST-1 single-crystal growth are the internal flows in an evaporating droplet and consequently aggregation induced by the combination of metallic Cu(II) and BTC ions. Understanding the formation of different morphologies of HKUST-1 crystals is useful to guide the production of crystals with desired shapes for various applications.

---

1. Introduction

Metal–organic frameworks (MOFs) are ultra-porous and highly crystalline materials due to the framework produced by metal ions coordinated to organic linkers.^1–3 As future porous materials, MOFs offer the highest surface area per gram of any known material.⁴ Therefore, these MOFs show numerous potential applications for sensing,⁵ drug delivery,⁶ energy production,^7,8 bioreactors,⁹ etc.^10–14 For the utilization of MOFs in these applications, miniaturization is essential to fabricate multiple-functional devices.¹⁵ Therefore, the ability to confine MOF properties to a desired location is of great importance to realize device miniaturization. Several techniques have been reported to achieve spatial control over the location of MOF materials, such as microcontact printing (μCP),¹⁶ surface functionalization (e.g., self-assembled monolayers, SAMs) combined with layer-by-layer (LbL) assembly,¹⁷ liquid-phase epitaxy (LPE),¹⁸ microfluidics¹⁹ and pen-type lithography.²⁰ However, each of these methods has its advantages and disadvantages. These existing techniques exhibit several drawbacks, such as restricted throughput and small patterning area, random positioning on the substrate, large distribution in the droplet sizes, the necessity for expensive equipment or complex operation.¹⁵ These drawbacks have constrained the practical use of these techniques where uniform droplet volumes, precise positioning and large-scale patterning in ordered arrays are desirable.

We developed a novel miniaturized, high-throughput and straightforward method to realize positioned MOF growth on a surface. In this work, we show that circumventing the above limitations is possible through confining droplets on wettable pre-patterned arrays on a nonwettable substrate. We applied the proposed method to form HKUST-1 [Cu₃(BTC)₂] crystals, a much-studied MOF material consisting of metallic Cu(II) and 1,3,5-benzenetricarboxylate (BTC or trimesate).²¹ This method is based on surface-tension-confined (STC) technology.²² STC devices confine small volumes of liquid to specific surface areas that exhibit higher surface energy compared to the background surface, resulting in liquid droplets guidance along patterning arrays. To date, most strategies¹⁵ developed to achieve positioned MOF growth require functionalizing the substrate surface with SAMs, which can provide a high contact angle between the HKUST-1 precursor solution and the surface and induce oriented growth. However, our method does not require this specific functionalization. Therefore, the surface-tension confinement of patterned wettable (lyophilic)/nonwettable (lyophobic) arrays on HKUST-1 precursor droplets seems to lead to oriented growth of HKUST-1 crystals. Our approach take advantage of STC technology, such as high-throughput processing (250 kHz), uniform droplet volumes and facile operation, to deposit monodisperse MOFs crystals in patterns down to the single-crystallite level by in situ crystallization, to achieve smaller droplet volumes and denser array networks than existing positioning methods.^16,19,20

2. Experimental

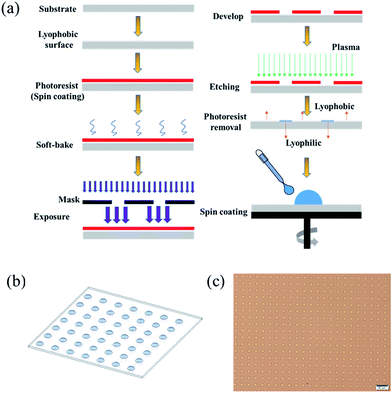
The schematic diagram of STC technology is shown in Fig. 1. First, we fabricated wettable patterns on nonwettable substrates through photolithography. To prepare the nonwettable substrates, [100]-oriented silicon wafers growing (Wenhao Microfluidic Technology Company, Suzhou, China) and glass substrates (Guluo Glass, Beijing, China) were cleaned using a plasma cleaner (PDC-002, Harrick Plasma, USA). Then, the substrates were modified with 1H,1H,2H,2H-perfluorooctyltriethoxysilane (POTS, Sigma-Aldrich, USA) by heating for 2 h at 120° in a sealed crisper containing an open vial with POTS, followed by heating in a drying oven (FD115, Binder, Germany). Next, a positive photoresist (AZ9620, Wenhao Microfluidic Technology Company, Suzhou, China) was spin coated on the nonwettable substrates using a spin-coater (AC100, Jiatu-Tech, Jiangyin, China), followed by pre-baking the resist at ∼105° on a hot plate (HP6, Jiatu-Tech, Jiangyin, China), exposing the resist to ultraviolet (UV) light through a transparent mask using a mask aligner (MJB4, SUSS MicroTec, Germany), and removing the polymerized photoresist in a developer (Wenhao Microfluidic Technology Company, Suzhou, China). The average roughness of the photoresist was approximately 10 μm. After rinsing the substrates in a developer solution and deionized (DI) water, the unprotected circular domains were exposed. DI water was obtained from a water purifier (S30CF, Master Touch, Shanghai). Then, a plasma etching treatment was performed to produce wettable patterns on the nonwettable substrate. Afterwards, the nonwettable background was exposed by removing the photoresist coating on the silicon wafer or glass substrate in acetone and ethanol (Sinopharm Chemical Reagent Co. Ltd, Shanghai).

Fig. 1 Schematic illustration of the process followed for fabricating high-throughput patterned surface droplet arrays through the STC technology and optical micrographs of HKUST-1 precursor droplet arrays. (a) Schematic view of the process flow for the preparation of patterned wettable/nonwettable substrate and formation of droplet arrays. (b) Concept diagram of the surface droplet arrays. (c) Optical micrograph of HKUST-1 precursor droplet array. Scale bars in (c) is 50 μm.

Then, we formed the surface droplet array of SoF (sodium fluorescein, Aladdin Industrial Corporation, Shanghai) solution and HKUST-1 precursor solution on the pre-patterned surface. The HKUST-1 precursor solution was prepared by adding [Cu(NO₃)₂] (5 mmol, 1.22 g, Aladdin Industrial Corporation, Shanghai) and trimesate (2.5 mmol, 0.58 g, Aladdin Industrial Corporation, Shanghai) to dimethyl sulphoxide (DMSO, 5 g, Aladdin Industrial Corporation, Shanghai) and keeping the solution at 20 °C. The SoF solution was prepared by adding SoF to DI water/glycerol (1 : 1, glycerol was purchased from Aladdin Industrial Corporation, Shanghai) to reduce droplet evaporation and maintain a similar viscosity as the HKUST-1 precursor solution. The concentration was 0.5 mmol L⁻¹. Droplet arrays were then produced on the patterned wettable/nonwettable surface through spin-coating, as illustrated in Fig. 1. Briefly, the patterned wettable/nonwettable substrate was placed on a holder of spinner (KW-4B, Beijing), followed by adding 2 mL of SoF solution or HKUST-1 precursor solution, and then spinning at a speed of 2000 rad min⁻¹ for 30 s. Next, the HKUST-1 precursor droplet arrays were placed under ambient conditions for 48 h until the DMSO solvent was completely evaporated to form HKUST-1 crystals before studying with optical microscopy (IX73, Olympus; LV100ND, Nikon), scanning electron microscopy (SEM, Hitachi SU5000, Japan) and X-ray diffraction (XRD, PANalytical Empyrean, Netherlands). SEM images were collected on a SEM at acceleration voltages of 15 kV, using the secondary electron detector in vacuum environment. And XRD patterns of surface samples were collected on Empyrean instrument in Bragg–Brentano mode (θ–2θ; Cu Kα₁) using a position-sensitive detector: generator voltage is 45 kV and divergence slit is fixed in 0.38 mm (2θ = 5–20°; Δθ = 0.01°). In addition, the SoF droplet arrays were characterized by confocal fluorescence microscopy (FV31S-SW, Olympus), and the contact angles were measured using a contact angle measuring instrument (XG-CAMC3, XYCXIE, Shanghai) under ambient conditions.

3. Results and discussion

We successfully demonstrate the high-throughput patterning of surface droplets in arrays prepared through STC technology. In addition, we also take the advantage of this method to fabricate femtoliter MOF single-crystal arrays.

We designed a mask including holes in an array with a droplet diameter of 10 μm, and a total number of droplets of more than 9 million, as shown in Fig. S1.† These 9 million droplets are formed using a spinning-coating method in 35 s, and thus, the deposition rate exceeds 250 kHz, achieving higher-throughput procession compared to other methods.^16,19,20 Because of the higher rate in the spinning-coating process to produce droplet arrays, the average height of each droplet is around 4.8 ± 0.5 μm, which should be higher than those achieved by other methods using a slower formation speeds.^19,23 Essentially, the spin-coating process produced droplet arrays is based on wetting and dewetting phenomenon. Dewetting is a spontaneous process where a thin film on a surface rearranges into an ensemble of separated objects which can be seen as the reverse process of wetting. During the discontinuous dewetting process, liquid is moved along a surface possessing strong dewettability (lyophobic section), with pinning on highly wettable sections (lyophilic arrays) to create an array of pinned droplets. As a result, the large droplet in the Fig. 1a spreads in all directions due to wetting process caused by centrifugal force, forming a uniform thin film on a surface. Then the thin film becomes thinner and thinner due to centrifugal force, till the film rupture to create an array of pinned droplets. Through spin-coating method, we can achieve high-throughput procession, uniform droplet volumes, precise positioning and large-scale patterned region in ordered arrays.

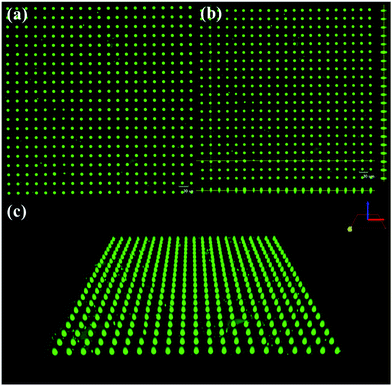
As a proof-of-concept, we first evaluate the feasibility of creating highly ordered arrays of surface droplets by spreading SoF solution on a patterned wettable/nonwettable substrate. Fig. 2 shows fluorescent images and a three-dimensional image of SoF droplet arrays on the surface, and droplet diameter is 11.4 μm ± 1.25 μm, and therefore, the volume is estimated to be approximately 297.6 ± 47.2 fL. Based on geometric analysis of surface droplets, we can obtain the following formula:

where h, d and α are the droplet height, bottom diameter of the droplet and contact angle between the water–air interfacial tension (γ_WA) and the substrate–water interfacial tension (γ_SW), respectively. Accordingly, we calculate the contact angle α of a 10 μm surface droplet prepared through STC technology to be 82.2°. As shown in Fig. S2,† the static contact angles of the SoF solution on the nonwettable and wettable substrate surfaces are 96.8° and 9.1°, respectively, which confirms that the surface-tension confinement effect of the wettable/nonwettable array on the surface droplet is highly remarkable.

Fig. 2 Fluorescent images and three-dimensional image of SoF droplet arrays. (a) Fluorescent images of SoF surface droplets in arrays through the STC technology. (b) Sectional view of the droplets formed on pre-patterned surface. And the image was taken by a fluorescence confocal microscopy. (c) Three-dimensional images of SoF droplet arrays. Scale bars in (a), (b) are 30 μm.

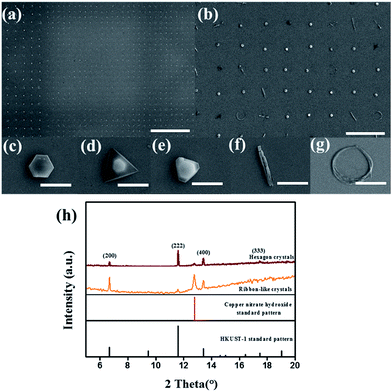
We then chose our method to form HKUST-1 crystals. For the surface droplet reaction, a droplet can represent a microreactor because crystallization can only be performed in a limited space. As a result, this droplet reaction is straightforward and is achieved in a short-time for all the experimental operations compared to conventional experimental methods.²⁴ Fig. 3a and b shows the patterned HKUST-1 crystals in an array grown by evaporation-induced self-assembly (EISA) on a patterned wettable/nonwettable substrate. In addition, representative morphologies of HKUST-1 crystals are shown in Fig. 3c–g. The HKUST-1 crystal arrays are highly uniform, showing very high-quality single crystals on the wettable section. Specifically, the diameters of these single crystals are measured to be approximately 4 μm. In addition, five typical morphologies (i.e., hexagonal, irregular hexagonal, triangular, arc-like and ribbon-like crystals) are observed in the large area on the patterned substrates during crystallization, but most HKUST-1 crystals are hexagonal shaped.

Fig. 3 The patterning HKUST-1 crystal arrays and their representative morphologies with corresponding XRD patterns. (a and b) The patterning HKUST-1 crystal arrays grown on a patterned wettable/nonwettable substrate after surface droplet evaporated. (c–g) Representative morphologies of HKUST-1 crystals. (h) XRD patterns of HKUST-1 crystals with different morphologies. Scale bars in (a), (b), (c–g) are 200 μm, 50 μm, 5 μm, respectively.

Most of HKUST-1 structures using existing techniques are hexagonal and irregular hexagonal shapes, no arc-like and ribbon-like HKUST-1 crystals appeared in the previous research.

The similar appearance of the crystals (Fig. 3b) suggests a common preferred orientation, as confirmed by the XRD pattern. The XRD pattern in Fig. 3h clearly demonstrates not only the formation of HKUST-1 crystals but also a crystal growth orientation preference along the [111] and [100] directions.¹⁶ Because of the relatively weak X-ray reflection on a single crystal, we obtained the XRD pattern by scanning a square millimeter region containing the corresponding HKUST-1 crystal arrays to accumulate reflected signal. Before measuring XRD pattern, we first observe the HKUST-1 crystal arrays by optical microscopy to obtain HKUST-1 crystals which are same morphology in certain region, then mark them. Notably, the hexagon crystals and ribbon-like crystals in the XRD pattern represent the clear majority of the HKUST-1 crystals are the corresponding morphology in the scanning region; a few ribbon-like crystals exist in the hexagonal crystal regions. We also find some remaining copper nitrate in the HKUST-1 crystal arrays due to the excessive amount of the [Cu(NO₃)₂] reactant in the HKUST-1 precursor solution. As shown in the XRD pattern, the hexagonal crystals are oriented along the [111] direction, which is coincident with the previous research by Rob Ameloot et al.¹⁶ and the ribbon-like crystals are oriented along the [100] direction due to the spatial confinement present during the crystallization.¹⁶ These above results also confirm that the HKUST-1 crystal shapes agree well with the Gibbs–Curie–Wulff theorem.²⁵

Gibbs believed that crystals grow in a form in which their total surface area multiplies the surface free energy is at a minimum in a balanced state. Curie indicated that the normal growth rate of a crystal surface is directly proportional to the surface free energy. Wulff stated that, at equilibrium, the central distances of the crystal face from a point within the crystal (Wulff point) are proportional to the corresponding specific surface free energies of these faces, i.e., γ_i/h_i = constant (where γ_i is the specific surface free energy of crystal face i, and h_i is the central distance from the Wulff point). According to the Gibbs–Curie–Wulff theorem, the equilibrium shape of a crystal is closely related to the free energy of the corresponding crystal surfaces.

Due to the droplet diameter reaching 10 μm, micro- and even nanometer-sized “small” HKUST-1 crystals can be investigated, which provides us the opportunity to study the crystal growth progress and observe experimental evidence to support the Gibbs–Curie–Wulff theorem. Furthermore, HKUST-1 crystals can rapidly change their shape to lower the total surface free energy due to the flexible structure of the MOF and smooth evaporation at room temperature. Due to the nearly ideal conditions described above, the HKUST-1 crystals approach their equilibrium shapes. Part of HKUST-1 crystals are oriented along the [111] direction, indicating that the HKUST-1 molecules are arranged in an ABCABCABC closest packing mode to lower the total free energy and that the final HKUST-1 crystals have a hexagonal equilibrium shapes.²¹ According to the Gibbs–Curie–Wulff theorem, any of the six lateral planes of hexagon crystals can grow solely due to the free energies of the corresponding crystal surfaces. Because of environmental fluctuations, such as temperature, pressure and gas flow, crystallization may occur under slightly different conditions. In fact, crystals with growth along other lateral planes and different morphologies are found in our experiment, and some examples, such as irregular hexagons and triangle crystals, are exemplified in Fig. 3d and e. Understanding how different morphologies of HKUST-1 crystals form is useful to guide the production of crystals with desired shapes for various applications.

While polydispersity in bulk MOF syntheses has been explained by simultaneous nucleation and growth,²⁶ this mechanism is clearly not applicable to the confined droplets discussed here. Our research can provide a better understanding of the formation mechanism of MOF crystals in a confined sessile droplet. We find the key factor determining HKUST-1 single-crystal growth is the hydrodynamics of an evaporating droplet and the droplet volume. Of course, evaporation rate can also influence crystal growth.²⁰

Fluid motion inside an evaporating sessile droplet spontaneously occurs due to a non-uniform evaporation rate along the vapor–liquid interface of the droplet. Two different flows, including capillary flow and Marangoni flow, occur in the evaporating droplet.²⁷ The existence of capillary flow and Marangoni flow in evaporating droplets has been previously described,^28,29 and the related schematic illustrations of these two evaporation models is shown in Fig. 4a and b. Capillary flow³⁰ is the most commonly and easily observed flow pattern in an evaporating droplet and follows a two-stage process. In the first stage, the contact line is confined to the substrate, and both the contact angle and droplet height decrease; this stage is often termed the constant contact line (CCL) mode. The edges of the droplet evaporate at a higher rate than the center of the droplet, and thus, to maintain the pinned contact line, solvent must flow according to two-dimensional radial motion outward to the edges to compensate for this loss of liquid, as shown in Fig. 4a. The droplet remains a distinct coffee-ring stain, known as capillary flow. The second stage happens when the droplet reaches a critical contact angle (2–4°), and the contact line starts to recede; more than 80% of the initial volume disappears during this stage.

Fig. 4 Schematic illustration of two droplet evaporation models. (a) Schematic illustration of capillary flow. (b) Schematic illustration of Marangoni flow.

The secondary flow in an evaporating droplet, often referred to as Marangoni flow³¹ or recirculating flow, are believed to be caused by a surface temperature gradient and a corresponding surface-tension gradient (known as Marangoni stress), which represents a constant contact angle (CCA) model. Owing to the non-uniform evaporative flux along the droplet surface, a temperature gradient arises from cooling effects, causing the surface-tension gradient to drive Marangoni flow. As shown in Fig. 4b, fluid flows from the low-surface-tension regions to high-surface-tension regions, in response to the temperature gradient, which creates symmetrical flow fields through the cross section of the droplet. Fluid inside the droplet flows along the substrate toward the center of the droplet then turns toward the air–dimethyl sulfoxide (DMSO) interface and flows in the direction of the contact line along the droplet surface. Under the effect of recirculating flow, the droplet height and diameter are uniformly shrunk, and the contact line recedes to leave a circle, carrying the solution to the center of the droplet and increasing the solution concentration. Moreover, non-uniform evaporative cooling effects are determined, in part, by the heat transfer rate from the isothermal substrate to the air–liquid interface.³² These heat transfer rates are, in part, a function of both the droplet height and the thermal conductivities of the substrate and liquid. As for our experiment, the 6 cm × 6 cm droplet arrays (9 million droplets) is on the same silicon wafer. The thermal conductivities of the substrate cause same effect on all the droplets in array. So the thermal conductivities of the substrate are not the key factors to explain the different morphologies of HKUST-1 crystals, and its effect is not considered.

Using a numerical simulation, Hu et al. showed that the presence of Marangoni flow is dependent on the drop contact angle.³¹ The authors estimated that the surface-tension-induced Marangoni flow ceases at contact angles below ∼14°. In our experiment, the contact angle α of the 10 μm surface droplets prepared through STC technology is calculated between 80° and 90°. Marangoni flow seems to coexist with capillary flow in the HKUST-1 precursor droplets, but Marangoni flow plays a more important role in the evaporation progress of the sessile droplets. These internal flows and consequently aggregation induced by the combination of metallic Cu(II) and BTC ions are the basic elements of our approach to deposit monodisperse HKUST-1 crystals in patterns down to the single-crystallite level by in situ crystallization. As the solution concentration increases in the evaporation progress, a HKUST-1 crystal seed forms at an uncertain position, as depicted in Fig. 5a. Upon forming the crystal seed inside the droplet due to an oversaturated reactant, the seed settles to the substrate and then is transported to the droplet center by the Marangoni flow, resulting in a concentrated spot. Next, center-directed Marangoni flow transports more metallic Cu(II) and BTC ions to grow a HKUST-1 single crystal. Consequently, the concentration rises of HKUST-1 building blocks caused by ongoing evaporation is countered by the growth of the crystal seed formed in the early stage. In the final stage of the evaporation progress, a regular-hexagonal HKUST-1 crystal forms in the microreactor. The schematic diagram of this progress is depicted in Fig. 5b.

Fig. 5 Schematic diagram of the progress how different HKUST-1 crystal morphologies form. (a) Optical micrograph of HKUST-1 crystal seeds in the evaporation progress on glass substrate. (b) Schematic illustration of the progress how hexagonal HKUST-1 crystal forms; (c) schematic illustration of the progress how arc-like and ribbon-like HKUST-1 crystal form. Scale bars in (a) is 20 μm. Notably, we use little balls inside the droplet to simulate elementary particles in the HKUST-1 precursor solution.

However, the specific position of the HKUST-1 crystal seed in the early stage is uncertain. Some fraction of crystal seeds become entrapped at the air–liquid interface due to the surface-tension confinement effect of wettable/nonwettable arrays. In this case, minimal aggregation occurs at the droplet center because the HKUST-1 building blocks remain mostly monodispersed; thus, the metallic Cu(II) and BTC ions continue to circulate under Marangoni flow. Finally, the HKUST-1 building blocks in the sessile droplet eventually deposit at the droplet edge due to the outwardly directed flow along the droplet surface, which is superimposed with capillary flow, achieving growth of arc-like HKUST-1 crystals. Notably, the electrical charge of the ions inside the droplet and their interactions can greatly affect the arc pattern formations. Because of the metallic Cu(II) and BTC ions inside the droplet, positive and negative ions combine with the formed crystal seed at the air–liquid interface. The HKUST-1 crystals spontaneously grow along the radial direction, forming ribbon-like crystals due to the inwardly directed flow along the substrate toward the droplet center. A schematic diagram of this progress is illustrated in Fig. 5c.

After the 10 μm droplets in an array have completely evaporated, hexagonal, ribbon-like and arc-like crystals remain, coinciding with the optical micrographs of the HKUST-1 crystals in Fig. 6a and b. Consequently, two basic elements, internal flow in an evaporating droplet of the HKUST-1 precursor solution and consequently aggregation induced by the combination of metallic Cu(II) and BTC ions, play a dominant role in the HKUST-1 single-crystal growth. The droplet volume also influences the single-crystal growth. Only a droplet approaching a femtoliter volume can realize HKUST-1 single-crystal growth. As the droplet volume increase, multiple-crystals will form.

Fig. 6 Optical micrograph of HKUST-1 crystal arrays on glass substrate with different directional light. (a) Optical micrograph of HKUST-1 crystal arrays with light spreading from down to up. (b) Optical micrograph of HKUST-1 crystal arrays in same position with opposite light direction. Scale bars in (a and b) are 10 μm.

4. Conclusions

In conclusion, we achieved the STC assembly of MOFs in femtoliter droplet arrays. Our approach took advantage of STC technology, such as high-throughput processing (250 kHz), smaller droplet volumes and denser array networks. Highly uniform HKUST-1 crystal arrays grown by EISA were observed, showing very high-quality single crystals on a patterned wettable/nonwettable substrate. Five typical crystal morphologies (i.e., hexagonal, irregular hexagonal, triangular, arc-like and ribbon-like crystals) were found in the large area on the patterned substrates during crystallization, but most of the HKUST-1 crystals possessed hexagonal shapes. The hexagonal crystals were oriented along the [111] direction and the arc-like and ribbon-like crystals were oriented along the [100] direction during crystallization. Moreover, the HKUST-1 crystal shapes also agreed well with the Gibbs–Curie–Wulff theorem. When the droplet diameter reached 10 μm, the surface-tension confinement effect of the wettable/nonwettable arrays on the surface droplet became highly remarkable. In addition, the surface-tension confinement on the HKUST-1 precursor droplet and internal flows in the evaporating droplet both led to oriented growth of the HKUST-1 crystals. These internal flows and consequently aggregation induced by the combination of metallic Cu(II) and BTC ions are the basic elements of our approach to deposit monodisperse HKUST-1 crystals in patterns down to the single-crystallite level by in situ crystallization. Understanding the hydrodynamics of an evaporating droplet will facilitate knowledge on the formation mechanism of MOF crystals in a confined sessile droplet. Finally, we are cautiously optimistic that the STC crystallization in femtoliter droplet arrays is applicable to not only HKUST-1 crystals, but also MOF-5 and ZIF-8 and even other functional materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for financial support from the Shanghai Science and Technology Committee (Grant 16DZ2260601) and the Shanghai Pujiang Program (Grant 16PJ1403200).

References

1. H. L. Li, M. Eddaoudi and O. M. Yaghi, Nature, 1999, 402, 276.
2. O. M. Yaghi, N. W. Ockwig and H. K. Chae, Nature, 2003, 423, 705.
3. H. Deng, S. Grunder and K. E. Cordova, Science, 2012, 336, 1018.
4. S. Kitagawa, Acc. Chem. Res., 2017, 50, 514.
5. W. J. Shen, Y. Zhuo and Y. Q. Chai, Anal. Chem., 2015, 87, 11345.
6. K. Liang, R. Ricco and C. M. Doherty, Nat. Commun., 2015, 6, 7240.
7. R. Wang, L. Gu and J. J. Zhou, Adv. Mater. Interfaces, 2015, 2, 1500037.
8. Z. Xie, Z. He and X. Feng, ACS Appl. Mater. Interfaces, 2016, 8, 10324.
9. J. S. Kahn, L. Freage and N. Enkin, Adv. Mater., 2017, 29, 102782.
10. F. Y. Zhang, L. F. Liu and X. N. Tan, Soft Matter, 2017, 13, 7365.
11. L. He, M. Brasino and C. Mao, Small, 2017, 13, 1700504.
12. F. Y. Zhang, L. Y. Liu and X. N. Tan, Soft Matter, 2017, 13, 7365.
13. M. Usman, S. Mendiratta and K. L. Lu, Adv. Mater., 2017, 29, 1605071.
14. M. X. Wu and Y. W. Yang, Adv. Mater., 2017, 29, 1606134.
15. P. Falcaro, R. Ricco and C. M. Doherty, Chem. Soc. Rev., 2014, 43, 5513.
16. R. Ameloot, E. Gobechiya and H. Uji-i, Adv. Mater., 2010, 22, 2685.
17. A. Huang, H. Bux and F. Steinbach, Angew. Chem., Int. Ed. Engl., 2010, 49, 4958.
18. A. Schoedel, C. Scherb and T. Bein, Angew. Chem., Int. Ed. Engl., 2010, 49, 7225.
19. D. Witters, N. Vergauwe and R. Ameloot, Adv. Mater., 2012, 24, 1316.
20. A. Carbonell, I. Imaz and D. Maspoch, J. Am. Chem. Soc., 2011, 133, 2144.
21. S. Li, G. Lu and X. Huang, Chem. Commun., 2012, 48, 11901.
22. I. You, N. Yun and H. Lee, ChemPhysChem, 2013, 14, 471.
23. H. Z. Li, Q. Yang and G. N. Li, ACS Appl. Mater. Interfaces, 2015, 7, 9060.
24. A. Zacher, A. Baunemann and S. Hermes, J. Mater. Chem., 2007, 17, 2785.
25. R. Li, X. Zhang and H. Dong, Adv. Mater., 2016, 28, 1697.
26. A. Zacher, J. Liu and K. Huber, Chem. Commun., 2009, 9, 1031.
27. I. L. Garcia-Cordero and Z. H. Fan, Lab Chip, 2017, 17, 2150.
28. T. S. Wong, T. H. Chen and X. Shen, Anal. Chem., 2011, 83, 1871.
29. I. R. Trantum, M. L. Baglia and Z. E. Eagleton, Lab Chip, 2014, 14, 315.
30. H. Hu and R. G. Larson, Langmuir, 2005, 21, 3963.
31. H. Hu and R. G. Larson, Langmuir, 2005, 21, 3972.
32. W. D. Ristenpart, P. G. Kim and C. Domingues, Phys. Rev. Lett., 2007, 99, 234502.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13250f

---