Open Access Article
Open Access ArticleInitiation mechanisms and kinetic analysis of the isothermal decomposition of poly(α-methylstyrene): a ReaxFF molecular dynamics study
Shide Hu *ab,
Weiguo Sun*ac,
Jia Fuc,
Zhanwen Zhangd,
Weidong Wud and
Yongjian Tangd
*ab,
Weiguo Sun*ac,
Jia Fuc,
Zhanwen Zhangd,
Weidong Wud and
Yongjian Tangd
aInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, Sichuan 610065, P. R. China
bSchool of Sciences, Southwest Petroleum University, Chengdu, Sichuan 610500, P. R. China. E-mail: hushide@swpu.edu.cn
cSchool of Science, Research Center for Advanced Computation, Xihua University, Chengdu, Sichuan 610039, P. R. China. E-mail: swg@mail.xhu.edu.cn
dResearch Center of Laser Fusion, CAEP, Mianyang, Sichuan 621900, P. R. China
First published on 17th January 2018
Abstract
This study investigates the thermal decomposition initiation mechanisms and kinetics of poly(α-methylstyrene) (PαMS) under isothermal conditions, using molecular dynamics simulations with the ReaxFF reactive force field. The unimolecular pyrolysis simulations show that the thermal decomposition of the PαMS molecule is initiated mainly by carbon–carbon backbone cleavage in two types at random points along the main chain that leads to different intermediates, and is accompanied by depolymerization reactions that lead to the formation of the final products. The time evolution of typical species in the process of PαMS thermal decomposition at various temperatures presents specific evolution profiles and shows a temperature-dependence effect. Isothermal decomposition kinetic analysis based on PαMS pyrolysis shows that the activation energy varies with the degree of conversion during the thermal decomposition processes, which infers that the decomposition process at different conversions may have different reaction mechanisms.
1 Introduction
It is well known that most polymers will experience unavoidable degradation, owing to heat, light and other environmental factors. Thermal decomposition, which is caused by heat, is the most common type of degradation. This process involves complex physical and chemical reactions for the reduction of the molecular weight or the decomposition of macromolecules into smaller fragments. Also, the pyrolysis characteristics may vary with several factors such as the heating rate, temperature and additives.1 The study of the kinetics of thermal decomposition is helpful toward revealing the impact of various factors and predicting the optimum reaction conditions in order to achieve the desired outcome.2–4 Kinetic analysis is aimed at determining basic kinetic parameters such as the rate constant, activation energy, and reaction model. The activation energy represents the minimum energy required for reaction, and can be used to evaluate the thermal stability. The reaction model is usually used to describe the mechanisms of thermal processes. Therefore, the study of thermal decomposition mechanisms and kinetics is important to understand the pyrolysis process.Over the years, the process of polymer thermal decomposition has been studied using experimental and theoretical methods.5–7 In experimental studies, the thermal decomposition behaviour of polymers is usually investigated by thermogravimetric analysis or the differential scanning calorimetry technique.8 There are two categories of thermogravimetry, isothermal or static thermogravimetry, where the sample is maintained at a constant temperature, and non-isothermal or dynamic thermogravimetry, where the sample is heated up gradually.2 In practical experiments, non-isothermal thermogravimetry is preferred due to the convenience of performing a quick scan over the whole continuous temperature ranges in a single experiment. However, isothermal kinetic data are easier to analyze since the Arrhenius-type rate equation can be readily applied, although multiple mass loss curves at different temperatures are required, which is time-consuming. It is considered that kinetic analysis based on several curves presents a lower uncertainty than that based on a single curve. Therefore, these methods are complementary, and it is worth performing both kinds of measurement in order to obtain a complete description of the decomposition process.9
However, it is difficult to independently examine the influence of a specified factor on pyrolysis in experiments because the experimental results are usually due to the combined effects of multiple factors. Therefore, theoretical methods are often used to investigate thermal decomposition processes. With the advancement of computational technology, quantum chemistry methods can give microscopic insight into elementary reactions. However, they are still restricted to simple processes of small molecular systems due to the computational expense and methodology limitations. For large systems, such as polymers, the molecular dynamics (MD) method based on classical mechanics and empirical force fields is a more practical approach for studying the behaviour of thermal decomposition at the atomic/molecular level, which significantly reduces the computational cost.10 However, in traditional MD simulations, nonreactive force fields are not capable of investigating chemical reactions.11
In recent decades, reactive force fields such as the Tersoff potential,12 reactive empirical bond order (REBO),13,14 and ReaxFF15 have been developed by employing the bond-order concept.16 These bond-order potentials allow for the formation and dissociation of chemical bonds during the MD simulations and this feature extends MD simulations to reactive processes. In particular, the ReaxFF reactive force field, originally developed by van Duin and colleagues in 2001, has been successfully utilized for modeling a wide variety of chemical reactions including explosion of high-energy materials, combustion of fuel, and thermal decomposition of polymers.7,17–25 Compared with the high computational cost of quantum chemistry methods, it is significantly reduced in reactive MD simulations. However, under realistic experimental conditions, thermal decomposition reactions are observed within hours or even days, which is many orders of magnitude larger than the typical MD time scales. Therefore, in reactive MD simulations, much higher temperatures and/or higher pressures are usually chosen to accelerate the reaction, so that the reactions can be observed within a computationally feasible simulation time. Although the high temperatures may introduce some uncertainty in the mechanism analysis, previous research studies of ReaxFF MD simulations have proven that the results acquired using elevated temperature are in agreement with experimental observations.26–29
Poly(α-methylstyrene) (PαMS) is a homopolymer of the α-methylstyrene (αMS, formula C9H10) monomer, where αMS is an alkene with an aromatic aliphatic hydrocarbon side chain. The feature of its appropriate thermal degradability makes PαMS useful for preparing hollow microspheres in the application of inertial confinement fusion (ICF).30,31 In the ICF experiment, a depolymerizable mandrel technique has been developed to prepare glow discharge polymer (GDP) shells for the cryotarget. The starting PαMS bead with the desired size is overcoated with GDP. Then, the GDP-overcoated PαMS mandrel is heated, and the PαMS mandrel decomposes into gases that diffuse out through the GDP coating. This leaves the GDP coating as the final hollow shell material. In the process of PαMS mandrel thermal decomposition, a proper pyrolysis rate is important for the quality of the final hollow microspheres.30
In our previous works, the non-isothermal decomposition of PαMS has been studied using theoretical methods and molecular simulations.6,32 The overall pyrolysis mechanisms and a kinetic equation were obtained, and the effect of the heating rate on the thermal decomposition was investigated by comparing the kinetics at different heating rates. Because of the time-consuming nature of isothermal thermogravimetry experiments as mentioned above, to our knowledge, kinetics insight based on isothermal decomposition of PαMS is still lacking. Therefore, the study of PαMS thermal decomposition under isothermal conditions is necessary to reveal its mechanisms and kinetics.
In order to systematically study the molecular thermal decomposition mechanisms of the PαMS molecule and kinetic characteristics of the thermal decomposition process, this study investigates the isothermal decomposition process of PαMS using a MD method with the ReaxFF force field. The unimolecular PαMS system was simulated at 3000 K, and the detailed thermal decomposition initiation mechanisms were obtained. The thermal decomposition of the PαMS system consisting of ten chains was simulated at a series of constant temperatures ranging from 1800 K to 2600 K with intervals of 200 K, and the influence of temperature on the pyrolysis and the dependence of the activation energy on the degree of conversion during the thermal decomposition processes were analyzed.
2 PαMS models and simulation details
2.1 PαMS models
To perform molecular dynamics simulation on the PαMS system, a PαMS molecule was created from 50 α-methylstyrene units and was geometrically optimized. The molecular structure of a PαMS molecule consisting of 50 αMS units is illustrated in Fig. 1(a), in which an αMS repeat unit is enlarged and displayed in the inset for a clear view. | ||
| Fig. 1 Molecular structures of (a) the PαMS molecule and (b) the equilibrated amorphous PαMS system. | ||
Then, ten PαMS molecules were packed in a periodic cubic box to construct an amorphous PαMS system at an initial density of 0.5 g cm−3 using the PACKMOL package.33 The relatively low density was used to avoid the overlap of atoms. And, then, the packed PαMS system was equilibrated at 300 K for 10 ps. The required density was obtained by imposing an external pressure of 0.2 GPa. With the progress of this compression simulation, the volume of the simulation box was shrunk and the density increased gradually. The imposed high pressure will produce a large density at equilibrium. According to the general theory of reaction kinetics, the large density may have an influence on the reaction rate.34 In order to minimize the potential impact of the large density on the reaction and obtain the density closest to the experimental value, during the process of the compression, while the expected density was reached, the configuration was chosen as the initial structure with the expected density, and the final equilibrium properties of the system would not depend on the choice of the initial conditions.10 At 14.0 ps of the compression, the density was 1.041 g cm−3, which is approximately equal to the experimental value of 1.04 g cm−3.35 Therefore, this configuration was chosen as the initial structure to represent the realistic PαMS system.
Finally, the equilibrated structure was achieved by performing an annealing simulation for 10 ps between 300 K and 500 K, and a following dynamics simulation at 300 K for 40 ps in the NVT ensemble. The final PαMS system at the equilibrated configuration in a cubic periodic box of side length 45.51 Å is illustrated in Fig. 1(b).
2.2 Protocol of reactive molecular dynamics simulations
After equilibration, the PαMS system was subjected to molecular dynamics simulations with the ReaxFF reactive force field in the NVT ensemble for 50 ps at a series of temperatures of 1800 K, 2000 K, 2200 K, 2400 K, and 2600 K using the open source package LAMMPS36 (version 14 May 2016, available from http://lammps.sandia.gov). Here, a relatively high temperature was chosen to accommodate the chemical reactions within a practical simulation time. This strategy in reactive MD simulations is favored to accelerate chemical reactions, and it has been shown that the high temperatures may not affect initiation reaction mechanisms.26,28 The temperature of the simulated PαMS system was controlled using a Nose–Hoover thermostat, and the integration time step was set to 0.1 fs to ensure the correct dynamics at high temperatures.In the ReaxFF force field, the total system energy (Etot) is expressed as follows,37
| Etot = Ebond + Elp + Eover + Eunder + Eval + Epen + Ecoa + EC2 + Etriple + Etors + Econj + EH-bond + EvdWaals + ECoulomb | (1) |
The C/H ReaxFF parameters reported in ref. 37 were used in this study. These parameters had been trained and validated for compounds containing aromatic hydrocarbons for a wide range of temperatures.26,37 Also, in the theoretical framework of ReaxFF development, the parameter sets are transferable within the same development branch in ReaxFF.20
3 Results and discussion
In this section, the detailed decomposition initiation mechanisms and the influence of temperature on the product evolution of the pyrolysis of PαMS were studied and discussed. Based on the simulations at various temperatures, the kinetics of the thermal decomposition of PαMS was analyzed using the Arrhenius law and isoconversional method.3.1 Detailed decomposition initiation mechanisms of the PαMS molecule
To investigate the detailed thermal decomposition mechanisms, a unimolecular PαMS system was constructed and equilibrated. In this amorphous PαMS system, there was a single PαMS molecule which consisted of 50 αMS repeat units. The procedures for the construction and equilibrium were similar to those for the PαMS system containing ten molecules. Firstly, a single PαMS molecule was packed in a cubic cell. And, then, an NPT simulation was performed and the obtained density was 1.04 g cm−3, which is equal to the experimental value.35 Finally, the PαMS system was equilibrated by performing an annealing simulation and NVT dynamics. The final equilibrated configuration in a cubic periodic box of side length 21.13 Å is illustrated in Fig. 2(a). Because the simulated PαMS system was a minuscule system compared with the realistic system, a single trajectory would not provide general information. In order to get statistical characteristics of the initiation reaction, ten independent simulations with unique initial velocities were carried out on the equilibrated unimolecular PαMS system at 3000 K for 50 ps. Here, the elevated temperature was also employed to observe the reaction within a feasible computation time. | ||
| Fig. 2 Snapshots of the unimolecular PαMS system at (a) t = 0 ps and (b) t = 1.0 ps (the purple dashed lines in subfigure (b) represent the broken bonds). | ||
As pointed out in our previous work,6 during the thermal decomposition of the PαMS system under non-isothermal conditions, the main decomposition mechanisms involved random chain scission and depolymerization processes. These processes were also observed under isothermal conditions. Fig. 2(b) shows a snapshot of one of the simulations at 1.0 ps, where the PαMS chain is broken into some fragments by the fracture of the C–C backbone. By this initiation reaction, the molecular weight was decreased and the intermediates were generated. Afterwards, these low polymerized intermediates were further depolymerized into small fragments, and a large number of monomers and other small molecules were generated rapidly by depolymerization, radical recombination, hydrogen transfer, and other reactions.
These processes can be demonstrated by the time evolution of the total number of molecules/fragments during the simulation, as shown in Fig. 3. At the beginning of the simulation, there was only one PαMS molecule in the system. With the progression of the simulation, the backbone of the PαMS molecule was fractured and the total number of the fragments increased gradually. During the stage of the first 6 ps, the total number of fragments increased rapidly, indicating rapid decomposition at this stage. And, then, the total number of fragments increased to about 50. The fluctuation of the total number of fragments was due to radical eliminations and recombinations, especially at the final stage.
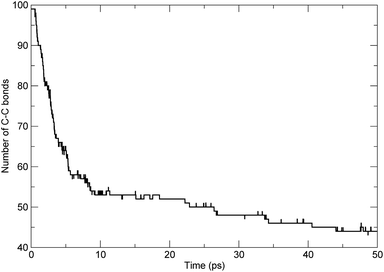
To investigate the scission of the backbone of the PαMS molecule in detail, based on bond-orders with a cutoff of 0.3,7,34 we analyzed the time evolution of the bond number between adjacent carbon atoms along the main chain. The number of C–C bonds along the backbone varying with time was obtained. For the simulated unimolecular PαMS system, which consisted of 50 αMS repeat units, there were 99 C–C bonds connecting the 100 C atoms along the backbone. The time evolution of the number of bonds between adjacent C atoms is shown in Fig. 4. It can be seen that the number decreased from 99 to about 44 during the simulation. At the first stage before 6 ps, the number decreased rapidly, which indicates the rapid breaking of C–C bonds, and, at the later stage, the number decreased gradually. The time evolution characteristics of the number of bonds were consistent with the conclusion based on the evolution of the total number of fragments.
To obtain detailed information on the bond breaking along the backbone, several representative adjacent C atoms along the backbone were chosen to demonstrate the bond-order evolution with the simulation time. The selected portion of the PαMS molecule is illustrated in Fig. 5, where the backbone is highlighted in purple and the corresponding carbon atoms are labelled by the atomic symbol with an index number.
 | ||
| Fig. 5 The representative portion of the PαMS molecule (the drawing style is set as lines for a clear view, and purple lines represent the backbone). | ||
The bond-orders between the adjacent C atoms (C134–C135, C135–C153, C153–C154, C154–C172, and C172–C173) during the first 10 ps of the decomposition process were calculated, and the time evolution of each bond-order is shown in Fig. 6. For the bond-orders of C153–C154 and C172–C173, as shown in Fig. 6(a), they firstly fluctuated around 0.98, and drastically reduced to nearly 0. Based on the bond-order cutoff of 0.3, the bond-orders of C153–C154 and C172–C173 were smaller than 0.3 after 0.61 ps and 0.81 ps, respectively. This indicates that these bonds were broken. This breaking can also be seen from the evolution of the bond-order between C154 and C172, as shown in Fig. 6(b). The bond-order between C154 and C172 firstly fluctuated around 0.98, and at the time from 0.61 ps to 0.81 ps, it increased gradually and then fluctuated around 1.55. This indicates that after the breaking of the C153–C154 bond, an αMS monomer was generated by scission of the C172–C173 bond. For the bond-order between C134 and C135, as shown in Fig. 6(a), it decreased sharply at 7.89 ps, indicating that the bond was broken. At the same time, the bond-order between C135 and C153 began to increase from 0.98 to 1.55, as shown in Fig. 6(c), which indicates that another αMS monomer was generated.
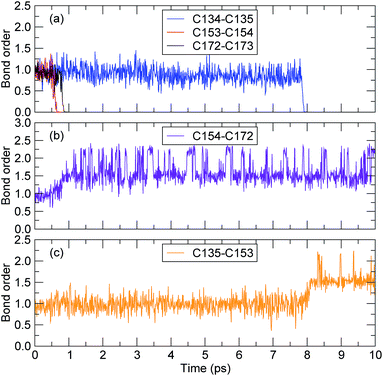 | ||
| Fig. 6 The time evolution of the bond-order between adjacent carbon atoms (the time axes in all of the subfigures are the same). | ||
In order to investigate the possible position of the initial cleavage along the backbone of the PαMS molecule, each trajectory of ten independent simulations was analyzed. The first observed reactions of chain scissions of the PαMS molecules (C450H502) during the initiation process, along with the time of each reaction taking place, were extracted and are listed in Table 1, where each reaction corresponds to each trajectory of the ten simulations.
| No. | Reaction | Time (ps) |
|---|---|---|
| R1 | C450H502 → C315H351 + C135H151 | 0.52 |
| R2 | C450H502 → C370H413 + C80H89 | 0.44 |
| R3 | C450H502 → C377H419 + C73H83 | 0.61 |
| R4 | C450H502 → C341H378 + C64H73 + C45H51 | 0.60 |
| R5 | C450H502 → C9H10 + C198H221 + C243H271 | 0.20 |
| R6 | C450H502 → C360H401 + C90H101 | 0.41 |
| R7 | C450H502 → C324H361 + C125H138 + CH3 | 0.77 |
| R8 | C450H502 → C432H481 + C18H20 + H | 0.41 |
| R9 | C450H502 → C9H10 + C36H40 + C288H321 + C117H131 | 0.33 |
| R10 | C450H502 → C423H471 + C27H31 | 0.21 |
In the process of the initiation, the PαMS molecule was broken into two or more segments with free radicals at each end through C–C bond dissociation. As listed in Table 1, the chain scission of the PαMS molecule in each simulation took place in the time range from 0.20 ps to 0.77 ps. Furthermore, the products of this process were different for each simulation. This variety of the generated fragments indicates that scission of the C–C bond occurred at different positions of the backbone. For the reaction R1, the PαMS molecular chain (C450H502) was ruptured into C315H351 and C135H151 at 0.52 ps, but for reaction R2, the PαMS chain was broken into C370H413 and C80H89. It is noted that these two reactions belong to two types of initiation reaction, as represented in Scheme 1.
 | ||
| Scheme 1 Initiation reaction types of the PαMS molecule (Ph represents phenyl. The objects in the dashed line boxes represent the αMS repeat unit). | ||
Owing to the isotacticity of the PαMS molecule with a configuration of head-to-tail for each αMS repeat unit, there were two types of C–C bond along the backbone, denoted as a and b in Scheme 1. Type a was considered as the linkage between the tail and the head of the adjacent αMS repeat unit, and b was the internal C–C connection of each αMS repeat unit. Except for the chain ends, these two types of C–C bond were identical; therefore, they had the same probability of bond breaking, but these two types of breakpoint position could lead to different intermediates. If the breakpoint occurred at the position of a, the degrees of polymerization of the intermediates were integers (denoted as k1 in Scheme 1). If it occurred at b, the degrees of polymerization of the intermediates were not integers (denoted as k2 in Scheme 1). For the observed reactions listed in Table 1, reactions R2 and R3 belonged to the k2 type, R4 included both types of reaction, and the others belonged to the k1 type.
It was generally believed that random scission occurred at the position of a and the subsequent depolymerization reactions generated monomers directly by peeling off the monomer unit from the chain end. In the simulations, random scission reactions that occurred at the position of b and radical recombination reactions were also observed. The simulations indicated that the chain scission would take place at a random position, either at the position of a or b.
The intermediates from the two initiation types were different, but further fracture of all of them might produce active radicals such as CH2 and (C6H5)–C–(CH3), which would generate monomers (C9H10) quickly by recombination reactions as represented in Scheme 2. Because of the high activity of the radicals having two unpaired electrons, they would undergo subsequent reactions to produce other products quickly, therefore only the reduced reactions would be observed within a long period of time. This is why fewer k2 type initiations were observed compared to the k1 type in the simulations.
During the process of initiation, two or more random scissions might occur simultaneously at different positions, which would result in more than two fragments in one reaction. Also, due to the two initiation types of random scission, occasionally, the αMS monomer could be formed directly from the PαMS chain, such as for reactions R5 and R9 listed in Table 1.
Along with the main chain scissions, radical elimination was also observed in the simulations. As listed in Table 1, radicals such as CH3 and H were produced in reactions R7 and R8.
3.2 Effect of temperature on the decomposition of the PαMS system
To investigate the influence of temperature, NVT-MD simulations on the PαMS system consisting of ten PαMS molecules (as shown in Fig. 1(b)) were carried out for 50 ps at five different temperatures of 1800 K, 2000 K, 2200 K, 2400 K, and 2600 K. Based on the simulations at different temperatures, the influence of temperature on the decomposition of the PαMS system is discussed in terms of the time evolution of the chemical species. Also, the evolution profile of the PαMS molecules with time was used for kinetic analysis in the next subsection.In the practice of molecular simulations, one trajectory usually includes statistical noise that may cause uncertainty in the observations. In order to obtain statistically better results, for each temperature, a set of eight independent simulations were performed with unique initial velocities, and the average over the eight trajectories was taken as the simulation result for analysis.
In Fig. 7, the quantities of each simulation along with their averages of the PαMS molecules and αMS monomers versus time at 2000 K are shown. It can be seen that the evolution tendency of each independent simulation was similar. As the simulation progressed, the number of PαMS molecules (C450H502) decayed from the initial amounts of 10 to finally zero, and the dominant product species αMS monomers (C9H10) were generated gradually. Also, the average of PαMS and that of αMS showed the improvement of the statistics. In what follows, we only show the average values of the simulations.
To compare the influence of temperature, the evolution profiles of the PαMS molecules with time at various temperatures are shown in Fig. 8. It can be seen that the number of PαMS molecules decreased with the progression of the simulation time, and the higher the temperature, the shorter the time for completing the pyrolysis. For the simulation at a temperature of 2600 K, the number of PαMS molecules quickly decreased to zero within 2 ps, which indicates that the thermal decomposition reaction rate was fast at high temperature. For the case of 1800 K, at the end of the simulation of 50 ps, the final number of the PαMS molecules was 0.75 on average, and to complete the decomposition, it would need a longer time.
The influence of temperature on the PαMS thermal decomposition can also be investigated from the evolution of the main products. The αMS monomers were the major products generated during pyrolysis of the PαMS system. The observed generation of the αMS monomers with time at various temperatures is shown in Fig. 9. It is obvious that the rate of monomer generation was faster at higher temperature. At the relatively lower temperatures of 1800 K and 2000 K, the number of monomers increased approximately linearly with the simulation time, and at the time of 50 ps, the final numbers were 60 and 219, respectively. At the moderate temperature of 2200 K, the number of monomers also increased approximately linearly before 20 ps, but the increasing of the number of monomers became mild after 30 ps. Meanwhile, at the higher temperatures of 2400 K and 2600 K, the number of monomers increased rapidly at the beginning of the decomposition process and then reached a plateau, and the final numbers were 328 and 351 for 2400 K and 2600 K at the end of the simulation.
These results are consistent with general collision theory, in which more frequent collisions at high temperatures will result in a higher probability of occurrence of the reaction. Hence, the reaction rate increased with the increase of temperature. Also, the simulations presented the specific evolution profiles of the PαMS molecules and αMS monomers during the decomposition at different temperatures.
3.3 Kinetic analysis of thermal decomposition
In order to investigate the kinetic characteristics of PαMS pyrolysis, based on the time evolution of the PαMS molecules at different temperatures, kinetic analysis of the PαMS thermal decomposition was carried out using the Arrhenius law and isoconversional method.The kinetics of decomposition in a solid sample is generally expressed as2
 | (2) |
The conversion α is calculated using
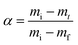 | (3) |
Solid pyrolysis is a complex chemical reaction, but for kinetic analysis it is usually considered as a one-step process, where the overall rate can be described using the first-order reaction rate equation. The behaviour of the simulated time evolution profiles for the decomposition of the PαMS system, as shown in Fig. 8, indicates that this assumption is applicable to the present study.
Thus, first-order reaction kinetics was employed to evaluate the rate constant, and the model function is described as
| f(α) = 1 − α | (4) |
Substituting this into eqn (2), considering k as a constant at temperature T, and rearranging and integrating, one can get the following expression,
| ln(1 − α) = −kt | (5) |
By plotting the left hand side of eqn (5) versus time, the rate constant can be determined from the slope.
Using eqn (5) and the simulated data as shown in Fig. 8, the rate constants of the decomposition reaction of the PαMS system at each simulation temperature were obtained and are listed in Table 2.
| T (K) | 1800 | 2000 | 2200 | 2400 | 2600 |
| k (1/ps) | 0.05316 | 0.2099 | 0.4823 | 1.270 | 2.179 |
The rate constant is usually described by the Arrhenius law38
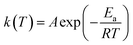 | (6) |
Taking the natural logarithm of both sides of eqn (6), one can obtain an expression for kinetics analysis,
 | (7) |
Based on the calculated rate constants as listed in Table 2, by plotting the left hand side of eqn (7) versus 1/T, as shown in Fig. 10, the activation energy and pre-exponential factor were estimated from the slope and intercept, respectively. The solid line in Fig. 10 represents the linear fitting based on eqn (7), exhibiting typical linear behaviour for the decomposition reaction of the PαMS system. The obtained activation energy and pre-exponential factor were 180.94 ± 6.14 kJ mol−1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140.58 ± 1.41 1/ps, respectively. The estimated activation energy of pyrolysis of the PαMS system is within the range of the reported values which varied from 153.8 to 235.8 kJ mol−1 and were obtained from experimental thermogravimetric analysis.6 In the experiment, the PαMS thermal decomposition was performed at a temperature range from ambient temperature to 620 K at different constant heating rates. The wide range of the reported experimental values of activation energy was due to the different heating rates and the molecular weight of the sample in the experiment.6
140.58 ± 1.41 1/ps, respectively. The estimated activation energy of pyrolysis of the PαMS system is within the range of the reported values which varied from 153.8 to 235.8 kJ mol−1 and were obtained from experimental thermogravimetric analysis.6 In the experiment, the PαMS thermal decomposition was performed at a temperature range from ambient temperature to 620 K at different constant heating rates. The wide range of the reported experimental values of activation energy was due to the different heating rates and the molecular weight of the sample in the experiment.6
It is noted that the direct Arrhenius plot method described above only produces an overall activation energy for the whole process of thermal decomposition, and the complexity of the process is not detected. Isoconversional methods are capable of determining the activation energy as a function of conversion without pre-assumptions of the reaction model.39 This model-free approach is considered as a reliable method for obtaining kinetic information and revealing the complexity of the reactions.
According to the isoconversional method,39 under isothermal conditions, substituting eqn (6) into (2), and rearranging and integrating leads to the following equation,
 | (8) |
Using the natural logarithmic form of eqn (8), we have the linear relationship of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t versus 1/T,
t versus 1/T,
 | (9) |
For a set of kinetic curves recorded at different temperatures, at a given conversion, there is a reaction time that corresponds to each temperature. Thus, the activation energy at a given conversion can be determined from the slope of the plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t versus 1/T. Repeating this procedure for each given conversion will lead to the activation energy as a function of the extent of conversion.
t versus 1/T. Repeating this procedure for each given conversion will lead to the activation energy as a function of the extent of conversion.
Based on the isothermal simulations at five temperatures from 1800 K to 2600 K as shown in Fig. 8, the isoconversional plots, namely the plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t versus 1/T, for the conversions from 0.1 to 0.9, are shown in Fig. 11. The activation energy for each conversion was obtained by linear fitting of the corresponding data at five temperatures, and the evaluated activation energies (Ea) as a function of conversion (α) are depicted in Fig. 12. It can be seen from Fig. 12 that the activation energy varies with the conversion. This indicates that the reaction mechanisms were different at the different decomposition stages. At the lower conversions of less than 0.2, Ea remained at around 112 kJ mol−1, which did not significantly change, but had a higher standard error. This showed that only one mechanism governed the initial reaction. The higher standard error might be attributed to the fact that a few decomposition reactions took place in a relatively short period of time at the initial stage, which resulted in the difficulty in accurately determining the time corresponding to each temperature at the lower conversion. Also, in the conversion range from 0.3 to 0.9, Ea increased from 118.9 kJ mol−1 to 180.6 kJ mol−1, which indicates that there were complex mechanisms at the later stages of the thermal decomposition. As discussed in the above context of the mechanism analyses, after initiation, the intermediates were depolymerized into monomers and other small fragments, and were accompanied by reactions of free radical recombination, hydrogen transfer, diffusion, and so on. These parallel reactions resulted in the increase of the activation energy. The variation in the activation energy with the conversion also indicates that the thermal stability of PαMS varied with the degree of the conversion. Lower values of the activation energy signified that the decomposition might occur at a faster rate. In the application of the depolymerizable mandrel technique, the thermal decomposition rate of PαMS is important for the quality of the final hollow microsphere. Therefore, this result suggests that the experimental conditions should be adjusted to obtain an appropriate pyrolysis rate at different stages during the thermal decomposition process.
t versus 1/T, for the conversions from 0.1 to 0.9, are shown in Fig. 11. The activation energy for each conversion was obtained by linear fitting of the corresponding data at five temperatures, and the evaluated activation energies (Ea) as a function of conversion (α) are depicted in Fig. 12. It can be seen from Fig. 12 that the activation energy varies with the conversion. This indicates that the reaction mechanisms were different at the different decomposition stages. At the lower conversions of less than 0.2, Ea remained at around 112 kJ mol−1, which did not significantly change, but had a higher standard error. This showed that only one mechanism governed the initial reaction. The higher standard error might be attributed to the fact that a few decomposition reactions took place in a relatively short period of time at the initial stage, which resulted in the difficulty in accurately determining the time corresponding to each temperature at the lower conversion. Also, in the conversion range from 0.3 to 0.9, Ea increased from 118.9 kJ mol−1 to 180.6 kJ mol−1, which indicates that there were complex mechanisms at the later stages of the thermal decomposition. As discussed in the above context of the mechanism analyses, after initiation, the intermediates were depolymerized into monomers and other small fragments, and were accompanied by reactions of free radical recombination, hydrogen transfer, diffusion, and so on. These parallel reactions resulted in the increase of the activation energy. The variation in the activation energy with the conversion also indicates that the thermal stability of PαMS varied with the degree of the conversion. Lower values of the activation energy signified that the decomposition might occur at a faster rate. In the application of the depolymerizable mandrel technique, the thermal decomposition rate of PαMS is important for the quality of the final hollow microsphere. Therefore, this result suggests that the experimental conditions should be adjusted to obtain an appropriate pyrolysis rate at different stages during the thermal decomposition process.
4 Conclusions
The thermal decomposition process of poly(α-methylstyrene), namely PαMS, was simulated using molecular dynamics with the ReaxFF reactive force field at various temperatures. The chemical events in the initial thermal decomposition were observed, and the time evolutions of the PαMS molecules and αMS monomers were obtained at five different temperatures. The influence of temperature on the product evolution and the effects of the degree of conversion on the activation energy of the PαMS thermal decomposition were analyzed.The unimolecular pyrolysis simulations showed that two types of initiation reaction occurred at random points along the backbone due to the isotacticity of the PαMS molecule with a head-to-tail configuration. The intermediates generated from two initiation types were different and further decomposed into the final products by depolymerization, radical recombination, and other reactions.
The time evolution of the PαMS molecule decomposition and the αMS monomer formation at different temperatures presented specific evolution profiles, and showed that the rates of consumption of the reactants were faster and the yield of the products was larger at higher temperature.
The kinetic analysis based on the thermal decomposition of PαMS at various temperatures showed that the activation energy varied with the degree of decomposition conversion, which characterized the thermal decomposition mechanisms and the thermal stability of the PαMS system at different stages. This outcome reveals that the detailed reaction mechanisms of the decomposition process were different at different conversions. Also, the dependence of the activation energy on the degree of conversion provides options for the application of the depolymerizable mandrel technique.
These results might be useful to better understand the molecular mechanisms and fundamental processes of the thermal decomposition of PαMS material.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Ministry of Education “chunhui plan” (Grant No. Z2016160), Xihua University key research project (Grant No. Z1513323) and a fund of the research center of laser fusion, CAEP of China.Notes and references
- C. E. Carraher, Carraher’s Polymer Chemistry, CRC Press, Boca Raton, 9th edn, 2013 Search PubMed.
- S. Vyazovkin and C. A. Wight, Int. Rev. Phys. Chem., 1998, 17, 407–433 CrossRef CAS.
- S. Vyazovkin, Int. Rev. Phys. Chem., 2000, 19, 45–60 CrossRef CAS.
- S. Vyazovkin, Phys. Chem. Chem. Phys., 2016, 18, 18643–18656 RSC.
- Z. Zhang, Y. Huang, X. Luo, X. Qi, S. Chen, Y. Liu and B. Li, High Power Laser Part. Beams, 2010, 22, 2079–2081 CrossRef CAS.
- J. Fu, W. Sun, Y. Jiang, Q. Fan, Y. Zhang and Z. Zhang, Polym. Degrad. Stab., 2014, 110, 415–421 CrossRef CAS.
- K. Chenoweth, S. Cheung, A. C. T. van Duin, W. A. Goddard and E. M. Kober, J. Am. Chem. Soc., 2005, 127, 7192–7202 CrossRef CAS PubMed.
- E. Turi, Thermal characterization of polymeric materials, Academic Press, New York, 1981 Search PubMed.
- K. Pielichowski and J. Njuguna, Thermal Degradation of Polymeric Materials, Rapra Technology Limited, Shawbury, 2005 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, New York, 2nd edn, 2002 Search PubMed.
- T. Liang, Y. K. Shin, Y.-T. Cheng, D. E. Yilmaz, K. G. Vishnu, O. Verners, C. Zou, S. R. Phillpot, S. B. Sinnott and A. C. T. van Duin, Annu. Rev. Mater. Res., 2013, 43, 109–129 CrossRef CAS.
- J. Tersoff, Phys. Rev. B, 1988, 37, 6991–7000 CrossRef.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- T. C. O’Connor, J. Andzelm and M. O. Robbins, J. Chem. Phys., 2015, 142, 024903 CrossRef PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- D. W. Brenner, Phys. Rev. B, 1990, 42, 9458–9471 CrossRef CAS.
- L. Huang, K. L. Joshi, A. C. T. van Duin, T. J. Bandosz and K. E. Gubbins, Phys. Chem. Chem. Phys., 2012, 14, 11327–11332 RSC.
- Z. Zhang, K. Yan and J. Zhang, RSC Adv., 2013, 3, 6401–6407 RSC.
- M. Alaghemandi and J. R. Green, Phys. Chem. Chem. Phys., 2016, 18, 2810–2817 RSC.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- S. Bhoi, T. Banerjee and K. Mohanty, RSC Adv., 2016, 6, 2559–2570 RSC.
- C. Ashraf, A. Jain, Y. Xuan and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2017, 19, 5004–5017 RSC.
- S. Monti, G. Barcaro, L. Sementa, V. Carravetta and H. Ågren, RSC Adv., 2017, 7, 49655–49663 RSC.
- X. Zhang, Y. Li, D. Chen, S. Xiao, S. Tian, J. Tang and R. Zhuo, RSC Adv., 2017, 7, 50663–50671 RSC.
- Y. Cao, C. Liu, H. Zhang, X. Xu and Q. Li, Appl. Therm. Eng., 2017, 126, 330–338 CrossRef CAS.
- E. Salmon, A. C. T. van Duin, F. Lorant, P.-M. Marquaire and W. A. Goddard III, Org. Geochem., 2009, 40, 416–427 CrossRef CAS.
- E. Salmon, A. C. T. van Duin, F. Lorant, P.-M. Marquaire and W. A. Goddard III, Org. Geochem., 2009, 40, 1195–1209 CrossRef CAS.
- Q.-D. Wang, X.-X. Hua, X.-M. Cheng, J.-Q. Li and X.-Y. Li, J. Phys. Chem. A, 2012, 116, 3794–3801 CrossRef CAS PubMed.
- M. Zheng, Z. Wang, X. Li, X. Qiao, W. Song and L. Guo, Fuel, 2016, 177, 130–141 CrossRef CAS.
- S. A. Letts, E. M. Fearon, L. M. Allison and R. Cook, J. Vac. Sci. Technol., A, 1996, 14, 1015–1018 CAS.
- Z.-W. Zhang, X.-B. Qi and B. Li, Acta Phys. Sin., 2012, 61, 145204 Search PubMed.
- S. Hu, W. Sun, J. Fu, L. Zhang, Q. Fan, Z. Zhang, W. Wu and Y. Tang, J. Mol. Model., 2017, 23, 179 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- L. Zhang, S. V. Zybin, A. C. T. van Duin, S. Dasgupta, W. A. Goddard and E. M. Kober, J. Phys. Chem. A, 2009, 113, 10619–10640 CrossRef CAS PubMed.
- L. J. Fetters, D. J. Lohse and R. H. Colby, in Chain Dimensions and Entanglement Spacings, ed. J. E. Mark, Springer, New York, 2007, pp. 447–454, book section 25 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- K. J. Laidler, Pure Appl. Chem., 1996, 68, 149–192 CrossRef CAS.
- S. Vyazovkin and N. Sbirrazzuoli, Macromol. Rapid Commun., 2006, 27, 1515–1532 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |