DOI:
10.1039/C7RA12163F
(Paper)
RSC Adv., 2018,
8, 302-310
Valence of Ti cations and its effect on magnetic properties of spinel ferrites TixM1−xFe2O4 (M = Co, Mn)
Received
6th November 2017
, Accepted 13th December 2017
First published on 2nd January 2018
Abstract
Powder samples of TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4) and TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3) were synthesized using a conventional method for preparing ceramics. X-ray diffraction analysis confirmed that the samples consisted of a single phase with a cubic (A)[B]2O4 spinel structure. The average molecular magnetic moment (μexp) measured at 10 K decreased monotonically with increasing x for two series of samples. According to previous investigations, Ti2+ and Ti3+ cations are present in these ferrites, but there are no Ti4+ cations; the magnetic moments of the Ti2+, Ti3+, and Mn3+ cations are assumed to couple antiferromagnetically with those of the Mn2+, Co2+, Co3+, Fe2+, and Fe3+ cations whenever they are at the (A) or [B] sublattice. The dependence of μexp of the two series of samples on the doping level x was fitted using a quantum-mechanical potential barrier, and the cation distributions in the two series of samples were obtained.
1 Introduction
Spinel ferrites have received much attention in recent years because of their application in spintronics and multiferroics.1–7 In a (A)[B]2O4 spinel ferrite, each unit cell contains eight formula units, in which the 32 larger oxygen anions form a close-packed face-centered-cubic structure with the 24 smaller metal cations occupying two types of interstitial position: the tetrahedral (8a) or (A) sites and the octahedral (16d) or [B] sites,8–11 which form the (A) and [B] sublattices.
Many studies were carried out on the magnetic moment of and cation distribution in Ti-doped spinel ferrites.12–16 In these investigations, all of the Ti cations were assumed to be tetravalent, but there have been disputes regarding the cation distribution. Dwivedi et al. prepared a series of samples, Co(Fe1−xTix)2O4 (x = 0, 0.05, or 0.1), by conventional solid-phase reactions; using X-ray photoelectron spectroscopy (XPS) they discovered that all Ti cations went into the octahedral sites.12 Srinivasa Rao et al. prepared samples of the CoTixFe2−xO4 (0.0 ≤ x ≤ 0.3) series; they thought that the Ti4+ ions had the tendency to go to the [B] site, which affected the cation distribution in the samples.13 Schmidbauer prepared samples of the Fe1+xCr2−2xTixO4 (0 ≤ x ≤ 1) series and concluded that there were Fe2+ ions at the (A) and [B] sites, and all Cr and Ti cations occupied the B-sites.14 Schmidbauer also prepared samples of two spinel ferrite series, Fe2.4−tCr0.6TitO4 (0 ≤ t ≤ 0.7) and Fe2.1−tCr0.9TitO4 (0 ≤ t ≤ 0.55), and assumed that all of the Ti4+ ions entered the [B] sites.15 However, when Kale et al. prepared TixNi1+xFe2−2xO4 (0.0 ≤ x ≤ 0.7), they estimated the cation distribution at the (A) and [B] sites using X-ray diffraction and came to the conclusion that the fraction of Ti4+ cations entering the (A) sites increased with increasing x, and it reached 0.5 when x = 0.7.16
In order to resolve these discrepancies regarding cation distributions in spinel ferrites, Xu et al. investigated the valence, distribution of cations and the magnetic structure of Ti-doped spinel ferrites17–19 by using an O 2p itinerant-electron model.20–22 They found an additional antiferromagnetic phase when Ti cations replaced a portion of the Ni or Fe cations in the spinel ferrites Ni0.68Fe2.32O4 (ref. 17 and 18) and NiFe2O4,19 and they offered the following explanation for the phenomenon: most of the Ti cations were Ti2+ cations that occupied the [B] sites; the remaining Ti cations were Ti3+ cations and there were no Ti4+ cations; the magnetic moments of the Ti cations coupled antiferromagnetically with those of Fe and Ni cations whenever they were at the (A) or [B] sites.
The absence of Ti4+ in an oxide has been confirmed by theoretical and experimental investigations. Cohen23 and Cohen and Krakauer24 used density functional theory to calculate the densities of states for valence electrons in the perovskite oxide BaTiO3. Their results indicated that the average valence of Ba is +2, which is the same as the traditionally accepted value, but the average valences of Ti and O are +2.89 and −1.63, respectively, which are different from the conventional results of +4 and −2, respectively. This calculation result was confirmed by the X-ray photoelectron spectra obtained by Wu et al.,25 who found that the average valence of O anions, ValO, is −1.55, which is close to the value (−1.63) calculated by Cohen. In addition, using XPS analysis, Dupin et al. found that the average valence of O anions is −1.15 for TiO2,26 which indicates that there are Ti2+ and Ti3+ cations, but no Ti4+ cations, in TiO2. Ji et al. proposed a method to estimate the valences of cations and anions in (A)[B]2O4 spinel ferrites; they obtained estimated values between −1.6 and −1.8 for ValO of spinel ferrites, and they also defined the ionicity of an oxide as fi = |ValO|/2, accompanied by calculated values of the iconicity of several cations in spinel ferrites.27
Taking into account that there are O1− ions in addition to O2− ions, our group uses the O 2p itinerant-electron model20 and the quantum mechanical potential barrier method21,22 to investigate the cation distribution in several series of spinel ferrites.28–35 In the study reported here, we prepared spinel ferrite samples of TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4) and TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3) and measured the magnetic moment, μexp, of the samples at 10 K. The cation distribution in the samples was estimated by fitting the measured values of μexp.
2 Experimental
2.1 Sample preparation
Spinel ferrites TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4; hereafter referred to as the Co-series) and TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3; hereafter referred to as the Mn-series) were prepared using the method of solid-phase reaction.17 The analytical reagent (AR)-grade chemicals CoO, MnO2, Fe2O3, and TiO2 were used as the starting materials. First, stoichiometric amounts of each chemical were mixed together, ground for 8 h in an agate mortar, and then calcined at 1173 K for 5 h. The calcined materials were then ground again for 1 h. The ground powder was calcined at 1473 K for an additional 5 h, and then further ground for 1 h. Next, the twice calcined and thrice ground powder was pressed into pellets at a pressure of 104 kg cm−2 and then sintered at 1673 K for 10 h in a tube furnace under an argon flow. The sintered pellets were then ground for 30 min in an agate mortar, and the resulting powder was used for the measurements.
2.2 Sample characterization
The crystal structure of the samples was determined by analyzing their X-ray diffraction (XRD) patterns, which were measured with an X-ray diffractometer (X'pert Pro, PANalytical, The Netherlands) with Cu Kα (λ = 1.5406 Å) radiation at room temperature. The data were collected in the 2θ range of 15–120° with a step size of 0.0167°. The working current and voltage were 40 mA and 40 kV, respectively. The magnetic hysteresis loops of the samples were measured using a physical properties measurement system (PPMS, Quantum Design Corporation, USA) at 10 and 300 K.
3 Experimental results
3.1 Analysis of X-ray diffraction patterns
Fig. 1(a) and (b) show the XRD patterns of the TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4) and TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3) samples, which indicate that they consisted of a single-phase with a cubic spinel structure of space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The XRD data were fitted using the X'Pert HighScore Plus software (PANalytical, The Netherlands) and the Rietveld powder-diffraction profile-fitting technique.36 The ions O (32e), A (8b) and B (16c) were located at the positions (u, u, u), (0.375, 0.375, 0.375), and (0, 0, 0), respectively. We obtained the crystal structure data, including the crystal lattice constant, a, the oxygen position parameters, u, the distances from the O anions to the cations at the (A) and [B] sites, dAO and dBO; and the distance between the cations at the (A) sites and those at the [B] sites, dAB; the data are summarized in Table 1. For the cubic spinel structure, the ideal values (assuming u = 0.25) of dAO, dBO, and dAB are
m. The XRD data were fitted using the X'Pert HighScore Plus software (PANalytical, The Netherlands) and the Rietveld powder-diffraction profile-fitting technique.36 The ions O (32e), A (8b) and B (16c) were located at the positions (u, u, u), (0.375, 0.375, 0.375), and (0, 0, 0), respectively. We obtained the crystal structure data, including the crystal lattice constant, a, the oxygen position parameters, u, the distances from the O anions to the cations at the (A) and [B] sites, dAO and dBO; and the distance between the cations at the (A) sites and those at the [B] sites, dAB; the data are summarized in Table 1. For the cubic spinel structure, the ideal values (assuming u = 0.25) of dAO, dBO, and dAB are 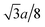 , a/4, and
, a/4, and 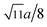 , respectively; however, the observed values of dAO and dBO (Table 1) are 1.0400 and 0.9805 (or 1.0918 and 0.9565) times, respectively, of the ideal values for the Co-series (or Mn-series) samples. On the other hand, the observed values of dAB are equal to the ideal values for the two series. The volume-averaged crystallite sizes of all samples were calculated using the X'Pert HighScore Plus software, and they were found to be greater than 100 nm. Therefore, surface effects of the crystallites are expected to be very weak in all samples.
, respectively; however, the observed values of dAO and dBO (Table 1) are 1.0400 and 0.9805 (or 1.0918 and 0.9565) times, respectively, of the ideal values for the Co-series (or Mn-series) samples. On the other hand, the observed values of dAB are equal to the ideal values for the two series. The volume-averaged crystallite sizes of all samples were calculated using the X'Pert HighScore Plus software, and they were found to be greater than 100 nm. Therefore, surface effects of the crystallites are expected to be very weak in all samples.
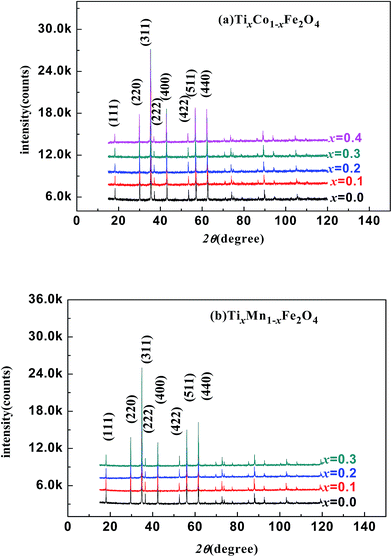 |
| | Fig. 1 X-ray diffraction patterns of various samples: (a) TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4); (b) TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3). | |
Table 1 Rietveld fitting results of XRD patterns of the two series of samples, obtained using the X'Pert HighScore Plus software. a is the lattice parameter; dAO and dBO are the distances from the O anion to the cations at the (A) and [B] sites, respectively; and dAB is the distance from the cations at the (A) sites to those at the [B] sites
| x |
a (Å) |
dAO (Å) |
dBO (Å) |
dAB (Å) |
u (Å) |
| TixCo1−xFe2O4 |
| 0.0 |
8.3871 |
1.888 |
2.056 |
3.477 |
0.24503 |
| 0.1 |
8.3987 |
1.891 |
2.059 |
3.482 |
0.24501 |
| 0.2 |
8.4089 |
1.893 |
2.061 |
3.486 |
0.24500 |
| 0.3 |
8.4203 |
1.896 |
2.064 |
3.491 |
0.24499 |
| 0.4 |
8.4343 |
1.898 |
2.066 |
3.497 |
0.24498 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| TixMn1−xFe2O4 |
| 0.0 |
8.5197 |
2.014 |
2.037 |
3.532 |
0.23856 |
| 0.1 |
8.5190 |
2.016 |
2.038 |
3.531 |
0.23857 |
| 0.2 |
8.5172 |
2.012 |
2.036 |
3.530 |
0.23858 |
| 0.3 |
8.5118 |
2.011 |
2.035 |
3.529 |
0.23859 |
Fig. 2 shows the dependence of the lattice parameter a on the Ti-doping level, x, in the two series of samples. It can be seen that with increasing x, a increased for the Co-series and decreased for the Mn-series. The different trends in the lattice constant were related to the cation radii, magnetic ordering, and cohesive energies of the samples.
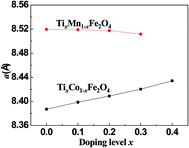 |
| | Fig. 2 Curves of lattice constant, a, versus the Ti-doping level, x, for the two series of samples. | |
3.2 Analysis of magnetic properties of the samples
Fig. 3 and 4 show the magnetic hysteresis loops of the two series of samples measured at 10 and 300 K. From these figures, we obtained the specific saturation magnetization (σS) measured at 10 and 300 K and the magnetic moment (μexp) per formula unit of each sample at 10 K, as listed in Table 2. It can be seen that the values of σS for the two series of samples gradually decreased with increasing x at both 10 and 300 K.
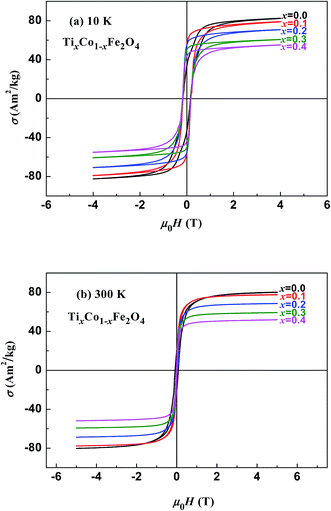 |
| | Fig. 3 Magnetic hysteresis loops measured at (a) 10 K and (b) 300 K for samples of TixCo1−xFe2O4. | |
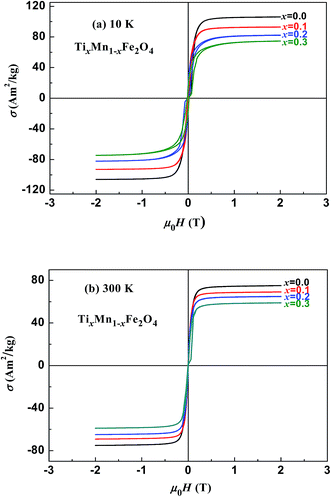 |
| | Fig. 4 Magnetic hysteresis loops measured at (a) 10 K and (b) 300 K for samples of TixMn1−xFe2O4. | |
Table 2 Specific saturation magnetization measured at 10 K (σS-10 K) and 300 K (σS-300 K) for the two series of samples; μexp is the experimental magnetic moment per formula unit of a sample, which was calculated using σS-10K
| x |
σS-10 K (A m2 kg−1) |
σS-300 K (A m2 kg−1) |
μexp (μB per formula) |
| TixCo1−xFe2O4 |
| 0.0 |
77.73 |
77.39 |
3.266 |
| 0.1 |
74.19 |
76.32 |
3.102 |
| 0.2 |
66.30 |
67.34 |
2.759 |
| 0.3 |
59.97 |
58.03 |
2.484 |
| 0.4 |
51.02 |
50.12 |
2.103 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| TixMn1−xFe2O4 |
| 0.0 |
105.23 |
74.41 |
4.346 |
| 0.1 |
92.28 |
68.47 |
3.799 |
| 0.2 |
81.06 |
64.31 |
3.327 |
| 0.3 |
72.91 |
58.18 |
2.983 |
4 Estimation of cation distributions by fitting the samples' magnetic moments at 10 K
Following the procedure reported by Xu et al.,18–20 we used the O 2p itinerant-electron model20 and the quantum mechanical potential barrier method21,22 to fit the magnetic moments measured at 10 K as a function of x and estimate the cation distribution in all samples. During the fitting process, the following factors were taken into account:
Factor 1: since there were O1− ions in addition to O2− ions, the ionicity of the cations in the samples was distinctly lower than 1.0, as shown in Table 3; the values listed in Table 3 were calculated using the method reported by Ji et al.27 In (A)[B]2O4 spinel ferrites, the total valence and the total number of trivalent cations per formula unit (N3) are both less than the traditional values of 8 and 2, respectively.
Table 3 Cation parameters used in the magnetic-moment fitting process, including the second and third ionization energies, V(M2+) and V(M3+); effective radii, r, of the divalent cations with coordination number 6; ionicity, fi;27 and the magnetic moments of the divalent and trivalent cations, m2 and m3
| Element, M |
V(M2+) (eV) |
V(M3+) (eV) |
r37 (nm) |
fi27 |
m2 (μB) |
m3 (μB) |
| Ti |
13.58 |
27.49 |
0.0860 |
0.9716 |
−1 |
−2 |
| Mn |
15.64 |
33.67 |
0.0830 |
0.8293 |
5 |
−4 |
| Fe |
16.18 |
30.65 |
0.0780 |
0.8790 |
4 |
5 |
| Co |
17.06 |
33.50 |
0.0745 |
0.8314 |
3 |
4 |
Factor 2: the O 2p itinerant-electron model is characterized by certain features:20 (i) in a given sublattice, an O 2p electron with constant spin direction can hop from an O2− anion to the O 2p hole of an adjacent O1− anion, with a cation acting as an intermediary. (ii) The two O 2p electrons in the outer orbit of an O2− anion, which have opposite spin directions, become itinerant electrons in the two different sublattices (the (A) or [B] sublattice). (iii) In a given sublattice that is constrained by Hund's rules and by the fact that an itinerant electron has constant spin direction, the direction of the magnetic moments of cations with the 3d electron number of nd ≤ 4 will couple antiferromagnetically to those of the cations with nd ≥ 5 at either the (A) sites or the [B] sites of a spinel ferrite. Therefore, the directions of the magnetic moments of Ti3+(3d1), Ti2+(3d2), and Mn3+(3d4) were antiparallel to those of the magnetic moments of Mn2+, Co2+, Co3+, Fe3+, and Fe2+ in the same sample at either the (A) sublattice or the [B] sublattice. Therefore, in the following calculations, we set the moment of the cations to the values shown in Table 3.
Factor 3: we assumed that there is a square potential barrier between a pair of anion and cation.21 The height and the width of the potential barrier are related to the cation ionization energy and the distance between the cation–anion pair. The content ratio (R) of the different cations is therefore related to the probability of the last ionized electrons transmitted through the potential barriers, and the following equation can be obtained:
| |
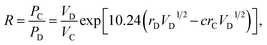 | (1) |
where nanometers (nm) and electron-volts (eV) are used as the units of length and energy;
PC (or
PD) stands for the probability of the last ionized electron of the C (or D) cation jumping to the anions through the potential barrier with the height
VC (or
VD) and the width
rC (or
rD).
VC and
VD are the ionization energies of the last ionized electron of the cations C and D, and
rC and
rD are the distances from the cations C and D to the anions. The parameter
c is a barrier shape-correcting constant related to the different extents to which the shapes of the two potential barriers deviate from a square barrier. When
VC =
VD and
rC =
rD, it is obvious that
c = 1.0.
Factor 4: we considered the Pauli repulsion energy of the electron cloud between adjacent cations and anions. This can be taken into account using the effective ionic radius:37 smaller ions tend to enter the sites with smaller available space in the lattice. It is worth noting that the volumes of the (A) sites are smaller than those of the [B] sites in spinel ferrites.
Factor 5: during the thermal treatment of the samples, the tendency to balance the electrical charge density forced some of the divalent cations (with large effective ionic radii) to enter the (A) sites (with smaller available space) from the [B] sites (with large available space), jumping over an equivalent potential barrier, VBA, because cations at the (A) sites have four adjacent oxygen ions while cations at the [B] sites have six adjacent oxygen ions. VBA is related to the ionization energy, ionic radius, and the thermal-treatment temperature. We assumed VBA of the ferrite samples can be expressed by the following equations:34
| |
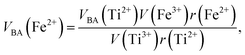 | (2) |
| |
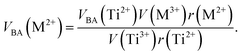 | (3) |
where M = Co or Mn;
V(M
3+),
V(Ti
3+), and
V(Fe
3+) are the third ionization energies of Co, Mn, Ti and Fe, respectively; and
r(M
2+),
r(Ti
2+), and
r(Fe
2+) are the effective radii of the divalent cations with coordination number 6, as shown in
Table 3.
The chemical formulae of the ferrite samples TixCo1−xFe2O4 and TixMn1−xFe2O4, are rewritten here as Tix1Mx2Fe3−x1−x2O4 (M = Co, Mn) so that the cation distributions can be described by the equation
| | |
(Tiy13+My23+Fey33+Tiy42+My52+Fey62+)[Tix1−y1−y4−z12+Mx2−y2−y5−z22+Fe3−x1−x2−y3−y6−z32+Tiz13+Mz23+Fez33+]O4.
| (4) |
It can be seen from eqn (4) that
| | |
y1 + y2 + y3 + y4 + y5 + y6 = 1,
| (5) |
| | |
y1 + y2 + y3 + z1 + z2 + z3 = N3,
| (6) |
| |
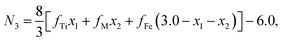 | (7) |
where
N3 is the number of trivalent cations per formula unit. The parameters
fTi,
fFe, and
fM =
fCo (or
fMn) represent the ionicities of the Ti, Fe, and Co (or Mn) ions,
27 whose values are shown in
Table 3.
Eqn (7) suggests that when the ionicity of all cations are 1.00, the sum of the valence of all cations is 8.00, while
N3 = 2.00. In fact, the ionicity of each cation is lower than 1.00 (see
Table 3), resulting in
N3 < 2.00. From
eqn (4), we have
| |
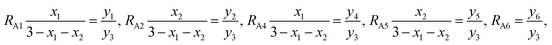 | (8) |
| |
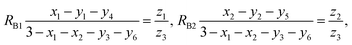 | (9) |
where
RA1,
RA2,
RA4,
RA5, and
RA6 represent the probability ratios of the Ti
3+, Co
3+(Mn
3+), Ti
2+, Co
2+(Mn
2+), and Fe
2+ ions, respectively, with respect to the Fe
3+ ions at the (A) sites, while
RB1 and
RB2 represent the probability ratios of the Ti
3+ and Co
3+(Mn
3+) ions with respect to the Fe
3+ ions at the [B] sites. From
eqn (5) and
(8), we can obtain
| |
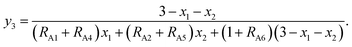 | (10) |
From eqn (6) and (9), we have
| |
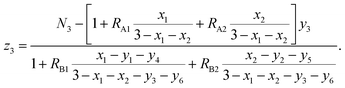 | (11) |
According to the above-mentioned quantum mechanical potential barrier method for estimating the cation distributions in spinel ferrites,21,22 which is similar to eqn (1), the content ratios RA1, RA2, RA4, RA5, and RA6 at the (A) sites and RB1 and RB2 at the [B] sites can be rewritten as
| |
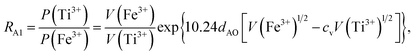 | (12) |
| |
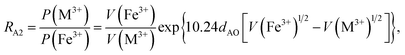 | (13) |
| |
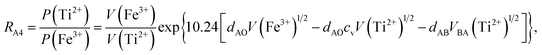 | (14) |
| |
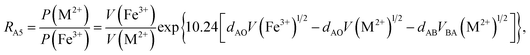 | (15) |
| |
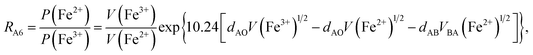 | (16) |
| |
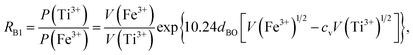 | (17) |
| |
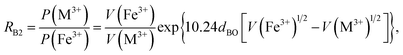 | (18) |
where M = Co or Mn; and
V(M
2+),
V(M
3+),
V(Ti
2+),
V(Ti
3+),
V(Fe
2+), and
V(Fe
3+) are the second and third ionization energies of Co, Mn, Ti, and Fe, respectively, as shown in
Table 3. The parameter
cv is a barrier shape-correcting constant related to the potential barrier of Ti
2+ and Ti
3+ cations; we assume that
cv = 1.0 for other cations because the second and third ionization energies of Ti cations are distinctly lower than those of other cations.
VBA(M
2+),
VBA(Ti
2+), and
VBA(Fe
2+) are the heights of the equivalent potential barriers (all have a width of
dAB), which must be transmitted through by the M
2+, Ti
2+, and Fe
2+ ions as they move from the [B] sites to the (A) sites during thermal treatment. The values of,
dAO,
dBO, and
dAB are the observed values in the XRD patterns, as listed in
Table 1.
According to the O 2p itinerant-electron model, the magnetic moments of the Mn3+, Ti2+, and Ti3+ cations are antiparallel to those of Co2+, Co3+, Mn2+, Fe3+, and Fe2+ cations in the same sublattice of a spinel ferrite (see Table 3). Therefore, we can calculate the average magnetic moment per formula unit of a sample from eqn (4):
| |
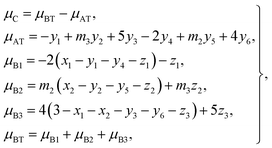 | (19) |
where
μC is the calculated magnetic moment of a sample;
μAT and
μBT are the magnetic moments of the (A) and [B] sublattices; and
μB1,
μB2, and
μB3 are magnetic moments contributed by the Ti, Co (or Mn), and Fe ions, respectively, at the [B] sublattice.
For each sample, there are 22 parameters: y1–y6; z1–z3; N3; RA1, RA2, RA4, RA5, and RA6; RB1 and RB2; VBA(Ti2+), VBA(M2+), and VBA(Fe2+); μC; and cv. Altogether, there are 20 independent equations, including eqn (2), (3), (5)–(9), and (12)–(19), where eqn (8) contains five equations and eqn (9) contains two equations. Therefore, we needed to obtain the values of at least two independent parameters, such as cv and VBA(Ti2+), in order to fit the observed values of μexp of a sample at 10 K.
Using the above parameters and equations, we fitted the dependence of μexp on x for the two series of samples. The points and curves in Fig. 5 represent the observed and calculated magnetic moments, μexp and μC, of the samples. It can be seen that the fitted curves are very close to the experimental results. In the fitting process, we obtained the cation distribution and other data, as listed in Tables 4 and 5. The cation distribution is shown as a function of x for the two series of samples in Fig. 6 and 7.
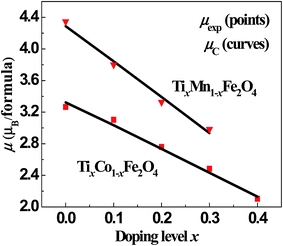 |
| | Fig. 5 Fitted magnetic moments, μC (line), and observed values, μexp (points), as functions of x for the two series of samples. | |
Table 4 Cation distributions obtained by fitting the dependence of the magnetic moments in the samples TixCo1−xFe2O4 on x. The parameters VBA(Ti2+), VBA(Co2+), and VBA(Fe2+) are the heights of the potential barriers that must be transmitted though by the Ti2+, Co2+, and Fe2+ ions when moving from the [B] sites to the (A) sites during thermal treatment of the samples; N3 is the total average number of trivalent cations per formula unit; μAT and μBT are the magnetic moments per formula unit of the (A) and [B] sublattices, respectively; and μC = μBT − μAT is the calculated magnetic moment per formula unit
| x |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
| N3 |
0.9070 |
0.9496 |
0.9906 |
1.0297 |
1.0675 |
| VBA(Ti2+) (eV) |
1.0933 |
1.2900 |
1.4867 |
1.6833 |
1.8800 |
| VBA(Co2+) (eV) |
1.1542 |
1.3618 |
1.5694 |
1.7770 |
1.9847 |
| VBA(Fe2+) (eV) |
1.1056 |
1.3045 |
1.5034 |
1.7022 |
1.9011 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| A sites |
| Ti3+ |
0.0000 |
0.0168 |
0.0372 |
0.0602 |
0.0849 |
| Co3+ |
0.1164 |
0.1193 |
0.1172 |
0.1106 |
0.1002 |
| Fe3+ |
0.4159 |
0.4822 |
0.5392 |
0.5864 |
0.6244 |
| Ti2+ |
0.0000 |
0.0178 |
0.0283 |
0.0332 |
0.0343 |
| Co2+ |
0.1286 |
0.0919 |
0.0637 |
0.0429 |
0.0280 |
| Fe2+ |
0.3392 |
0.2706 |
0.2121 |
0.1639 |
0.1252 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| B sites |
| Ti2+ |
0.0000 |
0.0578 |
0.1202 |
0.1859 |
0.2536 |
| Co2+ |
0.6674 |
0.6173 |
0.5610 |
0.4992 |
0.4331 |
| Fe2+ |
0.9578 |
0.9935 |
1.0219 |
1.0424 |
1.0553 |
| Ti3+ |
0.0000 |
0.0091 |
0.0165 |
0.0228 |
0.0289 |
| Co3+ |
0.0931 |
0.0739 |
0.0586 |
0.0468 |
0.0377 |
| Fe3+ |
0.2816 |
0.2483 |
0.2219 |
0.2029 |
0.1914 |
| μBT (μB per formula) |
7.6142 |
7.2385 |
6.8574 |
6.4745 |
6.0925 |
| μAT (μB per formula) |
4.2909 |
4.2040 |
4.1225 |
4.0427 |
3.9621 |
| μC (μB per formula) |
3.3233 |
3.0345 |
2.7349 |
2.4318 |
2.1303 |
Table 5 Cation distributions obtained by fitting the dependence of the magnetic moments in the samples TixMn1−xFe2O4 on x. The parameters VBA(Ti2+), VBA(Mn2+), and VBA(Fe2+) are the heights of the potential barriers that must be transmitted though by the Ti2+, Mn2+, and Fe2+ ions when moving from the [B] sites to the (A) sites during thermal treatment of the samples; N3 is the total average number of trivalent cations per formula unit; μAT and μBT are the magnetic moments per formula unit of the (A) and [B] sublattices, respectively; and μC = μBT − μAT is the calculated magnetic moment per formula unit
| x |
0.0 |
0.1 |
0.2 |
0.3 |
| N3 |
0.8994 |
0.9373 |
0.9753 |
1.0132 |
| VBA(Ti2+) (eV) |
0.8960 |
1.0200 |
1.0800 |
1.1400 |
| VBA(Mn2+) (eV) |
1.1348 |
1.2057 |
1.2766 |
1.3476 |
| VBA(Fe2+) (eV) |
0.9708 |
1.0315 |
1.0921 |
1.1528 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| A sites |
| Ti3+ |
0.0000 |
0.0042 |
0.0090 |
0.0145 |
| Mn3+ |
0.0872 |
0.0847 |
0.0808 |
0.0755 |
| Fe3+ |
0.3319 |
0.3579 |
0.3840 |
0.4101 |
| Ti2+ |
0.0000 |
0.0104 |
0.0200 |
0.0290 |
| Mn2+ |
0.1789 |
0.1543 |
0.1312 |
0.1097 |
| Fe2+ |
0.4019 |
0.3885 |
0.3749 |
0.3612 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| B sites |
| Ti2+ |
0.0000 |
0.0795 |
0.1585 |
0.2371 |
| Mn2+ |
0.6225 |
0.5566 |
0.4911 |
0.4262 |
| Fe2+ |
0.8972 |
0.8734 |
0.8489 |
0.8235 |
| Ti3+ |
0.0000 |
0.0059 |
0.0124 |
0.0194 |
| Mn3+ |
0.1114 |
0.1044 |
0.0969 |
0.0885 |
| Fe3+ |
0.3689 |
0.3802 |
0.3922 |
0.4052 |
| μBT (μB per formula) |
8.1005 |
7.5945 |
7.0953 |
6.6036 |
| μAT (μB per formula) |
3.8129 |
3.7513 |
3.7033 |
3.6690 |
| μC (μB per formula) |
4.2876 |
3.8433 |
3.3921 |
2.9347 |
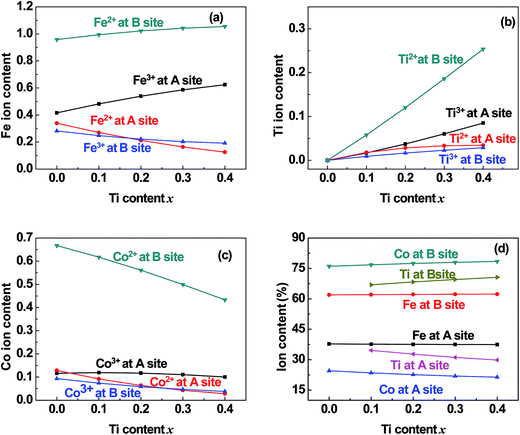 |
| | Fig. 6 Distribution of (a) Fe, (b) Ti, and (c) Co cations and (d) the total content percentages of different valence cations at the (A) and [B] sites in samples of TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4). | |
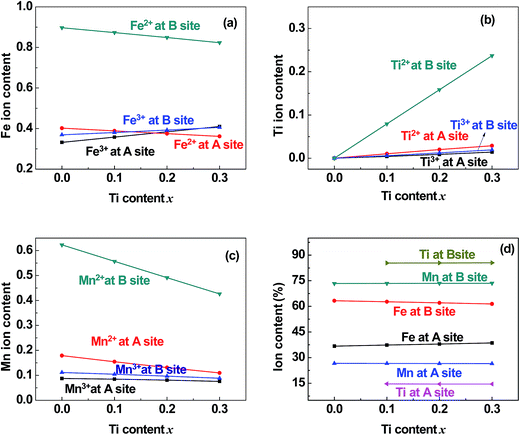 |
| | Fig. 7 Distribution of (a) Fe, (b) Ti, and (c) Mn cations and (d) the total content percentages of different valence cations at the (A) and [B] sites in samples of TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3). | |
5 Discussion
From Tables 4, 5, Fig. 6 and 7, we found that the fitting parameters and the cation distribution in the samples had certain characteristics, as discussed in the following subsections.
5.1 Fitting parameters: cv and VBA
During the fitting process, we determined that the potential barrier shape-correcting constant cv was equal to 1.1 and 1.2 for the pair of ions, Ti–O, in the Co-series and Mn-series, respectively. Both values are reasonable when compared with cv = 1.0 for other cation–anion pairs.
The Ti2+ ions must transmit though the equivalent potential barrier VBA(Ti2+) as they moved from the [B] sites to the (A) sites during the thermal treatment. We obtained the values of VBA(Ti2+) in the fitting process, and they increased from 1.093 eV (x = 0.0) to 1.880 eV (x = 0.4) for the Co-series and from 0.896 eV (x = 0.0) to 1.140 eV (x = 0.3) for the Mn-series. The values of VBA(Fe2+), VBA(Co2+), and VBA(Mn2+) were calculated from eqn (2) and (3), and they appear reasonable in the context of a physics problem.
5.2 Valence and distribution of Ti cations
(i) The ratio of Ti2+ ions at the (A) and [B] sites to the Ti-doping level, x, is more than 72% in the Co-series samples (Fig. 6(b)) and about 89% in the Mn-series samples (Fig. 7(b)). This result is similar to that measured using XPS and reported by Dupin et al.; they found that the average O ionic valence is −1.15 for TiO2, which suggests that 70% of Ti cations in TiO2 are Ti2+ ions.26 Therefore, the conventional view12–16 that all Ti cations in an oxide are Ti4+ ions needs to be modified.
(ii) The ratio of Ti2+ cations that entered the [B] sites to x increased from 58% (x = 0.1) to 63% (x = 0.4) in the Co-series samples (Fig. 6(b)), and this ratio remained at 79% from x = 0.1 to x = 0.3 in the Mn-series samples (Fig. 7(b)). This result is similar to that reported by Xu et al., who found the ratio of Ti2+ cations that entered the [B] sites to x was 81% in Ti-doped ferrite Ni0.68Fe2.32O4.18
(iii) The ratio of Ti cations, including Ti2+ and Ti3+, that entered the [B] sites to x increased from 67% (x = 0.1) to 72% (x = 0.4) in the Co-series samples (Fig. 6(d)), and this ratio was 85% in the Mn-series samples (Fig. 7(d)). This result appears to be a balance between the contrasting results reported by several authors:12–16 Kale et al. concluded that 71% of Ti cations entered the (A) sites in Ti0.7Ni1.7Fe0.6O4,16 while other authors assumed that all of the Ti ions entered the [B] sites of the spinel ferrite samples.12–15
5.3 Distribution of Co cations in Co-series
(i) The ratio of Co cations, including Co2+ and Co3+, that entered the [B] sites to the total Co cation content ranged from 76% to 78% (Fig. 6(d)). This ratio is very close to that reported by Shang et al.30 for Co1−xCrxFe2O4. This result is also close to that reported by Wakabayashi et al. for a CoFe2O4 film with thickness of 11 nm, which was based on soft X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD) combined with cluster model calculations.38
(ii) The ratio of Co2+ cations that entered the [B] sites to the total Co cation content increased from 67% (x = 0.0) to 73% (x = 0.4). This result is similar to that reported by Shang et al., who found that the ratio of Co2+ cations that entered the [B] sites ranged from 64% (x = 0.0) to 59% (x = 0.8) in Co1−xCrxFe2O4.30
5.4 Distribution of Mn cations in Mn-series
The ratio of Mn2+ cations that entered the [B] sites to the total Mn cation content was 61%. The ratio of Mn ions, including Mn2+ and Mn3+ cations, that entered the [B] sites to the total Mn cation content was 73%. This result is similar to that reported by Xu et al.20
5.5 Entry of few Co and Mn cations into the (A) sites
It can be seen from Fig. 6(c) and 7(c) that a few of the Co (Mn) cations entered the (A) sites of the Co (Mn) series samples. This is in accordance with the observed results from XRD mentioned in Section 3.1: the ratio of observed to ideal values of A–O distance for MnFe2O4, 1.09, is higher than that for CoFe2O4, 1.04, because the effective radius of Mn is greater than that of Co (see Table 3). This suggested that a few of the Mn (Co) cations entered the (A) sites of MnFe2O4 (CoFe2O4).
6 Conclusions
The single-phase spinel ferrites TixCo1−xFe2O4 (0.0 ≤ x ≤ 0.4) and TixMn1−xFe2O4 (0.0 ≤ x ≤ 0.3) were prepared using the conventional method for preparing ceramics. The samples were found to consist of a single phase with a cubic spinel structure. The lattice constant increased in the Co-series samples and decreased in the Mn-series samples with increases in the dopant level, x. The values of μexp of the two series of samples, measured at 10 K, decreased approximate linearly with increasing x.
The dependence of μexp on x for the two series of samples was fitted using a quantum-mechanical potential barrier method. The fitted magnetic moments were very close to the experimental results. In the fitting process, the cation distributions of the two series of samples were obtained.
The cation distributions and the magnetic structure obtained in this study are distinctly different from those reported by other groups: (i) there were Ti2+ and Ti3+ ions, but no Ti4+ ions, in our samples. (ii) The ratio of Ti2+ cations that entered the [B] sites to the Ti-doping level, x, increased from 58% (x = 0.1) to 63% (x = 0.4) in the Co-series samples, and this ratio was 79% from x = 0.1 to x = 0.3 in the Mn-series samples. (iii) The magnetic moments of Ti2+, Ti3+, and Mn3+ ions (with 3d electron number of nd ≤ 4) coupled antiferromagnetically with other cations (nd ≥ 5) whenever they were at the (A) or [B] sublattice.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSF-11174069), the Natural Science Foundation of Hebei Province (A2015205111), the Key item Science Foundation of Hebei Province (Grant No. 16961106D), and the Young scholar Science Foundation of the Education Department of Hebei Province (QN2016015).
References
- W. M. Xu, G. R. Hearne, S. Layek, D. Levy, J.-P. Itié, M. P. Pasternak, G. Kh. Rozenberg and E. Greenberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 045108 CrossRef.
- K. Ugendar, S. Samanta, S. Rayaprol, V. Siruguri, G. Markandeyulu and B. R. K. Nanda, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 035138 CrossRef.
- O. Kuschel, R. Buß, W. Spiess, T. Schemme, J. Wollermann, K. Balinski, A. T. N'Diaye, T. Kuschel, J. Wollschlager and K. Kuepper, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 094423 CrossRef.
- G. Lavorato, E. Winkler, B. Rivas-Murias and F. Rivadulla, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 054405 CrossRef.
- M. Abes, C. T. Koops, S. B. Hrkac, J. McCord, N. O. Urs, N. Wolff, L. Kienle, W. J. Ren, L. Bouchenoire, B. M. Murphy and O. M. Magnussen, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 195427 CrossRef.
- T. Watanabe, S. Takita, K. Tomiyasu and K. Kamazawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174420 CrossRef.
- D. Fritsch and C. Ederer, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014406 CrossRef.
- D. Venkateshvaran, M. Althammer, A. Nielsen, S. Geprägs, M. S. Ramachandra Rao, S. T. B. Goennenwein, M. Opel and R. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134405 CrossRef.
- M. Reehuis, M. Tovar, D. M. Többens, P. Pattison, A. Hoser and B. Lake, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024407 CrossRef.
- C. W. Chen, Magnetism and Metallurgy of Soft Magnetic Materials, North-Holland Publishing Company, 1977, pp. 171–417 Search PubMed.
- J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, 2010, pp. 414–427 Search PubMed.
- G. D. Dwivedi, A. G. Joshi, H. Kevin, P. Shahi, A. Kumar, A. K. Ghosh, H. D. Yang and S. Chatterjee, Solid State Commun., 2012, 152, 360–363 CrossRef CAS.
- K. Srinivasa Rao, A. Mahesh Kumar a, M. Chaitanya Varma, G. S. V. R. K. Choudary and K. H. Rao, J. Alloys Compd., 2009, 488, 6–9 CrossRef.
- E. Schmidbauer, Solid State Commun., 1976, 18, 301–303 CrossRef CAS.
- E. Schmidbauer, Phys. Chem. Miner., 1983, 9, 124–126 CrossRef CAS.
- C. M. Kale, P. P. Bardapurkar, S. J. Shukla and K. M. Jadhav, J. Magn. Magn. Mater., 2013, 331, 220–224 CrossRef CAS.
- J. Xu, D. H. Ji, Z. Z. Li, W. H. Qi, G. D. Tang, Z. F. Shang and X. Y. Zhang, J. Alloys Compd., 2015, 619, 228–234 CrossRef CAS.
- J. Xu, D. H. Ji, Z. Z. Li, W. H. Qi, G. D. Tang, X. Y. Zhang, Z. F. Shang and L. L. Lang, Phys. Status Solidi B, 2015, 252, 411–420 CrossRef CAS.
- J. Xu, W. H. Qi, D. H. Ji, Z. Z. Li, G. D. Tang, X. Y. Zhang, Z. F. Shang and L. L. Lang, Acta Phys. Sin., 2015, 64, 017501 Search PubMed.
- J. Xu, L. Ma, Z. Z. Li, L. L. Lang, W. H. Qi, G. D. Tang, L. Q. Wu, L. C. Xue and G. H. Wu, Phys. Status Solidi B, 2015, 252, 2820–2829 CrossRef CAS.
- G. D. Tang, D. H. Ji, Y. X. Yao, S. P. Liu, Z. Z. Li, W. H. Qi, Q. J. Han, X. Hou and D. L. Hou, Appl. Phys. Lett., 2011, 98, 072511 CrossRef.
- S. R. Liu, D. H. Ji, J. Xu, Z. Z. Li, G. D. Tang, R. R. Bian, W. H. Qi, Z. F. Shang and X. Y. Zhang, J. Alloys Compd., 2013, 581, 616–624 CrossRef CAS.
- R. E. Cohen, Nature, 1992, 358, 136–138 CrossRef CAS.
- R. E. Cohen and H. Krakauer, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 6416–6423 CrossRef CAS.
- L. Q. Wu, Y. C. Li, S. Q. Li, Z. Z. Li, G. D. Tang, W. H. Qi, L. C. Xue, X. S. Ge and L. L. Ding, AIP Adv., 2015, 5, 097210 CrossRef.
- J. C. Dupin, D. Gonbeau, P. Vinatier and A. Levasseur, Phys. Chem. Chem. Phys., 2000, 2, 1319–1324 RSC.
- D. H. Ji, G. D. Tang, Z. Z. Li, X. Hou, Q. J. Han, W. H. Qi, R. R. Bian and S. R. Liu, J. Magn. Magn. Mater., 2013, 326, 197–200 CrossRef CAS.
- G. D. Tang, Q. J. Han, J. Xu, D. H. Ji, W. H. Qi, Z. Z. Li, Z. F. Shang and X. Y. Zhang, Phys. B, 2014, 438, 91–96 CrossRef CAS.
- L. L. Lang, J. Xu, W. H. Qi, Z. Z. Li, G. D. Tang, Z. F. Shang, X. Y. Zhang, L. Q. Wu and L. C. Xue, J. Appl. Phys., 2014, 116, 123901 CrossRef.
- Z. F. Shang, W. H. Qi, D. H. Ji, J. Xu, G. D. Tang, X. Y. Zhang, Z. Z. Li and L. L. Lang, Chin. Phys. B, 2014, 23, 107503 CrossRef.
- X. Y. Zhang, J. Xu, Z. Z. Li, W. H. Qi, G. D. Tang, Z. F. Shang, D. H. Ji and L. L. Lang, Phys. B, 2014, 446, 92–99 CrossRef CAS.
- L. L. Lang, J. Xu, Z. Z. Li, W. H. Qi, G. D. Tang, Z. F. Shang, X. Y. Zhang, L. Q. Wu and L. C. Xue, Phys. B, 2015, 462, 47–53 CrossRef CAS.
- G. D. Tang, Z. F. Shang, X. Y. Zhang, J. Xu, Z. Z. Li, C. M. Zhen, W. H. Qi and L. L. Lang, Phys. B, 2015, 463, 26–29 CrossRef CAS.
- L. C. Xue, L. L. Lang, J. Xu, Z. Z. Li, W. H. Qi, G. D. Tang and L. Q. Wu, AIP Adv., 2015, 5, 097167 CrossRef.
- L. L. Ding, L. C. Xue, Z. Z. Li, S. Q. Li, G. D. Tang, W. H. Qi, L. Q. Wu and X. S. Ge, AIP Adv., 2016, 6, 105012 CrossRef.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- Y. K. Wakabayashi, Y. Nonaka, Y. Takeda, S. Sakamoto, K. Ikeda, Z. Chi, G. Shibata, A. Tanaka, Y. Saitoh, H. Yamagami, M. Tanaka, A. Fujimori and R. Nakane, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 104410 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac,
J. J. Qiana,
M. Y. Chena and
W. H. Qia
*ac,
J. J. Qiana,
M. Y. Chena and
W. H. Qia
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The XRD data were fitted using the X'Pert HighScore Plus software (PANalytical, The Netherlands) and the Rietveld powder-diffraction profile-fitting technique.36 The ions O (32e), A (8b) and B (16c) were located at the positions (u, u, u), (0.375, 0.375, 0.375), and (0, 0, 0), respectively. We obtained the crystal structure data, including the crystal lattice constant, a, the oxygen position parameters, u, the distances from the O anions to the cations at the (A) and [B] sites, dAO and dBO; and the distance between the cations at the (A) sites and those at the [B] sites, dAB; the data are summarized in Table 1. For the cubic spinel structure, the ideal values (assuming u = 0.25) of dAO, dBO, and dAB are
m. The XRD data were fitted using the X'Pert HighScore Plus software (PANalytical, The Netherlands) and the Rietveld powder-diffraction profile-fitting technique.36 The ions O (32e), A (8b) and B (16c) were located at the positions (u, u, u), (0.375, 0.375, 0.375), and (0, 0, 0), respectively. We obtained the crystal structure data, including the crystal lattice constant, a, the oxygen position parameters, u, the distances from the O anions to the cations at the (A) and [B] sites, dAO and dBO; and the distance between the cations at the (A) sites and those at the [B] sites, dAB; the data are summarized in Table 1. For the cubic spinel structure, the ideal values (assuming u = 0.25) of dAO, dBO, and dAB are 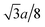 , a/4, and
, a/4, and 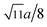 , respectively; however, the observed values of dAO and dBO (Table 1) are 1.0400 and 0.9805 (or 1.0918 and 0.9565) times, respectively, of the ideal values for the Co-series (or Mn-series) samples. On the other hand, the observed values of dAB are equal to the ideal values for the two series. The volume-averaged crystallite sizes of all samples were calculated using the X'Pert HighScore Plus software, and they were found to be greater than 100 nm. Therefore, surface effects of the crystallites are expected to be very weak in all samples.
, respectively; however, the observed values of dAO and dBO (Table 1) are 1.0400 and 0.9805 (or 1.0918 and 0.9565) times, respectively, of the ideal values for the Co-series (or Mn-series) samples. On the other hand, the observed values of dAB are equal to the ideal values for the two series. The volume-averaged crystallite sizes of all samples were calculated using the X'Pert HighScore Plus software, and they were found to be greater than 100 nm. Therefore, surface effects of the crystallites are expected to be very weak in all samples.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
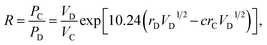
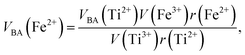
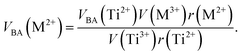
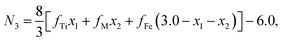
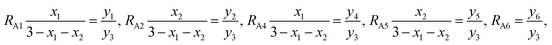
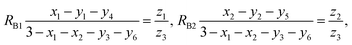
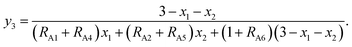
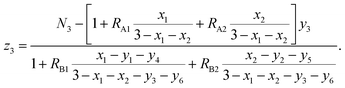
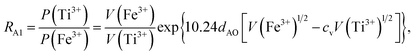
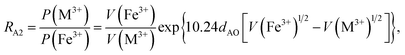
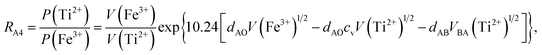
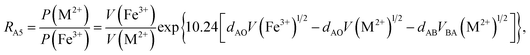
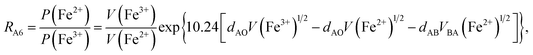
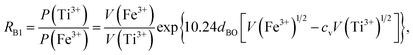
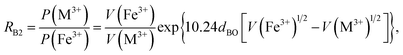
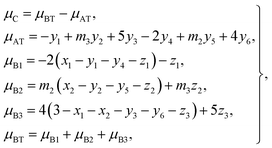

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)





