Theoretical study on the gigantic effect of external static electric field application on the nonlinear optical properties of 1,2,3,5-dithiadiazolyl π-radical dimers†
Hiroshi
Matsui
a,
Masaki
Yamane
a,
Takayoshi
Tonami
a,
Takanori
Nagami
a,
Kenichiro
Watanabe
a,
Ryohei
Kishi
a,
Yasutaka
Kitagawa
ab and
Masayoshi
Nakano
 *ab
*ab
aDepartment of Materials Engineering Science, Graduate School of Engineering Science, Osaka University, Toyonaka, Osaka 560-8531, Japan. E-mail: mnaka@cheng.es.osaka-u.ac.jp
bCenter for Spintronics Research Network (CSRN), Graduate School of Engineering Science, Osaka University, Toyonaka, Osaka 560-8531, Japan
First published on 6th February 2018
Abstract
Using the spin-unrestricted density functional theory method, we investigate the effect of external static electric field application on the first and second hyperpolarizabilities (β and γ) – nonlinear optical (NLO) properties at the molecular scale – of a 1,2,3,5-dithiadiazolyl π-radical dimer. It is found that these properties drastically vary depending on the external electric field intensity, and that such drastic variation occurs with gigantically enhanced peaks around the transition region from the diradical to charge transfer state. These results qualitatively accord with the previous theoretical prediction based on the asymmetric two-site diradical model. It also turns out that the field-induced enhancement ratio of γ amplitude reaches 9 × 104 in the maximum positive peak and −3 × 105 in the maximum negative peak for the dimer with an intermolecular distance d = 4.8 Å. This result demonstrates the promising potential of open-shell molecular aggregates as a novel class of highly-active external-field-driven NLO switches.
Introduction
In the last several decades, the nonlinear optical (NLO) properties of organic molecules have been studied with great interest due to their versatile future applications such as fabrication of hyperfine structures,1 huge-capacity optical memory,2,3 ultrafast optical switching,4etc. These fascinating NLO phenomena originate from nonlinear terms in the power series expansion of induced dipole moment μ with respect to the applied electric field F:| μ = μ0 + αF + βFF + γFFF + …, | (1) |
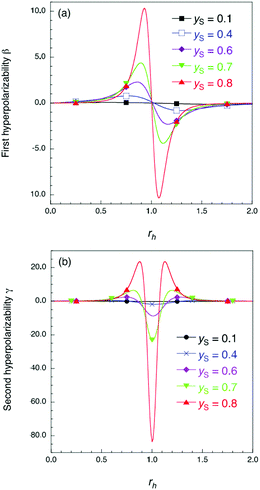 | ||
| Fig. 1 Results of the theoretical model in ref. 12 for dimensionless first hyperpolarizability β (a) and second hyperpolarizability γ (b). The rh and yS values denote asymmetricity and diradical character in the absence of asymmetricity, respectively (see the ESI† for details of rh and yS). | ||
In this study, therefore, we investigate the effect of external static electric field application on the NLO properties of realistic π-radical dimer models with a wide range of diradical characters yS. It is known that π-radical dimers often possess covalent-like intermolecular interaction so-called pancake-bonding25,26 and that they exhibit diradical character depending on their intermolecular distance.27,28 Because π-radical dimers without static electric field application are symmetric in swapping the monomers, it is easy to evaluate yS. Application of an external static electric field is also predicted to induce asymmetricity continuously in the π-radical dimer. Therefore, the investigation of the electric field application effect on the NLO properties of the realistic dimer models is an appropriate way for the comprehensive understanding for the previous results obtained by a two-site model study. In addition, it is expected to provide the potential of the external-field-driven NLO switching mechanism since the previous theoretical model study predicts a remarkable variation in NLO properties induced by introducing asymmetricity into open-shell singlet systems.
Theory and calculation method
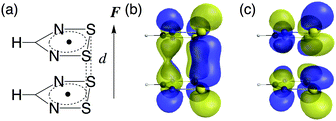
We consider 1,2,3,5-dithiadiazolyl (DTDA) as a π-radical monomer. It has been experimentally synthesized and reported to form a dimer with a close intermolecular distance (3.1 Å) in its crystal phase.29 This intermolecular distance can be modified by chemical substitution27,30 and doping31 to some extent. Kertesz et al. also clarified that this dimer bears pancake bonding and indicates a wide range of diradical characters depending on its intermolecular distance.27 The geometry optimization was performed for the DTDA monomer using the spin-unrestricted (U) Møller–Plesset second-order perturbation (MP2) method with the 6-311+G* basis set under the constraint of C2v symmetry. The geometries of the DTDA dimers were not optimized but were constructed from the face-to-face π–π stacked monomers with a wide range of intermolecular distances d (3.0 Å ≤ d ≤ 4.8 Å). The external static electric field is applied along the stacking direction (Fig. 2). Note here that although it is known that the DTDA dimer can take several kinds of stacking structures depending on substituents,27,30 we examine the cis-cofacial structure in this study as an example of pancake bonding. Since the present results are found to originate from the strength of pancake bonding (open-shell character) and field-induced asymmetricity in the stacking direction as shown below, the qualitative structure–property relationships obtained in this study are expected to also hold for different types of cofacial pancake bonded DTDA aggregates.The diradical character y is defined as the occupation number of the lowest unoccupied natural orbital (LUNO),32 and is evaluated using the long-range corrected UBLYP (LC-UBLYP) method with the 6-31+G* basis set. The range separating parameter μ of the LC-UBLYP functional is set to 0.33 bohr−1.33 The natural charge distribution is also evaluated using the LC-UBLYP(μ = 0.33)/6-31+G* method.
The NLO properties (diagonal components along the stacking direction of first hyperpolarizability β and second hyperpolarizability γ) are investigated in order to clarify their diradical character dependences. These properties were evaluated using the LC-UBLYP(μ = 0.33)/6-31+G* method because the long-range corrected functional is found to obtain reliable NLO properties as mentioned below. It is known that the LC-BLYP method can avoid catastrophic increases of optical properties as observed in global hybrid functionals.34–36 In addition, the LC-UBLYP method is found to semi-quantitatively reproduce the γ values of open-shell singlet systems calculated by the strong-correlated ab initio molecular orbital (MO) method like the UCCSD(T) method.33 Although solutions obtained by single reference methods are known to suffer from discontinuity at the boundary between open-shell and closed-shell solutions, they are known to still give qualitatively meaningful results.33 The 6-31+G* basis set is employed since an extended basis set with diffuse functions is found to be necessary for semi-quantitatively reliable calculation of (hyper)polarizabilities.37–39 The β and γ values were calculated by the coupled perturbed Kohn–Sham (CPKS) method and the finite field (FF) method,40 respectively.
To clarify the spatial contribution of radical electrons to y of the systems, we performed odd electron density analysis.41,42 The odd electron Dodd(r) is defined by the mth natural orbital φm and its occupation number nm as
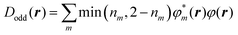 | (2) |
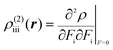 | (3) |
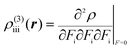 | (4) |
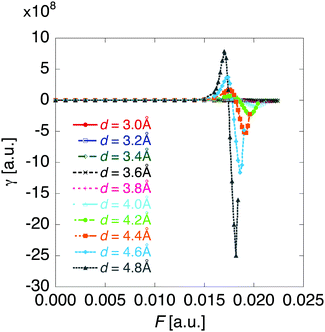
The βiii and γiiii values are obtained, respectively, using these densities as
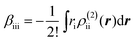 | (5) |
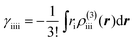 | (6) |
All calculations were carried out using the Gaussian 09 program package.44
Results and discussion
Electric field application effects on the electronic structure of the DTDA dimer
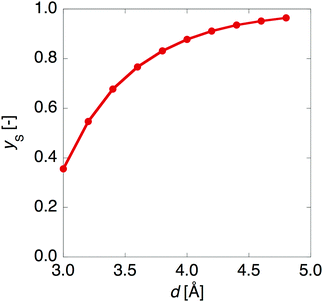
Fig. 3 shows that yS increases with increasing d, which indicates that an increase of d leads to an increase of yS. This is caused by reducing the singly-occupied MO (SOMO)–SOMO overlap, which constructs the pancake bond.27Fig. 4 shows the applied electric field amplitude dependences of the sum of natural charge transfer from the one monomer to the other monomer (from the upper to the lower monomer in the present case) for the DTDA dimers. As seen from Fig. 4, charge transfer from one molecule to the other is increased with an increase of the applied electric field amplitude F, which indicates that the applied electric field induces asymmetricity along the stacking direction of the DTDA dimer. In addition, it turns out that the larger d in the dimer, the more drastically charge transfer occurs around F = 0.016 a.u. This drastic charge transfer is predicted to be caused by the decrease of overlap between the monomers with large d. It is found that under small F the dimer with large d is insensitive to F due to small overlap, while under rather large F the dimer cannot retain electrons between the monomers due to the small overlap, causing such drastic charge transfer.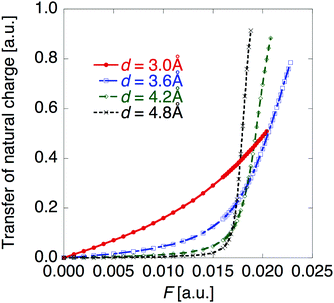 | ||
| Fig. 4 Applied electric field amplitude F dependences of charge transfer from the upper to the lower monomer in the DTDA dimer with intermolecular distance d. | ||
Electric field application effects on the nonlinear optical properties of the DTDA dimer
Fig. 5 shows the electric field amplitude dependence of β for the DTDA dimers with a wide range of d. First, for any d, the β value of the dimer exhibits a maximum positive peak and a maximum negative peak as F increases. In addition, in the 3.0 ≤ d ≤ 4.8 Å range, the larger d, the more drastically the β value varies. Because increases in d and F are shown to increase the yS and asymmetricity, respectively, the tendency of variation in β as a function of F for different d is found to well accord with that in a previous theoretical model study (see Fig. 1(a)).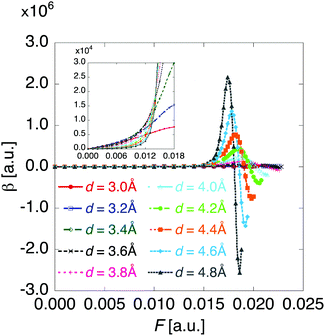 | ||
| Fig. 5 Applied electric field amplitude F dependences of first hyperpolarizability β for the DTDA dimer with intermolecular distance d ranging from 3.0 to 4.8 Å. The magnified inset is also shown. | ||
Fig. 6 shows the electric field amplitude dependence of γ for the DTDA dimers with a wide range of d. For any d, the γ value of the dimer exhibits a maximum positive peak and a maximum negative peak as F increases. The latter amplitude is found to be much larger than the former one. Similar to β, the variation in γ is shown to be intensified in the dimer with large d, i.e., large yS. These tendencies of γ variation are also found to accord with the theoretical model study (see Fig. 1(b)). Furthermore, it is found that the intensifying ratio of γ, which is defined as the ratio of the peak amplitude of γ to γ at F = 0, exhibits gigantic values. For the dimer with d = 3.4 Å, the intensifying ratio for the maximum positive peak exhibits 17.3 and that for the maximum negative peak exhibits 40.5. For the dimer with d = 4.8 Å, the intensifying ratio for the maximum positive peak reaches 9 × 104 and that for the maximum negative peak reaches 3 × 105. These results demonstrate that electric field application causes drastic variations in β and γ, which contributes to realizing highly-active NLO switches with gigantic switching ratios.
 | ||
| Fig. 6 Applied electric field amplitude F dependences of second hyperpolarizability γ for the DTDA dimer with intermolecular distance d ranging from 3.0 to 4.8 Å. | ||
The comparison in F dependences between natural charge and NLO properties reveals that drastic variations in NLO properties occur in the transition region between the diradical state and charge transfer state. This fact is in qualitative agreement with the previous theoretical result: NLO properties exhibit drastic peaks around the region where the domination of the neutral/ionic configuration inverses.12
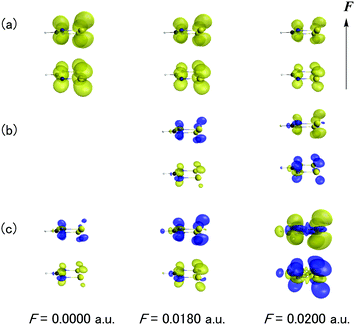
Fig. 7 shows the F dependences of odd electron density, β density and γ density for the dimer with d = 4.2 Å. As seen from Fig. 7a, the odd electron density of the dimer originates from the singly occupied MO (SOMO) of DTDA forming the pancake bond and its amplitude diminishes with an increase of F. This behavior corresponds to the occurrence of charge transfer in Fig. 4. From the definitions (eqn (5) and (6)), the signs of the contributions of the β and γ densities are positive when the direction from the positive to negative hyperpolarizability density coincides with the direction of F. As seen from Fig. 7b and c, the main contribution to β and γ originates from the pancake bond. Indeed, although both β and γ exhibit positive and negative values under F = 0.0180 a.u. and 0.0200 a.u., respectively, the β and γ density contributions of the pancake bond well reproduce those features.
Conclusions
In this study, the external static electric field application effect on the β and γ of the DTDA dimer has been investigated. The β and γ of the DTDA dimer are found to drastically vary depending on the amplitude of the applied electric field, and to exhibit gigantically enhanced maximum positive and maximum negative peak values. These drastic variations are shown to be intensified in the dimer with large d, i.e., large yS, the feature of which well accords with the results obtained in a previous theoretical two-site model study. It is also found that the switching ratio of γ can reach gigantic values, e.g., ∼102 (d = 3.4 Å)–105 (d = 4.8 Å). Hyperpolarizability density analyses have clarified that the pancake bond primarily contributes to such a gigantic enhancement of NLO properties. Thus, the present results show the applicability of the previous model results to real molecular dimer systems and demonstrate the promising potential of highly-active external-electric-field induced NLO switches based on asymmetric open-shell molecular systems. To realize such applications, further experimental and theoretical investigations are strongly desired for the synthetic development and mechanistic analysis of a wide range of one-dimensional pancake bonded open-shell singlet aggregates composed of various π-radical molecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI, Grants-in-Aid for Scientific Research on Innovative Areas “π-System Figuration” (JP17H05157) and “Photosynergetics” (JP26107004), a JSPS Research Fellowship for Young Scientists (JP15J05489), and JSPS KAKENHI Grant in Scientific Research (A) (No. JP25248007). This was also partly supported by King Khalid University through grant RCAMS/KKU/001-16 under the Research Center for Advanced Materials Science at King Khalid University, Kingdom of Saudi Arabia. Theoretical calculations were partly performed using facilities at the Research Center for Computational Science, Okazaki, Japan.References
- S. Kawata, H. B. Sun, T. Tanaka and K. Takada, Nature, 2001, 412, 697 CrossRef CAS PubMed.
- S. Kawata and Y. Kawata, Chem. Rev., 2000, 100, 1777 CrossRef CAS PubMed.
- D. Day, M. Gu and a. Smallridge, Adv. Mater., 2001, 13, 1005 CrossRef CAS.
- S. Tao, T. Miyagoe, a. Maeda, H. Matsuzaki, H. Ohtsu, M. Hasegawa, S. Takaishi, M. Yamashita and H. Okamoto, Adv. Mater., 2007, 19, 2707 CrossRef CAS.
- C. W. Dirk, L.-T. Cheng and M. G. Kuzyk, Int. J. Quantum Chem., 1992, 43, 27–36 CrossRef CAS.
- J. L. Brédas, C. Adant, P. Tackx and A. Persoons, Chem. Rev., 1994, 94, 243 CrossRef.
- R. R. Tykwinski, U. Gubler, R. E. Martin, C. Bosshard and P. Gu, J. Phys. Chem. B, 1998, 102, 4451 CrossRef CAS.
- F. Terenziani, C. Katan, E. Badaeva, S. Tretiak and M. Blanchard-Desce, Adv. Mater., 2008, 20, 4641 CrossRef CAS.
- M. Spassova, B. Champagne and B. Kirtman, Chem. Phys. Lett., 2005, 412, 217 CrossRef CAS.
- M. Nakano, R. Kishi, T. Nitta, T. Kubo, K. Nakasuji, K. Kamada, K. Ohta, B. Champagne, E. Botek and K. Yamaguchi, J. Phys. Chem. A, 2005, 109, 885 CrossRef CAS PubMed.
- M. Nakano, R. Kishi, S. Ohta, H. Takahashi, T. Kubo, K. Kamada, K. Ohta, E. Botek and B. Champagne, Phys. Rev. Lett., 2007, 99, 033001 CrossRef PubMed.
- M. Nakano and B. Champagne, J. Chem. Phys., 2013, 138, 244306 CrossRef PubMed.
- H. Matsui, M. Nakano and B. Champagne, Phys. Rev. Appl., 2016, 94, 42515 Search PubMed.
- E. F. Hayes and A. K. Q. Siu, J. Am. Chem. Soc., 1971, 93, 2090 CrossRef CAS.
- K. Yamaguchi, T. Fueno and H. Fukutome, Chem. Phys. Lett., 1973, 22, 461 CrossRef CAS.
- M. Nakano and B. Champagne, J. Phys. Chem. Lett., 2015, 6, 3236 CrossRef CAS.
- M. Nakano and B. Champagne, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 198 CrossRef CAS.
- M. Nakano, Chem. Rec., 2017, 17, 27 CrossRef CAS PubMed.
- H. S. Quah, W. Chen, M. K. Schreyer, H. Yang, M. W. Wong, W. Ji and J. J. Vittal, Nat. Commun., 2015, 6, 7954 CrossRef CAS PubMed.
- K. Kamada, K. Ohta, T. Kubo, A. Shimizu, Y. Morita, K. Nakasuji, R. Kishi, S. Ohta, S. Furukawa, H. Takahashi and M. Nakano, Angew. Chem., Int. Ed. Engl., 2007, 46, 3544–3546 CrossRef CAS PubMed.
- K. Kamada, S. Fuku-en, S. Minamide, K. Ohta, R. Kishi, M. Nakano, H. Matsuzaki, H. Okamoto, H. Higashikawa, K. Inoue, S. Kojima and Y. Yamamoto, J. Am. Chem. Soc., 2013, 135, 232 CrossRef CAS PubMed.
- M. Nakano and K. Fukuda, J. Phys. Chem. C, 2016, 120, 1193 CAS.
- M. Nakano, K. Fukuda, S. Ito, H. Matsui, T. Nagami, S. Takamuku and Y. Kitagawa, J. Phys. Chem. A, 2017, 121, 861 CrossRef CAS PubMed.
- Z. Zeng, S. Lee, M. Son, K. Fukuda, P. M. Burrezo, X. Zhu, Q. Qi, R. Li, J. T. Lo, J. Ding, J. Casado, M. Nakano, D. Kim and J. Wu, J. Am. Chem. Soc., 2015, 137, 8572 CrossRef CAS PubMed.
- R. S. Mulliken and W. B. Person, Molecular Complexes, Wiley, New York, 1969 Search PubMed.
- S. Suzuki, Y. Morita, K. Fukui, K. Sato, D. Shiomi, T. Takui and K. Nakasuji, J. Am. Chem. Soc., 2006, 128, 2530–2531 CrossRef CAS PubMed.
- H. Z. Beneberu, Y.-H. Tian and M. Kertesz, Phys. Chem. Chem. Phys., 2012, 14, 10713 RSC.
- K. Yoneda, M. Nakano, K. Fukuda, H. Matsui, S. Takamuku, Y. Hirosaki, T. Kubo, K. Kamada and B. Champagne, Chemistry, 2014, 20, 11129 CrossRef CAS PubMed.
- A. W. Cordes, C. D. Bryan, W. M. Davis, R. H. de Laat, H. S. Glarum, J. D. Goddard, R. C. Haddon, R. G. Hicks, D. K. Kennepohl, R. T. Oakley, S. R. Scotf and N. P. C. Westwoodlb, J. Am. Chem. Soc., 1993, 115, 7232 CrossRef CAS.
- R. G. Hicks, in Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, ed. R. G. Hicks, Wiley, West Sussex, 2010 Search PubMed.
- C. D. Bryan, A. W. Cordes, R. C. Haddon, R. G. Hicks, D. K. Kennepohl, C. D. Mackinnon, R. T. Oakley, J. T. T. M. Palstra, A. S. Perel, S. R. Scott, L. F. Schneemeyer and J. V. Waszczak, J. Am. Chem. Soc., 1994, 116, 1205 CrossRef CAS.
- K. Yamaguchi, in Self-Consistent Field, ed. R. Carbo and M. Klobukowsiki, Amsterdam, 1990, p. 727 Search PubMed.
- R. Kishi, S. Bonness, K. Yoneda, H. Takahashi, M. Nakano, E. Botek, B. Champagne, T. Kubo, K. Kamada, K. Ohta and T. Tsuneda, J. Chem. Phys., 2010, 132, 94107 CrossRef PubMed.
- B. Champagne, E. A. Perpète, S. J. A. Van Gisbergen, E. J. Baerends, J. G. Snijders, C. Soubra-Ghaoui, K. A. Robins and B. Kirtman, J. Chem. Phys., 1998, 109, 10489–10498 CrossRef CAS.
- H. Sekino, Y. Maeda, M. Kamiya and K. Hirao, J. Chem. Phys., 2007, 126, 14107 CrossRef PubMed.
- B. Kirtman, S. Bonness, A. Ramirez-Solis, B. Champagne, H. Matsumoto and H. Sekino, J. Chem. Phys., 2008, 128, 114108 CrossRef PubMed.
- G. Maroulis, J. Chem. Phys., 1999, 111, 583 CrossRef CAS.
- G. Maroulis, D. Xenides, U. Hohm and a. Loose, J. Chem. Phys., 2001, 115, 7957 CrossRef CAS.
- M. de Wergifosse, F. Wautelet, B. Champagne, R. Kishi, K. Fukuda, H. Matsui and M. Nakano, J. Phys. Chem. A, 2013, 117, 4709 CrossRef CAS PubMed.
- H. D. Cohen and C. Roothaan, J. Chem. Phys., 1965, 43, S34 CrossRef CAS.
- M. Head-Gordon, Chem. Phys. Lett., 2003, 372, 508 CrossRef CAS.
- M. Nakano, H. Fukui, T. Minami, K. Yoneda, Y. Shigeta, R. Kishi, B. Champagne, E. Botek, T. Kubo, K. Ohta and K. Kamada, Theor. Chem. Acc., 2011, 130, 711 CrossRef CAS.
- M. Nakano, I. Shigemoto, S. Yamada and K. Yamaguchi, J. Chem. Phys., 1995, 103, 4175 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7qm00549k |
| This journal is © the Partner Organisations 2018 |