Unlocking the action mechanisms of molecular nonlinear optical absorption for optical conjugated polymers under aggregation states†
Jin
Huang
 ab,
Dong
Zheng
ac,
Bang'an
Peng
a,
Menghao
Kong
b,
Yixiao
Hang
b,
Jing
Ma
ab,
Dong
Zheng
ac,
Bang'an
Peng
a,
Menghao
Kong
b,
Yixiao
Hang
b,
Jing
Ma
 *ac and
Xudong
Jia
*a
*ac and
Xudong
Jia
*a
aState Key Laboratory of Coordination Chemistry, Department of Polymer Science & Engineering, Nanjing University, Nanjing 210023, PR China. E-mail: jiaxd@nju.edu.cn; Fax: +86-25-89682485
bInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, Nanjing 211816, China
cKey Laboratory of Mesoscopic Chemistry of MOE, School of Chemistry & Chemical Engineering, Nanjing University, Nanjing 210023, PR China. E-mail: majing@nju.edu.cn
First published on 14th November 2018
Abstract
The intense interactions of optical conjugated polymers (OCPs) under molecular aggregation states attenuate their molecular nonlinear optical absorption (MNOA) performances. An effective route to unlock the action mechanisms of MNOA for OCPs under aggregation states by auxiliary theoretical calculations is developed in this work. Three typical molecular structures of OCPs (donor 1–donor 2 (D1–D2)-type, donor 1–acceptor (D1–A)-type and donor 1–donor 2–donor 1–acceptor (D1–D2–D1–A)-type) applied to nonlinear optical absorption materials are constructed by thienyl, carbazolyl and fluorenyl moieties. The relationships between the molecular structure and nonlinear optical absorption performance for the three types of OCPs are then predicted by theoretical calculations, and the D1-A-type and D1–D2–D1–A-type OCPs are verified to possess better MNOA performances. Furthermore, based on the experimental data, the optimum proportions of the donor unit and the acceptor unit are determined to obtain the best MNOA performance for D1–D2–D1–A-type OCPs. The MNOA for different doping mass ratios of the D1–D2–D1–A-type OCP in OCP/PMMA and OCP/PS composite films is also discussed, and the action mechanism of the aggregation state in solid composite films is revealed. These results suggest that this new strategy to prepare MNOA materials could promote further applications of OCPs in the field of nonlinear optical (NLO) devices.
Introduction
Optical conjugated polymers (OCPs) have attracted extensive attention due to their great application prospects in the fields of organic photovoltaics (OPVs),1 polymer light-emitting diodes (PLEDs),2 nonlinear optics,3 sensing,4 photodynamic therapy,5 optical data storage,6etc. Generally, two main influencing factors determine the optical performance of OCPs. One factor is the molecular microstructure under different conditions. A typical example is aggregation-induced emission (AIE), which results from the change of the molecular microstructure in OCPs. Tang's group reported AIE OCPs with blue- to red-light emission, which covered the entire visible range.7 Another typical example is poly(dialkylfluorenes), which could form a β-phase morphology derived from an intriguing “planar zigzag” chain conformation,8 and thus lead to an enhanced effective conjugation length, a larger Förster radius for excitation transfer9 and better photoelectric properties.10 In other words, the optical properties of OCPs could be improved by controlling the molecular β-phase morphology to acquire more planar molecules.11 However, very few studies have explored the relationship between the molecular nonlinear optical (NLO) absorption (MNOA) performance and the molecular β-phase morphology for poly(dialkylfluorenes). Another influencing factor on the optical performance of OCPs is the molecular aggregation state or mode under different conditions. A common aggregation mode in OCPs was π–π stacking. Strong π–π stacking and dipole–dipole interactions between the chromophores, which resulted from the rigid structure of the aromatic rings in OCPs, led to strong optical-quenching effects.12 Thus, the application of OCPs in the field of photoelectric devices has been hindered.The two main influencing factors mentioned above play crucial roles in the MNOA performance of OCPs. Therefore, understanding of the relationship between the MNOA performance and these two main influencing factors for OCPs is urgently needed to provide a guide for the preparation of high-performance polymeric NLO materials. More specifically, for alkyl-fluorene-type polymers as a common kind of NLO molecule, on the one hand, the molecular microstructures tend to be in more planar configurations upon the formation of the β-phase.13 The nearly co-planar molecular configuration under the aggregation state implies a greater delocalization range of π electrons to achieve better MNOA performance.11c,14 On the other hand, according to the theory of nonlinear anti-saturation absorption, the MNOA performance was evaluated from the excited-state absorption cross section in the π-conjugated system.15 However, strong dipole–dipole interactions between the chromophores, resulting from molecular aggregation and π–π stacking in solid films, would weaken the MNOA performance in some cases. Few literature reports have studied and expounded the relationship between the molecular microstructure and MNOA performance of OCPs in the aggregation state at the molecular level, and until now, little is known about the methods to control molecular aggregation to improve the MNOA performance.
Based on the reasons mentioned above and stemming from the former knowledge and understanding about controlling the molecular aggregation state,16 a new and effective route guided by theoretical calculations to construct NLO materials was developed by exploring the relationship between the MNOA performance and molecular microstructure or molecular aggregation state under different conditions. This understanding provided further comprehension of the action mechanism of MNOA for OCPs under different aggregation states, which could provide a guide for the molecular design of high-performance MNOA materials. To achieve such a purpose in this work, three typical molecular structures of OCPs (D1–D2-type, D1–A-type and D1–D2–D1–A-type) were first constructed by using thienyl, carbazolyl and fluorenyl groups (Scheme 1). Theoretical calculations were very useful to find the type of OCP with the best MNOA performance, which was verified by experimental results. In addition, combined with theoretical calculations, the influence of the β-phase morphology on the OCP MNOA performance under different concentrations in solution was further discussed. Derived from the theoretical calculations and experimental data, the optimal doping proportions of nitrothiophene for D1–A-type and D1–D2–D1–A-type OCPs were screened. For the OCP composite films, clarifying the relationships of the MNOA with the molecular microstructure or arrangement under the solid aggregation state was important. To this end, OCPs mixed with polymethyl methacrylate (PMMA) in different ratios were prepared to investigate the main influencing factors on the MNOA performance. Based on the determined action mechanisms under different aggregation states, MNOA composite materials with high performance were obtained. An effective route to unlock MNOA would encourage pursuit to improve the performances of D–A-type OCPs and promote their further applications in the field of NLO devices.
 | ||
| Scheme 1 (a) Structures of D1–D2-type, D1–A-type and D1–D2–D1–A-type OCPs. (b) Illustration of preparing a D1–D2–D1–A-type OCP/PMMA composite film. | ||
Results and discussion
Architecture of typical nonlinear OCPs and their MNOA performance in solution
Thienyl, carbazolyl and fluorenyl groups are often used as NLO absorption fragments in the backbone of OCPs. In this work, the fluorenyl moiety is introduced as donor 1, the carbazolyl moiety is introduced as donor 2, and the dinitro-thienyl moiety is used as an acceptor. The chemical structures of D1–D2-type, D1–A-type and D1–D2–D1–A-type OCPs are shown in Scheme 1b. The synthetic routes toward the OCPs are outlined in Fig. S1 (ESI†). Efficient palladium-catalyzed Suzuki cross-coupling polymerizations occurred between the dibromo monomers and double dioxaborinan monomer. The D1–D2-type OCP (P0) and D1–A-type OCP (P1) were first synthesized with M1 and M2 or with M1 and M3 in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The D1–D2–D1–A-type OCPs with different doping ratios of nitrothiophene (P0.05, P0.1, P0.2, P0.3, P0.4) were then synthesized by adjusting the different proportions of donors and acceptors (see the ESI†). The yields were between 52% and 82% after removing small molecules via Soxhlet extraction (Table 1). Because of the different reactivities of the dibromo monomers (M2 and M3), the actual feed ratios of the fluorenyl-carbazolyl unit (FC unit) and fluorenyl-dinitrothienyl unit (FD unit) in the D1–A–D1–D2-type OCPs were different, which were analyzed via1H NMR spectra of the OCPs (see Table S1 and Fig. S2–S10, ESI†). The molecular weights of the polymers were estimated using gel permeation chromatography (GPC) measured in tetrahydrofuran (THF) relative to polystyrene (PS) standards, as summarized in Table 1. The thermal properties of the polymers were evaluated using thermal gravimetric analysis (TGA) under a N2 atmosphere. The 5% weight loss temperatures (Td) of the polymers occurred between 307 °C and 343 °C (Table 1, Fig. S11, ESI†). The glass transition temperature (Tg) of the OCPs would increase with the increase of nitro-thiophene content (Fig. S12†). Tg of (D1–D2)-type (P0) was 251 °C, and Tg of P0.1 was 267 °C while P0.4 and D1–A-type OCP (P1) did not show obvious glass phase transition from 50 °C to 300 °C in DSC curves. These results indicated that the OCPs have excellent thermal stability.
1. The D1–D2–D1–A-type OCPs with different doping ratios of nitrothiophene (P0.05, P0.1, P0.2, P0.3, P0.4) were then synthesized by adjusting the different proportions of donors and acceptors (see the ESI†). The yields were between 52% and 82% after removing small molecules via Soxhlet extraction (Table 1). Because of the different reactivities of the dibromo monomers (M2 and M3), the actual feed ratios of the fluorenyl-carbazolyl unit (FC unit) and fluorenyl-dinitrothienyl unit (FD unit) in the D1–A–D1–D2-type OCPs were different, which were analyzed via1H NMR spectra of the OCPs (see Table S1 and Fig. S2–S10, ESI†). The molecular weights of the polymers were estimated using gel permeation chromatography (GPC) measured in tetrahydrofuran (THF) relative to polystyrene (PS) standards, as summarized in Table 1. The thermal properties of the polymers were evaluated using thermal gravimetric analysis (TGA) under a N2 atmosphere. The 5% weight loss temperatures (Td) of the polymers occurred between 307 °C and 343 °C (Table 1, Fig. S11, ESI†). The glass transition temperature (Tg) of the OCPs would increase with the increase of nitro-thiophene content (Fig. S12†). Tg of (D1–D2)-type (P0) was 251 °C, and Tg of P0.1 was 267 °C while P0.4 and D1–A-type OCP (P1) did not show obvious glass phase transition from 50 °C to 300 °C in DSC curves. These results indicated that the OCPs have excellent thermal stability.
| Polymer | Yield (%) | M n (kDa) | M w (kDa) | PDI | T d (°C) | T g (°C) |
|---|---|---|---|---|---|---|
| P0 (D1–D2 type) | 82 | 18.3 | 38.1 | 2.08 | 343 | 251 |
| P0.05 | 77 | 13.3 | 32.8 | 2.47 | 338 | — |
| P0.1 | 81 | 11.2 | 28.6 | 2.56 | 335 | 267 |
| P0.2 | 68 | 10.2 | 27.1 | 2.65 | 331 | — |
| P0.3 | 73 | 9.06 | 25.9 | 2.86 | 330 | — |
| P0.4 | 66 | 8.37 | 25.2 | 3.01 | 326 | — |
| P1 | ||||||
| (D1–A type) | 52 | 4.77 | 17.6 | 3.69 | 307 | — |
Additionally, there were also some empirical or qualitative rules to improve the efficiency of the NLO properties at the microscopic molecular level. The molecular polarizability was defined in eqn (1) by a Taylor series expansion of the total dipole moment in the small perturbing field E and effective field F that induces charge separation and geometry relaxation.
 | (1) |
At a given value of F, the static polarizabilities were obtained from the formula shown in eqn (2), where the n-th expansion parameter of the induced dipole moment, μ(F), was related to the derivative, with respect to E, of the dipole moment or the (n − 1)-th order polarizability.17
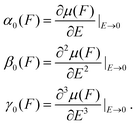 | (2) |
The ground-state dipole moment (μg), the polarizability (α0) and the first hyperpolarizability (β0) were calculated using density functional theory (DFT) with the B3LYP functional and the 6-31+G(d) basis set, based on the finite field approach. The polarizabilities (α0, β0, and γ0) and transition dipole moment between the ground and excited states of organic chromophores have been shown to be closely correlated with relevant chemically parameters, such as bond length alternation (BLA, δ), which was widely used to characterize the extent of π-electron delocalization. As shown in Fig. 1, the BLA values, defined in Fig. S13,† of the studied building units M1, M2, and M3 and oligomeric combinations M1 + M2, M1 + M3, and 2 M1 + M2 + M3 are close to zero (δ = 0.03–0.05), indicating the strong π-conjugation and thus high polarizability of the π-electron distributions even in the ground states. Furthermore, the efficiencies of the chromophores for NLO applications were evaluated by the product of β0 and the chromophore ground-state dipole moment, μg, i.e., the chromophore figure of merit (μg × β0).18 The thiophene (M2)-containing oligomers, M1 + M2 (D1–A-type) and 2 M1 + M2 + M3 (D1–D2–D1–A-type), stand out from the series for their much larger ground-state dipole moments and μg × β0 values.
Notably, the calculated μg × β0 values of the D1–A-type OCPs were slightly higher than those of the D1–D2–D1–A-type OCPs. In addition, the calculated nonlinear properties for the D1–D2–D1–A1-type and D1–A-type OCPs could be correlated with experiments considering the electronic structures of the various architecture combinations (Fig. 1 and Table S2†). DFT calculations were a preliminary step to screen promising material building units to explore novel NLO materials, and further research must provide insight into the experimental fabrication of D–A-type OCPs considering the possibility of forming the β-phase conformation under aggregation states in concentrated solution. According to our previous work,19 the β-phase conformation, which was a nearly planar conformation, was determined by the small torsion angle, D < 15°, between two adjacent units. The following study will demonstrate that the enhanced planarity of the chromophores (with a small inter-ring torsion angle D) in the conjugate main chain of the OCPs correlates well with satisfactory MNOA performance.
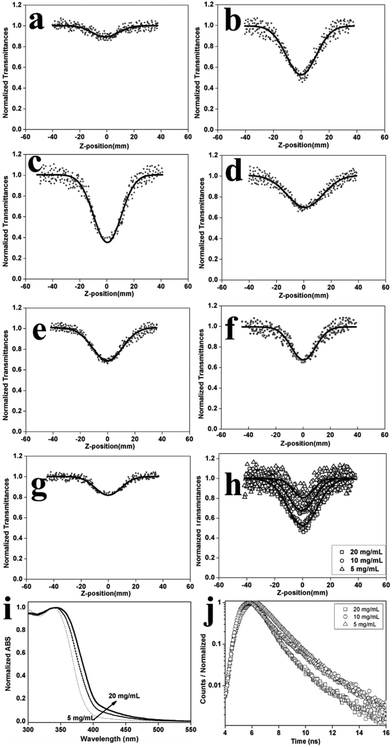
The relative MNOA performances of the D1–D2-type, D1–A-type and D1–D2–D1–A-type OCPs were predicted according to the theoretical calculations of the dipole moment or the first hyperpolarizability in the molecular chain segments. The MNOA performances of the two kinds of D–A type OCPs were superior to those of the D1–D2-type OCPs. To verify the results, the third-order nonlinear absorption coefficients (β) of the three types of OCPs were acquired from open-aperture Z-scan curves (Fig. 2a–g) (see the Experimental section), as shown in Table S2.† The trend of the β values for the three types of OCPs was β(PD1–D2–D1–A) > β(PD1–A) > β(PD1–D2) (PD1–D2–D1–A represents P0.05, P0.1, P0.2, P0.3 and P0.4; PD1–A represents P1; PD1–D2 represents P0), which was consistent with that of theoretical calculations. These results revealed that the introduction of the nitrothiophene moiety into poly(fluorene-co-carbazole) to construct a push–pull electron effect in the main chain was an effective way to improve the MNOA performance.
To acquire preferable MNOA performance in the conjugated polymers, balancing the ratio of the electron donating group and the electron drawing group was necessary to adjust the molecular polarization of the OCPs, as suggested by previous reports.20 In this work, for the D1–D2–D1–A-type OCPs, the MNOA performance was adjusted by controlling the nitrothiophene unit proportion in the molecular skeleton. As a result, P0.1 was found to have the highest β value among all the D1–D2–D1–A-type OCPs (Fig. 2a–g, Table S2†).
Under ideal conditions, the concentration of an OCP in solution has little effect on the MNOA performance.21 However, for some very polar systems, aggregation in concentrated solutions may affect the MNOA performance, leading to a contrary result. In this work, third-order nonlinear absorption coefficients of P0.1 under three different concentrations (5 mg mL−1, 10 mg mL−1 and 20 mg mL−1) were calculated from their respective open-aperture Z-scan curves (Fig. 2h). The results indicated that β(P0.1, 20 mg mL−1) = 5.96 × 10−10 m W−1 > β(P0.1, 10 mg mL−1) = 3.18 × 10−10 m W−1 > β(P0.1, 5 mg mL−1) = 2.85 × 10−10 m W−1. With an increase in the concentration of P0.1 in THF solution, the β values also increased, among which the value of 20 mg mL−1 P0.1 in THF solution was the highest. For the three different concentrations, the absorption enhanced in the range of 400 nm–450 nm in the UV-vis spectra (Fig. 2i) indicating that the β-phase content increased with the increase of the concentration of P0.1.22
To rationalize the above experimental results, the typical molecular conformations of P0.1 were studied via simulated calculations (Fig. 3a and S14†). The abovementioned small torsion angle (D) was a direct indicator of the β-phase conformation (Fig. 3b). Such a direct indicator was closely related to the co-planarity of the chromophores in the main chain and directly affected the nonlinear absorption properties of the OCPs. Usually, the statistics of 0° < D < 15°, 15° < D < 30° and 30° < D < 45° were classified into the β-phase, g-phase, and α-phase conformations, respectively.19,23 The β-phase conformation was taken as a nearly planar conformation, and the g-phase conformation was nearly a planar conformation,19 whose percentages (β-and g-phase conformation percentages) for 10 mg mL−1 and 20 mg mL−1 P0.1 in THF solution could be obtained from statistical analysis of the molecular dynamics (MD) simulations. The content of the β-phase conformation increased from 5% at 10 mg mL−1 to 8% at 20 mg mL−1, and the content of the g-phase conformation increased from 27% at 10 mg mL−1 to 30% at 20 mg mL−1. These results could explain the better nonlinear absorption properties under higher concentrations for the OCPs.
In conjugated π-electron systems of OCP molecules, the effective conjugate lengths (ECLs) have a great effect on the MNOA performance.24 The planarity between the chromophores is reflected not only by the torsion angle value D but also by the ECL proportions. According to the simulation strategy used in our previous studies on packing structures of oligo thiophenes and oligo fluorenols,19,25 the ECLs of P0.1 under the two concentrations in THF solution (10 mg mL−1 and 20 mg mL−1) were calculated. The ECL was closely related to the MNOA properties, where a longer effective conjugate length corresponded to a higher third-order nonlinear absorption coefficient.17,18,26 The numerical distribution of ECLs under the two concentrations ranged from 2 to 10 (Fig. 3c) according to MD simulations. From a statistical average perspective, the average ECL under 10 mg mL−1 was δL(10 mg mL−1) = 4.97, and the average value under 20 mg mL−1 was δL(20 mg mL−1) = 5.06 (for details of the calculation procedure, see the ESI†), which were consistent with the experimental conclusions. From the analysis of the main content, the main distributions of the ECLs were 3, 4, 5, and 6 for the molecular chain of P0.1, and their respective percentages were above 10%. In the 20 mg mL−1 THF solution, the percentages of the ECLs of 4 or 5 were obviously higher than those in the 10 mg mL−1 THF solution. However, the percentage of the ECL of 3 in the 20 mg mL−1 THF solution was obviously decreased compared to that in the 10 mg mL−1 THF solution. The larger concentration also favors the appearance of the β-phase conformation, as the population of the planar structure (with an ECL larger than 6) slightly increased from 10 mg ml−1 to 20 mg ml−1.
The photoluminescent properties of P0.1 under different concentrations (0.3 mg mL−1, 5 mg mL−1, 10 mg mL−1, and 20 mg mL−1) were measured (Fig. S15†). In the dilute solution of 0.3 mg mL−1, the maximum emission peak of P0.1 was about 420 nm. While in the 10 mg mL−1 and 20 mg mL−1 THF solution, the emission peaks at approximately 450 nm corresponding to the β-phase morphology were stronger than that in the 0.3 mg mL−1 THF solution. Meanwhile, the time-resolved fluorescence decay curves had not obviously changed at 420 nm and 450 nm (Fig. S16†). In dilute solution, the fluorescence decay curve showed a single exponential mode and the fluorescence lifetime was 1.27 ns (Table S4†). According to the fitting and calculation of time-resolved fluorescence decay curves at 450 nm (belonged to β-phase peak) in the THF solution of P0.1 (5 mg mL−1–20 mg mL−1, Fig. 2j), a bi-exponential fluorescence decay with two decay components of (τ1) 1.67 ns–1.96 ns and (τ2) 3.38 ns–4.72 ns (Table S4†) is shown. It indicated that there were dual emission sources existing in these systems belonging to the main chains of polymeric molecules and their aggregates.27 And the state of aggregation was closely related to a more planar conformation when the molecular chain of the OCPs formed the β-phase.22a The average fluorescence lifetime (τ) had reduced and the fluorescence quantum yield (QY) had increased with the increase of concentration (Table S4†). These phenomena were also explained by the increasing β-phase content in high concentration solutions. The fluorescence properties were also related to the β-phase morphology content of P0.1 in solution.
According to the PL results, MNOA measurements and theoretical calculations, we deduced that the increased β-phase content would considerably enhance the MNOA performance for OCPs. From a molecular microstructure perspective, when the system contains a higher β-phase content of OCP molecules, the dihedral angle of the molecular plane would decrease, and the molecules would become more planar, leading to longer ECLs. This conclusion could also be validated from the experimental results of the opposite angle, indicating that there was decreased β-phase morphology content and feeble nonlinear absorption for P0.1 in dilute THF solution (0.3 mg mL−1) (Fig. S17†). Meanwhile, by comparison of the nonlinear absorption performances of the three kinds of pure solid films (P0, P1 and P0.1), we could find that the nonlinear absorption property of the OCPs was worse than that in the solution state (Fig. S18a†). In particular, there was almost no nonlinear absorption in the solid film of P1. This might be related to the greater nitro-thiophene content in the main chain, which would lead to stronger π–π stacking interactions. It could also be seen that an increase of the nitro-thiophene unit would lead to a redshift of absorption spectra of the OCP solid films (Fig. S18b†).
Action mechanism of the aggregation state in solid OCP composite films
Studying the action mechanism of the aggregation state would provide an understanding of the relationship between the MNOA performance of an OCP and the molecular microstructure or arrangement under the solid aggregation state. The abundant β-phase morphology and strong π–π stacking in pure solid OCP films pose great challenges, difficulties and intricate problems to research. In addition, the strong aggregation effect in pure solid OCP films would lead to MNOA performance (Fig. S18a†), and the fluorescence emission property was significantly decreased (Table S5†). In the photoluminescence (PL) spectrum of pure polymeric films (taking a P0.1 film as an example), the broad emission peaks at about 480 nm and 520 nm belonged to strong π–π stacking generated by the rigid conjugate group in the polymer main chain (Fig. S19†). Fixing chromophores in composite films to force them under specific aggregation states is an effective method to study the interaction mechanisms of chromophores, which could also help overcome the problem of the severe aggregation effect of chromophores. The interaction or π–π stacking effect of chromophores in composite films is weaker than that in pure solid OCP films. Therefore, the investigation of the action mechanism of the aggregation state in composite films is relatively simple. Thus, different doping ratios of P0.1/PMMA and P0.1/PS in composite films were prepared, and the nonlinear absorption properties were acquired via their open-aperture Z-scan curves (Fig. 4a, b, S20 and S21†). Table 2 shows the nonlinear absorption coefficients β for the two kinds of OCP composite films at different doping ratios. At relatively low doping mass fractions, the β values of OCP composite films rapidly increased with an increase of the doping mass fraction, from 4.26 × 10−10 m W−1 at a mass fraction of 0.01% to 12.25 × 10−10 m W−1 at a mass fraction of 0.08% in the OCP/PMMA films and from 4.79 × 10−10 m W−1 at a mass fraction of 0.01% to 12.95 × 10−10 m W−1 at a mass fraction of 0.08% in the OCP/PS films. With a further increase in the doping mass fraction from 0.08% to 0.3%, the β value of the OCP composite film changed only slightly.| PMMA as the matrix P0.1 mass fraction (%) | Nonlinear absorption coefficient (10−10 m W−1) | PS as the matrix P0.1 mass fraction (%) | Nonlinear absorption coefficient (10−10 m W−1) |
|---|---|---|---|
| 0 | 0.21 | 0 | 0.87 |
| 0.01 | 4.26 | 0.01 | 4.79 |
| 0.03 | 7.57 | 0.03 | 8.02 |
| 0.05 | 9.63 | 0.05 | 10.66 |
| 0.08 | 12.25 | 0.08 | 12.95 |
| 0.1 | 12.46 | 0.1 | 13.12 |
| 0.3 | 12.67 | 0.3 | 13.81 |
To explain the above results, PL and UV-vis spectra of the OCP/PMMA and OCP/PS composite films were measured. In the UV-vis spectra without doping (Fig. S22†), the maximum absorption peak at 348 nm was attributed to PMMA. Under a 0.01% doping mass fraction, no obvious changes to the maximum absorption peak were observed (Fig. 4c) due to the small amount of P0.1 in these composite films. In addition, upon increasing the doping mass fraction of the OCP in the PMMA films from 0.05% to 0.1%, the maximum absorption peak redshifted from 369 nm to 401 nm (the emission peak corresponding to the FC unit of P0.1),16b,c which could be attributed to an increase in the β-phase morphology content in the composite films, leading to an increase in conjugation length.28 The maximum absorption peaks of the OCP/PMMA composite films in the UV-vis spectra did not display obvious continuous redshifts at a 0.3% doping mass fraction, suggesting that the conjugation did not further increase in the system, which is consistent with the above conclusion. Therefore, strong dipole–dipole and π–π stacking interactions played dominant roles in these films and greatly impacted the MNOA performances of the OCP composite films.
In the PL spectra at 0.01 wt% of OCP in the PMMA films (Fig. 4d), the maximum emission peak at 426 nm corresponded to the α-phase morphology of the FC unit.29 The shoulder emission peak at about 450 nm was ascribed to β-phase morphology, and the weak broad emission peak longer than 480 nm corresponded to the exciplex in the composite film.10a,22,30 Upon increasing the mass fraction of the OCP to 0.05% in the PMMA films, the β-phase morphology peak at about 450 nm and the exciplex peak between 480 nm and 510 nm greatly increased, which indicated that their contents greatly increased. The strong peak at about 450 nm suggested that the β-phase morphology content played a leading role in the OCP composite films. By comparison with the 0.01% doping mass fraction, the absolute fluorescence quantum yields (QY) had remarkably increased (Table S6†). Upon further increasing the doping mass fraction to 0.1% and 0.3%, a major emission peak appeared at 502 nm, which revealed that the exciplex played a primary role in the P0.1/PMMA composite films. In this situation, more planar conformations via β-phase transition could make the rigidity of polymeric molecular chains significantly enhanced. As a result, strong dipole–dipole and π–π stacking interactions took place to produce a large amount of exciplex, which could generate fluorescence quenching, and the QY value had declined from 0.05% to 0.3% (Table S6†).
Time-resolved fluorescence decay curves showed a bi-exponential mode (Fig. 4e). The bi-exponential fluorescence decay of P0.1/PMMA composite films was also closely related to a more planar conformation when the molecular chains of OCPs formed the β-phase.29 By a comparison with a low (0.01%) and a high doping (0.05%) mass fraction (Table S6†), the average fluorescence lifetime (τ) was significantly reduced and QY increased with an increase of the doping mass fraction. Such results were similar to those in OCP solution, due to the increase of β-phase content in the composite films. The MNOA performances of P0.1/PMMA composite films would become better with the increase of doping mass fraction. With the relatively higher doping mass fraction (0.3%), the QY would decline, which resulted from the strong dipole–dipole and π–π stacking interaction to generate a large amount of exciplex. The MNOA performances of P0.1/PMMA composite films could not become significantly better in this situation.
Base on the above research results, time-resolved emission spectroscopy (TRES) was used to study the aggregation states of three typical doping mass fractions in P0.1/PMMA composite films (Fig. 4f–h), in order to further explain the change of aggregation state in the composite film. TRES were measured by time correlated single photon counting mode using EI-FLS980. TRES of three typical doping concentrations were selected on the basis of the above research results. When the fluorescence emissive intensity of P0.1/PMMA films reached a maximum, the window time (Δt) was 5.42 ns for 0.01%, 5.74 ns for 0.05% and 5.42 ns for 0.3% doping mass fractions, respectively. The β-phase peak played a dominant role from 0.01% to 0.05% doping mass fractions. The exciplex peak played a primary role in the 0.3% doping mass fraction at 5.42 ns. Meanwhile, single emission peaks longer than 480 nm, which were attributed to the exciplex formation, could be clearly seen at 13.39 ns for 0.01%, 13.35 ns for 0.05% and 13.03 ns for 0.3% doping mass fractions, respectively. This result revealed that the exciplex could exist even with a low doping mass fraction of P0.1/PMMA composite films.
Briefly, for relatively low doping mass fractions, the MNOA performances of OCP composite films would be greatly enhanced by increasing the doping mass fraction, as the β-phase morphology content rapidly increased, leading to an increased effective conjugation length. In other words, the β-phase morphology content had a marked impact on the MNOA performances of OCP composite films. When the doping mass fraction reached higher values (0.08%–0.3%), the MNOA performance was no longer significantly increased. The interaction between the chromophore groups in this system was dominated by strong dipole–dipole and π–π stacking interactions. The effective conjugate lengths were not further increased in this situation. Similarly, the change of the MNOA performance and fluorescence properties in these OCP/PS composite films (Fig. S23†) could also be explained by the above action mechanism, which could be applied in other composite systems of OCPs under aggregation states.
Experimental
General procedure for the synthesis of D1–D2-type, D1–A-type and D1–D2–D1–A-type OCPs
M1 (112 mg, 0.20 mmol), tetrakis(triphenylphosphine) palladium(0) (24 mg, 5 mol%), different proportions of M2 and M3 monomers (M2 + M3 = 0.20 mmol, see Table S1†), toluene (6 mL), 4 mL of K2CO3 (2 mol L−1) and tetrabutylammonium bromide (2 mg) were added into a Schlenk flask in a nitrogen-filled glovebox. After stirring at 85–100 °C for 48–72 h, bromobenzene (1 mg soluble in 2 mL methanol) as a reaction terminating/end-capping reagent was added into the mixture, and the reaction was continued for 1 h. The mixture was filtered and then was precipitated into methanol. The solid was filtered and washed in a Soxhlet extractor with methanol followed by acetone to remove residual catalyst and low-molecular-weight material.MD simulations
The polymer consistent force field (PCFF)31 was employed in simulations of the conformational changes using the explicit solvent model in solutions of P0.1 with different concentrations (10 and 20 mg mL−1 in THF). The MD simulations were carried out in the canonical (NVT) ensemble at 298 K using an Andersen thermostat.32 The cutoff of van der Waals interactions was set to 15.5 Å. Electrostatic interactions were evaluated by the Ewald summation. Motion equations were integrated using the velocity Verlet algorithm with a time step of 1 fs. The 1 ns simulation was subsequently carried out after the equilibrium state was reached at 298 K. All the MD simulations were performed with the discover module in the Materials Studio package.33P0.1 and THF were introduced into the PBC model. Detailed information on the numbers of the solute and solvent molecules, the density, and the cell parameters is tabulated in Table S3.† The force field formulation, PCFF parameters for the water model, and the validation of PCFF in describing the intermolecular interactions between o-cresol and water have previously been presented in our recent work.34 From the MD trajectories, a series of snapshots of the oligomer were selected to calculate the NLO properties of the P0.1 building block.
DFT calculations
All ab initio calculations of the electronic structures of the building block under vacuum were carried out using the Gaussian 09 program.35 The geometry optimizations of the gaseous structures were performed at the B3LYP level of DFT with the 6-31+G(d,) basis set. At the same theoretical level, frequency calculations were also performed to identify all the stationary points as minima. To investigate the NLO properties of P0.1, the ground-state dipole moment (μg), the polarizability (α0) and the mean first hyperpolarizability (β0) were calculated using the B3LYP method with the 6-31+G(d) basis set based on the finite field approach. The μg, α0 and β0 values were calculated using eqn (3).36 | (3) |
Molecular structure characterization
IR spectra were obtained using a Bruker VECTOR 22 Fourier transform infrared (FT-IR) spectrometer. The 1H NMR and 13C NMR spectra were recorded in trichloromethane-d using tetramethylsilane as an internal standard on a Bruker 500 instrument (500 MHz). Elemental Analysis data were obtained using a CHN-O-Rapid elemental analyzer (Foss Heraeus, Germany).Molecular weights of polymers were measured on a GPC apparatus equipped with a Wyatt Optilab rEX refractive index detector and a Waters 1515 HPLC pump. THF was used as a carrier solvent at a flow rate of 1.0 mL min−1 at 25 °C. A calibration curve was prepared to determine the Mn and Mw/Mn values with PS standards (Mw = 900–1.74 × 106 g mol−1, D < 1.1). Simultaneously, a TG-DTA Netzsch STA 449F3 instrument was used to investigate the thermal stability of the polymers under a nitrogen atmosphere from ambient temperature to 700 °C at a heating rate of 10 C min−1. The DSC experiment was conducted using a PerkinElmer Pyris 1 DSC. Samples (≈ 3 mg) were heated from 50 °C to 300 °C at a heating rate of 10 °C min −1 under a nitrogen flow of 50 mL min−1.
Steady-state fluorescence spectra of OCPs were measured by using an EI-FLS980 instrument. Absolute fluorescence quantum yields in solid polymer films, composite films and solutions were determined using an integrating sphere on an Edinburgh Instruments FLS980 instrument. Time-resolved fluorescence decay curves, time-resolved emission spectra and fluorescence lifetime were measured by time correlated single photon counting mode (TCSPC) using an Edinburgh Instruments FLS980 instrument, the excitation light source was a 375 nm picosecond laser, and the frequency was 20 MHz. UV-vis spectra in solution, composite films and pure solid polymer films were measured by using a PerkinElmer Lambda750 instrument.
Preparation of nonlinear absorption OCP/PMMA or OCPs/PS composite films
1.10 g PMMA or PS and chloroform (5 mL) were added to a single-necked bottle with a magnetic stir bar at room temperature. The mixture was used as the matrix solution. Chloroform solutions of P0.1 (5 mg ml−1) were prepared, and different volumes of the P0.1 chloroform solution, according to the different mass fractions of P0.1 in the composite films, were added to the former matrix solution with magnetic stirring. The mixture was then added to a Teflon plate. The solvent was evaporated over 24 h at room temperature and then was placed in an oven at 60 °C for 2 days. Finally, the residual solvent was evaporated under vacuum at 30 °C for 10 h.Z-Scan measurements
The linear absorption spectra of P0.1 in THF solution and P0.1/PMMA composite films showed that there was nearly no linear absorption at 532 nm (see the Results and discussion section, Fig. 2i and 4c). The results indicated low intensity loss and little temperature change via photon absorption during the nonlinear optical measurements using a nanosecond laser. Open-aperture Z-scan measurements used an Nd-YAG laser with a pulse duration of 4 ns at 532 nm. The laser pulses with near-Gaussian spatial and temporal profiles were focused on the sample cell using a lens with a focal length of 30 cm. In theory, the normalized transmittance for the open aperture is defined using the following equations:37 | (4) |
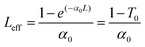 | (5) |
Conclusions
In summary, three typical D1–D2-type, D1–A-type and D1–A–D1–D2-type OCPs were successfully synthesized. From a combination of theoretical and experimental studies, the action mechanisms for OCPs under different molecular aggregation states were explored. The D1–A–D1–D2-type OCPs were shown to have the best MNOA performance among the three kinds of OCPs, and the optimal proportion (approximately 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of the donor unit and the acceptor unit in the main chain of the OCPs was found. In the solution state, the β-phase morphology content determined the MNOA properties. High β-phase morphology content enhanced the MNOA performances of the OCPs. It had better molecular planarity for the OCPs in that situation, which led to longer ECLs. In the composite films, in a certain doping mass fraction range (<0.08% doping mass fraction), the MNOA performance of the OCP composite films was greatly enhanced with an increase of doping mass fraction because the β-phase morphology content rapidly increased. In the relatively high doping mass fraction range (from 0.08% to 0.3%), the interactions between the chromophore groups in the composite films, which were dominated by strong dipole–dipole and π–π stacking interactions, and the MNOA performance was no longer considerably enhanced with a further increase in the doping mass fraction. Based on the analysis of the action mechanism, these results could be attributed to control over the molecular microstructures and adjustment of the interactions between the chromophores under different aggregation states, leading to higher-performance NLO materials. In addition, the nonlinear absorption coefficient was enhanced from 2.85 × 10−10 m W−1 in solution (5 mg mL−1 THF solution) to 13.81 × 10−10 m W−1 in the OCP/PS composite film (0.3% doping mass fraction). An effective route to unravel the action mechanism of MNOA for OCPs would encourage pursuit to improve the performances of D–A-type OCPs and promote their further applications in the field of NLO devices.
1) of the donor unit and the acceptor unit in the main chain of the OCPs was found. In the solution state, the β-phase morphology content determined the MNOA properties. High β-phase morphology content enhanced the MNOA performances of the OCPs. It had better molecular planarity for the OCPs in that situation, which led to longer ECLs. In the composite films, in a certain doping mass fraction range (<0.08% doping mass fraction), the MNOA performance of the OCP composite films was greatly enhanced with an increase of doping mass fraction because the β-phase morphology content rapidly increased. In the relatively high doping mass fraction range (from 0.08% to 0.3%), the interactions between the chromophore groups in the composite films, which were dominated by strong dipole–dipole and π–π stacking interactions, and the MNOA performance was no longer considerably enhanced with a further increase in the doping mass fraction. Based on the analysis of the action mechanism, these results could be attributed to control over the molecular microstructures and adjustment of the interactions between the chromophores under different aggregation states, leading to higher-performance NLO materials. In addition, the nonlinear absorption coefficient was enhanced from 2.85 × 10−10 m W−1 in solution (5 mg mL−1 THF solution) to 13.81 × 10−10 m W−1 in the OCP/PS composite film (0.3% doping mass fraction). An effective route to unravel the action mechanism of MNOA for OCPs would encourage pursuit to improve the performances of D–A-type OCPs and promote their further applications in the field of NLO devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from Nanjing Tech University and a SICAM Fellowship from Jiangsu National Synergetic Innovation Center for Advanced Materials. This work was supported by the National Natural Science Foundation of China (Grant No. 21673111).Notes and references
- (a) Y. Kim, S. Cook, S. M. Tuldhar, S. A. Choulis, J. J. Nelson, R. Durrant, D. D. C. Bradley, M. Giles, I. McCulloch, C.-S. Ha and M. Ree, Nat. Mater., 2006, 5, 197–203 CrossRef CAS; (b) R. F. Chen, C. H. Zheng, C. Li, H. H. Li, Z. X. Wang, Y. T. Tang, H. J. Jiang, Z. N. Tan and W. Huang, Polym. Chem., 2016, 7, 780–784 RSC; (c) T. Kim, J. H. Kim, T. E. Kang, C. Lee, H. Kang, M. Shin, C. Wang, B. Ma, U. Jeong, T.-S. Kim and B. J. Kim, Nat. Commun., 2015, 6, 8547 CrossRef CAS PubMed; (d) S. H. Chen, Y. J. Li and Y. L. Li, Polym. Chem., 2013, 4, 5162–5180 RSC; (e) T. Earmme, Y.-J. Hwang, N. M. Murari, S. Subramaniyan and S. A. Jenekhe, J. Am. Chem. Soc., 2013, 135, 14960–14963 CrossRef CAS.
- (a) H. Zheng, Y. Zheng, N. Liu, N. Ai, Q. Wang, S. Wu, J. Zhou, D. Hu, S. Yu, S. Han, W. Xu, C. Luo, Y. Meng, Z. Jiang, Y. Chen, D. Li, F. Huang, J. Wang, J. B. Peng and Y. Cao, Nat. Commun., 2013, 4, 1971 CrossRef; (b) C. Liu, Y. H. Li, Y. F. Li, C. Yang, H. Wu, J. Qin and Y. Cao, Chem. Mater., 2013, 25, 3320–3327 CrossRef CAS; (c) S. Y. Lee, T. Yasuda, H. Komiyama, J. Lee and C. Adachi, Adv. Mater., 2016, 28, 4019–4024 CrossRef CAS; (d) C.-Y. Chen, W.-K. Lee, Y.-J. Chen, C.-Y. Lu, H. Y. Lin and C.-C. Wu, Adv. Mater., 2015, 27, 4883–4888 CrossRef CAS.
- (a) A. Camposeo, P. D. Carro, L. Persano and D. Pisignano, Adv. Mater., 2012, 24, OP221–OP225 CrossRef CAS; (b) J. Schmitt, V. Heitz, A. Sour, F. Bolze, H. Ftouni, J.-F. Nicoud, L. Flamigni and B. Ventura, Angew. Chem., Int. Ed., 2015, 54, 171–175 CrossRef; (c) B. Guzelturk, A. L. Kanibolotsky, C. Orofino-Pena, N. Laurand, M. D. Dawson, P. J. Skabara and H. V. Demir, J. Mater. Chem. C, 2015, 44, 12018–12025 RSC.
- (a) W. Wu, R. Tang, Q. Lia and Z. Li, Chem. Soc. Rev., 2015, 44, 3997–4022 RSC; (b) H. Shi, H. Sun, H. Yang, S. Liu, G. Jenkins, W. Feng, F. Li, Q. Zhao, B. Liu and W. Huang, Adv. Funct. Mater., 2013, 23, 3268–3276 CrossRef CAS.
- (a) P. Liu, C. X. Yue, Z. H. Sheng, G. H. Gao, M. X. Li, H. Q. Yi, C. F. Zheng, B. Wang and L. T. Cai, Polym. Chem., 2014, 5, 874–881 RSC; (b) J. Kim, E. Lee, Y. Hong, B. Kim, M. Ku, D. Heo, J. Choi, J. Na, J. You, S. Haam, Y.-M. Huh, J.-S. Suh, E. Kim and J. Yang, Adv. Funct. Mater., 2015, 25, 2260–2269 CrossRef CAS.
- I. F. A. Mariz, F. Siopa, C. A. B. Rodrigues, C. A. M. Afonso, X. Chen, J. M. G. Martinho and E. M. S. Maçôas, J. Mater. Chem. C, 2015, 3, 10775–10782 RSC.
- (a) J. Mei, N. L. C. Leung, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Chem. Rev., 2015, 115, 11718–11940 CrossRef CAS; (b) L. L. Wang, Z. Sun, M. M. Ye, Y. Shao, L. Fang and X. W. Liu, Polym. Chem., 2016, 7, 3669–3673 RSC; (c) W. Z. Yuan, Y. Gong, S. Chen, X. Y. Shen, J. W. Y. Lam, P. Lu, Y. Lu, Z. Wang, R. Hu, N. Xie, H. S. Kwok, Y. Zhang, J. Z. Sun and B. Z. Tang, Chem. Mater., 2012, 24, 1518–1528 CrossRef CAS; (d) C. K. W. Jim, A. Qin, J. W. Y. Lam, F. Mahtab, Y. Yu and B. Z. Tang, Adv. Funct. Mater., 2010, 20, 1319–1328 CrossRef CAS; (e) Y. Liu, J. Roose, J. W. Y. Lam and B. Z. Tang, Macromolecules, 2015, 48, 8098–8107 CrossRef CAS.
- (a) M. Grell, D. D. C. Bradley, X. Long, T. Chamberlain, M. Inbasekaran, E. P. Woo and M. Soliman, Acta Polym., 1998, 49, 439–444 CrossRef CAS; (b) W. Chunwaschirasiri, B. Tanto, D. L. Huber and M. J. Winokur, Phys. Rev. Lett., 2005, 94, 107402 CrossRef CAS; (c) G. Ryu, P. N. Stavrinou and D. D. C. Bradley, Adv. Funct. Mater., 2009, 19, 3237–3242 CrossRef CAS; (d) Y. Zhao, H. L. Chen, L. Yin, X. X. Cheng, W. Zhang and X. L. Zhu, Polym. Chem., 2018, 9, 2295–2301 RSC.
- (a) M. Knaapila, F. B. Dias, V. M. Garamus, L. Almásy, M. Torkkeli, K. Leppänen, F. Galbrecht, E. Preis, H. D. Burrows, U. Scherf and A. P. Monkman, Macromolecules, 2007, 40, 9398–9405 CrossRef CAS; (b) C. Liu, Q. Wang, H. Tian, J. Liu, Y. Geng and D. Yan, Macromolecules, 2013, 46, 3025–3030 CrossRef CAS; (c) D. W. Bright, F. Galbrecht, U. Scherf and A. P. Monkman, Macromolecules, 2010, 43, 7860–7863 CrossRef CAS.
- (a) J. Y. Lin, W. S. Zhu, F. Liu, L. H. Xie, L. Zhang, R. Xia, G. C. Xing and W. Huang, Macromolecules, 2014, 47, 1001–1007 CrossRef CAS; (b) H. F. Shi, Y. Nakai, S. J. Liu, Q. Zhao, Z. F. An, T. Tsuboi and W. Huang, J. Phys. Chem. C, 2011, 115, 11749–11757 CrossRef CAS; (c) M.-C. Hung, J.-L. Liao, S.-A. Chen, S.-H. Chen and A.-C. Su, J. Am. Chem. Soc., 2005, 127, 14576–14577 CrossRef CAS; (d) J. X. He, L. Y. Du, C. Wang, M. J. Jiang, L. L. Liu, Y. Q. Mo, Z. Q. Xie, B. Yang and Y. G. Ma, Polym. Chem., 2017, 8, 1255–1262 RSC.
- (a) Z. Bai, Y. Liu, T. Li, X. Li, B. Liu and D. Lu, J. Phys. Chem. C, 2016, 120, 27820–27828 CrossRef CAS; (b) M. Torkkeli, F. Galbrecht, U. Scherf and M. Knaapila, Macromolecules, 2015, 48, 5244–5250 CrossRef CAS; (c) X. Li, Z. Bai, B. Liu, T. Li and D. Lu, J. Phys. Chem. C, 2017, 121, 14443–14450 CrossRef CAS.
- S. W. Thomas III, G. D. Joly and T. M. Swager, Chem. Rev., 2007, 107, 1339–1386 CrossRef.
- (a) L. Huang, X. Huang, G. Sun, C. Gu, D. Lu and Y. Ma, J. Phys. Chem. C, 2012, 116, 7993–7999 CrossRef CAS; (b) T. Li, B. Liu, H. Zhang, J. Ren, Z. Bai, X. Li, T. Ma and D. Lu, Polymer, 2016, 103, 299–306 CrossRef CAS.
- (a) A. J. C. Kuehne, M. Kaiser, A. R. Mackintosh, B. H. Wallikewitz, D. Hertel, R. A. Pethrick and K. Meerholz, Adv. Funct. Mater., 2011, 21, 2564–2570 CrossRef CAS; (b) H. Ling, J. Lin, M. Yi, B. Liu, W. Li, Z. Lin, L. Xie, Y. Bao, F. Guo and W. Huang, ACS Appl. Mater. Interfaces, 2016, 8, 18969–18977 CrossRef CAS.
- (a) V. Butkus, L. Valkunas and D. Abramavicius, J. Chem. Phys., 2014, 140, 034306 CrossRef; (b) R. Sun, B. L. Yan, J. F. Ge, Q. F. Xu, N. J. Li, X. Z. Wu, Y. L. Song and J. M. Lu, Dyes Pigm., 2013, 96, 189–195 CrossRef CAS.
- (a) J. Huang, W. Wang, J. Gu, W. Li, Q. Zhang, Y. Ding, K. Xi, Y. Zheng and X. Jia, Polymer, 2014, 55, 6696–6707 CrossRef CAS; (b) J. Huang, J. Gu, Z. Meng, X. Jia and K. Xi, Nanoscale, 2015, 7, 15413–15420 RSC; (c) J. Huang, B. Peng, W. Wang, H. Ji, L. Li, K. Xi, W. Lai, X. Zhang and X. Jia, Adv. Funct. Mater., 2016, 26, 1646–1655 CrossRef CAS.
- S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J.-L. Bredas and B. M. Pierce, Science, 1994, 265, 632–635 CrossRef CAS.
- Y. Kutuvantavida, G. V. M. Williams, M. D. H. Bhuiyan, S. G. Raymond and A. J. Kay, J. Phys. Chem. B, 2015, 119, 3273–3280 CrossRef CAS.
- X. Yuan, W. Zhang, L. H. Xie, J. Ma, W. Huang and W. Liu, J. Phys. Chem. B, 2015, 119, 10316–10333 CrossRef CAS.
- (a) X. Wang, S. Y. Guang, H. Y. Xu, X. Y. Su, J. Y. Yang, Y. L. Song, N. B. Lin and X. Y. Liu, J. Mater. Chem., 2008, 18, 4204–4209 RSC; (b) Q. D. Zheng, S. K. Gupta, G. S. He, L. S. Tan and P. N. Prasad, Adv. Funct. Mater., 2008, 18, 2770–2779 CrossRef CAS; (c) K. Susumu, J. A. N. Fisher, J. Zheng, D. N. Beratan, A. G. Yodh and M. J. Therien, J. Phys. Chem. A, 2011, 115, 5525–5539 CrossRef CAS.
- (a) Z. A. Li, T. R. Ensley, H. H. Hu, Y. D. Zhang, S. H. Jang, S. R. Marder, D. J. Hagan, E. W. Van Stryland and A. K.-Y. Jen, Adv. Opt. Mater., 2015, 3, 900–906 CrossRef CAS; (b) J. Qian, Z. F. Zhu, A. J. Qin, W. Qin, L. L. Chu, F. H. Cai, H. Q. Zhang, Q. Wu, R. R. Hu and B. Z. Tang, Adv. Mater., 2015, 27, 2332–2339 CrossRef CAS.
- (a) B. Liu, J. Lin, M. Yu, B. Li, L. Xie, C. Ou, F. Liu, T. Li, D. Lu and W. Huang, J. Phys. Chem. C, 2017, 121, 19087–19096 CrossRef CAS; (b) W. Xue, J. Y. Lin, B. Liu, N. E. Shi, M. N. Yu, W. D. Wu, W. S. Zhu, L. H. Xie, L. H. Wang and W. Huang, Polymer, 2018, 153, 338–343 CrossRef CAS.
- A. Perevedentsev, S. Aksel, K. Feldman, P. Smith, P. N. Stavrinou and D. D. C. Bradley, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 22–38 CrossRef CAS.
- (a) Z. B. Zeng, Z. P. Guan, Q. H. Xu and J. S. Wu, Chem. – Eur. J., 2011, 17, 3837–3841 CrossRef CAS; (b) Y. H. Jiang, Y. C. Wang, B. Wang, J. B. Yang, N. N. He, S. X. Qian and J. L. Hua, Chem. – Asian J., 2011, 6, 157–165 CrossRef CAS; (c) J. Z. Liu, J. W. Y. Lam, C. K. W. Jim, J. C. Y. Ng, J. B. Shi, H. M. Su, K. F. Yeung, Y. N. Hong, M. Faisal, Y. Yu, K. S. Wong and B. Z. Tang, Macromolecules, 2011, 44, 68–79 CrossRef CAS.
- J. Hong, S. K. Jeon, J. J. Kim, D. Devi, K. Chacon-Madrid, W. Lee, S. M. Koo, J. Wildeman, M. Y. Sfeir, L. A. Peteanu, J. Wen and J. Ma, J. Phys. Chem. A, 2014, 118, 10464–10473 CrossRef CAS.
- J. L. Bredas, C. Adant, P. Tackx and A. Persoons, Chem. Rev., 1994, 94, 243–278 CrossRef CAS.
- J. Teetsov and F. M. Anne, J. Mater. Chem., 1999, 9, 2117–2122 RSC.
- (a) A. Perevedentsev, Y. Sonnefraud, C. R. Belton, S. Sharma, A. E. G. Cass, S. A. Maier, J. Kim, P. N. Stavrinou and D. D. C. Bradley, Nat. Commun., 2015, 6, 5977 CrossRef CAS; (b) M. Ariu, M. Sims, M. D. Rahn, J. Hill, A. M. Fox, D. G. Lidzey, M. Oda, J. Cabanillas-Gonzalez and D. D. C. Bradley, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 195333 CrossRef.
- (a) R. Tkachov, V. Senkovskyy, M. Horecha, U. Oertel, M. Stamm and A. Kiriy, Chem. Commun., 2010, 46, 1425–1427 RSC; (b) M. J. Tapia, M. Monteserín, H. D. Burrows, J. S. S. de Melo, J. Pina, R. A. E. Castro, S. García and J. Estelrich, J. Phys. Chem. B, 2011, 115, 5794–5800 CrossRef CAS; (c) R. R. Rosencrantz, K. Rahimi and A. J. C. Kuehne, J. Phys. Chem. B, 2014, 118, 6324–6328 CrossRef CAS.
- B. Liu, J. Lin, F. Liu, M. Yu, X. Zhang, R. Xia, T. Yang, Y. Fang, L. Xie and W. Huang, ACS Appl. Mater. Interfaces, 2016, 8, 21648–21655 CrossRef CAS.
- (a) M. Hwang, T. Stockfisch and A. Hagler, J. Am. Chem. Soc., 1994, 116, 2515–2525 CrossRef CAS; (b) H. Sun, Macromolecules, 1995, 28, 701–712 CrossRef CAS; (c) H. Sun, S. Mumby, J. Maple and A. Hagler, J. Phys. Chem., 1995, 99, 5873–5882 CrossRef CAS.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- Materials studio, Version 4.0, Accelrys, Inc., San Diego, USA, 2006 Search PubMed.
- X. Yuan, D. Zheng, X. Wang, P. Liu and J. Ma, J. Phys. Chem. A, 2016, 120, 10196–10206 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, J. B. Farkas, J. V. O. Foresman, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, USA, 2010 Search PubMed.
- K. Chandrasekaran and R. T. Kumar, Spectrochim. Acta, Part A, 2015, 150, 974–991 CrossRef CAS.
- (a) X. H. Ouyang, H. P. Zeng and W. Ji, J. Phys. Chem. B, 2009, 113, 14565–14573 CrossRef CAS; (b) N. Lin, X. Y. Liu, Y. Y. Diao, H. Xu, C. Chen, X. Ouyang, H. Yang and W. Ji, Adv. Funct. Mater., 2012, 22, 361–368 CrossRef CAS; (c) Z. M. Htwe, Y. D. Zhang, C. B. Yao, H. Li, H. Y. Li and P. Yuan, Opt. Mater., 2016, 52, 6–13 CrossRef CAS; (d) X. Y. Su, S. Y. Guang, C. W. Li, H. Y. Xu, X. Y. Liu, X. Wang and Y. L. Song, Macromolecules, 2010, 43, 2840–2845 CrossRef CAS; (e) I. Papadakis, Z. Bouza, A. Stathis, I. Orfanos, S. Couris, T. Miletić and D. Bonifaz, J. Phys. Chem. A, 2018, 122, 5142–5152 CrossRef CAS; (f) Z. Li, P. Cui, C. Wang, S. Kilina and W. Sun, J. Phys. Chem. C, 2014, 118, 28764–28775 CrossRef CAS; (g) L. Kamath, K. B. Manjunatha, S. Shettigar, G. Umesh, B. Narayana, S. Samshuddin and B. K. Sarojini, Opt. Laser Technol., 2014, 56, 425–429 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and supporting data. See DOI: 10.1039/c8py01268g |
| This journal is © The Royal Society of Chemistry 2019 |