Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Short-lived intermediates in photochemistry of an OsCl62− complex in aqueous solutions†
Marina V.
Rogozina
*ab,
Vladislav V.
Yudanov
ab,
Roman G.
Fedunov
b,
Ivan P.
Pozdnyakov
ac,
Alexey A.
Melnikov
d,
Sergey V.
Chekalin
d and
Evgeni M.
Glebov
 ac
ac
aVoevodsky Institute of Chemical Kinetics and Combustion, 3 Institutskaya Str., 630090, Novosibirsk, Russian Federation. E-mail: glebov@kinetics.nsc.ru; Fax: +7 383 3307350; Tel: +7 383 3309150
bVologograd State University, 100 University Ave., 400062, Volgograd, Russian Federation. E-mail: rogozina@volsu.ru
cNovosibirsk State University, 2 Pirogova Str., 630090, Novosibirsk, Russian Federation
dInstitute of Spectroscopy, Russian Academy of Sciences, 5 Fizicheskaya Str., 119333 Troitsk, Moscow, Russian Federation. E-mail: melnikov@isan.troitsk.ru
First published on 2nd November 2017
Abstract
Two mechanisms of OsIVCl62− photolysis were studied by means of quantum chemical calculations in gas and aqueous phases. The difference between these mechanisms is in the nature of the possible Os(IV) key intermediates (KI). According to calculations, the intermediate is an OsIVCl5− complex of square pyramidal coordination geometry. The calculations do not give an opportunity to make an unambiguous choice between the triplet and quintet multiplicities of OsIVCl5−. The calculated CASSCF/IMCP-SR1 transition energies for 5OsIVCl5− are lower than for 3OsIVCl5−, while the calculated XMC-QDPT2/SBKJC spectra for the triplet state are in better agreement with the experimental absorption spectrum of the KI than for the quintet state.
1. Introduction
Ultrafast dynamics of transition metal complexes is an active area of research in chemical physics.1–9 A combination of ultrafast (femtosecond), nanosecond and stationary experimental data accompanied by quantum chemical calculations allows one to identify the short-lived intermediates and construct the verified reaction mechanism.Recently, we have reviewed the efforts in studying primary photophysical and photochemical processes for hexahalide complexes of tetravalent ions of platinum group metals (see ref. 10 and references there). Five complexes of this type were the subjects of femtosecond studies, namely, PtIVCl62−, PtIVBr62−, IrIVCl62−, IrIVBr62−, and OsIVBr62−. Among them, the photophysics and photochemistry of PtIVBr62− in aqueous and alcoholic solutions have been experimentally examined in the time range from absorption of a light quantum to the formation of final photolysis products, and supported by quantum chemistry.11,12 In aqueous solutions the only photochemical process is photoaquation.13,14 It was shown that the main reactive intermediate is the pentacoordinated PtBr5− complex in the singlet state.11
For the other mentioned complexes, the mechanisms are not as complete as for PtIVBr62−. For PtIVCl62− the overall photochemical process is also photoaquation, yielding the PtIVCl5(H2O)− complex at the first stage.15 The mechanism includes redox reactions with the participation of short-lived Pt(III) intermediates.16 As a result, the chain pathway of solvation is realized in aqueous15 and acetonitrile17 solutions. The identification of Pt(III) intermediates was based on the Xα calculations performed by Goursot et al. in the 1980s.18 No verification of the results by modern quantum chemical methods was done.
Low quantum yields of IrIVCl62− photolysis in aqueous solutions19 did not allow one to correlate photochemical20 and photophysical21 pulsed experiments, as there were no observable precursors of the stable photoproducts.
Photochemistry of OsIVBr62− in aqueous and methanolic solutions is similar to the case of PtIVBr62−.11,12 The difference is that the ground state of the pentacoordinated intermediate OsIVBr5− is a triplet, while for the case of PtIVBr5− it is a singlet. Additional data on the stationary and nanosecond laser flash photolysis of OsIVBr62− are required to complete its photolysis mechanism.
No chemical reactions were detected in aqueous IrIVBr62− solutions upon ultrafast excitation at 770 nm,12 unlike the gas phase photodissociation of the complex.22 Actually, very little is known about photochemistry of IrIVBr62−, with additional complications due to its instability in the absence of free Br− anions.
Recently we examined ultrafast processes for the pseudohexahalide complex PtIV(SCN)62−.23 Its photophysics and photochemistry were found to be similar to those of PtIVBr62−.
In addition to the mentioned hexahalide complexes of platinum metals, we have recently performed experiments on ultrafast spectroscopy of OsIVCl62− in aqueous solutions.24 Irradiation of this complex in water,25,26 methanol,26 acetonitrile and pyridine25 resulted in photosolvation, while irradiation in chloroform gave rise to photooxidation of Os(IV) to Os(V).27
The quantum yield of photoaquation was found to be wavelength-dependent, dropping to the longer irradiation wavelengths.24 The main result of ref. 24 was the registration of the intermediate (further – key intermediate, KI) with the maximum in the region of 450–470 nm and a plateau in the region of 550–650 nm. The characteristic lifetime of the KI is about 20 ps. Because of a low quantum yield of photoaquation (0.005 at the irradiation wavelength of 405 nm (ref. 24)) the main channel of the intermediate's decay was identified as the transition to the ground state of OsIVCl62−. Two possibilities of the KI identification were proposed:24 either the lowest electronic excited state of OsIVCl62− or a pentacoordinated complex of Os(IV), OsIVCl5− situated in the solvent cage with the chloride anion. Based on analogy with photophysics of OsIVBr62−,11,12 it was proposed that the ground state of OsIVCl5− is most likely a triplet.
Corresponding to the method of the KI identification, two possible tentative mechanisms of OsIVCl62− photoaquation are presented in ref. 24. In the following equations, OsIVCl62− is considered as the octahedral low-spin complex.28 In this case, the ground state and lowest electronic excited state of OsIVCl62− are 3T1g and 1T2g correspondingly.29
Mechanism 1 (KI is the lowest electronic excited state of OsIVCl62−, namely OsIVCl62−(1T2g))
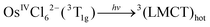 | (1) |
| 3(LMCT)hot → OsIVCl62−(1T2g*)hot | (2) |
| OsIVCl62−(1T2g*)hot → OsIVCl62−(1T2g*) | (3) |
| OsIVCl62−(1T2g*) → OsIVCl62−(3T1g) | (4) |
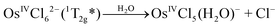 | (5) |
Mechanism 2 (KI is the ionic pair {3OsIVCl5−…Cl−}cage)
| 3(LMCT)hot → {OsIVCl5−…Cl−}cagehot | (6) |
| 3{OsIVCl5−…Cl−}cagehot → {OsIVCl5−…Cl−}cage | (7) |
| 3{OsIVCl5−…Cl−}cage → {OsIVCl62−(3T1g)} | (8) |
 | (9) |
The OsIVCl5(H2O)− complex demonstrates acidic properties:24
| OsIVCl5(H2O)− ⇌ OsIVCl5(OH)2− + H+ | (10) |
When OsIVCl62− is irradiated in the solutions with neutral pH, equilibrium (10) is right-shifted, and the OsIVCl5(OH)2− hydroxocomplex is the product of photoaquation.24
In this work we describe our efforts in the identification of the KI by means of quantum chemical calculations.
2. Experiment and quantum chemical calculations
2.1. Ultrafast spectroscopy
In this work we analyze the results obtained using the experimental setup described in detail in ref. 30. The samples were excited by ∼60 fs pulses (energy ca. 1 μJ, pulse repetition rate 1 kHz) at ∼400 nm (second harmonic of a Ti:sapphire generator–amplifier system, CDP Ltd, Moscow, Russia). 200 pulses were used to record a single time-resolved spectrum. Each kinetic curve contained 110 points (60 points with a 100 fs step, 20 points with a 500 fs step, and 30 points with a 3 ps step). The investigated solutions (total volume of 20 ml) were pumped through a 1 mm cell at room temperature to provide uniform irradiation and avoid possible degradation due to photochemical reactions. The experimental data were globally fitted by a three-exponential model. The fitting program performed corrections of the group velocity dispersion and calculated the response time of the instrument.2.2. Quantum chemical calculations
Ground-state gas-phase geometry optimization was performed at the Hartree–Fock level of theory (RHF, ROHF and UHF) using the SBKJC, Def2-TZVP, IMCP-NR1 and IMCP-SR1 basis sets.31,32 The calculations were carried out using the GAMESS-US package33 for the Def2-TZVP, IMCP-NR1 and IMCP-SR1 basis sets and FireFly version 8.1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 for the SBKJC basic set. The effect of solvent (water) was taken into account in the framework of the polarizable continuum model (PCM).
34 for the SBKJC basic set. The effect of solvent (water) was taken into account in the framework of the polarizable continuum model (PCM).
In the course of GAMESS-US package calculations, electronic excitation terms were computed at the complete active space configuration interaction (state-specific CASSCF) with 8 active orbitals and 10 active electrons using the same basis sets. When SCF convergence failure happened the active space was lowered to 6 active orbitals and 6 active electrons.
In the course of FireFly calculations, electronic spectra were computed at the framework of Extended Multi-Configuration Quasi-Degenerate Perturbation Theory (XMCQDPT)34 with the same active space (state-averaged CASSCF). All the molecular systems were calculated with prescribed multiplicity and total electronic charge.
3. Results and discussion
3.1. Geometry of ground state and electronic excited states of OsIVCl62−
OsIVCl62− is a low spin complex with the 5d4 electronic configuration. To clarify the further description, the approximate structure of orbitals (based on the results of Jørgensen28,35 obtained in the assumption on the octahedral symmetry of the complex) is shown in Fig. 1. In the framework of the simple crystal field approach with the Oh symmetry the ground state of OsIVCl62− is a triplet (3T1g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29). In the literature, the octahedral symmetry is typically used in the studies on OsIVCl62− spectroscopy28,29 in spite of the Jahn–Teller distortion to lower symmetry.
29). In the literature, the octahedral symmetry is typically used in the studies on OsIVCl62− spectroscopy28,29 in spite of the Jahn–Teller distortion to lower symmetry.
 | ||
| Fig. 1 The structure of molecular orbitals of the OsCl62− complex in the framework of Oh symmetry according to ref. 27 (non-relativistic approximation). Arrows correspond to LMCT transitions. Wavelengths of the band maxima are indicated for aqueous solutions. | ||
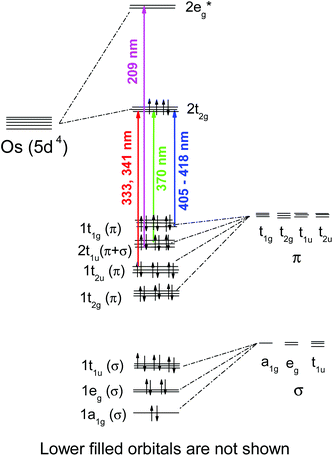
Quantum chemical calculations performed in this work resulted in slight distortions from the octahedral geometry to the D2h symmetry. The geometrical structure of OsIVCl62− is shown in Fig. 2 (and in Fig. S1 of the ESI†). The detailed results of calculations performed with different methods are collected in Table S1 of the ESI.† Two axial Os–Cl bonds are 90° with an equatorial plane, and the Cl–Os–Cl bond angles of atoms lying in the equatorial plane may be slightly (not more than 2°) different from 90° for different methods. Os–Cl bond lengths for the singlet and triplet states vary from 2.355 to 2.478 Å. Axial Os–Cl bonds for quintet states (2.65 ÷ 2.73 Å) are sufficiently longer than the covalent Os–Cl bonds. This is an indication of the dissociative character of the quintet states.
 | ||
| Fig. 2 Geometry of the OsCl62− ground state according to quantum chemical calculations. For details see Table S1 in the ESI.† | ||
All equatorial Os–Cl bond lengths and chlorine charges calculated with one method are close to each other. Typically (with a couple of exclusions), for the triplet states the calculated axial Os–Cl bond lengths and chlorine atom charges are less than corresponding parameters for equatorial chlorine atoms. For singlet states the prevailing picture is opposite. Atomic charges on the axial chlorine atoms for quintet states are more negative than ones on the equatorial chlorines.
3.2. UV spectrum of OsIVCl62−
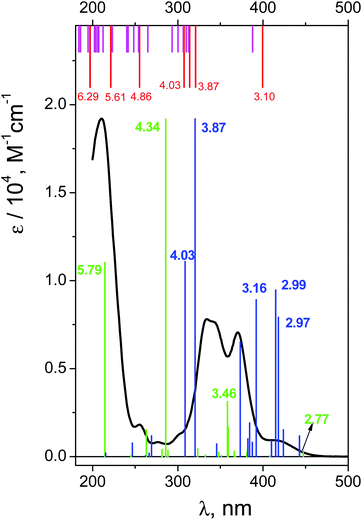
The UV spectrum of OsIVCl62− in aqueous solutions (pH ∼ 7) is shown in Fig. 3 (black line). We use here the molar absorption coefficients obtained in ref. 24, which are close to those reported by Jørgensen.28The interpretation of absorption bands of the initial complex in the framework of octahedral symmetry (according to ref. 28) is presented in Fig. 1. A low intense band appearing as a shoulder in the region of 405–418 nm was assigned to an LMCT transition. According to Jørgensen interpretation28,35 this band corresponds to the πCl(t1g) → Os(t2g) promotion. The LMCT bands in the region of 320–375 nm are represented by a doublet (λmax = 333 and 341 nm) and a single band with a maximum at 370 nm. These bands correspond to πCl(t2u) → Os(t2g) and (π + σ)Cl(t1u) → Os(t2g) promotions.28 The most intense LMCT band at 210 nm was assigned to the πCl → Os(eg) promotion.28 Low intense bands in the regions of 301, 278 and 255 nm were interpreted by the d–d transitions;28 they are partially superimposed with the LMCT bands.
In spite of the undoubted interpretation of the OsIVCl62− electronic absorption spectrum in the literature, we have performed its quantum chemical calculations. The necessity of these calculations stems from the use of quantum chemistry for the assignment of short-lived reactive intermediates of Os(IV) in this work. Before using calculations for the assignment of the absorption bands obtained in time-resolved experiments, we had to ensure that the calculated spectrum of the OsIVCl62− ground state did not contradict the experimental one.
The calculations of excited state energy levels were performed by different methods using the GAMESS-US package (by means of CASSCF(8,10)/IMCP-SR1, CASSCF(8,10)/IMCP-NR1, and CASSCF(8,10)/Def2-TZVP methods) and FireFly package. In the case of GAMESS calculations the oscillator strengths could not be figured out, while in the case of FireFly calculations it was possible. The results of the calculations of energies and orbital populations are presented in the ESI.† Tables S2 and S3† contain the gas phase data obtained from GAMESS-US and FireFly calculations, while Tables S4 and S5† contain the results of calculations performed in the aqueous phase.
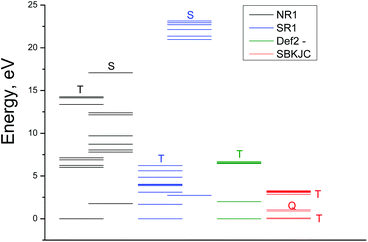
The excitation energies obtained by GAMESS and FireFly calculations in the gas phase using different basis sets are schematically shown in Fig. 4. Only for the triplet ground state the results of calculations are comparable with the experimental spectrum. The calculations performed in basis sets IMCP-SR1 (triplet manifold) and SBKJC give the best agreement between the calculated excitation energies and the experimentally observed spectra. Thus further analysis has been carried out only with these basis sets. These calculations are represented in Fig. 3 as red vertical lines under the upper scale (CASSCF(10,8)/IMCP-SR1) and green vertical lines above the lower scale (SBKJC).
Let us analyze the results of the IMCP-SR1 calculations. First of all, to evaluate the possible solvent effect, calculations in the framework of PCM with 32 excited states were performed (see Table S4 of the ESI†). The results are shown in Fig. 3 (magenta vertical lines under the upper scale). Consideration of the solvent in calculation reduces molecular symmetry, resulting in an increase in the number of spectral lines that complicate the analysis of transitions. In spite of this, one can see that the difference between the results of gas phase and aqueous solution calculations is not large. This is true for both structures (Table S1 of the ESI†) and spectra (Fig. 3, upper scale). For these reasons, further analysis was performed only for the results obtained in the gas phase.
Let us compare the experimental (Fig. 3) and calculated (Fig. 3 and Table S2 of the ESI†) spectra. The lowest energy band (T1 → T2) was assigned to an electron transfer from the HOMO (for the image of active orbitals see Fig. S2†), including only the dyz(Os) atomic orbital, to the LUMO composed of dxx, dyy, dzz(Os) and px(Cl(2, 2′)) atomic orbitals. Calculated energy for this transition is 3.1 eV (399 nm), which corresponds to the shoulder in the experimental spectrum. The group of transitions from T1 to T3, T4 and T5 with energies 3.86, 3.95 and 4.03 eV (321, 314 and 307 nm) is mainly constituted from the same atomic orbitals as (T1 → T2) transition, but with slightly different occupancies. These transitions could be placed in compliance with LMCT bands in the region of 320–370 nm in the experimental spectrum. Furthermore, triplet level T7 with energy equal to 5.6 eV (221 nm) could be assigned as the (LUMO+1) orbital. The states T6, T8 and T9 with energies 4.86, 6.29 and 6.30 eV (255 and 197 nm) are constituted from the HOMO, LUMO and (LUMO+1) orbitals with different populations. Transitions from (T1 → T6) to (T1 → T9) could be considered as responsible for the most intense LMCT band at 210 nm and the low intense band at 255 nm. Therefore, (CASSCF(8,10)/IMCP-SR1, M = 3) calculations do not contradict the experimental spectrum (but note that the absence of oscillator strengths allows one to make only tentative conclusions).
Now let us consider the results of XMCQDPT(10,8)/SBKJC calculations. Gas phase FireFly calculations are presented as green vertical lines in Fig. 3 (see also Table S3 in the ESI†). The oscillator strengths were normalized to the maximal value of the molar absorption coefficient of the experimental spectrum (green vertical line at 4.34 eV (286 nm) in Fig. 3). The XMCQDPT (10,8)/SBKJC/PCM(water) spectrum is presented in Fig. 3 as blue vertical lines. The oscillator strengths were normalized to the maximal value of the molar absorption coefficient of the experimental spectrum (blue vertical line at 3.87 eV (320) nm in Fig. 3).
The impact of the solvent on the position of the spectral lines is ambiguous (Fig. 3 and Table S5 of the ESI†). The line corresponding to the highest energy is shifted to the shortwave region and all other lines are shifted to the longwave region. Apparently this is because the whole range was narrower compared to the spectrum calculated in the gas phase, although the shape of the spectrum in water qualitatively matches the shape of the spectrum in the gas phase. There is some difference; the additional line at 3.16 eV (392 nm) appears to be at the left from the doublet 2.99 and 2.97 eV (415 and 418 nm). The following analysis was performed for the gas phase spectrum (Table S3 in the ESI†).
The first energy band with non-vanishing oscillator strength (T1 → T4) was assigned to an electron transfer from the HOMO−2, including the dyz(Os) main atomic orbitals, to the LUMO including the following main atomic orbitals: dyz, dyy, dzz(Os) and py(Cl(5, 4)), pz(Cl(3, 2)). Calculated energy for this transition is 2.77 eV (447 nm), which corresponds to the shoulder in the experimental spectrum (Fig. 3).
The interim energy band for transition (T1 → T11) (3.46 eV, 358 nm) was assigned to the electron transfer from the composition of the HOMO−2 and HOMO to the composition of the LUMO and LUMO+1 of average molecular orbitals. The main atomic orbitals in the HOMO include dxy(Os) and dxz(Os) parts. The composition of both the LUMO and LUMO+1 for the T11 state includes the following main atomic orbitals: dxy, dxz(Os) and py(Cl(1′)) for the LUMO and dyy, dzz(Os), py(Cl(3, 3′)) and pz(Cl(2, 2′)) for the LUMO+1.
The energy band with the maximal oscillator strength (T1 → T17) (4.34 eV, 286 nm) was assigned to the electron transfer from the composition of the HOMO−2, HOMO−1 and HOMO to the composition of the LUMO and LUMO+1 of averaged molecular orbitals. The HOMO and HOMO−2 were described earlier, and the HOMO−1 consists of dxy(Os), dxz(Os) and a small part of pz(Cl(1, 1′)) atomic orbitals. The LUMO orbital for the T17 state is the same as the LUMO orbital for the T11 state but excluding part of the py(Cl(1′)) orbital and including px(Cl(1, 1′)) and py(Cl(3, 3′)) orbitals. The LUMO+1 for the T17 state includes the following main atomic orbitals: dzz, dyy (Os) and py(Cl(3, 3′)), pz(Cl(2, 2′)). The energy band (T1 → T22) (5.79 eV, 214 nm) was assigned to the electron transfer from the HOMO−2 to the LUMO. The LUMO orbital for the T22 state includes the following main atomic orbitals: dxx, dyy, dzz(Os) and px(Cl(1, 1′)), py(Cl(3, 3′)), pz(Cl(2, 2′)).
Therefore, we can conclude that both GAMESS and FireFly quantum chemical calculations do not contradict the experimental spectrum of the OsIVCl62− complex. It is reasonable to use these types of calculations for the assignment of LMCT states and the short-lived intermediates observed in the course of the ultrafast kinetic spectroscopy experiments.
It should be noted that (CASSCF(8,10)/IMCP-SR1, M = 3) calculations predict the existence of the low-lying excited quintet (Q1) and singlet (S0) energy levels with the energies 1.68 and 2.74 eV above the ground state correspondingly (see Table S2 of the ESI†). The quintet level, which is dissociative, probably plays a sufficient role in the photolysis mechanism.
3.3. Electronic absorption spectra of possible intermediates of OsIVCl62−photolysis
The results of ultrafast measurements for the OsIVCl62− complex in aqueous solutions were analyzed24 in the framework of the sequential decay of the transient absorption A → B → C → (ground state + products). Intermediate C, which is the precursor of the photoaquation product, was considered as the key intermediate (KI). The Species Associated Differential Spectra (SADS) of the intermediates are calculated in ref. 24 using formulae derived in ref. 36 (see paragraph “Species Associated Differential Spectra (SADS)” in the ESI†).The SADS of the KI obtained in ref. 24 is shown in Fig. 5 (blue dots). Because OsIVCl62− has no significant absorption in the region of probing (440–680 nm), the SADS coincides with the electronic absorption spectrum of the KI. According to the shape of the spectrum, there are at least two different absorption bands in the observed wavelength range. The decay of intermediate absorption was described by the monoexponential kinetic law with a characteristic lifetime of 23 ± 3 ps.24
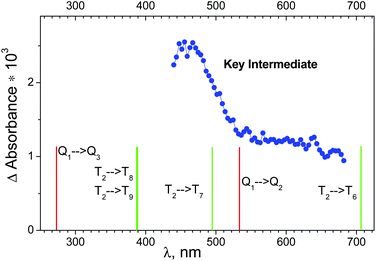 | ||
| Fig. 5 Blue dots – species associated difference spectrum (SADS) of the key intermediate recorded in an ultrafast kinetic spectroscopy experiment (λpump = 400 nm) with OsIVCl62− (2.3 × 10−4 M) in aqueous solution (taken from ref. 24). Lines above the bottom axis mark positions of possible transitions from the lowest quintet (red lines) and triplet (green lines) electronic excited states of OsIVCl62− (for details see Table S2 of the ESI†). | ||
Let us discuss the possibility of KI interpretation as one of the lowest electronic absorption states of OsIVCl62−. According to (CASSCF(8,10)/IMCP-SR1, M = 3) calculations (Table S2 of the ESI†) the three lowest electronic excited states have different multiplicities. They are quintet Q1, singlet S0 and triplet T2 states, whose energies are 1.7, 2.7 and 3.1 eV above the ground state T1.
Wavelengths of possible transitions from Q1 to the other quintet states Q2 and Q3 are shown in Fig. 5 as red lines above the bottom axis. One can see that the position of the lowest Q1 → Q2 transition lies in the range of the observed spectrum, and the second band Q1 → Q3 is far in the UV region. As a matter of fact, the description of the KI spectrum given by transitions within the quintet manifold cannot be considered as satisfactory.
The possibility of KI interpretation as the lowest singlet state S0 should be ruled out, because calculations do not show any transitions from S0 to other singlet states in the visible and near UV spectral range.
The wavelengths of transitions from the lowest excited triplet state T2 to the other triplet states are shown in Fig. 5 as green lines above the bottom axis. One can see that the transitions inside the set of triplet energy levels can provide better description of the experimental spectrum than the transitions inside the set of quintet levels. Nevertheless, the possibility of T2 state partial stabilization (the lifetime of KI is 23 ps, as was mentioned) seems improbable.
Finally, we can conclude that calculations do not support the interpretation of KI as one of the lowest electronic excited states of OsIVCl62−, and Mechanism 1 seems improbable. On the other side, the dissociative character of the lowest excited state Q1 allows one to consider it as a precursor of the ion pair in Mechanism 2.
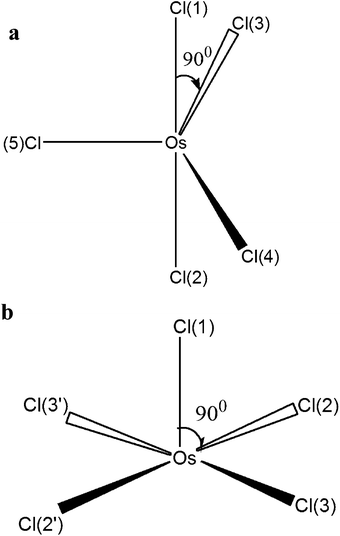
The pentacoordinated intermediate OsIVCl5− plays a key role in Mechanism 2. GAMESS calculations with the use of the IMCP-SR1 basis set show the existence of two modifications of OsIVCl5− (Fig. 6 and also Fig. S3 of the ESI†). The first modification (Fig. 6a) is further marked as OsIVCl5− (planar). It was obtained from the OsIVCl62− complex by the removal of one chlorine atom lying in the equatorial plane. The second modification (Fig. 6b) marked as OsIVCl5− (axial) was obtained by the detachment of one axial chlorine atom. The detailed results of geometry calculations performed for both planar and axial modifications are collected in Tables S6a and S6b of the ESI.† The OsIVCl5− complex in the singlet state tends to a trigonal bipyramidal coordination geometry and in the triplet state to a square pyramidal coordination geometry.
The optimization of all geometrical parameters of OsIVCl5− (axial) was carried out at a low Cl symmetry. Under optimization of the geometrical parameters for the OsIVCl5− (planar) complex a high degree of symmetry (D3h) was preserved only for the singlet state. In the triplet state the SCF procedure fails for the given high symmetry. Therefore, the optimization of geometrical parameters of the OsIVCl5− (planar) complex was carried out at a predetermined low Cl symmetry with fixed values of the Cl–Os–Cl angles in the equatorial plane. For this reason, the electronic structure of planar modification in the triplet state is similar to the electronic structure of axial modification in the triplet state. That is manifested in the asymmetric distribution of charges on the chlorine atoms in the equatorial plane as well as in different bond lengths between osmium and equatorial chlorine atoms (Tables S6a and S6b†). A similar result was obtained for the quintet state. After the optimization of geometry, the quintet state of the OsIVCl5− (planar) complex in fact transits to the axial configuration with a low Cl symmetry.
Therefore, GAMESS calculations show that the singlet state of OsIVCl5− can exist both in planar and axial configurations, while for the triplet and quintet states only the low symmetry axial configuration is realized. That is why the FireFly calculations for triplets and quintets were performed only for the OsIVCl5− (axial) modification. FireFly calculations performed in the SBKJC basis set are in accordance with the GAMESS results. The geometrical and electronic structures are shown in Table S7.†
The electronic absorption spectra of OsIVCl5− with different multiplicities were calculated in the FireFly package only (because FireFly provides oscillator strengths). The results of gas phase calculations for the triplet and quintet states are collected in Tables S8 and S9 of the ESI† correspondingly. Table S10 of the ESI† gives the results of calculation for 3OsIVCl5− in aqueous solutions. A comparison of the calculated spectra of the possible pentacoordinated intermediates and the experimental spectrum of the KI is shown in Fig. 7.
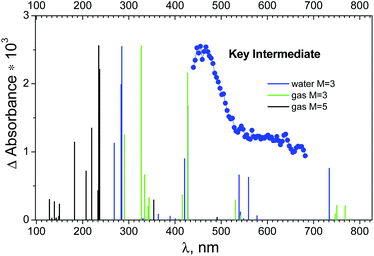 | ||
| Fig. 7 Blue dots – species associated difference spectrum (SADS) of the key intermediate recorded in an ultrafast kinetic spectroscopy experiment (λpump = 400 nm) with OsIVCl62− (2.3 × 10−4 M) in aqueous solution (taken from ref. 24). Lines above lower axes mark positions of possible transitions from the lowest quintet and triplet electronic excited states of OsIVCl5− according to calculations. | ||
The XMCQDPT (10,8)/SBKJC in the gas phase in the triplet and quintet states are shown in Fig. 7 as vertical green and black lines. The singlet state OsIVCl5− spectra are not shown, because the transition energy is 8.51 eV for the axial configuration and exceeds 21.96 eV for the planar configuration. One can see that the spectrum in the triplet state has two pronounced peaks, shifted to the short wavelength region relative to the experimental maximum. Several lines of smaller intensity in the longer wavelength region form the shoulder of the spectrum, which qualitatively coincides with the experimental spectrum. The XMCQDPT (10,8)/SBKJC/PCM(water) in the aqueous phase in the triplet state spectrum are presented in Fig. 7 as blue vertical lines.
The calculated energies of different OsIVCl5− modifications are collected in Tables S8–S10 of the ESI.† The axial modification for the triplet state is characterized by the lowest total energy among all triplet modifications (the UHF/IMCP-SR1 result should be excluded from consideration because the wave function has a high degree of spin contamination, S2 = 3.05). Indeed, for the quintet state the axial modification is characterized by lower energy than the planar modification. Thus, for both the quintet and triplet states the axial modification is energetically more favorable, whereas for the singlet state it is energetically favorable to be in the planar modification.
Table S8 (ESI†) shows that for the triplet, the total energy (CASSCF) of the ground state T1 is −4465.532 eV, and for the quintet the energy (CASSCF) of the Q1 state is −4465.50 eV (Table S9†), there is a slight difference. Including the additional electron correlation (XMC-QDPT2 energy of transition) gives a picture similar to the GAMESS calculations, where the quintet is lower in energy than the triplet. GAMESS calculations (Table S6b†) show that the quintet is indeed lower in energy than the triplet, but the difference is not much. At the same time, the qualitative coincidence with the experimental spectrum in FireFly (Fig. 7) for the triplet state is much better than for the quintet state (especially in the aqueous phase).
Additional calculations were performed by both methods for the free Os4+ cation (Table S11 of the ESI†). The results show that the state with multiplicity M = 5 is the most energetically favorable. As can be seen from the previous calculations, the presence of six ligands makes the state M = 3 in OsIVCl62− more favorable. We can assume that the removal of one Cl− anion reduces the influence of the ligands on the electronic structure of the Os4+ ion. Thus, the quintet state could also be expected to be the most favorable in the OsIVCl5− complex.
As a result, we conclude that the OsIVCl5− complex for sure is the key intermediate of OsIVCl62− photoaquation. As for the multiplicity of the OsIVCl5− ground state, both M = 3 and M = 5 cases could not be ruled out from the results of calculations.
4. Conclusions
In this work the quantum chemical calculations were performed to determine the nature of the key intermediate (KI) of the OsIVCl62− complex photoaquation.The calculations were carried out using program packages FireFly 8.1 and GAMESS-US both in gas and aqueous phases. Different methods were used; the best fitting to the experimental data was obtained by means of the CASSCF(8,10) method with the basis sets IMCP-SR1 (GAMESS-US) and SBKJC (FireFly).
The geometric and electronic structures and spectra were obtained for the initial OsIVCl62− complex and the OsIVCl5− complex as the probable KI. Analysis of electronic transitions and absorption spectra indicates the possibility of the reaction of OsIVCl62− photoaquation through a sequence of stages close to the Mechanism 2 (reactions (6)–(9)).
According to quantum-chemical calculations both in GAMESS and FireFly the KI is OsIVCl5− of square pyramidal coordination geometry. As for the multiplicity of its ground state, no unambiguous choice between the triplet and quintet state could be made. On the one hand, the calculated electronic absorption spectrum of 3OsIVCl5− is closer to the experimental one than the 5OsIVCl5− spectrum (Fig. 7). On the other hand, the calculated energy of the quintet state seems to be lower than for the triplet state. One can see that according to the results of CASSCF GAMESS calculations the OsIVCl5− complex is in the quintet state, while according to FireFly calculations the triplet state is favourable. Perhaps this difference stems from the fact that the used IMCP-SR1 basis set takes into account scalar relativistic pseudopotentials, which are ignored by the SBKJC basis set. This is manifested in the compression of the complex; the bond lengths calculated by the IMCP-SR1 are less than the bond lengths calculated by the SBKJC. The results of calculations taking into account relativistic amendments seem to be more reliable. The calculation of the total energy of a free osmium ion with charge Q = 4 also indicates that the quintet state is more energetically favorable.
The results of CASSCF GAMESS calculations include only the static correlation within the active space. Multireference perturbation theory (such as XMCQDPT) corrects the absolute state energies through the inclusion of dynamical correlation. This correction is different for the states of different nature and different multiplicity. As a result, the transition energies and the order of states in CASSCF and XMCQDPT calculations may differ substantially. Thus, the XMCQDPT results seem more reliable than CASSCF data. Nevertheless, it should be noted that the differences in total energies determining the order of energy levels are rather small.
Thus we can conclude that the reaction of photoaquation passes through Mechanism 2, and the key intermediate is the OsIVCl5− complex either in the triplet or in the quintet state.
It should be noted that the use of the time-consuming methods taking into account the spin–orbit coupling could change the order of energy levels.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Russian Science Foundation (Grant No. 15-13-10012) is gratefully acknowledged.Notes and references
- A. Vlcek Jr., Coord. Chem. Rev., 2000, 200–202, 933 CrossRef.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876 CrossRef CAS PubMed.
- L. S. Forster, Coord. Chem. Rev., 2006, 250, 2023 CrossRef CAS.
- E. A. Juban, A. L. Smeigh, J. E. Monat and J. K. McCusker, Coord. Chem. Rev., 2006, 250, 1783 CrossRef CAS.
- J. N. Schrauben, K. L. Dillman, W. F. Beck and J. K. McCusker, Chem. Sci., 2010, 1, 405 RSC.
- R. Compton, H. K. Gerardi, D. Weidinger, D. J. Brown, W. J. Dressick, E. J. Heilweil and J. C. Owrutsky, Chem. Phys., 2013, 422, 135 CrossRef CAS.
- J. P. Lomont, S. C. Nguyen and C. B. Harris, Acc. Chem. Res., 2014, 47, 1634 CrossRef CAS PubMed.
- A. Marino, P. Chakraborty, M. Servol, M. Lorenc, E. Collet and A. Hauser, Angew. Chem., Int. Ed., 2014, 53, 3863 CrossRef CAS PubMed.
- C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem. – Eur. J., 2013, 19, 17541 CrossRef CAS PubMed.
- E. M. Glebov, I. P. Pozdnyakov, V. F. Plyusnin and I. Khmelinskii, J. Photochem. Photobiol., C, 2015, 24, 1 CrossRef CAS.
- I. L. Zheldakov, M. N. Ryazantsev and A. N. Tarnovsky, J. Phys. Chem. Lett., 2011, 2, 1540 CrossRef CAS.
- I. L. Zheldakov, Ultrafast Photophysics and Photochemistry of Hexacoordinated Bromides of Pt(IV), Os(IV), and Ir(IV) in the Condensed Phase Studied by Femtosecond Pump-Probe Spectroscopy, Ph. D. Thesis, Bowling Green State University, 2010 Search PubMed.
- V. Balzani, M. F. Manfrin and L. Moggi, Inorg. Chem., 1967, 6, 354 CrossRef CAS.
- E. M. Glebov, V. F. Plyusnin, V. P. Grivin, A. B. Venediktov and S. V. Korenev, Russ. Chem. Bull., 2007, 56, 2357 CrossRef CAS.
- (a) L. E. Cox, D. G. Peters and E. L. Wehry, J. Inorg. Nucl. Chem., 1972, 14, 297 CrossRef; (b) K. P. Balashev, V. V. Vasil'ev, A. M. Zimnyakov and G.A. Shagisultanova, Russ. J. Coord. Chem., 1984, 10, 976 CAS (in Russian); (c) K. P. Balashev, I. I. Blinov and G.A. Shagisultanova, Russ. J. Inorg. Chem., 1987, 32, 2470 CAS (in Russian); (d) I. V. Znakovskaya and E. M. Glebov, Mendeleev Commun., 2016, 26, 35 CrossRef CAS.
- (a) R. C. Wright and G. S. Laurence, J. Chem. Soc., Chem. Commun., 1972, 132–133 RSC; (b) I. V. Znakovskaya, Yu. A. Sosedova, E. M. Glebov, V. P. Grivin and V. F. Plyusnin, Photochem. Photobiol. Sci., 2005, 4, 897 RSC; (c) E. M. Glebov, A. V. Kolomeets, I. P. Pozdnyakov, V. F. Plyusnin, V. P. Grivin, N. V. Tkachenko and H. Lemmetyinen, RSC Adv., 2012, 2, 5768 RSC; (d) E. M. Glebov, A. V. Kolomeets, I. P. Pozdnyakov, V. P. Grivin, V. F. Plyusnin, N. V. Tkachenko and H. Lemmetyinen, Russ. Chem. Bull., 2013, 62, 1540 CrossRef CAS; (e) I. P. Pozdnyakov, E. M. Glebov, S. G. Matveeva, V. F. Plyusnin, A. A. Melnikov and S. V. Chekalin, Russ. Chem. Bull., 2015, 64, 1784 CrossRef CAS.
- S. G. Matveeva, I. P. Pozdnyakov, V. P. Grivin, V. F. Plyusnin, A. S. Mereshchenko, A. A. Melnikov, S. V. Chekalin and E. M. Glebov, J. Photochem. Photobiol., A, 2016, 325, 13 CrossRef CAS.
- (a) A. Goursot, H. Chermette, E. Peigault, M. Chanon and W. L. Waltz, Inorg. Chem., 1984, 23, 3618 CrossRef CAS; (b) A. Goursot, H. Chermette, E. Peigault, M. Chanon and W. L. Waltz, Inorg. Chem., 1985, 24, 1042 CrossRef CAS; (c) A. Goursot, A. D. Kirk, W. L. Waltz, G. B. Porter and D. K. Sharma, Inorg. Chem., 1987, 26, 14 CrossRef CAS; (d) A. Goursot, H. Chermette, W. L. Waltz and J. Lillie, Inorg. Chem., 1989, 28, 2241 CrossRef CAS; (e) W. L. Waltz, J. Lillie, A. Goursot and H. Chermette, Inorg. Chem., 1989, 28, 2247 CrossRef CAS.
- L. Moggi, G. Varani, M. F. Manfrin and V. Balzani, Inorg. Chim. Acta, 1970, 4, 335 CrossRef CAS.
- E. M. Glebov, V. F. Plyusnin, N. V. Tkachenko and H. Lemmetyinen, Chem. Phys., 2000, 257, 79 CrossRef CAS.
- (a) E. M. Glebov, A. V. Kolomeets, I. P. Pozdnyakov, V. F. Plyusnin, N. V. Tkachenko and H. Lemmetyinen, Photochem. Photobiol. Sci., 2011, 10, 1709 RSC; (b) E. M. Glebov, I. P. Pozdnyakov, A. A. Melnikov and S. V. Chekalin, J. Photochem. Photobiol., A, 2014, 292, 34 CrossRef CAS.
- C. Rensing, O. T. Ehrler, J.-P. Yang, A.-N. Unterreiner and M. M. Kappes, J. Chem. Phys., 2009, 130, 234306 CrossRef PubMed.
- (a) E. M. Glebov, V. P. Chernetsov, V. P. Grivin, V. F. Plyusnin and A. B. Venediktov, Mendeleev Commun., 2014, 24, 111 CrossRef CAS; (b) E. M. Glebov, I. P. Pozdnyakov, V. P. Chernetsov, V. P. Grivin, A. B. Venediktov, A. A. Melnikov, S. V. Chekalin and V. F. Plyusnin, Russ. Chem. Bull., 2017, 66, 418 CrossRef CAS.
- E. M. Glebov, I. P. Pozdnyakov, S. G. Matveeva, A. A. Melnikov, S. V. Chekalin, M. V. Rogozina, V. V. Yudanov, V. P. Grivin and V. F. Plyusnin, Photochem. Photobiol. Sci., 2017, 16, 220 CAS.
- W. Casenpusch and W. Preetz, Z. Anorg. Allg. Chem., 1977, 432, 107 CrossRef.
- E. M. Glebov, V. F. Plyusnin, V. P. Grivin and Yu. V. Ivanov, Russ. J. Coord. Chem., 1997, 23, 580 CAS.
- L. A. Pena and P. E. Hoggard, Photochem. Photobiol., 2010, 86, 467 CrossRef CAS PubMed.
- C. K. Jørgensen, Mol. Phys., 1959, 2, 309 CrossRef.
- S. M. Khan, H. H. Patterson and H. Engstrom, Mol. Phys., 1978, 35, 1623 CrossRef CAS.
- S. V. Chekalin, Phys. Usp., 2006, 49, 634 CAS.
- C. C. Lovallo and M. Klobukowski, J. Comput. Chem., 2003, 24, 1009 CrossRef CAS PubMed.
- C. C. Lovallo and M. Klobukowski, J. Comput. Chem., 2004, 25, 1206 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS.
- (a) A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed; (b) FireFly Project homepage: http://classic.chem.msu.su/gran/firefly/index.html.
- C. K. Jørgensen and W. Preetz, Z. Naturforsch., A: Astrophys. Phys. Phys. Chem., 1967, 22, 945 Search PubMed.
- A. S. Rury and R. J. Sension, Chem. Phys., 2013, 422, 220 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Raw data of quantum chemical calculations. See DOI: 10.1039/c7pp00299h |
| This journal is © The Royal Society of Chemistry and Owner Societies 2018 |