Weak anti-localization of two-dimensional holes in germanium beyond the diffusive regime†
Abstract
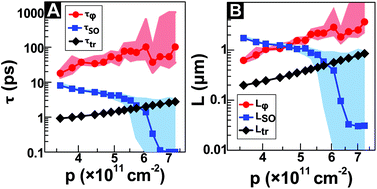
Gate-controllable spin–orbit coupling is often one requisite for spintronic devices. For practical spin field-effect transistors, another essential requirement is ballistic spin transport, where the spin precession length is shorter than the mean free path such that the gate-controlled spin precession is not randomized by disorder. In this letter, we report the observation of a gate-induced crossover from weak localization to weak anti-localization in the magneto-resistance of a high-mobility two-dimensional hole gas in a strained germanium quantum well. From the magneto-resistance, we extract the phase-coherence time, spin–orbit precession time, spin–orbit energy splitting, and cubic Rashba coefficient over a wide density range. The mobility and the mean free path increase with increasing hole density, while the spin precession length decreases due to increasingly stronger spin–orbit coupling. As the density becomes larger than ∼6 × 1011 cm−2, the spin precession length becomes shorter than the mean free path, and the system enters the ballistic spin transport regime. We also report here the numerical methods and code developed for calculating the magneto-resistance in the ballistic regime, where the commonly used HLN and ILP models for analyzing weak localization and anti-localization are not valid. These results pave the way toward silicon-compatible spintronic devices.


 Please wait while we load your content...
Please wait while we load your content...
